Redpoll's 60
Home / 3Dプログラミング入門 / 付録 B $§$B-1
付録 B ベータ版プログラム
| $§$B-1 衝突判定 (楕円 vs 楕円 ; β版) | $§$B-2 衝突判定 S |
$§$B-1 衝突判定 (楕円 vs 楕円 ; β版)
本節で扱う衝突判定は楕円同士の衝突判定である。この衝突判定に関してはニュートン法による反復的アプローチ、あるいはまともに4次方程式を解いて両者の交点を求めるアプローチ、あるいは楕円を適当な図形で置き換える近似的なアプローチなどが見られるが、いまだに定番となるアルゴリズムが存在しない。
以下で解説するアルゴリズムは楕円同士の衝突判定であるが数値解析や4次方程式を使うわけでもなく、近似的なアプローチというわけでもない。普通に2つの楕円が衝突しているかどうかを調べるものである。

図1 楕円 vs 楕円 (Code1 実行結果)
上図は今回の実装の実行結果であるが、図に示されるように今回の実装は楕円同士の衝突判定として特に問題なく動作する。特に問題なく動作するといってもこの実装は数学的に完全なわけではなく、見た目で区別のつかない部分についてはあえて精度を放棄しているケースもある (この点についてはいずれ別の機会に述べる)。
簡単にいえばこの実装は実用的な使用、例えば上図のように2つの楕円が画面内に収まっているようなケースにおいては正しく動作する (現時点で問題らしい問題が見つかっていないだけなのかもしれないが)。
ただ解説に入る前にあらかじめ言っておくが、ここで述べる実装には1つ注意しなければいけない点がある。それはこの実装は今までにテストした限りでは確かに正しく動作するが、それがなぜ正しく動作するのかについては詳しいことはよく分かっていない。つまり以下の解説を読んでも読者は楕円同士の衝突判定に関しての数学的な裏付けのようなものは何ら得ることはできない。解説を読んだだけではこの実装が正しく動作するという明らかな印象を持つことはできないはずである。
(注意 1) 本節では「アフィン変換」という用語が頻繁に使われるが、本節におけるアフィン変換は具体的には「スケール」「回転」「平行移動」の3つの変換、あるいはそれらを任意回数、任意の順序で合成したものを意味する。実際のアフィン変換は「スケール」「回転」「平行移動」だけでなく他にも何種類かあるが、本節ではこの3種類の変換(及びそれらを合成したもの)のみを指す。
(注意 2 : 以前に何度か述べたが、この講義におけるスケール行列は各軸の倍率が $0$ より大きい値であり、非一様スケール(各軸の倍率が異なるスケール)に関しては変換の一番最初に実行し、それ以降のスケールは一様スケールのみを用いると制限していた。しかし、本節においては非一様スケールはどこで何度使っても構わないものとして進める。つまり本節におけるスケール行列は各軸の倍率が $0$ より大きい値であればどこで何度使っても構わない。例えば上記の $S_1, S_2, \ldots, S_n$ がすべて非一様スケールであっても構わない)
上記の $(\mathrm{i})$ は明らかである。平面上に置かれた楕円の長径を $a$、短径を $b$ とし、長径と x軸とのなす角を $\theta$ とする (下図2)。位置はどこで考えても同じであるためここでは簡単のため原点としている。右図3の半径 $1$ の正円がこの楕円になるようにするためには x軸方向の倍率を $a$、y軸方向の倍率を $b$ としたスケール行列を $S$、角度 $\theta$ の回転行列を $R$ とすればこれらの積 $RS$ を正円に対して実行すればよい。
またもちろんスケール倍率及び回転角度を適当に変えても正円に対してスケール、回転の順で変換を行えば適当な長径、短径を持ち、適当な方向を向いた楕円になる。

図2 楕円 
図3 半径 1 の正円
$(\mathrm{ii})$ もまた明らかである。ここでいう「アフィン変換」とは具体的には平行移動、回転、スケールのいずれかあるいはそれらを有限回数合成したものを意味する。
アフィン変換を表す行列を $M$ とする。今述べたように $M$ は有限個の平行移動行列 $T_i$、回転行列 $R_i$、スケール行列 $S_i$ を適当な順序で掛け合わせたものであるから\[ M = S_n T_l R_m \ldots R_2S_2T_2R_1S_1T_1\]として表される。
また $M$ の逆行列 $M^{-1}$ は次の形で表される。\[ M^{-1} = T{_1}^{-1}S{_1}^{-1}R{_1}^{-1}T{_2}^{-1}S{_2}^{-1}R{_2}^{-1}\ldots R{_m}^{-1}T{_l}^{-1}S{_n}^{-1} \]平行移動行列の逆行列は平行移動行列であり、回転行列の逆行列も回転行列である。同様にスケール行列の逆行列もスケール行列である。したがって上記の $M^{-1}$ も有限個の平行移動行列、回転行列、スケール行列の積であるからアフィン変換を表している。
平面上の2つの図形が衝突しているとき、両者は少なくとも1点を共有しているがその点を $\boldsymbol{p}$ とする。この2つの図形にアフィン変換を行うものとし、それを表す行列 $M$ をとする。$\boldsymbol{p'} = M\boldsymbol{p}$ とすれば、変換前の両者の共有点 $\boldsymbol{p}$ は $\boldsymbol{p'}$ に移ることを意味するが、これは変換後においても両者は(少なくとも)1つの点 $\boldsymbol{p'}$ を共有することを意味する。つまりアフィン変換前に2つの図形が衝突しているならば変換後においても衝突しているのである。
アフィン変換を表す行列 $M$ の逆行列 $M^{-1}$ も何らかのアフィン変換を表すことに注意すれば上記の逆もいえる。すなわちアフィン変換後において2つの図形が衝突しているならば変換前においても衝突している。したがって、その対偶によりアフィン変換前に2つの図形が衝突していないのであれば変換後においても衝突はしていない。
まとめると、アフィン変換前に2つの図形が衝突しているのであれば変換後においても両者は衝突している。変換前に衝突していないのであれば変換後においても衝突はしていない。つまりアフィン変換によって両者の衝突状態は変化しないのである。
$(\mathrm{iii})$ はそれほど簡単には導けない。
上記 $(\mathrm{i})$ で見たように原点に置かれている任意の楕円は、原点に置かれた半径 $1$ の正円に対し適当な回転行列 $R$、スケール行列 $S$ の積 $RS$ を実行すれば得られる。したがって平面上の任意の位置に置かれた楕円は適当な平行移動行列 $T$ を追加することで、原点に置かれた半径 $1$ の正円に対し $TRS$ を実行すれば得られるわけである。
例えば下図4の楕円であれば原点から点 $P_0$ までの移動を表す平行移動行列を $T_0$、角度 $\theta$ の回転を表す回転行列を $R_0$、 x軸方向の倍率が $a$、y軸方向の倍率が $b$ であるスケール行列を $S_0$ とし、その積 $M_0 = T_0R_0S_0$ を下図3の正円に実行すればこの正円は目的の楕円に変換されることになる。
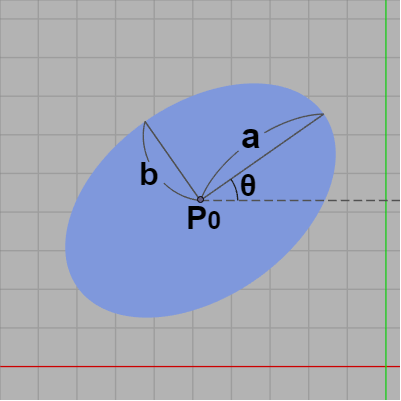
図4 
図3 半径 1 の正円
ここで適当なアフィン変換を表す行列 $M$ を以下のように定める (以下の $T_i$ は平行移動行列、$R_i$ は回転行列、$S_i$ はスケール行列)。\[ M = S_n T_l R_m \ldots R_2S_2T_2R_1S_1T_1\]そしてこの $M$ を上図4の楕円に実行した結果、下図に示される状態になったとしよう。点 $P$ は変換後の図形のオブジェクト原点(ローカル座標系の原点)である。

図5
上図の図形を楕円と簡単に決めることはできない。なぜなら、この図形は上図4の楕円に対し $M$ を実行した結果であるが、それは図3の正円に対し $MM_0$ を実行した結果ともいえる。つまり図5の図形は半径 $1$ の正円に対し\[ MM_0 = (S_n T_l R_m \ldots R_2S_2T_2R_1S_1T_1)(T_0R_0S_0) \]を実行した結果である。ここで重要なのはこの $MM_0$ を $MM_0 = TRS$ のように分解することが(一般には)できないという点である。もし $MM_0 = TRS$ のように分解することができるのであれば $(\mathrm{i})$ で述べたように図5の図形は楕円である。しかし、14‐2節で述べたように $TRS$ 分解が可能であるためには、非一様スケールは変換の一番最初でしか使えないという制限がある。本節の場合は上で述べたように非一様スケールはどこで何度使っても構わないのでこの制限を守っているわけではない。したがって、上記の $MM_0$ は $MM_0 = TRS$ の形に分解できる保証はないのである。
それでも結論からいえば上図5の図形は楕円なのである (それが $(\mathrm{iii})$ の主張である)。
ここで使われる変換行列は平面図形を対象としているため $3\times3$ 行列であり、具体的には下のような形になっている。
\[\begin{pmatrix}\color{red}{a} &\color{red}{b} &e\\ \color{red}{c} &\color{red}{d} &f\\ 0 &0 &1\\\end{pmatrix}\]この行列に対し回転行列あるいはスケール行列を掛けると左上の $2\times2$ 成分($\color{red}{a}$、$\color{red}{b}$、$\color{red}{c}$、$\color{red}{d}$)は変化するが、平行移動行列を掛けてもこの左上の $2\times2$ 成分は変化しない (平行移動によってオブジェクトはその位置のみが変化することを考えればこのことは明らかである。つまり平行移動によって回転成分やスケール成分は変化しない)。
したがって先程の\[ MM_0 = (S_n T_l R_m \ldots R_2S_2T_2R_1S_1T_1)(T_0R_0S_0) \]から平行移動行列をすべて取り除いた積を\[ A = S_n R_m \ldots R_2S_2R_1S_1R_0S_0 \] 
図3 半径 1 の正円 とすれば、$MM_0$ と $A$ の左上 $2\times2$ 成分は同じである。そのため右図の正円にこの変換行列 $A$ を実行すると位置は原点から動かないがその形状は図5の図形と全く同じ形になる。そして図5の図形は点 $P$ の位置に置かれているから、$P$ だけの平行移動を表す平行移動行列を $T$ とすると、右図の正円に変換行列 $TA$ を実行した結果は図5の図形と全く同じになるわけである。つまり図5の図形は半径 $1$ の正円に変換行列 $MM_0$ を実行した結果であるが、$TA$ を実行しても同じ結果になるということである。
そして上記の変換行列 $A$ は回転行列とスケール行列のみで構成されている (各スケール行列の倍率はいずれも $0$ より大きい値)。このような場合、この $A$ を2つの回転行列 $R$、$Q$ と倍率が $0$ より大きいスケール行列 $S$ を用いて次のように表すことができる (以下を詳しくは特異値分解という。この原理については 14-12節参照)。\[ A = RSQ \]先程述べたように図3の正円に対し変換行列 $TA$ を実行すると図5の図形になるのであった。この図形は実際には楕円であるが、以下この点について解説する。
$A = RSQ$ と書き換えられるのであれば $TA = TRSQ$ となるが、これは正円に対し $Q$、$S$、$R$、$T$ の順で変換が行われることを意味する。このとき回転行列 $R$ の第1列目、第2列目を $\boldsymbol{lx}$、$\boldsymbol{ly}$ とすれば、この変換($TRSQ$)によって正円は $\boldsymbol{lx}$、$\boldsymbol{ly}$ を短軸あるいは長軸の方向とする楕円になるのである。さらにこのときスケール行列 $S$ の各軸方向の倍率を $\large{s_x}$、$\large{s_y}$ とすればそれらは長軸あるいは短軸の長さに等しくなる (下図6)。
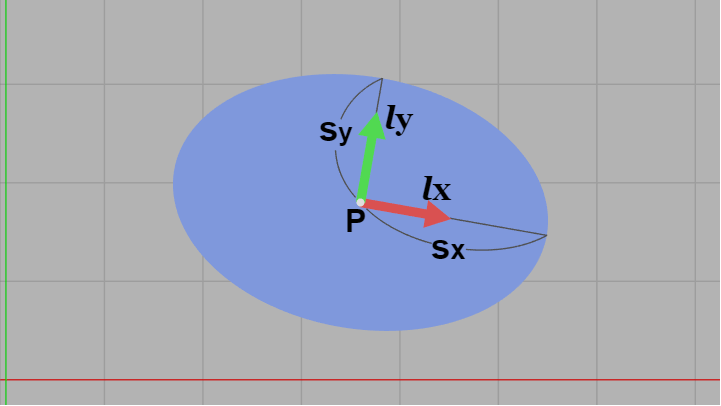
図6
これは次のように考えればよい。例えば最初の回転行列 $Q$ の回転角度が $\theta$ であったとしよう。図3に示されるように正円は原点に置かれておりこの時点では初期状態、すなわち何も回転が行われていないため正円のローカル座標系の各軸とXY平面の x軸、y軸は重なっている。ここで、正円のローカル座標系と $-\theta$ の角をなす仮想的なローカル座標系を考える。
図3の正円に対し最初の回転行列 $Q$ が実行されると見た目上は正円は何も変化しないが、この仮想的なローカル座標系はXY平面の x軸、y軸と重なった状態になる。この後に行われる変換は $S$、$R$、$T$ であるが、これらの変換をこの仮想的なローカル座標系に対して実行することを考えれば、$S$ の各倍率が短径あるいは長径になり、$R$ の各列が短軸あるいは長軸の方向になることは明らかであろう。
正円も楕円の一種であることを考えれば正円に対してどのようなアフィン変換を行っても確かに何らかの楕円にはなる。しかし、その楕円のローカル座標系と短軸、長軸は一般には重ならない。例えば簡単な例として初期状態ではなく何らかの回転($90^\circ$ や $180^\circ$ ではない回転)の行われている正円に対して非一様スケール、回転、平行移動の順で変換を行っても確かに楕円にはなるが、その楕円のローカル座標系の各軸と短軸、長軸は重ならない。さらにその場合には楕円のローカル座標系の各軸は直交性が失われている。
つまり初期状態の正円に対して何らかのアフィン変換を実行しても楕円にはなるが、その楕円の本来のローカル座標系と短軸、長軸が重なっているという保証はないので、本来のローカル座標系からは楕円の短軸や長軸の方向、及びそれらの長さを求めることは簡単にはいかないのである (そのために上記のような仮想的なローカル座標系を考えるわけである)。
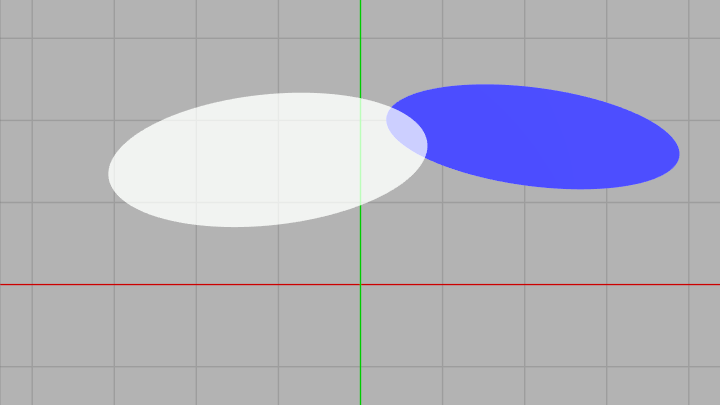
図7
ここで青い楕円を原点に置かれた半径 $1$ の正円に変換するとしよう。それは青い楕円を初期状態に戻すことを意味するから、青い楕円に実行されている変換行列を $M$ とすれば上図の青い楕円に対しその逆行列 $M^{-1}$ を実行すればよい。さらに上図の白い楕円に対してもこの $M^{-1}$ を実行し、その結果下図のようになったとする。
上でも述べたように $M^{-1}$ は平行移動行列や回転行列及びスケール行列の積に過ぎないから $M^{-1}$ はアフィン変換を表す行列である。そして上記の $(\mathrm{iii})$ により楕円にアフィン変換を行った結果もまた何らかの楕円になる。したがって下図の白い図形は楕円である。
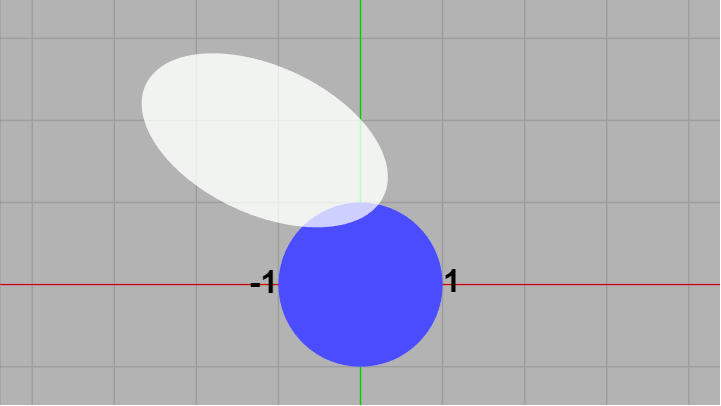
図8
ここで白い楕円のローカル座標系と完全に重なる座標系、ij 座標系を用意する (下図9)。ij 座標系においては白い楕円は原点に置かれた軸平行な楕円であり、この座標系における正円の位置をここでは $C$ とする。
(注意 : すぐ上で述べたようにアフィン変換実行後の楕円はそのローカル座標系と短軸、長軸が重なっている保証はない。しかし、以下の解説では便宜上 楕円の短軸、長軸と重なっている座標系としてローカル座標系という語を用いている。これは単に解説の便宜のためであり他に意味はない)
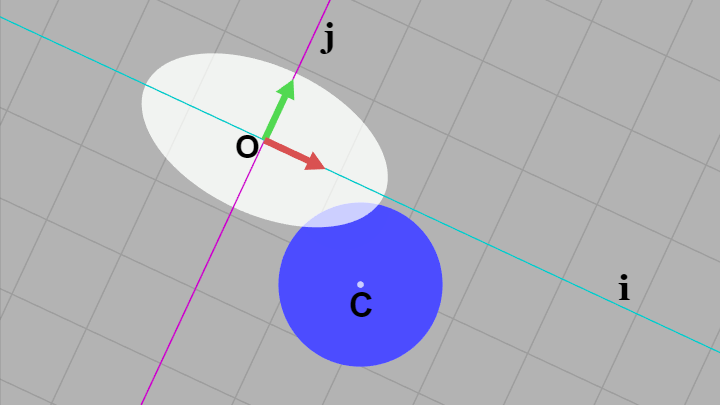
図9
さらに楕円と正円をともに $-C$ だけ移動させ、カメラを適当に回転させて ij 座標系が(斜めではなく)画面の縦横に平行に表示されるようにした結果が以下の図である。この状態においては楕円の中心が $-C$、正円は原点に置かれることになる。
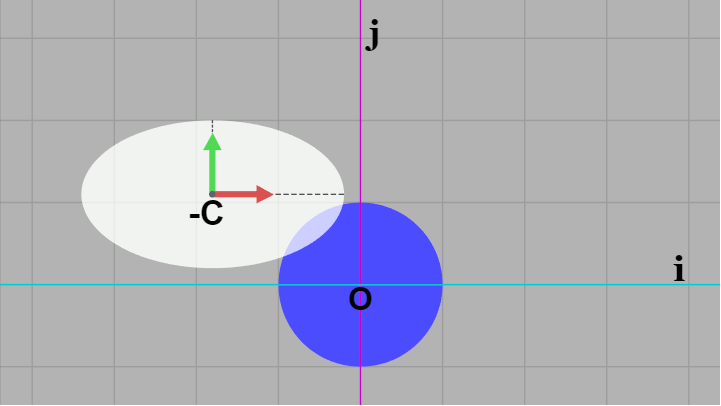
図10
上図は ij 座標系における楕円と正円であるが、XY平面で考えても同じであるから i 軸、j 軸を x軸、y軸とみなして、以下ではXY平面上の軸平行な楕円と原点に置かれた正円として考える。
正円は原点に置かれているので x軸、y軸に関して対称である。そのため楕円が平面上どの位置にあったとしても適当な場所に対称移動させて考えることができる。例えば下図11の場合は第1象限の楕円を第2象限に対象移動させているが、これによって両者の衝突状態が変わることはない。
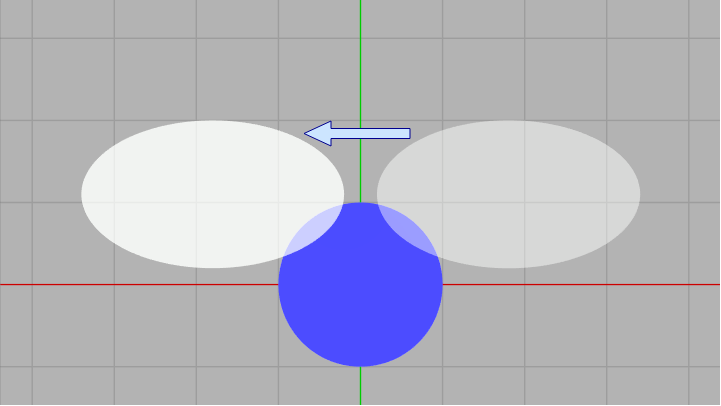
図11
また、第2象限にある軸平行な楕円の場合は直線 $y = -x$ に関して対象移動させれば横長の楕円は縦長になり、縦長の楕円は横長になる。そしてこの対称移動を行った場合でも下の2つの図に示されるように衝突状態が変わることはない。
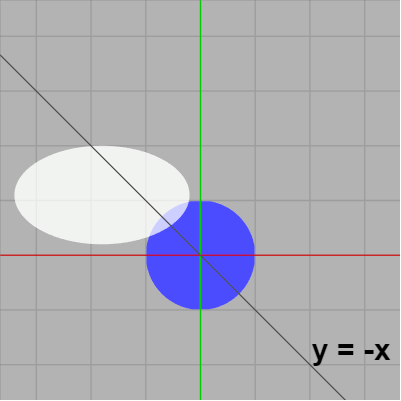
図12 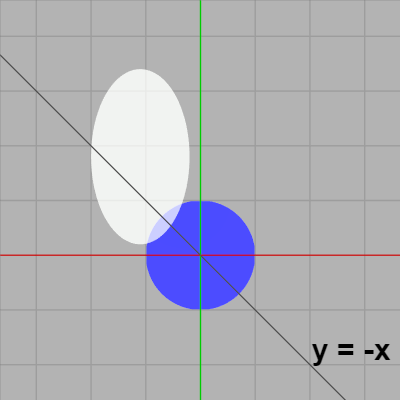
図13
これらのことから今回の実装では上図10の状態から軸平行な楕円の方は、常に第2象限の縦長の楕円に変換して使用する。
つまり2つの楕円が以下の状態であったときに上で述べたアフィン変換や対象移動を有限回実行することによって、

図7
両者を下図のような配置に変換する。上の $(\mathrm{ii})$ にあるようにアフィン変換を行っても両者の衝突状態は変わらないので衝突判定を下図のように簡単な状況で考えるわけである。
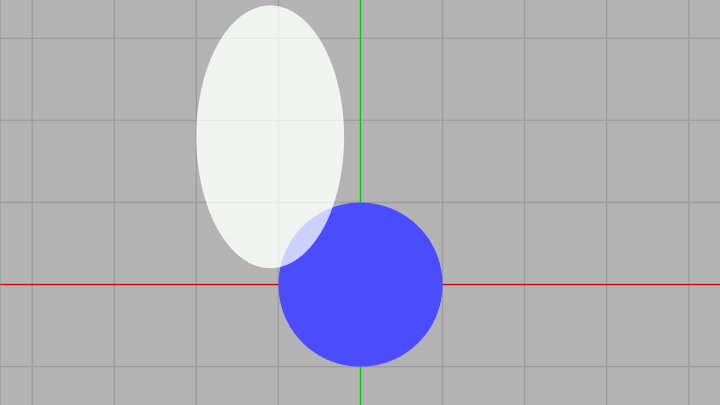
図14
以上、準備的な説明が長くなったが楕円同士の衝突判定はまず両者を図14の状態に変換してからが始まりである。今回の実装では2つの楕円の衝突判定を、第2象限に置かれた軸平行な縦長の楕円と原点に置かれた半径 $1$ の正円の衝突判定に帰着して考えるのである。
(本節では「アフィン変換」を平行移動、回転、スケールの3つの変換に限定したが、上で述べた対称移動も実際にはアフィン変換の一種である)
上で述べたようにこの実装では最終的には第2象限に置かれた軸平行な縦長の楕円と原点に置かれた半径 $1$ の正円の衝突に帰着して考えるので、両者が衝突する場合は上図に示されるように楕円右下と正円左上が衝突する。そのため楕円や正円の接線を考える場合には、楕円であればその右下部分(楕円のローカル座標系の第4象限)、正円であればその左上部分(第2象限)のみを対象とすればよい。
楕円の短径を $a$、長径を $b$、その中心を $E$ とし、楕円円周上において短軸と $\beta$ の角をなす点を $L$ とする (下図)。
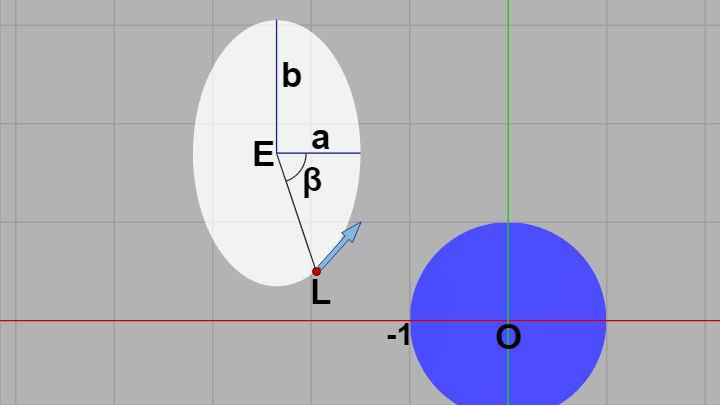
図15
このとき $L$ の座標は $(E_x + a\cos\beta,\ E_y + b\sin\beta)$ である。$L$ における接線ベクトル(図に示されるベクトル)の方向は、$L$ の各成分を微分したものであるから、\[ (\frac{d}{d\beta}(E_x + a\cos\beta),\ \frac{d}{d\beta}(E_y + b\sin\beta)) = (-a\sin\beta,\ b\cos\beta)\]であり、この接線(ベクトル)の傾きは $\displaystyle\frac{b\cos\beta}{-a\sin\beta}$ となる。
逆に $L$ における接線の傾きだけがわかっているものとしその傾きを $m$ とすれば、$L$ の座標は以下のように求められる。$L$ と短軸のなす角をここでも $\beta$ とすれば、この場合の $\beta$ は未知数であるが $L$ における座標や接線ベクトルの表し方は上記と同じである。したがって接線の傾き $m$ は $\beta$ を用いれば\[ m = \frac{b\cos\beta}{-a\sin\beta} = -\frac{1}{k\tan\beta} \qquad (k = \frac{a}{b})\]と表される。すなわち、\[ \tan\beta = -\frac{1}{mk} \]であり、(楕円の右下部分のみを対象としているため) $\beta$ は必ず $-\pi/2 < \beta < 0$ の範囲にあることに注意すれば $\cos\beta$、$\sin\beta$ は\[\cos\beta = +\sqrt{\frac{1}{1 + \tan^2\beta}}\qquad,\qquad \sin\beta = \tan\beta\cos\beta \]として求められる。これにより $L$ の座標も求められるわけである。
正円の場合はその円周上の位置や接線ベクトルはほとんど明らかであるが、今回の実装では1つ注意しておかなければならないことがある。それは正円の接線ベクトルに関しては通常のものとは逆向きのものを使うという点である。
正円円周上の点(第2象限の点)を $R$ とし、$R$ と x軸プラス方向のなす角を $\alpha$ とする (下図)。
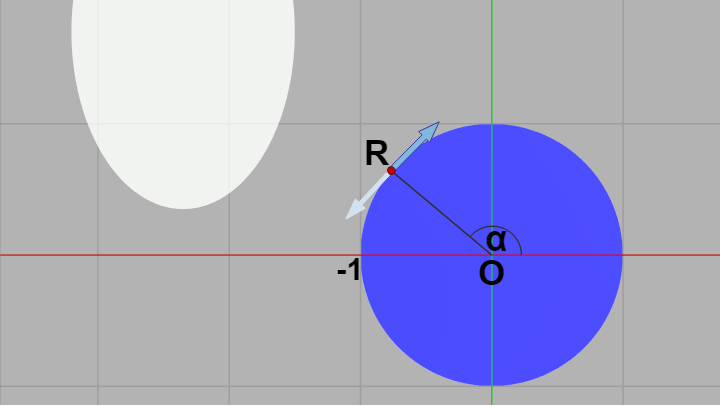
図16 第2象限における正円の接線ベクトルは本来は左下を向いているが、今回の実装ではその逆向きの右上を向いたものを接線ベクトルとして使用する。
$R$ の座標は $(\cos\alpha,\ \sin\alpha)$ であり、$R$ における接線ベクトルはこの各成分を微分した $(-\sin\alpha,\ \cos\alpha)$ が本来のものであるが、今回の実装ではこの逆向きのベクトル $(\sin\alpha,\ -\cos\alpha)$ を正円の接線ベクトルとして使用する。正円は第2象限のみが対象となるため、その領域の接線ベクトルは本来は左下を向いている。しかし、以下の解説においてはその逆方向である右上を向いたものを正円の接線ベクトルとして扱う。
ただし $R = (\cos\alpha,\ \sin\alpha)$ における接線ベクトルとして使うものが左下を向いたものであっても右上を向いたものであってもその傾きはいずれの場合も $\displaystyle -\frac{\cos\alpha}{\sin\alpha}$ である。
まずは衝突しているかしていないかが明らかなケースから始める。例えば次の2つのケースは明らかに衝突していない。左図は楕円の右端(短軸の先端)が直線 $x=-1$ よりも左側にある場合であり、具体的には $E_x + a < -1$、右図は楕円の下端(長軸の先端)が直線 $y=1$ よりも上にある場合であり、この場合には $E_y - b > 1$ である。
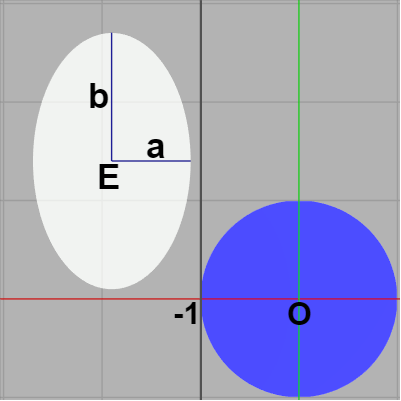
図17 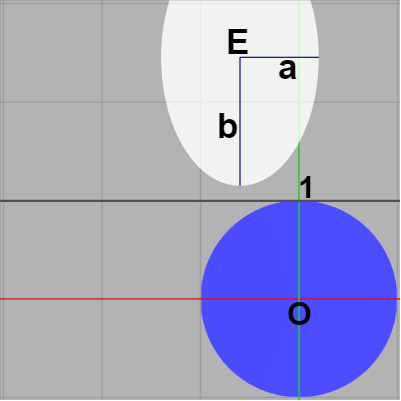
図18
以下では楕円右端は直線 $x=-1$ よりも右、下端は直線 $y=1$ よりも下にあるものとする。このとき楕円の中心 $E$ が直線 $x = -1$ より左にあるか右にあるかで処理が分かれるが、しばらくは $x=-1$ より左側にある場合($E_x < -1$)で進める (図19)。

図19 E が x=-1 よりも左側にある 
図20 E が x=-1 よりも右側にある
楕円中心が $x=-1$ よりも左にあり楕円右端が $x=-1$ よりも右にある場合には楕円と直線 $x=-1$ は必ず交点を持つが、2つの交点のうち楕円中心 $E$ より下側の交点を $P = (P_x,\ P_y)$ とする (図21 ; 接している場合でも2つの交点が重なっているものとして考える)。
このとき図22のように $P$ が直線 $y=1$ よりも上にあるならば明らかに衝突していない。
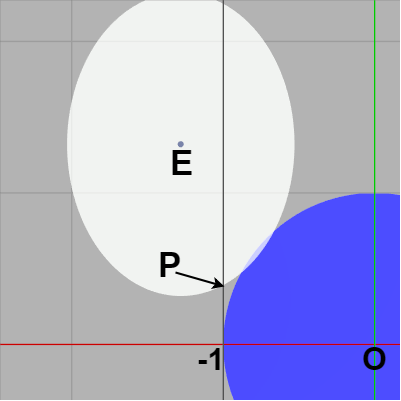
図21 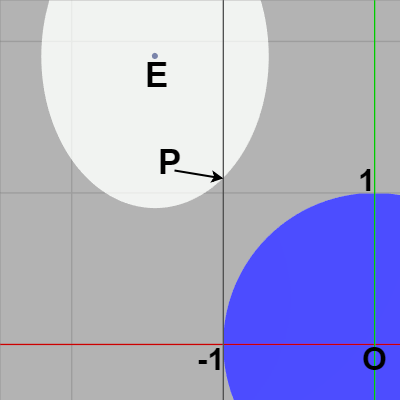
図22
下図23の場合は $P$ が x軸より下にあるが、このケースでは明らかに楕円と正円は衝突する。具体的には $P_y <= 0$ であれば楕円と正円は衝突している。
また、楕円上の点 $P$ と同じ高さにある円周上の点を $P'$ とするとき($P_y = P'_y$)、$P$ における接線の傾きが $P'$ における接線の傾きよりも大きい場合には下図24に示されるように両者は明らかに衝突はしていない。
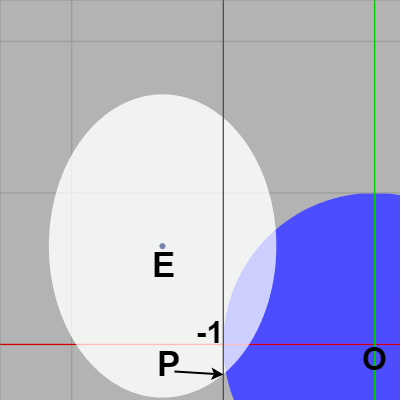
図23 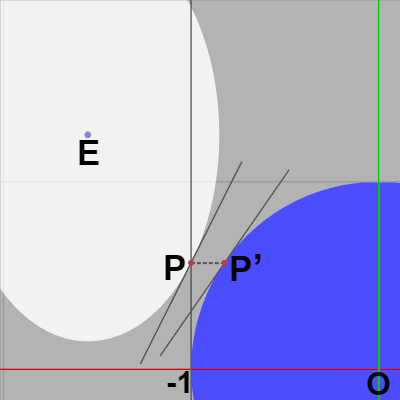
図24
以上が衝突判定の自明なケースであるが、両者が衝突している場合にはこのような簡単な方法では判定できない場合が多い。以下では上記のような簡単な方法では判定できない場合について見ていく。
今回は楕円と正円を常に第2象限で考えるため、両者が衝突している場合には楕円右下と正円左上が衝突している (下図25)。
先程と同じく楕円上の点 $P$ と同じ高さにある円周上の点を $P'$ とする ($P_y = P'_y$)。楕円の短軸 $EF$ と $EP$ のなす角を $\beta$、正円においては x軸プラス方向と $OP'$ のなす角を $\alpha$ とする。このとき、$\pi/2 \leq \alpha < \pi$、$-\pi/2 < \beta < 0$ である。また楕円と正円の2つの交点を $M$、$N$ とし、正円の上端 $(0,\ 1)$ を $H$ とする。
$P$ や $P'$ の求め方は簡単である。$P = (E_x + a\cos\beta,\ E_y + b\sin\beta)$ であるが、$P_x = -1$ であるから $E_x + a\cos\beta = -1$、すなわち\[ \cos\beta = \frac{-1 - E_x}{a} \]として $\cos\beta$ が求められるので、これにより $\sin\beta$ も求められる (この場合 $\sin\beta$ は必ず $\sin\beta < 0$)。
$P$ の座標がわかれば $P_y = P'_y$ であり $P' = (\cos\alpha,\ \sin\alpha)$ であるから、$\sin\alpha = P_y$ として $\sin\alpha$ が求められ、自動的に $\cos\alpha$ も求められる (ただし常に $\cos\alpha \leq 0$)。
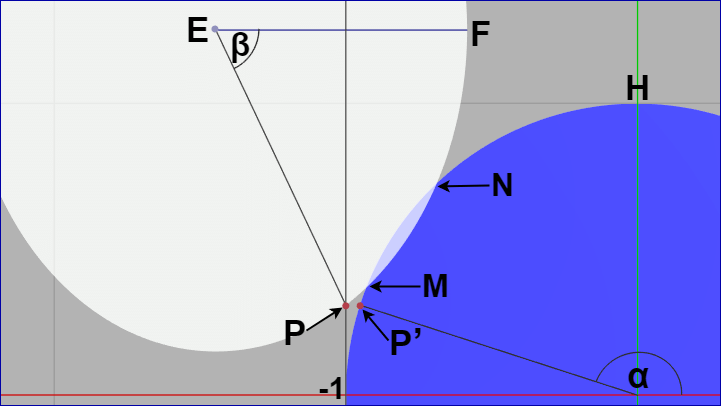
図25
楕円右下と正円左上が衝突している場合、$P$ における楕円の接線の傾きは $P'$ における正円の接線の傾きよりも必ず小さくなる。
例えば上の状況では $P$ における楕円の接線ベクトルは $(-a\sin\beta,\ b\cos\beta)$ であるから、傾きは $\displaystyle\frac{b\cos\beta}{-a\sin\beta}$、正円の $P'$ における接線ベクトルは $(\sin\alpha,\ -\cos\alpha)$ であるから、傾きは $\displaystyle\frac{-\cos\alpha}{\sin\alpha}$ となる。したがって楕円右下と正円左上が衝突している場合には\[\frac{b\cos\beta}{-a\sin\beta} < \frac{-\cos\alpha}{\sin\alpha}\]となっているということである。
そしてこの状況では楕円円周上を $P$ から $F$ に移動する際、接線の傾きは連続的に増加する。正円円周上を $P'$ から $H$ に移動する際、接線の傾きは連続的に減少する。したがって楕円上においては $P$ から一定量ずつ角度を増加させ、正円上においては $P'$ から同じ量ずつ角度を減少させていくとある時点において両者の接線の傾きは等しくなる。
すなわち、\[\frac{b\cos(\beta + x)}{-a\sin(\beta + x)} = \frac{-\cos(\alpha - x)}{\sin(\alpha - x)} \tag{1} \]を満たす角度 $x$ が存在する。さらに上図より、$P$ から楕円円周上を移動し交点 $N$ に達する時点では楕円と正円の接線の傾きは逆転している ($N$ の位置においては楕円の接線の傾きは明らかに正円の接線の傾きよりも大きい)。つまり $P$ から $N$ に移動するまでに両者の接線の傾きが等しくなる状況が起こるわけである ($N$ に移動するまでに起こらないこともあるが、その場合でも $F$ に移動するまでには必ず1回は両者の接線の傾きは等しくなる)。そしてその状況においては図から明らかに $-\pi/2 < \beta + x < 0$ である。
上記 $(1)$ を変形すれば \begin{align*}&\frac{\sin(\alpha - x)}{\cos(\alpha - x)} = \frac{a}{b}\frac{\sin(\beta + x)}{\cos(\beta + x)} \\\\=\ &\tan(\alpha - x) = k\tan(\beta + x) \tag{2}\end{align*}となる。ただし $k = a/b$ である。
上記 $(2)$ を三角関数の公式によって書き換えると\[\frac{\tan\alpha - \tan x}{1 + \tan\alpha\tan x} = k\frac{\tan\beta + \tan x}{1 - \tan\beta\tan x} \tag{3}\]となるが、ここで表記を簡単にするために $A = \tan\alpha$、$B = \tan\beta$、$X = \tan x$ と置くと $(3)$ は以下のように表される。
\[\frac{A - X}{1 + AX} = k\frac{B + X}{1 - BX} \tag{4}\]ここで分母をはらえば、\[(A - X)(1 - BX) = k(B + X)(1 + AX) \tag{5}\]であるが、この左辺を右辺に移動させて $X$ についてまとめると次の形に変形される。
\[(kA - B)X^2 + (k + 1)(AB + 1)X + (kB - A) = 0 \tag{6}\]すなわち、$X$ の2次方程式になるわけである。
$\tan\beta$ (及び $\tan\alpha$)は既知であり、この方程式から $X\ (= \tan x)$ が求められるので $\tan(\beta + x)$ や$\tan(\alpha - x)$ も上述のように以下の形で求められる。
\begin{align*}&\tan(\beta + x) = \frac{\tan\beta + \tan x}{1 - \tan\beta\tan x} \\\\&\tan(\alpha - x) = k\tan(\beta + x)\end{align*}
今までは楕円の中心 $E$ が直線 $x=-1$ よりも左側にある場合について見てきたが、ここで一旦 $E$ が直線 $x=-1$ より右にある場合の処理について簡単に解説する。楕円の中心 $E$ は第2象限に置かれることを前提としているからこの場合においては $-1 < E_x \leq 0$ である。
楕円の下端の点を $P$ とする。縦長の楕円であるから長径を $b$ とすれば $P = (E_x,\ E_y - b)$ である。このとき次の2つのケースにおける判定は明らかである。
左のケースは $P$ が正円に含まれる場合であり、右のケースは $P$ が x軸よりも下側にある場合である。この2つのケースでは両者は必ず衝突している。
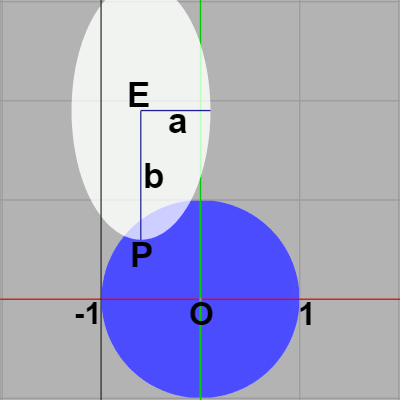
図26 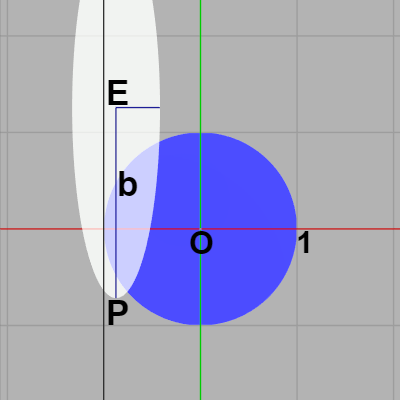
図27
$E$ が直線 $x=-1$ よりも右にあり上記のような自明な判定ができない場合、両者が衝突している際には以下のような状態になっている。しかしこの場合における判定方法は先程述べたやり方と同じであり、ここでも $P$ と同じ高さにある正円円周上の点を $P'$ とする ($P_y = P'_y$)。
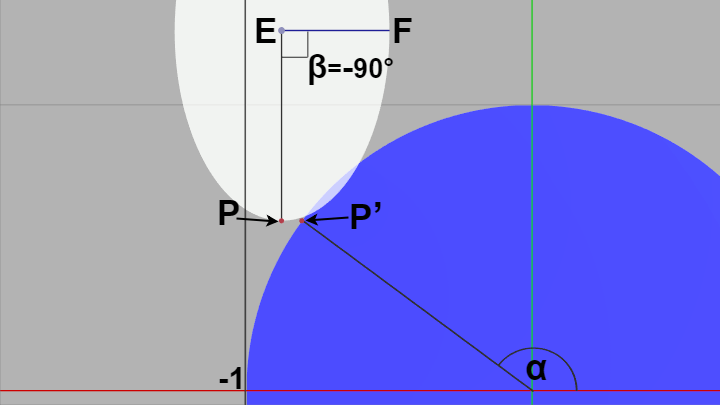
図28
楕円の短軸 $EF$ と $EP$ のなす角を $\beta$ とし、正円においては x軸プラス方向と $OP'$ のなす角を $\alpha$ とする。ここで再び角度 $\beta$ を少しずつ増加させ、角度 $\alpha$ は同じ量ずつ減少させていくと、ある時点において楕円上の点 $P$ における接線の傾きと、正円上の点 $P'$ における接線の傾きは等しくなる。つまり、\[\frac{b\cos(\beta + x)}{-a\sin(\beta + x)} = \frac{-\cos(\alpha - x)}{\sin(\alpha - x)} \tag{1} \]を成り立たたせる角度 $x$ が存在する。
したがって三角関数の公式によってこの式を書き換えれば先程と同じように\[\frac{\tan\alpha - \tan x}{1 + \tan\alpha\tan x} = k\frac{\tan\beta + \tan x}{1 - \tan\beta\tan x} \tag{3}\]が得られるが、今回は角度 $\beta$ は $-90^\circ$ であることがわかっているから $\displaystyle \tan\beta = \tan(-\frac{\pi}{2}) = -\infty$ である。これによって上記 $(3)$ の右辺は次のように書き換えられる。
\[\frac{A - X}{1 + AX} = -\frac{k}{X} \tag{8}\]分母をはらって $X$ についてまとめると先程のものよりも簡単な次の2次方程式が得られる。
\[X^2 - (A + kA)X - k = 0 \tag{9}\]さらにこの場合には $(7)$ より\[ \tan(\beta + x) = \frac{\tan\beta + \tan x}{1 - \tan\beta\tan x} = -\frac{1}{\tan x}\]である。
ここまでに楕円及び正円の接線の傾きが一致する角度を求めたわけであるが、楕円上において接線の傾きが一致する点を $Q$、正円上において接線の傾きが一致する点を $Q'$ とする (下図29)。
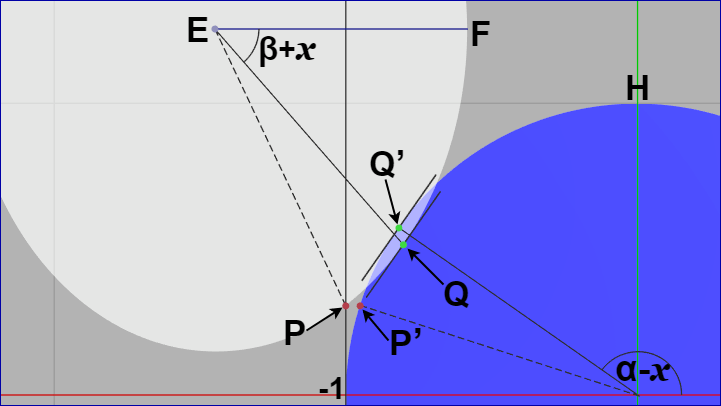
図29
図に示されるように $-\pi/2 < \beta + x < 0$ であるから $\theta = \beta + x$ と置けば、\[ \cos\theta = +\sqrt{\frac{1}{1 + \tan^2\theta}}\ ,\qquad \sin\theta = \tan\theta\cos\theta\ \tag{10}\]となる。したがって楕円上の位置 $Q$ は\[ Q = (E_x + a\cos\theta,\ E_y + b\sin\theta) \tag{11} \]として求められる。
同様にして正円上の位置 $Q'$ も求められる。$\pi/2 < \alpha - x < \pi$ であるから $\varphi = \alpha - x$ と置けば、\[ \cos\varphi = -\sqrt{\frac{1}{1 + \tan^2\varphi}}\ ,\qquad \sin\varphi = \tan\varphi\cos\varphi\ \tag{12}\]となる (ここでは $\cos\varphi$ の符号はマイナスになることに注意)。
正円の半径は $1$ であり中心は原点にあるから\[ Q' = (\cos\varphi,\ \sin\varphi) \tag{13} \]である。
このとき $Q$ と $Q'$ の位置関係について次の4つのケースが考えられる。
$\rm{I}.$ $Q$ が正円の中にある
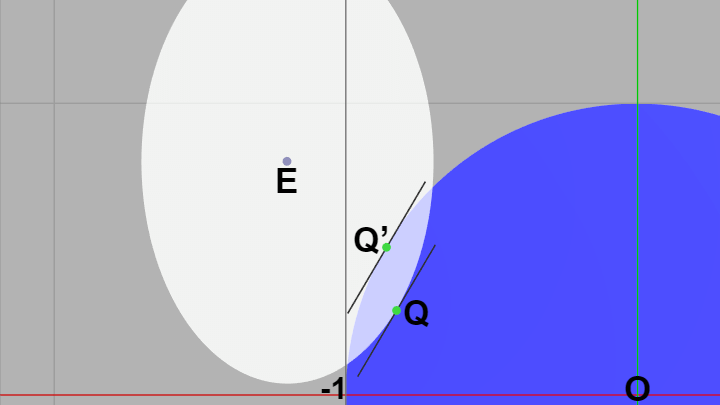
図30
このケースは単に $|OQ| \leq 1$ であるかを調べればよい (上図では $Q'$ は楕円の中にあるが衝突の仕方によっては $Q'$ が楕円の外に位置することもある)。
$\rm{I}\hspace{-1.0pt}\rm{I}.$ ($Q$ は正円の中にはないが) $Q'$ が楕円の中にある
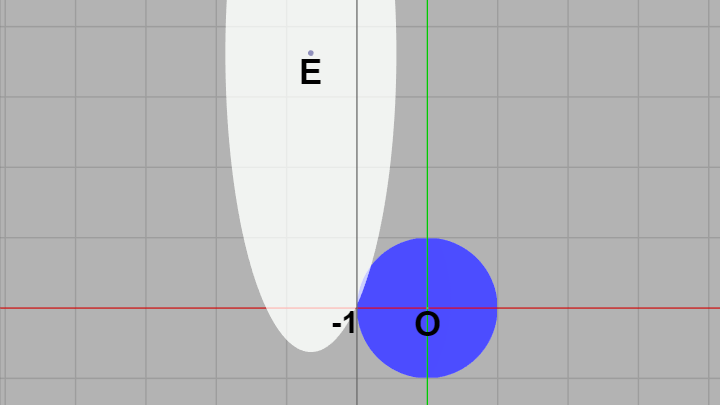
図31
状況としては上図のような衝突状態のときである。このときの両者の衝突部分を拡大したものを以下に示す。
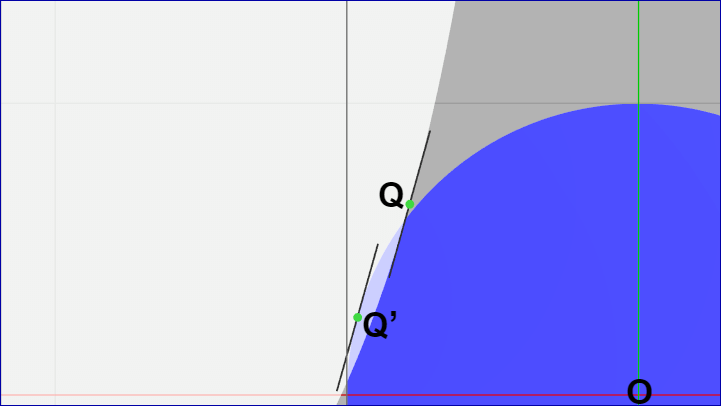
図32
このケースでは $Q'$ が楕円の中にあるかを調べるために、楕円を正円にスケールして判定を行う。
上記 $(9)$ より $Q'=(\cos\varphi,\ \sin\varphi)$ であるが、この座標は楕円の中心 $E$ を原点としたローカル座標系では $(\cos\varphi - E_x,\ \sin\varphi - E_y)$ となるが便宜上のこの座標を\[K = (K_x,\ K_y) = (\cos\varphi - E_x,\ \sin\varphi - E_y) \]で表す。
$Q'$ が $E$ を中心とする短径 $a$、長径 $b$ の楕円に含まれるかどうかは、この $K$ が原点を中心とする短径 $a$、長径 $b$ の楕円に含まれるかを調べることと同じである。さらにその場合には原点中心のその楕円と $K$ を縦方向に $a/b$ だけ縮小して、半径 $a$ の正円に含まれるかどうかを調べることと同じである。したがって $K = (K_x,\ K_y)$ を縦方向に $a/b$ だけ縮小した座標 $(K_x,\ \displaystyle\frac{a}{b}K_y)$ が半径 $a$ の正円に含まれるかを調べればよい。
$\rm{I}\hspace{-1.0pt}\rm{I}\hspace{-1.0pt}\rm{I}.$ 楕円と正円の2つの交点を $M$、$N$ とするとき、$Q$ が $M$ の手前にあり、$Q'$ は $N$ を過ぎた位置にある
この場合には両者は下図のような衝突状態になっている。
(第3のケース及び次の第4のケースで扱う衝突は下図のような境界部分における衝突の判定である。下図の場合は両者にわずかな重なりがあることが見てわかるが、第3、第4のケースで扱う衝突のほとんどはカメラをかなり近づけなければ目で確認することはできない)
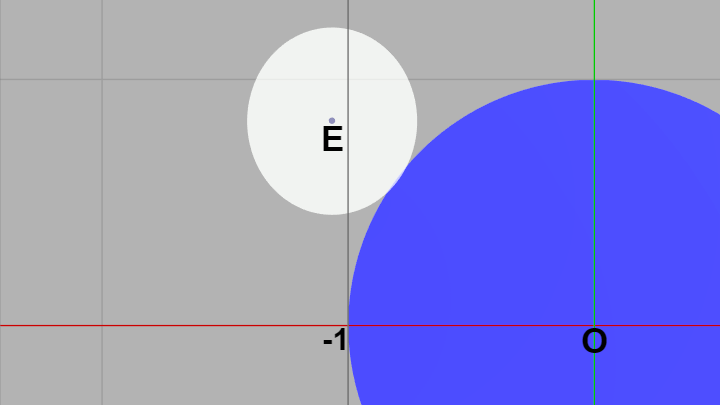
図33
下図はこのときの両者の衝突部分を拡大したものである。
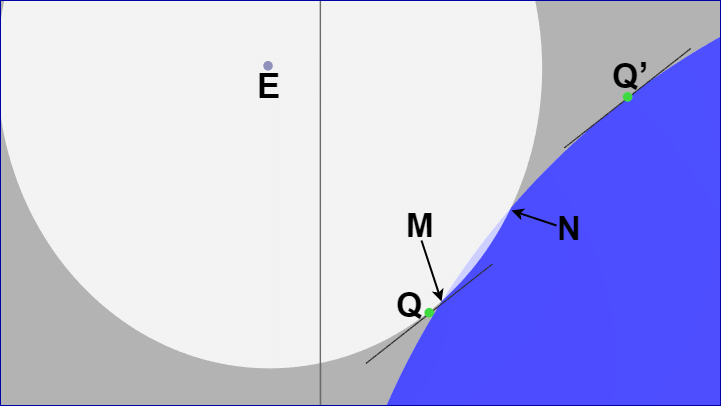
図34
$Q$ が正円の中になく、さらに $Q'$ も楕円の中にないというケースである。この場合 $Q$ が上図の $M$ より手前にあるのであれば、($Q$ と $Q'$ の接線の傾きが同じであることに注意すれば) $Q'$ が $M$ より手前に来ることがないのは明らかである。
このケースにおいて両者が衝突している状況では、ほとんどすべての場合において $Q$ は正円に極めて近い位置に来る。そこで $Q$ から接線を引き、その接線と正円との交点を $R'$ とする。次にこの(正円上の点) $R'$ における接線の傾きと一致する楕円上の点 $R$ を求め、この $R$ が正円に含まれるかを調べる (下図35 ; この図では見やすさのために楕円の形状をやや変えている)。
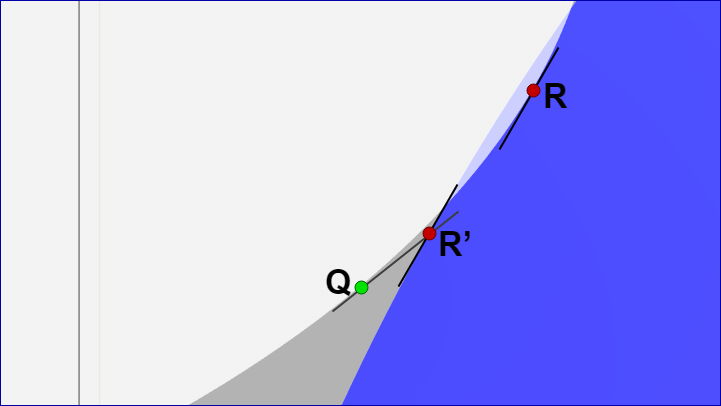
図35
$Q = (E_x + a\cos\theta,\ E_y + b\sin\theta)$ とすれば、その位置における接線ベクトルは上の C) の部分で述べたように $(-a\sin\theta,\ b\cos\theta)$ であるから、$Q$ からこの方向に延びる直線と正円との衝突点を求めればそれが $R'$ である。
$R' = (R'_x,\ R'_y)$ とすれば接線ベクトルは $(R'_y,\ -R'_x)$ であり、この接線ベクトルの傾きを $m$ とすれば $\displaystyle{m= -\frac{R'_x}{R'_y}}$ である。
一方傾きが $m$ となる楕円上の位置が $R$ であるがその角度を $\gamma$ とすれば、$R$ の座標は $(E_X + a\cos\gamma,\ E_y + b\sin\gamma)$ であり、$R$ における接線ベクトルは $(-a\sin\gamma,\ b\cos\gamma)$ となる。そしてこの接線ベクトルの傾きが $m$ であることから $\sin\gamma$、$\cos\gamma$ は次のように求められる。
\[ m = -\frac{b\cos\gamma}{a\sin\gamma} = -\frac{1}{k\tan\gamma} \qquad (k = \frac{a}{b}) \]であるから、\[\tan\gamma = -\frac{1}{mk}\]したがって、\[\cos\gamma = +\sqrt{\frac{1}{1 + \tan^2\gamma}}\qquad,\qquad \sin\gamma = \tan\gamma\cos\gamma \]となる ($\cos\gamma$ の符号は必ずプラス)。
$\rm{I}\hspace{-1.0pt}\rm{V}.$ 上記 $\rm{I}\hspace{-1.0pt}\rm{I}\hspace{-1.0pt}\rm{I}$ と同じく2つの交点を $M$、$N$ とするとき、$Q'$ が $M$ の手前にあり、$Q$ は $N$ を過ぎた位置にある
このケースは次のような状況において起こる。下図では両者は接しているようにしか見えないが、カメラを近づけると楕円と正円は非常にわずかな幅で重なっていることがわかる。

図36
以下はその重なり部分の拡大図である。確かに両者はわずかな幅で重なっており、$Q'$ が交点 $M$ の手前、$Q$ は交点 $N$ を過ぎた位置に来ている。
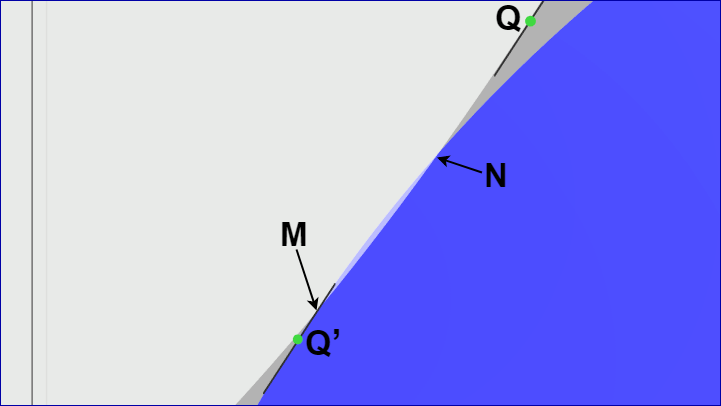
図37
ここで $Q'_x$ と同じ x座標を持つ楕円上の位置を $L$ とする。第4のケースではまず $L$ における接線ベクトルを求めるが、その際 $L$ 及びその接線ベクトルは楕円のローカル座標系で計算する。したがって $L_x = Q'_x - E_x$ である。楕円のローカル座標系で考えたときには $L_x$、$L_y$ に関して $\ \displaystyle{\frac{L{_x}^2}{a^2} + \frac{L{_y}^2}{b^2} = 1}\ $ であるから $L_y$ は\[ L_y = -\sqrt{b^2(1 - \frac{L{_x}^2}{a^2})} = -b\sqrt{1 - \frac{L{_x}^2}{a^2}}\]として求められる (楕円のローカル座標系においては $L$ は必ず y軸よりも下に位置するので $L_y$ の符号はマイナス)。
$L = (L_x,\ L_y) = (a\cos\psi,\ b\sin\psi)$ とすれば $L$ における接線ベクトルは $(-a\sin\psi,\ b\cos\psi)$ であるから、これを $L_x$、$L_y$ で表せば $\displaystyle{(-a\sin\psi,\ b\cos\psi) = (-\frac{a}{b}L_y,\ \frac{b}{a}L_x) }$ となる。
$Q'$ における(単位)接線ベクトルを $\boldsymbol{\mathsf{v_1}}$、$L$ における(単位)接線ベクトルを $\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{\mathsf{v_1}} + \boldsymbol{\mathsf{v_2}}$ を正規化したベクトルを $\boldsymbol{\mathsf{v_3}}$ とし、$\boldsymbol{\mathsf{v_3}}$ を接線ベクトルとして持つ正円上の点を $S'$ とする (下図 ; この図においても見やすさのため楕円の形状をやや変えている)。
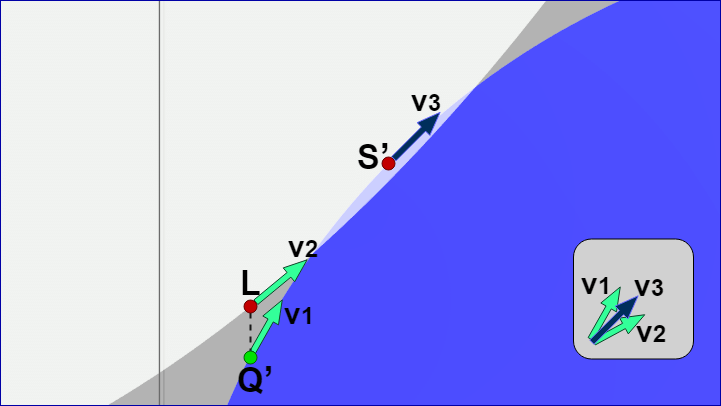
図38 v1 はQ'における接線ベクトル、v2 はLにおける接線ベクトル。v3 は v1+v2 を正規化したベクトルで、v3 を接線ベクトルとして持つ正円上の点が S'。
第4のケースではこの $S'$ が楕円の中に含まれるかどうかを調べる。処理としては第2のケースと同じであり、$S'$ を再び楕円のローカル座標系での座標 $S$ に変換し ( $S = (S'_x - E_x,\ S'_y - E_y)$ )、この $S$ を縦方向に $a/b$ だけ縮小した座標が半径 $a$ の正円に含まれるかどうかを調べればよい。
以下のメソッド CollisionTest_AAEllipse_UnitCircle(..) は軸平行な楕円と正円の衝突判定を行うものであるが、軸平行な楕円はその中心が第2象限に置かれた縦長の楕円、正円は原点に置かれた半径 $1$ の正円であることを前提としている。引数の E は楕円の中心、a、b は短径、長径である (縦長の楕円であるから短軸は x軸に平行、長軸は y軸に平行)。
[CollisionTest_AAEllipse_UnitCircle(..)]
上の解説では軸平行な楕円の中心が直線 $x=-1$ の左にあるか右にあるかで処理を分けたが、9行目のifブロックが左にある場合、38行目の else ブロックが右にある場合である。これらの if/else ブロックやメソッド冒頭で処理を返すif文があるがそれらはいずれも自明な判定のケースである。
プログラム中の cosBt、sinBt は $\cos\beta$、$\sin\beta$ のことであり、cosAl、sinAl は $\cos\alpha$、$\sin\alpha$ のことである。また上の解説では $\tan x$ を求めるために最後に2次方程式が現れたが(式 $(6)$ や $(9)$)、プログラム中ではその2次方程式は $sX^2 + tX + u = 0$ として使われている。つまりメソッド内の s は $X^2$ の係数、t は $X$ の係数、u は定数項である。
60行目の Q、71行目の Qd は上の解説における $Q$、$Q'$ のことであり、この2つの行は上記の式 $(11)$ や $(13)$ と同じである。
任意の2つの楕円同士の衝突判定用のメソッド CollisionTest_Ellipse_Ellipse(..) は上のメソッドを利用することで次のように記述される。
このメソッドでは2つの楕円が、原点に置かれた半径 $1$ の正円に対しスケール、回転、平行移動をこの順序で1回ずつ行ってできたものであることを前提としている。引数の E は楕円の中心、lx、ly はローカル座標系の x軸、y軸方向を表す単位ベクトル、sx、sy はローカル座標系の x軸方向、y軸方向の倍率である。
ここで使われる楕円は原点に置かれた正円に対しスケール、回転、平行移動をこの順で実行して得られるものであるから、楕円の短軸、長軸はそのローカル座標系の各軸と重なっており、したがってローカル座標系の各軸の方向や倍率はそのまま短軸や長軸の方向や長さとして使うことができる。
[CollisionTest_Ellipse_Ellipse(..)]
一方の楕円に実行された変換行列を $M_1$、もう一方の楕円に実行された変換行列を $M_2$ とすれば16行目までに行っていることは $M{_2}^{-1}M_1$ の計算である。これは一方の楕円を初期状態に戻すために逆行列を実行し、もう一方の楕円にもその逆行列を実行して適当な楕円に変換する処理に相当する。$A = M{_2}^{-1}M_1$ とすれば18~35行目は特異値分解の処理であり、31、32行目の u1、u2 は変換された楕円の短軸あるいは長軸の方向、34、35行目の r_a、r_b は短軸あるいは長軸の長さになる。これらは上の解説における図6の $\boldsymbol{lx}$、$\boldsymbol{ly}$、$\large{s_x}$、$\large{s_y}$ に相当する。
11行目の CalcInverseRows(..) は送られてくる引数から逆行列を計算しその各行を Vecotr3[] で返すものであり、具体的には以下の内容である。
41行目の E は楕円のローカル座標系の各軸に平行な座標系(上の解説における ij 座標系)において、正円を原点に移動させたときの楕円の位置を表しているが、この位置は対象移動によって第2象限に移されている。43行目のifブロックは楕円が横長であれば縦長の楕円にする処理である。
この43行目のifブロックが終わる時点では2つの楕円は原点に置かれた半径 $1$ の正円と第2象限に置かれた軸平行な縦長の楕円に変換されているのであとは上記の CollisionTest_AAEllipse_UnitCircle(..) を実行すればよい。
以上が今回の実装の詳細である。2つの楕円が画面上に収まるような大きさで、楕円を普通に動かしている場合には、ほとんどすべての衝突は自明な衝突でない限り上記の第1のケースで検出される ($99\%$ に近い)。つまり両者が衝突している状況ではほとんどすべての場合において上の解説における $Q$ が正円の中に含まれるということであるが、なぜそうなるのかはわかっていない。
また $Q$ が正円に含まれない場合においても両者が衝突しているのであれば $Q$ は極めて正円に近い位置に来る。それが必ず成り立つのかどうかについても詳細は不明である。
楕円を'手動'で動かすような場合には(自明な場合を除いて)両者の衝突は第1のケースで検出されることがほとんどであるが、2つの楕円の位置、形状をランダムに変えてテストする場合にはその割合は状況によって変化する。第2のケースで一番多く検出されることもあるが、第3や第4のケースで検出される割合はやはり少ない。ただし、こういったことも確かなことは残念ながら不明である。
冒頭で述べたように今回の実装は目で確認できるような誤動作は起こらない。しかし、この衝突判定は数学的に完全なわけではないので境界部分において実際には衝突の検出ができていないケースがある。ただしそういった誤動作はカメラをかなり近づけなければ判別できないため今回はそのレベルの精度については放棄している。
繰り返しになるが、このアルゴリズムは肝心な点については何もわかっていないので過信してはいけない (まだ発見されていない明らかな誤動作が含まれている可能性も十分にあり得る)。
本節では上で述べたことに関連した2つのプログラムが用意されている。
(UnityにおけるSceneファイルは「PNX_B」、プログラムは「sPNX_B」フォルダ内の「SecB01」である)
2つの楕円は以下のキー操作によって大きさや向きあるいは位置を変えることができる。
H、J、K、L : 楕円を縦横に移動させる
S、T : 楕円を軸方向に拡大させる (+Shift の場合は縮小)
R : 楕円を回転させる (+Shift の場合は逆回転)
Shift + A : 操作対象の楕円の変更
[Code1] (実行結果 図1)
キー操作は以下のとおり。
H、J、K、L : 楕円を縦横に移動させる
S、T : 楕円を軸方向に拡大させる (+Shift の場合は縮小)
[Code2]
以下で解説するアルゴリズムは楕円同士の衝突判定であるが数値解析や4次方程式を使うわけでもなく、近似的なアプローチというわけでもない。普通に2つの楕円が衝突しているかどうかを調べるものである。

上図は今回の実装の実行結果であるが、図に示されるように今回の実装は楕円同士の衝突判定として特に問題なく動作する。特に問題なく動作するといってもこの実装は数学的に完全なわけではなく、見た目で区別のつかない部分についてはあえて精度を放棄しているケースもある (この点についてはいずれ別の機会に述べる)。
簡単にいえばこの実装は実用的な使用、例えば上図のように2つの楕円が画面内に収まっているようなケースにおいては正しく動作する (現時点で問題らしい問題が見つかっていないだけなのかもしれないが)。
ただ解説に入る前にあらかじめ言っておくが、ここで述べる実装には1つ注意しなければいけない点がある。それはこの実装は今までにテストした限りでは確かに正しく動作するが、それがなぜ正しく動作するのかについては詳しいことはよく分かっていない。つまり以下の解説を読んでも読者は楕円同士の衝突判定に関しての数学的な裏付けのようなものは何ら得ることはできない。解説を読んだだけではこの実装が正しく動作するという明らかな印象を持つことはできないはずである。
A) 準備 1
まず準備的な説明から始める (以下の $(\mathrm{i})$~$(\mathrm{iii})$ が読者にとって明らかなのであれば、この部分を飛ばして「B) 準備 2」へ進んで構わない)。(注意 1) 本節では「アフィン変換」という用語が頻繁に使われるが、本節におけるアフィン変換は具体的には「スケール」「回転」「平行移動」の3つの変換、あるいはそれらを任意回数、任意の順序で合成したものを意味する。実際のアフィン変換は「スケール」「回転」「平行移動」だけでなく他にも何種類かあるが、本節ではこの3種類の変換(及びそれらを合成したもの)のみを指す。
| ($\mathrm{i}$) | 任意の楕円は半径 $1$ の正円に対し適当なスケールと適当な回転をこの順序で行うことで得られる。逆に、半径 $1$ の正円に適当なスケールと適当な回転をこの順序で行った結果は必ず楕円になる。 |
| ($\mathrm{ii}$) | 平面上の2つの図形に対して同じアフィン変換を行った場合、そのアフィン変換の前後で両者の衝突状態は変化しない。変換を行う前に衝突しているならば変換後においても両者は衝突している。変換前に衝突していないのであれば変換後においても両者は衝突していない。 |
| ($\mathrm{iii}$) | 平面上の楕円に対して任意のアフィン変換を行った結果もまた楕円になる。 $T_1, T_2, \ldots , T_l$ を平行移動行列、$R_1, R_2, \ldots, R_m$ を回転行列、$S_1, S_2, \ldots, S_n$ をスケール行列とし、それらを適当な順序で並べた積を\[ M = R_m S_n T_l \ldots S_2T_2S_1R_2T_1R_1\]とすれば、楕円に対しこの $M$ を実行した結果も楕円になる。 |
(注意 2 : 以前に何度か述べたが、この講義におけるスケール行列は各軸の倍率が $0$ より大きい値であり、非一様スケール(各軸の倍率が異なるスケール)に関しては変換の一番最初に実行し、それ以降のスケールは一様スケールのみを用いると制限していた。しかし、本節においては非一様スケールはどこで何度使っても構わないものとして進める。つまり本節におけるスケール行列は各軸の倍率が $0$ より大きい値であればどこで何度使っても構わない。例えば上記の $S_1, S_2, \ldots, S_n$ がすべて非一様スケールであっても構わない)
上記の $(\mathrm{i})$ は明らかである。平面上に置かれた楕円の長径を $a$、短径を $b$ とし、長径と x軸とのなす角を $\theta$ とする (下図2)。位置はどこで考えても同じであるためここでは簡単のため原点としている。右図3の半径 $1$ の正円がこの楕円になるようにするためには x軸方向の倍率を $a$、y軸方向の倍率を $b$ としたスケール行列を $S$、角度 $\theta$ の回転行列を $R$ とすればこれらの積 $RS$ を正円に対して実行すればよい。
またもちろんスケール倍率及び回転角度を適当に変えても正円に対してスケール、回転の順で変換を行えば適当な長径、短径を持ち、適当な方向を向いた楕円になる。


$(\mathrm{ii})$ もまた明らかである。ここでいう「アフィン変換」とは具体的には平行移動、回転、スケールのいずれかあるいはそれらを有限回数合成したものを意味する。
アフィン変換を表す行列を $M$ とする。今述べたように $M$ は有限個の平行移動行列 $T_i$、回転行列 $R_i$、スケール行列 $S_i$ を適当な順序で掛け合わせたものであるから\[ M = S_n T_l R_m \ldots R_2S_2T_2R_1S_1T_1\]として表される。
また $M$ の逆行列 $M^{-1}$ は次の形で表される。\[ M^{-1} = T{_1}^{-1}S{_1}^{-1}R{_1}^{-1}T{_2}^{-1}S{_2}^{-1}R{_2}^{-1}\ldots R{_m}^{-1}T{_l}^{-1}S{_n}^{-1} \]平行移動行列の逆行列は平行移動行列であり、回転行列の逆行列も回転行列である。同様にスケール行列の逆行列もスケール行列である。したがって上記の $M^{-1}$ も有限個の平行移動行列、回転行列、スケール行列の積であるからアフィン変換を表している。
平面上の2つの図形が衝突しているとき、両者は少なくとも1点を共有しているがその点を $\boldsymbol{p}$ とする。この2つの図形にアフィン変換を行うものとし、それを表す行列 $M$ をとする。$\boldsymbol{p'} = M\boldsymbol{p}$ とすれば、変換前の両者の共有点 $\boldsymbol{p}$ は $\boldsymbol{p'}$ に移ることを意味するが、これは変換後においても両者は(少なくとも)1つの点 $\boldsymbol{p'}$ を共有することを意味する。つまりアフィン変換前に2つの図形が衝突しているならば変換後においても衝突しているのである。
アフィン変換を表す行列 $M$ の逆行列 $M^{-1}$ も何らかのアフィン変換を表すことに注意すれば上記の逆もいえる。すなわちアフィン変換後において2つの図形が衝突しているならば変換前においても衝突している。したがって、その対偶によりアフィン変換前に2つの図形が衝突していないのであれば変換後においても衝突はしていない。
まとめると、アフィン変換前に2つの図形が衝突しているのであれば変換後においても両者は衝突している。変換前に衝突していないのであれば変換後においても衝突はしていない。つまりアフィン変換によって両者の衝突状態は変化しないのである。
$(\mathrm{iii})$ はそれほど簡単には導けない。
上記 $(\mathrm{i})$ で見たように原点に置かれている任意の楕円は、原点に置かれた半径 $1$ の正円に対し適当な回転行列 $R$、スケール行列 $S$ の積 $RS$ を実行すれば得られる。したがって平面上の任意の位置に置かれた楕円は適当な平行移動行列 $T$ を追加することで、原点に置かれた半径 $1$ の正円に対し $TRS$ を実行すれば得られるわけである。
例えば下図4の楕円であれば原点から点 $P_0$ までの移動を表す平行移動行列を $T_0$、角度 $\theta$ の回転を表す回転行列を $R_0$、 x軸方向の倍率が $a$、y軸方向の倍率が $b$ であるスケール行列を $S_0$ とし、その積 $M_0 = T_0R_0S_0$ を下図3の正円に実行すればこの正円は目的の楕円に変換されることになる。


ここで適当なアフィン変換を表す行列 $M$ を以下のように定める (以下の $T_i$ は平行移動行列、$R_i$ は回転行列、$S_i$ はスケール行列)。\[ M = S_n T_l R_m \ldots R_2S_2T_2R_1S_1T_1\]そしてこの $M$ を上図4の楕円に実行した結果、下図に示される状態になったとしよう。点 $P$ は変換後の図形のオブジェクト原点(ローカル座標系の原点)である。

上図の図形を楕円と簡単に決めることはできない。なぜなら、この図形は上図4の楕円に対し $M$ を実行した結果であるが、それは図3の正円に対し $MM_0$ を実行した結果ともいえる。つまり図5の図形は半径 $1$ の正円に対し\[ MM_0 = (S_n T_l R_m \ldots R_2S_2T_2R_1S_1T_1)(T_0R_0S_0) \]を実行した結果である。ここで重要なのはこの $MM_0$ を $MM_0 = TRS$ のように分解することが(一般には)できないという点である。もし $MM_0 = TRS$ のように分解することができるのであれば $(\mathrm{i})$ で述べたように図5の図形は楕円である。しかし、14‐2節で述べたように $TRS$ 分解が可能であるためには、非一様スケールは変換の一番最初でしか使えないという制限がある。本節の場合は上で述べたように非一様スケールはどこで何度使っても構わないのでこの制限を守っているわけではない。したがって、上記の $MM_0$ は $MM_0 = TRS$ の形に分解できる保証はないのである。
それでも結論からいえば上図5の図形は楕円なのである (それが $(\mathrm{iii})$ の主張である)。
ここで使われる変換行列は平面図形を対象としているため $3\times3$ 行列であり、具体的には下のような形になっている。
\[\begin{pmatrix}\color{red}{a} &\color{red}{b} &e\\ \color{red}{c} &\color{red}{d} &f\\ 0 &0 &1\\\end{pmatrix}\]この行列に対し回転行列あるいはスケール行列を掛けると左上の $2\times2$ 成分($\color{red}{a}$、$\color{red}{b}$、$\color{red}{c}$、$\color{red}{d}$)は変化するが、平行移動行列を掛けてもこの左上の $2\times2$ 成分は変化しない (平行移動によってオブジェクトはその位置のみが変化することを考えればこのことは明らかである。つまり平行移動によって回転成分やスケール成分は変化しない)。
したがって先程の\[ MM_0 = (S_n T_l R_m \ldots R_2S_2T_2R_1S_1T_1)(T_0R_0S_0) \]から平行移動行列をすべて取り除いた積を\[ A = S_n R_m \ldots R_2S_2R_1S_1R_0S_0 \]

そして上記の変換行列 $A$ は回転行列とスケール行列のみで構成されている (各スケール行列の倍率はいずれも $0$ より大きい値)。このような場合、この $A$ を2つの回転行列 $R$、$Q$ と倍率が $0$ より大きいスケール行列 $S$ を用いて次のように表すことができる (以下を詳しくは特異値分解という。この原理については 14-12節参照)。\[ A = RSQ \]先程述べたように図3の正円に対し変換行列 $TA$ を実行すると図5の図形になるのであった。この図形は実際には楕円であるが、以下この点について解説する。
$A = RSQ$ と書き換えられるのであれば $TA = TRSQ$ となるが、これは正円に対し $Q$、$S$、$R$、$T$ の順で変換が行われることを意味する。このとき回転行列 $R$ の第1列目、第2列目を $\boldsymbol{lx}$、$\boldsymbol{ly}$ とすれば、この変換($TRSQ$)によって正円は $\boldsymbol{lx}$、$\boldsymbol{ly}$ を短軸あるいは長軸の方向とする楕円になるのである。さらにこのときスケール行列 $S$ の各軸方向の倍率を $\large{s_x}$、$\large{s_y}$ とすればそれらは長軸あるいは短軸の長さに等しくなる (下図6)。

これは次のように考えればよい。例えば最初の回転行列 $Q$ の回転角度が $\theta$ であったとしよう。図3に示されるように正円は原点に置かれておりこの時点では初期状態、すなわち何も回転が行われていないため正円のローカル座標系の各軸とXY平面の x軸、y軸は重なっている。ここで、正円のローカル座標系と $-\theta$ の角をなす仮想的なローカル座標系を考える。
図3の正円に対し最初の回転行列 $Q$ が実行されると見た目上は正円は何も変化しないが、この仮想的なローカル座標系はXY平面の x軸、y軸と重なった状態になる。この後に行われる変換は $S$、$R$、$T$ であるが、これらの変換をこの仮想的なローカル座標系に対して実行することを考えれば、$S$ の各倍率が短径あるいは長径になり、$R$ の各列が短軸あるいは長軸の方向になることは明らかであろう。
正円も楕円の一種であることを考えれば正円に対してどのようなアフィン変換を行っても確かに何らかの楕円にはなる。しかし、その楕円のローカル座標系と短軸、長軸は一般には重ならない。例えば簡単な例として初期状態ではなく何らかの回転($90^\circ$ や $180^\circ$ ではない回転)の行われている正円に対して非一様スケール、回転、平行移動の順で変換を行っても確かに楕円にはなるが、その楕円のローカル座標系の各軸と短軸、長軸は重ならない。さらにその場合には楕円のローカル座標系の各軸は直交性が失われている。
つまり初期状態の正円に対して何らかのアフィン変換を実行しても楕円にはなるが、その楕円の本来のローカル座標系と短軸、長軸が重なっているという保証はないので、本来のローカル座標系からは楕円の短軸や長軸の方向、及びそれらの長さを求めることは簡単にはいかないのである (そのために上記のような仮想的なローカル座標系を考えるわけである)。
B) 準備 2
2つの楕円が下図のように置かれていたとする。本節で使われる楕円はいずれも初期状態においては原点に置かれた半径 $1$ の正円であり、その正円に対し適当なスケール、回転、平行移動をこの順序で実行し楕円として使っている。
ここで青い楕円を原点に置かれた半径 $1$ の正円に変換するとしよう。それは青い楕円を初期状態に戻すことを意味するから、青い楕円に実行されている変換行列を $M$ とすれば上図の青い楕円に対しその逆行列 $M^{-1}$ を実行すればよい。さらに上図の白い楕円に対してもこの $M^{-1}$ を実行し、その結果下図のようになったとする。
上でも述べたように $M^{-1}$ は平行移動行列や回転行列及びスケール行列の積に過ぎないから $M^{-1}$ はアフィン変換を表す行列である。そして上記の $(\mathrm{iii})$ により楕円にアフィン変換を行った結果もまた何らかの楕円になる。したがって下図の白い図形は楕円である。

ここで白い楕円のローカル座標系と完全に重なる座標系、ij 座標系を用意する (下図9)。ij 座標系においては白い楕円は原点に置かれた軸平行な楕円であり、この座標系における正円の位置をここでは $C$ とする。
(注意 : すぐ上で述べたようにアフィン変換実行後の楕円はそのローカル座標系と短軸、長軸が重なっている保証はない。しかし、以下の解説では便宜上 楕円の短軸、長軸と重なっている座標系としてローカル座標系という語を用いている。これは単に解説の便宜のためであり他に意味はない)

さらに楕円と正円をともに $-C$ だけ移動させ、カメラを適当に回転させて ij 座標系が(斜めではなく)画面の縦横に平行に表示されるようにした結果が以下の図である。この状態においては楕円の中心が $-C$、正円は原点に置かれることになる。

上図は ij 座標系における楕円と正円であるが、XY平面で考えても同じであるから i 軸、j 軸を x軸、y軸とみなして、以下ではXY平面上の軸平行な楕円と原点に置かれた正円として考える。
正円は原点に置かれているので x軸、y軸に関して対称である。そのため楕円が平面上どの位置にあったとしても適当な場所に対称移動させて考えることができる。例えば下図11の場合は第1象限の楕円を第2象限に対象移動させているが、これによって両者の衝突状態が変わることはない。

また、第2象限にある軸平行な楕円の場合は直線 $y = -x$ に関して対象移動させれば横長の楕円は縦長になり、縦長の楕円は横長になる。そしてこの対称移動を行った場合でも下の2つの図に示されるように衝突状態が変わることはない。


これらのことから今回の実装では上図10の状態から軸平行な楕円の方は、常に第2象限の縦長の楕円に変換して使用する。
つまり2つの楕円が以下の状態であったときに上で述べたアフィン変換や対象移動を有限回実行することによって、

両者を下図のような配置に変換する。上の $(\mathrm{ii})$ にあるようにアフィン変換を行っても両者の衝突状態は変わらないので衝突判定を下図のように簡単な状況で考えるわけである。

以上、準備的な説明が長くなったが楕円同士の衝突判定はまず両者を図14の状態に変換してからが始まりである。今回の実装では2つの楕円の衝突判定を、第2象限に置かれた軸平行な縦長の楕円と原点に置かれた半径 $1$ の正円の衝突判定に帰着して考えるのである。
(本節では「アフィン変換」を平行移動、回転、スケールの3つの変換に限定したが、上で述べた対称移動も実際にはアフィン変換の一種である)
C) 楕円及び正円の接線について
今回の実装では楕円及び正円の接線が中心的な役割を担う。実装の詳細に入る前にここで楕円及び正円の接線に関連した事柄について簡単に復習する。上で述べたようにこの実装では最終的には第2象限に置かれた軸平行な縦長の楕円と原点に置かれた半径 $1$ の正円の衝突に帰着して考えるので、両者が衝突する場合は上図に示されるように楕円右下と正円左上が衝突する。そのため楕円や正円の接線を考える場合には、楕円であればその右下部分(楕円のローカル座標系の第4象限)、正円であればその左上部分(第2象限)のみを対象とすればよい。
楕円の短径を $a$、長径を $b$、その中心を $E$ とし、楕円円周上において短軸と $\beta$ の角をなす点を $L$ とする (下図)。

このとき $L$ の座標は $(E_x + a\cos\beta,\ E_y + b\sin\beta)$ である。$L$ における接線ベクトル(図に示されるベクトル)の方向は、$L$ の各成分を微分したものであるから、\[ (\frac{d}{d\beta}(E_x + a\cos\beta),\ \frac{d}{d\beta}(E_y + b\sin\beta)) = (-a\sin\beta,\ b\cos\beta)\]であり、この接線(ベクトル)の傾きは $\displaystyle\frac{b\cos\beta}{-a\sin\beta}$ となる。
逆に $L$ における接線の傾きだけがわかっているものとしその傾きを $m$ とすれば、$L$ の座標は以下のように求められる。$L$ と短軸のなす角をここでも $\beta$ とすれば、この場合の $\beta$ は未知数であるが $L$ における座標や接線ベクトルの表し方は上記と同じである。したがって接線の傾き $m$ は $\beta$ を用いれば\[ m = \frac{b\cos\beta}{-a\sin\beta} = -\frac{1}{k\tan\beta} \qquad (k = \frac{a}{b})\]と表される。すなわち、\[ \tan\beta = -\frac{1}{mk} \]であり、(楕円の右下部分のみを対象としているため) $\beta$ は必ず $-\pi/2 < \beta < 0$ の範囲にあることに注意すれば $\cos\beta$、$\sin\beta$ は\[\cos\beta = +\sqrt{\frac{1}{1 + \tan^2\beta}}\qquad,\qquad \sin\beta = \tan\beta\cos\beta \]として求められる。これにより $L$ の座標も求められるわけである。
正円の場合はその円周上の位置や接線ベクトルはほとんど明らかであるが、今回の実装では1つ注意しておかなければならないことがある。それは正円の接線ベクトルに関しては通常のものとは逆向きのものを使うという点である。
正円円周上の点(第2象限の点)を $R$ とし、$R$ と x軸プラス方向のなす角を $\alpha$ とする (下図)。

$R$ の座標は $(\cos\alpha,\ \sin\alpha)$ であり、$R$ における接線ベクトルはこの各成分を微分した $(-\sin\alpha,\ \cos\alpha)$ が本来のものであるが、今回の実装ではこの逆向きのベクトル $(\sin\alpha,\ -\cos\alpha)$ を正円の接線ベクトルとして使用する。正円は第2象限のみが対象となるため、その領域の接線ベクトルは本来は左下を向いている。しかし、以下の解説においてはその逆方向である右上を向いたものを正円の接線ベクトルとして扱う。
ただし $R = (\cos\alpha,\ \sin\alpha)$ における接線ベクトルとして使うものが左下を向いたものであっても右上を向いたものであってもその傾きはいずれの場合も $\displaystyle -\frac{\cos\alpha}{\sin\alpha}$ である。
D) 実装の流れ
以下の解説においては楕円の中心を $E = (E_x,\ E_y)$ とし、短軸の長さを $a$、長軸の長さを $b$ とする。この衝突判定では軸平行な縦長の楕円を使うので短軸は x軸に平行であり、長軸は y軸に平行になる。まずは衝突しているかしていないかが明らかなケースから始める。例えば次の2つのケースは明らかに衝突していない。左図は楕円の右端(短軸の先端)が直線 $x=-1$ よりも左側にある場合であり、具体的には $E_x + a < -1$、右図は楕円の下端(長軸の先端)が直線 $y=1$ よりも上にある場合であり、この場合には $E_y - b > 1$ である。


以下では楕円右端は直線 $x=-1$ よりも右、下端は直線 $y=1$ よりも下にあるものとする。このとき楕円の中心 $E$ が直線 $x = -1$ より左にあるか右にあるかで処理が分かれるが、しばらくは $x=-1$ より左側にある場合($E_x < -1$)で進める (図19)。


楕円中心が $x=-1$ よりも左にあり楕円右端が $x=-1$ よりも右にある場合には楕円と直線 $x=-1$ は必ず交点を持つが、2つの交点のうち楕円中心 $E$ より下側の交点を $P = (P_x,\ P_y)$ とする (図21 ; 接している場合でも2つの交点が重なっているものとして考える)。
このとき図22のように $P$ が直線 $y=1$ よりも上にあるならば明らかに衝突していない。


下図23の場合は $P$ が x軸より下にあるが、このケースでは明らかに楕円と正円は衝突する。具体的には $P_y <= 0$ であれば楕円と正円は衝突している。
また、楕円上の点 $P$ と同じ高さにある円周上の点を $P'$ とするとき($P_y = P'_y$)、$P$ における接線の傾きが $P'$ における接線の傾きよりも大きい場合には下図24に示されるように両者は明らかに衝突はしていない。


以上が衝突判定の自明なケースであるが、両者が衝突している場合にはこのような簡単な方法では判定できない場合が多い。以下では上記のような簡単な方法では判定できない場合について見ていく。
今回は楕円と正円を常に第2象限で考えるため、両者が衝突している場合には楕円右下と正円左上が衝突している (下図25)。
先程と同じく楕円上の点 $P$ と同じ高さにある円周上の点を $P'$ とする ($P_y = P'_y$)。楕円の短軸 $EF$ と $EP$ のなす角を $\beta$、正円においては x軸プラス方向と $OP'$ のなす角を $\alpha$ とする。このとき、$\pi/2 \leq \alpha < \pi$、$-\pi/2 < \beta < 0$ である。また楕円と正円の2つの交点を $M$、$N$ とし、正円の上端 $(0,\ 1)$ を $H$ とする。
$P$ や $P'$ の求め方は簡単である。$P = (E_x + a\cos\beta,\ E_y + b\sin\beta)$ であるが、$P_x = -1$ であるから $E_x + a\cos\beta = -1$、すなわち\[ \cos\beta = \frac{-1 - E_x}{a} \]として $\cos\beta$ が求められるので、これにより $\sin\beta$ も求められる (この場合 $\sin\beta$ は必ず $\sin\beta < 0$)。
$P$ の座標がわかれば $P_y = P'_y$ であり $P' = (\cos\alpha,\ \sin\alpha)$ であるから、$\sin\alpha = P_y$ として $\sin\alpha$ が求められ、自動的に $\cos\alpha$ も求められる (ただし常に $\cos\alpha \leq 0$)。

楕円右下と正円左上が衝突している場合、$P$ における楕円の接線の傾きは $P'$ における正円の接線の傾きよりも必ず小さくなる。
例えば上の状況では $P$ における楕円の接線ベクトルは $(-a\sin\beta,\ b\cos\beta)$ であるから、傾きは $\displaystyle\frac{b\cos\beta}{-a\sin\beta}$、正円の $P'$ における接線ベクトルは $(\sin\alpha,\ -\cos\alpha)$ であるから、傾きは $\displaystyle\frac{-\cos\alpha}{\sin\alpha}$ となる。したがって楕円右下と正円左上が衝突している場合には\[\frac{b\cos\beta}{-a\sin\beta} < \frac{-\cos\alpha}{\sin\alpha}\]となっているということである。
そしてこの状況では楕円円周上を $P$ から $F$ に移動する際、接線の傾きは連続的に増加する。正円円周上を $P'$ から $H$ に移動する際、接線の傾きは連続的に減少する。したがって楕円上においては $P$ から一定量ずつ角度を増加させ、正円上においては $P'$ から同じ量ずつ角度を減少させていくとある時点において両者の接線の傾きは等しくなる。
すなわち、\[\frac{b\cos(\beta + x)}{-a\sin(\beta + x)} = \frac{-\cos(\alpha - x)}{\sin(\alpha - x)} \tag{1} \]を満たす角度 $x$ が存在する。さらに上図より、$P$ から楕円円周上を移動し交点 $N$ に達する時点では楕円と正円の接線の傾きは逆転している ($N$ の位置においては楕円の接線の傾きは明らかに正円の接線の傾きよりも大きい)。つまり $P$ から $N$ に移動するまでに両者の接線の傾きが等しくなる状況が起こるわけである ($N$ に移動するまでに起こらないこともあるが、その場合でも $F$ に移動するまでには必ず1回は両者の接線の傾きは等しくなる)。そしてその状況においては図から明らかに $-\pi/2 < \beta + x < 0$ である。
上記 $(1)$ を変形すれば \begin{align*}&\frac{\sin(\alpha - x)}{\cos(\alpha - x)} = \frac{a}{b}\frac{\sin(\beta + x)}{\cos(\beta + x)} \\\\=\ &\tan(\alpha - x) = k\tan(\beta + x) \tag{2}\end{align*}となる。ただし $k = a/b$ である。
上記 $(2)$ を三角関数の公式によって書き換えると\[\frac{\tan\alpha - \tan x}{1 + \tan\alpha\tan x} = k\frac{\tan\beta + \tan x}{1 - \tan\beta\tan x} \tag{3}\]となるが、ここで表記を簡単にするために $A = \tan\alpha$、$B = \tan\beta$、$X = \tan x$ と置くと $(3)$ は以下のように表される。
\[\frac{A - X}{1 + AX} = k\frac{B + X}{1 - BX} \tag{4}\]ここで分母をはらえば、\[(A - X)(1 - BX) = k(B + X)(1 + AX) \tag{5}\]であるが、この左辺を右辺に移動させて $X$ についてまとめると次の形に変形される。
\[(kA - B)X^2 + (k + 1)(AB + 1)X + (kB - A) = 0 \tag{6}\]すなわち、$X$ の2次方程式になるわけである。
$\tan\beta$ (及び $\tan\alpha$)は既知であり、この方程式から $X\ (= \tan x)$ が求められるので $\tan(\beta + x)$ や$\tan(\alpha - x)$ も上述のように以下の形で求められる。
\begin{align*}&\tan(\beta + x) = \frac{\tan\beta + \tan x}{1 - \tan\beta\tan x} \\\\&\tan(\alpha - x) = k\tan(\beta + x)\end{align*}
今までは楕円の中心 $E$ が直線 $x=-1$ よりも左側にある場合について見てきたが、ここで一旦 $E$ が直線 $x=-1$ より右にある場合の処理について簡単に解説する。楕円の中心 $E$ は第2象限に置かれることを前提としているからこの場合においては $-1 < E_x \leq 0$ である。
楕円の下端の点を $P$ とする。縦長の楕円であるから長径を $b$ とすれば $P = (E_x,\ E_y - b)$ である。このとき次の2つのケースにおける判定は明らかである。
左のケースは $P$ が正円に含まれる場合であり、右のケースは $P$ が x軸よりも下側にある場合である。この2つのケースでは両者は必ず衝突している。


$E$ が直線 $x=-1$ よりも右にあり上記のような自明な判定ができない場合、両者が衝突している際には以下のような状態になっている。しかしこの場合における判定方法は先程述べたやり方と同じであり、ここでも $P$ と同じ高さにある正円円周上の点を $P'$ とする ($P_y = P'_y$)。

楕円の短軸 $EF$ と $EP$ のなす角を $\beta$ とし、正円においては x軸プラス方向と $OP'$ のなす角を $\alpha$ とする。ここで再び角度 $\beta$ を少しずつ増加させ、角度 $\alpha$ は同じ量ずつ減少させていくと、ある時点において楕円上の点 $P$ における接線の傾きと、正円上の点 $P'$ における接線の傾きは等しくなる。つまり、\[\frac{b\cos(\beta + x)}{-a\sin(\beta + x)} = \frac{-\cos(\alpha - x)}{\sin(\alpha - x)} \tag{1} \]を成り立たたせる角度 $x$ が存在する。
したがって三角関数の公式によってこの式を書き換えれば先程と同じように\[\frac{\tan\alpha - \tan x}{1 + \tan\alpha\tan x} = k\frac{\tan\beta + \tan x}{1 - \tan\beta\tan x} \tag{3}\]が得られるが、今回は角度 $\beta$ は $-90^\circ$ であることがわかっているから $\displaystyle \tan\beta = \tan(-\frac{\pi}{2}) = -\infty$ である。これによって上記 $(3)$ の右辺は次のように書き換えられる。
\[ k\frac{\tan\beta + \tan x}{1 - \tan\beta\tan x} = k\dfrac{1 + \dfrac{\tan x}{\tan\beta}}{\dfrac{1}{\tan\beta} - \tan x} = k\dfrac{1 + \dfrac{\tan x}{-\infty}}{\dfrac{1}{-\infty} - \tan x} = -\frac{k}{\tan x} \tag{7}\]
ここで表記を簡単にするために $A = \tan\alpha$、$B = \tan\beta$、$X = \tan x$ と置くと $(3)$ は以下のように表される。\[\frac{A - X}{1 + AX} = -\frac{k}{X} \tag{8}\]分母をはらって $X$ についてまとめると先程のものよりも簡単な次の2次方程式が得られる。
\[X^2 - (A + kA)X - k = 0 \tag{9}\]さらにこの場合には $(7)$ より\[ \tan(\beta + x) = \frac{\tan\beta + \tan x}{1 - \tan\beta\tan x} = -\frac{1}{\tan x}\]である。
ここまでに楕円及び正円の接線の傾きが一致する角度を求めたわけであるが、楕円上において接線の傾きが一致する点を $Q$、正円上において接線の傾きが一致する点を $Q'$ とする (下図29)。

図に示されるように $-\pi/2 < \beta + x < 0$ であるから $\theta = \beta + x$ と置けば、\[ \cos\theta = +\sqrt{\frac{1}{1 + \tan^2\theta}}\ ,\qquad \sin\theta = \tan\theta\cos\theta\ \tag{10}\]となる。したがって楕円上の位置 $Q$ は\[ Q = (E_x + a\cos\theta,\ E_y + b\sin\theta) \tag{11} \]として求められる。
同様にして正円上の位置 $Q'$ も求められる。$\pi/2 < \alpha - x < \pi$ であるから $\varphi = \alpha - x$ と置けば、\[ \cos\varphi = -\sqrt{\frac{1}{1 + \tan^2\varphi}}\ ,\qquad \sin\varphi = \tan\varphi\cos\varphi\ \tag{12}\]となる (ここでは $\cos\varphi$ の符号はマイナスになることに注意)。
正円の半径は $1$ であり中心は原点にあるから\[ Q' = (\cos\varphi,\ \sin\varphi) \tag{13} \]である。
このとき $Q$ と $Q'$ の位置関係について次の4つのケースが考えられる。
$\rm{I}.$ $Q$ が正円の中にある

このケースは単に $|OQ| \leq 1$ であるかを調べればよい (上図では $Q'$ は楕円の中にあるが衝突の仕方によっては $Q'$ が楕円の外に位置することもある)。
$\rm{I}\hspace{-1.0pt}\rm{I}.$ ($Q$ は正円の中にはないが) $Q'$ が楕円の中にある

状況としては上図のような衝突状態のときである。このときの両者の衝突部分を拡大したものを以下に示す。

このケースでは $Q'$ が楕円の中にあるかを調べるために、楕円を正円にスケールして判定を行う。
上記 $(9)$ より $Q'=(\cos\varphi,\ \sin\varphi)$ であるが、この座標は楕円の中心 $E$ を原点としたローカル座標系では $(\cos\varphi - E_x,\ \sin\varphi - E_y)$ となるが便宜上のこの座標を\[K = (K_x,\ K_y) = (\cos\varphi - E_x,\ \sin\varphi - E_y) \]で表す。
$Q'$ が $E$ を中心とする短径 $a$、長径 $b$ の楕円に含まれるかどうかは、この $K$ が原点を中心とする短径 $a$、長径 $b$ の楕円に含まれるかを調べることと同じである。さらにその場合には原点中心のその楕円と $K$ を縦方向に $a/b$ だけ縮小して、半径 $a$ の正円に含まれるかどうかを調べることと同じである。したがって $K = (K_x,\ K_y)$ を縦方向に $a/b$ だけ縮小した座標 $(K_x,\ \displaystyle\frac{a}{b}K_y)$ が半径 $a$ の正円に含まれるかを調べればよい。
$\rm{I}\hspace{-1.0pt}\rm{I}\hspace{-1.0pt}\rm{I}.$ 楕円と正円の2つの交点を $M$、$N$ とするとき、$Q$ が $M$ の手前にあり、$Q'$ は $N$ を過ぎた位置にある
この場合には両者は下図のような衝突状態になっている。
(第3のケース及び次の第4のケースで扱う衝突は下図のような境界部分における衝突の判定である。下図の場合は両者にわずかな重なりがあることが見てわかるが、第3、第4のケースで扱う衝突のほとんどはカメラをかなり近づけなければ目で確認することはできない)

下図はこのときの両者の衝突部分を拡大したものである。

$Q$ が正円の中になく、さらに $Q'$ も楕円の中にないというケースである。この場合 $Q$ が上図の $M$ より手前にあるのであれば、($Q$ と $Q'$ の接線の傾きが同じであることに注意すれば) $Q'$ が $M$ より手前に来ることがないのは明らかである。
このケースにおいて両者が衝突している状況では、ほとんどすべての場合において $Q$ は正円に極めて近い位置に来る。そこで $Q$ から接線を引き、その接線と正円との交点を $R'$ とする。次にこの(正円上の点) $R'$ における接線の傾きと一致する楕円上の点 $R$ を求め、この $R$ が正円に含まれるかを調べる (下図35 ; この図では見やすさのために楕円の形状をやや変えている)。

$Q = (E_x + a\cos\theta,\ E_y + b\sin\theta)$ とすれば、その位置における接線ベクトルは上の C) の部分で述べたように $(-a\sin\theta,\ b\cos\theta)$ であるから、$Q$ からこの方向に延びる直線と正円との衝突点を求めればそれが $R'$ である。
$R' = (R'_x,\ R'_y)$ とすれば接線ベクトルは $(R'_y,\ -R'_x)$ であり、この接線ベクトルの傾きを $m$ とすれば $\displaystyle{m= -\frac{R'_x}{R'_y}}$ である。
一方傾きが $m$ となる楕円上の位置が $R$ であるがその角度を $\gamma$ とすれば、$R$ の座標は $(E_X + a\cos\gamma,\ E_y + b\sin\gamma)$ であり、$R$ における接線ベクトルは $(-a\sin\gamma,\ b\cos\gamma)$ となる。そしてこの接線ベクトルの傾きが $m$ であることから $\sin\gamma$、$\cos\gamma$ は次のように求められる。
\[ m = -\frac{b\cos\gamma}{a\sin\gamma} = -\frac{1}{k\tan\gamma} \qquad (k = \frac{a}{b}) \]であるから、\[\tan\gamma = -\frac{1}{mk}\]したがって、\[\cos\gamma = +\sqrt{\frac{1}{1 + \tan^2\gamma}}\qquad,\qquad \sin\gamma = \tan\gamma\cos\gamma \]となる ($\cos\gamma$ の符号は必ずプラス)。
$\rm{I}\hspace{-1.0pt}\rm{V}.$ 上記 $\rm{I}\hspace{-1.0pt}\rm{I}\hspace{-1.0pt}\rm{I}$ と同じく2つの交点を $M$、$N$ とするとき、$Q'$ が $M$ の手前にあり、$Q$ は $N$ を過ぎた位置にある
このケースは次のような状況において起こる。下図では両者は接しているようにしか見えないが、カメラを近づけると楕円と正円は非常にわずかな幅で重なっていることがわかる。

以下はその重なり部分の拡大図である。確かに両者はわずかな幅で重なっており、$Q'$ が交点 $M$ の手前、$Q$ は交点 $N$ を過ぎた位置に来ている。

ここで $Q'_x$ と同じ x座標を持つ楕円上の位置を $L$ とする。第4のケースではまず $L$ における接線ベクトルを求めるが、その際 $L$ 及びその接線ベクトルは楕円のローカル座標系で計算する。したがって $L_x = Q'_x - E_x$ である。楕円のローカル座標系で考えたときには $L_x$、$L_y$ に関して $\ \displaystyle{\frac{L{_x}^2}{a^2} + \frac{L{_y}^2}{b^2} = 1}\ $ であるから $L_y$ は\[ L_y = -\sqrt{b^2(1 - \frac{L{_x}^2}{a^2})} = -b\sqrt{1 - \frac{L{_x}^2}{a^2}}\]として求められる (楕円のローカル座標系においては $L$ は必ず y軸よりも下に位置するので $L_y$ の符号はマイナス)。
$L = (L_x,\ L_y) = (a\cos\psi,\ b\sin\psi)$ とすれば $L$ における接線ベクトルは $(-a\sin\psi,\ b\cos\psi)$ であるから、これを $L_x$、$L_y$ で表せば $\displaystyle{(-a\sin\psi,\ b\cos\psi) = (-\frac{a}{b}L_y,\ \frac{b}{a}L_x) }$ となる。
$Q'$ における(単位)接線ベクトルを $\boldsymbol{\mathsf{v_1}}$、$L$ における(単位)接線ベクトルを $\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{\mathsf{v_1}} + \boldsymbol{\mathsf{v_2}}$ を正規化したベクトルを $\boldsymbol{\mathsf{v_3}}$ とし、$\boldsymbol{\mathsf{v_3}}$ を接線ベクトルとして持つ正円上の点を $S'$ とする (下図 ; この図においても見やすさのため楕円の形状をやや変えている)。

第4のケースではこの $S'$ が楕円の中に含まれるかどうかを調べる。処理としては第2のケースと同じであり、$S'$ を再び楕円のローカル座標系での座標 $S$ に変換し ( $S = (S'_x - E_x,\ S'_y - E_y)$ )、この $S$ を縦方向に $a/b$ だけ縮小した座標が半径 $a$ の正円に含まれるかどうかを調べればよい。
以下のメソッド CollisionTest_AAEllipse_UnitCircle(..) は軸平行な楕円と正円の衝突判定を行うものであるが、軸平行な楕円はその中心が第2象限に置かれた縦長の楕円、正円は原点に置かれた半径 $1$ の正円であることを前提としている。引数の E は楕円の中心、a、b は短径、長径である (縦長の楕円であるから短軸は x軸に平行、長軸は y軸に平行)。
[CollisionTest_AAEllipse_UnitCircle(..)]
bool CollisionTest_AAEllipse_UnitCircle(Vector2 E, float a, float b)
{
if (E.x + a < -1.0f || E.y - b > 1.0f) { return false; }
float k = a / b;
float inv_a = 1.0f / a;
float tanTh, x;
if (E.x < -1.0f)
{
float d = -1.0f - E.x;
float cosBt = d * inv_a; // d / a;
float sinBt = -Mathf.Sqrt(1 - cosBt * cosBt);
Vector2 P = new Vector2(E.x + d, E.y + b * sinBt); // d == a*cosBt
if (P.y <= 0.0f) { return true; }
else if (P.y >= 1.0f) { return false; }
float sinAl = P.y;
float cosAl = -(Mathf.Sqrt(1.0f - sinAl * sinAl));
float mEll = -(b * cosBt) / (a * sinBt);
float mCir = -cosAl / sinAl;
if(mEll >= mCir) { return false; }
float A = sinAl / cosAl; // tanAl
float B = sinBt / cosBt; // tanBt
float s = k * A - B;
float t = (k + 1) * (A * B + 1);
float u = k * B - A;
float D = t * t - 4 * s * u;
float sqD = Mathf.Sqrt(D);
x = (-t + sqD) / (2 * s);
tanTh = (B + x) / (1.0f - B * x); // tan(Beta + x)
}
else
{
Vector2 P = new Vector2(E.x, E.y - b);
if(P.sqrMagnitude <= 1.0f || P.y <= 0.0f) { return true; }
float sinAl = P.y;
float cosAl = -(Mathf.Sqrt(1.0f - sinAl * sinAl));
float A = sinAl / cosAl; // tanAl
// float s = 1.0f;
float t = -(A + k * A);
float u = -k;
float D = t * t - 4 * u;
float sqD = Mathf.Sqrt(D);
x = (-t + sqD) * 0.5f;
tanTh = -1.0f / x;
}
float cosTh = Mathf.Sqrt(1.0f / (1.0f + tanTh * tanTh));
float sinTh = tanTh * cosTh;
Vector2 Q = new Vector2(E.x + a * cosTh, E.y + b * sinTh);
if(Q.sqrMagnitude <= 1.0f) { return true; }
// [CASE 2]
//
//tanPh = (A - x) / (1.0f + A * x);
float tanPh = k * tanTh; // tan(A-x) == k*tan(B+x)
float cosPh = -Mathf.Sqrt(1.0f / (1.0f + tanPh * tanPh));
float sinPh = tanPh * cosPh;
Vector2 Qd = new Vector2(cosPh, sinPh); // Q'
Vector2 L = Qd - E; // new Vector2(Qd.x - E.x, Qd.y - E.y);
L.y *= k;
float a2 = a * a;
if (L.sqrMagnitude <= a2) { return true; }
// [CASE 3]
const float EPS = 0.0002f;
if(Q.x < Qd.x)
{
Vector2 dirQ = new Vector2(-a * sinTh, b * cosTh).normalized;
float t = Vector2.Dot(Q, dirQ);
float u = Q.sqrMagnitude - 1.0f;
float D = t * t - u;
if (D < 0.0f || (-t - Mathf.Sqrt(D)) < 0.0f)
{ return false; }
Vector2 Rd = Q + (-t - Mathf.Sqrt(D)) * dirQ; // R'
float m = -Rd.x / Rd.y; // = -1 / (k*tanR)
float tanGm = -1.0f / (k * m);
float cosGm = Mathf.Sqrt(1.0f / (1.0f + tanGm * tanGm));
float sinGm = tanGm * cosGm;
Vector2 R = new Vector2(E.x + a * cosGm, E.y + b * sinGm);
if (R.magnitude <= 1.0f + EPS) { return true; }
}
// [CASE 4 (and CASE 3)]
{
Vector2 v1 = -new Vector2(-Qd.y, Qd.x);
L.y = -b * Mathf.Sqrt(1.0f - (L.x * L.x) / a2);
Vector2 v2 = new Vector2(-L.y * k, L.x * b * inv_a).normalized; // L.x * (b / a)
Vector2 v3 = (v1 + v2).normalized;
Vector2 Sd = new Vector2(-v3.y, v3.x);
Vector2 S = Sd - E;
S.y *= k;
return (S.magnitude * inv_a) <= (1.0f + EPS);
}
}
上の解説では軸平行な楕円の中心が直線 $x=-1$ の左にあるか右にあるかで処理を分けたが、9行目のifブロックが左にある場合、38行目の else ブロックが右にある場合である。これらの if/else ブロックやメソッド冒頭で処理を返すif文があるがそれらはいずれも自明な判定のケースである。
プログラム中の cosBt、sinBt は $\cos\beta$、$\sin\beta$ のことであり、cosAl、sinAl は $\cos\alpha$、$\sin\alpha$ のことである。また上の解説では $\tan x$ を求めるために最後に2次方程式が現れたが(式 $(6)$ や $(9)$)、プログラム中ではその2次方程式は $sX^2 + tX + u = 0$ として使われている。つまりメソッド内の s は $X^2$ の係数、t は $X$ の係数、u は定数項である。
60行目の Q、71行目の Qd は上の解説における $Q$、$Q'$ のことであり、この2つの行は上記の式 $(11)$ や $(13)$ と同じである。
任意の2つの楕円同士の衝突判定用のメソッド CollisionTest_Ellipse_Ellipse(..) は上のメソッドを利用することで次のように記述される。
このメソッドでは2つの楕円が、原点に置かれた半径 $1$ の正円に対しスケール、回転、平行移動をこの順序で1回ずつ行ってできたものであることを前提としている。引数の E は楕円の中心、lx、ly はローカル座標系の x軸、y軸方向を表す単位ベクトル、sx、sy はローカル座標系の x軸方向、y軸方向の倍率である。
ここで使われる楕円は原点に置かれた正円に対しスケール、回転、平行移動をこの順で実行して得られるものであるから、楕円の短軸、長軸はそのローカル座標系の各軸と重なっており、したがってローカル座標系の各軸の方向や倍率はそのまま短軸や長軸の方向や長さとして使うことができる。
[CollisionTest_Ellipse_Ellipse(..)]
bool CollisionTest_Ellipse_Ellipse(Vector2 E1, Vector2 lx1, Vector2 ly1, float sx1, float sy1,
Vector2 E2, Vector2 lx2, Vector2 ly2, float sx2, float sy2)
{
Vector3[] m1c = new Vector3[] // cols, M1
{
new Vector3(sx1 * lx1.x, sx1 * lx1.y, 0),
new Vector3(sy1 * ly1.x, sy1 * ly1.y, 0),
new Vector3(E1.x, E1.y, 1)
};
Vector3[] im2r = CalcInverseRows(E2, lx2, ly2, sx2, sy2); // rows, invM2
//// A = (col1, col2, col3) = invM2 * M1
Vector3 col1 = new Vector3(Vector3.Dot(im2r[0], m1c[0]), Vector3.Dot(im2r[1], m1c[0]), 0);
Vector3 col2 = new Vector3(Vector3.Dot(im2r[0], m1c[1]), Vector3.Dot(im2r[1], m1c[1]), 0);
Vector3 col3 = new Vector3(Vector3.Dot(im2r[0], m1c[2]), Vector3.Dot(im2r[1], m1c[2]), 1);
float a = col1.x;
float c = col1.y;
float b = col2.x;
float d = col2.y;
float e = a * a + b * b;
float f = a * c + b * d;
float g = c * c + d * d;
float ja = e + g;
float jb = Mathf.Sqrt((e - g) * (e - g) + 4.0f * f * f);
float G1 = (ja + jb) * 0.5f;
float G2 = (ja - jb) * 0.5f;
Vector2 u1 = new Vector2(1.0f, (G1 - e) / f).normalized;
Vector2 u2 = new Vector2(-u1.y, u1.x);
float r_a = Mathf.Sqrt(G1);
float r_b = Mathf.Sqrt(G2);
Vector2 wp = col3;
float x0 = Vector2.Dot(-wp, u1);
float y0 = Vector2.Dot(-wp, u2);
Vector2 E = new Vector2(-Mathf.Abs(-x0), Mathf.Abs(-y0));
if (r_a > r_b)
{
float w = r_a;
r_a = r_b;
r_b = w;
w = E.x;
E.x = -E.y;
E.y = -w;
}
return CollisionTest_AAEllipse_UnitCircle(E, r_a, r_b);
}
一方の楕円に実行された変換行列を $M_1$、もう一方の楕円に実行された変換行列を $M_2$ とすれば16行目までに行っていることは $M{_2}^{-1}M_1$ の計算である。これは一方の楕円を初期状態に戻すために逆行列を実行し、もう一方の楕円にもその逆行列を実行して適当な楕円に変換する処理に相当する。$A = M{_2}^{-1}M_1$ とすれば18~35行目は特異値分解の処理であり、31、32行目の u1、u2 は変換された楕円の短軸あるいは長軸の方向、34、35行目の r_a、r_b は短軸あるいは長軸の長さになる。これらは上の解説における図6の $\boldsymbol{lx}$、$\boldsymbol{ly}$、$\large{s_x}$、$\large{s_y}$ に相当する。
11行目の CalcInverseRows(..) は送られてくる引数から逆行列を計算しその各行を Vecotr3[] で返すものであり、具体的には以下の内容である。
Vector3[] CalcInverseRows(Vector2 pos, Vector2 lx, Vector2 ly, float sx, float sy)
{
float p = pos.x;
float q = pos.y;
float a = lx.x;
float b = ly.x;
float c = lx.y;
float d = ly.y;
float inv_s = 1.0f / sx;
float inv_t = 1.0f / sy;
Vector3[] rows =
{
new Vector3(a * inv_s, c * inv_s, -(a * p + c * q) * inv_s),
new Vector3(b * inv_t, d * inv_t, -(b * p + d * q) * inv_t),
new Vector3(0, 0, 1)
};
return rows;
}
41行目の E は楕円のローカル座標系の各軸に平行な座標系(上の解説における ij 座標系)において、正円を原点に移動させたときの楕円の位置を表しているが、この位置は対象移動によって第2象限に移されている。43行目のifブロックは楕円が横長であれば縦長の楕円にする処理である。
この43行目のifブロックが終わる時点では2つの楕円は原点に置かれた半径 $1$ の正円と第2象限に置かれた軸平行な縦長の楕円に変換されているのであとは上記の CollisionTest_AAEllipse_UnitCircle(..) を実行すればよい。
以上が今回の実装の詳細である。2つの楕円が画面上に収まるような大きさで、楕円を普通に動かしている場合には、ほとんどすべての衝突は自明な衝突でない限り上記の第1のケースで検出される ($99\%$ に近い)。つまり両者が衝突している状況ではほとんどすべての場合において上の解説における $Q$ が正円の中に含まれるということであるが、なぜそうなるのかはわかっていない。
また $Q$ が正円に含まれない場合においても両者が衝突しているのであれば $Q$ は極めて正円に近い位置に来る。それが必ず成り立つのかどうかについても詳細は不明である。
楕円を'手動'で動かすような場合には(自明な場合を除いて)両者の衝突は第1のケースで検出されることがほとんどであるが、2つの楕円の位置、形状をランダムに変えてテストする場合にはその割合は状況によって変化する。第2のケースで一番多く検出されることもあるが、第3や第4のケースで検出される割合はやはり少ない。ただし、こういったことも確かなことは残念ながら不明である。
冒頭で述べたように今回の実装は目で確認できるような誤動作は起こらない。しかし、この衝突判定は数学的に完全なわけではないので境界部分において実際には衝突の検出ができていないケースがある。ただしそういった誤動作はカメラをかなり近づけなければ判別できないため今回はそのレベルの精度については放棄している。
繰り返しになるが、このアルゴリズムは肝心な点については何もわかっていないので過信してはいけない (まだ発見されていない明らかな誤動作が含まれている可能性も十分にあり得る)。
本節では上で述べたことに関連した2つのプログラムが用意されている。
(UnityにおけるSceneファイルは「PNX_B」、プログラムは「sPNX_B」フォルダ内の「SecB01」である)
# Code1
次のプログラムは2つの楕円同士の衝突判定を行うものである (2つの楕円はプログラムでは White、Blue という名前で使われている)。2つの楕円は以下のキー操作によって大きさや向きあるいは位置を変えることができる。
H、J、K、L : 楕円を縦横に移動させる
S、T : 楕円を軸方向に拡大させる (+Shift の場合は縮小)
R : 楕円を回転させる (+Shift の場合は逆回転)
Shift + A : 操作対象の楕円の変更
[Code1] (実行結果 図1)
if (!i_INITIALIZED)
{
White.scaleX = 2.34f;
White.scaleY = 1.23f;
White.degree = 25.0f;
White.position = new Vector2(-3.55f, 1.25f);
Blue.scaleX = 1.25f;
Blue.scaleY = 2.21f;
Blue.degree = 26.5f;
Blue.position = new Vector2(2.65f, 0.2f);
i_INITIALIZED = true;
}
ObjectMotion();
Vector2 E1 = White.position;
Vector2 lx1 = White.localX;
Vector2 ly1 = White.localY;
float sx1 = White.scaleX;
float sy1 = White.scaleY;
Vector2 E2 = Blue.position;
Vector2 lx2 = Blue.localX;
Vector2 ly2 = Blue.localY;
float sx2 = Blue.scaleX;
float sy2 = Blue.scaleY;
bool bColl = CollisionTest_Ellipse_Ellipse(E1, lx1, ly1, sx1, sy1, E2, lx2, ly2, sx2, sy2);
Hit(bColl);
# Code2
次のプログラムは軸平行な楕円と原点に置かれた半径 $1$ の正円との衝突判定を行うものである (プログラム中のWhiteが楕円)。楕円は自由に移動を行えるが正円は静止したままである。また楕円はどこに位置していても判定の前に第2象限の縦長の楕円に変換される。キー操作は以下のとおり。
H、J、K、L : 楕円を縦横に移動させる
S、T : 楕円を軸方向に拡大させる (+Shift の場合は縮小)
[Code2]
if (!i_INITIALIZED)
{
White.scaleX = 0.9f;
White.scaleY = 1.7f;
White.position = new Vector2(-2.4f, 2.3f);
i_INITIALIZED = true;
}
ObjectMotion();
Vector2 E = White.position;
float sx = White.scaleX;
float sy = White.scaleY;
E.x = -Mathf.Abs(E.x);
E.y = Mathf.Abs(E.y);
float a = sx;
float b = sy;
if (sx > sy)
{
a = sy;
b = sx;
float w = E.x;
E.x = -E.y;
E.y = -w;
}
bool bColl = CollisionTest_AAEllipse_UnitCircle(E, a, b);
Hit(bColl);
B-2 >>
衝突判定 S
衝突判定 S
© 2020-2025 Redpoll's 60 (All rights reserved)