Redpoll's 60
Home / 3Dプログラミング入門 / 第14章 $§$14-1
第14章 数学的事柄についての補足
| $§$14-1 外積の導出 | $§$14-8 球面線形補間の実装 |
| $§$14-2 TRS分解における回転行列 | $§$14-9 ベクトルを一致させる回転 |
| $§$14-3 三角形の重心座標 (barycentric coordinates) | $§$14-10 Quaternion、回転行列、オイラー角の相互変換 |
| $§$14-4 Möller-Trumbore algorithm (レイ vs 三角形) | $§$14-11 二線分間の最短距離 |
| $§$14-5 法線ベクトルの変換 | $§$14-12 「直方体 vs 直方体」における分離軸 |
| $§$14-6 Quaternion 基礎 | $§$14-13 2D空間における特異値分解 |
| $§$14-7 Quaternionによる回転の表現 |
$§$14-1 外積の導出
2つの3次元ベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ が与えられたとき、ベクトルの外積 $\boldsymbol{a} \times \boldsymbol{b}$ は以下の ($\mathrm{i}$)~($\mathrm{iii}$) を満たすベクトルとして定義されるのであった。
(今までと同様本節においても外積は左手系の外積として考える。また上記 ($\mathrm{iii}$) から2つのベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ のなす角が $0^\circ$ あるいは $180^\circ$ のときは外積は定義されないので、$\boldsymbol{a}$、$\boldsymbol{b}$ のなす角を $\theta$ とするとき以下の解説においては $0^\circ < \theta < 180^\circ$ であることを前提とする)
今までの解説やプログラムにおいては外積は何度も使われたが、それは実用的な立場からのものであり外積それ自体に深く立ち入るようなものではなかった。例えば外積の成分はどのようにして導出されるのか、あるいは外積の向きが常に中指の方向を指すとなぜいえるのかなどについては特に数学的な議論をすることはなかった。
以下では上の定義からベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ の外積 $\boldsymbol{a} \times \boldsymbol{b}$ を導出するが、その結果として向き及び大きさがどのような場合においても定義通りのものになることも示されるのである。
(証明) まず $\boldsymbol{a}$、$\boldsymbol{b}$ に直交するようなベクトル $\boldsymbol{\mathsf{v}} = (\mathsf{v_x}, \mathsf{v_y}, \mathsf{v_z})$ がどのような成分になるのかを求める。$\boldsymbol{\mathsf{v}}$ が $\boldsymbol{a}$、$\boldsymbol{b}$ に直交するのであれば\begin{align*}\boldsymbol{a} \cdot \boldsymbol{\mathsf{v}} = a_x \mathsf{v_x} + a_y \mathsf{v_y} + a_z \mathsf{v_z} = 0 \\\\\boldsymbol{b} \cdot \boldsymbol{\mathsf{v}} = b_x \mathsf{v_x} + b_y \mathsf{v_y} + b_z \mathsf{v_z} = 0 \end{align*}であるが、$\boldsymbol{a} \cdot \boldsymbol{\mathsf{v}}$ に $b_y$ を掛け、$\boldsymbol{b} \cdot \boldsymbol{\mathsf{v}}$ に $a_y$ を掛けてその差を計算すると
\[ (a_xb_y - a_yb_x)\mathsf{v_x} + (a_zb_y - a_yb_z)\mathsf{v_z} = 0 \]したがって、\[ \frac{\mathsf{v_x}}{\mathsf{v_z}} = \frac{a_yb_z - a_zb_y}{a_xb_y - a_yb_x} \tag{1} \]である。
同様に、$\boldsymbol{a} \cdot \boldsymbol{\mathsf{v}}$ に $b_x$ を掛け、$\boldsymbol{b} \cdot \boldsymbol{\mathsf{v}}$ に $a_x$ を掛けてその差を計算すると
\[ (a_yb_x - a_xb_y)\mathsf{v_y} + (a_zb_x - a_xb_z)\mathsf{v_z} = 0 \]となるから、\[ \frac{\mathsf{v_y}}{\mathsf{v_z}} = \frac{a_zb_x - a_xb_z}{a_xb_y - a_yb_x} \tag{2} \]である。
ここで上の式 $(1)$、$(2)$ からベクトル $\boldsymbol{\mathsf{v}}$ を一意的に\[ \boldsymbol{\mathsf{v}} = (\mathsf{v_x}, \mathsf{v_y}, \mathsf{v_z}) = (a_yb_z - a_zb_y,\ a_zb_x - a_xb_z,\ a_xb_y - a_yb_x)\]と決めることはできない。なぜなら、$\boldsymbol{\mathsf{v}}$ の各成分に $0$ でない任意の実数 $k$ を掛けた以下のベクトルでも $(1)$、$(2)$ は成り立つからである。
そこでまず以下のような簡単な状況を考える。
2つのベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ はいずれもXY平面上にあり、特に $\boldsymbol{b}$ は y軸上に置かれている。2つのベクトルの始点はいずれも原点であり、両者のなす角をここでは $\theta$ としている (図では $\theta$ は $90^\circ$ より小さいが、$0^\circ < \theta < 180^\circ$ であればどのような値でも構わない)。XY平面上にあるためそれぞれの成分は $\boldsymbol{a} = (A_x,\ A_y,\ 0)$、$\boldsymbol{b} = (B_x,\ B_y,\ 0)$ の形で表されるが、より詳しくは $A_x$、$A_y$、$B_y$ は $0$ よりも大きい値であり、$B_x = 0$ である ($\theta$ が $90^\circ$ より大きい場合は $A_y < 0$ となる)。
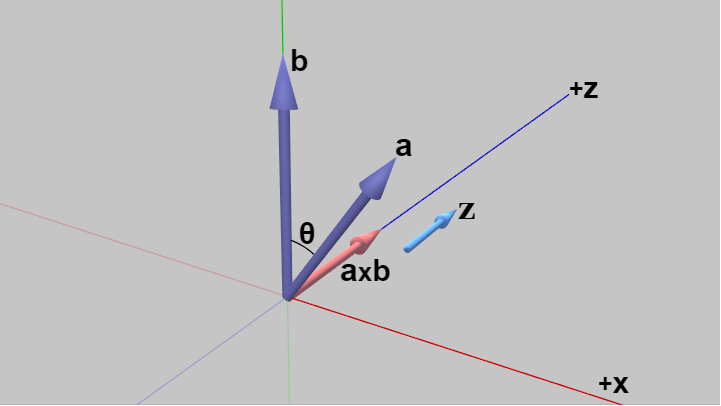
図1
上の定義 ($\mathrm{ii}$) から外積 $\boldsymbol{a} \times \boldsymbol{b}$ は、$\boldsymbol{a}$ に左手の親指を合わせ、$\boldsymbol{b}$ に左手の人差し指を合わせたときの中指の指す方向であるから、この場合にはその方向は z軸プラス方向である。
$\boldsymbol{a} = (A_x,\ A_y,\ 0)$、$\boldsymbol{b} = (0,\ B_y,\ 0)$ を上式 $(3)$ に代入すると\[\boldsymbol{a} \times \boldsymbol{b} = (0,\ 0,\ kA_xB_y) \tag{4} \]となるが、$A_x$、$B_y$ はいずれも $0$ より大きいからこのベクトルが z軸プラス方向を向くためには $k > 0$ でなければならないことがわかる。
また定義 ($\mathrm{iii}$) から、外積 $\boldsymbol{a} \times \boldsymbol{b}$ の大きさは $\boldsymbol{a}$、$\boldsymbol{b}$ によって張られる平行四辺形の大きさであることが要求されるが、以下この点について見ていこう。
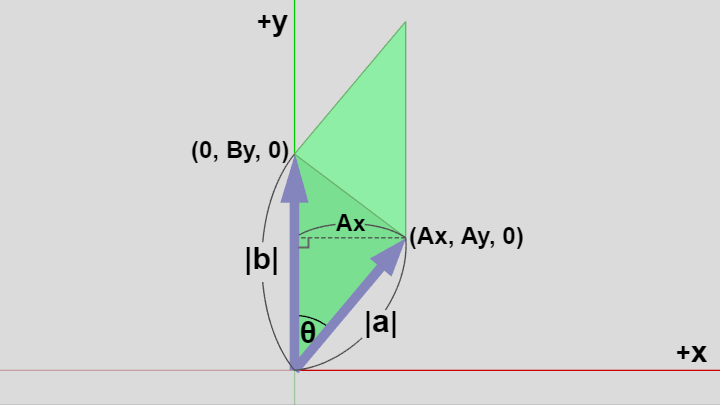
図2
上の状況では2つのベクトル $\boldsymbol{a} = (A_x,\ A_y,\ 0)$、$\boldsymbol{b} = (0,\ B_y,\ 0)$ の始点はいずれも原点であるから、両者の成分はいずれも終点の座標に一致する。例えば $\boldsymbol{b}$ は y軸上のベクトルで始点が原点にあるので、その大きさは $|\boldsymbol{b}| = B_y$ である。
この2つのベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ で張られる三角形は、$\boldsymbol{b}$ を底辺とするとき図中の点線部分が高さに相当する。この点線の長さは $|\boldsymbol{a}|sin\theta$ であるが、ベクトル $\boldsymbol{a}$ の始点も原点に置かれているのでこの $|\boldsymbol{a}|sin\theta$ という値は $\boldsymbol{a}$ の終点の x座標に等しい。すなわち点線部分の長さは $|\boldsymbol{a}|sin\theta = A_x$ である。
したがって $\boldsymbol{a}$、$\boldsymbol{b}$ で張られる三角形の面積は\[ \frac{1}{2}|\boldsymbol{a}||\boldsymbol{b}|sin\theta = \frac{1}{2}A_xB_y \]として計算される。$\boldsymbol{a}$、$\boldsymbol{b}$ によって張られる平行四辺形の面積はこの三角形の面積の2倍であるから、その面積は $A_xB_y$ であることがわかる。
そして今回の状況においては外積 $\boldsymbol{a} \times \boldsymbol{b}$ は $k > 0$ として、\[\boldsymbol{a} \times \boldsymbol{b} = (0,\ 0,\ kA_xB_y) \]の形になることが先程示されたが、このベクトルの向きは z軸プラス方向、大きさは $|\boldsymbol{a} \times \boldsymbol{b}| = |kA_xB_y| = kA_xB_y$ である。この値が今求めた平行四辺形の大きさに等しくなるためには、$k = 1$ でなければならない。したがって $\boldsymbol{a} \times \boldsymbol{b} = (0,\ 0,\ A_xB_y)$ となるが、z軸プラス方向を表す単位ベクトルを $\boldsymbol{z} = (0, 0, 1)$ とすれば簡単な計算により\[\boldsymbol{z}\cdot(\boldsymbol{a} \times \boldsymbol{b}) = A_xB_y\]である。
つまり上図1のような状況においてはベクトルの外積は $(3)$ の係数 $k$ の値を $1$ とした以下の形
では次に $(5)$ の形で表されるベクトルが一般の状況において外積の定義を満たすかどうかを調べよう。
一般の状況とは単に上図1の2つのベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ に対し適当な回転(同じ回転)を実行した場合であるが、回転後のそれぞれのベクトルを $\boldsymbol{a'}$、$\boldsymbol{b'}$ と表記する。またこのとき同じ回転を z軸プラス方向の単位ベクトル $\boldsymbol{z} = (0, 0, 1)$ に対しても実行し、回転後の $\boldsymbol{z}$ を $\boldsymbol{z'}$ と表記する (図3)。
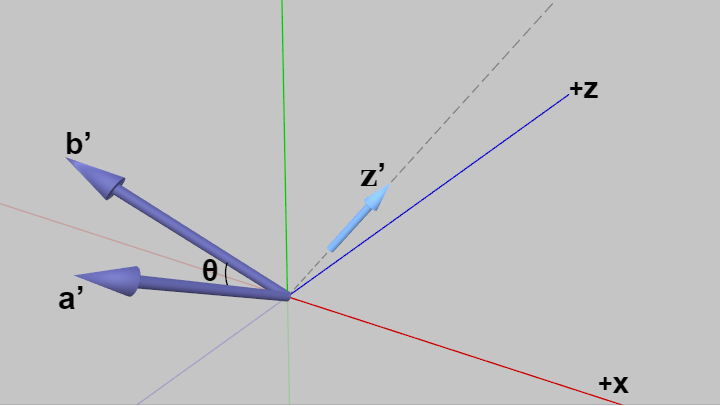
図3
ここで $\boldsymbol{a'} = (a_x', a_y', a_z')$、$\boldsymbol{b'} = (b_x', b_y', b_z')$ とおくと $(5)$ より、
図3の $\boldsymbol{a'}$、$\boldsymbol{b'}$、$\boldsymbol{z'}$ は図1の $\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{z}$ に対し同じ回転を実行したものであるから、それぞれのベクトルの間の相対的な位置関係は変わらない。例えば $\boldsymbol{a'}$ と $\boldsymbol{b'}$ のなす角は $\theta$ であり、$\boldsymbol{z'}$ は $\boldsymbol{a'}$、$\boldsymbol{b'}$ と直交し、さらに $\boldsymbol{a'}$ を左手の親指、$\boldsymbol{b'}$ を人差し指としたときの中指の方向になっている。また回転によってベクトルの大きさは変化しないので $|\boldsymbol{a'}| = |\boldsymbol{a}|$、$|\boldsymbol{b'}| = |\boldsymbol{b}|$、$|\boldsymbol{z'}| = |\boldsymbol{z}|$ である。そのため $\boldsymbol{a'}$、$\boldsymbol{b'}$ によって張られる平行四辺形の面積は、$\boldsymbol{a}$、$\boldsymbol{b}$ によって張られる平行四辺形の面積と同じであり、その値は上で求めた $A_xB_y$ である。
ここで調べるべきは $(6)$ の成分で表されるベクトル $\boldsymbol{a'} \times \boldsymbol{b'}$ が $\boldsymbol{z'}$ と同じ方向を向いているか、またその大きさが $\boldsymbol{a'}$、$\boldsymbol{b'}$ によって張られる平行四辺形の面積 $A_xB_y$ に等しいかの2つである。
そのためには $\boldsymbol{a'} \times \boldsymbol{b'}$ と $\boldsymbol{z'}$ の内積を計算し、その値が $A_xB_y$ であるかを調べればよい。なぜなら、その内積は $\boldsymbol{a'} \times \boldsymbol{b'}$ と $\boldsymbol{z'}$ のなす角を $\varphi$ とすれば (上でも注意したように $(6)$ の成分で表されるベクトルは $\boldsymbol{a'}$、$\boldsymbol{b'}$ と直交することはわかっている。したがって $\varphi$ は $0^\circ$ か $180^\circ$ のいずれかである)\[ \boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) = |\boldsymbol{z'}||\boldsymbol{a'} \times \boldsymbol{b'}|cos\varphi\]となるが、$\boldsymbol{a'} \times \boldsymbol{b'}$ が $\boldsymbol{z'}$ と同じ方向を向いているのであれば $\varphi = 0^\circ$ であり、$|\boldsymbol{z'}| = 1$ であるから、結局\[ \boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) = |\boldsymbol{a'} \times \boldsymbol{b'}|\]となるため、$\boldsymbol{a'} \times \boldsymbol{b'}$ の大きさが $\boldsymbol{a'}$、$\boldsymbol{b'}$ によって張られる平行四辺形の大きさに等しいのであれば、この計算結果は $A_xB_y$ とならなければならない (これはその逆もいえる。すなわち $\boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) = A_xB_y$ であれば、$\boldsymbol{a'} \times \boldsymbol{b'}$ は $\boldsymbol{z'}$ と同じ方向であり、その大きさは平行四辺形の大きさに等しい)。
$\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{z}$ を $\boldsymbol{a'}$、$\boldsymbol{b'}$、$\boldsymbol{z'}$ に移す回転行列を $R$ とする。なおここでは $R$ をオイラー角による回転行列とする (6-8節で述べたように任意の回転はオイラー角回転で表すことができる)。
このとき $\boldsymbol{a'} = R\boldsymbol{a}$、$\boldsymbol{b'} = R\boldsymbol{b}$、$\boldsymbol{z'} = R\boldsymbol{z}$ であるから、$\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{z}$ を列ベクトルとして持つ $3\times3$ 行列を $(\boldsymbol{a},\ \boldsymbol{b},\ \boldsymbol{z})$ として表すことにすれば、\[(\boldsymbol{a'},\ \boldsymbol{b'},\ \boldsymbol{z'}) = R(\boldsymbol{a},\ \boldsymbol{b},\ \boldsymbol{z})\]である。
では以上をふまえて $\boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) = A_xB_y$ を示す。
スカラー三重積により $\boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) = det(\boldsymbol{a'},\ \boldsymbol{b'},\ \boldsymbol{z'})$ であること、及び回転行列の行列式が $1$ であることに注意すれば、\begin{align*}\boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) &= det(\boldsymbol{a'},\ \boldsymbol{b'},\ \boldsymbol{z'}) \\\\&= det\{R(\boldsymbol{a},\ \boldsymbol{b},\ \boldsymbol{z})\} = det R\!.det(\boldsymbol{a},\ \boldsymbol{b},\ \boldsymbol{z}) \\\\&= det (\boldsymbol{a},\ \boldsymbol{b},\ \boldsymbol{z}) = \boldsymbol{z} \cdot (\boldsymbol{a} \times \boldsymbol{b}) = A_xB_y\end{align*}となる。これにより一般の場合においても $(5)$ の形で表されるベクトルは外積の定義を満たすことが示された。 (証明終)
| ($\mathrm{i}$) | $\boldsymbol{a} \times \boldsymbol{b}$ は2つのベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ と直交する。 |
| ($\mathrm{ii}$) | $\boldsymbol{a}$ を左手の親指に、$\boldsymbol{b}$ を左手の人差し指に合わせたとき、$\boldsymbol{a} \times \boldsymbol{b}$ の向きは中指の方向を指す。 |
| ($\mathrm{iii}$) | $\boldsymbol{a} \times \boldsymbol{b}$ の大きさは $\boldsymbol{a}$、$\boldsymbol{b}$ によって張られる平行四辺形の大きさに等しい。 |
(今までと同様本節においても外積は左手系の外積として考える。また上記 ($\mathrm{iii}$) から2つのベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ のなす角が $0^\circ$ あるいは $180^\circ$ のときは外積は定義されないので、$\boldsymbol{a}$、$\boldsymbol{b}$ のなす角を $\theta$ とするとき以下の解説においては $0^\circ < \theta < 180^\circ$ であることを前提とする)
今までの解説やプログラムにおいては外積は何度も使われたが、それは実用的な立場からのものであり外積それ自体に深く立ち入るようなものではなかった。例えば外積の成分はどのようにして導出されるのか、あるいは外積の向きが常に中指の方向を指すとなぜいえるのかなどについては特に数学的な議論をすることはなかった。
以下では上の定義からベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ の外積 $\boldsymbol{a} \times \boldsymbol{b}$ を導出するが、その結果として向き及び大きさがどのような場合においても定義通りのものになることも示されるのである。
2つの3次元ベクトル $\boldsymbol{a} = (a_x, a_y, a_z)$、$\boldsymbol{b} = (b_x, b_y, b_z)$ が与えられたとき、上の定義を満たす外積 $\boldsymbol{a} \times \boldsymbol{b}$ は一意的に\[ \boldsymbol{a} \times \boldsymbol{b}\ =\ (a_yb_z - a_zb_y,\ a_zb_x - a_xb_z,\ a_xb_y - a_yb_x) \]として決定される。
(証明) まず $\boldsymbol{a}$、$\boldsymbol{b}$ に直交するようなベクトル $\boldsymbol{\mathsf{v}} = (\mathsf{v_x}, \mathsf{v_y}, \mathsf{v_z})$ がどのような成分になるのかを求める。$\boldsymbol{\mathsf{v}}$ が $\boldsymbol{a}$、$\boldsymbol{b}$ に直交するのであれば\begin{align*}\boldsymbol{a} \cdot \boldsymbol{\mathsf{v}} = a_x \mathsf{v_x} + a_y \mathsf{v_y} + a_z \mathsf{v_z} = 0 \\\\\boldsymbol{b} \cdot \boldsymbol{\mathsf{v}} = b_x \mathsf{v_x} + b_y \mathsf{v_y} + b_z \mathsf{v_z} = 0 \end{align*}であるが、$\boldsymbol{a} \cdot \boldsymbol{\mathsf{v}}$ に $b_y$ を掛け、$\boldsymbol{b} \cdot \boldsymbol{\mathsf{v}}$ に $a_y$ を掛けてその差を計算すると
\[ (a_xb_y - a_yb_x)\mathsf{v_x} + (a_zb_y - a_yb_z)\mathsf{v_z} = 0 \]したがって、\[ \frac{\mathsf{v_x}}{\mathsf{v_z}} = \frac{a_yb_z - a_zb_y}{a_xb_y - a_yb_x} \tag{1} \]である。
同様に、$\boldsymbol{a} \cdot \boldsymbol{\mathsf{v}}$ に $b_x$ を掛け、$\boldsymbol{b} \cdot \boldsymbol{\mathsf{v}}$ に $a_x$ を掛けてその差を計算すると
\[ (a_yb_x - a_xb_y)\mathsf{v_y} + (a_zb_x - a_xb_z)\mathsf{v_z} = 0 \]となるから、\[ \frac{\mathsf{v_y}}{\mathsf{v_z}} = \frac{a_zb_x - a_xb_z}{a_xb_y - a_yb_x} \tag{2} \]である。
ここで上の式 $(1)$、$(2)$ からベクトル $\boldsymbol{\mathsf{v}}$ を一意的に\[ \boldsymbol{\mathsf{v}} = (\mathsf{v_x}, \mathsf{v_y}, \mathsf{v_z}) = (a_yb_z - a_zb_y,\ a_zb_x - a_xb_z,\ a_xb_y - a_yb_x)\]と決めることはできない。なぜなら、$\boldsymbol{\mathsf{v}}$ の各成分に $0$ でない任意の実数 $k$ を掛けた以下のベクトルでも $(1)$、$(2)$ は成り立つからである。
\begin{align*}\boldsymbol{\mathsf{v}} &= (\mathsf{v_x}, \mathsf{v_y}, \mathsf{v_z}) \\\\&= (\ k(a_yb_z - a_zb_y),\ k(a_zb_x - a_xb_z),\ k(a_xb_y - a_yb_x)\ ) \tag{3}\end{align*}
つまり、$\boldsymbol{a}$ と $\boldsymbol{b}$ に直交するという定義 ($\mathrm{i}$) からだけでは外積を一意的に決めることはできないので他の定義から $k$ が具体的にどのような値になるかを調べる必要があるわけである。ただし $(3)$ の成分で表されるベクトルは $k (\neq 0)$ の値が不定なだけで $\boldsymbol{a}$、$\boldsymbol{b}$ とは直交するという点には注意しよう。そこでまず以下のような簡単な状況を考える。
2つのベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ はいずれもXY平面上にあり、特に $\boldsymbol{b}$ は y軸上に置かれている。2つのベクトルの始点はいずれも原点であり、両者のなす角をここでは $\theta$ としている (図では $\theta$ は $90^\circ$ より小さいが、$0^\circ < \theta < 180^\circ$ であればどのような値でも構わない)。XY平面上にあるためそれぞれの成分は $\boldsymbol{a} = (A_x,\ A_y,\ 0)$、$\boldsymbol{b} = (B_x,\ B_y,\ 0)$ の形で表されるが、より詳しくは $A_x$、$A_y$、$B_y$ は $0$ よりも大きい値であり、$B_x = 0$ である ($\theta$ が $90^\circ$ より大きい場合は $A_y < 0$ となる)。

上の定義 ($\mathrm{ii}$) から外積 $\boldsymbol{a} \times \boldsymbol{b}$ は、$\boldsymbol{a}$ に左手の親指を合わせ、$\boldsymbol{b}$ に左手の人差し指を合わせたときの中指の指す方向であるから、この場合にはその方向は z軸プラス方向である。
$\boldsymbol{a} = (A_x,\ A_y,\ 0)$、$\boldsymbol{b} = (0,\ B_y,\ 0)$ を上式 $(3)$ に代入すると\[\boldsymbol{a} \times \boldsymbol{b} = (0,\ 0,\ kA_xB_y) \tag{4} \]となるが、$A_x$、$B_y$ はいずれも $0$ より大きいからこのベクトルが z軸プラス方向を向くためには $k > 0$ でなければならないことがわかる。
また定義 ($\mathrm{iii}$) から、外積 $\boldsymbol{a} \times \boldsymbol{b}$ の大きさは $\boldsymbol{a}$、$\boldsymbol{b}$ によって張られる平行四辺形の大きさであることが要求されるが、以下この点について見ていこう。

上の状況では2つのベクトル $\boldsymbol{a} = (A_x,\ A_y,\ 0)$、$\boldsymbol{b} = (0,\ B_y,\ 0)$ の始点はいずれも原点であるから、両者の成分はいずれも終点の座標に一致する。例えば $\boldsymbol{b}$ は y軸上のベクトルで始点が原点にあるので、その大きさは $|\boldsymbol{b}| = B_y$ である。
この2つのベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ で張られる三角形は、$\boldsymbol{b}$ を底辺とするとき図中の点線部分が高さに相当する。この点線の長さは $|\boldsymbol{a}|sin\theta$ であるが、ベクトル $\boldsymbol{a}$ の始点も原点に置かれているのでこの $|\boldsymbol{a}|sin\theta$ という値は $\boldsymbol{a}$ の終点の x座標に等しい。すなわち点線部分の長さは $|\boldsymbol{a}|sin\theta = A_x$ である。
したがって $\boldsymbol{a}$、$\boldsymbol{b}$ で張られる三角形の面積は\[ \frac{1}{2}|\boldsymbol{a}||\boldsymbol{b}|sin\theta = \frac{1}{2}A_xB_y \]として計算される。$\boldsymbol{a}$、$\boldsymbol{b}$ によって張られる平行四辺形の面積はこの三角形の面積の2倍であるから、その面積は $A_xB_y$ であることがわかる。
そして今回の状況においては外積 $\boldsymbol{a} \times \boldsymbol{b}$ は $k > 0$ として、\[\boldsymbol{a} \times \boldsymbol{b} = (0,\ 0,\ kA_xB_y) \]の形になることが先程示されたが、このベクトルの向きは z軸プラス方向、大きさは $|\boldsymbol{a} \times \boldsymbol{b}| = |kA_xB_y| = kA_xB_y$ である。この値が今求めた平行四辺形の大きさに等しくなるためには、$k = 1$ でなければならない。したがって $\boldsymbol{a} \times \boldsymbol{b} = (0,\ 0,\ A_xB_y)$ となるが、z軸プラス方向を表す単位ベクトルを $\boldsymbol{z} = (0, 0, 1)$ とすれば簡単な計算により\[\boldsymbol{z}\cdot(\boldsymbol{a} \times \boldsymbol{b}) = A_xB_y\]である。
つまり上図1のような状況においてはベクトルの外積は $(3)$ の係数 $k$ の値を $1$ とした以下の形
\[ \boldsymbol{a} \times \boldsymbol{b}\ =\ (a_yb_z - a_zb_y,\ a_zb_x - a_xb_z,\ a_xb_y - a_yb_x) \tag{5} \]
になることがわかった。では次に $(5)$ の形で表されるベクトルが一般の状況において外積の定義を満たすかどうかを調べよう。
一般の状況とは単に上図1の2つのベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ に対し適当な回転(同じ回転)を実行した場合であるが、回転後のそれぞれのベクトルを $\boldsymbol{a'}$、$\boldsymbol{b'}$ と表記する。またこのとき同じ回転を z軸プラス方向の単位ベクトル $\boldsymbol{z} = (0, 0, 1)$ に対しても実行し、回転後の $\boldsymbol{z}$ を $\boldsymbol{z'}$ と表記する (図3)。

ここで $\boldsymbol{a'} = (a_x', a_y', a_z')$、$\boldsymbol{b'} = (b_x', b_y', b_z')$ とおくと $(5)$ より、
\[ \boldsymbol{a'} \times \boldsymbol{b'}\ =\ (a_y'b_z' - a_z'b_y',\ a_z'b_x' - a_x'b_z',\ a_x'b_y' - a_y'b_x') \tag{6} \]
である。図3の $\boldsymbol{a'}$、$\boldsymbol{b'}$、$\boldsymbol{z'}$ は図1の $\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{z}$ に対し同じ回転を実行したものであるから、それぞれのベクトルの間の相対的な位置関係は変わらない。例えば $\boldsymbol{a'}$ と $\boldsymbol{b'}$ のなす角は $\theta$ であり、$\boldsymbol{z'}$ は $\boldsymbol{a'}$、$\boldsymbol{b'}$ と直交し、さらに $\boldsymbol{a'}$ を左手の親指、$\boldsymbol{b'}$ を人差し指としたときの中指の方向になっている。また回転によってベクトルの大きさは変化しないので $|\boldsymbol{a'}| = |\boldsymbol{a}|$、$|\boldsymbol{b'}| = |\boldsymbol{b}|$、$|\boldsymbol{z'}| = |\boldsymbol{z}|$ である。そのため $\boldsymbol{a'}$、$\boldsymbol{b'}$ によって張られる平行四辺形の面積は、$\boldsymbol{a}$、$\boldsymbol{b}$ によって張られる平行四辺形の面積と同じであり、その値は上で求めた $A_xB_y$ である。
ここで調べるべきは $(6)$ の成分で表されるベクトル $\boldsymbol{a'} \times \boldsymbol{b'}$ が $\boldsymbol{z'}$ と同じ方向を向いているか、またその大きさが $\boldsymbol{a'}$、$\boldsymbol{b'}$ によって張られる平行四辺形の面積 $A_xB_y$ に等しいかの2つである。
そのためには $\boldsymbol{a'} \times \boldsymbol{b'}$ と $\boldsymbol{z'}$ の内積を計算し、その値が $A_xB_y$ であるかを調べればよい。なぜなら、その内積は $\boldsymbol{a'} \times \boldsymbol{b'}$ と $\boldsymbol{z'}$ のなす角を $\varphi$ とすれば (上でも注意したように $(6)$ の成分で表されるベクトルは $\boldsymbol{a'}$、$\boldsymbol{b'}$ と直交することはわかっている。したがって $\varphi$ は $0^\circ$ か $180^\circ$ のいずれかである)\[ \boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) = |\boldsymbol{z'}||\boldsymbol{a'} \times \boldsymbol{b'}|cos\varphi\]となるが、$\boldsymbol{a'} \times \boldsymbol{b'}$ が $\boldsymbol{z'}$ と同じ方向を向いているのであれば $\varphi = 0^\circ$ であり、$|\boldsymbol{z'}| = 1$ であるから、結局\[ \boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) = |\boldsymbol{a'} \times \boldsymbol{b'}|\]となるため、$\boldsymbol{a'} \times \boldsymbol{b'}$ の大きさが $\boldsymbol{a'}$、$\boldsymbol{b'}$ によって張られる平行四辺形の大きさに等しいのであれば、この計算結果は $A_xB_y$ とならなければならない (これはその逆もいえる。すなわち $\boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) = A_xB_y$ であれば、$\boldsymbol{a'} \times \boldsymbol{b'}$ は $\boldsymbol{z'}$ と同じ方向であり、その大きさは平行四辺形の大きさに等しい)。
$\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{z}$ を $\boldsymbol{a'}$、$\boldsymbol{b'}$、$\boldsymbol{z'}$ に移す回転行列を $R$ とする。なおここでは $R$ をオイラー角による回転行列とする (6-8節で述べたように任意の回転はオイラー角回転で表すことができる)。
このとき $\boldsymbol{a'} = R\boldsymbol{a}$、$\boldsymbol{b'} = R\boldsymbol{b}$、$\boldsymbol{z'} = R\boldsymbol{z}$ であるから、$\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{z}$ を列ベクトルとして持つ $3\times3$ 行列を $(\boldsymbol{a},\ \boldsymbol{b},\ \boldsymbol{z})$ として表すことにすれば、\[(\boldsymbol{a'},\ \boldsymbol{b'},\ \boldsymbol{z'}) = R(\boldsymbol{a},\ \boldsymbol{b},\ \boldsymbol{z})\]である。
では以上をふまえて $\boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) = A_xB_y$ を示す。
スカラー三重積により $\boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) = det(\boldsymbol{a'},\ \boldsymbol{b'},\ \boldsymbol{z'})$ であること、及び回転行列の行列式が $1$ であることに注意すれば、\begin{align*}\boldsymbol{z'} \cdot (\boldsymbol{a'} \times \boldsymbol{b'}) &= det(\boldsymbol{a'},\ \boldsymbol{b'},\ \boldsymbol{z'}) \\\\&= det\{R(\boldsymbol{a},\ \boldsymbol{b},\ \boldsymbol{z})\} = det R\!.det(\boldsymbol{a},\ \boldsymbol{b},\ \boldsymbol{z}) \\\\&= det (\boldsymbol{a},\ \boldsymbol{b},\ \boldsymbol{z}) = \boldsymbol{z} \cdot (\boldsymbol{a} \times \boldsymbol{b}) = A_xB_y\end{align*}となる。これにより一般の場合においても $(5)$ の形で表されるベクトルは外積の定義を満たすことが示された。 (証明終)
© 2020-2025 Redpoll's 60 (All rights reserved)