Redpoll's 60
Home / 3Dプログラミング入門 / 第14章 $§$14-7
第14章 数学的事柄についての補足
| $§$14-1 外積の導出 | $§$14-8 球面線形補間 |
| $§$14-2 TRS分解における回転行列 | $§$14-9 ベクトルを重ね合わせる回転 |
| $§$14-3 Möller-Trumbore algorithm (レイ vs 三角形) | $§$14-10 Quaternion、回転行列、オイラー角の相互変換 |
| $§$14-4 三角形とBarycentric Coordinates | $§$14-11 二線分間の最短距離 |
| $§$14-5 法線ベクトルの変換 | $§$14-12 「直方体 vs 直方体」における分離軸 |
| $§$14-6 Quaternion 基礎 | $§$14-13 2D空間における特異値分解 |
| $§$14-7 Quaternionによる回転の表現 | $§$14-14 Perspecive Projection Matrix |
$§$14-7 Quaternionによる回転の表現
前節でも見たように大きさ $1$ の単位 $Quaternion$ $q$ は適当な $\sin\theta$、$\cos\theta$、及び単位ベクトル $\boldsymbol{u}$ を用いて\[ q = (\sin\theta\,\boldsymbol{u},\ \cos\theta) \]のように表される。
ベクトル部だけの任意の $Quaternion$ を $\boldsymbol{\mathsf{v}}_q = (\boldsymbol{\mathsf{v}},\ 0)$ とするとき、よく知られるようにベクトル $\boldsymbol{\mathsf{v}}$ を回転軸 $\boldsymbol{u}$ の周りに角度 $\theta$ 回転させるには、角度 $\displaystyle \frac{\theta}{2}$ の単位 $Quaternion$ $\displaystyle q = \Big(\sin\frac{\theta}{2}\,\boldsymbol{u},\ \cos\frac{\theta}{2}\Big)$ とその共役 $\displaystyle q^* = \Big(-\sin\frac{\theta}{2}\,\boldsymbol{u},\ \cos\frac{\theta}{2}\Big)$ を用いて\[q\,\boldsymbol{\mathsf{v}}_q\,q^*\]の形の計算を行う。つまり $Quaternion$ をこのように使うことで、$Quaternion$ は3次元空間における任意軸周りの回転を表すことができるのである。
ではなぜ $Quaternion$ による回転は2つの $Quaternion$ を使って挟み込む形の積にしなければならないのか、またなぜ角度 $\theta$ の回転に角度 $\displaystyle \frac{\theta}{2}$ の $Quaternion$ を使うのか。
この点について謎のように感じる者は多いであろうが、その原理自体は難しいものではない。面倒な計算は現れないし、特別な想像力を働かせる必要もない。
以下本節ではこの謎の解決を通して $Quaternion$ が3次元空間における回転を表すことについて解説する。
まずは前節の内容を簡単に復習する。
($\mathrm{i}$) 2つの $Quaternion$ を $q_1 = (\boldsymbol{\mathsf{v_1}},\ w_1)$、$q_2 = (\boldsymbol{\mathsf{v_2}},\ w_2)$ とするとき $Quaternion$ の積 $q_1q_2$ は\begin{align*}q_1q_2 &= (\boldsymbol{\mathsf{v_1}},\ w_1)(\boldsymbol{\mathsf{v_2}},\ w_2) \\&= (\boldsymbol{\mathsf{v_1}}\times \boldsymbol{\mathsf{v_2}} + w_1\boldsymbol{\mathsf{v_2}} + w_2\boldsymbol{\mathsf{v_1}},\ w_1w_2 - \boldsymbol{\mathsf{v_1}} \cdot \boldsymbol{\mathsf{v_2}}) \end{align*}として定義される。
($\mathrm{ii}$) スカラーと $Quaternion$ の積は可換である。すなわち $s$ をスカラー、$q = (\boldsymbol{\mathsf{v}},\ w)$ を $Quaternion$ とすれば\[sq = qs = (s\boldsymbol{\mathsf{v}},\ sw)\]である。
($\mathrm{iii}$) $q = (\boldsymbol{\mathsf{v}},\ w)$ を任意の $Quaternion$ とするとき、$q$ の大きさを $|q| = k$ とすれば適当な角度 $\theta$ 及び単位ベクトル $\boldsymbol{n}$ を用いて\[ q = (\boldsymbol{\mathsf{v}},\ w) = k(\sin\theta\,\boldsymbol{n},\ \cos\theta)\]と表すことができる。ここで $(\sin\theta\,\boldsymbol{n},\ \cos\theta)$ は単位 $Quaternion$ である。
($\mathrm{iv}$) $Quaternion$ はその積に関して結合法則及び分配法則が成り立つ。$q_1$、$q_2$、$q_3$ を任意の $Quaternion$ とすれば、\begin{align*}q_1(q_2q_3) &= (q_1q_2)q_3 \\\\q_1(q_2 + q_3) &= q_1q_2 + q_1q_3 \\\\(q_2 + q_3)q_1 &= q_2q_1 + q_3q_1 \end{align*}である。
単位 $Quaternion$ $q$ は適当な角度 $\theta$ と単位ベクトル $\boldsymbol{u}$ を用いて $q = (\sin\theta\,\boldsymbol{u},\ \cos\theta)$ の形で表されるが、以下の解説では簡単のためこのベクトル部で使われている単位ベクトル $\boldsymbol{u}$ を「回転軸」と呼ぶことにする (まだ $Quaternion$ が回転を表すことを示していないので細かいことを言えばこの呼び方はフライングである)。
同様に以下の解説においては回転軸 $\boldsymbol{u}$、角度 $\theta$ の単位 $Quaternion$ $q = (\sin\theta\,\boldsymbol{u},\ \cos\theta)$ を簡単に\[q(\theta)\]の形で表すものとする。
($\mathrm{v}$) 一般に $Quaternion$ の積は可換ではないが、回転軸が同じで角度だけが異なる2つの単位 $Quaternion$ $q_1$、$q_2$ の積は可換である。具体的には $q_1 = (\sin\theta_1\,\boldsymbol{u},\ \cos\theta_1)$、$q_2 = (\sin\theta_2\,\boldsymbol{u},\ \cos\theta_2)$ とするとき、積 $q_1q_2$ は回転軸 $\boldsymbol{u}$、角度 $\theta_1 + \theta_2$ の単位 $Quaternion$ になる。
すなわち、\begin{align*}q_2q_1 &= q_1q_2 \\ &= (\sin\theta_1\,\boldsymbol{u},\ \cos\theta_1)(\sin\theta_2\,\boldsymbol{u},\ \cos\theta_2) \\&= (\sin(\theta_1 + \theta_2)\,\boldsymbol{u},\ \cos(\theta_1 + \theta_2)) \\\end{align*}である。
上で定めた表記によって $q_1 = q(\theta_1)$、$q_2 = q(\theta_2)$ と書けるから上の式は\[q(\theta_2)q(\theta_1) = q(\theta_1)q(\theta_2) = q(\theta_1 + \theta_2) \tag{1}\]のように簡潔な形にすることができる。
角度 $\theta$ の単位 $Quaternion$ $q = (\sin\theta\,\boldsymbol{u},\ \cos\theta)$ の共役は $q^* = (-\sin\theta\,\boldsymbol{u},\ \cos\theta)$ であるが、$-\sin\theta = \sin(-\theta)$、$\cos\theta = \cos(-\theta)$ であるから\[q^* = (-\sin\theta\,\boldsymbol{u},\ \cos\theta) = (\sin(-\theta)\,\boldsymbol{u},\ \cos(-\theta))\]である。先程の表記を用いれば上の式は $q^*(\theta) = q(-\theta)$ であることを意味している。
($\mathrm{vi}$) 上記の $q_1 = (\sin\theta_1\,\boldsymbol{u},\ \cos\theta_1)$、$q_2 = (\sin\theta_2\,\boldsymbol{u},\ \cos\theta_2)$ に関して、一方を共役にしても両者の回転軸は同じであるからその積は可換である。すなわち $q{_2}^*q_1 = q_1q{_2}^*$ であるが、$q{_2}^* = q^*(\theta_2) = q(-\theta_2)$ であることに注意すればこの積は\[q^*(\theta_2)q(\theta_1) = q(\theta_1)q^*(\theta_2) = q(\theta_1 - \theta_2) \tag{2}\]として表すことができる。
($\mathrm{vii}$) 単位ベクトル $\boldsymbol{u}$ だけを含む $(\boldsymbol{u},\ 0)$ のようなスカラー部 $0$ の $Quaternion$ は、$\displaystyle\sin\frac{\pi}{2} = 1$、$\displaystyle\cos\frac{\pi}{2} = 0$ であることから $\sin$、$\cos$ を用いて $\displaystyle (\boldsymbol{u},\ 0) = \Big(\sin\frac{\pi}{2}\boldsymbol{u},\ \cos\frac{\pi}{2}\Big)$ として表される。上で定めた表記を使えば $\displaystyle (\boldsymbol{u},\ 0) = q\Big(\frac{\pi}{2}\Big)$ である。
$\boldsymbol{u}$ に適当なスカラー $a$ を掛けたベクトル $a\boldsymbol{u}$ の場合でも事情は同じであり、$\displaystyle (a\boldsymbol{u},\ 0) = a(\boldsymbol{u},\ 0)$ であるから、\[(a\boldsymbol{u},\ 0) = a(\boldsymbol{u},\ 0) = aq\Big(\frac{\pi}{2}\Big) \tag{3}\]である。
特に上の式 (1)、(2) から $q(\theta)$ あるいは $q^*(\theta)$ と $\displaystyle aq\Big(\frac{\pi}{2}\Big)$ の積は次のように計算される。\begin{align*}q(\theta)\Big\lbrace aq\Big(\frac{\pi}{2}\Big)\Big\rbrace = aq\Big(\frac{\pi}{2}\Big)q(\theta) = aq\Big(\frac{\pi}{2} + \theta\Big) \\\\q^*(\theta)\Big\lbrace aq\Big(\frac{\pi}{2}\Big)\Big\rbrace = aq\Big(\frac{\pi}{2}\Big)q^*(\theta) = aq\Big(\frac{\pi}{2} - \theta\Big) \\\\\end{align*}
回転軸 $\boldsymbol{u}$、角度 $\theta$ の単位 $Quaternion$ $q(\theta) = (\sin\,\boldsymbol{u},\ \cos\theta)$ に対して回転対象のベクトルを $\boldsymbol{\mathsf{v}}$ とするとき、冒頭でも述べたように $\boldsymbol{\mathsf{v}}$ を軸 $\boldsymbol{u}$ の周りに $\theta$ 回転させる場合、角度 $\displaystyle \frac{\theta}{2}$ の単位 $Quaternion$ $\displaystyle q\Big(\frac{\theta}{2}\Big)$ とその共役 $\displaystyle q^*\Big(\frac{\theta}{2}\Big)$ を用いて\[ \displaystyle q\Big(\frac{\theta}{2}\Big)\,\boldsymbol{\mathsf{v}}_q\,q^*\Big(\frac{\theta}{2}\Big)\]という計算を行う ($\boldsymbol{\mathsf{v}}_q = (\boldsymbol{\mathsf{v}},\ 0)$)。
しかし回転対象のベクトルに対してある条件を付けると、回転行列によってベクトルを回転させる場合と同じくその計算を $R\,\boldsymbol{\mathsf{v}}$ の形にすることができるのである。さらにその場合には角度を $\displaystyle \frac{\theta}{2}$ にする必要もない。$Quaternion$ に関してこの性質はほとんど言及されることはないが、$Quaternion$ が3次元空間における回転を表すことを示す際には非常に重要な役割を務めるのである。
具体的には次の命題が成り立つ。
証明は容易である。積の定義に従って計算をすればよい。
\begin{align*}q(\theta)\,\boldsymbol{\mathsf{v}}_q &= (\sin\theta\,\boldsymbol{u},\ \cos\theta)(\boldsymbol{\mathsf{v}},\ 0) \\\\&= (\sin\theta\,\boldsymbol{u} \times \boldsymbol{\mathsf{v}} + \cos\theta\,\boldsymbol{\mathsf{v}},\ - \sin\theta\,\boldsymbol{u}\cdot\boldsymbol{\mathsf{v}}) \\\\&= (\sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}}) + \cos\theta\,\boldsymbol{\mathsf{v}},\ 0)\end{align*}
$\boldsymbol{u}$ は単位ベクトルであり、$\boldsymbol{u}$ と $\boldsymbol{\mathsf{v}}$ は直交しているからそのなす角は $\displaystyle\frac{\pi}{2}$、したがって\[ |\boldsymbol{u} \times \boldsymbol{\mathsf{v}}| = |\boldsymbol{u}||\boldsymbol{\mathsf{v}}|\sin\Big(\frac{\pi}{2}\Big) = |\boldsymbol{\mathsf{v}}|\]である。すなわちこの場合には $\boldsymbol{u} \times \boldsymbol{\mathsf{v}}$ の大きさと $\boldsymbol{\mathsf{v}}$ の大きさは等しいわけであるが、以下この大きさを $r$ で表す。
$q(\theta)\,\boldsymbol{\mathsf{v}}_q = ( \cos\theta\,\boldsymbol{\mathsf{v}} + \sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}}),\ 0)$ が何を表しているかは以下の図を見れば明らかであろう。ただし図においては $\boldsymbol{\mathsf{v}_1} = \cos\theta\,\boldsymbol{\mathsf{v}} + \sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}})$ としている。
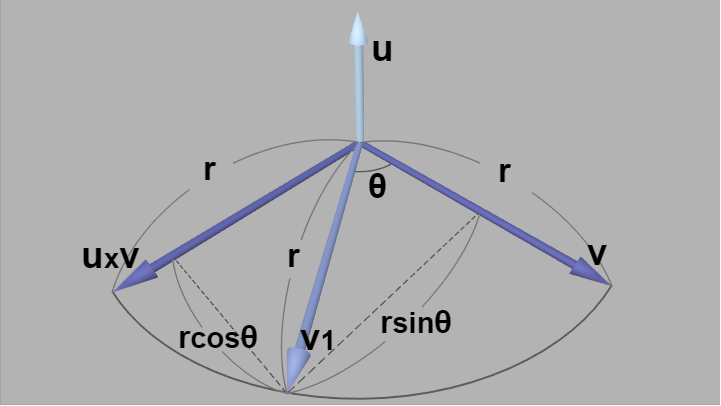
図1 $\large\boldsymbol{u}$、$\large\boldsymbol{\mathsf{v}}$、$\large\boldsymbol{u} \times \boldsymbol{\mathsf{v}}$ は互いに直交している。また、$\large\boldsymbol{\mathsf{v}_1} = \cos\theta\,\boldsymbol{\mathsf{v}} + \sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}})$ である。
3つのベクトル $\boldsymbol{u}$、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{u} \times \boldsymbol{\mathsf{v}}$ は互いに直交しており、$|\boldsymbol{u} \times \boldsymbol{\mathsf{v}}| = |\boldsymbol{\mathsf{v}}| = r$ であるが、図から明らかなように $\boldsymbol{\mathsf{v}_1}$ の大きさも\[ |\boldsymbol{\mathsf{v}_1}| = \sqrt{(r\cos\theta)^2 + (r\sin\theta)^2} = r \]である。$\boldsymbol{\mathsf{v}}$ を x軸、$\boldsymbol{u} \times \boldsymbol{\mathsf{v}}$ を y軸と見れば $\boldsymbol{\mathsf{v}_1}$ の指す位置は $r(\cos\theta,\ \sin\theta)$ に相当する。つまり、$\boldsymbol{\mathsf{v}_1} = \cos\theta\,\boldsymbol{\mathsf{v}} + \sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}})$ は(軸 $\boldsymbol{u}$ と直交するベクトル) $\boldsymbol{\mathsf{v}}$ を軸 $\boldsymbol{u}$ の周りに角度 $\theta$ 回転させたときの位置であることがわかる。すなわち回転軸 $\boldsymbol{u}$ と直交するベクトル $\boldsymbol{\mathsf{v}}$ に対しては、$q(\theta)\,\boldsymbol{\mathsf{v}}_q = ( \cos\theta\,\boldsymbol{\mathsf{v}} + \sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}}),\ 0)$ は軸 $\boldsymbol{u}$ 周りの角度 $\theta$ の回転を表すのである。
$\boldsymbol{\mathsf{v}}_q\,q^*(\theta)$ も同様の回転であることは、以下に示されるように計算結果が同じになることから明らかである。
\begin{align*}\boldsymbol{\mathsf{v}}_q\,q^*(\theta) &= (\boldsymbol{\mathsf{v}},\ 0)(-\sin\theta\,\boldsymbol{u},\ \cos\theta) \\\\&= (\boldsymbol{\mathsf{v}} \times (-\sin\theta\,\boldsymbol{u}) + \cos\theta\,\boldsymbol{\mathsf{v}},\ - \boldsymbol{\mathsf{v}}\cdot(-\sin\theta\,\boldsymbol{u})) \\\\&= (-\sin\theta(\boldsymbol{\mathsf{v}} \times \boldsymbol{u}) + \cos\theta\,\boldsymbol{\mathsf{v}},\ 0) \\\\&= (\sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}}) + \cos\theta\,\boldsymbol{\mathsf{v}},\ 0)\end{align*}
ここで、今までに述べてきたことをまとめよう。
回転軸 $\boldsymbol{u}$、角度 $\theta$ の単位 $Quaternion$ を $q(\theta) = (\sin\theta\,\boldsymbol{u},\ \cos\theta)$ とする。
回転軸 $\boldsymbol{u}$ と直交する任意のベクトルを $\boldsymbol{\mathsf{v}}$ とし、$\boldsymbol{\mathsf{v}}$ を軸 $\boldsymbol{u}$ の周りに角度 $\theta$ 回転させた位置を $\boldsymbol{\mathsf{v}_1}$ とするとき、\begin{align*}q(\theta)\,\boldsymbol{\mathsf{v}}_q = \boldsymbol{\mathsf{v}_1}{_q} \tag{4} \\\\\boldsymbol{\mathsf{v}}_q\,q^*(\theta) = \boldsymbol{\mathsf{v}_1}{_q} \tag{5}\end{align*}である (ただし $\boldsymbol{\mathsf{v}}_q = (\boldsymbol{\mathsf{v}},\ 0)$、$\boldsymbol{\mathsf{v}_1}{_q} = (\boldsymbol{\mathsf{v}}_1,\ 0)$)。$\boldsymbol{\mathsf{v}}_1$ も軸 $\boldsymbol{u}$ と直交しているから $\boldsymbol{\mathsf{v}}_1$ をさらに $\theta$ 回転させた位置を $\boldsymbol{\mathsf{v}}_2$ とすれば、$q(\theta)\,\boldsymbol{\mathsf{v}_1}{_q} = \boldsymbol{\mathsf{v}_1}{_q}\,q^*(\theta) = \boldsymbol{\mathsf{v}_2}{_q}$ となる。
回転軸 $\boldsymbol{u}$ に平行な任意のベクトルは適当なスカラー $a$ を用いて $a\boldsymbol{u}$ と表される。この $a\boldsymbol{u}$ をベクトル部に持つ $Quaternion$ $(a\boldsymbol{u},\ 0)$ は $\sin$、$\cos$ を用いて表すと上記 (3) より $\displaystyle (a\boldsymbol{u},\ 0) = a\Big(\sin\frac{\pi}{2}\boldsymbol{u},\ \cos\frac{\pi}{2}\Big) = aq\Big(\frac{\pi}{2}\Big)$ であるが、この $\displaystyle aq\Big(\frac{\pi}{2}\Big)$ に $q(\theta)$ あるいは $q^*(\theta)$ を掛けると\begin{align*}q(\theta)\Big\lbrace aq\Big(\frac{\pi}{2}\Big)\Big\rbrace = aq\Big(\frac{\pi}{2}\Big)q(\theta) = aq\Big(\frac{\pi}{2} + \theta\Big) \tag{6} \\\\q^*(\theta)\Big\lbrace aq\Big(\frac{\pi}{2}\Big)\Big\rbrace = aq\Big(\frac{\pi}{2}\Big)q^*(\theta) = aq\Big(\frac{\pi}{2} - \theta\Big) \tag{7}\end{align*}である。
以上の準備をもとにして $Quaternion$ が3次元空間における回転になることを示すが、あとは単なる足し算と引き算の問題に過ぎない。
回転軸を $\boldsymbol{u}$ とし、回転対象のベクトルを $\boldsymbol{r}$ とする。$\boldsymbol{r}$ を $\boldsymbol{u}$ に直交する方向と平行な方向に分解するとき、$\boldsymbol{u}$ に直交する方向を $\boldsymbol{\mathsf{v}}$、平行な方向を $\boldsymbol{\mathsf{w}}$ とすれば $\boldsymbol{r} = \boldsymbol{\mathsf{v}} + \boldsymbol{\mathsf{w}}$ であるが、$|\boldsymbol{\mathsf{w}}| = a$ とすれば $\boldsymbol{\mathsf{w}} = a\boldsymbol{u}$ であるから、$\boldsymbol{r}$ は\[ \boldsymbol{r} = \boldsymbol{\mathsf{v}} + a\boldsymbol{u} \]の形に分解される (下図)。簡単のため以下では $\boldsymbol{\mathsf{v}}$ を「$\boldsymbol{r}$ の直交成分」、$a\boldsymbol{u}$ を「$\boldsymbol{r}$ の平行成分」と呼ぶことにする。
ここで $\boldsymbol{r}$ を軸 $\boldsymbol{u}$ の周りに角度 $\theta$ 回転させた位置を $\boldsymbol{r}_1$ とし、$\boldsymbol{\mathsf{v}}$ を軸 $\boldsymbol{u}$ の周りに角度 $\theta$ 回転させた位置を $\boldsymbol{\mathsf{v}}_1$ とする。このとき下図に示されるように\[ \boldsymbol{r}_1 = \boldsymbol{\mathsf{v}}_1 + a\boldsymbol{u} \]である。
また、$\boldsymbol{\mathsf{v}}_1$ をさらに軸 $\boldsymbol{u}$ の周りに $\theta$ 回転させた位置を図では $\boldsymbol{\mathsf{v}}_2$ としている。

図2 $\large\boldsymbol{\mathsf{v}}$ は回転軸 $\large\boldsymbol{u}$ と直交するベクトル。軸 $\large\boldsymbol{u}$ の周りに $\large\boldsymbol{r}$ を角度 $\large\theta$ 回転させた位置が $\large\boldsymbol{r}_1$ であり、軸 $\large\boldsymbol{u}$ の周りに $\large\boldsymbol{\mathsf{v}}$ を角度 $\large\theta$ 回転させた位置が $\large\boldsymbol{\mathsf{v}}_1$、$\large\boldsymbol{\mathsf{v}}_1$ をさらに $\large\theta$ 回転させた位置が $\large\boldsymbol{\mathsf{v}}_2$ 。
回転行列を使って $\boldsymbol{r}$ の回転後の位置を求める場合、軸 $\boldsymbol{u}$ 周りの角度 $\theta$ の回転行列を $R$ とすればその計算は以下のような形で行われる。\begin{align*}R\boldsymbol{r} &= R(\boldsymbol{\mathsf{v}} + a\boldsymbol{u}) = R\boldsymbol{\mathsf{v}} + aR\boldsymbol{u} \\\\&= \boldsymbol{\mathsf{v}}_1 + a\boldsymbol{u} = \boldsymbol{r}_1\end{align*}(軸 $\boldsymbol{u}$ 周りの回転によって $\boldsymbol{u}$ は変化しないので $R\boldsymbol{u} = \boldsymbol{u}$ である)
これと同じことを単位 $Quaternion$ $q(\theta)$、$q^*(\theta)$ を使ってできないかを調べてみよう (以下ではこれまでと同様にベクトル部だけの $Quaternion$ を $\boldsymbol{\mathsf{v}}_q = (\boldsymbol{\mathsf{v}},\ 0)$、$\boldsymbol{\mathsf{v}_1}{_q} = (\boldsymbol{\mathsf{v}_1},\ 0)$ のように表す。ただし $(\boldsymbol{u},\ 0)$ の場合は $\displaystyle (\boldsymbol{u},\ 0) = q\Big(\frac{\pi}{2}\Big)$ として表す)。
$\boldsymbol{r} = \boldsymbol{\mathsf{v}} + a\boldsymbol{u}$ であるからこれを $Quaternion$ として表せば、\begin{align*}\boldsymbol{r}_q &= (\boldsymbol{r},\ 0) = (\boldsymbol{\mathsf{v}} + a\boldsymbol{u},\ 0) \\\\&= (\boldsymbol{\mathsf{v}},\ 0) + a(\boldsymbol{u},\ 0) = \boldsymbol{\mathsf{v}}_q + aq\Big(\frac{\pi}{2}\Big)\end{align*}であり、回転後の位置 $\boldsymbol{r}_1$ を $Quaternion$ で表すと\[\boldsymbol{r_1}{_q} = (\boldsymbol{\mathsf{v}_1} + a\boldsymbol{u},\ 0) = \boldsymbol{\mathsf{v}_1}{_q} + aq\Big(\frac{\pi}{2}\Big)\]である。つまり $q(\theta)$ あるいは $q^*(\theta)$ を使って $\displaystyle \boldsymbol{r}_q = \boldsymbol{\mathsf{v}}_q + aq\Big(\frac{\pi}{2}\Big)$ を $\displaystyle \boldsymbol{r_1}{_q} = \boldsymbol{\mathsf{v}_1}{_q} + aq\Big(\frac{\pi}{2}\Big)$ にすることができればよいわけである。そのために $q(\theta)\,\boldsymbol{r}_q$ 及び $\boldsymbol{r}_q\,q^*(\theta)$ を計算すると上記 (4)、(5)、(6)、(7) より\begin{align*}q(\theta)\,\boldsymbol{r}_q &= q(\theta)\Big\lbrace\boldsymbol{\mathsf{v}}_q + aq\Big(\frac{\pi}{2}\Big)\Big\rbrace = q(\theta)\boldsymbol{\mathsf{v}}_q + q(\theta)\Big\lbrace aq\Big(\frac{\pi}{2}\Big)\Big\rbrace \\\\ &= \boldsymbol{\mathsf{v}_1}{_q} + aq\Big(\frac{\pi}{2} + \theta\Big) \\\\\boldsymbol{r}_q\,q^*(\theta) &= \Big\lbrace\boldsymbol{\mathsf{v}}_q + aq\Big(\frac{\pi}{2}\Big)\Big\rbrace q^*(\theta) = \boldsymbol{\mathsf{v}}_q\,q^*(\theta) + aq\Big(\frac{\pi}{2}\Big)\,q^*(\theta) \\\\ &= \boldsymbol{\mathsf{v}_1}{_q} + aq\Big(\frac{\pi}{2} - \theta\Big) \end{align*}となる。計算結果に示されるように確かに $\boldsymbol{r}$ の直交成分 $\boldsymbol{\mathsf{v}}$ は目的の値である $\boldsymbol{\mathsf{v}}_1$ になるが、$\boldsymbol{r}$ の平行成分は $\displaystyle aq\Big(\frac{\pi}{2} + \theta\Big)$ あるいは $\displaystyle aq\Big(\frac{\pi}{2} - \theta\Big)$ となってしまっている。平行成分は本来ならば $\displaystyle aq\Big(\frac{\pi}{2}\Big) = a(\boldsymbol{u},\ 0)$ にならなければいけないが、上記の計算では $+\theta$ あるいは $-\theta$ だけ余計な $\theta$ が残ってしまう。
$\boldsymbol{r}_q$ に対して $q(\theta)$ だけを掛ける、あるいは $q^*(\theta)$ だけを掛けるとこのような余計な $\theta$ が残ることになる。そのため片方だけでなく $q(\theta)$ と $q^*(\theta)$ の両方を使ってこの余計な $\theta$ を何とか相殺することができないかを考えたときに、例の挟み込む形が必要になるわけである。
すなわち、次の形で計算すればよい。
最終的に軸 $\boldsymbol{u}$ 周りの角度 $\theta$ の回転は\[q\Big(\frac{\theta}{2}\Big)\,\boldsymbol{r}_q\,q^*\Big(\frac{\theta}{2}\Big)\]とすればよいことがわかる。
このように $Quaternion$ が回転を表すことを理解するだけならば大した困難にはぶつからない。しかし、$Quaternion$ において最も重要なものは積の定義である。積の定義こそが $Quaternion$ のいわば核心部分であり、回転を含めて $Quaternion$ に関する幾多な性質はこの積の定義から導かれるのである。
もし読者が積の定義に関して興味があるならば下記の参考資料の論文を読むとよい。この論文は多少の想像力を必要とするため容易な内容ではないが、学生向けの参考書のように丁寧に書かれているため代数学の基本的な部分を理解していれば読めるであろう。
(参考資料)
Ronald N. Goldman , Understanding quaternions, 2011 .
ベクトル部だけの任意の $Quaternion$ を $\boldsymbol{\mathsf{v}}_q = (\boldsymbol{\mathsf{v}},\ 0)$ とするとき、よく知られるようにベクトル $\boldsymbol{\mathsf{v}}$ を回転軸 $\boldsymbol{u}$ の周りに角度 $\theta$ 回転させるには、角度 $\displaystyle \frac{\theta}{2}$ の単位 $Quaternion$ $\displaystyle q = \Big(\sin\frac{\theta}{2}\,\boldsymbol{u},\ \cos\frac{\theta}{2}\Big)$ とその共役 $\displaystyle q^* = \Big(-\sin\frac{\theta}{2}\,\boldsymbol{u},\ \cos\frac{\theta}{2}\Big)$ を用いて\[q\,\boldsymbol{\mathsf{v}}_q\,q^*\]の形の計算を行う。つまり $Quaternion$ をこのように使うことで、$Quaternion$ は3次元空間における任意軸周りの回転を表すことができるのである。
ではなぜ $Quaternion$ による回転は2つの $Quaternion$ を使って挟み込む形の積にしなければならないのか、またなぜ角度 $\theta$ の回転に角度 $\displaystyle \frac{\theta}{2}$ の $Quaternion$ を使うのか。
この点について謎のように感じる者は多いであろうが、その原理自体は難しいものではない。面倒な計算は現れないし、特別な想像力を働かせる必要もない。
以下本節ではこの謎の解決を通して $Quaternion$ が3次元空間における回転を表すことについて解説する。
まずは前節の内容を簡単に復習する。
($\mathrm{i}$) 2つの $Quaternion$ を $q_1 = (\boldsymbol{\mathsf{v_1}},\ w_1)$、$q_2 = (\boldsymbol{\mathsf{v_2}},\ w_2)$ とするとき $Quaternion$ の積 $q_1q_2$ は\begin{align*}q_1q_2 &= (\boldsymbol{\mathsf{v_1}},\ w_1)(\boldsymbol{\mathsf{v_2}},\ w_2) \\&= (\boldsymbol{\mathsf{v_1}}\times \boldsymbol{\mathsf{v_2}} + w_1\boldsymbol{\mathsf{v_2}} + w_2\boldsymbol{\mathsf{v_1}},\ w_1w_2 - \boldsymbol{\mathsf{v_1}} \cdot \boldsymbol{\mathsf{v_2}}) \end{align*}として定義される。
($\mathrm{ii}$) スカラーと $Quaternion$ の積は可換である。すなわち $s$ をスカラー、$q = (\boldsymbol{\mathsf{v}},\ w)$ を $Quaternion$ とすれば\[sq = qs = (s\boldsymbol{\mathsf{v}},\ sw)\]である。
($\mathrm{iii}$) $q = (\boldsymbol{\mathsf{v}},\ w)$ を任意の $Quaternion$ とするとき、$q$ の大きさを $|q| = k$ とすれば適当な角度 $\theta$ 及び単位ベクトル $\boldsymbol{n}$ を用いて\[ q = (\boldsymbol{\mathsf{v}},\ w) = k(\sin\theta\,\boldsymbol{n},\ \cos\theta)\]と表すことができる。ここで $(\sin\theta\,\boldsymbol{n},\ \cos\theta)$ は単位 $Quaternion$ である。
($\mathrm{iv}$) $Quaternion$ はその積に関して結合法則及び分配法則が成り立つ。$q_1$、$q_2$、$q_3$ を任意の $Quaternion$ とすれば、\begin{align*}q_1(q_2q_3) &= (q_1q_2)q_3 \\\\q_1(q_2 + q_3) &= q_1q_2 + q_1q_3 \\\\(q_2 + q_3)q_1 &= q_2q_1 + q_3q_1 \end{align*}である。
単位 $Quaternion$ $q$ は適当な角度 $\theta$ と単位ベクトル $\boldsymbol{u}$ を用いて $q = (\sin\theta\,\boldsymbol{u},\ \cos\theta)$ の形で表されるが、以下の解説では簡単のためこのベクトル部で使われている単位ベクトル $\boldsymbol{u}$ を「回転軸」と呼ぶことにする (まだ $Quaternion$ が回転を表すことを示していないので細かいことを言えばこの呼び方はフライングである)。
同様に以下の解説においては回転軸 $\boldsymbol{u}$、角度 $\theta$ の単位 $Quaternion$ $q = (\sin\theta\,\boldsymbol{u},\ \cos\theta)$ を簡単に\[q(\theta)\]の形で表すものとする。
($\mathrm{v}$) 一般に $Quaternion$ の積は可換ではないが、回転軸が同じで角度だけが異なる2つの単位 $Quaternion$ $q_1$、$q_2$ の積は可換である。具体的には $q_1 = (\sin\theta_1\,\boldsymbol{u},\ \cos\theta_1)$、$q_2 = (\sin\theta_2\,\boldsymbol{u},\ \cos\theta_2)$ とするとき、積 $q_1q_2$ は回転軸 $\boldsymbol{u}$、角度 $\theta_1 + \theta_2$ の単位 $Quaternion$ になる。
すなわち、\begin{align*}q_2q_1 &= q_1q_2 \\ &= (\sin\theta_1\,\boldsymbol{u},\ \cos\theta_1)(\sin\theta_2\,\boldsymbol{u},\ \cos\theta_2) \\&= (\sin(\theta_1 + \theta_2)\,\boldsymbol{u},\ \cos(\theta_1 + \theta_2)) \\\end{align*}である。
上で定めた表記によって $q_1 = q(\theta_1)$、$q_2 = q(\theta_2)$ と書けるから上の式は\[q(\theta_2)q(\theta_1) = q(\theta_1)q(\theta_2) = q(\theta_1 + \theta_2) \tag{1}\]のように簡潔な形にすることができる。
角度 $\theta$ の単位 $Quaternion$ $q = (\sin\theta\,\boldsymbol{u},\ \cos\theta)$ の共役は $q^* = (-\sin\theta\,\boldsymbol{u},\ \cos\theta)$ であるが、$-\sin\theta = \sin(-\theta)$、$\cos\theta = \cos(-\theta)$ であるから\[q^* = (-\sin\theta\,\boldsymbol{u},\ \cos\theta) = (\sin(-\theta)\,\boldsymbol{u},\ \cos(-\theta))\]である。先程の表記を用いれば上の式は $q^*(\theta) = q(-\theta)$ であることを意味している。
($\mathrm{vi}$) 上記の $q_1 = (\sin\theta_1\,\boldsymbol{u},\ \cos\theta_1)$、$q_2 = (\sin\theta_2\,\boldsymbol{u},\ \cos\theta_2)$ に関して、一方を共役にしても両者の回転軸は同じであるからその積は可換である。すなわち $q{_2}^*q_1 = q_1q{_2}^*$ であるが、$q{_2}^* = q^*(\theta_2) = q(-\theta_2)$ であることに注意すればこの積は\[q^*(\theta_2)q(\theta_1) = q(\theta_1)q^*(\theta_2) = q(\theta_1 - \theta_2) \tag{2}\]として表すことができる。
($\mathrm{vii}$) 単位ベクトル $\boldsymbol{u}$ だけを含む $(\boldsymbol{u},\ 0)$ のようなスカラー部 $0$ の $Quaternion$ は、$\displaystyle\sin\frac{\pi}{2} = 1$、$\displaystyle\cos\frac{\pi}{2} = 0$ であることから $\sin$、$\cos$ を用いて $\displaystyle (\boldsymbol{u},\ 0) = \Big(\sin\frac{\pi}{2}\boldsymbol{u},\ \cos\frac{\pi}{2}\Big)$ として表される。上で定めた表記を使えば $\displaystyle (\boldsymbol{u},\ 0) = q\Big(\frac{\pi}{2}\Big)$ である。
$\boldsymbol{u}$ に適当なスカラー $a$ を掛けたベクトル $a\boldsymbol{u}$ の場合でも事情は同じであり、$\displaystyle (a\boldsymbol{u},\ 0) = a(\boldsymbol{u},\ 0)$ であるから、\[(a\boldsymbol{u},\ 0) = a(\boldsymbol{u},\ 0) = aq\Big(\frac{\pi}{2}\Big) \tag{3}\]である。
特に上の式 (1)、(2) から $q(\theta)$ あるいは $q^*(\theta)$ と $\displaystyle aq\Big(\frac{\pi}{2}\Big)$ の積は次のように計算される。\begin{align*}q(\theta)\Big\lbrace aq\Big(\frac{\pi}{2}\Big)\Big\rbrace = aq\Big(\frac{\pi}{2}\Big)q(\theta) = aq\Big(\frac{\pi}{2} + \theta\Big) \\\\q^*(\theta)\Big\lbrace aq\Big(\frac{\pi}{2}\Big)\Big\rbrace = aq\Big(\frac{\pi}{2}\Big)q^*(\theta) = aq\Big(\frac{\pi}{2} - \theta\Big) \\\\\end{align*}
回転軸 $\boldsymbol{u}$、角度 $\theta$ の単位 $Quaternion$ $q(\theta) = (\sin\,\boldsymbol{u},\ \cos\theta)$ に対して回転対象のベクトルを $\boldsymbol{\mathsf{v}}$ とするとき、冒頭でも述べたように $\boldsymbol{\mathsf{v}}$ を軸 $\boldsymbol{u}$ の周りに $\theta$ 回転させる場合、角度 $\displaystyle \frac{\theta}{2}$ の単位 $Quaternion$ $\displaystyle q\Big(\frac{\theta}{2}\Big)$ とその共役 $\displaystyle q^*\Big(\frac{\theta}{2}\Big)$ を用いて\[ \displaystyle q\Big(\frac{\theta}{2}\Big)\,\boldsymbol{\mathsf{v}}_q\,q^*\Big(\frac{\theta}{2}\Big)\]という計算を行う ($\boldsymbol{\mathsf{v}}_q = (\boldsymbol{\mathsf{v}},\ 0)$)。
しかし回転対象のベクトルに対してある条件を付けると、回転行列によってベクトルを回転させる場合と同じくその計算を $R\,\boldsymbol{\mathsf{v}}$ の形にすることができるのである。さらにその場合には角度を $\displaystyle \frac{\theta}{2}$ にする必要もない。$Quaternion$ に関してこの性質はほとんど言及されることはないが、$Quaternion$ が3次元空間における回転を表すことを示す際には非常に重要な役割を務めるのである。
具体的には次の命題が成り立つ。
回転軸 $\boldsymbol{u}$、角度 $\theta$ の単位 $Quaternion$ を $q(\theta) = (\sin\theta\,\boldsymbol{u},\ \cos\theta)$ とし、回転対象のベクトル $\boldsymbol{\mathsf{v}}$ を回転軸 $\boldsymbol{u}$ と直交する任意のベクトルとする。このとき軸 $\boldsymbol{u}$ 周りの角度 $\theta$ の回転は
として表される ($\boldsymbol{\mathsf{v}}_q = (\boldsymbol{\mathsf{v}},\ 0)$)。
$q(\theta)\,\boldsymbol{\mathsf{v}}_q$ あるいは $\boldsymbol{\mathsf{v}}_q\,q^*(\theta)$
として表される ($\boldsymbol{\mathsf{v}}_q = (\boldsymbol{\mathsf{v}},\ 0)$)。
証明は容易である。積の定義に従って計算をすればよい。
\begin{align*}q(\theta)\,\boldsymbol{\mathsf{v}}_q &= (\sin\theta\,\boldsymbol{u},\ \cos\theta)(\boldsymbol{\mathsf{v}},\ 0) \\\\&= (\sin\theta\,\boldsymbol{u} \times \boldsymbol{\mathsf{v}} + \cos\theta\,\boldsymbol{\mathsf{v}},\ - \sin\theta\,\boldsymbol{u}\cdot\boldsymbol{\mathsf{v}}) \\\\&= (\sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}}) + \cos\theta\,\boldsymbol{\mathsf{v}},\ 0)\end{align*}
$\boldsymbol{u}$ は単位ベクトルであり、$\boldsymbol{u}$ と $\boldsymbol{\mathsf{v}}$ は直交しているからそのなす角は $\displaystyle\frac{\pi}{2}$、したがって\[ |\boldsymbol{u} \times \boldsymbol{\mathsf{v}}| = |\boldsymbol{u}||\boldsymbol{\mathsf{v}}|\sin\Big(\frac{\pi}{2}\Big) = |\boldsymbol{\mathsf{v}}|\]である。すなわちこの場合には $\boldsymbol{u} \times \boldsymbol{\mathsf{v}}$ の大きさと $\boldsymbol{\mathsf{v}}$ の大きさは等しいわけであるが、以下この大きさを $r$ で表す。
$q(\theta)\,\boldsymbol{\mathsf{v}}_q = ( \cos\theta\,\boldsymbol{\mathsf{v}} + \sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}}),\ 0)$ が何を表しているかは以下の図を見れば明らかであろう。ただし図においては $\boldsymbol{\mathsf{v}_1} = \cos\theta\,\boldsymbol{\mathsf{v}} + \sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}})$ としている。

3つのベクトル $\boldsymbol{u}$、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{u} \times \boldsymbol{\mathsf{v}}$ は互いに直交しており、$|\boldsymbol{u} \times \boldsymbol{\mathsf{v}}| = |\boldsymbol{\mathsf{v}}| = r$ であるが、図から明らかなように $\boldsymbol{\mathsf{v}_1}$ の大きさも\[ |\boldsymbol{\mathsf{v}_1}| = \sqrt{(r\cos\theta)^2 + (r\sin\theta)^2} = r \]である。$\boldsymbol{\mathsf{v}}$ を x軸、$\boldsymbol{u} \times \boldsymbol{\mathsf{v}}$ を y軸と見れば $\boldsymbol{\mathsf{v}_1}$ の指す位置は $r(\cos\theta,\ \sin\theta)$ に相当する。つまり、$\boldsymbol{\mathsf{v}_1} = \cos\theta\,\boldsymbol{\mathsf{v}} + \sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}})$ は(軸 $\boldsymbol{u}$ と直交するベクトル) $\boldsymbol{\mathsf{v}}$ を軸 $\boldsymbol{u}$ の周りに角度 $\theta$ 回転させたときの位置であることがわかる。すなわち回転軸 $\boldsymbol{u}$ と直交するベクトル $\boldsymbol{\mathsf{v}}$ に対しては、$q(\theta)\,\boldsymbol{\mathsf{v}}_q = ( \cos\theta\,\boldsymbol{\mathsf{v}} + \sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}}),\ 0)$ は軸 $\boldsymbol{u}$ 周りの角度 $\theta$ の回転を表すのである。
$\boldsymbol{\mathsf{v}}_q\,q^*(\theta)$ も同様の回転であることは、以下に示されるように計算結果が同じになることから明らかである。
\begin{align*}\boldsymbol{\mathsf{v}}_q\,q^*(\theta) &= (\boldsymbol{\mathsf{v}},\ 0)(-\sin\theta\,\boldsymbol{u},\ \cos\theta) \\\\&= (\boldsymbol{\mathsf{v}} \times (-\sin\theta\,\boldsymbol{u}) + \cos\theta\,\boldsymbol{\mathsf{v}},\ - \boldsymbol{\mathsf{v}}\cdot(-\sin\theta\,\boldsymbol{u})) \\\\&= (-\sin\theta(\boldsymbol{\mathsf{v}} \times \boldsymbol{u}) + \cos\theta\,\boldsymbol{\mathsf{v}},\ 0) \\\\&= (\sin\theta(\boldsymbol{u} \times \boldsymbol{\mathsf{v}}) + \cos\theta\,\boldsymbol{\mathsf{v}},\ 0)\end{align*}
ここで、今までに述べてきたことをまとめよう。
回転軸 $\boldsymbol{u}$、角度 $\theta$ の単位 $Quaternion$ を $q(\theta) = (\sin\theta\,\boldsymbol{u},\ \cos\theta)$ とする。
回転軸 $\boldsymbol{u}$ と直交する任意のベクトルを $\boldsymbol{\mathsf{v}}$ とし、$\boldsymbol{\mathsf{v}}$ を軸 $\boldsymbol{u}$ の周りに角度 $\theta$ 回転させた位置を $\boldsymbol{\mathsf{v}_1}$ とするとき、\begin{align*}q(\theta)\,\boldsymbol{\mathsf{v}}_q = \boldsymbol{\mathsf{v}_1}{_q} \tag{4} \\\\\boldsymbol{\mathsf{v}}_q\,q^*(\theta) = \boldsymbol{\mathsf{v}_1}{_q} \tag{5}\end{align*}である (ただし $\boldsymbol{\mathsf{v}}_q = (\boldsymbol{\mathsf{v}},\ 0)$、$\boldsymbol{\mathsf{v}_1}{_q} = (\boldsymbol{\mathsf{v}}_1,\ 0)$)。$\boldsymbol{\mathsf{v}}_1$ も軸 $\boldsymbol{u}$ と直交しているから $\boldsymbol{\mathsf{v}}_1$ をさらに $\theta$ 回転させた位置を $\boldsymbol{\mathsf{v}}_2$ とすれば、$q(\theta)\,\boldsymbol{\mathsf{v}_1}{_q} = \boldsymbol{\mathsf{v}_1}{_q}\,q^*(\theta) = \boldsymbol{\mathsf{v}_2}{_q}$ となる。
回転軸 $\boldsymbol{u}$ に平行な任意のベクトルは適当なスカラー $a$ を用いて $a\boldsymbol{u}$ と表される。この $a\boldsymbol{u}$ をベクトル部に持つ $Quaternion$ $(a\boldsymbol{u},\ 0)$ は $\sin$、$\cos$ を用いて表すと上記 (3) より $\displaystyle (a\boldsymbol{u},\ 0) = a\Big(\sin\frac{\pi}{2}\boldsymbol{u},\ \cos\frac{\pi}{2}\Big) = aq\Big(\frac{\pi}{2}\Big)$ であるが、この $\displaystyle aq\Big(\frac{\pi}{2}\Big)$ に $q(\theta)$ あるいは $q^*(\theta)$ を掛けると\begin{align*}q(\theta)\Big\lbrace aq\Big(\frac{\pi}{2}\Big)\Big\rbrace = aq\Big(\frac{\pi}{2}\Big)q(\theta) = aq\Big(\frac{\pi}{2} + \theta\Big) \tag{6} \\\\q^*(\theta)\Big\lbrace aq\Big(\frac{\pi}{2}\Big)\Big\rbrace = aq\Big(\frac{\pi}{2}\Big)q^*(\theta) = aq\Big(\frac{\pi}{2} - \theta\Big) \tag{7}\end{align*}である。
以上の準備をもとにして $Quaternion$ が3次元空間における回転になることを示すが、あとは単なる足し算と引き算の問題に過ぎない。
回転軸を $\boldsymbol{u}$ とし、回転対象のベクトルを $\boldsymbol{r}$ とする。$\boldsymbol{r}$ を $\boldsymbol{u}$ に直交する方向と平行な方向に分解するとき、$\boldsymbol{u}$ に直交する方向を $\boldsymbol{\mathsf{v}}$、平行な方向を $\boldsymbol{\mathsf{w}}$ とすれば $\boldsymbol{r} = \boldsymbol{\mathsf{v}} + \boldsymbol{\mathsf{w}}$ であるが、$|\boldsymbol{\mathsf{w}}| = a$ とすれば $\boldsymbol{\mathsf{w}} = a\boldsymbol{u}$ であるから、$\boldsymbol{r}$ は\[ \boldsymbol{r} = \boldsymbol{\mathsf{v}} + a\boldsymbol{u} \]の形に分解される (下図)。簡単のため以下では $\boldsymbol{\mathsf{v}}$ を「$\boldsymbol{r}$ の直交成分」、$a\boldsymbol{u}$ を「$\boldsymbol{r}$ の平行成分」と呼ぶことにする。
ここで $\boldsymbol{r}$ を軸 $\boldsymbol{u}$ の周りに角度 $\theta$ 回転させた位置を $\boldsymbol{r}_1$ とし、$\boldsymbol{\mathsf{v}}$ を軸 $\boldsymbol{u}$ の周りに角度 $\theta$ 回転させた位置を $\boldsymbol{\mathsf{v}}_1$ とする。このとき下図に示されるように\[ \boldsymbol{r}_1 = \boldsymbol{\mathsf{v}}_1 + a\boldsymbol{u} \]である。
また、$\boldsymbol{\mathsf{v}}_1$ をさらに軸 $\boldsymbol{u}$ の周りに $\theta$ 回転させた位置を図では $\boldsymbol{\mathsf{v}}_2$ としている。

回転行列を使って $\boldsymbol{r}$ の回転後の位置を求める場合、軸 $\boldsymbol{u}$ 周りの角度 $\theta$ の回転行列を $R$ とすればその計算は以下のような形で行われる。\begin{align*}R\boldsymbol{r} &= R(\boldsymbol{\mathsf{v}} + a\boldsymbol{u}) = R\boldsymbol{\mathsf{v}} + aR\boldsymbol{u} \\\\&= \boldsymbol{\mathsf{v}}_1 + a\boldsymbol{u} = \boldsymbol{r}_1\end{align*}(軸 $\boldsymbol{u}$ 周りの回転によって $\boldsymbol{u}$ は変化しないので $R\boldsymbol{u} = \boldsymbol{u}$ である)
これと同じことを単位 $Quaternion$ $q(\theta)$、$q^*(\theta)$ を使ってできないかを調べてみよう (以下ではこれまでと同様にベクトル部だけの $Quaternion$ を $\boldsymbol{\mathsf{v}}_q = (\boldsymbol{\mathsf{v}},\ 0)$、$\boldsymbol{\mathsf{v}_1}{_q} = (\boldsymbol{\mathsf{v}_1},\ 0)$ のように表す。ただし $(\boldsymbol{u},\ 0)$ の場合は $\displaystyle (\boldsymbol{u},\ 0) = q\Big(\frac{\pi}{2}\Big)$ として表す)。
$\boldsymbol{r} = \boldsymbol{\mathsf{v}} + a\boldsymbol{u}$ であるからこれを $Quaternion$ として表せば、\begin{align*}\boldsymbol{r}_q &= (\boldsymbol{r},\ 0) = (\boldsymbol{\mathsf{v}} + a\boldsymbol{u},\ 0) \\\\&= (\boldsymbol{\mathsf{v}},\ 0) + a(\boldsymbol{u},\ 0) = \boldsymbol{\mathsf{v}}_q + aq\Big(\frac{\pi}{2}\Big)\end{align*}であり、回転後の位置 $\boldsymbol{r}_1$ を $Quaternion$ で表すと\[\boldsymbol{r_1}{_q} = (\boldsymbol{\mathsf{v}_1} + a\boldsymbol{u},\ 0) = \boldsymbol{\mathsf{v}_1}{_q} + aq\Big(\frac{\pi}{2}\Big)\]である。つまり $q(\theta)$ あるいは $q^*(\theta)$ を使って $\displaystyle \boldsymbol{r}_q = \boldsymbol{\mathsf{v}}_q + aq\Big(\frac{\pi}{2}\Big)$ を $\displaystyle \boldsymbol{r_1}{_q} = \boldsymbol{\mathsf{v}_1}{_q} + aq\Big(\frac{\pi}{2}\Big)$ にすることができればよいわけである。そのために $q(\theta)\,\boldsymbol{r}_q$ 及び $\boldsymbol{r}_q\,q^*(\theta)$ を計算すると上記 (4)、(5)、(6)、(7) より\begin{align*}q(\theta)\,\boldsymbol{r}_q &= q(\theta)\Big\lbrace\boldsymbol{\mathsf{v}}_q + aq\Big(\frac{\pi}{2}\Big)\Big\rbrace = q(\theta)\boldsymbol{\mathsf{v}}_q + q(\theta)\Big\lbrace aq\Big(\frac{\pi}{2}\Big)\Big\rbrace \\\\ &= \boldsymbol{\mathsf{v}_1}{_q} + aq\Big(\frac{\pi}{2} + \theta\Big) \\\\\boldsymbol{r}_q\,q^*(\theta) &= \Big\lbrace\boldsymbol{\mathsf{v}}_q + aq\Big(\frac{\pi}{2}\Big)\Big\rbrace q^*(\theta) = \boldsymbol{\mathsf{v}}_q\,q^*(\theta) + aq\Big(\frac{\pi}{2}\Big)\,q^*(\theta) \\\\ &= \boldsymbol{\mathsf{v}_1}{_q} + aq\Big(\frac{\pi}{2} - \theta\Big) \end{align*}となる。計算結果に示されるように確かに $\boldsymbol{r}$ の直交成分 $\boldsymbol{\mathsf{v}}$ は目的の値である $\boldsymbol{\mathsf{v}}_1$ になるが、$\boldsymbol{r}$ の平行成分は $\displaystyle aq\Big(\frac{\pi}{2} + \theta\Big)$ あるいは $\displaystyle aq\Big(\frac{\pi}{2} - \theta\Big)$ となってしまっている。平行成分は本来ならば $\displaystyle aq\Big(\frac{\pi}{2}\Big) = a(\boldsymbol{u},\ 0)$ にならなければいけないが、上記の計算では $+\theta$ あるいは $-\theta$ だけ余計な $\theta$ が残ってしまう。
$\boldsymbol{r}_q$ に対して $q(\theta)$ だけを掛ける、あるいは $q^*(\theta)$ だけを掛けるとこのような余計な $\theta$ が残ることになる。そのため片方だけでなく $q(\theta)$ と $q^*(\theta)$ の両方を使ってこの余計な $\theta$ を何とか相殺することができないかを考えたときに、例の挟み込む形が必要になるわけである。
すなわち、次の形で計算すればよい。
\begin{align*}q(\theta)\,\boldsymbol{r}_q\,q^*(\theta) &= q(\theta)\lbrace\boldsymbol{r}_q\,q^*(\theta)\rbrace = q(\theta)\Big\lbrace\boldsymbol{\mathsf{v}_1}{_q} + aq\Big(\frac{\pi}{2} - \theta\Big)\Big\rbrace \\\\&= q(\theta)\,\boldsymbol{\mathsf{v}_1}{_q} + q(\theta)\Big\lbrace aq\Big(\frac{\pi}{2} - \theta\Big)\Big\rbrace = \boldsymbol{\mathsf{v}_2}{_q} + aq\Big(\frac{\pi}{2} - \theta + \theta\Big) \\\\&= \boldsymbol{\mathsf{v}_2}{_q} + aq\Big(\frac{\pi}{2}\Big) \end{align*}
この形の積にすることで確かに平行成分は $\displaystyle aq\Big(\frac{\pi}{2}\Big)$ として目的の値になったが、今度は直交成分の方が $\theta$ 回転させた位置 $\boldsymbol{\mathsf{v}}_1$ ではなく、$2\theta$ 回転させた位置 $\boldsymbol{\mathsf{v}}_2$ になってしまっている。しかし、この修正は容易である。最終的に軸 $\boldsymbol{u}$ 周りの角度 $\theta$ の回転は\[q\Big(\frac{\theta}{2}\Big)\,\boldsymbol{r}_q\,q^*\Big(\frac{\theta}{2}\Big)\]とすればよいことがわかる。
このように $Quaternion$ が回転を表すことを理解するだけならば大した困難にはぶつからない。しかし、$Quaternion$ において最も重要なものは積の定義である。積の定義こそが $Quaternion$ のいわば核心部分であり、回転を含めて $Quaternion$ に関する幾多な性質はこの積の定義から導かれるのである。
もし読者が積の定義に関して興味があるならば下記の参考資料の論文を読むとよい。この論文は多少の想像力を必要とするため容易な内容ではないが、学生向けの参考書のように丁寧に書かれているため代数学の基本的な部分を理解していれば読めるであろう。
(参考資料)
Ronald N. Goldman , Understanding quaternions, 2011 .
<< 14-6
Quaternion 基礎
Quaternion 基礎
14-8 >>
球面線形補間
球面線形補間
© 2020-2025 Redpoll's 60 (All rights reserved)