Redpoll's 60
Home / 3Dプログラミング入門 / 第5章 $§$5-2
第5章 変換のオブジェクト化
| $§$5-1 要旨 | $§$5-6 Transformクラスの実装 2 |
| $§$5-2 Unityにおける標準的な変換方法 1 | $§$5-7 Transformクラスの実装 3 |
| $§$5-3 Unityにおける標準的な変換方法 2 | $§$5-8 いくつかの使用例 |
| $§$5-4 Unityにおける標準的な変換方法 3 | $§$5-9 課題 |
| $§$5-5 Transformクラスの実装 1 |
$§$5-2 Unityにおける標準的な変換方法 1
この講義では、オブジェクトの運動は いくつかの例を除いて全て行列を通して実装された。オブジェクトに対するすべての変換は、最終的にはただ1つの変換行列にまとめられ、その変換行列をオブジェクトの SetMatrix(..) の引数にセットして、オブジェクトを動かしてきたのであった。
しかし、この方法は講義用に独自に実装したものであり、Unityの標準的な機能ではないことは すでに述べた。前節で少し触れたように、Unityでは、オブジェクトに対する何らかの変換の実行は Transformクラスを通して行われる。具体的には、オブジェクトを動かすためには、そのオブジェクトが所有する Transform型の transform というプロパティを経由して、Transformクラスの各プロパティに適切な値をセットしていく (プロパティとは C#において、独自のアクセス定義がされているメンバ変数のことである。ここでは単にメンバ変数と捉えても構わない)。
まずは、Transformクラスで主に使用する3つのプロパティから始める。
localPosition localRotation localScale
それぞれの型は、localPosition が Vector3型、localRotation が Quaternion型、localScale が Vector3型である。Vector3 は今までのプログラムで何度も使われてきているので、説明は不要であろう。Quaternion(クォータニオン、四元数)とは回転を表す形式の1つである。今までのプログラムでは、回転は行列によって表されていたが、3Dコンピューターグラフィックスにおいては、回転を表す形式として Quaternionを使用する場合が非常に多い。Quaternionについては、第6章以降で本格的に使用していくが、本節での使用や解説は必要最小限に留める。
では実際に、この3つのプロパティを用いて、オブジェクトに変換を実行していく。
使用するオブジェクトは、図1に示される各辺の長さが $2$の立方体オブジェクト Cubeである (図2は Cubeを反対側から見たときのもの)。

図1 Cube 初期状態 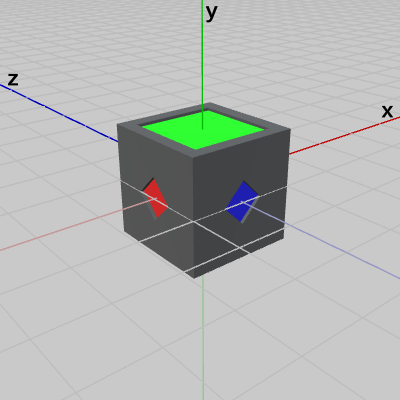
図2 Cube 初期状態 (反対側から見たとき)
オブジェクトを初期状態にするためには、各プロパティに次のようにセットする。
Vector3.zero、Quaternion.identity、Vector3.one は、いずれも Unity側に用意されている定数である。
Vector3.zero は、new Vector3(0, 0, 0) を表しており、これは移動量が $(0, 0, 0)$、すなわち平行移動が行われないことを意味する。
Quaternion.identity は、new Quaternion(0, 0, 0, 1) を表しており、これは何も回転を行わない Quaternion を意味する。詳しくは第6章で解説するが、オブジェクトに対して回転を行わない場合には、localRotation に Quaternion.identity をセットするのである。
Vector3.one は、new Vector3(1, 1, 1) を表しており、これは各軸の倍率が $1$倍、すなわちスケールが行われないことを意味する。
したがって、localPosition、localRotation、localScale に Vector3.zero、Quaternion.identity、Vector3.one をセットすると、平行移動も行われず、回転も行われず、スケールも行われない、すなわち、オブジェクトは何の変換も実行されていない状態、初期状態になるのである。
図1は Cubeの初期状態であるが、Cubeに対して次のコードを実行した結果である。
(注意 : Unity側に用意されている Vector3 や Quaternion は、クラスではなく、構造体である。したがって、参照型ではなく、値型である。つまり、上のコードにおける代入では、Vector3.zero、Quaternion.identity、Vector3.one の複製がセットされることになる)
では、次に Cubeに対して平行移動だけを実行する。
図3は 初期状態の Cubeであり、図4は Cubeを $(6, 0, 0)$ だけ平行移動させる次のコードを実行した結果である。
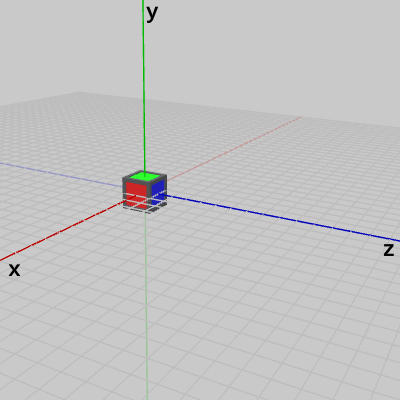
図3 Cube 初期状態 
図4 (6, 0, 0) の平行移動を実行した結果
続いて、Cubeに対して回転だけを実行した場合、スケールだけを実行した場合を示す。
図5は Cubeを y軸周りに $-90$° 回転させる次のコードを実行した結果である。
ここで使用されているメソッド AngleAxis(..) は、Unity側に用意されている Quaternion の staticメソッドで、第1引数に回転角度(float型)、第2引数に回転軸(Vector3型)を指定する。つまり、Quaternion は任意軸回転が可能であり、この staticメソッドによって指定した軸周りに、指定の角度だけ回転させる Quaternion が返される。ここでは、y軸周りに $-90$°回転させる Quaternionを取得するために、第1引数に $-90$、第2引数に Vector3.up (y軸プラス方向 $(0, 1, 0)$ を表す定数)を指定している。
図6は Cubeを 各軸方向に $2$倍拡大する次のコードを実行した結果である。

図5 y軸周り -90°の回転を実行した結果 
図6 各軸方向に 2倍の拡大を実行した結果
行列の場合、変換の合成は、それらの変換を表す変換行列の積によって表されていた。そして、変換行列の積においては、変換の実行順序は積の右から左へ進むのであった (列優先の場合 ; 3-8節参照)。
まずは、上で見てきた3つの変換を行列によって合成し、それを Cubeに実行することから始める。
Cube に実行する変換は次の3つである。
--> $(6, 0, 0)$ の平行移動
--> y軸周り $-90$°の回転
--> 各軸方向に $2$倍の拡大
(1) スケール、回転、平行移動の順序での実行 (実行結果 図7)
(2) スケール、平行移動、回転の順序での実行 (実行結果 図8 ; プログラムの 1行目から 3行目は (1)と同じ)
(3) 平行移動、回転、スケールの順序での実行 (実行結果 図9 ; プログラムの 1行目から 3行目は (1)と同じ)
図7は、(1)の実行結果で、スケール、回転が(原点において)先に行われ、平行移動が最後に実行されるので、最終的な Cubeの位置は x軸上に移動している。
図8は、(2)の実行結果で、スケール、平行移動、そして最後に回転が実行される。平行移動が行われた時点では、Cubeは x軸上に移動しているが、そこから y軸周りに $-90$°の回転が実行されるので、最終的には z軸上に移ることになる。
図9は、(3)の実行結果で、まず始めに平行移動が行われ、x軸上に移動、次に y軸周り $-90$°の回転によって z軸上に移される。さらに、そこから各軸方向への $2$倍の拡大が実行される。これによって、Cubeの各頂点は原点からの距離が $2$倍になる。結果的には、(2)の実行結果の位置から z軸方向へ $2$倍離れた位置に移動する。
つまり、行列による変換の合成では、実行順序を変えた場合には実行結果が異なってしまうわけである (「実行結果は同じになるとは限らない」という表現の方がより適切である)。
変換の実行順序を入れ替えた場合に、実行結果が変わることについては、1-8節や 3-13節で見てきたことであり、ここでの結果は いささか自明なことであったかもしれない。
では、localPosition、localRotation、localScale について、上で行ったように実行順序を入れ替えた場合、どのような結果になるかについて見ていこう (実行される変換は、上と同じく $(6, 0, 0)$ の平行移動、y軸周り $-90$°の回転、各軸方向への $2$倍の拡大 である)。
(1) スケール、回転、平行移動の順序での実行 (実行結果 図10)
(2) スケール、平行移動、回転の順序での実行 (実行結果 図11)
(3) 平行移動、回転、スケールの順序での実行 (実行結果 図12)
上の図から明らかなように、localPosition、localRotation、localScale を使った変換では、順序を入れ替えて実行した場合でも、実行結果はすべて同じ結果になっている。そして、この結果は行列を使用した場合の (1)の実行順序、スケール、回転、平行移動の順で変換を実行した場合と同じ結果である(図7)。
では、この変換の原理について解説しよう。
4-6節では、(1つ以上の変換の合成による)任意の変換を表す変換行列$M$に対して、次のような書き換えを行った (「任意の変換を表す変換行列$M$」は3-13節や4-6節で述べたスケールについての取り決めに従っているものとする)。
3-9節で述べたように、平行移動行列を作成するために必要なデータは、第4列目の1行目から3行目に指定する、x軸方向の移動量、y軸方向の移動量、z軸方向の移動量の3つである ($T$においては、その3つのデータは、$t_x$, $t_y$, $t_z$ で表されている)。Unityでは、3つの(浮動点小数)データを1つの Vector3インスタンスに保持することができる。したがって、平行移動行列$T$を作成するためには、1つの Vector3インスタンスがあればよいことになる。
また、3-12節で述べたように、スケール行列を作成するために必要なデータは、1行1列目、2行2列目、3行3列目に指定する、x軸方向の倍率、y軸方向の倍率、z軸方向の倍率の3つである ($S$においては、その3つのデータは、$s_x$, $s_y$, $s_z$ で表されている)。したがって、スケール行列$S$を作成する場合にも、1つの Vector3インスタンスがあればよいことになる。
回転行列については、やや事情が異なる。3-11節では、ロドリゲスの回転公式による任意軸周りの回転行列について扱った。オブジェクトを回転させるために、プログラム内で頻繁に使用したカスタムライブラリのメソッド TH3DMath.GetRotation4x4(float deg, Vector3 axis) も、ロドリゲスの回転公式に基づいた $4\times 4$の回転行列を返すものであることは、そこで述べた。また、上で述べたように、Unityでは、基本的に回転は Quaternionで表す。
そして、Quaternionと回転行列の間では相互変換が可能なのである。つまり、ある回転が Quaternionで表されている場合、その回転を$4\times 4$回転行列に、逆に、ある回転が $4\times 4$回転行列で表されている場合、その回転を Quaternionで表すことも可能なのである (Quaternionも回転を表す1つの形式に過ぎない。今までのプログラムでは、回転はすべて行列という形式で表していたのである)。
Unityには、Quaternionを行列に変換するために、以下のメソッドが用意されている。
このメソッドは、Matrix4x4の staticメソッドで、引数の Quaternionインスタンスが表す回転を、Matrix4x4に変換して、その Matrix4x4インスタンスを返すものである。
また、Unityでは任意軸周りの回転を表す Quaternionインスタンスを、上でも使用した次のメソッドで取得できる。
したがって、回転行列$R$を作成するためには、1つの Quaternionインスタンスを使って、以下のような変換を行えばよい。すなわち、回転行列$R$を作成するためには、1つの Quaternionインスタンスがあればよいのである。
上で述べてきたことをまとめると次のようになる。
(注) 以下の文章中における「変換行列$M$」はオブジェクトのローカル行列を表すものである (ワールド行列ではない)。
(1つ以上の変換の合成による)任意の変換を表す変換行列$M$は、ただ1つの平行移動行列$T$と、ただ1つの回転行列$R$、及び ただ1つのスケール行列$S$の積として、\[M = TRS\]と表される。
そして、平行移動行列$T$の作成に必要となるデータは Vector3インスタンス1つであり、回転行列$R$の作成に必要となるデータは Quaternionインスタンス1つであり、スケール行列$S$の作成に必要となるデータは Vector3インスタンス1つである。
つまり、任意の変換を表す変換行列を作成するためには、平行移動のための1つの Vector3インスタンスと、回転のための1つの Quaternionインスタンスと、スケールのための1つの Vector3インスタンスがあればよいということである。
逆の言い方をすれば、平行移動のための1つの Vector3インスタンスと、回転のための1つの Quaternionインスタンスと、スケールのための1つの Vector3インスタンスがあれば任意の変換を表現できるということである。
ではここで、プログラムに着眼点を戻す。
上記では、Cubeに対して localPosition、localRotation、localScale を用いた次のコードによって変換を実行した。
そして、これらの記述順序、すなわち localPosition、localRotation、localScale に対してデータをセットする順序を変えても実行結果は変わらなかった。
つまり、コードにおける記述順序(各プロパティへのデータのセット順序)は、変換の実行順序には影響していないということである。
実際には、localPosition、localRotation、localScale に対するデータのセットは次の意味を持っている。
(先程も述べたように、ここで使われている変換行列$M$はオブジェクトのローカル行列を表している。したがって、「オブジェクトに実行される変換」とはそのオブジェクトの親座標系の中で実行される変換を意味しており、ワールド座標系の中での実行を意味してはいない。ただし、親オブジェクトを持たないオブジェクトの場合は親座標系とワールド座標系は一致する)
では、具体的な例で見ていく。
(1) (実行結果 図10)
これは、先ほどのコードであるが、このコードの意味することは、
「Cubeに対しては、スケール、回転、平行移動の順で変換を実行するが、各変換の内容は、
スケール : 各軸方向への $2$倍の拡大
回転 : y軸周り $-90$°の回転
平行移動 : $(6, 0, 0)$ の移動
である。」
(2) (実行結果 図11)
これは、上のコードの実行順序を入れ替えたもので、本節の中程で見たとおり実行結果は上のコードと変わらない。以下に示すこのコードの処理内容を見ればその理由は明らかであろう。
「Cubeに対しては、スケール、回転、平行移動の順で変換を実行するが、各変換の内容は、
スケール : 各軸方向への $2$倍の拡大
回転 : y軸周り $-90$°の回転
平行移動 : $(6, 0, 0)$ の移動
である。」
(3) (実行結果 図13)
このコードの処理内容は次のとおり。
「Cubeに対しては、スケール、回転、平行移動の順で変換を実行するが、各変換の内容は、
スケール : y軸方向のみ $1.5$倍の拡大
回転 : z軸周り $180$°の回転
平行移動 : $(5,\ 1.5,\ 10)$ の移動
である。」
(2行目の Vector3.forward は z軸プラス方向 $(0, 0, 1)$ を表す定数)
(4) (実行結果 図14)
このコードでは、1行目と3行目に localPosition へのデータセットがあり、2行目と4行目に localRotation へのデータセットがある。このように、1つのプロパティに対して複数回のデータセットがある場合、一番最後にセットしたデータが反映される (これは プログラミングにおいて変数へデータをセットする場合と同様である)。したがって、この場合は1行目の localPosition、3行目の localRotation へのデータセットは2行目、4行目において上書きされてしまう (つまり、フレーム描画前に このようにオブジェクト変換用の同一プロパティに何度もデータをセットすることは意味がない)。
このコードの処理内容は次のとおり。
「Cubeに対しては、スケール、回転、平行移動の順で変換を実行するが、各変換の内容は、
スケール : y軸方向のみ $1.5$倍の拡大
回転 : z軸周り $180$°の回転
平行移動 : $(5,\ 1.5,\ 10)$ の移動
である。」

図13 (3) 実行結果 
図14 (4) 実行結果
繰り返しになるが、標準的な変換方法では、オブジェクトに対して実行される変換は、常に スケール、回転、平行移動の順で行われる。そして、それらの3つの変換の内容は localScale、localRotation、localPosition に対して指定するのである。
本節では、Unityにおける標準的な変換方法についての基本的な事柄を一通り解説した。第4章までのプログラムでは、一貫して行列を使ってきたが、本節において、標準的な方法への’橋渡し’が行われたわけである。しかし、標準的な変換方法についても、その根底には行列が重要な意味を持って存在していることは本節において見てきたとおりである。
極端な言い方をすれば、標準的な方法で使われる3つのプロパティ localScale、localRotation、localPosition は、行列が姿形を変えて使われているに過ぎないのである。
上でも述べたように 3つのプロパティ localPosition、localRotation、localScale はローカル行列を作成するためのものである。したがって、その値は親座標系における値である。簡単に言えば、localPosition は親座標系における位置であり、localRotation は親座標系における向き、localScale は親座標系における大きさである。
UnityのTransformクラスにはこの他に position (Vector3型)、rotation (Quaternion型)、lossyScale (Vector3型)というプロパティがあるが、これらのプロパティが表すものはワールド座標系における値、すなわち、ワールド座標系における位置、向き、大きさである。
オブジェクトが他のオブジェクトと親子関係を持たない単独のオブジェクトの場合は、そのオブジェクトの親座標系はワールド座標系であるから、localPosition、localRotation、localScale と position、rotation、lossyScale の内容は同じものである。
例えば、上のプログラムで使われているCubeは親子関係を持たない単独のオブジェクトであるから、プログラム中の localPosition を position に、localRotation を rotation に変えても同じ結果になる (lossyScaleは読み込み専用なのでlocalScaleの代わりに使うことはできない)。
しかし、この方法は講義用に独自に実装したものであり、Unityの標準的な機能ではないことは すでに述べた。前節で少し触れたように、Unityでは、オブジェクトに対する何らかの変換の実行は Transformクラスを通して行われる。具体的には、オブジェクトを動かすためには、そのオブジェクトが所有する Transform型の transform というプロパティを経由して、Transformクラスの各プロパティに適切な値をセットしていく (プロパティとは C#において、独自のアクセス定義がされているメンバ変数のことである。ここでは単にメンバ変数と捉えても構わない)。
まずは、Transformクラスで主に使用する3つのプロパティから始める。
A) localPosition, localRotation, localScale
Transformクラスは、オブジェクトの変換に関連する さまざまなプロパティやメソッドを持っている。それらのうち、この講義で主として使用するのは、以下の3つのプロパティである。localPosition localRotation localScale
それぞれの型は、localPosition が Vector3型、localRotation が Quaternion型、localScale が Vector3型である。Vector3 は今までのプログラムで何度も使われてきているので、説明は不要であろう。Quaternion(クォータニオン、四元数)とは回転を表す形式の1つである。今までのプログラムでは、回転は行列によって表されていたが、3Dコンピューターグラフィックスにおいては、回転を表す形式として Quaternionを使用する場合が非常に多い。Quaternionについては、第6章以降で本格的に使用していくが、本節での使用や解説は必要最小限に留める。
では実際に、この3つのプロパティを用いて、オブジェクトに変換を実行していく。
使用するオブジェクトは、図1に示される各辺の長さが $2$の立方体オブジェクト Cubeである (図2は Cubeを反対側から見たときのもの)。


オブジェクトを初期状態にするためには、各プロパティに次のようにセットする。
Obj.transform.localPosition = Vector3.zero; Obj.transform.localRotation = Quaternion.identity; Obj.transform.localScale = Vector3.one;
Vector3.zero、Quaternion.identity、Vector3.one は、いずれも Unity側に用意されている定数である。
Vector3.zero は、new Vector3(0, 0, 0) を表しており、これは移動量が $(0, 0, 0)$、すなわち平行移動が行われないことを意味する。
Quaternion.identity は、new Quaternion(0, 0, 0, 1) を表しており、これは何も回転を行わない Quaternion を意味する。詳しくは第6章で解説するが、オブジェクトに対して回転を行わない場合には、localRotation に Quaternion.identity をセットするのである。
Vector3.one は、new Vector3(1, 1, 1) を表しており、これは各軸の倍率が $1$倍、すなわちスケールが行われないことを意味する。
したがって、localPosition、localRotation、localScale に Vector3.zero、Quaternion.identity、Vector3.one をセットすると、平行移動も行われず、回転も行われず、スケールも行われない、すなわち、オブジェクトは何の変換も実行されていない状態、初期状態になるのである。
図1は Cubeの初期状態であるが、Cubeに対して次のコードを実行した結果である。
Cube.transform.localPosition = Vector3.zero; Cube.transform.localRotation = Quaternion.identity; Cube.transform.localScale = Vector3.one;
(注意 : Unity側に用意されている Vector3 や Quaternion は、クラスではなく、構造体である。したがって、参照型ではなく、値型である。つまり、上のコードにおける代入では、Vector3.zero、Quaternion.identity、Vector3.one の複製がセットされることになる)
では、次に Cubeに対して平行移動だけを実行する。
図3は 初期状態の Cubeであり、図4は Cubeを $(6, 0, 0)$ だけ平行移動させる次のコードを実行した結果である。
// (6, 0, 0) の平行移動 Cube.transform.localPosition = new Vector3(6, 0, 0);


続いて、Cubeに対して回転だけを実行した場合、スケールだけを実行した場合を示す。
図5は Cubeを y軸周りに $-90$° 回転させる次のコードを実行した結果である。
// y軸周り -90°の回転 Cube.transform.localRotation = Quaternion.AngleAxis(-90, Vector3.up);
ここで使用されているメソッド AngleAxis(..) は、Unity側に用意されている Quaternion の staticメソッドで、第1引数に回転角度(float型)、第2引数に回転軸(Vector3型)を指定する。つまり、Quaternion は任意軸回転が可能であり、この staticメソッドによって指定した軸周りに、指定の角度だけ回転させる Quaternion が返される。ここでは、y軸周りに $-90$°回転させる Quaternionを取得するために、第1引数に $-90$、第2引数に Vector3.up (y軸プラス方向 $(0, 1, 0)$ を表す定数)を指定している。
図6は Cubeを 各軸方向に $2$倍拡大する次のコードを実行した結果である。
// x軸、y軸、z軸方向に 2倍拡大 Cube.transform.localScale = new Vector3(2, 2, 2);


B) 標準的な変換方法
では次に、localPosition、localRotation、localScale を使った場合の変換の合成について見ていく。行列の場合、変換の合成は、それらの変換を表す変換行列の積によって表されていた。そして、変換行列の積においては、変換の実行順序は積の右から左へ進むのであった (列優先の場合 ; 3-8節参照)。
まずは、上で見てきた3つの変換を行列によって合成し、それを Cubeに実行することから始める。
Cube に実行する変換は次の3つである。
--> $(6, 0, 0)$ の平行移動
--> y軸周り $-90$°の回転
--> 各軸方向に $2$倍の拡大
(1) スケール、回転、平行移動の順序での実行 (実行結果 図7)
Matrix4x4 S = TH3DMath.GetScale4x4(2.0f); Matrix4x4 R = TH3DMath.GetRotation4x4(-90, Vector3.up); Matrix4x4 T = TH3DMath.GetTranslation4x4(6, 0, 0); Matrix4x4 M = T * R * S; Cube.SetMatrix(M);
(2) スケール、平行移動、回転の順序での実行 (実行結果 図8 ; プログラムの 1行目から 3行目は (1)と同じ)
Matrix4x4 M = R * T * S; Cube.SetMatrix(M);
(3) 平行移動、回転、スケールの順序での実行 (実行結果 図9 ; プログラムの 1行目から 3行目は (1)と同じ)
Matrix4x4 M = S * R * T; Cube.SetMatrix(M);
 図7 (1) スケール、回転、平行移動
図7 (1) スケール、回転、平行移動 図8 (2) スケール、平行移動、回転
図8 (2) スケール、平行移動、回転 図9 (3) 平行移動、回転、スケール
図9 (3) 平行移動、回転、スケール
図7は、(1)の実行結果で、スケール、回転が(原点において)先に行われ、平行移動が最後に実行されるので、最終的な Cubeの位置は x軸上に移動している。
図8は、(2)の実行結果で、スケール、平行移動、そして最後に回転が実行される。平行移動が行われた時点では、Cubeは x軸上に移動しているが、そこから y軸周りに $-90$°の回転が実行されるので、最終的には z軸上に移ることになる。
図9は、(3)の実行結果で、まず始めに平行移動が行われ、x軸上に移動、次に y軸周り $-90$°の回転によって z軸上に移される。さらに、そこから各軸方向への $2$倍の拡大が実行される。これによって、Cubeの各頂点は原点からの距離が $2$倍になる。結果的には、(2)の実行結果の位置から z軸方向へ $2$倍離れた位置に移動する。
つまり、行列による変換の合成では、実行順序を変えた場合には実行結果が異なってしまうわけである (「実行結果は同じになるとは限らない」という表現の方がより適切である)。
変換の実行順序を入れ替えた場合に、実行結果が変わることについては、1-8節や 3-13節で見てきたことであり、ここでの結果は いささか自明なことであったかもしれない。
では、localPosition、localRotation、localScale について、上で行ったように実行順序を入れ替えた場合、どのような結果になるかについて見ていこう (実行される変換は、上と同じく $(6, 0, 0)$ の平行移動、y軸周り $-90$°の回転、各軸方向への $2$倍の拡大 である)。
(1) スケール、回転、平行移動の順序での実行 (実行結果 図10)
Cube.transform.localScale = new Vector3(2, 2, 2); Cube.transform.localRotation = Quaternion.AngleAxis(-90, Vector3.up); Cube.transform.localPosition = new Vector3(6, 0, 0);
(2) スケール、平行移動、回転の順序での実行 (実行結果 図11)
Cube.transform.localScale = new Vector3(2, 2, 2); Cube.transform.localPosition = new Vector3(6, 0, 0); Cube.transform.localRotation = Quaternion.AngleAxis(-90, Vector3.up);
(3) 平行移動、回転、スケールの順序での実行 (実行結果 図12)
Cube.transform.localPosition = new Vector3(6, 0, 0); Cube.transform.localRotation = Quaternion.AngleAxis(-90, Vector3.up); Cube.transform.localScale = new Vector3(2, 2, 2);
 図10 (1) スケール、回転、平行移動
図10 (1) スケール、回転、平行移動 図11 (2) スケール、平行移動、回転
図11 (2) スケール、平行移動、回転 図12 (3) 平行移動、回転、スケール
図12 (3) 平行移動、回転、スケール
上の図から明らかなように、localPosition、localRotation、localScale を使った変換では、順序を入れ替えて実行した場合でも、実行結果はすべて同じ結果になっている。そして、この結果は行列を使用した場合の (1)の実行順序、スケール、回転、平行移動の順で変換を実行した場合と同じ結果である(図7)。
では、この変換の原理について解説しよう。
4-6節では、(1つ以上の変換の合成による)任意の変換を表す変換行列$M$に対して、次のような書き換えを行った (「任意の変換を表す変換行列$M$」は3-13節や4-6節で述べたスケールについての取り決めに従っているものとする)。
\[M = \begin{pmatrix}m_{11} &m_{12} &m_{13} &m_{14} \\m_{21} &m_{22} &m_{23} &m_{24} \\m_{31} &m_{32} &m_{33} &m_{34} \\0 &0 &0 &1 \end{pmatrix} =\begin{pmatrix}s_x r_{11} &s_y r_{12} &s_z r_{13} &t_x \\s_x r_{21} &s_y r_{22} &s_z r_{23} &t_y \\s_x r_{31} &s_y r_{32} &s_z r_{33} &t_z \\0 &0 &0 &1 \end{pmatrix} \]
さらに、この書き換えの行われた $M$は、以下に示される 平行移動行列$T$、回転行列$R$、スケール行列$S$\[T = \begin{pmatrix}1 &0 &0 &t_x \\0 &1 &0 &t_y \\ 0 &0 &1 &t_z \\0 &0 &0 &1\end{pmatrix} \qquad R = \begin{pmatrix}r_{11} &r_{12} &r_{13} &0 \\r_{21} &r_{22} &r_{23} &0 \\r_{31} &r_{32} &r_{33} &0 \\0 &0 &0 &1 \end{pmatrix} \qquad S = \begin{pmatrix}s_x &0 &0 &0 \\0 &s_y &0 &0 \\ 0 &0 &s_z &0 \\0 &0 &0 &1\end{pmatrix}\]
の積として、次のように、求められるのであった。\begin{align*}M = TRS &= \begin{pmatrix}1 &0 &0 &t_x \\0 &1 &0 &t_y \\ 0 &0 &1 &t_z \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}r_{11} &r_{12} &r_{13} &0 \\r_{21} &r_{22} &r_{23} &0 \\r_{31} &r_{32} &r_{33} &0 \\0 &0 &0 &1 \end{pmatrix}\begin{pmatrix}s_x &0 &0 &0 \\0 &s_y &0 &0 \\ 0 &0 &s_z &0 \\0 &0 &0 &1\end{pmatrix} \\\\&=\begin{pmatrix}s_x r_{11} &s_y r_{12} &s_z r_{13} &t_x \\s_x r_{21} &s_y r_{22} &s_z r_{23} &t_y \\s_x r_{31} &s_y r_{32} &s_z r_{33} &t_z \\0 &0 &0 &1 \end{pmatrix} \\\\\end{align*}
ここで、着眼点を3つの変換行列 $T$、$R$、$S$ に移して話を進める。3-9節で述べたように、平行移動行列を作成するために必要なデータは、第4列目の1行目から3行目に指定する、x軸方向の移動量、y軸方向の移動量、z軸方向の移動量の3つである ($T$においては、その3つのデータは、$t_x$, $t_y$, $t_z$ で表されている)。Unityでは、3つの(浮動点小数)データを1つの Vector3インスタンスに保持することができる。したがって、平行移動行列$T$を作成するためには、1つの Vector3インスタンスがあればよいことになる。
また、3-12節で述べたように、スケール行列を作成するために必要なデータは、1行1列目、2行2列目、3行3列目に指定する、x軸方向の倍率、y軸方向の倍率、z軸方向の倍率の3つである ($S$においては、その3つのデータは、$s_x$, $s_y$, $s_z$ で表されている)。したがって、スケール行列$S$を作成する場合にも、1つの Vector3インスタンスがあればよいことになる。
回転行列については、やや事情が異なる。3-11節では、ロドリゲスの回転公式による任意軸周りの回転行列について扱った。オブジェクトを回転させるために、プログラム内で頻繁に使用したカスタムライブラリのメソッド TH3DMath.GetRotation4x4(float deg, Vector3 axis) も、ロドリゲスの回転公式に基づいた $4\times 4$の回転行列を返すものであることは、そこで述べた。また、上で述べたように、Unityでは、基本的に回転は Quaternionで表す。
そして、Quaternionと回転行列の間では相互変換が可能なのである。つまり、ある回転が Quaternionで表されている場合、その回転を$4\times 4$回転行列に、逆に、ある回転が $4\times 4$回転行列で表されている場合、その回転を Quaternionで表すことも可能なのである (Quaternionも回転を表す1つの形式に過ぎない。今までのプログラムでは、回転はすべて行列という形式で表していたのである)。
Unityには、Quaternionを行列に変換するために、以下のメソッドが用意されている。
// Quaternionを行列に変換する (Matrix4x4インスタンスが返される) Matrix4x4.Rotate(Quaternion q)
また、Unityでは任意軸周りの回転を表す Quaternionインスタンスを、上でも使用した次のメソッドで取得できる。
// 回転軸axisの周りに、角度degだけ回転させる Quaternionを返す Quaternion.AngleAxis(float deg, Vector3 axis)
Quaternion q = Quaternion.AngleAxis(deg, axis); Matrix4x4 R = Matrix4x4.Rotate(q);
上で述べてきたことをまとめると次のようになる。
(注) 以下の文章中における「変換行列$M$」はオブジェクトのローカル行列を表すものである (ワールド行列ではない)。
(1つ以上の変換の合成による)任意の変換を表す変換行列$M$は、ただ1つの平行移動行列$T$と、ただ1つの回転行列$R$、及び ただ1つのスケール行列$S$の積として、\[M = TRS\]と表される。
そして、平行移動行列$T$の作成に必要となるデータは Vector3インスタンス1つであり、回転行列$R$の作成に必要となるデータは Quaternionインスタンス1つであり、スケール行列$S$の作成に必要となるデータは Vector3インスタンス1つである。
つまり、任意の変換を表す変換行列を作成するためには、平行移動のための1つの Vector3インスタンスと、回転のための1つの Quaternionインスタンスと、スケールのための1つの Vector3インスタンスがあればよいということである。
逆の言い方をすれば、平行移動のための1つの Vector3インスタンスと、回転のための1つの Quaternionインスタンスと、スケールのための1つの Vector3インスタンスがあれば任意の変換を表現できるということである。
ではここで、プログラムに着眼点を戻す。
上記では、Cubeに対して localPosition、localRotation、localScale を用いた次のコードによって変換を実行した。
Cube.transform.localScale = new Vector3(2, 2, 2); Cube.transform.localRotation = Quaternion.AngleAxis(-90, Vector3.up); Cube.transform.localPosition = new Vector3(6, 0, 0);
つまり、コードにおける記述順序(各プロパティへのデータのセット順序)は、変換の実行順序には影響していないということである。
実際には、localPosition、localRotation、localScale に対するデータのセットは次の意味を持っている。
オブジェクトに実行される変換は、必ずスケール、回転、平行移動の順序で実行される。つまり、それらの変換を表す変換行列を $S$、$R$、$T$ とし、オブジェクトに実行される変換行列の積を$M$とすれば、\[M = TRS\]となる。そして、各変換行列については、平行移動行列$T$は localPosition をもとに作成し、回転行列$R$は localRotation をもとに作成し、スケール行列$S$は localScale をもとに作成する。
(先程も述べたように、ここで使われている変換行列$M$はオブジェクトのローカル行列を表している。したがって、「オブジェクトに実行される変換」とはそのオブジェクトの親座標系の中で実行される変換を意味しており、ワールド座標系の中での実行を意味してはいない。ただし、親オブジェクトを持たないオブジェクトの場合は親座標系とワールド座標系は一致する)
では、具体的な例で見ていく。
(1) (実行結果 図10)
Cube.transform.localScale = new Vector3(2, 2, 2); Cube.transform.localRotation = Quaternion.AngleAxis(-90, Vector3.up); Cube.transform.localPosition = new Vector3(6, 0, 0);
「Cubeに対しては、スケール、回転、平行移動の順で変換を実行するが、各変換の内容は、
スケール : 各軸方向への $2$倍の拡大
回転 : y軸周り $-90$°の回転
平行移動 : $(6, 0, 0)$ の移動
である。」
(2) (実行結果 図11)
Cube.transform.localScale = new Vector3(2, 2, 2); Cube.transform.localPosition = new Vector3(6, 0, 0); Cube.transform.localRotation = Quaternion.AngleAxis(-90, Vector3.up);
「Cubeに対しては、スケール、回転、平行移動の順で変換を実行するが、各変換の内容は、
スケール : 各軸方向への $2$倍の拡大
回転 : y軸周り $-90$°の回転
平行移動 : $(6, 0, 0)$ の移動
である。」
(3) (実行結果 図13)
Cube.transform.localPosition = new Vector3(5f, 1.5f, 10f); Cube.transform.localRotation = Quaternion.AngleAxis(180, Vector3.forward); Cube.transform.localScale = new Vector3(1f, 1.5f, 1f);
「Cubeに対しては、スケール、回転、平行移動の順で変換を実行するが、各変換の内容は、
スケール : y軸方向のみ $1.5$倍の拡大
回転 : z軸周り $180$°の回転
平行移動 : $(5,\ 1.5,\ 10)$ の移動
である。」
(2行目の Vector3.forward は z軸プラス方向 $(0, 0, 1)$ を表す定数)
(4) (実行結果 図14)
Cube.transform.localPosition = new Vector3(-1f, -1f, 8f); Cube.transform.localRotation = Quaternion.AngleAxis(30, Vector3.right); Cube.transform.localPosition = new Vector3(5f, 1.5f, 10f); Cube.transform.localRotation = Quaternion.AngleAxis(180, Vector3.forward); Cube.transform.localScale = new Vector3(1f, 1.5f, 1f);
このコードの処理内容は次のとおり。
「Cubeに対しては、スケール、回転、平行移動の順で変換を実行するが、各変換の内容は、
スケール : y軸方向のみ $1.5$倍の拡大
回転 : z軸周り $180$°の回転
平行移動 : $(5,\ 1.5,\ 10)$ の移動
である。」


繰り返しになるが、標準的な変換方法では、オブジェクトに対して実行される変換は、常に スケール、回転、平行移動の順で行われる。そして、それらの3つの変換の内容は localScale、localRotation、localPosition に対して指定するのである。
本節では、Unityにおける標準的な変換方法についての基本的な事柄を一通り解説した。第4章までのプログラムでは、一貫して行列を使ってきたが、本節において、標準的な方法への’橋渡し’が行われたわけである。しかし、標準的な変換方法についても、その根底には行列が重要な意味を持って存在していることは本節において見てきたとおりである。
極端な言い方をすれば、標準的な方法で使われる3つのプロパティ localScale、localRotation、localPosition は、行列が姿形を変えて使われているに過ぎないのである。
# Code1
[Code1] (実行結果 図10)Cube.transform.localScale = new Vector3(2, 2, 2); Cube.transform.localRotation = Quaternion.AngleAxis(-90, Vector3.up); Cube.transform.localPosition = new Vector3(6, 0, 0);
# Code2
[Code2] (実行結果 図13)Cube.transform.localPosition = new Vector3(5f, 1.5f, 10f); Cube.transform.localRotation = Quaternion.AngleAxis(180, Vector3.forward); Cube.transform.localScale = new Vector3(1f, 1.5f, 1f);
上でも述べたように 3つのプロパティ localPosition、localRotation、localScale はローカル行列を作成するためのものである。したがって、その値は親座標系における値である。簡単に言えば、localPosition は親座標系における位置であり、localRotation は親座標系における向き、localScale は親座標系における大きさである。
UnityのTransformクラスにはこの他に position (Vector3型)、rotation (Quaternion型)、lossyScale (Vector3型)というプロパティがあるが、これらのプロパティが表すものはワールド座標系における値、すなわち、ワールド座標系における位置、向き、大きさである。
オブジェクトが他のオブジェクトと親子関係を持たない単独のオブジェクトの場合は、そのオブジェクトの親座標系はワールド座標系であるから、localPosition、localRotation、localScale と position、rotation、lossyScale の内容は同じものである。
例えば、上のプログラムで使われているCubeは親子関係を持たない単独のオブジェクトであるから、プログラム中の localPosition を position に、localRotation を rotation に変えても同じ結果になる (lossyScaleは読み込み専用なのでlocalScaleの代わりに使うことはできない)。
© 2020-2025 Redpoll's 60 (All rights reserved)