Redpoll's 60
Home / 3Dプログラミング入門 / 第5章 $§$5-4
第5章 変換のオブジェクト化
| $§$5-1 要旨 | $§$5-6 Transformクラスの実装 2 |
| $§$5-2 Unityにおける標準的な変換方法 1 | $§$5-7 Transformクラスの実装 3 |
| $§$5-3 Unityにおける標準的な変換方法 2 | $§$5-8 いくつかの使用例 |
| $§$5-4 Unityにおける標準的な変換方法 3 | $§$5-9 課題 |
| $§$5-5 Transformクラスの実装 1 |
$§$5-4 Unityにおける標準的な変換方法 3
本節では、以前に作成したいくつかのプログラムの書き換えを行う。それらのプログラムは、オブジェクトに対して変換行列を実行する形で実装されていたが、それを5-2節と5-3節で述べた Unityの標準的な変換方法を使用したものに書き換える。
[4-1節 Code5] (実行結果 図1)
Unityの標準的な変換方法によって実装したプログラムを以下に示す (実行結果は変わらない)。
[Code1] (実行結果 図1)
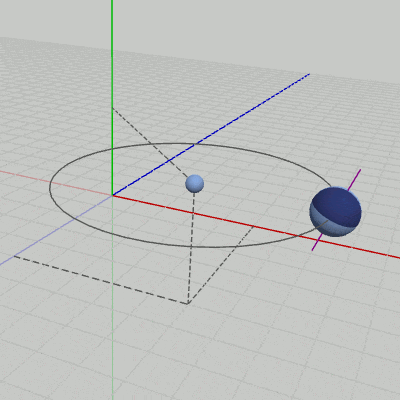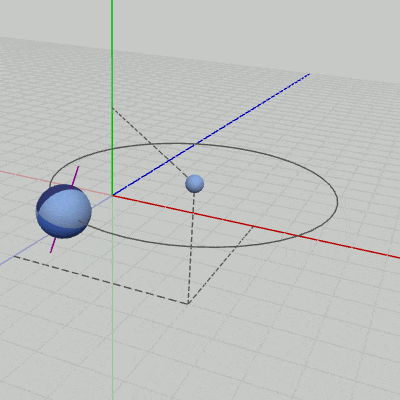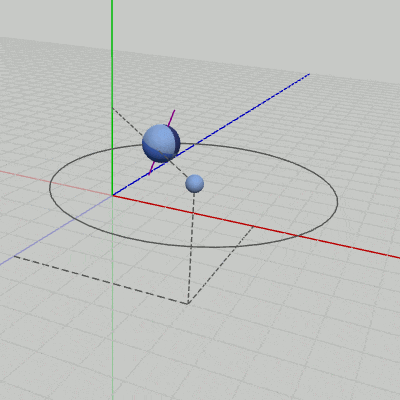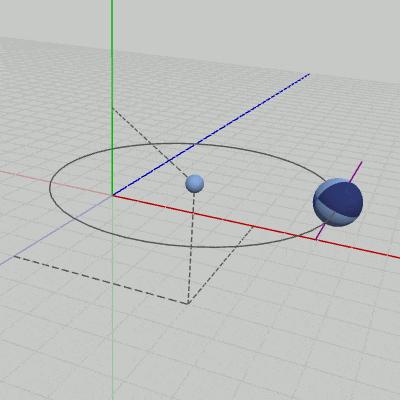
図1 Code1 実行結果 行列のプログラムにおいては、Sphereに最終的に実行される変換行列Mは平行移動行列Tと回転行列Rの積であるが、標準的変換のプログラムでは、11行目の localPosition が平行移動行列Tに対応し、12行目の localRotation が回転行列Rに対応している。すなわち localPosition、localRotation には、平行移動行列T、回転行列Rと同じ内容になるように値がセットされている。
標準的な変換方法では必要に応じて3つのプロパティ localPosition、localRotation、
localScale の値を更新すればよい。例えば、位置を変化させる必要がないのであれば localPosition の値を更新する必要はない (最後に設定された値の状態がずっと続く。つまり、localPositionを更新しなければ最後に設定された位置から動かない)。
なお Sphereは親オブジェクトを持たないので、変換に使われているプロパティ localPosition、localRotation を position、rotation としても結果は同じである。
[4-2節 Code2] (実行結果 図2)
Unityの標準的な変換方法によって実装したプログラムを以下に示す。
[Code2] (実行結果 図2)
1行目のifブロックは親子関係を設定するための初期化ブロックであり、プログラム実行開始時に1度だけ入るブロックである。i_INITIALIZEDは、初期化ブロックの処理が行われたかを示すbool型インスタンス変数であり初期値はfalseである。1度このifブロックに入ると、i_INITIALIZEDの値がtrueになるので、それ以降プログラムの実行中にこのブロックに入ることはない。
この初期化ブロックは親子関係の設定を行うための部分であり、ここでは Propellerの親オブジェクトとして Bodyを設定している。
今までの行列によるプログラムの場合、階層構造にあるオブジェクトの変換はプログラムにおいて次のように定義されていた。
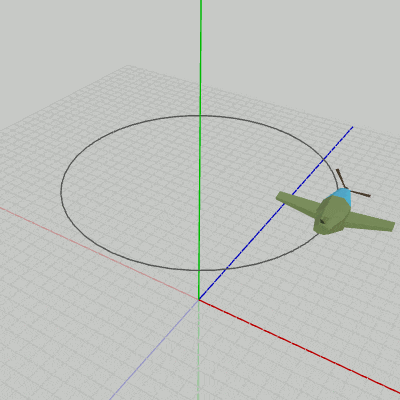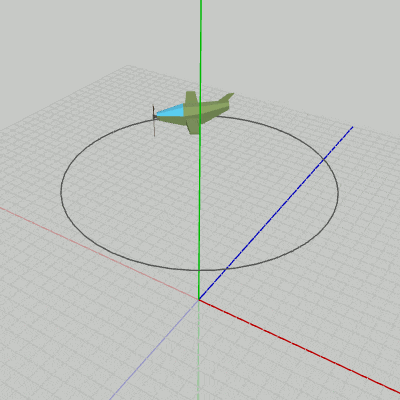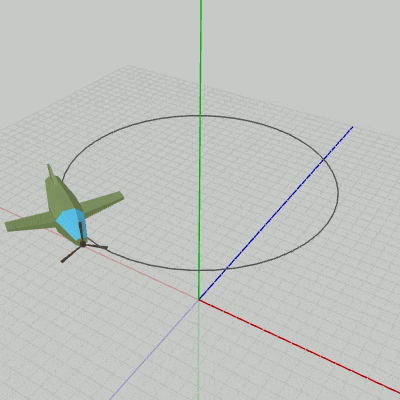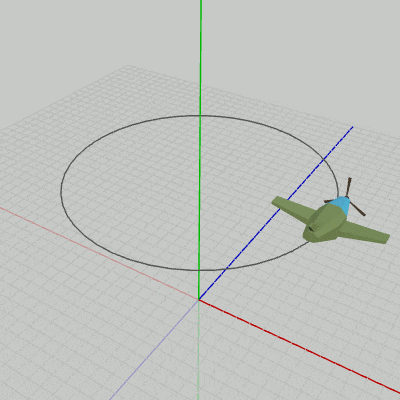
図2 Code2 実行結果 各オブジェクトのローカル行列はスケール行列、回転行列、平行移動行列の積であり、この順序で掛けられる。このローカル行列を求める際の平行移動行列、回転行列、スケール行列が、標準的な変換方法における localPosition、localRotation、localScale に対応している。
例えば、Obj3の localPosition に設定する値は、Obj3の平行移動行列traObj3の内容と同じものになるようにすればよい。Obj3の localRotation、localScale に設定する値についても同様に、Obj3の回転行列rotObj3、スケール行列sclObj3の内容と同じものになるようにすればよい。
上のCode2の場合を例にとると、行列による実装では Propellerのローカル行列localPropellerは回転行列rotPropと平行移動行列traPropの積である。回転行列rotPropの内容はz軸周りに角度i_degPropellerだけ回転させるというものであるが、標準的な変換方法のプログラムにおいても、Propellerの localRotation(13行目) には同じ内容の回転がセットされている。平行移動行列traPropの内容はアタッチポジションc_attachPos_Propellerへの平行移動であるが、標準的な変換方法のプログラムにおいても、Propellerの localPosition(12行目) には c_attachPos_Propeller がセットされるので同じ内容の平行移動が行われることになる。
Bodyの場合も同様に、行列による実装のプログラムでは Bodyのローカル行列は回転行列rotBodyと平行移動行列traBodyの積であるが、これらの行列の内容は標準的な変換方法のプログラムにおける Bodyの localRotation(20行目)、localPosition(19行目) の内容と同じものである。
なお、プログラム12行目では以下のように毎フレーム Propellerの localPositionには同じ定数ベクトルc_attachPos_Propellerがセットされるが、このようにプログラム実行中にプロパティの内容が変わらないのであれば、初期化処理のブロックにおいて1度だけセットすればよい。具体的には、この12行目を最初の初期化ブロックの中に移動すればよい (以下の9行目)。
このように、オブジェクトの localPosition、localRotation、localScaleのうちでプログラム実行中に変更しないと分かっているものは初期化時に1度だけ値を設定すれば、それ以降のフレームにおいても最初に設定した値のまま変わることはない。
[4-10節 Code5] (実行結果 図4)
このプログラムは3つのオブジェクト Disk、Arm、Sphere の一体化した運動を扱ったものであるが、図3はそれらのオブジェクトの階層構造であり、図4はプログラムの実行結果である。
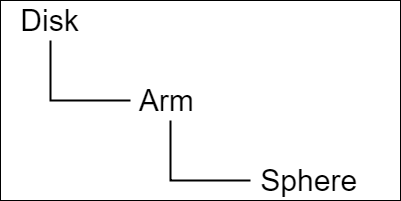
図3 オブジェクトの階層構造 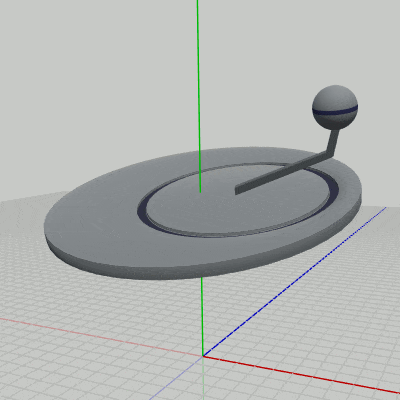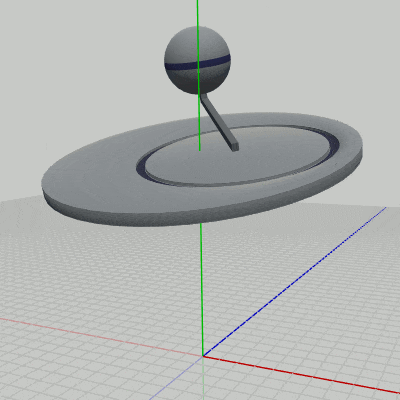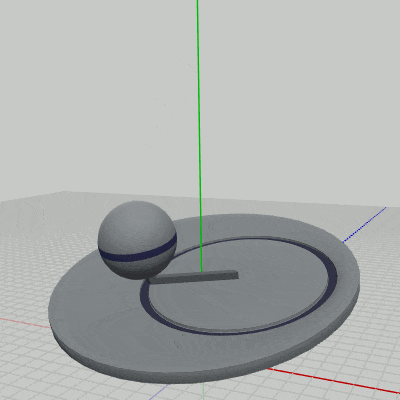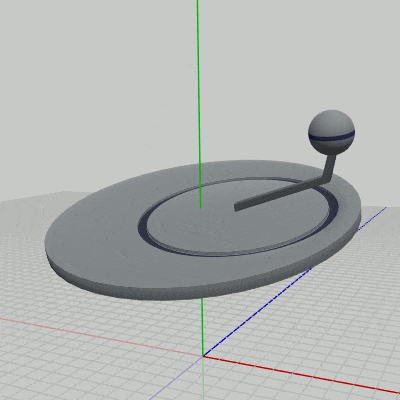
図4 Code3 実行結果
Unityの標準的な変換方法によって実装したプログラムを以下に示す。
[Code3] (実行結果 図4)
このプログラムにおいても13行目の Sphere.transform.localPosition、18行目の Arm.transform.localPosition、22行目の Disk.transform.localRotation には毎フレーム同じ値がセットされている。したがって、これらの処理を初期化ブロックに移しても結果は同じである。
[4-14節 Code2] (実行結果 図6)
このプログラムは4つのオブジェクト Pole、Arm0、Box0、Propeller0 の一体化した運動を扱ったものであるが、図5はそれらのオブジェクトの階層構造であり、図6はプログラムの実行結果である。
図5 オブジェクトの階層構造 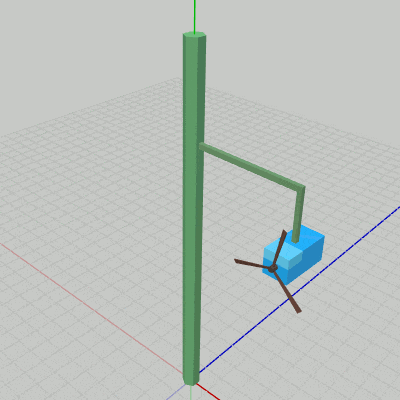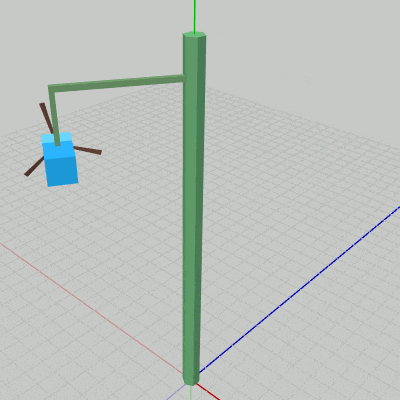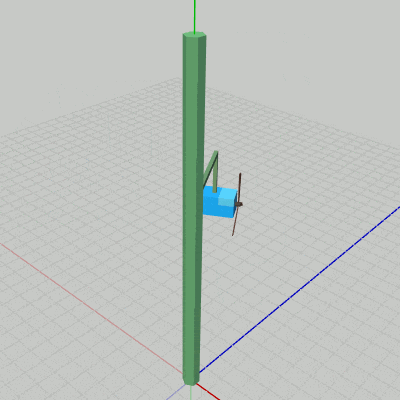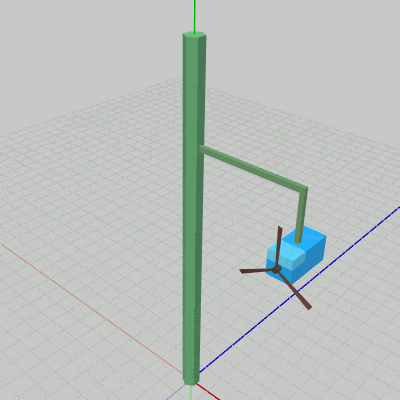
図6 Code4 実行結果
Unityの標準的な変換方法によって実装したプログラムを以下に示す。
(以下のプログラムではオブジェクトの名前が ArmArray、BoxArray、PropellerArray に変わっている)
[Code4] (実行結果 図6)
先程も述べたように、オブジェクトのプロパティのうちでプログラム実行中に1度設定すればよいものは初期化ブロックに記述すればよい。上のコードをそのように改めると以下のようになる。
[Code4 修正版] (実行結果 図6)
Propeller0のlocalPosition、Box0のlocalPositionは実行中に変更することがないので、それらに対するデータのセットが初期化ブロックに記述されている (9~10行目)。
[4-14節 Code5] (実行結果 図8)
このプログラムは3つのArm、3つのBox、3つのPropeller 及び Poleの一体化した運動を扱ったものである。図7はすべてのオブジェクトを一体化した際の階層構造であり、図8はプログラムの実行結果である。
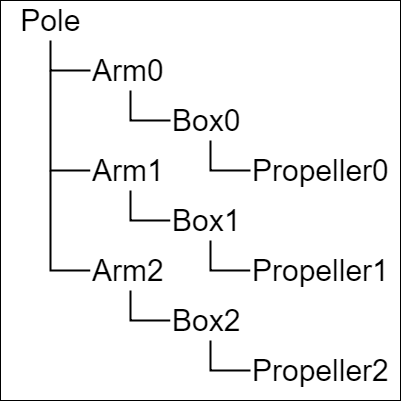
図7 オブジェクトの階層構造 
図8 Code4 実行結果
Unityの標準的な変換方法によって実装したプログラムを以下に示す。
(以下のプログラムにおいても Arm、Box、Propeller は ArmArray、BoxArray、PropellerArray として使われている)
[Code5] (実行結果 図8)
このプログラムにも、オブジェクトのプロパティへ毎フレーム同じ値をセットしている処理があるので、それらを初期化ブロックにまとめると以下のようになる。
[Code5 修正版] (実行結果 図8)
先程のプログラムでは各Propellerのアタッチポジションへの移動、各Boxのアタッチポジションへの移動、及び 各ArmをPoleの3つの面へ $120^\circ$ おきに配置する処理は、毎フレーム同じ値を各オブジェクトのプロパティへセットしていたが、この修正版ではそれらの処理は初期化ブロックへ移されている (17~22行目)。
[4-20節 Code1] (実行結果 図11)
このプログラムは下図9のオブジェクト Navy が3D空間内を飛行しながら細長い形のShell(図10)を連射するというプログラムであり、図11はその実行結果である。
Unityの標準的な変換方法によって実装したプログラムを以下に示す。
[Code6] (実行結果 図11)
行列による実装ではNavyに実行されている変換行列及びその回転成分を取得するために次のように記述されていた。
標準的な変換方法ではこの部分が次のように変更されている。
30行目の Navy.transform.localToWorldMatrix は Navy.GetMatrix() と内容は同じでありこの点は変わらないが、31行目ではQuaternion型のローカル変数 rotNavy に Navy.transform.rotation をセットしている。 transform.rotation はオブジェクトの現在の回転状態がセットされているQuaternion型のプロパティであるため、Navyに実行されている回転はこのプロパティから取得することができる。
Shellを発射開始位置にセットする処理は行列による実装では次のように記述されていた。
これはShellをNavyと同じ回転状態(同じ向き)にするために、まずShellのrotMatrixというプロパティにNavyに実行されている回転行列(R)をセットし、その回転行列と発射開始位置(startPos)に移動させる平行移動行列の積を求め、それをShellに実行するという手順である。
今回の position、rotation による実装では以下のように変更されている。
Shellを発射開始位置に移動させるために transform.position に startPos をセットし、Navyと同じ回転状態にするためには transform.rotation に rotNavy をセットすればよい。
発射されたShellは直進的に進んで行くが、行列版の実装ではその処理は次のように記述されていた。
50行目の mtx の内容はまずShellを発射されたときと同じ回転状態にして、新しい位置(newShellPos)に移動させるというものであり、Shellの移動中はこれが毎フレーム 実行される。しかし 移動中のShellの向きは変わることはないので、Shellに実行される回転行列 shell.rotMatrix の内容は常に同じである。
この処理は標準的な変換方法では次のように変更されている。
標準的な方法では、Shellが発射される際にNavyと同じ向きにするために transform.rotation に rotNavy がセットされる。そしてShellの移動中は位置だけが変化し、回転状態は変わらない。したがってShellの移動中には transform.position の内容だけを毎フレーム 更新すればよく、transform.rotation の内容は変える必要はない。
以下のプログラムは読者用の課題である。
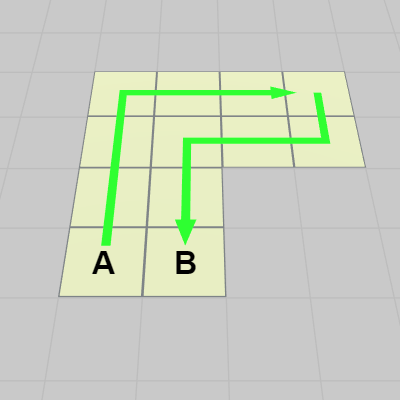
図12 サイコロの移動経路 
図13 開始時点ではサイコロはA地点に置かれている。
3-19節の課題はそのプログラムを行列で作成するものであったが、ここでの課題はこのサイコロの回転移動のプログラムを行列を使わずに、標準的な変換方法で実装することである (プログラムで使用するオブジェクト Dice は親オブジェクトを持たないので、変換に用いるプロパティはlocalPosition、localRotation であっても position、rotation であっても構わない)。
プログラムは Sec504.cs内のCode7に作成するものとする。Code7は最初の段階では以下のコードのみが記述されている。
[Code7]
使用するインスタンス変数や定数は 3-19節 Code1 のものと同じであり、ここではその説明については省略するが、1点だけ違いがある。3-19節ではサイコロの回転状態を保持するために i_curRotation というインスタンス変数が用意されていたが、今回はこの変数を使う必要はない。オブジェクトの現在の回転状態は Obj.transform.localRotation によって取得することができるので、オブジェクトを現在の状態からさらに回転させるには次のように記述すればよい。
このコードではオブジェクトの回転状態が変化するだけで、位置や大きさなどは変わらない。
なお 前節の終わりでも述べたが、回転後の新しい位置の計算は行列でもQuaternionでも、計算の仕方はほとんど変わらない。例えば、点$P = (a, b, c)$ を x軸周りに $120^\circ$ 回転させたときの位置は行列を使う場合は次のように記述される (回転後の位置を $Q$ とする)。
Quaternionで計算する場合は次のように書き換えればよい。
Quaternionによる計算では同次座標化する必要はないので、プログラム中の P は Vector3型のままで問題ない。
解答例については Sec504_Ans.txt内の Code7 を参照 (Sec504_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。

図14 立方体 展開された状態 (各数字はFace0~Face5を表している) 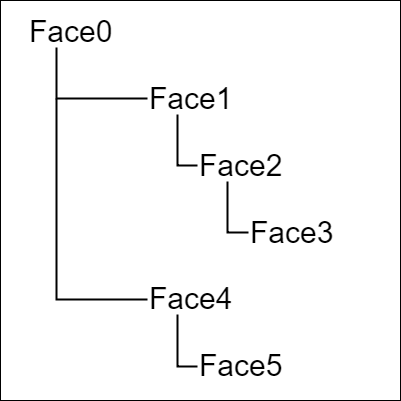
図15 オブジェクトの階層構造
ここでの課題も立方体の展開された状態、及び組み立てられた状態の間を行き来するプログラムの作成であるが、その際の展開された状態は図14の状態を使うものとする。そして、このプログラムもまた行列ではなく localPosition、localRotation によって実装するものとする。
以下の図16~18はこのプログラムで使用するオブジェクトの初期状態であり、上図15は各オブジェクトの階層構造である。
4-15節と同様に立方体の6個のそれぞれの面に対して6個のオブジェクト Face0 ~ Face5 が対応している。今回の立方体も1辺の長さは $1$ であり、Face0~Face5はいずれも1辺の長さが $1$ の正方形である。
Face0(図16)は立方体の底面で一番上の親オブジェクトであるが、初期状態における位置は x軸プラス側、z軸マイナス側に置かれている。
Face1~Face4は側面である。Face1、Face2、Face3の3つは初期状態において x軸プラス側、z軸プラス側に置かれており(図17)、Face4は初期状態において x軸マイナス側、z軸マイナス側に置かれている(図18)。
また、Face5は立方体の上の面であるが、この面もFace4と同じく初期状態においては x軸マイナス側、z軸マイナス側に置かれている(図18)。
4-15節 Code7では立方体を展開された状態にするためには、各Faceに対しアタッチポジションまでの平行移動だけを行えばよかったが、それはここでも同様である。図14は展開された状態の図であるが、各Faceに実行されている変換はアタッチポジションまでの平行移動のみである (図中の各数字はFace0~Face5を表している)。
このプログラムには以下のインスタンス変数が用意されている。
4-15節と同じく Face0~Face5はプログラム中ではFace[0]~Face[5]の配列として用意されている。
また、展開及び組み立ての際のキー操作については以下のキーを使用するものとする。
J : 立方体を組み立てる。
K : 立方体を展開する。
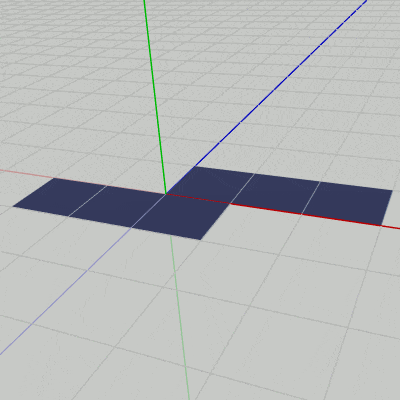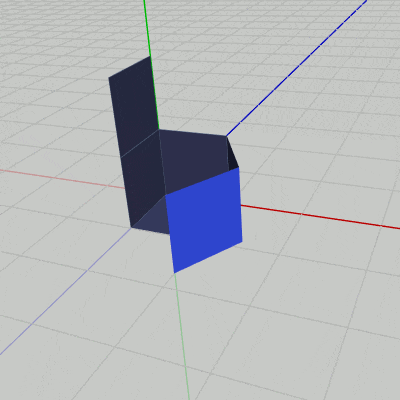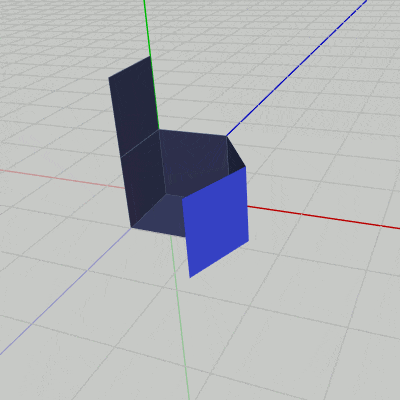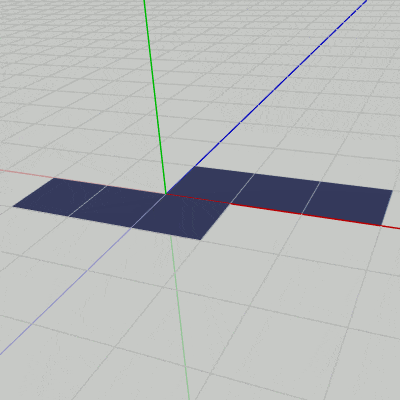
図19 Code8 実行結果 プログラムの作成は Sec504.cs内のCode8に行うものとする (Code8は最初の段階では空の初期化ブロックのみが記述されている)。
解答例については Sec504_Ans.txt内の Code8 を参照。
右図19は解答例のプログラムの実行結果であるが、一方の状態からもう一方の状態への変化にかかるフレーム数は240フレームである。
# Code1
以下のプログラムは 4-1節 Code5である (オブジェクトの変換は行列によって実装されている)。[4-1節 Code5] (実行結果 図1)
i_degRot += 4.0f; Matrix4x4 rotY = TH3DMath.GetRotation4x4(i_degRot, Vector3.up); Matrix4x4 rotZ = TH3DMath.GetRotation4x4(-20.0f, Vector3.forward); Matrix4x4 R = rotZ * rotY; i_degRev += 1.0f; Matrix4x4 rev = TH3DMath.GetRotation4x4(i_degRev, Vector3.up); Vector3 np = rev * new Vector4(3.0f, 0.0f, 0.0f, 1.0f); np += c_centerPos; Matrix4x4 T = TH3DMath.GetTranslation4x4(np); Matrix4x4 M = T * R; Sphere.SetMatrix(M);
Unityの標準的な変換方法によって実装したプログラムを以下に示す (実行結果は変わらない)。
[Code1] (実行結果 図1)
i_degRot += 4.0f; Quaternion rotY = Quaternion.AngleAxis(i_degRot, Vector3.up); Quaternion rotZ = Quaternion.AngleAxis(-20.0f, Vector3.forward); Quaternion rot = rotZ * rotY; i_degRev += 1.0f; Matrix4x4 rev = TH3DMath.GetRotation4x4(i_degRev, Vector3.up); Vector3 np = rev * new Vector4(3.0f, 0.0f, 0.0f, 1.0f); Vector3 pos = np + c_centerPos; Sphere.transform.localPosition = pos; Sphere.transform.localRotation = rot;

標準的な変換方法では必要に応じて3つのプロパティ localPosition、localRotation、
localScale の値を更新すればよい。例えば、位置を変化させる必要がないのであれば localPosition の値を更新する必要はない (最後に設定された値の状態がずっと続く。つまり、localPositionを更新しなければ最後に設定された位置から動かない)。
なお Sphereは親オブジェクトを持たないので、変換に使われているプロパティ localPosition、localRotation を position、rotation としても結果は同じである。
# Code2
以下のプログラムは 4-2節 Code2である (オブジェクトの変換は行列によって実装されている)。[4-2節 Code2] (実行結果 図2)
i_degPropeller += 15; Matrix4x4 rotProp = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward); Matrix4x4 traProp = TH3DMath.GetTranslation4x4(c_attachPos_Propeller); Matrix4x4 localPropeller = traProp * rotProp; i_degBody -= 2; Matrix4x4 rotBody = TH3DMath.GetRotation4x4(i_degBody, Vector3.up); Vector3 np = rotBody * new Vector4(8.0f, 10.0f, 0.0f, 1.0f); Matrix4x4 traBody = TH3DMath.GetTranslation4x4(np); Matrix4x4 localBody = traBody * rotBody; Matrix4x4 worldPropeller = localBody * localPropeller; Matrix4x4 worldBody = localBody; Propeller.SetMatrix(worldPropeller); Body.SetMatrix(worldBody);
Unityの標準的な変換方法によって実装したプログラムを以下に示す。
[Code2] (実行結果 図2)
if (!i_INITIALIZED)
{
i_INITIALIZED = true;
// 親子関係の設定
Propeller.transform.SetParent(Body.transform);
}
// Propeller
i_degPropeller += 15;
Quaternion rotProp = Quaternion.AngleAxis(i_degPropeller, Vector3.forward);
Propeller.transform.localPosition = c_attachPos_Propeller;
Propeller.transform.localRotation = rotProp;
// Body
i_degBody -= 2;
Quaternion rotBody = Quaternion.AngleAxis(i_degBody, Vector3.up);
Vector3 posBody = rotBody * new Vector3(8.0f, 10.0f, 0.0f);
Body.transform.localPosition = posBody;
Body.transform.localRotation = rotBody;
1行目のifブロックは親子関係を設定するための初期化ブロックであり、プログラム実行開始時に1度だけ入るブロックである。i_INITIALIZEDは、初期化ブロックの処理が行われたかを示すbool型インスタンス変数であり初期値はfalseである。1度このifブロックに入ると、i_INITIALIZEDの値がtrueになるので、それ以降プログラムの実行中にこのブロックに入ることはない。
この初期化ブロックは親子関係の設定を行うための部分であり、ここでは Propellerの親オブジェクトとして Bodyを設定している。
今までの行列によるプログラムの場合、階層構造にあるオブジェクトの変換はプログラムにおいて次のように定義されていた。
Matrix4x4 sclObj3 = ... ; Matrix4x4 rotObj3 = ... ; Matrix4x4 traObj3 = ... ; Matrix4x4 localObj3 = traObj3 * rotObj3 * sclObj3; Matrix4x4 sclObj2 = ... ; Matrix4x4 rotObj2 = ... ; Matrix4x4 traObj2 = ... ; Matrix4x4 localObj2 = traObj2 * rotObj2 * sclObj2; Matrix4x4 sclObj1 = ... ; Matrix4x4 rotObj1 = ... ; Matrix4x4 traObj1 = ... ; Matrix4x4 localObj1 = traObj1 * rotObj1 * sclObj1;

例えば、Obj3の localPosition に設定する値は、Obj3の平行移動行列traObj3の内容と同じものになるようにすればよい。Obj3の localRotation、localScale に設定する値についても同様に、Obj3の回転行列rotObj3、スケール行列sclObj3の内容と同じものになるようにすればよい。
上のCode2の場合を例にとると、行列による実装では Propellerのローカル行列localPropellerは回転行列rotPropと平行移動行列traPropの積である。回転行列rotPropの内容はz軸周りに角度i_degPropellerだけ回転させるというものであるが、標準的な変換方法のプログラムにおいても、Propellerの localRotation(13行目) には同じ内容の回転がセットされている。平行移動行列traPropの内容はアタッチポジションc_attachPos_Propellerへの平行移動であるが、標準的な変換方法のプログラムにおいても、Propellerの localPosition(12行目) には c_attachPos_Propeller がセットされるので同じ内容の平行移動が行われることになる。
Bodyの場合も同様に、行列による実装のプログラムでは Bodyのローカル行列は回転行列rotBodyと平行移動行列traBodyの積であるが、これらの行列の内容は標準的な変換方法のプログラムにおける Bodyの localRotation(20行目)、localPosition(19行目) の内容と同じものである。
なお、プログラム12行目では以下のように
Propeller.transform.localPosition = c_attachPos_Propeller;
if (!i_INITIALIZED)
{
i_INITIALIZED = true;
// 親子関係の設定
Propeller.transform.SetParent(Body.transform);
// 実行中に変更することのないデータの設定
Propeller.transform.localPosition = c_attachPos_Propeller;
}
このように、オブジェクトの localPosition、localRotation、localScaleのうちでプログラム実行中に変更しないと分かっているものは初期化時に1度だけ値を設定すれば、それ以降のフレームにおいても最初に設定した値のまま変わることはない。
# Code3
以下のプログラムは 4-10節 Code5である (オブジェクトの変換は行列によって実装されている)。[4-10節 Code5] (実行結果 図4)
i_shmSphere += 1.0f; float scale = 0.5f * Mathf.Sin(i_shmSphere * Mathf.Deg2Rad) + 1.5f; // 1から2の間を往復 Matrix4x4 sclSphere = TH3DMath.GetScale4x4(scale, scale, scale); Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); Matrix4x4 localSphere = traSphere * sclSphere; i_degArm--; Matrix4x4 rotArm = TH3DMath.GetRotation4x4(i_degArm, Vector3.up); Matrix4x4 traArm = TH3DMath.GetTranslation4x4(c_attachPos_Arm); Matrix4x4 localArm = traArm * rotArm; i_shmDisk += 1.0f; float posY = 4.0f * Mathf.Sin(i_shmDisk * Mathf.Deg2Rad) + 8.0f; // 4から12の間を往復 Matrix4x4 rotDisk = TH3DMath.GetRotation4x4(-15.0f, Vector3.right); Matrix4x4 traDisk = TH3DMath.GetTranslation4x4(0.0f, posY, 0.0f); Matrix4x4 localDisk = traDisk * rotDisk; Matrix4x4 worldSphere = localDisk * localArm * localSphere; Matrix4x4 worldArm = localDisk * localArm; Matrix4x4 worldDisk = localDisk; Sphere.SetMatrix(worldSphere); Arm.SetMatrix(worldArm); Disk.SetMatrix(worldDisk);
このプログラムは3つのオブジェクト Disk、Arm、Sphere の一体化した運動を扱ったものであるが、図3はそれらのオブジェクトの階層構造であり、図4はプログラムの実行結果である。


Unityの標準的な変換方法によって実装したプログラムを以下に示す。
[Code3] (実行結果 図4)
if (!i_INITIALIZED)
{
// 親子関係の設定
Sphere.transform.SetParent(Arm.transform);
Arm.transform.SetParent(Disk.transform);
i_INITIALIZED = true;
}
i_shmSphere += 1.0f;
float scale = 0.5f * Mathf.Sin(i_shmSphere * Mathf.Deg2Rad) + 1.5f; // 1から2の間を往復
Sphere.transform.localScale = new Vector3(scale, scale, scale);
Sphere.transform.localPosition = c_attachPos_Sphere;
i_degArm--;
Arm.transform.localRotation = Quaternion.AngleAxis(i_degArm, Vector3.up);
Arm.transform.localPosition = c_attachPos_Arm;
i_shmDisk += 1.0f;
float posY = 4.0f * Mathf.Sin(i_shmDisk * Mathf.Deg2Rad) + 8.0f; // 4から12の間を往復
Disk.transform.localRotation = Quaternion.AngleAxis(-15.0f, Vector3.right);
Disk.transform.localPosition = new Vector3(0.0f, posY, 0.0f);
このプログラムにおいても13行目の Sphere.transform.localPosition、18行目の Arm.transform.localPosition、22行目の Disk.transform.localRotation には毎フレーム同じ値がセットされている。したがって、これらの処理を初期化ブロックに移しても結果は同じである。
# Code4
以下のプログラムは 4-14節 Code2である (オブジェクトの変換は行列によって実装されている)。[4-14節 Code2] (実行結果 図6)
// Propeller i_degPropeller -= 6; Matrix4x4 rotPropeller = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward); Matrix4x4 traPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller); Matrix4x4 localPropeller = traPropeller * rotPropeller; // Box Matrix4x4 localBox = TH3DMath.GetTranslation4x4(c_attachPos_Box); // Arm i_shmArm += 1; float my = 3.0f * Mathf.Sin(i_shmArm * Mathf.Deg2Rad); // -3.0 -- 3.0 Matrix4x4 localArm = TH3DMath.GetTranslation4x4(0.0f, my, 0.0f); // Pole i_degPole += 1; Matrix4x4 localPole = TH3DMath.GetRotation4x4(i_degPole, Vector3.up); // world matrix Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller; Matrix4x4 worldBox = localPole * localArm * localBox; Matrix4x4 worldArm = localPole * localArm; Matrix4x4 worldPole = localPole; Propeller[0].SetMatrix(worldPropeller); Box[0].SetMatrix(worldBox); Arm[0].SetMatrix(worldArm); Pole.SetMatrix(worldPole);
このプログラムは4つのオブジェクト Pole、Arm0、Box0、Propeller0 の一体化した運動を扱ったものであるが、図5はそれらのオブジェクトの階層構造であり、図6はプログラムの実行結果である。


Unityの標準的な変換方法によって実装したプログラムを以下に示す。
(以下のプログラムではオブジェクトの名前が ArmArray、BoxArray、PropellerArray に変わっている)
[Code4] (実行結果 図6)
if (!i_INITIALIZED)
{
i_INITIALIZED = true;
// 親子関係の設定
ArmArray[0].transform.SetParent(Pole.transform);
BoxArray[0].transform.SetParent(ArmArray[0].transform);
PropellerArray[0].transform.SetParent(BoxArray[0].transform);
}
// Propeller
i_degPropeller -= 6;
PropellerArray[0].transform.localRotation = Quaternion.AngleAxis(i_degPropeller, Vector3.forward);
PropellerArray[0].transform.localPosition = c_attachPos_Propeller;
// Box
BoxArray[0].transform.localPosition = c_attachPos_Box;
// Arm
i_shmArm += 1;
float my = 3.0f * Mathf.Sin(i_shmArm * Mathf.Deg2Rad); // -3.0 -- 3.0
ArmArray[0].transform.localPosition = new Vector3(0.0f, my, 0.0f);
// Pole
i_degPole += 1;
Pole.transform.localRotation = Quaternion.AngleAxis(i_degPole, Vector3.up);
先程も述べたように、オブジェクトのプロパティのうちでプログラム実行中に1度設定すればよいものは初期化ブロックに記述すればよい。上のコードをそのように改めると以下のようになる。
[Code4 修正版] (実行結果 図6)
if (!i_INITIALIZED)
{
// 親子関係の設定
ArmArray[0].transform.SetParent(Pole.transform);
BoxArray[0].transform.SetParent(ArmArray[0].transform);
PropellerArray[0].transform.SetParent(BoxArray[0].transform);
// 実行中に変更することのないデータの設定
PropellerArray[0].transform.localPosition = c_attachPos_Propeller;
BoxArray[0].transform.localPosition = c_attachPos_Box;
i_INITIALIZED = true;
}
// Propeller
i_degPropeller -= 6;
PropellerArray[0].transform.localRotation = Quaternion.AngleAxis(i_degPropeller, Vector3.forward);
// Arm
i_shmArm += 1;
float my = 3.0f * Mathf.Sin(i_shmArm * Mathf.Deg2Rad); // -3.0 -- 3.0
ArmArray[0].transform.localPosition = new Vector3(0.0f, my, 0.0f);
// Pole
i_degPole += 1;
Pole.transform.localRotation = Quaternion.AngleAxis(i_degPole, Vector3.up);
Propeller0のlocalPosition、Box0のlocalPositionは実行中に変更することがないので、それらに対するデータのセットが初期化ブロックに記述されている (9~10行目)。
# Code5
以下のプログラムは 4-14節 Code5である (オブジェクトの変換は行列によって実装されている)。[4-14節 Code5] (実行結果 図8)
if (Input.GetKeyDown(KeyCode.J))
{
i_switch_Pole = !i_switch_Pole;
}
else if(Input.GetKeyDown(KeyCode.K))
{
i_switch_Arm = !i_switch_Arm;
}
else if(Input.GetKey(KeyCode.L)) // 長押しに対応
{
i_degBox0 = THUtil.IsShiftDown() ? i_degBox0 - 2 : i_degBox0 + 2;
}
// Propeller
i_degPropeller -= 6;
Matrix4x4 rotPropeller = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward);
Matrix4x4 traPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller);
Matrix4x4 localPropeller = traPropeller * rotPropeller;
// Box
Matrix4x4 traBox = TH3DMath.GetTranslation4x4(c_attachPos_Box);
Matrix4x4 lcBox = traBox; // Box1, Box2用のローカル行列
Matrix4x4 rotBox0 = TH3DMath.GetRotation4x4(i_degBox0, Vector3.up);
Matrix4x4 lcBox0 = traBox * rotBox0; // Box0用のローカル行列
// Pole
i_degPole = (i_switch_Pole) ? i_degPole + 1 : i_degPole;
Matrix4x4 localPole = TH3DMath.GetRotation4x4(i_degPole, Vector3.up);
i_shmArm = (i_switch_Arm) ? i_shmArm + 1 : i_shmArm;
for (int i = 0; i < 3; i++)
{
// Box
Matrix4x4 localBox = (i == 0) ? lcBox0 : lcBox;
// Arm
float my = 3.0f * Mathf.Sin((i_shmArm + i * 60) * Mathf.Deg2Rad); // -3.0 -- 3.0
Matrix4x4 traArm = TH3DMath.GetTranslation4x4(0.0f, my, 0.0f);
Matrix4x4 rotArm = TH3DMath.GetRotation4x4(i * 120, Vector3.up);
Matrix4x4 localArm = traArm * rotArm;
// world matrix : Propeller, Box, Arm
Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller;
Matrix4x4 worldBox = localPole * localArm * localBox;
Matrix4x4 worldArm = localPole * localArm;
Propeller[i].SetMatrix(worldPropeller);
Box[i].SetMatrix(worldBox);
Arm[i].SetMatrix(worldArm);
}
// world matrix : Pole
Matrix4x4 worldPole = localPole;
Pole.SetMatrix(worldPole);
このプログラムは3つのArm、3つのBox、3つのPropeller 及び Poleの一体化した運動を扱ったものである。図7はすべてのオブジェクトを一体化した際の階層構造であり、図8はプログラムの実行結果である。


Unityの標準的な変換方法によって実装したプログラムを以下に示す。
(以下のプログラムにおいても Arm、Box、Propeller は ArmArray、BoxArray、PropellerArray として使われている)
[Code5] (実行結果 図8)
if (!i_INITIALIZED)
{
// 親子関係の設定
ArmArray[0].transform.SetParent(Pole.transform);
ArmArray[1].transform.SetParent(Pole.transform);
ArmArray[2].transform.SetParent(Pole.transform);
BoxArray[0].transform.SetParent(ArmArray[0].transform);
BoxArray[1].transform.SetParent(ArmArray[1].transform);
BoxArray[2].transform.SetParent(ArmArray[2].transform);
PropellerArray[0].transform.SetParent(BoxArray[0].transform);
PropellerArray[1].transform.SetParent(BoxArray[1].transform);
PropellerArray[2].transform.SetParent(BoxArray[2].transform);
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.J))
{
i_switch_Pole = !i_switch_Pole;
}
else if(Input.GetKeyDown(KeyCode.K))
{
i_switch_Arm = !i_switch_Arm;
}
else if(Input.GetKey(KeyCode.L)) // 長押しに対応
{
// Box0のみ独自の回転を行う
i_degBox0 = THUtil.IsShiftDown() ? i_degBox0 - 2 : i_degBox0 + 2;
BoxArray[0].transform.localRotation = Quaternion.AngleAxis(i_degBox0, Vector3.up);
}
// Propeller
i_degPropeller -= 6;
for (int i = 0; i < 3; i++)
{
PropellerArray[i].transform.localRotation = Quaternion.AngleAxis(i_degPropeller, Vector3.forward);
PropellerArray[i].transform.localPosition = c_attachPos_Propeller;
}
// Box
for(int i = 0; i < 3; i++)
{
BoxArray[i].transform.localPosition = c_attachPos_Box;
}
// Arm
if (i_switch_Arm)
{
i_shmArm++;
for (int i = 0; i < 3; i++)
{
ArmArray[i].transform.localRotation = Quaternion.AngleAxis(i * 120, Vector3.up);
float my = 3.0f * Mathf.Sin((i_shmArm + i * 60) * Mathf.Deg2Rad); // -3.0 -- 3.0
ArmArray[i].transform.localPosition = new Vector3(0.0f, my, 0.0f);
}
}
// Pole
if (i_switch_Pole)
{
i_degPole++;
Pole.transform.localRotation = Quaternion.AngleAxis(i_degPole, Vector3.up);
}
このプログラムにも、オブジェクトのプロパティへ毎フレーム同じ値をセットしている処理があるので、それらを初期化ブロックにまとめると以下のようになる。
[Code5 修正版] (実行結果 図8)
if (!i_INITIALIZED)
{
// 親子関係の設定
ArmArray[0].transform.SetParent(Pole.transform);
ArmArray[1].transform.SetParent(Pole.transform);
ArmArray[2].transform.SetParent(Pole.transform);
BoxArray[0].transform.SetParent(ArmArray[0].transform);
BoxArray[1].transform.SetParent(ArmArray[1].transform);
BoxArray[2].transform.SetParent(ArmArray[2].transform);
PropellerArray[0].transform.SetParent(BoxArray[0].transform);
PropellerArray[1].transform.SetParent(BoxArray[1].transform);
PropellerArray[2].transform.SetParent(BoxArray[2].transform);
// 実行中に更新することのないデータの設定
for (int i = 0; i < 3; i++)
{
PropellerArray[i].transform.localPosition = c_attachPos_Propeller;
BoxArray[i].transform.localPosition = c_attachPos_Box;
ArmArray[i].transform.localRotation = Quaternion.AngleAxis(i * 120, Vector3.up);
}
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.J))
{
i_switch_Pole = !i_switch_Pole;
}
else if (Input.GetKeyDown(KeyCode.K))
{
i_switch_Arm = !i_switch_Arm;
}
else if (Input.GetKey(KeyCode.L)) // 長押しに対応
{
// Box0 (Box1、Box2は実行中のデータ更新はなし)
i_degBox0 = THUtil.IsShiftDown() ? i_degBox0 - 2 : i_degBox0 + 2;
BoxArray[0].transform.localRotation = Quaternion.AngleAxis(i_degBox0, Vector3.up);
}
// Propeller
i_degPropeller -= 6;
for (int i = 0; i < 3; i++)
{
PropellerArray[i].transform.localRotation = Quaternion.AngleAxis(i_degPropeller, Vector3.forward);
}
// Arm
if (i_switch_Arm)
{
i_shmArm++;
for (int i = 0; i < 3; i++)
{
float my = 3.0f * Mathf.Sin((i_shmArm + i * 60) * Mathf.Deg2Rad); // -3.0 -- 3.0
ArmArray[i].transform.localPosition = new Vector3(0.0f, my, 0.0f);
}
}
// Pole
if (i_switch_Pole)
{
i_degPole++;
Pole.transform.localRotation = Quaternion.AngleAxis(i_degPole, Vector3.up);
}
先程のプログラムでは各Propellerのアタッチポジションへの移動、各Boxのアタッチポジションへの移動、及び 各ArmをPoleの3つの面へ $120^\circ$ おきに配置する処理は、毎フレーム同じ値を各オブジェクトのプロパティへセットしていたが、この修正版ではそれらの処理は初期化ブロックへ移されている (17~22行目)。
# Code6
以下のプログラムは 4-20節 Code1である (オブジェクトの変換は行列によって実装されている)。[4-20節 Code1] (実行結果 図11)
if (!i_INITIALIZED)
{
Navy.lastShootFrame = 0;
Navy.shootInterval = 8;
Navy.shellSpeed = 1.0f;
Navy.initShootDirection = Vector3.forward;
Navy.initShootPositions = new Vector4[]
{
new Vector4( 0.358f, -0.13965f ,0.2371f, 1.0f),
new Vector4(-0.358f, -0.13965f ,0.2371f, 1.0f)
};
i_INITIALIZED = true;
}
NavyMotion();
i_frameCount++;
Matrix4x4 M = Matrix4x4.identity;
Matrix4x4 R = Matrix4x4.identity;
int numShooter = 0;
if (Input.GetKey(KeyCode.A))
{
if (i_frameCount >= Navy.lastShootFrame + Navy.shootInterval)
{
Navy.lastShootFrame = i_frameCount;
numShooter = 2;
M = Navy.GetMatrix();
R = M;
R.SetColumn(3, new Vector4(0, 0, 0, 1));
}
}
Vector3 posNavy = Navy.GetWorldPosition();
foreach (var shell in Shell)
{
if (shell.active)
{
Vector3 newShellPos = shell.position + shell.speed * shell.direction;
if ((posNavy - newShellPos).magnitude > 80.0f)
{
shell.active = false;
shell.position = new Vector3(-1000, 0, 0);
}
else
{
Matrix4x4 mtx = TH3DMath.GetTranslation4x4(newShellPos) * shell.rotMatrix;
shell.SetMatrix(mtx);
}
}
else
{
if (numShooter > 0)
{
Vector3 startPos = M * Navy.initShootPositions[2 - numShooter];
Vector3 shootDir = M * Navy.initShootDirection;
shell.active = true;
shell.direction = shootDir;
shell.speed = Navy.shellSpeed;
shell.rotMatrix = R;
Matrix4x4 mtx = TH3DMath.GetTranslation4x4(startPos) * shell.rotMatrix;
shell.SetMatrix(mtx);
numShooter--;
}
}
}
このプログラムは下図9のオブジェクト Navy が3D空間内を飛行しながら細長い形のShell(図10)を連射するというプログラムであり、図11はその実行結果である。
-
 図9 Navy 初期状態
図9 Navy 初期状態 -
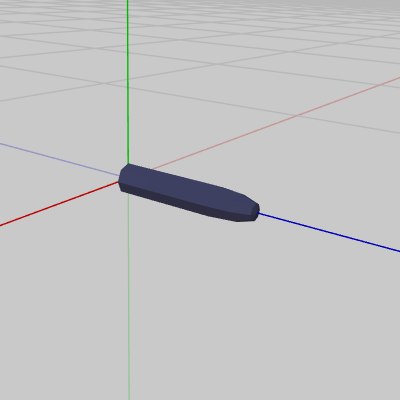 図10 Shell 初期状態
図10 Shell 初期状態 -
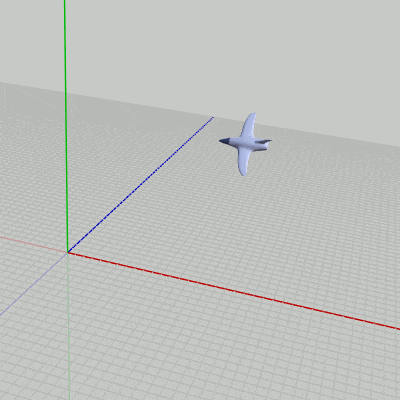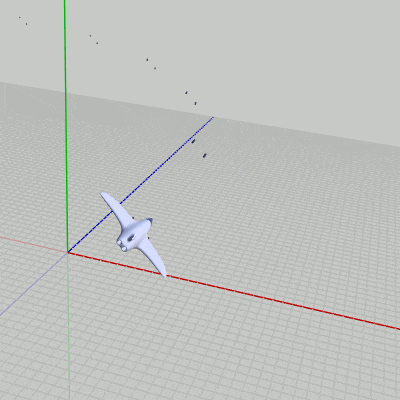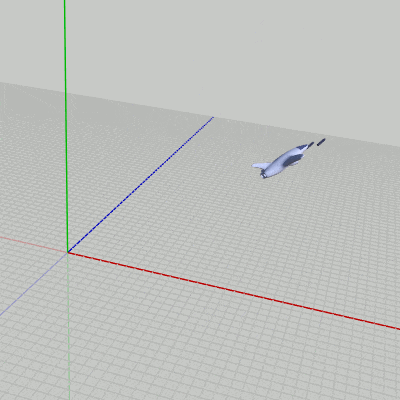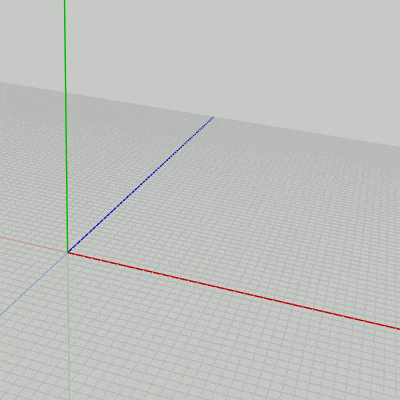 図11 Code6 実行結果
図11 Code6 実行結果
Unityの標準的な変換方法によって実装したプログラムを以下に示す。
[Code6] (実行結果 図11)
if (!i_INITIALIZED)
{
Navy.lastShootFrame = 0;
Navy.shootInterval = 8;
Navy.initShootDirection = Vector3.forward;
Navy.shellSpeed = 1.0f;
Navy.initShootPositions = new Vector4[]
{
new Vector4( 0.358f, -0.13965f ,0.2371f, 1.0f),
new Vector4(-0.358f, -0.13965f ,0.2371f, 1.0f)
};
i_INITIALIZED = true;
}
NavyMotion();
i_frameCount++;
Matrix4x4 M = Matrix4x4.identity;
Quaternion rotNavy = Quaternion.identity;
int numShooter = 0;
if (Input.GetKey(KeyCode.A))
{
if (i_frameCount >= Navy.lastShootFrame + Navy.shootInterval)
{
Navy.lastShootFrame = i_frameCount;
numShooter = 2;
M = Navy.transform.localToWorldMatrix;
rotNavy = Navy.transform.rotation;
}
}
Vector3 posNavy = Navy.GetWorldPosition();
foreach (var shell in Shell)
{
if (shell.active)
{
Vector3 newShellPos = shell.transform.position + shell.speed * shell.direction;
if ((posNavy - newShellPos).magnitude > 80.0f)
{
shell.active = false;
shell.transform.position = new Vector3(-1000, 0, 0);
}
else
{
shell.transform.position = newShellPos;
}
}
else
{
if (numShooter > 0)
{
Vector3 startPos = M * Navy.initShootPositions[2 - numShooter];
Vector3 shootDir = M * Navy.initShootDirection;
shell.active = true;
shell.direction = shootDir;
shell.speed = Navy.shellSpeed;
shell.transform.position = startPos;
shell.transform.rotation = rotNavy;
numShooter--;
}
}
}
行列による実装ではNavyに実行されている変換行列及びその回転成分を取得するために次のように記述されていた。
M = Navy.GetMatrix();
R = M;
R.SetColumn(3, new Vector4(0, 0, 0, 1));
標準的な変換方法ではこの部分が次のように変更されている。
M = Navy.transform.localToWorldMatrix;
rotNavy = Navy.transform.rotation;
30行目の Navy.transform.localToWorldMatrix は Navy.GetMatrix() と内容は同じでありこの点は変わらないが、31行目ではQuaternion型のローカル変数 rotNavy に Navy.transform.rotation をセットしている。 transform.rotation はオブジェクトの現在の回転状態がセットされているQuaternion型のプロパティであるため、Navyに実行されている回転はこのプロパティから取得することができる。
Shellを発射開始位置にセットする処理は行列による実装では次のように記述されていた。
shell.rotMatrix = R;
Matrix4x4 mtx = TH3DMath.GetTranslation4x4(startPos) * shell.rotMatrix;
shell.SetMatrix(mtx);
今回の position、rotation による実装では以下のように変更されている。
shell.transform.position = startPos;
shell.transform.rotation = rotNavy;
発射されたShellは直進的に進んで行くが、行列版の実装ではその処理は次のように記述されていた。
Matrix4x4 mtx = TH3DMath.GetTranslation4x4(newShellPos) * shell.rotMatrix;
shell.SetMatrix(mtx);
この処理は標準的な変換方法では次のように変更されている。
shell.transform.position = newShellPos;
以下のプログラムは読者用の課題である。
# Code7
3-19節のCode1はサイコロを以下の図に示される経路に沿って転がしていくという課題であった。

3-19節の課題はそのプログラムを行列で作成するものであったが、ここでの課題はこのサイコロの回転移動のプログラムを行列を使わずに、標準的な変換方法で実装することである (プログラムで使用するオブジェクト Dice は親オブジェクトを持たないので、変換に用いるプロパティはlocalPosition、localRotation であっても position、rotation であっても構わない)。
プログラムは Sec504.cs内のCode7に作成するものとする。Code7は最初の段階では以下のコードのみが記述されている。
[Code7]
if (!i_INITIALIZED)
{
Dice.transform.localPosition = A;
Dice.transform.localRotation = Quaternion.identity;
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S))
{
i_MOVE = true;
}
if (!i_MOVE) { return; }
使用するインスタンス変数や定数は 3-19節 Code1 のものと同じであり、ここではその説明については省略するが、1点だけ違いがある。3-19節ではサイコロの回転状態を保持するために i_curRotation というインスタンス変数が用意されていたが、今回はこの変数を使う必要はない。オブジェクトの現在の回転状態は Obj.transform.localRotation によって取得することができるので、オブジェクトを現在の状態からさらに回転させるには次のように記述すればよい。
Quaternion wr = ... 適当な回転 ...; Quaternion rot = wr * Obj.transform.localRotation; Obj.transform.localRotation = rot;
なお 前節の終わりでも述べたが、回転後の新しい位置の計算は行列でもQuaternionでも、計算の仕方はほとんど変わらない。例えば、点$P = (a, b, c)$ を x軸周りに $120^\circ$ 回転させたときの位置は行列を使う場合は次のように記述される (回転後の位置を $Q$ とする)。
Vector4 P = new Vector4(a, b, c, 1); Vector3 Q = TH3DMath.GetRotation4x4(120.0f, Vector3.right) * P;
Quaternionで計算する場合は次のように書き換えればよい。
Vector3 P = new Vector3(a, b, c); Vector3 Q = Quaternion.AngleAxis(120.0f, Vector3.right) * P;
解答例については Sec504_Ans.txt内の Code7 を参照 (Sec504_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
# Code8
4-15節 Code7は立方体を展開された状態から組み立てられた状態へ、あるいはその逆に組み立てられた状態から展開された状態へ変化させるものであった。立方体の展開図についてはいくつかの種類があるが、以下の図14もその1つである。

ここでの課題も立方体の展開された状態、及び組み立てられた状態の間を行き来するプログラムの作成であるが、その際の展開された状態は図14の状態を使うものとする。そして、このプログラムもまた行列ではなく localPosition、localRotation によって実装するものとする。
以下の図16~18はこのプログラムで使用するオブジェクトの初期状態であり、上図15は各オブジェクトの階層構造である。
-
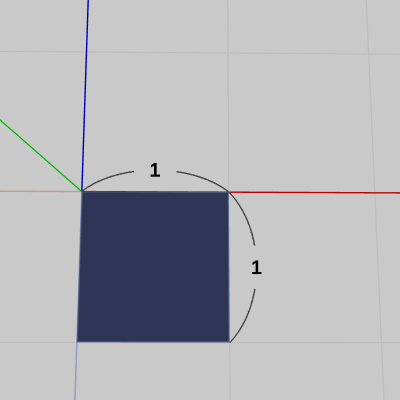 図16 Face0(底面) 初期状態
図16 Face0(底面) 初期状態 -
 図17 Face1~Face3(側面) 初期状態
図17 Face1~Face3(側面) 初期状態 -
 図18 Face4(側面)、Face5(上面) 初期状態
図18 Face4(側面)、Face5(上面) 初期状態
4-15節と同様に立方体の6個のそれぞれの面に対して6個のオブジェクト Face0 ~ Face5 が対応している。今回の立方体も1辺の長さは $1$ であり、Face0~Face5はいずれも1辺の長さが $1$ の正方形である。
Face0(図16)は立方体の底面で一番上の親オブジェクトであるが、初期状態における位置は x軸プラス側、z軸マイナス側に置かれている。
Face1~Face4は側面である。Face1、Face2、Face3の3つは初期状態において x軸プラス側、z軸プラス側に置かれており(図17)、Face4は初期状態において x軸マイナス側、z軸マイナス側に置かれている(図18)。
また、Face5は立方体の上の面であるが、この面もFace4と同じく初期状態においては x軸マイナス側、z軸マイナス側に置かれている(図18)。
4-15節 Code7では立方体を展開された状態にするためには、各Faceに対しアタッチポジションまでの平行移動だけを行えばよかったが、それはここでも同様である。図14は展開された状態の図であるが、各Faceに実行されている変換はアタッチポジションまでの平行移動のみである (図中の各数字はFace0~Face5を表している)。
このプログラムには以下のインスタンス変数が用意されている。
i_deg1, i_deg2, i_deg3, i_deg4, ,i_deg5
: Face1 ~ Face5 の回転角度を表すfloat型変数である。i_motionCounter
: 状態変化の過程において現在何フレーム目であるかを表すint型変数である (4-15節で使われていたものと役割は同じ)。4-15節と同じく Face0~Face5はプログラム中ではFace[0]~Face[5]の配列として用意されている。
また、展開及び組み立ての際のキー操作については以下のキーを使用するものとする。
J : 立方体を組み立てる。
K : 立方体を展開する。

解答例については Sec504_Ans.txt内の Code8 を参照。
右図19は解答例のプログラムの実行結果であるが、一方の状態からもう一方の状態への変化にかかるフレーム数は240フレームである。
© 2020-2025 Redpoll's 60 (All rights reserved)