Redpoll's 60
Home / 3Dプログラミング入門 / 第5章 $§$5-3
第5章 変換のオブジェクト化
| $§$5-1 要旨 | $§$5-6 Transformクラスの実装 2 |
| $§$5-2 Unityにおける標準的な変換方法 1 | $§$5-7 Transformクラスの実装 3 |
| $§$5-3 Unityにおける標準的な変換方法 2 | $§$5-8 いくつかの使用例 |
| $§$5-4 Unityにおける標準的な変換方法 3 | $§$5-9 課題 |
| $§$5-5 Transformクラスの実装 1 |
$§$5-3 Unityにおける標準的な変換方法 2
本節では、Unityの標準的な変換方法を使用して、一体化したオブジェクトに変換を実行する例をいくつか見ていく。
今までの行列を使用したプログラムでは、オブジェクトの一体化はプログラムの中で実装されていた。プログラムの終了部分は、必ず次のようなコードで終わっていたが、この処理が一体化の実装部分なのである (あるいは親子関係の実装部分である)。

図1 オブジェクトの階層構造 例えば、このコードでは3つのオブジェクト Obj1、Obj2、Obj3には図1に示されるような親子関係が築かれる。
後の節でも解説するが、オブジェクトの親子関係の構築は、具体的には上に示される数行程度の記述で実装されているのである。この数行のコードによってオブジェクトの親子関係が構築され、オブジェクトが一体化して運動するのである。
しかし、標準的な方法によってオブジェクトに変換を実行していく場合には、オブジェクトの親子関係は事前に Unity側に設定しておく必要がある。そして、親子関係の設定されたオブジェクトに対して、5-2節で見たように各プロパティに適当な値をセットして変換を実行していくのである (Unityでの親子関係の設定に関しては、本節の終わり部分で解説を載せている)。
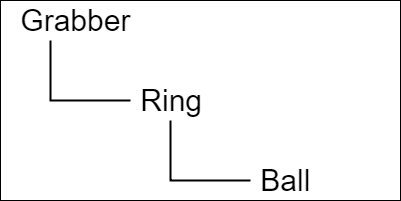
図5 オブジェクトの階層構造 これら3つのオブジェクトの階層構造は図5に示されるとおりである。
最初の2つのプログラム Beta1、Beta2では、Ballと Ringの2つのオブジェクトのみを表示して、それらに対する変換を見ていく。
まずは、行列を使って変換を行う。各オブジェクトに実行する変換は次のとおり。
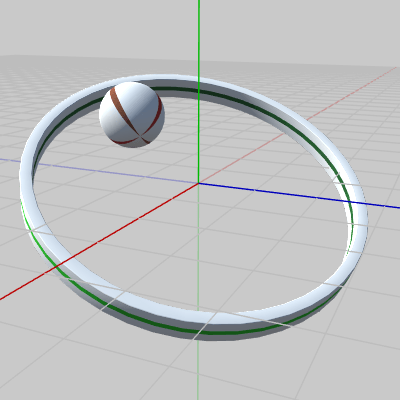
図6 Beta1、Beta2 実行結果 Ball : $1.5$倍のスケール、y軸周りに $-50$°の自転、さらに原点を中心とする z軸周りの半径 $2$の円周上を $(2, 0, 0)$を起点として $70$°公転する (これらの変換は Ballの親座標系である Ring座標系で実行される)。
Ring : x軸周りに $-60$°の回転、y軸周りに $45$°の回転をこの順で行う (これらの変換は Ringの親座標系であるワールド座標系で実行される ; Grabberはここでは使用されないため、Ringが一番上の親オブジェクトである)
プログラム自体は、今までに見てきた行列を使用したプログラムと構造的には同じであり、それらと比べて何か新しい要素があるわけではない。
[Beta1] (実行結果 図6)
続いて、今のものと同じ変換を標準的な変換方法によって実装した場合のプログラムを以下に示す (上でも述べたように、標準的な方法では Unity側に親子関係をあらかじめ設定した状態で実行している)。
[Beta2] (実行結果 図6)
Beta1、Beta2の実行結果はもちろん同じである(図6)。ただ、標準的な方法を使用した場合の方が、親子関係の構築処理の記述が不要になるためコードが簡潔になっている。
前節で解説したように、標準的な変換方法では各オブジェクトには、スケール、回転、平行移動の順で変換が実行される。そして、それらの変換の内容は、localPosition、localRotation、localScale に対して指定する。
例えば Ballの場合は、(Ring座標系の原点において) $1.5$倍の拡大、y軸周りに $-50$°の回転、さらに公転軌道上の計算された位置への平行移動がこの順序で実行されるのである。
Ringに実行される変換は2つの回転であるが、8~9行目ではそれは2つのQuaternionの積によって表されている。詳しくは第6章で解説するが、Quaternionの場合も複数の回転の合成は、複数のQuaternionの積によって表される。例えば、x軸周りの$10$°の回転を表すQuaternionをqx、y軸周りの$20$°の回転を表すQuaternionをqy、z軸周りの$30$°の回転を表すQuaternionをqz とすると、以下のプログラムにおける4行目の Quaternion wQ は、この3つの回転の合成を表すQuaternionである。つまり、wQによる回転は x軸周りの回転、y軸周りの回転、z軸周りの回転をこの順序で実行したものと同じ結果になる (以下の Vector3.right、Vector3.up、Vector3.forwardは、x軸プラス側、y軸プラス側、z軸プラス側を表す定数である)。
そして、(列優先)行列の積が右から左へ進むのと同じように、UnityにおけるQuaternionの積も右から左へ進む。つまり、あるQuaternionが複数のQuaternionの積によって表されている場合、1つ1つの回転は一番右のQuaternionから始まる。上の3つのQuaternionの積は、qz * qy * qx となっているが、この積の順序は上でも述べたように、x軸周りの回転、y軸周りの回転、z軸周りの回転の順になる。qy * qx * qz ならば、z軸周りの回転、x軸周りの回転、y軸周りの回転の順になる。
したがって、Beta2の8~9行目の
は、Ringに対して x軸周りに$-60$°、y軸周りに$45$°の順で回転を実行することを意味している。
この(Beta2の)実行結果に、各オブジェクトのローカル座標系を表示したものを以下に示す (図中のラベルは、x、y、zがワールド座標系の x軸、y軸、z軸を表し、R-x、R-y、R-zが Ring座標系の x軸、y軸、z軸、B-x、B-y、B-zが Ball座標系の x軸、y軸、z軸を表している)。

図7 
図8
図7は、プログラムの実行結果をワールド座標系から見たときのもので、Ring、Ballのそれぞれにローカル座標系が表示されている。
図8は、プログラムの実行結果を Ring座標系から見たときのものである (ここではワールド座標系を非表示にしている)。図では Ring座標系の $(2, 0, 0)$ の位置から、z軸周りに $70$°回転した位置に Ball(の中心)が移動していることが示されている。
さらに、このプログラムの実行結果に対して詳細な情報を追加した図を以下に示す (図中における W(##, ##, ##)はワールド座標系の値を表し、R(##, ##, ##)はRing座標系の値を表している)。

図9 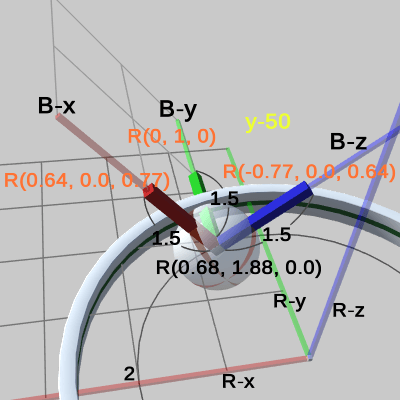
図10
以下の内容は、4-11節と重複する部分が多いが、復習の意味で読み進めていただきたい (ただし、ここで展開する内容は復習が目的ではない)。
図9は、プログラムの実行結果をワールド座標系において、Ring座標系の原点付近に近づけて見たときの様子である (図中の数値はすべてワールド座標系での値である)。
図10は、プログラムの実行結果を Ring座標系において、Ball座標系の原点付近に近づけて見たときの様子である (図中の数値はすべて Ring座標系での値である)。
これらは 4-11節でも見たように、ローカル座標系の単位ベクトル部分(各軸において原点からの長さが $1$までの部分)を強調して表示し、その単位ベクトル部分に関する情報を表示したものである。4-11節では、オブジェクトのローカル座標系は、その親座標系で見た場合には、そのオブジェクトのローカル行列を可視化したものになっているということについて学習した。
ここでは、簡単に各オブジェクトのローカル座標系とローカル行列との対応を見てみよう。
Beta1で使われている、Ring、Ballのローカル行列 localRing、localBall の内容を以下に示す (以下の それぞれの右辺は 4-6節 $(Ex1)$の書き換えを行った形である)。
図9、図10には黄色い数字で「x-60 y45」、「y-50」と表示されている。これらの数値は、オブジェクトに実行された回転を表しており、図9の場合は、Ringには、x軸周りに $-60$°、y軸周りに $45$°の順序で回転が実行されたことを示し、図10の場合は、Ballには、y軸周りに $-50$°の回転のみが実行されたことを示している。
4-8節から 4-11節で見てきたように、オブジェクトのローカル座標系には、そのオブジェクトに対して実行される変換と全く同じ変換が実行される。したがって、図9、図10の黄色い数値は、Ring座標系に実行された回転、Ball座標系に実行された回転でもある。すなわち、これらの図に表示されている黄色い数値は、ローカル座標系に対して実行された回転を表すものでもあるわけである。
4-11節で見てきたように、ローカル座標系の x軸、y軸、z軸の単位ベクトル表示(図9、図10のオレンジ色の数値)は、ローカル行列の第1列目、第2列目、第3列目の係数を除いたものに一致する。また、変換行列の左上3行3列において係数を除いたものを変換行列の回転成分と呼ぶことについても 4-6節で学習した。
例えば、図9の場合、すなわち Ring座標系の場合では各軸の単位ベクトル表示は、$(0.71, 0.0, -0.71)$、$(-0.61, 0.50, -0.61)$、$(0.35, 0.87, 0.35)$ であり、これは確かに Ringのローカル行列 localRing の回転成分(左上3行3列において係数を除いたもの)に一致している。そして、この localRing の回転成分の内容は、x軸周りに $-60$°、y軸周りに $45$°の順序で行う回転である。実際、x軸周り $-60$°の回転を $R_x$、y軸周り $45$°の回転を $R_y$とすれば、その積は、
繰り返しになるが、localRingの回転成分は、x軸周りに $-60$°、y軸周りに $45$°の順序の回転を意味している。言い換えれば、図9に示される黄色い数値「x-60 y45」は localRingの回転成分と同じ意味を持っているのである。
また、これも 4-11節で見てきたことだが、ローカル座標系の原点座標は、ローカル行列の平行移動成分(変換行列の第4列目)に等しく、ローカル座標系の各軸の単位ベクトル部分の長さは、ローカル行列のスケール成分(変換行列の第1列目、第2列目、第3列目に掛けられている係数)に等しいのであった。実際、図9の Ring座標系の原点座標、及び 単位ベクトル部分の長さと、localRingの平行移動成分、スケール成分を比較すれば このことは確かめられる。
図10においても同様で、Ball座標系に対して実行された回転を表す黄色い数値「y-50」は、localBallの回転成分と同じ意味を持っており (この回転成分の内容は y軸周り $-50$°の回転である)、Ball座標系の原点座標、及び Ball座標系の単位ベクトル部分の長さは、それぞれ localBallの平行移動成分、スケール成分に等しい。
上で述べたことは、以下の形で要約される。
ローカル座標系の原点座標は、ローカル行列の平行移動成分に等しい。
ローカル座標系に対して実行された回転を表す黄色い数値は、ローカル行列の回転成分と同じ意味を持っている。
ローカル座標系の単位ベクトル部分の長さは、ローカル行列のスケール成分に等しい。
では、ここで一旦話題を切り替える。

図11 3Dアプリケーションにおいて オブジェクトを動かす場合に、アプリケーション側では図11に示されるようなインターフェースを用意していることが一般的である。
図11は Unityにおけるインターフェースであるが、同様のものは、Unreal Engineにも備わっているし、Blender、MayaといったDCCツールにも用意されている。
図11は Unityにおいて Inspectorと呼ばれる領域で、Inspectorにはオブジェクトのさまざまな情報が表示される。
図に示されているのは Transformコンポーネントというものに関連したデータであり、ここには「Position」、「Rotation」、「Scale」の3つの項目のそれぞれに、x、y、z の値が表示されている。これらは、もちろんオブジェクトの Position、Rotation、Scaleのことであるが、具体的に何を意味しているのかについて以下で見ていこう。
上で示したプログラム Beta1、Beta2はオブジェクトの変換方法は異なるが、実行結果は同じであった。どちらのプログラムでも、実行結果は同じであるが、ここからは標準的な変換方法を使用した Beta2を実行した場合で話を進める (すなわち、Unity側には事前に親子関係の設定がなされている)。
Beta2 を実行した結果を再度示す。

図9 
図10
図9、図10は、プログラムの実行結果をワールド座標系、Ring座標系から見たときの様子であった。
このときの、Unityの Inspector上の Transformコンポーネントは次のような表示になっている。
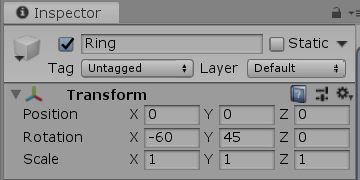
図12 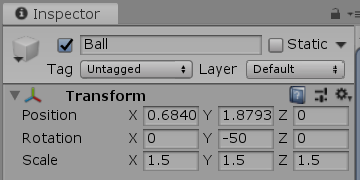
図13
図12は Ringの Transformコンポーネントであるが、ここに表示されているデータと図9の Ring座標系の各数値を見比べると次のような対応があることがわかる。
Transformコンポーネントの Position「x 0 y 0 z 0」は、Ring座標系の原点座標に等しい。
Transformコンポーネントの Rotation「x -60 y 45 z 0」は「z 0」を除外すれば、Ring座標系に実行された回転を表す黄色い数値に等しい。
Transformコンポーネントの Scale「x 1 y 1 z 1」は、Ring座標系の単位ベクトル部分の長さに等しい。
図13は Ballの Transformコンポーネントであるが、ここに表示されているデータと図10の Ball座標系の各数値を見比べた場合にも、同様の対応があることがわかる。
Transformコンポーネントの Position「x 0.6840 y 1.8793 z 0」は小数第3位を四捨五入すれば「x 0.68 y 1.88 z 0」であるが、これは Ball座標系の原点座標に等しい。
Transformコンポーネントの Rotation「x 0 y -50 z 0」は「x 0」「z 0」を除外すれば、Ball座標系に実行された回転を表す黄色い数値に等しい。
Transformコンポーネントの Scale「x 1.5 y 1.5 z 1.5」は、Ball座標系の単位ベクトル部分の長さに等しい。
オブジェクトの Transformコンポーネントとローカル座標系に関しての これら結果は、以下の形で要約される。
Transformコンポーネントの Positionは、ローカル座標系の原点座標に等しい。
Transformコンポーネントの Rotationは、ローカル座標系に実行された回転を表す黄色い数値に等しい。
Transformコンポーネントの Scaleは、ローカル座標系の単位ベクトル部分の長さに等しい。
ここで先程の、オブジェクトのローカル座標系とローカル行列に関しての要約を再度示す。
ローカル座標系の原点座標は、ローカル行列の平行移動成分に等しい。
ローカル座標系に対して実行された回転を表す黄色い数値は、ローカル行列の回転成分と同じ意味を持っている。
ローカル座標系の単位ベクトル部分の長さは、ローカル行列のスケール成分に等しい。
以上からわかるように、
ローカル座標系の原点座標、ローカル行列の平行移動成分、Transformコンポーネントの Position はすべて同じ内容を表しているのである。
また、ローカル座標系に実行された回転を表す黄色い数値、ローカル行列の回転成分、Transformコンポーネントの Rotation についても、3つとも同じ内容を表しているのである。
同様に、ローカル座標系の単位ベクトル部分の長さ、ローカル行列のスケール成分、Transformコンポーネントの Scale、この3つもやはり同じ内容を表しているのである。
簡単に言えば、ローカル座標系、ローカル行列、Inspector上の Transformコンポーネントは、'姿形'は異なるが同一のものなのである。
ただし、4-11節でも述べたが、ローカル座標系の各数値(原点座標、回転を表す黄色い数値、単位ベクトル部分の長さ)は親座標系で測ったときの値であることに注意する必要がある。上の図9の Ring座標系の各数値は親座標系であるワールド座標系での値であり、図10の Ball座標系の各数値は親座標系である Ring座標系での値である。例えば、図10の Ball座標系は、Ring座標系の $(0.68, 1.88, 0)$ に原点があり、Ring座標系の y軸周りに $-50$°の回転が実行されており、Ring座標系で測ったときに Ball座標系の単位ベクトル部分の長さ、すなわち、グリッド1マスの1辺の長さが $1.5$になるのである。Ring座標系の親座標系であるワールド座標系から Ball座標系を見たときには、原点座標や回転角度はこのような数値にはならない。
Inspector上の Transformコンポーネントは、ローカル座標系(及び ローカル行列)と同一のものであるので、そこに表示されている数値は親座標系での値である。Transformコンポーネントの各数値は、親座標系における数値であり、ワールド座標系での値ではない (もちろん、親座標系がワールド座標系であれば、表示される数値はワールド座標系での値になる ; 少なくとも、この解説で使用している Unityのバージョン 2019.2.9f1 においては、Transformコンポーネントには親座標系での値のみが表示される)。
では次に、上で使用した Ball、Ringの他に、Ringの親オブジェクトとして Grabberを追加し、親子階層を3階層にしたプログラムを使って、各オブジェクトに設定されるプロパティの値と、Inspector上のTransformコンポーネントの対応関係を簡単に確認する。
各オブジェクトに実行される変換は次のとおり。
Ball : $1.5$倍のスケール、y軸周りに $-135$°の自転、さらに原点を中心とする z軸周りの半径 $2$の円周上を $(2, 0, 0)$を起点として $150$°公転する (これらの変換は Ballの親座標系である Ring座標系で実行される)。
Ring : まず、y軸周りに $40$°の回転、次に、アタッチポジションである Grabber座標系の $(-11, 0, 0)$ への平行移動を行う (これらの変換は Ringの親座標系である Grabber座標系で実行される)。
Grabber : x軸周りに $15$°の回転、y軸周りに $50$°の回転をこの順で実行し、さらに y軸方向へ $8$だけ平行移動する (これらの変換は Grabberの親座標系であるワールド座標系で実行される)。
[Beta3] (実行結果 図14~図18 ; プログラムの実行にあたっては、事前に Unity側に親子関係の設定がなされている)

図14 Beta3 実行結果 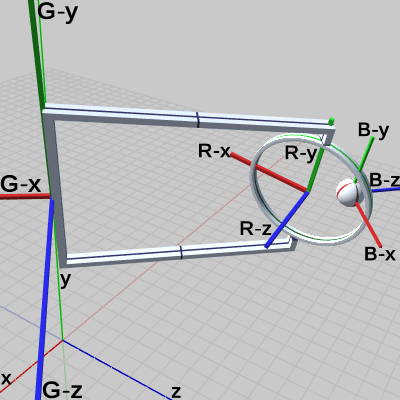
図15 Beta3 実行結果 (各オブジェクトのローカル座標系を表示)
図14は プログラムの実行結果をワールド座標系から見たときの様子であり、図15は さらに、各オブジェクトのローカル座標系を表示したものである。
続いて、この実行結果に関して各座標系から見たときの詳しい情報を付加した図、及び Inspector上の Transformコンポーネントを以下に示す (以下の図中における W(##, ##, ##)、G(##, ##, ##)、R(##, ##, ##) はワールド座標系の値、はGrabber座標系の値、Ring座標系の値を表している)。
図16は観察対象を Grabber座標系に定めたときのもので、図中の数値は、すべて親座標系であるワールド座標系での値である。Grabber座標系の原点位置は、y軸上の $8$の位置、すなわち $(0, 8, 0)$ に置かれている。Grabber(及び Grabber座標系)には、まず(初期状態の位置である)ワールド座標系の原点において、x軸周りに $15$°の回転、次に y軸周りに $50$°の回転がこの順序で行われる (その回転後に y軸上の $8$の位置への平行移動が行われる)。ワールド座標系のグリッド1マスの1辺の長さを $1$とすれば、Grabber座標系のグリッド1マスの1辺の長さも、ワールド座標系で測った場合には、同じく $1$である。
今述べたことは、図19に表示されている Grabberの Transformコンポーネントにも反映されていることがわかる。すなわち、
図16の Grabber座標系の原点座標 $(0, 8, 0)$ が、Transformコンポーネントの Positionに等しく、
図16に示される Grabber座標系に実行された回転を表す黄色い数値は、Transformコンポーネントの Rotationに等しく、
図16の Grabber座標系のグリッド1マスの1辺の長さは、ワールド座標系で測った場合には $1$であるが、この値は、Transformコンポーネントの Scaleに等しい (例えば、Grabberにz軸方向にだけ $2$倍の拡大が行われていれば、Grabber座標系のグリッド1マスの1辺の長さは、z軸方向だけ長さが $2$になる。その場合には、Transformコンポーネントの Scaleに表示される数値も zの値だけ $2$になる)。
図17は観察対象を Ring座標系に定めたときのもので、図中の数値は、すべて親座標系である Grabber座標系での値である。Ring座標系の原点位置は、Grabber座標系の x軸上(G-x軸上)の $-11$の位置、すなわち $(-11, 0, 0)$ に置かれている (ローカル座標系は基本的に各軸のプラス側のみの表示であるが、ここでは便宜上、Grabber座標系の x軸のマイナス側を半透明で表示している。また、表示されるグリッド領域も その分だけ増加している)。Ring(及び Ring座標系)には、(初期状態の位置である)Grabber座標系の原点において y軸周りに $40$°の回転が行われている (Ring座標系を図の位置から Grabber座標系の原点へ移動させれば、R-x軸と G-x軸は $40$°の角をなす)。Ringには拡大も縮小も行われていないので、Ring座標系のグリッド1マスの1辺の長さは、Grabber座標系のグリッド1マスの1辺の長さと同じく $1$である (ただし これは、Grabber座標系で測った時の長さ)。
図20は、Ringの Transformコンポーネントであるが、今述べたことが各データに反映されていることが確認できる。
図18は観察対象を Ball座標系に定めたときのもので、図中の数値は、すべて親座標系である Ring座標系での値である。また、図21は Ballの Transformコンポーネントであり、図18との間には以下のような対応関係を確認できる。
図18に表示されている座標値 $(-1.73,\ 1,\ 0)$ は Ball座標系の原点の位置を表しており、詳しくは Ball座標系の原点が Ring座標系の $(-1.73,\ 1,\ 0)$ に置かれているという意味である (この$(-1.73,\ 1,\ 0)$という位置は、Ring座標系の$(2, 0, 0)$から R-z軸周りに$150^\circ$回転したときの位置である)。そして、この値は Transformコンポーネントの Positionに等しい (正確には Positionの小数第3位を四捨五入した値)。
図18に示される Ball座標系に実行された回転を表す黄色い数値「y-135」は、Transformコンポーネントの Rotationに等しい (Ball座標系の原点をRing座標系の原点に移動させれば、B-x軸と R-x軸は $135^\circ$ の角をなす)。
図18の Ball座標系のグリッド1マスの1辺の長さは、Ring座標系で測った場合には $1.5$であるが、この値は、Transformコンポーネントの Scaleに等しい。
ここで、Transformコンポーネントの Rotationに関して1つ補足しておく。
説明を簡単にするため、使用するオブジェクトを Grabberのみとし、Grabberに対して次のプログラムを実行したとしよう。
このプログラムは、Grabberに3種類の回転のみを実行するもので、実行結果は図22のようになる。また、図23は そのときの Grabberの Transformコンポーネントである。
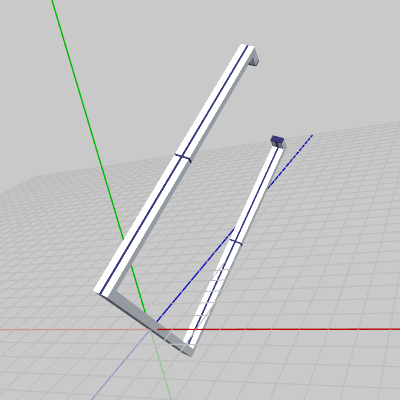
図22 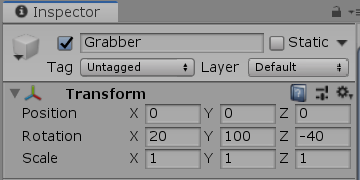
図23
プログラムの1行目から3行目に記述されているとおり、Grabberには、z軸周りに $-40$°の回転、x軸周りに $20$°の回転、y軸周りに $100$°の回転がこの順序で実行される。そして、図23に示される Transformコンポーネントの Rotationの各値を見れば、これらの数値は Grabberに実行された回転を確かに反映していることがわかる。
Transformコンポーネントの Rotationに表示される「x y z」の各値はもちろん、Grabberに対する回転を表す数値であるが、具体的には、これらの数値はオイラー角の各軸の回転角度を表しているのである。3-14節、3-15節で見てきたように、オイラー角は回転の指定方法の1つであり、オイラー角経由で回転を指定する場合には、3つの数値、すなわち、x軸周りの回転角度、y軸周りの回転角度、z軸周りの回転角度が必要なのであった (以下、これらを x-角度、y-角度、z-角度と表記する)。そして、この3つの回転角度をもとにして、3つの回転が実行されるが、その順序は Unityでは Z-X-Yオーダーであった。すなわち、最初に z軸周りの回転、次に x軸周りの回転、最後に y軸周りの回転の順で回転が行われる。
このプログラムで Grabberに実行される回転は、z軸周りの回転、x軸周りの回転、y軸周りの回転の順序であったので、これは Unityにおけるオイラー角指定での回転と実行順序が同じになる。このために、Transformコンポーネントの Rotationの「x y z」の各値が、プログラムで記述された回転角度と一致したのである。これは、自明なことと思われるかもしれないが、注意が必要である。
例えば、プログラムにおける回転の実行順序を Z-X-Y ではなく、X-Y-Z で行ったとしよう。つまり、x軸周りの回転、y軸周りの回転、z軸周りの回転の順で回転を行う次のようなコードを実行したとしよう。
このプログラムは先ほどのプログラムと比較して、回転軸とその軸に対する回転角度は同じであるが、回転順序だけが異なるものである。実行結果、及び Transformコンポーネントを以下に示す。

図24 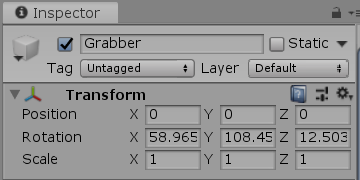
図25
図24に示される実行結果が、前のプログラムの実行結果(図22)と異なるのは、回転順序の違いから予想はできる。しかし、ここで注目すべきは、図25の Transformコンポーネントに示される Rotationの各値である。今回のプログラムでは、前回と同様に x軸周りの回転角度は $20$°、y軸周りの回転角度は $100$°、z軸周りの回転角度は $-40$°と指定していたが、図25における Rotationの各値は「x 58.965 y 108.451 z 12.503」という全く無関係な数値になっている。
なぜ このような数値が表示されるのかというと、やはりそこにはオイラー角の回転順序が関わってくるのである。
図25に示される Rotationの各値が意味することは、次のようなものである。
「Grabberに対して z軸周りに $12.503$°、x軸周りに $58.965$°、y軸周りに $108.451$°の順で回転を実行すると、Grabberは図24に示される状態と同じ状態になる」
実際、次のコードの実行結果は図24と同じである。
より詳しい言い方をすれば、x軸周りに $20$°の回転、y軸周りに $100$°の回転、z軸周りに $-40$°の回転をこの順序(X-Y-Z)で実行することは、z軸周りに $12.503$°の回転、x軸周りに $58.965$°の回転、y軸周りに $108.451$°の回転をこの順序(Z-X-Y)で実行することと同じ結果になるのである。
Transformコンポーネントの Rotationに表示される数値は、上でも述べたように Z-X-Yオーダーのオイラー角回転における3つの回転角度である。Unityでは、オブジェクトにどのような回転を実行しても、Z-X-Yオーダーのオイラー角回転に'翻訳'されて、Inspector上に表示されることになる。実行される回転がどのように複雑なものであったとしても、その回転と同じ結果になるような Z-X-Yオーダーのオイラー角回転を求めて、そのときの x-角度、y-角度、z-角度を Transformコンポーネントの Rotaionとして表示しているのである。
したがって、オブジェクトに実行する回転と Transformコンポーネントの Rotationの各値が一致するのは、オブジェクトに実行する回転が x軸周りの回転、y軸周りの回転、z軸周りの回転の3つだけで、その回転順序が Z-X-Yオーダーである場合のみである (ただし、3軸周りの回転をすべて行う必要はない。例えば、x軸周りの回転と y軸周りの回転のみを実行する場合は z軸周りの回転角度を $0$°と考えればよい)。
なお、Unityにはオイラー角経由の回転を求めるメソッドが用意されている。
これは、引数にオイラー角の x-角度、y-角度、z-角度を指定して、目的のオイラー角回転を表す Quaternionオブジェクトを取得するための staticメソッドである。
この staticメソッドを使って上のプログラムを書き換えると次のようになる。
ここでは、本節で扱った3つのオブジェクト Grabber、Ring、Ballの親子関係の設定を2つの方法によって行う。
(1) Hiecharchyウィンドウで設定する場合
画面上の Hiecharchyウィンドウには Scene内で使用するオブジェクトが並んでいるが、これらのオブジェクトに親子関係を設定する場合は、親子関係を設定するオブジェクトの間でドラッグ&ドロップを行えばよい。例えば、3つのオブジェクト Grabber、Ring、Ballに親子関係が設定されていない状態では、Hiecharchyウィンドウ内の表示は図26のようになっている。
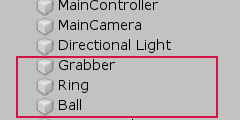
図26 親子関係が設定されていない状態 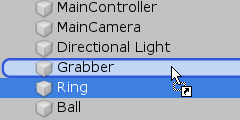
図27 ドラッグ&ドロップによって親子関係を設定する
ここで、図27のように Ringを Grabberの位置にドラッグ&ドロップし、さらに Ballを Ringの位置にドラッグ&ドロップすると、Hiecharchyウィンドウ内の表示は図28のようになる。
この図28の表示は、Grabber、Ring、Ballに図5のような親子関係が設定されていることを意味する。
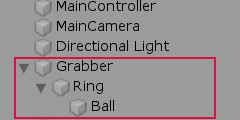
図28 親子関係が設定されている状態 
図5 オブジェクトの階層構造
(2) プログラムから設定する場合
オブジェクトの親子関係の設定はプログラムからも設定することができる。上記の3つのオブジェクトの親子関係を設定するプログラムは以下のようになる。
1行目では Ballの親オブジェクトとして Ringを設定し、2行目では Ringの親オブジェクトとして Grabberを設定している。このコードを実行すると Hiecharchyウィンドウ内の表示は図28のようになる。
各オブジェクトのtransformプロパティからSetParent(..)を実行し、その引数に親オブジェクトのtransformプロパティをセットする形になる。SetParent(..)はオブジェクトのtransformプロパティから呼び出すメソッドであり、オブジェクトが直接呼び出すものではない。例えば、次のような記述は誤りである。
この記述の方が自然に見えるが、Unityではオブジェクトの親子関係の設定は、オブジェクトのtransformプロパティを経由して行わなければいけない。
プログラムから親子関係を設定する場合は、プログラムの開始時点で1回だけ設定処理を行えばよい。例えば、次のようにプログラム開始後に1回だけ実行される初期化ブロックを設けて、このブロック内で親子関係を設定すればよい。
i_INITIALIZEDは、初期化ブロックの処理が行われたかを示すbool型インスタンス変数であり初期値はfalseである。1度このifブロックに入ると、i_INITIALIZEDの値がtrueになるので、それ以降プログラムの実行中にこのブロックに入ることはない。
本節で扱った2つのプログラム Beta2、Beta3は親子関係の設定に関する記述が省略されていたが、以下のプログラムはその設定を含めたものである。
[Code1] (実行結果 図6)
11行目では、x軸上の $(2, 0, 0)$ から z軸周りに $70^\circ$ 回転させた位置を計算している。この計算では行列が使われているが、Quaternionを使う場合は以下のように書き換えればよい。
TH3DMath.GetRotation4x4(70.0f, Vector3.forward) が Quaternion.AngleAxis(70.0f, Vector3.forward) に変わっているが、両方とも内容は同じであり、z軸周りの $70^\circ$ の回転である。行列の計算では $(2, 0, 0)$ が同次座標化されて $(2, 0, 0, 1)$ として使われているが、Quaternionによる計算では同次座標化する必要はないので、そのままQuaternionと $(2, 0, 0)$ の積を計算すればよい。
[Code2] (実行結果 図14)
今までの行列を使用したプログラムでは、オブジェクトの一体化はプログラムの中で実装されていた。プログラムの終了部分は、必ず次のようなコードで終わっていたが、この処理が一体化の実装部分なのである (あるいは親子関係の実装部分である)。
Matrix4x4 worldObj3 = localObj1 * localObj2 * localObj3; Matrix4x4 worldObj2 = localObj1 * localObj2; Matrix4x4 worldObj1 = localObj1; Obj3.SetMatrix(worldObj3); Obj2.SetMatrix(worldObj2); Obj1.SetMatrix(worldObj1);

後の節でも解説するが、オブジェクトの親子関係の構築は、具体的には上に示される数行程度の記述で実装されているのである。この数行のコードによってオブジェクトの親子関係が構築され、オブジェクトが一体化して運動するのである。
しかし、標準的な方法によってオブジェクトに変換を実行していく場合には、オブジェクトの親子関係は事前に Unity側に設定しておく必要がある。そして、親子関係の設定されたオブジェクトに対して、5-2節で見たように各プロパティに適当な値をセットして変換を実行していくのである (Unityでの親子関係の設定に関しては、本節の終わり部分で解説を載せている)。
A) 標準的な変換方法、及び Inspector
本節で使用するオブジェクトは以下の3つである。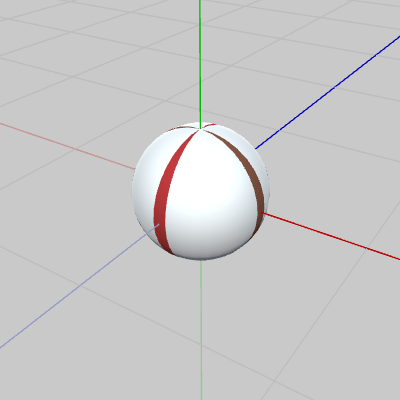 図2 Ball 初期状態
図2 Ball 初期状態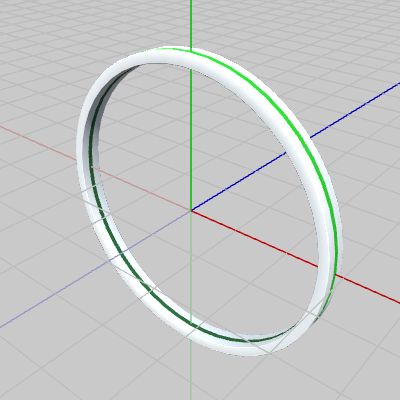 図3 Ring 初期状態
図3 Ring 初期状態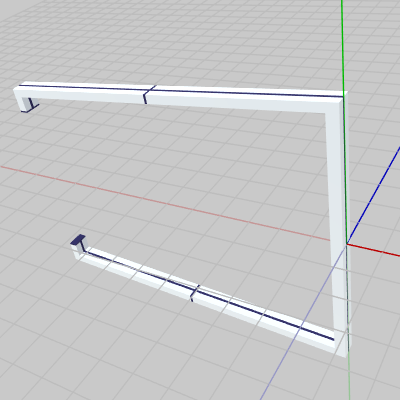 図4 Grabber 初期状態
図4 Grabber 初期状態

最初の2つのプログラム Beta1、Beta2では、Ballと Ringの2つのオブジェクトのみを表示して、それらに対する変換を見ていく。
まずは、行列を使って変換を行う。各オブジェクトに実行する変換は次のとおり。

Ring : x軸周りに $-60$°の回転、y軸周りに $45$°の回転をこの順で行う (これらの変換は Ringの親座標系であるワールド座標系で実行される ; Grabberはここでは使用されないため、Ringが一番上の親オブジェクトである)
プログラム自体は、今までに見てきた行列を使用したプログラムと構造的には同じであり、それらと比べて何か新しい要素があるわけではない。
[Beta1] (実行結果 図6)
// Ball
Matrix4x4 sclBall = TH3DMath.GetScale4x4(1.5f);
Matrix4x4 rotBall = TH3DMath.GetRotation4x4(-50.0f, Vector3.up);
Vector3 pos = TH3DMath.GetRotation4x4(70.0f, Vector3.forward) * new Vector4(2, 0, 0, 1);
Matrix4x4 traBall = TH3DMath.GetTranslation4x4(pos);
Matrix4x4 localBall = traBall * rotBall * sclBall;
// Ring
Matrix4x4 rotRing = TH3DMath.GetRotation4x4(45.0f, Vector3.up) *
TH3DMath.GetRotation4x4(-60.0f, Vector3.right);
Matrix4x4 localRing = rotRing;
Matrix4x4 worldBall = localRing * localBall;
Matrix4x4 worldRing = localRing;
Ball.SetMatrix(worldBall);
Ring.SetMatrix(worldRing);
続いて、今のものと同じ変換を標準的な変換方法によって実装した場合のプログラムを以下に示す (上でも述べたように、標準的な方法では Unity側に親子関係をあらかじめ設定した状態で実行している)。
[Beta2] (実行結果 図6)
// Ball
Ball.transform.localScale = new Vector3(1.5f, 1.5f, 1.5f);
Ball.transform.localRotation = Quaternion.AngleAxis(-50.0f, Vector3.up);
Ball.transform.localPosition = TH3DMath.GetRotation4x4(70.0f, Vector3.forward) *
new Vector4(2, 0, 0, 1);
// Ring
Ring.transform.localRotation = Quaternion.AngleAxis(45.0f, Vector3.up) *
Quaternion.AngleAxis(-60.0f, Vector3.right);
Beta1、Beta2の実行結果はもちろん同じである(図6)。ただ、標準的な方法を使用した場合の方が、親子関係の構築処理の記述が不要になるためコードが簡潔になっている。
前節で解説したように、標準的な変換方法では各オブジェクトには、スケール、回転、平行移動の順で変換が実行される。そして、それらの変換の内容は、localPosition、localRotation、localScale に対して指定する。
例えば Ballの場合は、(Ring座標系の原点において) $1.5$倍の拡大、y軸周りに $-50$°の回転、さらに公転軌道上の計算された位置への平行移動がこの順序で実行されるのである。
Ringに実行される変換は2つの回転であるが、8~9行目ではそれは2つのQuaternionの積によって表されている。詳しくは第6章で解説するが、Quaternionの場合も複数の回転の合成は、複数のQuaternionの積によって表される。例えば、x軸周りの$10$°の回転を表すQuaternionをqx、y軸周りの$20$°の回転を表すQuaternionをqy、z軸周りの$30$°の回転を表すQuaternionをqz とすると、以下のプログラムにおける4行目の Quaternion wQ は、この3つの回転の合成を表すQuaternionである。つまり、wQによる回転は x軸周りの回転、y軸周りの回転、z軸周りの回転をこの順序で実行したものと同じ結果になる (以下の Vector3.right、Vector3.up、Vector3.forwardは、x軸プラス側、y軸プラス側、z軸プラス側を表す定数である)。
Quaternion qx = Quaternion.AngleAxis(10.0f, Vector3.right); // x軸周りの回転 Quaternion qy = Quaternion.AngleAxis(20.0f, Vector3.up); // y軸周りの回転 Quaternion qz = Quaternion.AngleAxis(30.0f, Vector3.forward); // z軸周りの回転 Quaternion wQ = qz * qy * qx;
したがって、Beta2の8~9行目の
Ring.transform.localRotation = Quaternion.AngleAxis(45.0f, Vector3.up) *
Quaternion.AngleAxis(-60.0f, Vector3.right);
この(Beta2の)実行結果に、各オブジェクトのローカル座標系を表示したものを以下に示す (図中のラベルは、x、y、zがワールド座標系の x軸、y軸、z軸を表し、R-x、R-y、R-zが Ring座標系の x軸、y軸、z軸、B-x、B-y、B-zが Ball座標系の x軸、y軸、z軸を表している)。


図7は、プログラムの実行結果をワールド座標系から見たときのもので、Ring、Ballのそれぞれにローカル座標系が表示されている。
図8は、プログラムの実行結果を Ring座標系から見たときのものである (ここではワールド座標系を非表示にしている)。図では Ring座標系の $(2, 0, 0)$ の位置から、z軸周りに $70$°回転した位置に Ball(の中心)が移動していることが示されている。
さらに、このプログラムの実行結果に対して詳細な情報を追加した図を以下に示す (図中における W(##, ##, ##)はワールド座標系の値を表し、R(##, ##, ##)はRing座標系の値を表している)。


以下の内容は、4-11節と重複する部分が多いが、復習の意味で読み進めていただきたい (ただし、ここで展開する内容は復習が目的ではない)。
図9は、プログラムの実行結果をワールド座標系において、Ring座標系の原点付近に近づけて見たときの様子である (図中の数値はすべてワールド座標系での値である)。
図10は、プログラムの実行結果を Ring座標系において、Ball座標系の原点付近に近づけて見たときの様子である (図中の数値はすべて Ring座標系での値である)。
これらは 4-11節でも見たように、ローカル座標系の単位ベクトル部分(各軸において原点からの長さが $1$までの部分)を強調して表示し、その単位ベクトル部分に関する情報を表示したものである。4-11節では、オブジェクトのローカル座標系は、その親座標系で見た場合には、そのオブジェクトのローカル行列を可視化したものになっているということについて学習した。
ここでは、簡単に各オブジェクトのローカル座標系とローカル行列との対応を見てみよう。
Beta1で使われている、Ring、Ballのローカル行列 localRing、localBall の内容を以下に示す (以下の それぞれの右辺は 4-6節 $(Ex1)$の書き換えを行った形である)。
\[localRing=\begin{pmatrix}0.71 &-0.61 &0.35 &0.00 \\ 0.00 &0.50 &0.87 &0.00 \\ -0.71 &-0.61 &0.35 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix}=\begin{pmatrix}1\cdot 0.71 &1\cdot (-0.61) &1\cdot 0.35 &0.00 \\ 1\cdot 0.00 &1\cdot 0.50 &1\cdot 0.87 &0.00 \\ 1\cdot (-0.71) &1\cdot (-0.61) &1\cdot 0.35 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix}\]
\[localBall=\begin{pmatrix}0.96 &0.00 &-1.15 &0.68 \\ 0.00 &1.50 &0.00 &1.88 \\ 1.15 &0.00 &0.96 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix}=\begin{pmatrix}1.5\cdot 0.64 &1.5\cdot 0.00 &1.5\cdot (-0.77) &0.68 \\ 1.5\cdot 0.00 &1.5\cdot 1.00 &1.5\cdot 0.00 &1.88 \\ 1.5\cdot 0.77 &1.5\cdot 0.00 &1.5\cdot 0.64 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix}\]
図9、図10には黄色い数字で「x-60 y45」、「y-50」と表示されている。これらの数値は、オブジェクトに実行された回転を表しており、図9の場合は、Ringには、x軸周りに $-60$°、y軸周りに $45$°の順序で回転が実行されたことを示し、図10の場合は、Ballには、y軸周りに $-50$°の回転のみが実行されたことを示している。
4-8節から 4-11節で見てきたように、オブジェクトのローカル座標系には、そのオブジェクトに対して実行される変換と全く同じ変換が実行される。したがって、図9、図10の黄色い数値は、Ring座標系に実行された回転、Ball座標系に実行された回転でもある。すなわち、これらの図に表示されている黄色い数値は、ローカル座標系に対して実行された回転を表すものでもあるわけである。
4-11節で見てきたように、ローカル座標系の x軸、y軸、z軸の単位ベクトル表示(図9、図10のオレンジ色の数値)は、ローカル行列の第1列目、第2列目、第3列目の係数を除いたものに一致する。また、変換行列の左上3行3列において係数を除いたものを変換行列の回転成分と呼ぶことについても 4-6節で学習した。
例えば、図9の場合、すなわち Ring座標系の場合では各軸の単位ベクトル表示は、$(0.71, 0.0, -0.71)$、$(-0.61, 0.50, -0.61)$、$(0.35, 0.87, 0.35)$ であり、これは確かに Ringのローカル行列 localRing の回転成分(左上3行3列において係数を除いたもの)に一致している。そして、この localRing の回転成分の内容は、x軸周りに $-60$°、y軸周りに $45$°の順序で行う回転である。実際、x軸周り $-60$°の回転を $R_x$、y軸周り $45$°の回転を $R_y$とすれば、その積は、
\[R_y R_x = \begin{pmatrix}0.71 &0.00 &0.71 \\ 0.00 &1.00 &0.00 \\ -0.71 &0.00 &0.71 \end{pmatrix}\begin{pmatrix}1.00 &0.00 &0.00 \\ 0.00 &0.50 &0.87 \\ 0.00 &-0.87 &0.50 \end{pmatrix}=\begin{pmatrix}0.71 &-0.61 &0.35 \\ 0.00 &0.50 &0.87 \\ -0.71 &-0.61 &0.35 \end{pmatrix}\]
となり、確かに localRing の回転成分と等しいことが示される (回転行列同士の積なので $3\times 3$行列で計算している(3-10節参照) ; 行列の各成分は小数第3位を四捨五入して小数第2位までの表示としている)。繰り返しになるが、localRingの回転成分は、x軸周りに $-60$°、y軸周りに $45$°の順序の回転を意味している。言い換えれば、図9に示される黄色い数値「x-60 y45」は localRingの回転成分と同じ意味を持っているのである。
また、これも 4-11節で見てきたことだが、ローカル座標系の原点座標は、ローカル行列の平行移動成分(変換行列の第4列目)に等しく、ローカル座標系の各軸の単位ベクトル部分の長さは、ローカル行列のスケール成分(変換行列の第1列目、第2列目、第3列目に掛けられている係数)に等しいのであった。実際、図9の Ring座標系の原点座標、及び 単位ベクトル部分の長さと、localRingの平行移動成分、スケール成分を比較すれば このことは確かめられる。
図10においても同様で、Ball座標系に対して実行された回転を表す黄色い数値「y-50」は、localBallの回転成分と同じ意味を持っており (この回転成分の内容は y軸周り $-50$°の回転である)、Ball座標系の原点座標、及び Ball座標系の単位ベクトル部分の長さは、それぞれ localBallの平行移動成分、スケール成分に等しい。
上で述べたことは、以下の形で要約される。
ローカル座標系の原点座標は、ローカル行列の平行移動成分に等しい。
ローカル座標系に対して実行された回転を表す黄色い数値は、ローカル行列の回転成分と同じ意味を持っている。
ローカル座標系の単位ベクトル部分の長さは、ローカル行列のスケール成分に等しい。
では、ここで一旦話題を切り替える。

図11は Unityにおけるインターフェースであるが、同様のものは、Unreal Engineにも備わっているし、Blender、MayaといったDCCツールにも用意されている。
図11は Unityにおいて Inspectorと呼ばれる領域で、Inspectorにはオブジェクトのさまざまな情報が表示される。
図に示されているのは Transformコンポーネントというものに関連したデータであり、ここには「Position」、「Rotation」、「Scale」の3つの項目のそれぞれに、x、y、z の値が表示されている。これらは、もちろんオブジェクトの Position、Rotation、Scaleのことであるが、具体的に何を意味しているのかについて以下で見ていこう。
上で示したプログラム Beta1、Beta2はオブジェクトの変換方法は異なるが、実行結果は同じであった。どちらのプログラムでも、実行結果は同じであるが、ここからは標準的な変換方法を使用した Beta2を実行した場合で話を進める (すなわち、Unity側には事前に親子関係の設定がなされている)。
Beta2 を実行した結果を再度示す。


図9、図10は、プログラムの実行結果をワールド座標系、Ring座標系から見たときの様子であった。
このときの、Unityの Inspector上の Transformコンポーネントは次のような表示になっている。


図12は Ringの Transformコンポーネントであるが、ここに表示されているデータと図9の Ring座標系の各数値を見比べると次のような対応があることがわかる。
Transformコンポーネントの Position「x 0 y 0 z 0」は、Ring座標系の原点座標に等しい。
Transformコンポーネントの Rotation「x -60 y 45 z 0」は「z 0」を除外すれば、Ring座標系に実行された回転を表す黄色い数値に等しい。
Transformコンポーネントの Scale「x 1 y 1 z 1」は、Ring座標系の単位ベクトル部分の長さに等しい。
図13は Ballの Transformコンポーネントであるが、ここに表示されているデータと図10の Ball座標系の各数値を見比べた場合にも、同様の対応があることがわかる。
Transformコンポーネントの Position「x 0.6840 y 1.8793 z 0」は小数第3位を四捨五入すれば「x 0.68 y 1.88 z 0」であるが、これは Ball座標系の原点座標に等しい。
Transformコンポーネントの Rotation「x 0 y -50 z 0」は「x 0」「z 0」を除外すれば、Ball座標系に実行された回転を表す黄色い数値に等しい。
Transformコンポーネントの Scale「x 1.5 y 1.5 z 1.5」は、Ball座標系の単位ベクトル部分の長さに等しい。
オブジェクトの Transformコンポーネントとローカル座標系に関しての これら結果は、以下の形で要約される。
Transformコンポーネントの Positionは、ローカル座標系の原点座標に等しい。
Transformコンポーネントの Rotationは、ローカル座標系に実行された回転を表す黄色い数値に等しい。
Transformコンポーネントの Scaleは、ローカル座標系の単位ベクトル部分の長さに等しい。
ここで先程の、オブジェクトのローカル座標系とローカル行列に関しての要約を再度示す。
ローカル座標系の原点座標は、ローカル行列の平行移動成分に等しい。
ローカル座標系に対して実行された回転を表す黄色い数値は、ローカル行列の回転成分と同じ意味を持っている。
ローカル座標系の単位ベクトル部分の長さは、ローカル行列のスケール成分に等しい。
以上からわかるように、
ローカル座標系の原点座標、ローカル行列の平行移動成分、Transformコンポーネントの Position はすべて同じ内容を表しているのである。
また、ローカル座標系に実行された回転を表す黄色い数値、ローカル行列の回転成分、Transformコンポーネントの Rotation についても、3つとも同じ内容を表しているのである。
同様に、ローカル座標系の単位ベクトル部分の長さ、ローカル行列のスケール成分、Transformコンポーネントの Scale、この3つもやはり同じ内容を表しているのである。
簡単に言えば、ローカル座標系、ローカル行列、Inspector上の Transformコンポーネントは、'姿形'は異なるが同一のものなのである。
ただし、4-11節でも述べたが、ローカル座標系の各数値(原点座標、回転を表す黄色い数値、単位ベクトル部分の長さ)は親座標系で測ったときの値であることに注意する必要がある。上の図9の Ring座標系の各数値は親座標系であるワールド座標系での値であり、図10の Ball座標系の各数値は親座標系である Ring座標系での値である。例えば、図10の Ball座標系は、Ring座標系の $(0.68, 1.88, 0)$ に原点があり、Ring座標系の y軸周りに $-50$°の回転が実行されており、Ring座標系で測ったときに Ball座標系の単位ベクトル部分の長さ、すなわち、グリッド1マスの1辺の長さが $1.5$になるのである。Ring座標系の親座標系であるワールド座標系から Ball座標系を見たときには、原点座標や回転角度はこのような数値にはならない。
Inspector上の Transformコンポーネントは、ローカル座標系(及び ローカル行列)と同一のものであるので、そこに表示されている数値は親座標系での値である。Transformコンポーネントの各数値は、親座標系における数値であり、ワールド座標系での値ではない (もちろん、親座標系がワールド座標系であれば、表示される数値はワールド座標系での値になる ; 少なくとも、この解説で使用している Unityのバージョン 2019.2.9f1 においては、Transformコンポーネントには親座標系での値のみが表示される)。
Unityの User Manualには、Inspector上の Transformコンポーネントに関して次のような説明がある。
The position, rotation and scale values of a Transform are measured relative to the Transform’s parent. If the Transform has no parent, the properties are measured in world space.
これは 要するに、Transformコンポーネントの各数値は親座標系を基準にして測った数値であり、もしオブジェクトが親オブジェクトを持たない場合には、各数値はワールド座標系を基準にして測られるということを言っているのである。
The position, rotation and scale values of a Transform are measured relative to the Transform’s parent. If the Transform has no parent, the properties are measured in world space.
これは 要するに、Transformコンポーネントの各数値は親座標系を基準にして測った数値であり、もしオブジェクトが親オブジェクトを持たない場合には、各数値はワールド座標系を基準にして測られるということを言っているのである。
では次に、上で使用した Ball、Ringの他に、Ringの親オブジェクトとして Grabberを追加し、親子階層を3階層にしたプログラムを使って、各オブジェクトに設定されるプロパティの値と、Inspector上のTransformコンポーネントの対応関係を簡単に確認する。
各オブジェクトに実行される変換は次のとおり。
Ball : $1.5$倍のスケール、y軸周りに $-135$°の自転、さらに原点を中心とする z軸周りの半径 $2$の円周上を $(2, 0, 0)$を起点として $150$°公転する (これらの変換は Ballの親座標系である Ring座標系で実行される)。
Ring : まず、y軸周りに $40$°の回転、次に、アタッチポジションである Grabber座標系の $(-11, 0, 0)$ への平行移動を行う (これらの変換は Ringの親座標系である Grabber座標系で実行される)。
Grabber : x軸周りに $15$°の回転、y軸周りに $50$°の回転をこの順で実行し、さらに y軸方向へ $8$だけ平行移動する (これらの変換は Grabberの親座標系であるワールド座標系で実行される)。
[Beta3] (実行結果 図14~図18 ; プログラムの実行にあたっては、事前に Unity側に親子関係の設定がなされている)
// Ball
Ball.transform.localScale = new Vector3(1.5f, 1.5f, 1.5f);
Ball.transform.localRotation = Quaternion.AngleAxis(-135.0f, Vector3.up);
Ball.transform.localPosition = TH3DMath.GetRotation4x4(150.0f, Vector3.forward) *
new Vector4(2, 0, 0, 1);
// Ring
Ring.transform.localRotation = Quaternion.AngleAxis(40.0f, Vector3.up);
Ring.transform.localPosition = c_attachPos_Ring; // == (-11, 0, 0)
// Grabber
Grabber.transform.localRotation = Quaternion.AngleAxis(50.0f, Vector3.up) *
Quaternion.AngleAxis(15.0f, Vector3.right);
Grabber.transform.localPosition = new Vector3(0, 8, 0);


図14は プログラムの実行結果をワールド座標系から見たときの様子であり、図15は さらに、各オブジェクトのローカル座標系を表示したものである。
続いて、この実行結果に関して各座標系から見たときの詳しい情報を付加した図、及び Inspector上の Transformコンポーネントを以下に示す (以下の図中における W(##, ##, ##)、G(##, ##, ##)、R(##, ##, ##) はワールド座標系の値、はGrabber座標系の値、Ring座標系の値を表している)。
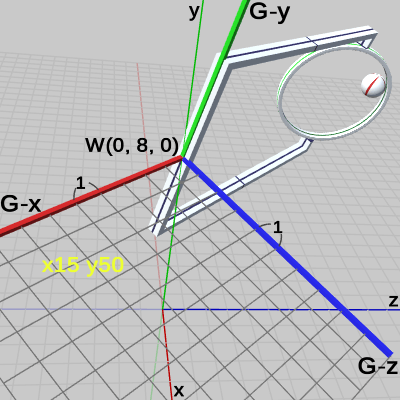 図16
図16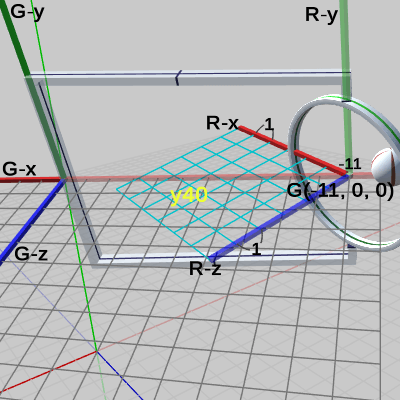 図17
図17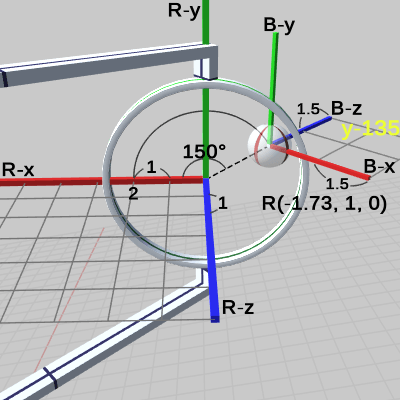 図18
図18
 図19
図19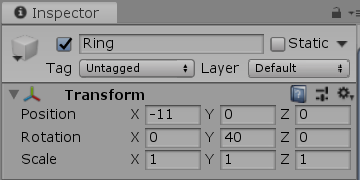 図20
図20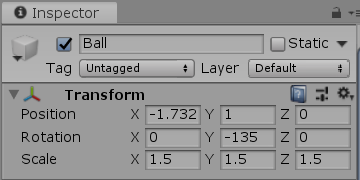 図21
図21
図16は観察対象を Grabber座標系に定めたときのもので、図中の数値は、すべて親座標系であるワールド座標系での値である。Grabber座標系の原点位置は、y軸上の $8$の位置、すなわち $(0, 8, 0)$ に置かれている。Grabber(及び Grabber座標系)には、まず(初期状態の位置である)ワールド座標系の原点において、x軸周りに $15$°の回転、次に y軸周りに $50$°の回転がこの順序で行われる (その回転後に y軸上の $8$の位置への平行移動が行われる)。ワールド座標系のグリッド1マスの1辺の長さを $1$とすれば、Grabber座標系のグリッド1マスの1辺の長さも、ワールド座標系で測った場合には、同じく $1$である。
今述べたことは、図19に表示されている Grabberの Transformコンポーネントにも反映されていることがわかる。すなわち、
図16の Grabber座標系の原点座標 $(0, 8, 0)$ が、Transformコンポーネントの Positionに等しく、
図16に示される Grabber座標系に実行された回転を表す黄色い数値は、Transformコンポーネントの Rotationに等しく、
図16の Grabber座標系のグリッド1マスの1辺の長さは、ワールド座標系で測った場合には $1$であるが、この値は、Transformコンポーネントの Scaleに等しい (例えば、Grabberにz軸方向にだけ $2$倍の拡大が行われていれば、Grabber座標系のグリッド1マスの1辺の長さは、z軸方向だけ長さが $2$になる。その場合には、Transformコンポーネントの Scaleに表示される数値も zの値だけ $2$になる)。
図17は観察対象を Ring座標系に定めたときのもので、図中の数値は、すべて親座標系である Grabber座標系での値である。Ring座標系の原点位置は、Grabber座標系の x軸上(G-x軸上)の $-11$の位置、すなわち $(-11, 0, 0)$ に置かれている (ローカル座標系は基本的に各軸のプラス側のみの表示であるが、ここでは便宜上、Grabber座標系の x軸のマイナス側を半透明で表示している。また、表示されるグリッド領域も その分だけ増加している)。Ring(及び Ring座標系)には、(初期状態の位置である)Grabber座標系の原点において y軸周りに $40$°の回転が行われている (Ring座標系を図の位置から Grabber座標系の原点へ移動させれば、R-x軸と G-x軸は $40$°の角をなす)。Ringには拡大も縮小も行われていないので、Ring座標系のグリッド1マスの1辺の長さは、Grabber座標系のグリッド1マスの1辺の長さと同じく $1$である (ただし これは、Grabber座標系で測った時の長さ)。
図20は、Ringの Transformコンポーネントであるが、今述べたことが各データに反映されていることが確認できる。
図18は観察対象を Ball座標系に定めたときのもので、図中の数値は、すべて親座標系である Ring座標系での値である。また、図21は Ballの Transformコンポーネントであり、図18との間には以下のような対応関係を確認できる。
図18に表示されている座標値 $(-1.73,\ 1,\ 0)$ は Ball座標系の原点の位置を表しており、詳しくは Ball座標系の原点が Ring座標系の $(-1.73,\ 1,\ 0)$ に置かれているという意味である (この$(-1.73,\ 1,\ 0)$という位置は、Ring座標系の$(2, 0, 0)$から R-z軸周りに$150^\circ$回転したときの位置である)。そして、この値は Transformコンポーネントの Positionに等しい (正確には Positionの小数第3位を四捨五入した値)。
図18に示される Ball座標系に実行された回転を表す黄色い数値「y-135」は、Transformコンポーネントの Rotationに等しい (Ball座標系の原点をRing座標系の原点に移動させれば、B-x軸と R-x軸は $135^\circ$ の角をなす)。
図18の Ball座標系のグリッド1マスの1辺の長さは、Ring座標系で測った場合には $1.5$であるが、この値は、Transformコンポーネントの Scaleに等しい。
ここで、Transformコンポーネントの Rotationに関して1つ補足しておく。
説明を簡単にするため、使用するオブジェクトを Grabberのみとし、Grabberに対して次のプログラムを実行したとしよう。
Grabber.transform.localRotation = Quaternion.AngleAxis(100.0f, Vector3.up) * // y軸周りの回転
Quaternion.AngleAxis( 20.0f, Vector3.right) * // x軸周りの回転
Quaternion.AngleAxis(-40.0f, Vector3.forward); // z軸周りの回転
このプログラムは、Grabberに3種類の回転のみを実行するもので、実行結果は図22のようになる。また、図23は そのときの Grabberの Transformコンポーネントである。


プログラムの1行目から3行目に記述されているとおり、Grabberには、z軸周りに $-40$°の回転、x軸周りに $20$°の回転、y軸周りに $100$°の回転がこの順序で実行される。そして、図23に示される Transformコンポーネントの Rotationの各値を見れば、これらの数値は Grabberに実行された回転を確かに反映していることがわかる。
Transformコンポーネントの Rotationに表示される「x y z」の各値はもちろん、Grabberに対する回転を表す数値であるが、具体的には、これらの数値はオイラー角の各軸の回転角度を表しているのである。3-14節、3-15節で見てきたように、オイラー角は回転の指定方法の1つであり、オイラー角経由で回転を指定する場合には、3つの数値、すなわち、x軸周りの回転角度、y軸周りの回転角度、z軸周りの回転角度が必要なのであった (以下、これらを x-角度、y-角度、z-角度と表記する)。そして、この3つの回転角度をもとにして、3つの回転が実行されるが、その順序は Unityでは Z-X-Yオーダーであった。すなわち、最初に z軸周りの回転、次に x軸周りの回転、最後に y軸周りの回転の順で回転が行われる。
このプログラムで Grabberに実行される回転は、z軸周りの回転、x軸周りの回転、y軸周りの回転の順序であったので、これは Unityにおけるオイラー角指定での回転と実行順序が同じになる。このために、Transformコンポーネントの Rotationの「x y z」の各値が、プログラムで記述された回転角度と一致したのである。これは、自明なことと思われるかもしれないが、注意が必要である。
例えば、プログラムにおける回転の実行順序を Z-X-Y ではなく、X-Y-Z で行ったとしよう。つまり、x軸周りの回転、y軸周りの回転、z軸周りの回転の順で回転を行う次のようなコードを実行したとしよう。
Grabber.transform.localRotation = Quaternion.AngleAxis(-40.0f, Vector3.forward) * // z軸周りの回転
Quaternion.AngleAxis(100.0f, Vector3.up) * // y軸周りの回転
Quaternion.AngleAxis(20.0f, Vector3.right); // x軸周りの回転
このプログラムは先ほどのプログラムと比較して、回転軸とその軸に対する回転角度は同じであるが、回転順序だけが異なるものである。実行結果、及び Transformコンポーネントを以下に示す。


図24に示される実行結果が、前のプログラムの実行結果(図22)と異なるのは、回転順序の違いから予想はできる。しかし、ここで注目すべきは、図25の Transformコンポーネントに示される Rotationの各値である。今回のプログラムでは、前回と同様に x軸周りの回転角度は $20$°、y軸周りの回転角度は $100$°、z軸周りの回転角度は $-40$°と指定していたが、図25における Rotationの各値は「x 58.965 y 108.451 z 12.503」という全く無関係な数値になっている。
なぜ このような数値が表示されるのかというと、やはりそこにはオイラー角の回転順序が関わってくるのである。
図25に示される Rotationの各値が意味することは、次のようなものである。
「Grabberに対して z軸周りに $12.503$°、x軸周りに $58.965$°、y軸周りに $108.451$°の順で回転を実行すると、Grabberは図24に示される状態と同じ状態になる」
実際、次のコードの実行結果は図24と同じである。
Grabber.transform.localRotation = Quaternion.AngleAxis(108.451f, Vector3.up) * // y軸周りの回転
Quaternion.AngleAxis(58.965f, Vector3.right) * // x軸周りの回転
Quaternion.AngleAxis(12.503f, Vector3.forward); // z軸周りの回転
より詳しい言い方をすれば、x軸周りに $20$°の回転、y軸周りに $100$°の回転、z軸周りに $-40$°の回転をこの順序(X-Y-Z)で実行することは、z軸周りに $12.503$°の回転、x軸周りに $58.965$°の回転、y軸周りに $108.451$°の回転をこの順序(Z-X-Y)で実行することと同じ結果になるのである。
Transformコンポーネントの Rotationに表示される数値は、上でも述べたように Z-X-Yオーダーのオイラー角回転における3つの回転角度である。Unityでは、オブジェクトにどのような回転を実行しても、Z-X-Yオーダーのオイラー角回転に'翻訳'されて、Inspector上に表示されることになる。実行される回転がどのように複雑なものであったとしても、その回転と同じ結果になるような Z-X-Yオーダーのオイラー角回転を求めて、そのときの x-角度、y-角度、z-角度を Transformコンポーネントの Rotaionとして表示しているのである。
したがって、オブジェクトに実行する回転と Transformコンポーネントの Rotationの各値が一致するのは、オブジェクトに実行する回転が x軸周りの回転、y軸周りの回転、z軸周りの回転の3つだけで、その回転順序が Z-X-Yオーダーである場合のみである (ただし、3軸周りの回転をすべて行う必要はない。例えば、x軸周りの回転と y軸周りの回転のみを実行する場合は z軸周りの回転角度を $0$°と考えればよい)。
なお、Unityにはオイラー角経由の回転を求めるメソッドが用意されている。
// 引数で指定されるオイラー角回転を表す Quaternionを返す Quaternion.Euler(float x, float y, float z)
この staticメソッドを使って上のプログラムを書き換えると次のようになる。
// 回転順序は Z-X-Yオーダー Grabber.transform.localRotation = Quaternion.Euler(58.965f, 108.451f, 12.503f);
B) Unityでの親子関係の設定
最後に、Unityにおいてオブジェクトの親子関係を設定する方法について簡単に解説する。ここでは、本節で扱った3つのオブジェクト Grabber、Ring、Ballの親子関係の設定を2つの方法によって行う。
(1) Hiecharchyウィンドウで設定する場合
画面上の Hiecharchyウィンドウには Scene内で使用するオブジェクトが並んでいるが、これらのオブジェクトに親子関係を設定する場合は、親子関係を設定するオブジェクトの間でドラッグ&ドロップを行えばよい。例えば、3つのオブジェクト Grabber、Ring、Ballに親子関係が設定されていない状態では、Hiecharchyウィンドウ内の表示は図26のようになっている。


ここで、図27のように Ringを Grabberの位置にドラッグ&ドロップし、さらに Ballを Ringの位置にドラッグ&ドロップすると、Hiecharchyウィンドウ内の表示は図28のようになる。
この図28の表示は、Grabber、Ring、Ballに図5のような親子関係が設定されていることを意味する。


(2) プログラムから設定する場合
オブジェクトの親子関係の設定はプログラムからも設定することができる。上記の3つのオブジェクトの親子関係を設定するプログラムは以下のようになる。
Ball.transform.SetParent(Ring.transform); Ring.transform.SetParent(Grabber.transform);
1行目では Ballの親オブジェクトとして Ringを設定し、2行目では Ringの親オブジェクトとして Grabberを設定している。このコードを実行すると Hiecharchyウィンドウ内の表示は図28のようになる。
各オブジェクトのtransformプロパティからSetParent(..)を実行し、その引数に親オブジェクトのtransformプロパティをセットする形になる。SetParent(..)はオブジェクトのtransformプロパティから呼び出すメソッドであり、オブジェクトが直接呼び出すものではない。例えば、次のような記述は誤りである。
// NG Ball.SetParent(Ring); Ring.SetParent(Grabber);
この記述の方が自然に見えるが、Unityではオブジェクトの親子関係の設定は、オブジェクトのtransformプロパティを経由して行わなければいけない。
プログラムから親子関係を設定する場合は、プログラムの開始時点で1回だけ設定処理を行えばよい。例えば、次のようにプログラム開始後に1回だけ実行される初期化ブロックを設けて、このブロック内で親子関係を設定すればよい。
if (!i_INITIALIZED)
{
i_INITIALIZED = true;
// 親子関係の設定
Obj5.transform.SetParent(Obj4.transform);
Obj4.transform.SetParent(Obj3.transform);
Obj3.transform.SetParent(Obj2.transform);
Obj2.transform.SetParent(Obj1.transform);
}
i_INITIALIZEDは、初期化ブロックの処理が行われたかを示すbool型インスタンス変数であり初期値はfalseである。1度このifブロックに入ると、i_INITIALIZEDの値がtrueになるので、それ以降プログラムの実行中にこのブロックに入ることはない。
本節で扱った2つのプログラム Beta2、Beta3は親子関係の設定に関する記述が省略されていたが、以下のプログラムはその設定を含めたものである。
# Code1
上記のプログラムBeta2に親子関係の設定を追加したものである。[Code1] (実行結果 図6)
if (!i_INITIALIZED)
{
Ball.transform.SetParent(Ring.transform);
i_INITIALIZED = true;
}
// Ball
Ball.transform.localScale = new Vector3(1.5f, 1.5f, 1.5f);
Ball.transform.localRotation = Quaternion.AngleAxis(-50.0f, Vector3.up);
Ball.transform.localPosition = TH3DMath.GetRotation4x4(70.0f, Vector3.forward) *
new Vector4(2, 0, 0, 1);
// Ring
Ring.transform.localRotation = Quaternion.AngleAxis(45.0f, Vector3.up) *
Quaternion.AngleAxis(-60.0f, Vector3.right);
11行目では、x軸上の $(2, 0, 0)$ から z軸周りに $70^\circ$ 回転させた位置を計算している。この計算では行列が使われているが、Quaternionを使う場合は以下のように書き換えればよい。
Ball.transform.localPosition = Quaternion.AngleAxis(70.0f, Vector3.forward) *
new Vector3(2, 0, 0);
TH3DMath.GetRotation4x4(70.0f, Vector3.forward) が Quaternion.AngleAxis(70.0f, Vector3.forward) に変わっているが、両方とも内容は同じであり、z軸周りの $70^\circ$ の回転である。行列の計算では $(2, 0, 0)$ が同次座標化されて $(2, 0, 0, 1)$ として使われているが、Quaternionによる計算では同次座標化する必要はないので、そのままQuaternionと $(2, 0, 0)$ の積を計算すればよい。
# Code2
上記のプログラムBeta3に親子関係の設定を追加したものである。[Code2] (実行結果 図14)
if (!i_INITIALIZED)
{
Ball.transform.SetParent(Ring.transform);
Ring.transform.SetParent(Grabber.transform);
i_INITIALIZED = true;
}
// Ball
Ball.transform.localScale = new Vector3(1.5f, 1.5f, 1.5f);
Ball.transform.localRotation = Quaternion.AngleAxis(-135.0f, Vector3.up);
Ball.transform.localPosition = TH3DMath.GetRotation4x4(150.0f, Vector3.forward) *
new Vector4(2, 0, 0, 1);
// Ring
Ring.transform.localRotation = Quaternion.AngleAxis(40.0f, Vector3.up);
Ring.transform.localPosition = c_attachPos_Ring;
// Grabber
Grabber.transform.localRotation = Quaternion.AngleAxis(50.0f, Vector3.up) *
Quaternion.AngleAxis(15.0f, Vector3.right);
Grabber.transform.localPosition = new Vector3(0, 8, 0);
© 2020-2025 Redpoll's 60 (All rights reserved)