Redpoll's 60
Home / 3Dプログラミング入門 / 第1章 $§$1-1
第1章 2D空間の基礎
| $§$1-1 点とベクトル | $§$1-6 行列による回転 |
| $§$1-2 ベクトルによる平行移動 | $§$1-7 行列によるスケール |
| $§$1-3 単位ベクトル | $§$1-8 変換行列の積 |
| $§$1-4 行列 | $§$1-9 フレームとフレームレート |
| $§$1-5 行列による平行移動 | $§$1-10 オブジェクトの基本的な運動 (往復運動と回転) |
$§$1-1 点とベクトル
本章では2D空間(2次元空間)の基礎的事項について解説する。
内容としては主にベクトルや行列の初歩的な使用例に関するものである。ベクトルや行列は2D、3Dを問わずコンピューターグラフィックスにおいて最も重要な概念であり、これらに対する理解は2Dあるいは3Dプログラミングを理解するうえで欠くことのできないものである。
なお、講義の中で使われる「2D空間」という用語はXY平面と同じものである。また、文章中で使用する図においては赤い軸がx軸、緑の軸がy軸である。
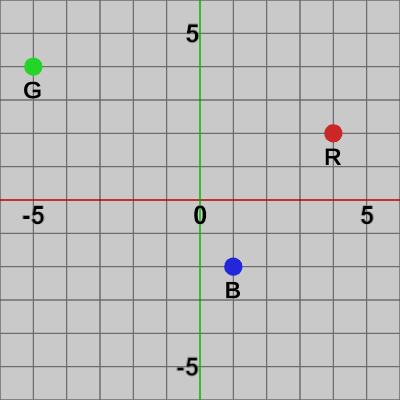
図1 点は2D(あるいは3D)空間上のある位置を示すために使われる。次の図1には3つの点$R$、$G$、$B$があり、それぞれの位置は
\[R : \begin{cases} x = 4 \\ y = 2 \end{cases}\quad G : \begin{cases} x = -5 \\ y = 4 \end{cases}\quad B : \begin{cases} x = 1 \\ y = -2 \end{cases}\]である。
コンピューターグラフィックスでは点も位置ベクトルというベクトルとして扱われる。例えば、上図の点$R$、$G$、$B$は位置ベクトルとして次のように表される。\[R = \begin{pmatrix}4 \\2 \end{pmatrix} \quad G = \begin{pmatrix}-5 \\4 \end{pmatrix} \quad B = \begin{pmatrix}1 \\-2 \end{pmatrix}\] 講義では基本的に縦並びの列ベクトルを使っていく。統一的に列ベクトルだけを使っていくのが理想であるが、スペース的な問題で文章中や図の中においては横並びの行ベクトルを用いる(この講義の中で行ベクトルを使う場合はあくまで見やすさのためである)。
ベクトルの加算、減算は次のように定義される。\begin{align*}\begin{pmatrix}x_{1} \\y_{1} \end{pmatrix} +\begin{pmatrix}x_{2} \\y_{2} \end{pmatrix} =\begin{pmatrix}x_{1} + x_{2}\\y_{1} + y_{2}\end{pmatrix} \\ \\\begin{pmatrix}x_{1} \\y_{1} \end{pmatrix} -\begin{pmatrix}x_{2} \\y_{2} \end{pmatrix} =\begin{pmatrix}x_{1} - x_{2}\\y_{1} - y_{2}\end{pmatrix} \end{align*}(計算例)\begin{align*}&\begin{pmatrix}3 \\4 \end{pmatrix} +\begin{pmatrix}8 \\-2 \end{pmatrix} =\begin{pmatrix}3 + 8\\4 + (-2)\end{pmatrix} =\begin{pmatrix}11\\2\end{pmatrix} \\ \\&\begin{pmatrix}-1 \\10 \end{pmatrix} -\begin{pmatrix}-5 \\5 \end{pmatrix} =\begin{pmatrix}-1 - (-5)\\10 - 5\end{pmatrix} =\begin{pmatrix}4\\5\end{pmatrix} \end{align*}
ベクトルは始点と終点を持っており、ベクトル自体は終点から始点を引くことで求められる。「終点から始点を引く」とは詳しく言えば始点、終点を位置ベクトルとして扱い、ベクトル同士の減算を行うのである。
以下にその例を示す(下図における矢の形をしたものはベクトルを可視化したものである。矢の先端がベクトルの終点を表している)。
図2のベクトル$\boldsymbol{\mathsf{v_1}}$は始点(1, 1)、終点(5、3)であり次のように求められる。\begin{equation} \boldsymbol{\mathsf{v_1}} = \begin{pmatrix}5 \\3 \end{pmatrix} -\begin{pmatrix}1 \\1 \end{pmatrix} =\begin{pmatrix}4 \\2 \end{pmatrix} \end{equation}図3のベクトル$\boldsymbol{\mathsf{v_2}}$は始点(0, 0)、終点(1、3)であり、図4のベクトル$\boldsymbol{\mathsf{v_3}}$は始点(-2, -5)、終点(-5, 4)である。これらのベクトルに関してもベクトル$\boldsymbol{\mathsf{v_1}}$の場合と同様に計算すればよい。\begin{align*} &\boldsymbol{\mathsf{v_2}} = \begin{pmatrix}1 \\3 \end{pmatrix} -\begin{pmatrix}0 \\0 \end{pmatrix} =\begin{pmatrix}1 \\3 \end{pmatrix} \\ \\ &\boldsymbol{\mathsf{v_3}} = \begin{pmatrix}-5 \\4 \end{pmatrix} -\begin{pmatrix}-2 \\-5\end{pmatrix} =\begin{pmatrix}-3 \\9 \end{pmatrix} \end{align*}
なお、この講義では図の中で点(位置)を表す数値については黒色のフォントを使用し、ベクトルを表す数値については緑色のフォントを使用している。例えば、図2のベクトル$\boldsymbol{\mathsf{v_1}}$は $(4, 2)$ であるが、この数値はベクトルを表すので緑色のフォントを使用し、$\boldsymbol{\mathsf{v_1}}$の始点 $(1, 1)$、終点 $(5, 3)$ は点(位置)を表すので黒色のフォントを使用している。図3のベクトル$\boldsymbol{\mathsf{v_2}}$、図4の$\boldsymbol{\mathsf{v_3}}$についても同様に始点、終点は黒色の数値で表され、各ベクトルの内容は緑色の数値で表されている。
また、始点から終点までの距離をベクトルの大きさ(Magnitude)、あるいは長さという。ベクトルの大きさは次のように計算される。
ベクトル $\boldsymbol{\mathsf{v}} = (x, y)$ の大きさ $|\boldsymbol{\mathsf{v}}|$\begin{equation} |\boldsymbol{\mathsf{v}}| = \sqrt{x^2 + y^2}\end{equation}( $|\ |$ はベクトルの大きさを表す時に用いる記号である)
上図2~4のベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{\mathsf{v_3}}$の大きさを計算し、図5～図7にその結果を表示する。
\begin{align*} &|\boldsymbol{\mathsf{v_1}}| = \sqrt{4^2 + 2^2} = \sqrt{20} = 4.4721\ldots \quad\risingdotseq 4.47 \\ &|\boldsymbol{\mathsf{v_2}}| = \sqrt{1^2 + 3^2} = \sqrt{10} = 3.1622\ldots \quad\risingdotseq 3.16 \\ &|\boldsymbol{\mathsf{v_3}}| = \sqrt{(-3)^2 + 9^2} = \sqrt{90} = 9.4868\ldots \quad\risingdotseq 9.49\end{align*}
ここで示されているように 2点間の距離は、それら2点を結ぶベクトルの大きさに等しい。 すなわち、2点間の距離を求めるには 2点のうちの一方を始点、もう一方を終点とするベクトルの大きさ求めればよい。
向きも大きさも等しいベクトルは、始点がどこにあろうとも、それらは皆ベクトルとしては同じものである。次の3つのベクトルを例に取ろう。
これらのベクトルは始点と終点の位置が違うだけで、以下に示すように全て同じベクトル $(1, 4)$ である。\begin{align*}&\boldsymbol{\mathsf{v_a}} = \begin{pmatrix}1 \\4 \end{pmatrix} -\begin{pmatrix}0 \\0 \end{pmatrix} =\begin{pmatrix}1 \\4 \end{pmatrix} \\ \\&\boldsymbol{\mathsf{v_b}} = \begin{pmatrix}-2 \\-1 \end{pmatrix} -\begin{pmatrix}-3 \\-5\end{pmatrix} =\begin{pmatrix}1 \\4 \end{pmatrix} \\ \\&\boldsymbol{\mathsf{v_c}} = \begin{pmatrix}4 \\2 \end{pmatrix} -\begin{pmatrix}3 \\-2\end{pmatrix} =\begin{pmatrix}1 \\4 \end{pmatrix} \\ \\&|\boldsymbol{\mathsf{v_a}}| = |\boldsymbol{\mathsf{v_b}}| = |\boldsymbol{\mathsf{v_c}}| = \sqrt{1^2 + 4^2} = \sqrt{17} \risingdotseq 4.12\end{align*}
実際、
このことは、ベクトルを$2$倍、$3$倍したときの大きさは、もとのベクトルの大きさの$2$倍、$3$倍になることを意味する。
例えば、図11に示されるベクトル$\boldsymbol{\mathsf{v}} = (-3, 2)$ を$3$倍したベクトル $3\boldsymbol{\mathsf{v}} = (-9, 6)$ (図12)、及び $-3$倍したベクトル $-3\boldsymbol{\mathsf{v}} = (9, -6)$ (図13)の大きさは以下の計算で示されるように、ベクトル$\boldsymbol{\mathsf{v}}$の大きさの$3$倍になる (以下の図においては、すべて始点は $(0, 0)$ である)。
各ベクトルの大きさを計算。
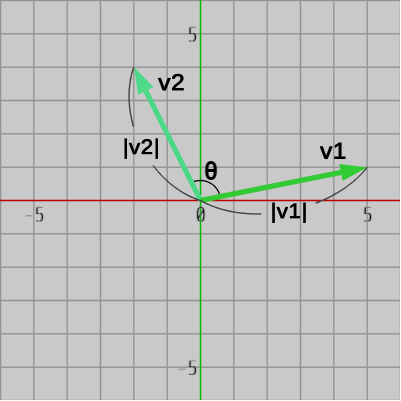
図14 2つの2次元ベクトル $\boldsymbol{\mathsf{v_1}} = (x_1, y_1)$、$\boldsymbol{\mathsf{v_2}} = (x_2, y_2)$ を用いて次のように計算される実数値を(2次元)ベクトルの内積(dot product)という。
\[\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = x_1 x_2 + y_1 y_2\]
内積は幾何的な意味を持っており、図14に示されるように 2つのベクトル $\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ のなす角を $\theta$ とすれば、内積 $\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}}$ は2つのベクトルのなす角の余弦を用いて次のように表される (ただし、なす角 $\theta$ は $0^\circ \leq \theta \leq 180^\circ$ とする)。\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = |\boldsymbol{\mathsf{v_1}}||\boldsymbol{\mathsf{v_2}}|cos\theta\]
(計算例)
(1) 2つのベクトル $\boldsymbol{a} = (2, 3)$、$\boldsymbol{b} = (5, 6)$ の内積 $\boldsymbol{a}\cdot\boldsymbol{b}$\[\boldsymbol{a}\cdot\boldsymbol{b} = 2\cdot5 + 3\cdot6 = 10 + 18 = 28\]
(2) 2つのベクトル $\boldsymbol{v} = (8, -4)$、$\boldsymbol{w} = (-11, -9)$ の内積 $\boldsymbol{v}\cdot\boldsymbol{w}$\[\boldsymbol{v}\cdot\boldsymbol{w} = 8\cdot(-11) + (-4)\cdot(-9) = -88 + 36 = -52\]
では最後に、本節で述べた内容に関するプログラムを作成する。
2D空間では主に2次元ベクトルか3次元ベクトルを使うので、プログラムでは主として Vector2構造体、Vector3構造体を使用する。
Vector2、Vector3型のインスタンス生成は次のように記述する。
[Code1] (実行結果 図16)
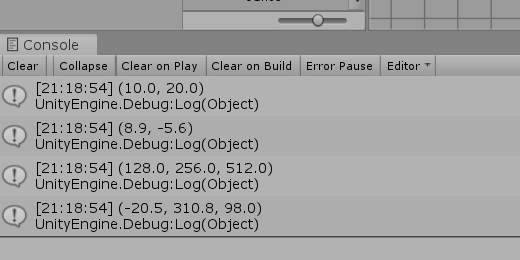
図15 UnityのConsoleウィンドウ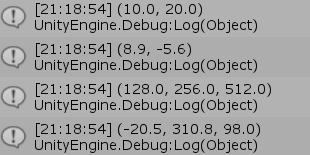 
図16 Code1 実行結果
v1、v2が Vector2型のインスタンスであり、v3、v4が Vector3型のインスタンスである。それぞれのコンストラクタに渡す引数は float型であり、int型を渡すと float型への暗黙的な型変換が行われる。
6行目以降で使われている Debug.Log(..) は、Unityの Consoleウィンドウ(図15)に文字列を表示するためのメソッドであり、引数には object型のインスタンスを渡す。ここでは Vector2型、Vector3型のインスタンス v1～v4を渡しているが、結果として表示されるのは図16に示されるように、それぞれのベクトルの内容である。ただし、Debug.Log(..) で Vector2、Vector3型のインスタンスを表示すると、自動的に小数第2位で四捨五入され、小数第1位までの表示になることに注意。
[Code2] (実行結果 図17)
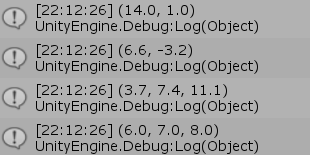
図17 Code2 実行結果 3行目、8行目、13行目、18行目に書かれているように、Vector2(あるいは Vector3)同士の加算、減算は数式と同じように、a + b、a - b と記述することが可能である。
上でも述べたように、点も位置ベクトルというベクトルとして扱われる。したがって、点$P = (-2, 8)$を始点、点$Q = (4, 1)$を終点とするベクトル$\boldsymbol{\mathsf{v}}$を求めるプログラムは次のように記述される。
[Code3] (実行結果 図18、図19)
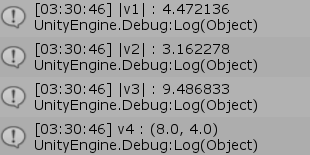
図18 Code3 実行結果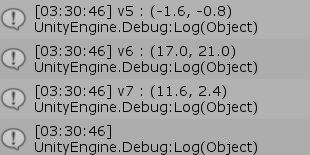 
図19 Code3 実行結果
Vector2や Vector3構造体には magnitude というfloat型のプロパティがあり、それは Vector2や Vector3型インスタンスの大きさを保持しているデータである。したがって、プログラム中の Vector2型のインスタンス v1の大きさは、4行目のように v1.magnitude と記述すれば取得することができる。
最初の3つのベクトルは本節の中程で使われたベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{\mathsf{v_3}}$ で、4～6行目の出力値は上で計算された値と(四捨五入すれば)確かに一致している。
8行目、9行目はv1の実数倍を計算する記述である。
13行目、14行目は実数倍されたベクトル同士の加算、減算であるが、これも通常の数式と同じように記述することができる。実際に、13行目、14行目の計算を数式で記述すると、
[Code4] (実行結果 図20)
図20 Code4 実行結果 このプログラムでは 2点 a、b を結ぶベクトルを Vector2 c = b - a; のように新しい変数にセットせずに、3行目で直接 (b - a) と記述している。この書き方でも通常のインスタンスと同じように、Vector2型のプロパティにアクセスすることができるのである。したがって、(b - a).magnitude と記述すれば (b - a) の大きさを取得できる。
また、2点を表す変数 a、b すら用意せずに、6行目のように直接 new Vector2(..) 同士を減算しても同じ結果が得られる。つまり、6行目の記述は (b - a).magnitude とした場合と同じ結果になる。
[Code5] (実行結果 図21)
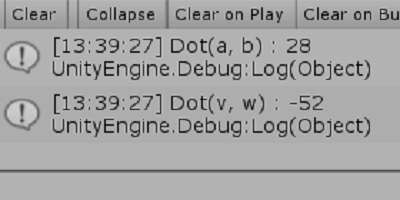
図21 Code5 実行結果 プログラム中で使われている Vector2.Dot(..) は Vector2構造体のstaticメソッドで、引数にセットされた2つの(2次元)ベクトルの内積を計算する。
ここでは2つ計算を行っているが、いずれも上記の内積の計算例で見たものである。
内容としては主にベクトルや行列の初歩的な使用例に関するものである。ベクトルや行列は2D、3Dを問わずコンピューターグラフィックスにおいて最も重要な概念であり、これらに対する理解は2Dあるいは3Dプログラミングを理解するうえで欠くことのできないものである。
なお、講義の中で使われる「2D空間」という用語はXY平面と同じものである。また、文章中で使用する図においては赤い軸がx軸、緑の軸がy軸である。
A) 点
\[R : \begin{cases} x = 4 \\ y = 2 \end{cases}\quad G : \begin{cases} x = -5 \\ y = 4 \end{cases}\quad B : \begin{cases} x = 1 \\ y = -2 \end{cases}\]である。
B) ベクトル
本章及び第2章では主に2D空間上のベクトルである2次元ベクトル(2Dベクトル)を扱う。2次元ベクトルとは、2つの実数値の組からなり次のように書き表される。\begin{equation*}\begin{pmatrix}1 \\0 \end{pmatrix} \qquad\begin{pmatrix}-20.5 \\6.32 \end{pmatrix} \qquad\begin{pmatrix}sin\theta \\cos\theta \end{pmatrix} \qquad\begin{pmatrix}1 \quad 0 \end{pmatrix} \qquad\begin{pmatrix}3.14 \quad 0.785 \end{pmatrix} \qquad\begin{pmatrix}v_x \quad v_y \end{pmatrix} \end{equation*}
要素が縦に並んだベクトル(左側3つ)を列ベクトル、要素が横に並んだベクトル(右側3つ)を行ベクトルという。列ベクトルでは上の要素がx座標、下の要素がy座標であり、行ベクトルでは左の要素がx座標、右の要素がy座標である。コンピューターグラフィックスでは点も位置ベクトルというベクトルとして扱われる。例えば、上図の点$R$、$G$、$B$は位置ベクトルとして次のように表される。\[R = \begin{pmatrix}4 \\2 \end{pmatrix} \quad G = \begin{pmatrix}-5 \\4 \end{pmatrix} \quad B = \begin{pmatrix}1 \\-2 \end{pmatrix}\] 講義では基本的に縦並びの列ベクトルを使っていく。統一的に列ベクトルだけを使っていくのが理想であるが、スペース的な問題で文章中や図の中においては横並びの行ベクトルを用いる(この講義の中で行ベクトルを使う場合はあくまで見やすさのためである)。
ベクトルの加算、減算は次のように定義される。\begin{align*}\begin{pmatrix}x_{1} \\y_{1} \end{pmatrix} +\begin{pmatrix}x_{2} \\y_{2} \end{pmatrix} =\begin{pmatrix}x_{1} + x_{2}\\y_{1} + y_{2}\end{pmatrix} \\ \\\begin{pmatrix}x_{1} \\y_{1} \end{pmatrix} -\begin{pmatrix}x_{2} \\y_{2} \end{pmatrix} =\begin{pmatrix}x_{1} - x_{2}\\y_{1} - y_{2}\end{pmatrix} \end{align*}(計算例)\begin{align*}&\begin{pmatrix}3 \\4 \end{pmatrix} +\begin{pmatrix}8 \\-2 \end{pmatrix} =\begin{pmatrix}3 + 8\\4 + (-2)\end{pmatrix} =\begin{pmatrix}11\\2\end{pmatrix} \\ \\&\begin{pmatrix}-1 \\10 \end{pmatrix} -\begin{pmatrix}-5 \\5 \end{pmatrix} =\begin{pmatrix}-1 - (-5)\\10 - 5\end{pmatrix} =\begin{pmatrix}4\\5\end{pmatrix} \end{align*}
ベクトルは始点と終点を持っており、ベクトル自体は終点から始点を引くことで求められる。「終点から始点を引く」とは詳しく言えば始点、終点を位置ベクトルとして扱い、ベクトル同士の減算を行うのである。
以下にその例を示す(下図における矢の形をしたものはベクトルを可視化したものである。矢の先端がベクトルの終点を表している)。
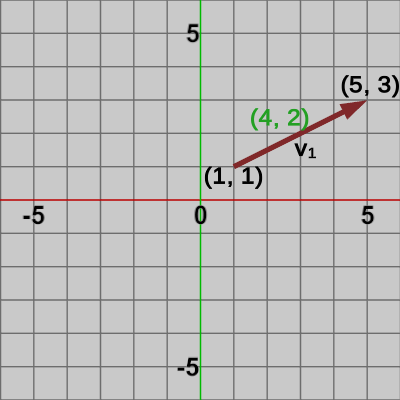図2 ベクトルv1
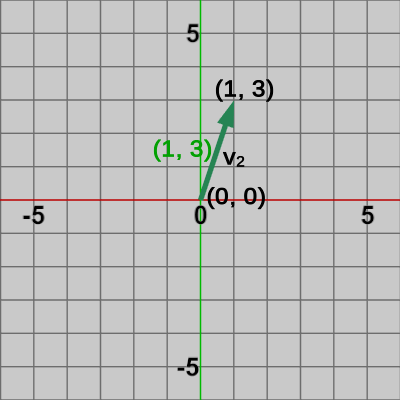図3 ベクトルv2
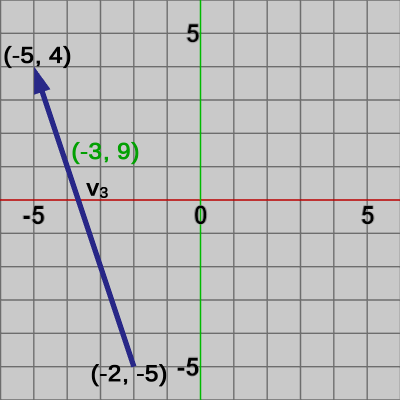図4 ベクトルv3
図2のベクトル$\boldsymbol{\mathsf{v_1}}$は始点(1, 1)、終点(5、3)であり次のように求められる。\begin{equation} \boldsymbol{\mathsf{v_1}} = \begin{pmatrix}5 \\3 \end{pmatrix} -\begin{pmatrix}1 \\1 \end{pmatrix} =\begin{pmatrix}4 \\2 \end{pmatrix} \end{equation}図3のベクトル$\boldsymbol{\mathsf{v_2}}$は始点(0, 0)、終点(1、3)であり、図4のベクトル$\boldsymbol{\mathsf{v_3}}$は始点(-2, -5)、終点(-5, 4)である。これらのベクトルに関してもベクトル$\boldsymbol{\mathsf{v_1}}$の場合と同様に計算すればよい。\begin{align*} &\boldsymbol{\mathsf{v_2}} = \begin{pmatrix}1 \\3 \end{pmatrix} -\begin{pmatrix}0 \\0 \end{pmatrix} =\begin{pmatrix}1 \\3 \end{pmatrix} \\ \\ &\boldsymbol{\mathsf{v_3}} = \begin{pmatrix}-5 \\4 \end{pmatrix} -\begin{pmatrix}-2 \\-5\end{pmatrix} =\begin{pmatrix}-3 \\9 \end{pmatrix} \end{align*}
なお、この講義では図の中で点(位置)を表す数値については黒色のフォントを使用し、ベクトルを表す数値については緑色のフォントを使用している。例えば、図2のベクトル$\boldsymbol{\mathsf{v_1}}$は $(4, 2)$ であるが、この数値はベクトルを表すので緑色のフォントを使用し、$\boldsymbol{\mathsf{v_1}}$の始点 $(1, 1)$、終点 $(5, 3)$ は点(位置)を表すので黒色のフォントを使用している。図3のベクトル$\boldsymbol{\mathsf{v_2}}$、図4の$\boldsymbol{\mathsf{v_3}}$についても同様に始点、終点は黒色の数値で表され、各ベクトルの内容は緑色の数値で表されている。
C) ベクトルの向きと大きさ
始点から終点へ向かう方向をベクトルの向き(Direction)という。上図においては矢印の方向がベクトルの向きである。また、始点から終点までの距離をベクトルの大きさ(Magnitude)、あるいは長さという。ベクトルの大きさは次のように計算される。
ベクトル $\boldsymbol{\mathsf{v}} = (x, y)$ の大きさ $|\boldsymbol{\mathsf{v}}|$\begin{equation} |\boldsymbol{\mathsf{v}}| = \sqrt{x^2 + y^2}\end{equation}( $|\ |$ はベクトルの大きさを表す時に用いる記号である)
上図2~4のベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{\mathsf{v_3}}$の大きさを計算し、図5～図7にその結果を表示する。
\begin{align*} &|\boldsymbol{\mathsf{v_1}}| = \sqrt{4^2 + 2^2} = \sqrt{20} = 4.4721\ldots \quad\risingdotseq 4.47 \\ &|\boldsymbol{\mathsf{v_2}}| = \sqrt{1^2 + 3^2} = \sqrt{10} = 3.1622\ldots \quad\risingdotseq 3.16 \\ &|\boldsymbol{\mathsf{v_3}}| = \sqrt{(-3)^2 + 9^2} = \sqrt{90} = 9.4868\ldots \quad\risingdotseq 9.49\end{align*}
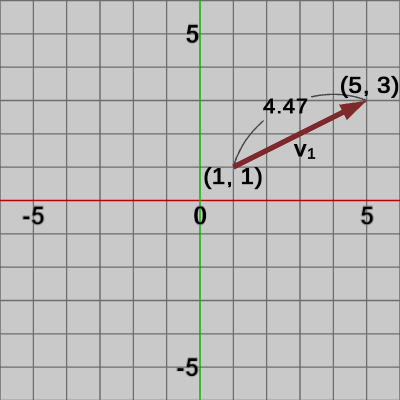図5 ベクトルv1 の大きさ
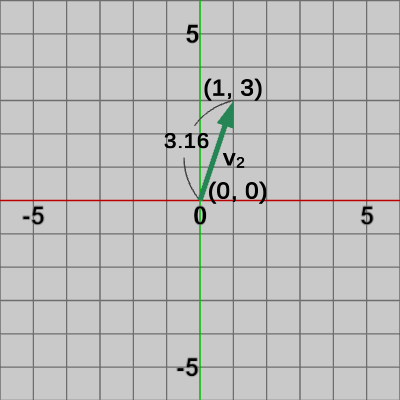図6 ベクトルv2 の大きさ
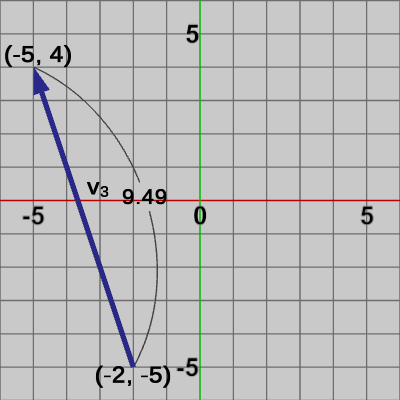図7 ベクトルv3 の大きさ
ここで示されているように 2点間の距離は、それら2点を結ぶベクトルの大きさに等しい。 すなわち、2点間の距離を求めるには 2点のうちの一方を始点、もう一方を終点とするベクトルの大きさ求めればよい。
向きも大きさも等しいベクトルは、始点がどこにあろうとも、それらは皆ベクトルとしては同じものである。次の3つのベクトルを例に取ろう。
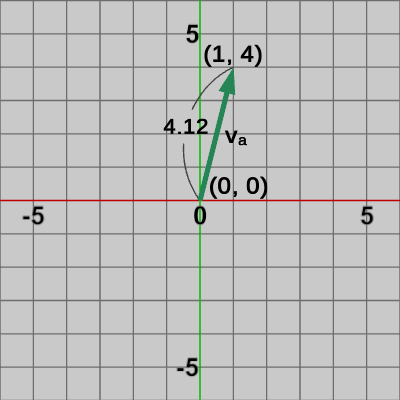図8 ベクトルva
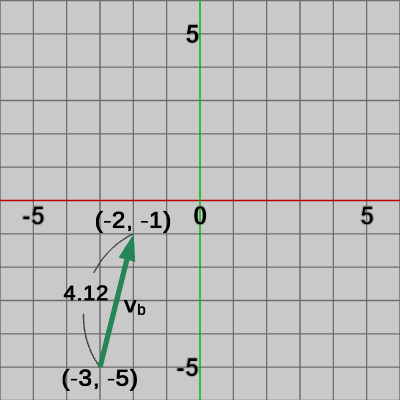図9 ベクトルvb
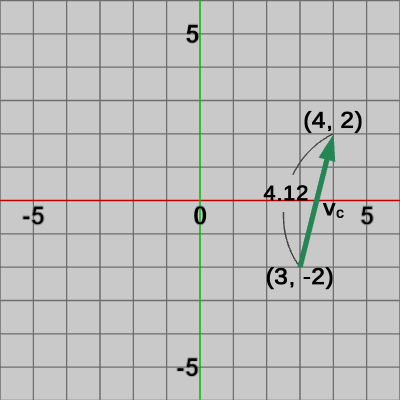図10 ベクトルvc
これらのベクトルは始点と終点の位置が違うだけで、以下に示すように全て同じベクトル $(1, 4)$ である。\begin{align*}&\boldsymbol{\mathsf{v_a}} = \begin{pmatrix}1 \\4 \end{pmatrix} -\begin{pmatrix}0 \\0 \end{pmatrix} =\begin{pmatrix}1 \\4 \end{pmatrix} \\ \\&\boldsymbol{\mathsf{v_b}} = \begin{pmatrix}-2 \\-1 \end{pmatrix} -\begin{pmatrix}-3 \\-5\end{pmatrix} =\begin{pmatrix}1 \\4 \end{pmatrix} \\ \\&\boldsymbol{\mathsf{v_c}} = \begin{pmatrix}4 \\2 \end{pmatrix} -\begin{pmatrix}3 \\-2\end{pmatrix} =\begin{pmatrix}1 \\4 \end{pmatrix} \\ \\&|\boldsymbol{\mathsf{v_a}}| = |\boldsymbol{\mathsf{v_b}}| = |\boldsymbol{\mathsf{v_c}}| = \sqrt{1^2 + 4^2} = \sqrt{17} \risingdotseq 4.12\end{align*}
D) ベクトルの実数倍
あるベクトル$\boldsymbol{\mathsf{v}} = (x, y)$に実数$s$を掛けたときのベクトル$s\boldsymbol{\mathsf{v}}$は、次のように表される。\[ s\boldsymbol{\mathsf{v}} = s\begin{pmatrix}x \\y \end{pmatrix} =\begin{pmatrix}sx \\sy \end{pmatrix} \]そして、このときのベクトル$s\boldsymbol{\mathsf{v}}$の大きさ$|s\boldsymbol{\mathsf{v}}|$は、ベクトル$\boldsymbol{\mathsf{v}}$の大きさ$|\boldsymbol{\mathsf{v}}|$の $|s|$倍である。すなわち、ベクトル$s\boldsymbol{\mathsf{v}}$の大きさは $|s||\boldsymbol{\mathsf{v}}|$である。実際、
\begin{align*}|s\boldsymbol{\mathsf{v}}| = \sqrt{(sx)^2 + (sy)^2} = \sqrt{s^2(x^2 + y^2)} = |s|\sqrt{x^2 + y^2} = |s||\boldsymbol{\mathsf{v}}|\end{align*}
となる。このことは、ベクトルを$2$倍、$3$倍したときの大きさは、もとのベクトルの大きさの$2$倍、$3$倍になることを意味する。
例えば、図11に示されるベクトル$\boldsymbol{\mathsf{v}} = (-3, 2)$ を$3$倍したベクトル $3\boldsymbol{\mathsf{v}} = (-9, 6)$ (図12)、及び $-3$倍したベクトル $-3\boldsymbol{\mathsf{v}} = (9, -6)$ (図13)の大きさは以下の計算で示されるように、ベクトル$\boldsymbol{\mathsf{v}}$の大きさの$3$倍になる (以下の図においては、すべて始点は $(0, 0)$ である)。
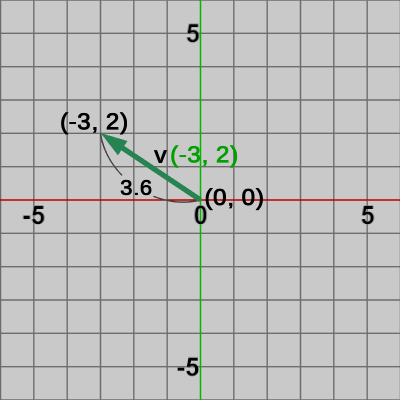図11 ベクトルv
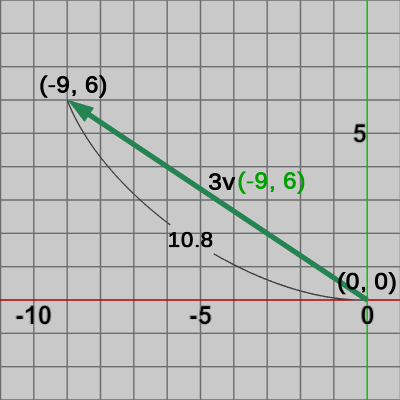図12 ベクトル 3v
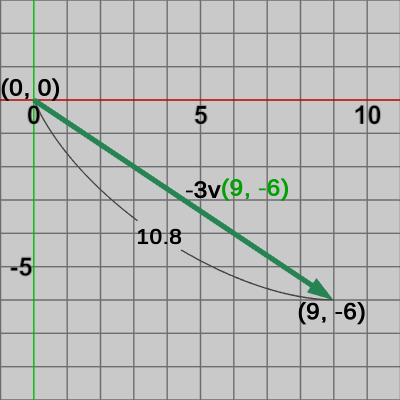図13 ベクトル -3v
各ベクトルの大きさを計算。
\begin{align*}|\boldsymbol{\mathsf{v}}| &= \sqrt{(-3)^2 + 2^2} = \sqrt{13} \quad(\risingdotseq 3.6) \\|3\boldsymbol{\mathsf{v}}| &= \sqrt{(-9)^2 + 6^2} = \sqrt{117} = \sqrt{9 \cdot 13} = 3\sqrt{13}\quad(\risingdotseq 10.8) \\|(-3)\boldsymbol{\mathsf{v}}| &= \sqrt{9^2 + (-6)^2} = \sqrt{117} = \sqrt{9 \cdot 13} = 3\sqrt{13}\quad(\risingdotseq 10.8) \\\end{align*}
E) ベクトルの内積
\[\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = x_1 x_2 + y_1 y_2\]
内積は幾何的な意味を持っており、図14に示されるように 2つのベクトル $\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ のなす角を $\theta$ とすれば、内積 $\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}}$ は2つのベクトルのなす角の余弦を用いて次のように表される (ただし、なす角 $\theta$ は $0^\circ \leq \theta \leq 180^\circ$ とする)。\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = |\boldsymbol{\mathsf{v_1}}||\boldsymbol{\mathsf{v_2}}|cos\theta\]
(計算例)
(1) 2つのベクトル $\boldsymbol{a} = (2, 3)$、$\boldsymbol{b} = (5, 6)$ の内積 $\boldsymbol{a}\cdot\boldsymbol{b}$\[\boldsymbol{a}\cdot\boldsymbol{b} = 2\cdot5 + 3\cdot6 = 10 + 18 = 28\]
(2) 2つのベクトル $\boldsymbol{v} = (8, -4)$、$\boldsymbol{w} = (-11, -9)$ の内積 $\boldsymbol{v}\cdot\boldsymbol{w}$\[\boldsymbol{v}\cdot\boldsymbol{w} = 8\cdot(-11) + (-4)\cdot(-9) = -88 + 36 = -52\]
では最後に、本節で述べた内容に関するプログラムを作成する。
# Code1
UnityのC#スクリプトにおいて、ベクトルを使う場合は以下の構造体を用いる。Vector2
: 2次元ベクトル用の構造体Vector3
: 3次元ベクトル用の構造体Vector4
: 4次元ベクトル用の構造体2D空間では主に2次元ベクトルか3次元ベクトルを使うので、プログラムでは主として Vector2構造体、Vector3構造体を使用する。
Vector2、Vector3型のインスタンス生成は次のように記述する。
[Code1] (実行結果 図16)
Vector2 v1 = new Vector2(10, 20); Vector2 v2 = new Vector2(8.91f, -5.643f); Vector3 v3 = new Vector3(128, 256, 512); Vector3 v4 = new Vector3(-20.5f, 310.83f, 98.048f); Debug.Log(v1); Debug.Log(v2); Debug.Log(v3); Debug.Log(v4);
v1、v2が Vector2型のインスタンスであり、v3、v4が Vector3型のインスタンスである。それぞれのコンストラクタに渡す引数は float型であり、int型を渡すと float型への暗黙的な型変換が行われる。
6行目以降で使われている Debug.Log(..) は、Unityの Consoleウィンドウ(図15)に文字列を表示するためのメソッドであり、引数には object型のインスタンスを渡す。ここでは Vector2型、Vector3型のインスタンス v1～v4を渡しているが、結果として表示されるのは図16に示されるように、それぞれのベクトルの内容である。ただし、Debug.Log(..) で Vector2、Vector3型のインスタンスを表示すると、自動的に小数第2位で四捨五入され、小数第1位までの表示になることに注意。
# Code2
ベクトルの加算、減算は次のように記述する。[Code2] (実行結果 図17)
Vector2 a = new Vector2(3, 5); Vector2 b = new Vector2(11, -4); Vector2 v = a + b; Debug.Log(v); // (14.0, 1.0) a = new Vector3(2.5f, 5.4f); b = new Vector3(-4.1f, 8.6f); v = a - b; Debug.Log(v); // (6.6, -3.2) Vector3 c = new Vector3(1.5f, 3.0f, 4.5f); Vector3 d = new Vector3(2.2f, 4.4f, 6.6f); Vector3 w = c + d; Debug.Log(w); // (3.7, 7.4, 11.1) c = new Vector3(10, 15, 20); d = new Vector3(4, 8, 12); w = c - d; Debug.Log(w); // (6.0, 7.0, 8.0)
上でも述べたように、点も位置ベクトルというベクトルとして扱われる。したがって、点$P = (-2, 8)$を始点、点$Q = (4, 1)$を終点とするベクトル$\boldsymbol{\mathsf{v}}$を求めるプログラムは次のように記述される。
Vector2 P = new Vector(-2, 8); Vector2 Q = new Vector(4, 1); Vector2 v = Q - P; // (6, -7)
# Code3
ベクトルの大きさ、及び ベクトルの実数倍の計算は以下のように記述される。[Code3] (実行結果 図18、図19)
Vector2 v1 = new Vector2(4, 2);
Vector2 v2 = new Vector2(1, 3);
Vector2 v3 = new Vector2(-3, 9);
Debug.Log("|v1| : " + v1.magnitude);
Debug.Log("|v2| : " + v2.magnitude);
Debug.Log("|v3| : " + v3.magnitude);
Vector2 v4 = 2.0f * v1;
Vector2 v5 = -0.4f * v1;
Debug.Log("v4 : " + v4);
Debug.Log("v5 : " + v5);
Vector2 v6 = 3.0f * v1 + 5.0f * v2;
Vector2 v7 = 6.2f * v2 - 1.8f * v3;
Debug.Log("v6 : " + v6);
Debug.Log("v7 : " + v7);
Vector2や Vector3構造体には magnitude というfloat型のプロパティがあり、それは Vector2や Vector3型インスタンスの大きさを保持しているデータである。したがって、プログラム中の Vector2型のインスタンス v1の大きさは、4行目のように v1.magnitude と記述すれば取得することができる。
最初の3つのベクトルは本節の中程で使われたベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{\mathsf{v_3}}$ で、4～6行目の出力値は上で計算された値と(四捨五入すれば)確かに一致している。
8行目、9行目はv1の実数倍を計算する記述である。
13行目、14行目は実数倍されたベクトル同士の加算、減算であるが、これも通常の数式と同じように記述することができる。実際に、13行目、14行目の計算を数式で記述すると、
\begin{align*}&3 \boldsymbol{\mathsf{v_1}} + 5\boldsymbol{\mathsf{v_2}} = 3\begin{pmatrix}4 \\2 \end{pmatrix} +5\begin{pmatrix}1 \\3 \end{pmatrix} =\begin{pmatrix}12 \\6 \end{pmatrix} +\begin{pmatrix}5 \\15 \end{pmatrix} =\begin{pmatrix}17 \\21 \end{pmatrix} \\ \\&6.2\boldsymbol{\mathsf{v_2}} - 1.8\boldsymbol{\mathsf{v_3}} = 6.2\begin{pmatrix}1 \\3 \end{pmatrix} -1.8\begin{pmatrix}-3 \\9 \end{pmatrix} =\begin{pmatrix}6.2 \\18.6 \end{pmatrix} -\begin{pmatrix}-5.4 \\16.2 \end{pmatrix} =\begin{pmatrix}11.6 \\2.4\end{pmatrix} \end{align*}
となる。# Code4
2点間の距離は、それら2点を結ぶベクトルの大きさであると述べたが、プログラムでは以下のように記述できる。[Code4] (実行結果 図20)
Vector2 a = new Vector2(7.4f, 4.1f); Vector2 b = new Vector2(11, -5); float len = (b - a).magnitude; Debug.Log(len); len = (new Vector2(11, -5) - new Vector2(7.4f, 4.1f)).magnitude; Debug.Log(len);
また、2点を表す変数 a、b すら用意せずに、6行目のように直接 new Vector2(..) 同士を減算しても同じ結果が得られる。つまり、6行目の記述は (b - a).magnitude とした場合と同じ結果になる。
# Code5
2次元ベクトルの内積はプログラムにおいては以下のように記述される。[Code5] (実行結果 図21)
Vector2 a = new Vector2(2, 3);
Vector2 b = new Vector2(5, 6);
float val = Vector2.Dot(a, b);
Debug.Log("Dot(a, b) : " + val);
Vector2 v = new Vector2(8, -4);
Vector2 w = new Vector2(-11, -9);
val = Vector2.Dot(v, w);
Debug.Log("Dot(v, w) : " + val);
ここでは2つ計算を行っているが、いずれも上記の内積の計算例で見たものである。
© 2020-2024 Redpoll's 60 (All rights reserved)