Redpoll's 60
Home / 3Dプログラミング入門 / 第1章 $§$1-4
第1章 2D空間の基礎
| $§$1-1 点とベクトル | $§$1-6 回転行列 |
| $§$1-2 ベクトルによる平行移動 | $§$1-7 スケール行列 |
| $§$1-3 単位ベクトル | $§$1-8 変換行列の積 |
| $§$1-4 行列の基礎 | $§$1-9 フレームとフレームレート |
| $§$1-5 平行移動行列 | $§$1-10 オブジェクトの基本的な運動 (往復運動と回転) |
$§$1-4 行列の基礎
A) 行列
以下のように、カッコに囲まれ縦横に配置された数値の組を行列(Matrix)という。左から順に、$2\times2$行列、$3\times3$行列、$4\times4$行列という($m \times n$ はm行n列を意味する)。
\begin{equation*}\begin{pmatrix}a_{11} &a_{12} \\a_{21} &a_{22}\end{pmatrix} \qquad\begin{pmatrix}a_{11} &a_{12} &a_{13} \\a_{21} &a_{22} &a_{23} \\a_{31} &a_{32} &a_{33}\end{pmatrix} \qquad\begin{pmatrix}a_{11} &a_{12} &a_{13} &a_{14} \\a_{21} &a_{22} &a_{23} &a_{24} \\a_{31} &a_{32} &a_{33} &a_{34} \\a_{41} &a_{42} &a_{43} &a_{44} \end{pmatrix}\end{equation*}
横に並んだ数値の組を行(row)といい、縦に並んだ数値の組を列(column)という。例えば、中央の$3\times3$行列の第1列目は $(a_{11}, a_{21}, a_{31})$ であり、第3行目は $(a_{31}, a_{32}, a_{33})$である。右側の$4\times4$行列の第4列目は $(a_{14}, a_{24}, a_{34}, a_{44})$であり、第2行目は $(a_{21}, a_{22}, a_{23}, a_{24})$である。上記のように行列の行数と列数が等しい行列を正方行列という。正方行列でない例を以下に示そう。
\begin{equation*}\begin{pmatrix}a_{11}\quad a_{12}\quad a_{13}\end{pmatrix} \qquad\begin{pmatrix}a_{11} \\a_{21} \\a_{31} \\a_{41} \end{pmatrix} \qquad\begin{pmatrix}a_{11} &a_{12} \\a_{21} &a_{22} \\a_{31} &a_{32} \end{pmatrix} \qquad\begin{pmatrix}a_{11} &a_{12} &a_{13} &a_{14} \\a_{21} &a_{22} &a_{23} &a_{24} \end{pmatrix}\end{equation*}
左から順に、$1\times3$行列、$4\times1$行列、$3\times2$行列、$2\times4$行列という。一番左の行列は、行が1行しかない行列であり、その次の行列は列が1列しかない行列である。こういったものも行列として扱われる。コンピューターグラフィックスで使われるのは主として正方行列である。2Dならば$2\times2$行列あるいは$3\times3$行列を使い、3Dならば$3\times3$行列あるいは$4\times4$行列を主として使う。第1章、第2章において扱う内容は2D空間を対象としているが、そこで主として使用する行列は$3\times3$行列である。文章中では、ときに $2\times2$行列を使用することもあるが、第1章、第2章で作成するプログラム内では$3\times3$行列のみを使う ($2\times2$行列ではなく$3\times3$行列を使うのは同次座標というものに対応させるためであるが、それらの事柄に関しては次節以降で解説する)。
Unityでは$4\times4$行列を表すための構造体は用意されているが、$3\times3$行列のための構造体はないので、プログラム内で使用する$3\times3$行列については以下のカスタムライブラリの構造体を使用する。
THMatrix3x3
: カスタムライブラリに用意されている $3\times3$行列を表す構造体2D空間におけるオブジェクトの運動は基本的に、この THMatrix3x3構造体を通して行われることになる。
B) 行列の積
次に行列同士の積について解説する。行列同士の演算は難しくはないが、その手続きは煩雑であり間違えやすいものである。コンピューターグラフィックスにおいては、これらの計算を行うのはCPUやGPUであるからプログラマーが紙の上にペンを走らせて計算するということはまずないであろう。それでも計算手順を知っておくことは3Dプログラミングを学習する上では絶対に必要なことなのである。$2\times2$行列、$3\times3$行列の積は次のように定義される。
\begin{align*}\begin{pmatrix}a_{11} &a_{12} \\a_{21} &a_{22}\end{pmatrix}\begin{pmatrix}\color{blue}{b_{11}} &\color{blue}{b_{12}} \\\color{blue}{b_{21}} &\color{blue}{b_{22}} \end{pmatrix}&=\begin{pmatrix}a_{11}\cdot\color{blue}{b_{11}}+a_{12}\cdot\color{blue}{b_{21}} &a_{11}\cdot\color{blue}{b_{12}}+a_{12}\cdot\color{blue}{b_{22}}\\a_{21}\cdot\color{blue}{b_{11}}+a_{22}\cdot\color{blue}{b_{21}} &a_{21}\cdot\color{blue}{b_{12}}+a_{22}\cdot\color{blue}{b_{22}}\end{pmatrix} \\ \\\begin{pmatrix}a_{11} &a_{12} &a_{13} \\a_{21} &a_{22} &a_{23} \\a_{31} &a_{32} &a_{33} \end{pmatrix}\begin{pmatrix}\color{blue}{b_{11}} &\color{blue}{b_{12}} &\color{blue}{b_{13}} \\\color{blue}{b_{21}} &\color{blue}{b_{22}} &\color{blue}{b_{23}} \\\color{blue}{b_{31}} &\color{blue}{b_{32}} &\color{blue}{b_{33}} \end{pmatrix}&=\begin{pmatrix}a_{11}\cdot\color{blue}{b_{11}}+a_{12}\cdot\color{blue}{b_{21}}+a_{13}\cdot\color{blue}{b_{31}}&a_{11}\cdot\color{blue}{b_{12}}+a_{12}\cdot\color{blue}{b_{22}}+a_{13}\cdot\color{blue}{b_{32}} &a_{11}\cdot\color{blue}{b_{13}}+a_{12}\cdot\color{blue}{b_{23}}+a_{13}\cdot\color{blue}{b_{33}}\\a_{21}\cdot\color{blue}{b_{11}}+a_{22}\cdot\color{blue}{b_{21}}+a_{23}\cdot\color{blue}{b_{31}}&a_{21}\cdot\color{blue}{b_{12}}+a_{22}\cdot\color{blue}{b_{22}}+a_{23}\cdot\color{blue}{b_{32}} &a_{21}\cdot\color{blue}{b_{13}}+a_{22}\cdot\color{blue}{b_{23}}+a_{23}\cdot\color{blue}{b_{33}}\\a_{31}\cdot\color{blue}{b_{11}}+a_{32}\cdot\color{blue}{b_{21}}+a_{33}\cdot\color{blue}{b_{31}}&a_{31}\cdot\color{blue}{b_{12}}+a_{32}\cdot\color{blue}{b_{22}}+a_{33}\cdot\color{blue}{b_{32}} &a_{31}\cdot\color{blue}{b_{13}}+a_{32}\cdot\color{blue}{b_{23}}+a_{33}\cdot\color{blue}{b_{33}}\end{pmatrix}\end{align*}
(計算例)
\begin{align*}\begin{pmatrix}1 &2 \\3 &4\end{pmatrix}\begin{pmatrix}\color{blue}{5} &\color{blue}{6} \\\color{blue}{7} &\color{blue}{8} \end{pmatrix}&=\begin{pmatrix}1\cdot\color{blue}{5}+2\cdot\color{blue}{7} &1\cdot\color{blue}{6}+2\cdot\color{blue}{8}\\3\cdot\color{blue}{5}+4\cdot\color{blue}{7} &3\cdot\color{blue}{6}+4\cdot\color{blue}{8}\end{pmatrix} \\&=\begin{pmatrix}5+14 &6+16\\15+28 &18+32\end{pmatrix} =\begin{pmatrix}19 &22\\43 &50\end{pmatrix} \\\\\begin{pmatrix}5 &6 \\7 &8\end{pmatrix}\begin{pmatrix}\color{blue}{1} &\color{blue}{2} \\\color{blue}{3} &\color{blue}{4} \end{pmatrix}&=\begin{pmatrix}5\cdot\color{blue}{1}+6\cdot\color{blue}{3} &5\cdot\color{blue}{2}+6\cdot\color{blue}{4}\\7\cdot\color{blue}{1}+8\cdot\color{blue}{3} &7\cdot\color{blue}{2}+8\cdot\color{blue}{4}\end{pmatrix} \\&=\begin{pmatrix}5+18 &10+24\\7+24 &14+32\end{pmatrix} =\begin{pmatrix}23 &34\\31 &46\end{pmatrix} \end{align*}
\begin{align*}\begin{pmatrix}1 &2 &3 \\4 &5 &6 \\7 &8 &9 \end{pmatrix}\begin{pmatrix}\color{blue}{11} &\color{blue}{14} &\color{blue}{17}\\\color{blue}{12} &\color{blue}{15} &\color{blue}{18}\\\color{blue}{13} &\color{blue}{16} &\color{blue}{19}\end{pmatrix}&=\begin{pmatrix}1\cdot\color{blue}{11}+2\cdot\color{blue}{12}+3\cdot\color{blue}{13} &1\cdot\color{blue}{14}+2\cdot\color{blue}{15}+3\cdot\color{blue}{16} &1\cdot\color{blue}{17}+2\cdot\color{blue}{18}+3\cdot\color{blue}{19} \\4\cdot\color{blue}{11}+5\cdot\color{blue}{12}+6\cdot\color{blue}{13} &4\cdot\color{blue}{14}+5\cdot\color{blue}{15}+6\cdot\color{blue}{16} &4\cdot\color{blue}{17}+5\cdot\color{blue}{18}+6\cdot\color{blue}{19} \\7\cdot\color{blue}{11}+8\cdot\color{blue}{12}+9\cdot\color{blue}{13} &7\cdot\color{blue}{14}+8\cdot\color{blue}{15}+9\cdot\color{blue}{16} &7\cdot\color{blue}{17}+8\cdot\color{blue}{18}+9\cdot\color{blue}{19} \end{pmatrix} \\&=\begin{pmatrix}11+24+39 &14+30+48 &17+36+57\\44+60+78 &56+75+96 &68+90+114\\77+96+117 &98+120+144 &119+144+171\\\end{pmatrix} \\&=\begin{pmatrix}74 &92 &110\\182 &227 &272\\290 &362 &434\end{pmatrix}\\\\\begin{pmatrix}11 &14 &17 \\12 &15 &18 \\13 &16 &19 \end{pmatrix}\begin{pmatrix}\color{blue}{1} &\color{blue}{2} &\color{blue}{3}\\\color{blue}{4} &\color{blue}{5} &\color{blue}{6}\\\color{blue}{7} &\color{blue}{8} &\color{blue}{9}\end{pmatrix}&=\begin{pmatrix}11\cdot\color{blue}{1}+14\cdot\color{blue}{4}+17\cdot\color{blue}{7} &11\cdot\color{blue}{2}+14\cdot\color{blue}{5}+17\cdot\color{blue}{8} &11\cdot\color{blue}{3}+14\cdot\color{blue}{6}+17\cdot\color{blue}{9} \\12\cdot\color{blue}{1}+15\cdot\color{blue}{4}+18\cdot\color{blue}{7} &12\cdot\color{blue}{2}+15\cdot\color{blue}{5}+18\cdot\color{blue}{8} &12\cdot\color{blue}{3}+15\cdot\color{blue}{6}+18\cdot\color{blue}{9} \\13\cdot\color{blue}{1}+16\cdot\color{blue}{4}+19\cdot\color{blue}{7} &13\cdot\color{blue}{2}+16\cdot\color{blue}{5}+19\cdot\color{blue}{8} &13\cdot\color{blue}{3}+16\cdot\color{blue}{6}+19\cdot\color{blue}{9} \end{pmatrix} \\&=\begin{pmatrix}11+56+119 &22+70+136 &33+84+153\\12+60+126 &24+75+144 &36+90+162\\13+64+133 &26+80+152 &39+96+171\\\end{pmatrix} \\&=\begin{pmatrix}186 &228 &270\\198 &243 &288\\210 &258 &306\end{pmatrix}\end{align*}
上の例から分かるように行列の積の順序を変えると、算出される行列は同じになるとは限らないので、積の順序は注意が必要である。
また、行列が $A$、$B$、$C$ のように変数で表されているときには、それらの積は $AB$、$ABC$ のように記述する (行列の積の場合は $A\times B$、$A\times B\times C$ のように積記号$\times$を使う必要はない)。
さらに行列の積に関して注意すべきことがある。それは、この講義において行列は列優先という形式にしたがっているので、行列の積の進行方向は右から左に進むということである (詳しくは 3-8節参照)。以下に例を示そう。
3つの $3\times3$行列$A$、$B$、$C$があり、それらの3つの積を $ABC$ とする。この積$ABC$は、具体的には まず$C$に$B$を掛け、その結果に$A$を掛けるという順序で行われる。つまり、$BC = M$ とすれば\[ ABC = A(BC) = AM \]である。
さらに、$3\times3$行列$D$を追加して、それら4つの積を $ABCD$ とする。この場合でも、まず始めに $D$と$C$の積が実行され、次に その積に対して$B$が掛けられるという順序で進んでいく。
$C$と$D$の積を$M_1$、$B$と$M_1$の積を$M_2$ とすれば\[ ABCD = AB(CD) = ABM_1 = A(BM_1) = AM_2 \]である。
(計算例) $2\times2$行列でも事情は変わらないので、次の3つの $2\times2$行列の積の算出過程を以下に示す。
\[A = \begin{pmatrix}4 &0 \\1 &-2 \end{pmatrix} \qquad B = \begin{pmatrix}3 &0 \\0 &3 \end{pmatrix} \qquad C = \begin{pmatrix}-5 &1 \\ 3 &-6 \end{pmatrix} \]
\begin{align*}ABC &= \begin{pmatrix}4 &0 \\1 &-2 \end{pmatrix}\begin{pmatrix}3 &0 \\0 &3 \end{pmatrix}\begin{pmatrix}-5 &1 \\ 3 &-6 \end{pmatrix} \\\\&= \begin{pmatrix}4 &0 \\1 &-2 \end{pmatrix}\begin{pmatrix}3\cdot(-5) + 0\cdot 3 &3\cdot 1 + 0\cdot (-6) \\0\cdot(-5) + 3\cdot 3 &0\cdot 1 + 3\cdot (-6)\end{pmatrix}=\begin{pmatrix}4 &0 \\1 &-2 \end{pmatrix}\begin{pmatrix}-15 &3 \\ 9 &-18\end{pmatrix} \\\\&=\begin{pmatrix}4\cdot(-15) + 0\cdot 9 &4\cdot 3 + 0\cdot (-18) \\1\cdot(-15) + (-2)\cdot 9 &1\cdot 3 + (-2)\cdot (-18)\end{pmatrix}=\begin{pmatrix}-60 &12 \\-33 &39\end{pmatrix} \\\\\end{align*}
C) 行列とベクトルの積
行列同士の積の特殊な例として行列とベクトルの積を以下に示す。次のベクトルは2次元ベクトル(2Dベクトル)、3次元ベクトル(3Dベクトル)に属するものであるが、見方を変えれば$2\times1$行列、$3\times1$行列でもあるので行列とベクトルの積は行列同士の積として扱うことができる。\begin{equation*}\begin{pmatrix}v_{x} \\v_{y} \end{pmatrix} \qquad\begin{pmatrix}\cos\theta \\\sin\theta \end{pmatrix} \qquad\begin{pmatrix}1 \\0\end{pmatrix} \qquad\begin{pmatrix}v_{x} \\v_{y} \\v_{z} \end{pmatrix} \qquad\begin{pmatrix}\cos\theta \\\sin\theta \\1\end{pmatrix} \qquad\begin{pmatrix}1 \\0 \\1\end{pmatrix} \end{equation*}
$2\times2$行列と2次元ベクトル、$3\times3$行列と3次元ベクトルの積
\begin{align*}\begin{pmatrix}a_{11} &a_{12} \\a_{21} &a_{22}\end{pmatrix}\begin{pmatrix}\color{blue}{v_x} \\\color{blue}{v_y} \end{pmatrix}&=\begin{pmatrix}a_{11}\cdot\color{blue}{v_x}+a_{12}\cdot\color{blue}{v_y} \\a_{21}\cdot\color{blue}{v_x}+a_{22}\cdot\color{blue}{v_y}\end{pmatrix} \\\\\begin{pmatrix}a_{11} &a_{12} &a_{13} \\a_{21} &a_{22} &a_{23} \\a_{31} &a_{32} &a_{33} \end{pmatrix}\begin{pmatrix}\color{blue}{v_x} \\\color{blue}{v_y} \\\color{blue}{v_z} \end{pmatrix}&=\begin{pmatrix}a_{11}\cdot\color{blue}{v_x}+a_{12}\cdot\color{blue}{v_y}+a_{13}\cdot\color{blue}{v_z}\\a_{21}\cdot\color{blue}{v_x}+a_{22}\cdot\color{blue}{v_y}+a_{23}\cdot\color{blue}{v_z}\\a_{31}\cdot\color{blue}{v_x}+a_{32}\cdot\color{blue}{v_y}+a_{33}\cdot\color{blue}{v_z}\end{pmatrix} \end{align*}
(計算例)
\begin{align*}\begin{pmatrix}3 &7 \\0 &8\end{pmatrix}\begin{pmatrix}\color{blue}{1} \\\color{blue}{2} \end{pmatrix}&=\begin{pmatrix}3\cdot\color{blue}{1}+7\cdot\color{blue}{2} \\0\cdot\color{blue}{1}+8\cdot\color{blue}{2}\end{pmatrix}=\begin{pmatrix}3+14 \\0+16\end{pmatrix}=\begin{pmatrix}17 \\16\end{pmatrix}\\\\\begin{pmatrix}\cos\theta &\sin\theta \\-\sin\theta &\cos\theta\end{pmatrix}\begin{pmatrix}\color{blue}{\cos\theta} \\\color{blue}{\sin\theta} \end{pmatrix}&=\begin{pmatrix}\cos\theta\cdot\color{blue}{\cos\theta}+\sin\theta\cdot\color{blue}{\sin\theta} \\-\sin\theta\cdot\color{blue}{\cos\theta}+\cos\theta\cdot\color{blue}{\sin\theta} \end{pmatrix}=\begin{pmatrix}\cos^2\theta+\sin^2\theta \\-\sin\theta\cos\theta+\cos\theta\sin\theta \\\end{pmatrix}=\begin{pmatrix}1 \\0\end{pmatrix}\\\\\begin{pmatrix}6 &1 &5\\3 &4 &2\\8 &0 &7\end{pmatrix}\begin{pmatrix}\color{blue}{5} \\\color{blue}{0} \\\color{blue}{1} \end{pmatrix}&=\begin{pmatrix}6\cdot\color{blue}{5}+1\cdot\color{blue}{0}+5\cdot\color{blue}{1}\\3\cdot\color{blue}{5}+4\cdot\color{blue}{0}+2\cdot\color{blue}{1}\\8\cdot\color{blue}{5}+0\cdot\color{blue}{0}+7\cdot\color{blue}{1}\end{pmatrix}=\begin{pmatrix}30+0+5 \\15+0+2 \\40+0+7\end{pmatrix}=\begin{pmatrix}35 \\17 \\47\end{pmatrix}\\\\\begin{pmatrix}1 &11 &2\\0 &9 &5\\13 &3 &0\end{pmatrix}\begin{pmatrix}\color{blue}{2} \\\color{blue}{4} \\\color{blue}{6} \end{pmatrix}&=\begin{pmatrix}1\cdot\color{blue}{2}+11\cdot\color{blue}{4}+2\cdot\color{blue}{6}\\0\cdot\color{blue}{2}+9\cdot\color{blue}{4}+5\cdot\color{blue}{6}\\13\cdot\color{blue}{2}+3\cdot\color{blue}{4}+0\cdot\color{blue}{6}\end{pmatrix}=\begin{pmatrix}2+44+12 \\0+36+30 \\26+12+0\end{pmatrix}=\begin{pmatrix}58 \\66 \\38\end{pmatrix}\end{align*}
D) 行列の和
この講義においては行列の和はほとんど扱うことはないが、一応 $2\times2$行列、$3\times3$行列同士の和の定義を以下に書いておこう。\begin{align*}\begin{pmatrix}a_{11} &a_{12} \\a_{21} &a_{22}\end{pmatrix}+\begin{pmatrix}\color{blue}{b_{11}} &\color{blue}{b_{12}} \\\color{blue}{b_{21}} &\color{blue}{b_{22}} \end{pmatrix}&=\begin{pmatrix}a_{11}+\color{blue}{b_{11}} &a_{12}+\color{blue}{b_{12}}\\a_{21}+\color{blue}{b_{21}} &a_{22}+\color{blue}{b_{22}}\end{pmatrix} \\ \\\begin{pmatrix}a_{11} &a_{12} &a_{13} \\a_{21} &a_{22} &a_{23} \\a_{31} &a_{32} &a_{33} \end{pmatrix}+\begin{pmatrix}\color{blue}{b_{11}} &\color{blue}{b_{12}} &\color{blue}{b_{13}} \\\color{blue}{b_{21}} &\color{blue}{b_{22}} &\color{blue}{b_{23}} \\\color{blue}{b_{31}} &\color{blue}{b_{32}} &\color{blue}{b_{33}} \end{pmatrix}&=\begin{pmatrix}a_{11}+\color{blue}{b_{11}} &a_{12}+\color{blue}{b_{12}} &a_{13}+\color{blue}{b_{13}}\\a_{21}+\color{blue}{b_{21}} &a_{22}+\color{blue}{b_{22}} &a_{23}+\color{blue}{b_{23}}\\a_{31}+\color{blue}{b_{31}} &a_{32}+\color{blue}{b_{32}} &a_{33}+\color{blue}{b_{33}}\end{pmatrix}\end{align*}
E) 変換と変換行列
3D空間や2D空間においてオブジェクトに対して行う平行移動や回転、スケールなどの操作を変換(Transformation)という。コンピューターグラフィックスでは、これらの変換を行列の形で表して使用する。変換を表す行列を変換行列(Transformation Matrix)といい、平行移動ならば平行移動行列、回転ならば回転行列、スケールならばスケール行列などがそれにあたる。また、変換を連続して行うことを変換の合成といい、平行移動、回転、スケールなどの変換の合成は、それらの変換を表す変換行列の積によって表される。この講義において扱う変換は平行移動(Translation)、回転(Rotation)、スケール(Scale)の3つである (注1)。3D空間や2D空間においてオブジェクトを運動させる場合には、何らかの変換をオブジェクトに実行する。オブジェクトに実行する変換は、ほとんどの場合には複数の変換の合成である。具体的には、それらは変換行列の積として1つの変換行列にまとめられ、その1つの変換行列をオブジェクトに対して実行する。
これらのことについては次節以降で1つ1つ詳しく解説していく。
(注1) 他にも「せん断(Shear)」という変換があるが、この講義では扱わない。
F) 単位行列
任意の$3\times3$行列$A$に対して、以下の性質を満たす$3\times3$行列$I$を($3\times3$の)単位行列(Identity Matrix)という。\[ AI = A \qquad\qquad IA = A \]この性質からわかるように、ある行列に単位行列を右から掛けても左から掛けても、その結果は掛ける前と変化しない (整数の掛け算でいえば$1$のような存在である)。$3\times3$の単位行列$I$の具体的な成分を以下に示す。\[I = \begin{pmatrix}1 &0 &0 \\0 &1 &0 \\0 &0 &1 \end{pmatrix} \](単位行列は対角成分がすべて$1$であり、それ以外の成分はすべて$0$である。このことは $2\times2$行列でも $4\times4$行列の場合でも同じである)
THMatrix3x3構造体には identity というstaticプロパティがあるが、その内容は上記の$I$と同じである。
THMatrix3x3.identity
: THMatrix3x3構造体のstaticプロパティで、$3\times3$の単位行列を表すG) 逆行列
$3\times3$行列$A$に対して、\[ AB = BA = I \]となる $3\times3$行列$B$が存在するとき、$B$を$A$の逆行列 (Inverse Matrix)という ($I$は$3\times3$の単位行列である)。$A$の逆行列は $A^{-1}$ として表される。すなわち、\[ AA^{-1} = A^{-1}A = I \]である。
行列の積が2つ以上の場合における逆行列は次のようになる。
$A$、$B$、$C$、$D$ を$3\times3$行列とし、それらに逆行列が存在し各逆行列を $A^{-1}$、$B^{-1}$、$C^{-1}$、$D^{-1}$ とすると、\begin{align*}&(AB)^{-1} = B^{-1}A^{-1} \\\\&(ABC)^{-1} = C^{-1}B^{-1}A^{-1} \\\\&(ABCD)^{-1} = D^{-1}C^{-1}B^{-1}A^{-1} \end{align*}である。
実際、$ABC$ の場合で計算すると
\begin{align*}&(ABC)(C^{-1}B^{-1}A^{-1}) = AB(CC^{-1})B^{-1}A^{-1} = ABIB^{-1}A^{-1} \\\\&= A(BB^{-1})A^{-1} = AIA^{-1} = AA^{-1} = I \\\\\\&(C^{-1}B^{-1}A^{-1})(ABC) = C^{-1}B^{-1}(A^{-1}A)BC = C^{-1}B^{-1}IBC \\\\&= C^{-1}(B^{-1}B)C = C^{-1}IC = C^{-1}C = I \end{align*}
となる (ただし、この計算には下で解説する結合法則が使われている)。$AB$、$ABCD$ の場合も同様に確認できる。
THMatrix3x3構造体には逆行列を表す inverse というプロパティがある。
inverse
: THMatrix3x3構造体のプロパティで、THMatrix3x3インスタンスの逆行列を表す。例えば、Aが THMatrix3x3のインスタンスであるとき、A.inverse は Aの逆行列を表している (つまり $A^{-1}$)。
一般に逆行列はn次正方行列(行数と列数の等しい行列)に対して定義されるものであるが、2D空間を扱う第1章、第2章では行列は$3\times3$行列のみを使うので、そこで使われる逆行列も$3\times3$行列である。また、3D空間を扱う第3章以降では行列は$4\times4$行列のみを使うので、そこにおいて使われる逆行列も$4\times4$行列である。
H) 結合法則
$A$、$B$、$C$ を$3\times3$行列とする。このとき、これらの行列同士の積に関しては結合法則が成り立つ。
すなわち、\[A(BC) = (AB)C\]である ($B$と$C$の積を先に計算してその結果と$A$を掛けても、$A$と$B$の積を先に計算してその結果と$C$を掛けても算出される行列は等しい)。
また、$D$ を$3\times3$行列とすると、\[(ABC)D = ABCD\]であるが、これはまず積$ABC$を計算し、その結果と$D$を掛けたものは積$ABCD$ ($D$から$A$に向かって順番に掛けていったもの)に等しいことを意味している。つまり、3つ以上の行列の積の場合には積の一部分を先に計算しても同じ結果が得られるのである。
結合法則の重要性を示すために、上で述べた行列の積の特別な場合である行列とベクトルの積を例にとって話を進める。
次節以降で解説するが、あるベクトル(ここでは点と考えて構わない)にスケールや回転、平行移動などの変換を実行する場合、スケールや回転、平行移動を表す行列をそのベクトルに対して掛ける。例えば、$2$倍のスケールを表す行列を $S$、$90$°の回転を表す行列を $R$、$(10, 5)$だけの平行移動を表す行列を $T$ とする。ここで、あるベクトル$\boldsymbol{\mathsf{v_1}}$に対し、$2$倍の拡大、$90$°の回転、$(10, 5)$だけの平行移動をこの順序で実行するものとすれば、これらの3つの変換実行後のベクトル$\boldsymbol{\mathsf{v_1}}$の位置を $\boldsymbol{\mathsf{w_1}}$ とすると $\boldsymbol{\mathsf{w_1}}$ は次のように求められる。\[ TRS\boldsymbol{\mathsf{v_1}} = \boldsymbol{\mathsf{w_1}} \]行列の積の場合には積の一部分を先に計算しても同じ結果が得られるので、ここでは先に積$TRS$を計算し、その結果を $M$ とする。それによって上記の計算は次のように改められる。\begin{align*}TRS = M \\\\M\boldsymbol{\mathsf{v_1}} = \boldsymbol{\mathsf{w_1}} \end{align*}ベクトル$\boldsymbol{\mathsf{v_1}}$ だけでなく、他のベクトル$\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{\mathsf{v_3}}$、$\boldsymbol{\mathsf{v_4}}$ に対しても $2$倍の拡大、$90$°の回転、$(10, 5)$だけの平行移動をこの順序で実行するものとし、それらのベクトルの変換実行後の位置を $\boldsymbol{\mathsf{w_2}}$、$\boldsymbol{\mathsf{w_3}}$、$\boldsymbol{\mathsf{w_4}}$ とすると $\boldsymbol{\mathsf{w_2}}$、$\boldsymbol{\mathsf{w_3}}$、$\boldsymbol{\mathsf{w_4}}$ は次のように求めればよい。\begin{align*}M\boldsymbol{\mathsf{v_2}} = \boldsymbol{\mathsf{w_2}} \\\\M\boldsymbol{\mathsf{v_3}} = \boldsymbol{\mathsf{w_3}} \\\\M\boldsymbol{\mathsf{v_4}} = \boldsymbol{\mathsf{w_4}} \end{align*}つまり、上で求めた $M$ をここでも再び使用しているわけである。複数のベクトルに対して実行する変換が同じものならば、先にその変換を表す変換行列の積を計算する。計算結果は1つの行列として算出されるので、その算出された1つの行列を複数のベクトルのそれぞれに掛ければ、各ベクトルの変換後の位置が求められる。
あるオブジェクトに対してスケール、回転、平行移動などの変換を実行することは、詳しくはそのオブジェクトを構成するすべての頂点に対してスケール、回転、平行移動などの変換を実行することになる。各頂点はベクトルによって表され、オブジェクトに実行される変換は変換行列によって表される。オブジェクトに対して何らかの変換を実行してオブジェクトの新しい位置を求めることは、そのオブジェクトを構成する全頂点の新しい位置を求めることに等しい。
したがって変換後のオブジェクトの位置を求めることは、具体的には、その変換を表す変換行列とオブジェクトを構成する全頂点ベクトルとの積を計算することに等しい (その計算の根底に結合法則が使われているのである)。
I) 分配法則
ここでも $A$、$B$、$C$ を$3\times3$行列とする。これらの行列同士の和と積に関しては分配法則が成り立つ。すなわち、
\begin{align*}A(B+C) = AB + AC \\\\(A+B)C = AC + BC\end{align*}である。
ここでは、$A$、$B$、$C$ を$3\times3$行列としたが、$A$、$B$、$C$ の間で計算に必要な積及び和が定義されているのであれば、$A$、$B$、$C$ はどのような行列でも構わない。
たとえば、$A$、$B$ が $3\times3$行列で $C$ が $3\times1$行列(=3次元ベクトル)であっても、$A$ と $C$、$B$ と $C$ の間では積が定義されており、$A$ と $B$ の間では和が定義されているので\begin{align*}&(A+B)C = AC + BC\end{align*}である (ただし、この場合は $A(B+C) = AB + AC$ は成り立たない。$B+C$ は$3\times3$行列と$3\times1$行列との和であるが、その和は定義されていないためである)。
行列とベクトルの積を用いて、分配法則の計算例をいくつか示す。
(1)
\begin{align*}&\begin{pmatrix}4 &-1 \\5 &2\end{pmatrix} \begin{pmatrix}-6 \\11\end{pmatrix} +\begin{pmatrix}4 &-1 \\5 &2\end{pmatrix} \begin{pmatrix}8 \\2\end{pmatrix} =\begin{pmatrix}4 &-1 \\5 &2\end{pmatrix} \left(\begin{pmatrix}-6 \\11\end{pmatrix} +\begin{pmatrix}8 \\2\end{pmatrix} \right)\\\\&=\begin{pmatrix}4 &-1 \\5 &2\end{pmatrix} \begin{pmatrix}2 \\13\end{pmatrix} =\begin{pmatrix}8 - 13 \\10 + 26\end{pmatrix} =\begin{pmatrix}-5 \\36\end{pmatrix} \end{align*}
(2)
\begin{align*}&\begin{pmatrix}18 &0 &3 \\-6 &4 &-5 \\0 &-12 &7 \\\end{pmatrix} \begin{pmatrix}21 \\34 \\-16\end{pmatrix} +\begin{pmatrix}18 &0 &3 \\-6 &4 &-5 \\0 &-12 &7 \\\end{pmatrix} \begin{pmatrix}-19 \\-34 \\17\end{pmatrix} \\\\&= \begin{pmatrix}18 &0 &3 \\-6 &4 &-5 \\0 &-12 &7 \\\end{pmatrix} \left(\begin{pmatrix}21 \\34 \\-16\end{pmatrix} +\begin{pmatrix}-19 \\-34 \\17\end{pmatrix} \right)\\\\&= \begin{pmatrix}18 &0 &3 \\-6 &4 &-5 \\0 &-12 &7 \\\end{pmatrix} \begin{pmatrix}2 \\0 \\1\end{pmatrix} =\begin{pmatrix}36 + 0 + 3 \\-12 + 0 -5 \\0 + 0 + 7\end{pmatrix} =\begin{pmatrix}39 \\-17 \\7\end{pmatrix} \end{align*}
(3)
\begin{align*}&\begin{pmatrix}2 &0 &4 \\0 &5 &-6 \\0 &0 &1 \\\end{pmatrix} \begin{pmatrix}5 \\5 \\1\end{pmatrix} -\begin{pmatrix}2 &0 &4 \\0 &5 &-6 \\0 &0 &1 \\\end{pmatrix} \begin{pmatrix}2 \\2 \\1\end{pmatrix} \\\\&= \begin{pmatrix}2 &0 &4 \\0 &5 &-6 \\0 &0 &1 \\\end{pmatrix} \left(\begin{pmatrix}5 \\5 \\1\end{pmatrix} -\begin{pmatrix}2 \\2 \\1\end{pmatrix} \right)\\\\&=\begin{pmatrix}2 &0 &4 \\0 &5 &-6 \\0 &0 &1 \\\end{pmatrix} \begin{pmatrix}3 \\3 \\0\end{pmatrix} =\begin{pmatrix}6 + 0 + 0 \\0 + 15 + 0 \\0 + 0 + 0\end{pmatrix} =\begin{pmatrix}6 \\15 \\0\end{pmatrix} \end{align*}
J) オブジェクトに変換行列を実行する
この講義ではオブジェクトを動かすにあたって、第5章まではオブジェクトに行列を実行するという方法をとる。UnityのC#スクリプトの標準機能を用いてオブジェクトを動かす場合は、Transformクラスを経由する。具体的には、TransformクラスのlocalPosition, localRotation, localScaleなどのプロパティに直接 値を設定するか、あるいはTransformクラスのメソッドを経由してそれらのプロパティに値を設定するなどの方法である。Transformクラスには行列を扱うメソッドがないため、行列を使ってオブジェクトを動かす場合には、講義用に用意したカスタムライブラリの機能を使う必要がある。この講義で使用するプログラムではさまざまなオブジェクトが使われるが、それらのオブジェクトはカスタムライブラリで用意されている THObject2Dクラス、THObject3Dクラス、及びそれらの派生クラスのインスタンスである (2D空間においては主に THObject2D、3D空間においては主に THObject3D を使用する)。
この2つのクラスには変換行列を実行するための次のメソッドが用意されている。
SetMatrix(THMatrix3x3 m)
: 2D空間のオブジェクトに対して、引数で指定された変換行列を実行する (THObject2Dクラスに用意されているメソッド)。SetMatrix(Matrix4x4 m)
: 3D空間のオブジェクトに対して、引数で指定された変換行列を実行する (THObject3Dクラスに用意されているメソッド)。第1章、第2章では2D空間を扱うので、プログラムで使用されるオブジェクトはすべて THObject2Dクラスのインスタンス(あるいはその派生クラスのインスタンス)であり、それらのオブジェクトに対して変換行列を実行する場合には2D空間用の SetMatrix(THMatrix3x3 m) を使用する。
UnityやUnreal Engineなどのゲームエンジン、あるいはBlenderやMayaなどのDCCツールでは、オブジェクトを動かす際には(正確にはある時点でのオブジェクトの状態を定める際には)「Position」「Rotation」「Scale」の3つのデータ(あるいはこれらに類似のデータ)に値をセットしていくことが普通であり、直接行列を経由するようなことはない。
しかし、コンピューターグラフィックスにおいてオブジェクトの運動をプログラムで実装する際には「Position」「Rotation」「Scale」による方法よりも行列による方法の方が直接的であり、初学者向きなのである。この点については、今後さまざまな箇所で解説する。
以下は本節の内容に関連したプログラムである。
# Code1
以下のプログラムは$3\times3$行列同士の積、$3\times3$行列とベクトルの積に関するものである。ここで記述されている計算は、すべて上の文章中で行った計算をプログラムで表したものに過ぎない。[Code1] (実行結果 図1、図2、図3)
// 行列と行列の積 Vector3 a1 = new Vector3(1, 4, 7); // 第1列 Vector3 a2 = new Vector3(2, 5, 8); // 第2列 Vector3 a3 = new Vector3(3, 6, 9); // 第3列 THMatrix3x3 A = new THMatrix3x3(a1, a2, a3); Vector3 b1 = new Vector3(11, 12, 13); // 第1列 Vector3 b2 = new Vector3(14, 15, 16); // 第2列 Vector3 b3 = new Vector3(17, 18, 19); // 第3列 THMatrix3x3 B = new THMatrix3x3(b1, b2, b3); THMatrix3x3 M = A * B; Debug.Log(M); // 図1 (A*B) M = B * A; Debug.Log(M); // 図2 (B*A) // 行列とベクトルの積 a1 = new Vector3(6, 3, 8); a2 = new Vector3(1, 4, 0); a3 = new Vector3(5, 2, 7); A = new THMatrix3x3(a1, a2, a3); Vector3 w = new Vector3(5, 0, 1); Vector3 v = A * w; Debug.Log(v); // 図3 a1 = new Vector3(1, 0, 13); a2 = new Vector3(11, 9, 3); a3 = new Vector3(2, 5, 0); A = new THMatrix3x3(a1, a2, a3); w = new Vector3(2, 4, 6); v = A * w; Debug.Log(v); // 図3
THMatrix3x3インスタンスをコンストラクタ経由で生成する場合は、以下に示されるようにコンストラクタの引数にVector3型の値を3つセットする
// 引数には3x3行列の 第1列目、第2列目、第3列目 をこの順序でセットする THMatrix3x3(Vector3 col1, Vector3 col2, Vector3 col3)
-
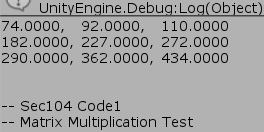 図1 Code1 実行結果 (行列と行列の積 A*B)
図1 Code1 実行結果 (行列と行列の積 A*B) -
 図2 Code1 実行結果 (行列と行列の積 B*A)
図2 Code1 実行結果 (行列と行列の積 B*A) -
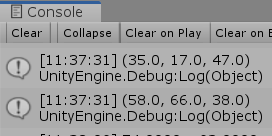 図3 Code1 実行結果 (行列とベクトルの積)
図3 Code1 実行結果 (行列とベクトルの積)
5行目と10行目で$3\times3$行列A、Bが作成され、13行目、15行目においてそれらの積を出力している。図1は積A*Bの計算結果であり、図2は積B*Aの計算結果である。いずれも上で見た結果に等しい。
図3は$3\times3$行列とベクトルの積の計算結果であり、具体的には24行目と32行目の出力である。
プログラム23行目、31行目に見られるように、THMatrix3x3とVector3の積は、
// AはTHMatrix3x3型、wはVector3型 Vector3 v = A * w;
# Code2
オブジェクトに変換行列を実行するには上で述べたように SetMatrix(..) を使う。具体的な変換行列の実行については次節以降で見ていくが、ここでは SetMatrix(..) の使用例として、オブジェクトに対してidentity行列(単位行列)を実行する場合について見る。オブジェクトを運動させるためには、オブジェクトに対してさまざまな変換行列を実行することになるが、オブジェクトに対してidentity行列を実行すると、オブジェクトは何の変換も受けていない状態になるのである。
[Code2] (実行結果 図4)
// Diskは何の変換も受けていない状態になる Disk.SetMatrix(THMatrix3x3.identity);
© 2020-2025 Redpoll's 60 (All rights reserved)