Redpoll's 60
Home / 3Dプログラミング入門 / 第1章 $§$1-7
第1章 2D空間の基礎
| $§$1-1 点とベクトル | $§$1-6 回転行列 |
| $§$1-2 ベクトルによる平行移動 | $§$1-7 スケール行列 |
| $§$1-3 単位ベクトル | $§$1-8 変換行列の積 |
| $§$1-4 行列の基礎 | $§$1-9 フレームとフレームレート |
| $§$1-5 平行移動行列 | $§$1-10 オブジェクトの基本的な運動 (往復運動と回転) |
$§$1-7 スケール行列
本節では2D空間上の点、及びオブジェクトの行列による拡大縮小変換、いわゆるスケール(Scale)を取り扱う。
図1に示される位置に、3点 $R = (2, 0)$、$G = (2, 2)$、$B = (0, 2)$ が置かれている。この3点に以下の3つのスケール行列を実行する。
$S_1$はx軸、y軸方向ともに$2$倍拡大。
$S_2$はx軸方向にのみ$0.5$倍縮小。
$S_3$はy軸方向にのみ$1.5$倍拡大。
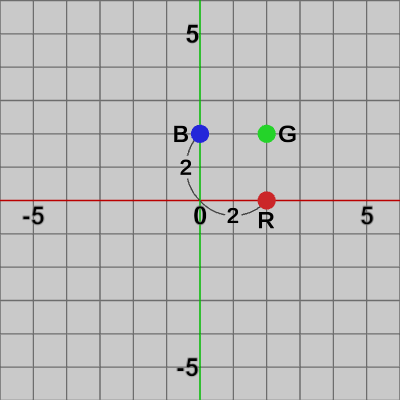
図1 3点R, G, Bの初期状態 
図2 x軸, y軸方向に2倍拡大
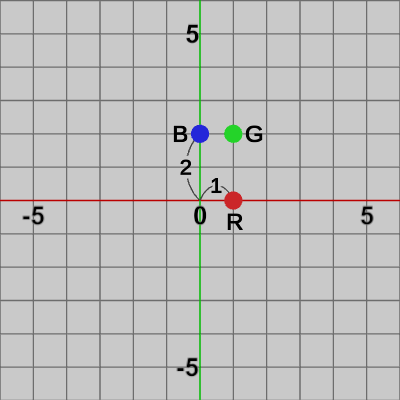
図3 x軸方向に0.5倍縮小 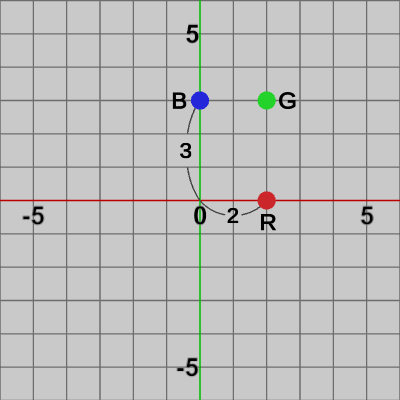
図4 y軸方向に1.5倍拡大
実際に計算してみよう。
$S_1$による変換(図2)
2D空間において、スケール行列による点の拡大縮小の具体的な意味は次の通りである。
ある点をx軸方向に$s$倍するということは、その点からy軸までの距離を$s$倍するということである。
同様に、ある点をy軸方向に$t$倍するということは、その点からx軸までの距離を$t$倍するということである。
点$(a, b)$をx軸方向に$s$倍、y軸方向に$t$倍する場合を以下の図に示す。
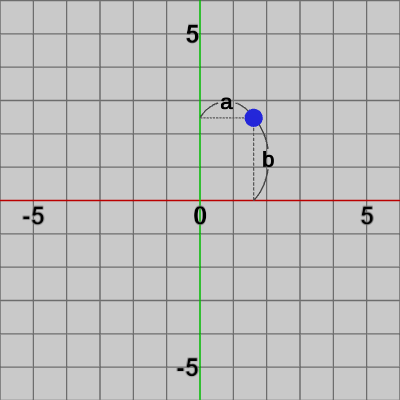
図5 点(a, b) 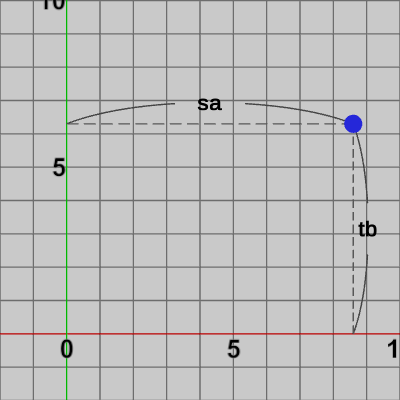
図6 x軸方向にs倍、y軸方向にt倍
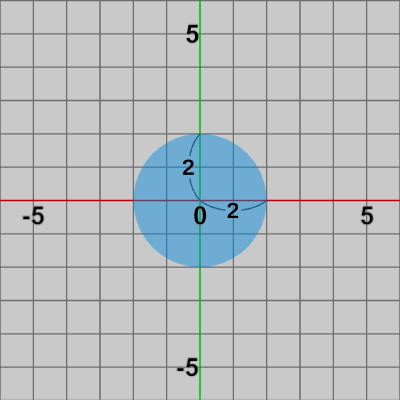
図7 Circle では以下に、オブジェクトに対しスケール行列を実行するプログラムを作成する。
図7に示されるオブジェクトCircleは半径$2$の円形オブジェクトで、その中心が原点に置かれている。このオブジェクトに対し、以下の3つのスケール行列$S_1$, $S_2$, $S_3$を実行するが、それぞれのスケールの内容は次の通り。
$S_1$はx軸方向にのみ$2$倍拡大。
$S_2$はy軸方向にのみ$0.5$倍縮小。
$S_3$はx軸方向に$2$倍拡大、y軸方向に$0.5$倍縮小。
これらのスケールを行列にすると次のようになる。
オブジェクトに対して実行するスケール行列は、カスタムライブラリの以下のメソッドを用いて取得できる。
また、次のように引数を1つだけ指定することもできる。
実際のプログラムを以下に示す。
実行結果は次の通り。
オブジェクトをx軸方向に$s$倍するということは、オブジェクトの各点からy軸までの距離を$s$倍するということである。
同様に、オブジェクトをy軸方向に$t$倍するということは、オブジェクトの各点からx軸までの距離を$t$倍するということである。
では最後に、本節で述べた内容に関するプログラムを作成する。
$S_1$はx軸、y軸方向ともに$2$倍拡大。
$S_2$はx軸方向にのみ$0.5$倍縮小。
$S_3$はy軸方向にのみ$1.5$倍拡大。
[Code1] (実行結果 図11、図12、図13)
1行目から3行目の Vector3型変数 R、G、B は $(2, 0)$、$(2, 2)$、$(0, 2)$ を同次座標化したものである。 プログラムで実行しているスケール行列は $S_1$であり、図11はその実行結果である。図12、図13は実行するスケール行列を $S_2$、$S_3$とした場合の結果である。いずれの結果も上での計算結果と一致する。なお、9行目から11行目の積は本来は Vector3型で返されるが、前節でも述べたように、Vector3型インスタンスを Vector2型変数に代入すると自動的に z成分が切り取られて、x成分、y成分のみがコピーされる。
半径$2$の円形オブジェクトCircleに対してスケール行列を実行する。
[Code2] (実行結果 図14)

図14 Code2 実行結果 1行目のスケール行列Sはx軸方向に$2.5$倍、y軸方向に$1.5$倍の拡大を実行する。
A) 点のスケール
2D空間において、x軸方向に$s$倍、y軸方向に$t$倍のスケールを実行するスケール行列(Scale Matrix)は次のように表される。\begin{pmatrix}s &0 \\0 &t\end{pmatrix}例えば、2D空間の点$(a, b)$を、x軸方向に$s$倍、y軸方向に$t$倍させる計算は次のように行われる。\[\begin{pmatrix}s &0 \\0 &t\end{pmatrix}\begin{pmatrix}a \\b\end{pmatrix}=\begin{pmatrix}sa \\tb\end{pmatrix}\]すなわち、x座標を$s$倍、y座標を$t$倍させた結果になる。図1に示される位置に、3点 $R = (2, 0)$、$G = (2, 2)$、$B = (0, 2)$ が置かれている。この3点に以下の3つのスケール行列を実行する。
\[S_1 =\begin{pmatrix}2 &0\\0 &2 \end{pmatrix}\qquad S_2 =\begin{pmatrix}0.5 &0\\0 &1 \end{pmatrix}\qquad S_3 =\begin{pmatrix}1 &0\\0 &1.5 \end{pmatrix}\]
それぞれの行列の意味は次の通りである。$S_1$はx軸、y軸方向ともに$2$倍拡大。
$S_2$はx軸方向にのみ$0.5$倍縮小。
$S_3$はy軸方向にのみ$1.5$倍拡大。




実際に計算してみよう。
$S_1$による変換(図2)
\[R : \begin{pmatrix}2 &0\\0 &2 \end{pmatrix}\begin{pmatrix}2\\0 \end{pmatrix}=\begin{pmatrix}4\\0 \end{pmatrix}\qquad G : \begin{pmatrix}2 &0\\0 &2 \end{pmatrix}\begin{pmatrix}2\\2 \end{pmatrix}=\begin{pmatrix}4\\4 \end{pmatrix}\qquad B : \begin{pmatrix}2 &0\\0 &2 \end{pmatrix}\begin{pmatrix}0\\2 \end{pmatrix}=\begin{pmatrix}0\\4 \end{pmatrix}\]
$S_2$による変換(図3)\[R : \begin{pmatrix}0.5 &0\\0 &1 \end{pmatrix}\begin{pmatrix}2\\0 \end{pmatrix}=\begin{pmatrix}1\\0 \end{pmatrix}\qquad G : \begin{pmatrix}0.5 &0\\0 &1 \end{pmatrix}\begin{pmatrix}2\\2 \end{pmatrix}=\begin{pmatrix}1\\2 \end{pmatrix}\qquad B : \begin{pmatrix}0.5 &0\\0 &1 \end{pmatrix}\begin{pmatrix}0\\2 \end{pmatrix}=\begin{pmatrix}0\\2 \end{pmatrix}\]
$S_3$による変換(図4)\[R : \begin{pmatrix}1 &0\\0 &1.5 \end{pmatrix}\begin{pmatrix}2\\0 \end{pmatrix}=\begin{pmatrix}2\\0 \end{pmatrix}\qquad G : \begin{pmatrix}1 &0\\0 &1.5 \end{pmatrix}\begin{pmatrix}2\\2 \end{pmatrix}=\begin{pmatrix}2\\3 \end{pmatrix}\qquad B : \begin{pmatrix}1 &0\\0 &1.5 \end{pmatrix}\begin{pmatrix}0\\2 \end{pmatrix}=\begin{pmatrix}0\\3 \end{pmatrix}\]
2D空間において、スケール行列による点の拡大縮小の具体的な意味は次の通りである。
ある点をx軸方向に$s$倍するということは、その点からy軸までの距離を$s$倍するということである。
同様に、ある点をy軸方向に$t$倍するということは、その点からx軸までの距離を$t$倍するということである。
点$(a, b)$をx軸方向に$s$倍、y軸方向に$t$倍する場合を以下の図に示す。


B) オブジェクトにスケール行列を実行する
2D空間のスケールは$2\times2$行列で表せるが、回転行列の場合と同様にスケール行列も、平行移動行列との積を可能にするために$3\times3$行列で表す必要がある。具体的には、x軸方向に$s$倍、y軸方向に$t$倍のスケールを実行するスケール行列は次のように表される。\begin{pmatrix}s &0 &0 \\0 &t &0 \\0 &0 &1\end{pmatrix}また、2D空間の点$(a, b)$を、x軸方向に$s$倍、y軸方向に$t$倍させる計算は以下のようになる (この場合には $(a, b)$は同次座標の形で $(a, b, 1)$と表す必要がある)。\[\begin{pmatrix}s &0 &0 \\0 &t &0 \\0 &0 &1\end{pmatrix}\begin{pmatrix}a \\b \\1\end{pmatrix}=\begin{pmatrix}sa \\tb \\1\end{pmatrix}\]
図7に示されるオブジェクトCircleは半径$2$の円形オブジェクトで、その中心が原点に置かれている。このオブジェクトに対し、以下の3つのスケール行列$S_1$, $S_2$, $S_3$を実行するが、それぞれのスケールの内容は次の通り。
$S_1$はx軸方向にのみ$2$倍拡大。
$S_2$はy軸方向にのみ$0.5$倍縮小。
$S_3$はx軸方向に$2$倍拡大、y軸方向に$0.5$倍縮小。
これらのスケールを行列にすると次のようになる。
\[S_1 =\begin{pmatrix}2 &0 &0\\0 &1 &0\\ 0 &0 &1\end{pmatrix}\qquad S_2 =\begin{pmatrix}1 &0 &0\\0 &0.5 &0\\ 0 &0 &1\end{pmatrix}\qquad S_3 =\begin{pmatrix}2 &0 &0\\0 &0.5 &0\\ 0 &0 &1\end{pmatrix}\]
オブジェクトに対して実行するスケール行列は、カスタムライブラリの以下のメソッドを用いて取得できる。
TH2DMath.GetScale3x3(float s, float t)
: 2D空間においてx軸方向に$s$倍、y軸方向に$t$倍の拡大縮小を実行するスケール行列を取得するための TH2DMathクラスの staticメソッドで、戻り値は THMatrix3x3型のインスタンス。また、次のように引数を1つだけ指定することもできる。
TH2DMath.GetScale3x3(float s)
: この場合には、x軸方向、y軸方向の倍率はともに$s$倍となる。実際のプログラムを以下に示す。
THMatrix3x3 S1 = TH2DMath.GetScale3x3(2.0f, 1.0f); THMatrix3x3 S2 = TH2DMath.GetScale3x3(1.0f, 0.5f); THMatrix3x3 S3 = TH2DMath.GetScale3x3(2.0f, 0.5f); Circle.SetMatrix(S1);
実行結果は次の通り。
 図8 S1(x軸方向に2倍)を実行した結果
図8 S1(x軸方向に2倍)を実行した結果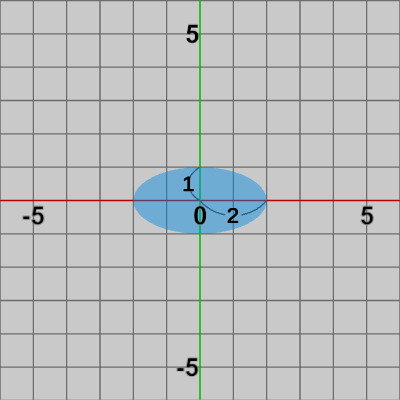 図9 S2(y軸方向に0.5倍)を実行した結果
図9 S2(y軸方向に0.5倍)を実行した結果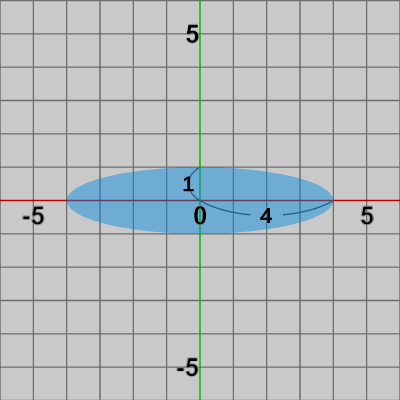 図10 S3(x軸方向に2倍、y軸方向に0.5倍)を実行した結果
図10 S3(x軸方向に2倍、y軸方向に0.5倍)を実行した結果
オブジェクトをx軸方向に$s$倍するということは、オブジェクトの各点からy軸までの距離を$s$倍するということである。
同様に、オブジェクトをy軸方向に$t$倍するということは、オブジェクトの各点からx軸までの距離を$t$倍するということである。
では最後に、本節で述べた内容に関するプログラムを作成する。
# Code1
3点 $R = (2, 0)$、$G = (2, 2)$、$B = (0, 2)$ に以下の3つのスケール行列を実行する。\[S_1 =\begin{pmatrix}2 &0 &0\\0 &2 &0\\0 &0 &1\end{pmatrix}\qquad S_2 =\begin{pmatrix}0.5 &0 &0\\0 &1 &0\\0 &0 &1\end{pmatrix}\qquad S_3 =\begin{pmatrix}1 &0 &0\\0 &1.5 &0\\ 0 &0 &1\end{pmatrix}\]
同次座標に対応させるために1次元拡張して $3\times3$行列の形で表されているが、それぞれの行列の意味は次の通りである。$S_1$はx軸、y軸方向ともに$2$倍拡大。
$S_2$はx軸方向にのみ$0.5$倍縮小。
$S_3$はy軸方向にのみ$1.5$倍拡大。
[Code1] (実行結果 図11、図12、図13)
Vector3 R = new Vector3(2, 0, 1);
Vector3 G = new Vector3(2, 2, 1);
Vector3 B = new Vector3(0, 2, 1);
THMatrix3x3 S1 = TH2DMath.GetScale3x3(2.0f);
THMatrix3x3 S2 = TH2DMath.GetScale3x3(0.5f, 1.0f);
THMatrix3x3 S3 = TH2DMath.GetScale3x3(1.0f, 1.5f);
Vector2 sR = S1 * R;
Vector2 sG = S1 * G;
Vector2 sB = S1 * B;
Debug.Log("S1 * R : " + sR);
Debug.Log("S1 * G : " + sG);
Debug.Log("S1 * B : " + sB);
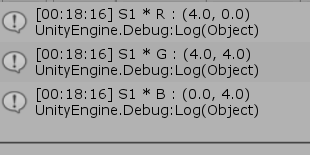 図11 S1(x軸方向、y軸方向に2倍拡大)を実行した場合
図11 S1(x軸方向、y軸方向に2倍拡大)を実行した場合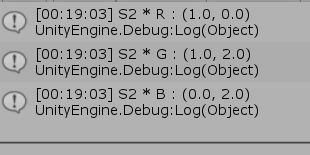 図12 S2(x軸方向に0.5倍縮小)を実行した場合
図12 S2(x軸方向に0.5倍縮小)を実行した場合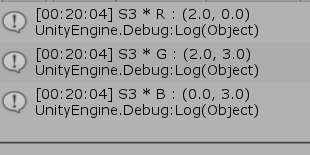 図13 S3(y軸方向に1.5倍拡大)を実行した場合
図13 S3(y軸方向に1.5倍拡大)を実行した場合
1行目から3行目の Vector3型変数 R、G、B は $(2, 0)$、$(2, 2)$、$(0, 2)$ を同次座標化したものである。 プログラムで実行しているスケール行列は $S_1$であり、図11はその実行結果である。図12、図13は実行するスケール行列を $S_2$、$S_3$とした場合の結果である。いずれの結果も上での計算結果と一致する。なお、9行目から11行目の積は本来は Vector3型で返されるが、前節でも述べたように、Vector3型インスタンスを Vector2型変数に代入すると自動的に z成分が切り取られて、x成分、y成分のみがコピーされる。
# Code2
スケール行列をオブジェクトに実行する場合のプログラムを以下に示す。半径$2$の円形オブジェクトCircleに対してスケール行列を実行する。
[Code2] (実行結果 図14)
THMatrix3x3 S = TH2DMath.GetScale3x3(2.5f, 1.5f); Circle.SetMatrix(S);

© 2020-2025 Redpoll's 60 (All rights reserved)