Redpoll's 60
Home / 3Dプログラミング入門 / 第1章 $§$1-2
第1章 2D空間の基礎
| $§$1-1 点とベクトル | $§$1-6 回転行列 |
| $§$1-2 ベクトルによる平行移動 | $§$1-7 スケール行列 |
| $§$1-3 単位ベクトル | $§$1-8 変換行列の積 |
| $§$1-4 行列の基礎 | $§$1-9 フレームとフレームレート |
| $§$1-5 平行移動行列 | $§$1-10 オブジェクトの基本的な運動 (往復運動と回転) |
$§$1-2 ベクトルによる平行移動
2D空間上の点$P$にベクトル$\boldsymbol{v}$を加算して別の地点に移動させることを考える。
ここでは、$P = (2, 1)$、$\boldsymbol{v} = (3, 2)$ とする。
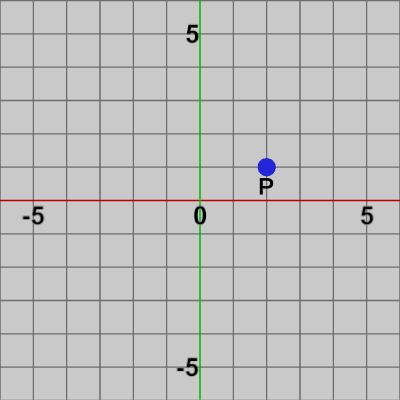
図1 点P=(2, 1) 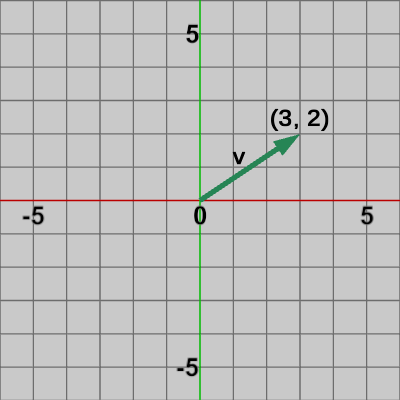
図2 ベクトルv=(3, 2)
前節で述べたようにコンピューターグラフィックスでは点も位置ベクトルというベクトルとして扱われる。例えば、上記の点$P$はx座標が$2$、y座標が$1$であるから位置ベクトルとして次のように表される。\[P = \begin{pmatrix}2 \\1 \end{pmatrix} \] 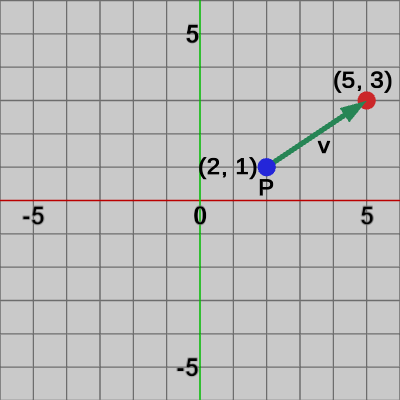
図3 点Pをベクトルvによって移動させる 点$P$にベクトル$\boldsymbol{v}$を加算することは詳しく言えば、位置ベクトル$P$に方向を表すベクトル$\boldsymbol{v}$を加算することを意味する。これは前節で見たベクトル同士の加算であり次のように計算される。
\[P + \boldsymbol{v} = \begin{pmatrix}2 \\1 \end{pmatrix} +\begin{pmatrix}3 \\2 \end{pmatrix} =\begin{pmatrix}5 \\3 \end{pmatrix} \] 図に示すと図3のようになる。ベクトル$\boldsymbol{v}$の始点を点$P$に一致させたときのベクトル$\boldsymbol{v}$の終点が点$P$の移動後の位置である(移動後の位置は赤い点で表示してある)。
続いて、ベクトルの加算によって移動させた点を元の位置に戻す処理について考えよう。
下図4のベクトル$w$の加算によって点$Q$を移動させた結果、図5の位置$(3, -1)$に移ったとする。
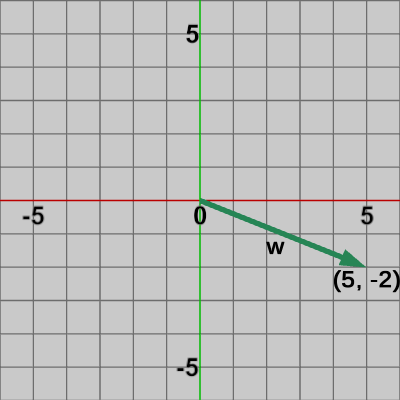
図4 ベクトルw=(5, -2) 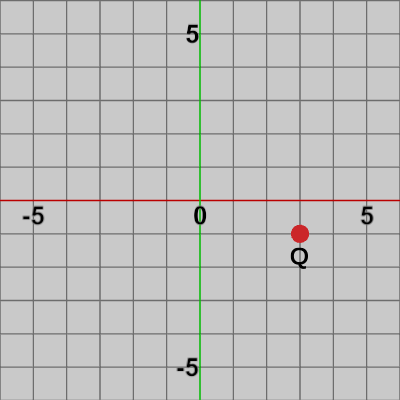
図5 移動後の点Q=(3, -1)
この点$Q$を移動前の位置に戻してみよう。
点$Q$の移動前の位置を(x, y)とする。点$Q$がベクトル$w = (5, -2)$の加算によって現在の位置$(3, -1)$に移った処理は次の式で表される(以下では赤い$\color{red}Q$が移動後の$Q$を表し、青い$\color{blue}Q$が移動前の$Q$を表している)。\[\color{blue}Q + \boldsymbol{w} = \begin{pmatrix}x \\y \end{pmatrix} +\begin{pmatrix}5 \\-2 \end{pmatrix} =\begin{pmatrix}3 \\-1 \end{pmatrix} = \color{red}Q \] したがって点$Q$の移動前の位置(x, y)は次のように求められる。\[\color{blue}Q =\begin{pmatrix}x \\y \end{pmatrix} =\begin{pmatrix}3 \\-1 \end{pmatrix} -\begin{pmatrix}5 \\-2 \end{pmatrix} = \color{red}Q - \boldsymbol{w}\] この式が意味することは、移動後の点 $Q = (3, -1)$ からベクトル $\boldsymbol{w} = (5, -2)$ を減算するということである。ベクトル $\boldsymbol{w} = (5, -2)$ を減算することは、ベクトル $\boldsymbol{w}$ の向きを反転させたベクトル $-\boldsymbol{w} = -(5, -2) = (-5, 2)$ を加算することに等しいから、結局上の式は、\[\color{blue}Q = \color{red}Q - \boldsymbol{w} = \color{red}Q + (-\boldsymbol{w})\]\[\begin{pmatrix}x \\y \end{pmatrix} =\begin{pmatrix}3 \\-1 \end{pmatrix} -\begin{pmatrix}5 \\-2 \end{pmatrix} =\begin{pmatrix}3 \\-1 \end{pmatrix} +\begin{pmatrix}-5 \\2 \end{pmatrix} =\begin{pmatrix}-2 \\1 \end{pmatrix} \] となり、移動前の点$Q = (-2, 1)$であることが分かる。
以上の結果を図6、図7に示す。
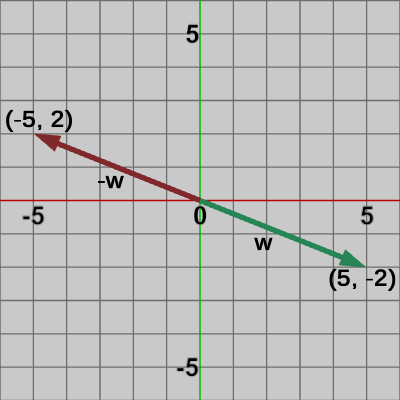
図6 ベクトルwの向きを反転させた ベクトル -w = (-5, 2) 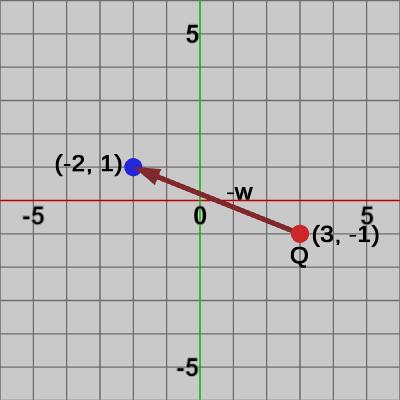
図7 点Qを元の位置(-2, 1)へ移動
図6はベクトル $w = (5, -2)$ とその向きを反転させたベクトル $-w = (-5, 2)$ (赤色のベクトル)である。
図7は移動後の点$Q$にベクトル $\boldsymbol{-w}$ を加算して、点$Q$を移動前の位置$(-2, 1)$に戻す様子を示している。ベクトル $\boldsymbol{-w}$ の始点を移動後の点$Q$に一致させたときのベクトル $\boldsymbol{-w}$ の終点が点$Q$の移動前の位置である(移動前の位置は青い点で表示してある)。
本節では2D空間上の点をベクトルによる加算(あるいは減算)によって別の位置へ直線的に移動させた。このように、2D空間上の点を別の位置へ直線的に移動させることを平行移動(Translation)という。
ここからは、本節で述べた内容に関するプログラムを作成する。
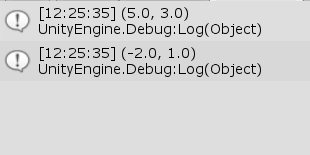
図8 Code1 実行結果 (1)は点$P = (2, 1)$をベクトル$\boldsymbol{\mathsf{v}} = (3, 2)$だけ移動させる計算である。
(2)はベクトル$\boldsymbol{\mathsf{w}} = (5, -2)$の加算によって、$(3, -1)$に移動した点$Q$の元の位置を求める計算である。
本節の始めに述べたように、点も位置ベクトルというベクトルとして表すことができるのでプログラムにおける点$P$、$Q$には、ベクトル$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$と同じく Vector2構造体が使われている。
[Code2] (実行結果 図9)

図9 Code2 実行結果 (1)は点$A$を$3\boldsymbol{\mathsf{v_a}}$だけ移動させた位置の計算である。\[ 3\boldsymbol{\mathsf{v_a}} = 3\begin{pmatrix}2 \\3 \end{pmatrix} =\begin{pmatrix}6 \\9 \end{pmatrix} \]であるから、移動後の位置は点$A = (-11,\ 6)$を$(6, 9)$だけ移動させた位置である。
\[A + 3\boldsymbol{\mathsf{v_a}} = \begin{pmatrix}-11 \\6 \end{pmatrix} +\begin{pmatrix}6 \\9 \end{pmatrix} =\begin{pmatrix}-5 \\15 \end{pmatrix} \]
(2)は点$B$を$-5\boldsymbol{\mathsf{v_b}}$だけ移動させた位置の計算である。\[ -5\boldsymbol{\mathsf{v_b}} = -5\begin{pmatrix}4 \\-6 \end{pmatrix} =\begin{pmatrix}-20 \\30 \end{pmatrix} \]であるから、移動後の位置は点$B = (22,\ 33)$を$(-20,\ 30)$だけ移動させた位置である。
\[B - 5\boldsymbol{\mathsf{v_b}} = B + (-5\boldsymbol{\mathsf{v_b}}) = \begin{pmatrix}22 \\33 \end{pmatrix} +\begin{pmatrix}-20 \\30 \end{pmatrix} =\begin{pmatrix}2 \\63 \end{pmatrix} \]
ここでは、$P = (2, 1)$、$\boldsymbol{v} = (3, 2)$ とする。


前節で述べたようにコンピューターグラフィックスでは点も位置ベクトルというベクトルとして扱われる。例えば、上記の点$P$はx座標が$2$、y座標が$1$であるから位置ベクトルとして次のように表される。\[P = \begin{pmatrix}2 \\1 \end{pmatrix} \]

\[P + \boldsymbol{v} = \begin{pmatrix}2 \\1 \end{pmatrix} +\begin{pmatrix}3 \\2 \end{pmatrix} =\begin{pmatrix}5 \\3 \end{pmatrix} \] 図に示すと図3のようになる。ベクトル$\boldsymbol{v}$の始点を点$P$に一致させたときのベクトル$\boldsymbol{v}$の終点が点$P$の移動後の位置である(移動後の位置は赤い点で表示してある)。
続いて、ベクトルの加算によって移動させた点を元の位置に戻す処理について考えよう。
下図4のベクトル$w$の加算によって点$Q$を移動させた結果、図5の位置$(3, -1)$に移ったとする。


この点$Q$を移動前の位置に戻してみよう。
点$Q$の移動前の位置を(x, y)とする。点$Q$がベクトル$w = (5, -2)$の加算によって現在の位置$(3, -1)$に移った処理は次の式で表される(以下では赤い$\color{red}Q$が移動後の$Q$を表し、青い$\color{blue}Q$が移動前の$Q$を表している)。\[\color{blue}Q + \boldsymbol{w} = \begin{pmatrix}x \\y \end{pmatrix} +\begin{pmatrix}5 \\-2 \end{pmatrix} =\begin{pmatrix}3 \\-1 \end{pmatrix} = \color{red}Q \] したがって点$Q$の移動前の位置(x, y)は次のように求められる。\[\color{blue}Q =\begin{pmatrix}x \\y \end{pmatrix} =\begin{pmatrix}3 \\-1 \end{pmatrix} -\begin{pmatrix}5 \\-2 \end{pmatrix} = \color{red}Q - \boldsymbol{w}\] この式が意味することは、移動後の点 $Q = (3, -1)$ からベクトル $\boldsymbol{w} = (5, -2)$ を減算するということである。ベクトル $\boldsymbol{w} = (5, -2)$ を減算することは、ベクトル $\boldsymbol{w}$ の向きを反転させたベクトル $-\boldsymbol{w} = -(5, -2) = (-5, 2)$ を加算することに等しいから、結局上の式は、\[\color{blue}Q = \color{red}Q - \boldsymbol{w} = \color{red}Q + (-\boldsymbol{w})\]\[\begin{pmatrix}x \\y \end{pmatrix} =\begin{pmatrix}3 \\-1 \end{pmatrix} -\begin{pmatrix}5 \\-2 \end{pmatrix} =\begin{pmatrix}3 \\-1 \end{pmatrix} +\begin{pmatrix}-5 \\2 \end{pmatrix} =\begin{pmatrix}-2 \\1 \end{pmatrix} \] となり、移動前の点$Q = (-2, 1)$であることが分かる。
以上の結果を図6、図7に示す。


図6はベクトル $w = (5, -2)$ とその向きを反転させたベクトル $-w = (-5, 2)$ (赤色のベクトル)である。
図7は移動後の点$Q$にベクトル $\boldsymbol{-w}$ を加算して、点$Q$を移動前の位置$(-2, 1)$に戻す様子を示している。ベクトル $\boldsymbol{-w}$ の始点を移動後の点$Q$に一致させたときのベクトル $\boldsymbol{-w}$ の終点が点$Q$の移動前の位置である(移動前の位置は青い点で表示してある)。
本節では2D空間上の点をベクトルによる加算(あるいは減算)によって別の位置へ直線的に移動させた。このように、2D空間上の点を別の位置へ直線的に移動させることを平行移動(Translation)という。
ここからは、本節で述べた内容に関するプログラムを作成する。
# Code1
[Code1] (実行結果 図8)// (1) Vector2 P = new Vector2(2, 1); Vector2 v = new Vector2(3, 2); Vector2 P1 = P + v; Debug.Log(P1); // (5, 3) // (2) Vector2 Q = new Vector2(3, -1); Vector2 w = new Vector2(5, -2); Vector2 Q1 = Q - w; Debug.Log(Q1); // (-2, 1)

(2)はベクトル$\boldsymbol{\mathsf{w}} = (5, -2)$の加算によって、$(3, -1)$に移動した点$Q$の元の位置を求める計算である。
本節の始めに述べたように、点も位置ベクトルというベクトルとして表すことができるのでプログラムにおける点$P$、$Q$には、ベクトル$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$と同じく Vector2構造体が使われている。
# Code2
次に点$A = (-11,\ 6)$、点$B = (22,\ 33)$ をベクトル$\boldsymbol{\mathsf{v_a}} = (2, 3)$、$\boldsymbol{\mathsf{v_b}} = (4, -6)$を使って移動させる。[Code2] (実行結果 図9)
// (1) Vector2 A = new Vector2(-11, 6); Vector2 va = new Vector2(2, 3); Vector2 A1 = A + 3.0f * va; Debug.Log(A1); // (-5, 15) // (2) Vector2 B = new Vector2(22, 33); Vector2 vb = new Vector2(4, -6); Vector2 B1 = B - 5.0f * vb; Debug.Log(B1); // (2, 63)

\[A + 3\boldsymbol{\mathsf{v_a}} = \begin{pmatrix}-11 \\6 \end{pmatrix} +\begin{pmatrix}6 \\9 \end{pmatrix} =\begin{pmatrix}-5 \\15 \end{pmatrix} \]
(2)は点$B$を$-5\boldsymbol{\mathsf{v_b}}$だけ移動させた位置の計算である。\[ -5\boldsymbol{\mathsf{v_b}} = -5\begin{pmatrix}4 \\-6 \end{pmatrix} =\begin{pmatrix}-20 \\30 \end{pmatrix} \]であるから、移動後の位置は点$B = (22,\ 33)$を$(-20,\ 30)$だけ移動させた位置である。
\[B - 5\boldsymbol{\mathsf{v_b}} = B + (-5\boldsymbol{\mathsf{v_b}}) = \begin{pmatrix}22 \\33 \end{pmatrix} +\begin{pmatrix}-20 \\30 \end{pmatrix} =\begin{pmatrix}2 \\63 \end{pmatrix} \]
© 2020-2025 Redpoll's 60 (All rights reserved)