Redpoll's 60
Home / 3Dプログラミング入門 / 第1章 $§$1-6
第1章 2D空間の基礎
| $§$1-1 点とベクトル | $§$1-6 回転行列 |
| $§$1-2 ベクトルによる平行移動 | $§$1-7 スケール行列 |
| $§$1-3 単位ベクトル | $§$1-8 変換行列の積 |
| $§$1-4 行列の基礎 | $§$1-9 フレームとフレームレート |
| $§$1-5 平行移動行列 | $§$1-10 オブジェクトの基本的な運動 (往復運動と回転) |
$§$1-6 回転行列
本節では2D空間上の点、及びオブジェクトを行列によって回転(Rotation)させることについて扱う。
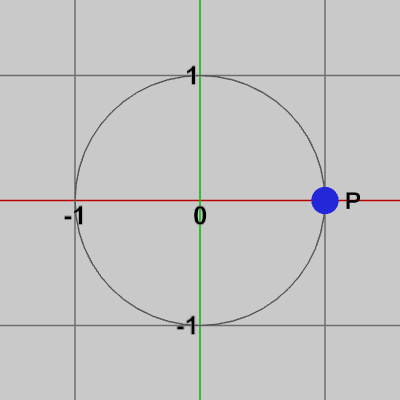
図1 点P=(1, 0) 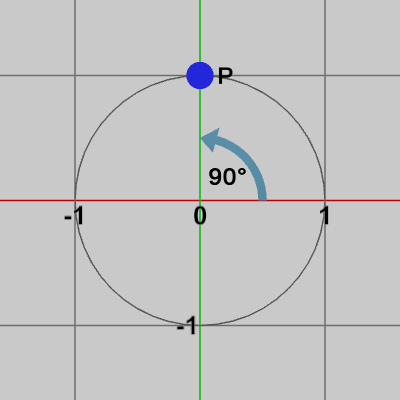
図2 点Pを90°回転させる(P=(0, 1)に移動する)
2D空間で原点を中心に角度 $\theta$ だけ回転させる回転行列(Rotation Matrix)は次のように表される。\begin{pmatrix}\cos\theta &-\sin\theta \\\sin\theta & \cos\theta \end{pmatrix}
例えば、2D空間の点 $(x, y)$ を原点周りに角度 $\theta$ 回転させる場合の計算は次のように行われる。回転後の座標を $(x', y')$ とすれば、\begin{align*}\begin{pmatrix}\cos\theta &-\sin\theta \\\sin\theta & \cos\theta \end{pmatrix}\begin{pmatrix}x \\y \end{pmatrix}= \begin{pmatrix}x\cos\theta - y\sin\theta \\x\sin\theta + y\cos\theta \end{pmatrix}=\begin{pmatrix}x' \\y' \end{pmatrix}\end{align*}
計算例として上記のケースをここで適用してみる。$P=(1, 0)$ を $90^\circ$ 回転させるには、$(x, y) = (1, 0)$、$\theta = 90^\circ$ とおいて
Unityにおける2D空間(XY平面)の回転は、プラス方向の回転が反時計回りであり、マイナス方向の回転が時計回りである。
例えば、$T > 0$ とし、角度 $+T$ 方向の回転と角度 $-T$ 方向の回転を示すと図3のようになる。また上記の点 $P = (1, 0)$ を $-90^\circ$ 回転させた場合を図4に示す。
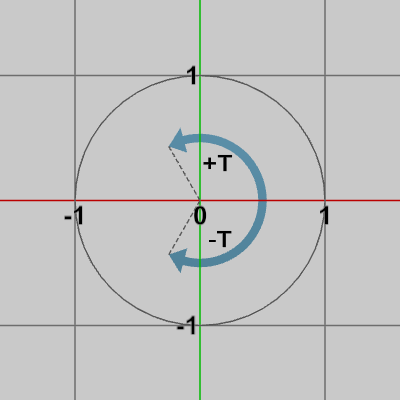
図3 +Tの回転と-Tの回転 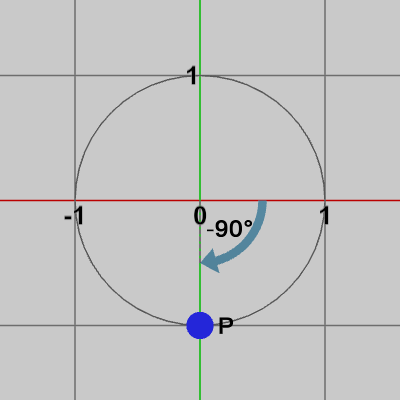
図4 点Pを-90°回転させる(P=(0, -1)に移動する)
2D空間上の点を回転行列によって回転させることは、その点と原点の間の距離を半径とする、原点中心の円周上において、その点を指定の角度分移動させることを意味する。図に示すと以下の図5から図7のようになる。
(計算例)
(1) まず$80$°回転させ、次に$70$°回転させる行列(最終的に$150$°の回転)。
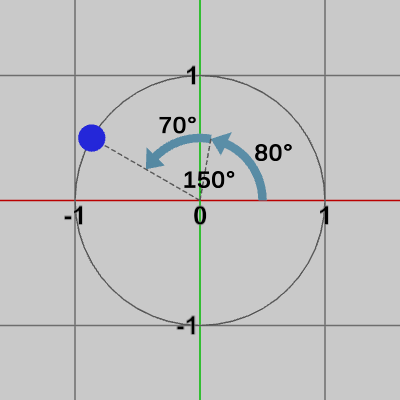
図8 (1)の回転 
図9 (2)の回転
それぞれの回転後の位置を計算すると、

図20 2点 P、Q 2次元の回転行列は加法定理を使うことで簡単に導出することができる。
例えば半径 $1$ の円周上において、$(1, 0)$ から角度 $A$ 離れた位置にある点を $P$ とすれば、$P = (\cos A,\ \sin A)$ であるが、$P$ を角度 $\theta$ 回転させた位置を $Q$ とすれば、その位置は $Q = (\cos(A + \theta),\ \sin(A + \theta))$ となる。
この $P$ から $Q$ への回転を行列を使って行う場合、行列の成分を $a$、$b$、$c$、$d$ とすればこの回転は以下の式で表される。
\[\begin{pmatrix}a &b \\c &d \\\end{pmatrix} \begin{pmatrix}\cos A \\\sin A\end{pmatrix} =\begin{pmatrix}\cos(A + \theta) \\\sin(A + \theta)\end{pmatrix} \]実際に左辺を計算し、右辺を加法定理を用いて展開すると、\[\begin{pmatrix}a\cos A + b \sin A \\c\cos A + d \sin A\\\end{pmatrix} =\begin{pmatrix}\cos A\cos \theta - \sin A\sin \theta \\\sin A\cos \theta + \cos A\sin \theta\end{pmatrix} \]右辺を左辺に移項し適当に整理すれば、\[\begin{pmatrix}(a - \cos \theta)\cos A + (b + \sin\theta) \sin A \\(c - \sin \theta)\cos A + (d - \cos\theta) \sin A\end{pmatrix} =\begin{pmatrix}0 \\0\end{pmatrix} \]この等式は角度 $A$ がどのような値であっても(言い換えれば $\cos A$、$\sin A$ がどのような値であっても)成り立つから、$a = \cos\theta$、$b = -\sin\theta$、$c = \sin\theta$、$d = \cos\theta$、
すなわち\[\begin{pmatrix}a &b \\c &d \\\end{pmatrix} =\begin{pmatrix}\cos\theta &-\sin\theta \\\sin\theta & \cos\theta \end{pmatrix}\]である。

図21 単位ベクトル $\boldsymbol{\mathsf{v_1}} = (a_1, b_1)$、$\boldsymbol{\mathsf{v_2}} = (a_2, b_2)$ 1-1節で見たようにベクトル $\boldsymbol{\mathsf{v_1}} = (a_1, b_1)$ と $\boldsymbol{\mathsf{v_2}} = (a_2, b_2)$ の内積は\[\boldsymbol{\mathsf{v_1}} \cdot \boldsymbol{\mathsf{v_2}} = a_1a_2 + b_1b_2\]として定義される。また $\boldsymbol{\mathsf{v}_1}$ と $\boldsymbol{\mathsf{v}_2}$ のなす角を $\theta$ とするとき、内積は $\cos\theta$ を用いて\[\boldsymbol{\mathsf{v_1}} \cdot \boldsymbol{\mathsf{v_2}} = |\boldsymbol{\mathsf{v}_1}||\boldsymbol{\mathsf{v}_2}|\cos\theta\]とも表される。$\boldsymbol{\mathsf{v}_1}$、$\boldsymbol{\mathsf{v}_2}$ がいずれも単位ベクトルであるとき、$\boldsymbol{\mathsf{v_1}} \cdot \boldsymbol{\mathsf{v_2}} = |\boldsymbol{\mathsf{v}_1}||\boldsymbol{\mathsf{v}_2}|\cos\theta\ = \cos\theta$ であるから、この場合には以下の等式が成り立つ。
\[a_1a_2 + b_1b_2 = \cos\theta\]ここでは回転行列を応用して、$\boldsymbol{\mathsf{v_1}} = (a_1, b_1)$、$\boldsymbol{\mathsf{v_2}} = (a_2, b_2)$ が単位ベクトルであるとき、その内積 $a_1a_2 + b_1b_2$ が実際に $\cos\theta$ に等しくなることを確かめよう。
$(a_1, b_1)$ と $(a_2, b_2)$ のなす角が $\theta$ であるから、$(a_1, b_1)$ を $\theta$ 回転させると $(a_2, b_2)$ に一致する。回転行列を使って表せば\[\begin{pmatrix}\cos\theta &-\sin\theta \\\sin\theta & \cos\theta \end{pmatrix}\begin{pmatrix}a_1 \\b_1 \end{pmatrix}=\begin{pmatrix}a_2 \\b_2 \end{pmatrix}\]である。左辺を計算すると\[\begin{pmatrix}a_1\cos\theta - b_1 \sin\theta \\a_1\sin\theta + b_1 \cos\theta \end{pmatrix}=\begin{pmatrix}a_2 \\b_2 \end{pmatrix}\]であるが、これは $\sin\theta$、$\cos\theta$ を未知数とする以下の形の連立方程式と同じである。\begin{equation}\left\{ \, \begin{aligned} & a_1\cos\theta - b_1 \sin\theta = a_2 \\\\ & a_1\sin\theta + b_1 \cos\theta = b_2 \end{aligned}\right.\end{equation}第1の式に $a_1$ を掛け、第2の式に $b_1$ を掛けると\begin{equation}\left\{ \, \begin{aligned} & {a_1}^2\cos\theta - a_1 b_1\sin\theta = a_1 a_2 \\\\ & a_1 b_1\sin\theta + {b_1}^2\cos\theta = b_1 b_2 \end{aligned}\right.\end{equation}2つの式を足し合わせると、\[{a_1}^2\cos\theta + {b_1}^2\cos\theta = a_1 a_2 + b_1 b_2\]となるが、${a_1}^2 + {b_1}^2 = 1$ であるから、結局\[a_1a_2 + b_1b_2 = \cos\theta\]であることが示される (同様にして $\sin\theta$ も簡単に求められるが、その値は $a_1 b_2 - b_1 a_2$ である。この値はベクトルの外積と呼ばれるものと密接な関わりがある。詳しくは3-6節参照)。
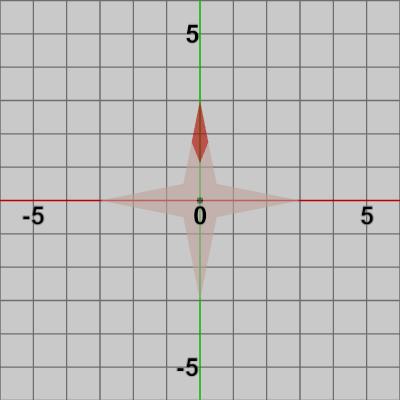
図10 Octagon (Orientation1 : 何も回転を実行していない状態) 図10のオブジェクトOctagonは(凹)八角形のオブジェクトで、その中心が原点に置かれている。ここでは、このオブジェクトに対し幾つかの回転行列を実行する。
しかしその前に平行移動行列の場合と同様に一つ重要な変更をしておかなければならない。
上で見たように、2D空間の回転は$2\times2$行列で表せる。しかし平行移動行列との積(1-8節で扱う)を可能にするために次元を1次元拡張する必要がある。すなわち回転行列を$2\times2$行列ではなく$3\times3$行列で表すのである。具体的には、原点を中心に角度$θ$だけ回転させる行列は次のように表される。\begin{pmatrix}\cos\theta &-\sin\theta &0 \\\sin\theta & \cos\theta &0 \\0 &0 &1\end{pmatrix}また、前節の平行移動行列の場合にもそうであったが2D空間上の点を2次元ベクトルではなく3次元ベクトルの形の同次座標で表す。すなわち2D空間上の点$(x, y)$は、次のように表される。\begin{pmatrix}x \\y \\1\end{pmatrix}上記のようにベクトルや行列を1次元拡張しても、2D空間上の点を回転行列で回転させる結果については本質的な違いはないことを以下に示そう。
2D空間の点$(x, y)$を原点周りに角度$θ$回転させる (回転後の座標を$(x', y')$とする)
オブジェクトに対して実行する回転行列は、カスタムライブラリの以下のメソッドを用いて取得できる。
例えば、原点周りに$60$°の回転を行う行列を取得し、その回転行列をオブジェクトに実行するためには、プログラムに以下のように記述する。
次の3つの行列は左から$30$°の回転、$120$°の回転、$270$°の回転を表す行列である。
1行目の GetRotation3x3(..) の引数を30、120、270としたときの結果が図11、図12、図13である。
点の回転のところでも述べたが、2D空間における回転は原点を中心とする回転になる。これらの図からもそのことは確認できる。
図10から図13の下部にOrientation1からOrientation4の表示があるが、それぞれについて説明すると以下のようになる。
Orientation1 : Octagonを$0$°回転させた状態(全く回転をしていない状態)。
Orientation2 : Octagonを$30$°回転させた状態。
Orientation3 : Octagonを$120$°回転させた状態。
Orientation4 : Octagonを$270$°回転させた状態。
オブジェクトがどこにあるかを表すのがPositionであり、オブジェクトがどの方向を向いているかを表すのがOrientationである (2Dオブジェクトの場合は「オブジェクトの向き」と「オブジェクトのOrientation」は同じ意味として使えるが、3Dオブジェクトの場合は厳密には両者は異なる。詳しくは第6章で解説する)。
前節では平行移動行列によってオブジェクトのPositionを設定したが、本節では回転行列によってオブジェクトのOrientationを設定しているのである。
(UnityのC#スクリプトの標準機能で、オブジェクトのPositionやOrientationを設定する場合はTransformクラスを経由して行うが、Transformクラスには「Orientation」という単語が含まれる変数やメソッドは存在しない。オブジェクトのOrientationを設定する際には、TransformクラスのlocalRotationやrotationといったQuaternion型のプロパティを介して設定することになる。オブジェクトのOrientationを設定する際に、Rotationという単語を含む変数やメソッドを使うのはUnityに限ったことではない。)
もしOctagonが何の変換も受けていない初期の状態が図10ではなく図14のような位置であるとしよう。この初期状態のOctagonに上記の$30$°、$120$°、$270$°の回転行列を実行すると以下の結果になる。
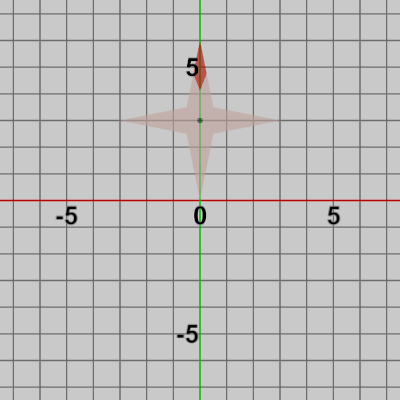
図14 初期状態 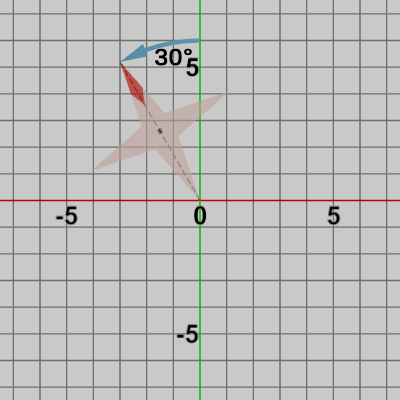
図15 30°回転
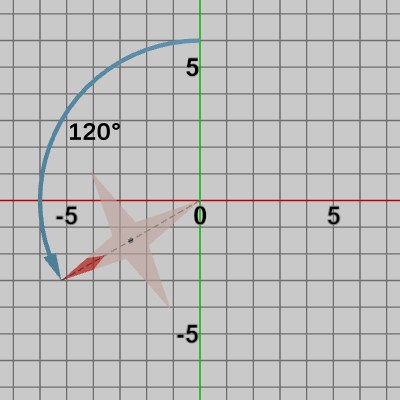
図16 120°回転 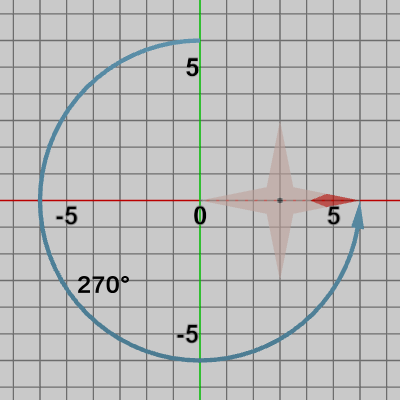
図17 270°回転
実行するプログラムは同じであるが、Octagonの初期状態が異なるのでこのような結果になるのである。2D空間における回転が原点を中心とする回転になることがこの例からも確認できるであろう。
では最後に、本節で述べた内容に関するプログラムを作成する。
(1) まず $80$°の回転、次に $70$°の回転を実行 (第1の回転行列を $R_1$、第2の回転行列を $R_2$とする)。
(2) まず $160$°の回転、次に $120$°の回転、最後に $-60$°の回転を実行 (第1の回転行列を $R_1$、第2の回転行列を $R_2$、第3の回転行列を $R_3$とする)。
いずれの回転も初期位置は $(1,\ 0)$ とする。
上で計算したように、それぞれの移動後の位置は以下のとおり (ただし、本節の中程における計算では $2\times2$行列と2次元ベクトルとの積であったが、ここでは同次座標で計算するために $3\times3$行列と3次元ベクトルとの積で表されていることに注意)。
[Code1] (実行結果 図18)
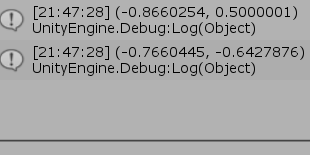
図18 Code1 実行結果 2行目から5行目が(1)の計算である。4行目の $3\times3$行列Mは、2つの平行移動行列 R1、R2を1つにまとめたものであり、Mの実行結果は R1、R2をこの順序で実行したものと同じである。5行目の Vector3(1, 0, 1) は回転の初期位置 $(1,\ 0)$ を同次座標で表したものである。$3\times3$行列Mと Vector3型インスタンスの積は Vector3型として返されるが、5行目では計算結果を Vector2型の変数P1に代入している。Unityでは、このように Vector3型インスタンスを Vector2型の変数に代入すると、自動的に z成分が切り取られて x成分と y成分のみがコピーされるのである。
9行目以降は(2)の計算であるが、これも(1)と手続きは同様である。
実行結果(図18)の出力値を小数第3位で四捨五入すれば、上に示される計算結果と一致する。
オブジェクトOctagon(図10)に対して回転行列を実行する。
[Code2] (実行結果 図19)
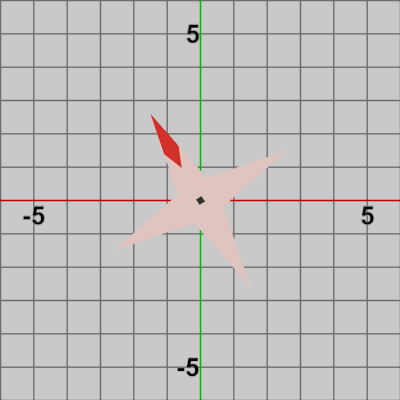
図19 Code2 実行結果 ここでの回転角度は$30$°であるが、この場合には Octagonは最初の向きから$30$°回転した状態になる (図19)。
A) 点の回転
今、点 $P$ が $(1, 0)$ の位置に置かれている。この点を原点を中心に $90^\circ$ 回転させることを考える。

2D空間で原点を中心に角度 $\theta$ だけ回転させる回転行列(Rotation Matrix)は次のように表される。\begin{pmatrix}\cos\theta &-\sin\theta \\\sin\theta & \cos\theta \end{pmatrix}
例えば、2D空間の点 $(x, y)$ を原点周りに角度 $\theta$ 回転させる場合の計算は次のように行われる。回転後の座標を $(x', y')$ とすれば、\begin{align*}\begin{pmatrix}\cos\theta &-\sin\theta \\\sin\theta & \cos\theta \end{pmatrix}\begin{pmatrix}x \\y \end{pmatrix}= \begin{pmatrix}x\cos\theta - y\sin\theta \\x\sin\theta + y\cos\theta \end{pmatrix}=\begin{pmatrix}x' \\y' \end{pmatrix}\end{align*}
計算例として上記のケースをここで適用してみる。$P=(1, 0)$ を $90^\circ$ 回転させるには、$(x, y) = (1, 0)$、$\theta = 90^\circ$ とおいて
\begin{align*}\begin{pmatrix}\cos{90^{\circ}} &-\sin{90^{\circ}} \\\sin{90^{\circ}} & \cos{90^{\circ}} \end{pmatrix}\begin{pmatrix}1 \\0 \end{pmatrix}&=\begin{pmatrix}0 &-1 \\1 &0 \end{pmatrix}\begin{pmatrix}1 \\0 \end{pmatrix} \\&=\begin{pmatrix}0\cdot1 + (-1)\cdot0 \\1\cdot1 + 0\cdot0 \end{pmatrix}=\begin{pmatrix}0 \\1 \end{pmatrix}\end{align*}
回転後の座標である $(0, 1)$ が求められる。Unityにおける2D空間(XY平面)の回転は、プラス方向の回転が反時計回りであり、マイナス方向の回転が時計回りである。
例えば、$T > 0$ とし、角度 $+T$ 方向の回転と角度 $-T$ 方向の回転を示すと図3のようになる。また上記の点 $P = (1, 0)$ を $-90^\circ$ 回転させた場合を図4に示す。


2D空間上の点を回転行列によって回転させることは、その点と原点の間の距離を半径とする、原点中心の円周上において、その点を指定の角度分移動させることを意味する。図に示すと以下の図5から図7のようになる。
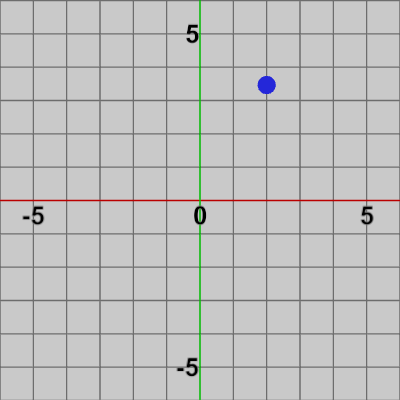 図5 2D空間上のある点
図5 2D空間上のある点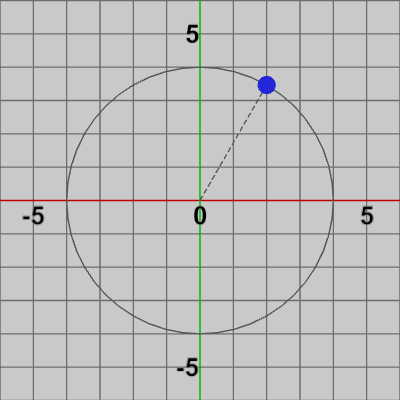 図6 2D空間上の点と原点の間の距離を半径とする円
図6 2D空間上の点と原点の間の距離を半径とする円 図7 点の回転(円周上において指定の角度だけ回転する)
図7 点の回転(円周上において指定の角度だけ回転する)
B) 回転行列の積
角度 $A$ 回転させる行列と角度 $B$ 回転させる行列の積は、角度 $A+B$ 回転させる行列になる。以下にそれを示す。\begin{align*}\begin{pmatrix}\cos{B} &-\sin{B} \\\sin{B} & \cos{B} \end{pmatrix}\begin{pmatrix}\cos{A} &-\sin{A} \\\sin{A} & \cos{A} \end{pmatrix}&= \begin{pmatrix}\cos{B}\cdot\cos{A} - \sin{B}\cdot\sin{A} &-\cos{B}\cdot\sin{A} - \sin{B}\cdot\cos{A} \\\sin{B}\cdot\cos{A} + \cos{B}\cdot\sin{A} &-\sin{B}\cdot\sin{A} + \cos{B}\cdot\cos{A}\end{pmatrix} \\&=\begin{pmatrix}\cos{A}\cdot\cos{B} - \sin{A}\cdot\sin{B} &-(\sin{A}\cdot\cos{B} + \cos{A}\cdot\sin{B}) \\\sin{A}\cdot\cos{B} + \cos{A}\cdot\sin{B} &\cos{A}\cdot\cos{B} - \sin{A}\cdot\sin{B} \end{pmatrix} \\&=\begin{pmatrix}\cos{(A+B)} &-\sin{(A+B)} \\\sin{(A+B)} & \cos{(A+B)} \end{pmatrix}\end{align*}
1-5節で述べたように変換行列の積の実行順序は右から左である。上記の場合は、まず角度 $A$ 回転させてから角度 $B$ 回転させるという順序で変換が行われる。(計算例)
(1) まず$80$°回転させ、次に$70$°回転させる行列(最終的に$150$°の回転)。
\begin{align*}\begin{pmatrix}\cos{70^{\circ}} &-\sin{70^{\circ}} \\\sin{70^{\circ}} & \cos{70^{\circ}} \end{pmatrix}\begin{pmatrix}\cos{80^{\circ}} &-\sin{80^{\circ}} \\\sin{80^{\circ}} & \cos{80^{\circ}} \end{pmatrix}&=\begin{pmatrix}\cos{(70^{\circ}+80^{\circ})} &-\sin{(70^{\circ}+80^{\circ})} \\\sin{(70^{\circ}+80^{\circ})} & \cos{(70^{\circ}+80^{\circ})} \end{pmatrix}\\&=\begin{pmatrix}\cos{150^{\circ}} &-\sin{150^{\circ}} \\\sin{150^{\circ}} & \cos{150^{\circ}} \end{pmatrix}\end{align*}
(2) まず$160$°回転させ、次に$120$°回転させ、さらに$-60$°回転させる行列(最終的に$220$°の回転)。\begin{align*}&\begin{pmatrix}\cos{(-60^{\circ})} &-\sin{(-60^{\circ})} \\\sin{(-60^{\circ})} & \cos{(-60^{\circ})} \end{pmatrix}\begin{pmatrix}\cos{120^{\circ}} &-\sin{120^{\circ}} \\\sin{120^{\circ}} & \cos{120^{\circ}} \end{pmatrix}\begin{pmatrix}\cos{160^{\circ}} &-\sin{160^{\circ}} \\\sin{160^{\circ}} & \cos{160^{\circ}} \end{pmatrix} \\=&\begin{pmatrix}\cos{(-60^{\circ}+120^{\circ}+160^{\circ})} &-\sin{(-60^{\circ}+120^{\circ}+160^{\circ})} \\\sin{(-60^{\circ}+120^{\circ}+160^{\circ})} & \cos{(-60^{\circ}+120^{\circ}+160^{\circ})} \end{pmatrix} \\=&\begin{pmatrix}\cos{220^{\circ}} &-\sin{220^{\circ}} \\\sin{220^{\circ}} & \cos{220^{\circ}} \end{pmatrix}\end{align*}
(1)、(2)の回転行列を初期位置が$(1, 0)$の点に実行した結果を図8, 図9に示す。

それぞれの回転後の位置を計算すると、
\begin{align*}\begin{pmatrix}\cos{150^{\circ}} &-\sin{150^{\circ}} \\\sin{150^{\circ}} & \cos{150^{\circ}} \end{pmatrix}\begin{pmatrix}1 \\ 0\end{pmatrix}=\begin{pmatrix}\cos{150^{\circ}}\cdot1 + (-\sin{150^{\circ}})\cdot0 \\\sin{150^{\circ}}\cdot1 + \cos{150^{\circ}}\cdot0 \\\end{pmatrix}=\begin{pmatrix}\cos{150^{\circ}} \\\sin{150^{\circ}}\end{pmatrix} \\\\\begin{pmatrix}\cos{220^{\circ}} &-\sin{220^{\circ}} \\\sin{220^{\circ}} & \cos{220^{\circ}} \end{pmatrix}\begin{pmatrix}1 \\ 0\end{pmatrix}=\begin{pmatrix}\cos{220^{\circ}}\cdot1 + (-\sin{220^{\circ}})\cdot0 \\\sin{220^{\circ}}\cdot1 + \cos{220^{\circ}}\cdot0 \\\end{pmatrix}=\begin{pmatrix}\cos{220^{\circ}} \\\sin{220^{\circ}}\end{pmatrix} \end{align*}
となる(初期位置が原点から$1$の距離にあったため半径$1$の円周上の回転になっている)。C) 回転行列の導出

例えば半径 $1$ の円周上において、$(1, 0)$ から角度 $A$ 離れた位置にある点を $P$ とすれば、$P = (\cos A,\ \sin A)$ であるが、$P$ を角度 $\theta$ 回転させた位置を $Q$ とすれば、その位置は $Q = (\cos(A + \theta),\ \sin(A + \theta))$ となる。
この $P$ から $Q$ への回転を行列を使って行う場合、行列の成分を $a$、$b$、$c$、$d$ とすればこの回転は以下の式で表される。
\[\begin{pmatrix}a &b \\c &d \\\end{pmatrix} \begin{pmatrix}\cos A \\\sin A\end{pmatrix} =\begin{pmatrix}\cos(A + \theta) \\\sin(A + \theta)\end{pmatrix} \]実際に左辺を計算し、右辺を加法定理を用いて展開すると、\[\begin{pmatrix}a\cos A + b \sin A \\c\cos A + d \sin A\\\end{pmatrix} =\begin{pmatrix}\cos A\cos \theta - \sin A\sin \theta \\\sin A\cos \theta + \cos A\sin \theta\end{pmatrix} \]右辺を左辺に移項し適当に整理すれば、\[\begin{pmatrix}(a - \cos \theta)\cos A + (b + \sin\theta) \sin A \\(c - \sin \theta)\cos A + (d - \cos\theta) \sin A\end{pmatrix} =\begin{pmatrix}0 \\0\end{pmatrix} \]この等式は角度 $A$ がどのような値であっても(言い換えれば $\cos A$、$\sin A$ がどのような値であっても)成り立つから、$a = \cos\theta$、$b = -\sin\theta$、$c = \sin\theta$、$d = \cos\theta$、
すなわち\[\begin{pmatrix}a &b \\c &d \\\end{pmatrix} =\begin{pmatrix}\cos\theta &-\sin\theta \\\sin\theta & \cos\theta \end{pmatrix}\]である。
D) 応用例

\[a_1a_2 + b_1b_2 = \cos\theta\]ここでは回転行列を応用して、$\boldsymbol{\mathsf{v_1}} = (a_1, b_1)$、$\boldsymbol{\mathsf{v_2}} = (a_2, b_2)$ が単位ベクトルであるとき、その内積 $a_1a_2 + b_1b_2$ が実際に $\cos\theta$ に等しくなることを確かめよう。
$(a_1, b_1)$ と $(a_2, b_2)$ のなす角が $\theta$ であるから、$(a_1, b_1)$ を $\theta$ 回転させると $(a_2, b_2)$ に一致する。回転行列を使って表せば\[\begin{pmatrix}\cos\theta &-\sin\theta \\\sin\theta & \cos\theta \end{pmatrix}\begin{pmatrix}a_1 \\b_1 \end{pmatrix}=\begin{pmatrix}a_2 \\b_2 \end{pmatrix}\]である。左辺を計算すると\[\begin{pmatrix}a_1\cos\theta - b_1 \sin\theta \\a_1\sin\theta + b_1 \cos\theta \end{pmatrix}=\begin{pmatrix}a_2 \\b_2 \end{pmatrix}\]であるが、これは $\sin\theta$、$\cos\theta$ を未知数とする以下の形の連立方程式と同じである。\begin{equation}\left\{ \, \begin{aligned} & a_1\cos\theta - b_1 \sin\theta = a_2 \\\\ & a_1\sin\theta + b_1 \cos\theta = b_2 \end{aligned}\right.\end{equation}第1の式に $a_1$ を掛け、第2の式に $b_1$ を掛けると\begin{equation}\left\{ \, \begin{aligned} & {a_1}^2\cos\theta - a_1 b_1\sin\theta = a_1 a_2 \\\\ & a_1 b_1\sin\theta + {b_1}^2\cos\theta = b_1 b_2 \end{aligned}\right.\end{equation}2つの式を足し合わせると、\[{a_1}^2\cos\theta + {b_1}^2\cos\theta = a_1 a_2 + b_1 b_2\]となるが、${a_1}^2 + {b_1}^2 = 1$ であるから、結局\[a_1a_2 + b_1b_2 = \cos\theta\]であることが示される (同様にして $\sin\theta$ も簡単に求められるが、その値は $a_1 b_2 - b_1 a_2$ である。この値はベクトルの外積と呼ばれるものと密接な関わりがある。詳しくは3-6節参照)。
E) オブジェクトに回転行列を実行する

しかしその前に平行移動行列の場合と同様に一つ重要な変更をしておかなければならない。
上で見たように、2D空間の回転は$2\times2$行列で表せる。しかし平行移動行列との積(1-8節で扱う)を可能にするために次元を1次元拡張する必要がある。すなわち回転行列を$2\times2$行列ではなく$3\times3$行列で表すのである。具体的には、原点を中心に角度$θ$だけ回転させる行列は次のように表される。\begin{pmatrix}\cos\theta &-\sin\theta &0 \\\sin\theta & \cos\theta &0 \\0 &0 &1\end{pmatrix}また、前節の平行移動行列の場合にもそうであったが2D空間上の点を2次元ベクトルではなく3次元ベクトルの形の同次座標で表す。すなわち2D空間上の点$(x, y)$は、次のように表される。\begin{pmatrix}x \\y \\1\end{pmatrix}上記のようにベクトルや行列を1次元拡張しても、2D空間上の点を回転行列で回転させる結果については本質的な違いはないことを以下に示そう。
2D空間の点$(x, y)$を原点周りに角度$θ$回転させる (回転後の座標を$(x', y')$とする)
\begin{align*}\begin{pmatrix}\cos\theta &-\sin\theta &0 \\\sin\theta & \cos\theta &0 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}x \\y \\1\end{pmatrix}&= \begin{pmatrix}x\cos\theta - y\sin\theta + 0\cdot1 \\x\sin\theta + y\cos\theta + 0\cdot1 \\0\cdot x + 0\cdot y + 1\cdot1\end{pmatrix}\\&= \begin{pmatrix}x\cos\theta - y\sin\theta \\x\sin\theta + y\cos\theta \\1\end{pmatrix}=\begin{pmatrix}x' \\y' \\1\end{pmatrix}\end{align*}
本節の始めの方に同じ計算を2次元ベクトルと$2\times2$行列を用いて行ったが、3次元ベクトルの$z$値を無視すれば結果は同じであることが分かる。オブジェクトに対して実行する回転行列は、カスタムライブラリの以下のメソッドを用いて取得できる。
TH2DMath.GetRotation3x3(float degree)
: 2D空間において原点周りに、degree で指定される角度の回転を実行する回転行列を取得する (TH2DMathクラスのstaticメソッドで、戻り値はTHMatrix3x3型のインスタンス)。例えば、原点周りに$60$°の回転を行う行列を取得し、その回転行列をオブジェクトに実行するためには、プログラムに以下のように記述する。
THMatrix3x3 R = TH2DMath.GetRotation3x3(60); Obj.SetMatrix(R);
次の3つの行列は左から$30$°の回転、$120$°の回転、$270$°の回転を表す行列である。
\begin{align*}\begin{pmatrix}\cos{30^{\circ}} &-\sin{30^{\circ}} &0 \\\sin{30^{\circ}} & \cos{30^{\circ}} &0 \\0 &0 &1\end{pmatrix}\qquad\quad\begin{pmatrix}\cos{120^{\circ}} &-\sin{120^{\circ}} &0 \\\sin{120^{\circ}} & \cos{120^{\circ}} &0 \\0 &0 &1\end{pmatrix}\qquad\quad\begin{pmatrix}\cos{270^{\circ}} &-\sin{270^{\circ}} &0 \\\sin{270^{\circ}} & \cos{270^{\circ}} &0 \\0 &0 &1\end{pmatrix}\end{align*}
この3つの行列をOctagonに実行するプログラムを以下に示す (実行結果は図11~図13)。THMatrix3x3 R = TH2DMath.GetRotation3x3(30); Octagon.SetMatrix(R);
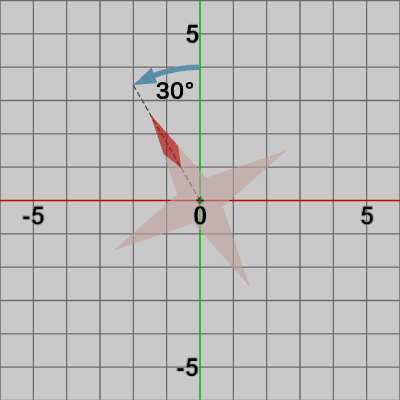 図11 Octagon (Orientation2)
図11 Octagon (Orientation2)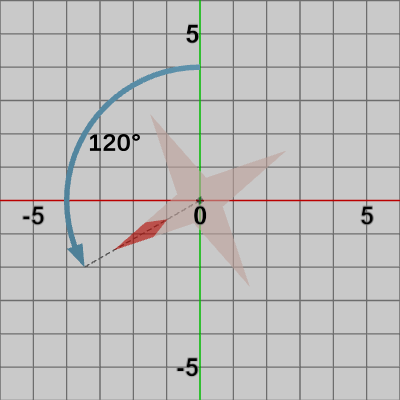 図12 Octagon (Orientation3)
図12 Octagon (Orientation3)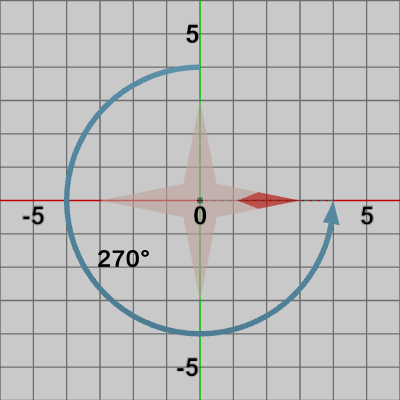 図13 Octagon (Orientation4)
図13 Octagon (Orientation4)
1行目の GetRotation3x3(..) の引数を30、120、270としたときの結果が図11、図12、図13である。
点の回転のところでも述べたが、2D空間における回転は原点を中心とする回転になる。これらの図からもそのことは確認できる。
F) オブジェクトのOrientation
Octagonに対して回転行列を実行した結果、Octagonが回転し、赤色の部分が回転角度の方向を向くようになった。このようにオブジェクトを回転させると、オブジェクトが一定の方向を向いた状態になるが、このオブジェクトの回転状態のことをオブジェクトのOrientation(オリエンテーション)という。図10から図13の下部にOrientation1からOrientation4の表示があるが、それぞれについて説明すると以下のようになる。
Orientation1 : Octagonを$0$°回転させた状態(全く回転をしていない状態)。
Orientation2 : Octagonを$30$°回転させた状態。
Orientation3 : Octagonを$120$°回転させた状態。
Orientation4 : Octagonを$270$°回転させた状態。
オブジェクトがどこにあるかを表すのがPositionであり、オブジェクトがどの方向を向いているかを表すのがOrientationである (2Dオブジェクトの場合は「オブジェクトの向き」と「オブジェクトのOrientation」は同じ意味として使えるが、3Dオブジェクトの場合は厳密には両者は異なる。詳しくは第6章で解説する)。
前節では平行移動行列によってオブジェクトのPositionを設定したが、本節では回転行列によってオブジェクトのOrientationを設定しているのである。
(UnityのC#スクリプトの標準機能で、オブジェクトのPositionやOrientationを設定する場合はTransformクラスを経由して行うが、Transformクラスには「Orientation」という単語が含まれる変数やメソッドは存在しない。オブジェクトのOrientationを設定する際には、TransformクラスのlocalRotationやrotationといったQuaternion型のプロパティを介して設定することになる。オブジェクトのOrientationを設定する際に、Rotationという単語を含む変数やメソッドを使うのはUnityに限ったことではない。)
G) 補足
最後に回転に関して補足的な例を挙げる。もしOctagonが何の変換も受けていない初期の状態が図10ではなく図14のような位置であるとしよう。この初期状態のOctagonに上記の$30$°、$120$°、$270$°の回転行列を実行すると以下の結果になる。




実行するプログラムは同じであるが、Octagonの初期状態が異なるのでこのような結果になるのである。2D空間における回転が原点を中心とする回転になることがこの例からも確認できるであろう。
では最後に、本節で述べた内容に関するプログラムを作成する。
# Code1
本節の中程で見た 計算例 をここではプログラムで実装する。(1) まず $80$°の回転、次に $70$°の回転を実行 (第1の回転行列を $R_1$、第2の回転行列を $R_2$とする)。
(2) まず $160$°の回転、次に $120$°の回転、最後に $-60$°の回転を実行 (第1の回転行列を $R_1$、第2の回転行列を $R_2$、第3の回転行列を $R_3$とする)。
いずれの回転も初期位置は $(1,\ 0)$ とする。
上で計算したように、それぞれの移動後の位置は以下のとおり (ただし、本節の中程における計算では $2\times2$行列と2次元ベクトルとの積であったが、ここでは同次座標で計算するために $3\times3$行列と3次元ベクトルとの積で表されていることに注意)。
\begin{align*}&(1)\qquad R_2R_1\begin{pmatrix}1 \\0 \\1\end{pmatrix}= \begin{pmatrix}\cos{150^{\circ}} &-\sin{150^{\circ}} &0\\\sin{150^{\circ}} & \cos{150^{\circ}} &0\\0 &0 &1\end{pmatrix}\begin{pmatrix}1 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}\cos{150^{\circ}} \\\sin{150^{\circ}} \\1\end{pmatrix} \risingdotseq\begin{pmatrix}-0.87 \\0.50 \\1\end{pmatrix} \\\\&(2)\qquad R_3R_2R_1 \begin{pmatrix}1 \\0 \\1\end{pmatrix}= \begin{pmatrix}\cos{220^{\circ}} &-\sin{220^{\circ}} &0\\\sin{220^{\circ}} & \cos{220^{\circ}} &0\\0 &0 &1\end{pmatrix}\begin{pmatrix}1 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}\cos{220^{\circ}} \\\sin{220^{\circ}} \\1\end{pmatrix} \risingdotseq\begin{pmatrix}-0.77 \\-0.64 \\1\end{pmatrix} \end{align*}
[Code1] (実行結果 図18)
// (1) 80°, 70°の順で回転
THMatrix3x3 R1 = TH2DMath.GetRotation3x3(80);
THMatrix3x3 R2 = TH2DMath.GetRotation3x3(70);
THMatrix3x3 M = R2 * R1;
Vector2 P1 = M * new Vector3(1, 0, 1);
Debug.Log("(" + P1.x + ", " + P1.y + ")");
// (2) 160°, 120°, -60°の順で回転
R1 = TH2DMath.GetRotation3x3(160);
R2 = TH2DMath.GetRotation3x3(120);
THMatrix3x3 R3 = TH2DMath.GetRotation3x3(-60);
M = R3 * R2 * R1;
Vector2 P2 = M * new Vector3(1, 0, 1);
Debug.Log("(" + P2.x + ", " + P2.y + ")");

9行目以降は(2)の計算であるが、これも(1)と手続きは同様である。
実行結果(図18)の出力値を小数第3位で四捨五入すれば、上に示される計算結果と一致する。
# Code2
オブジェクトに回転行列を実行する場合のプログラムであるが、これは本節中程で示したものと同じである。オブジェクトOctagon(図10)に対して回転行列を実行する。
[Code2] (実行結果 図19)
THMatrix3x3 R = TH2DMath.GetRotation3x3(30); Octagon.SetMatrix(R);

© 2020-2025 Redpoll's 60 (All rights reserved)