Redpoll's 60
Home / 3Dプログラミング入門 / 第1章 $§$1-10
第1章 2D空間の基礎
| $§$1-1 点とベクトル | $§$1-6 行列による回転 |
| $§$1-2 ベクトルによる平行移動 | $§$1-7 行列によるスケール |
| $§$1-3 単位ベクトル | $§$1-8 変換行列の積 |
| $§$1-4 行列 | $§$1-9 フレームとフレームレート |
| $§$1-5 行列による平行移動 | $§$1-10 オブジェクトの基本的な運動 (往復運動と回転) |
$§$1-10 オブジェクトの基本的な運動 (往復運動と回転)
本節では実際にオブジェクトを動かすプログラムを作成する。
平行移動、回転、スケールの3つの運動を扱うが、いずれも単純な構成であり今までの'静止映像'のプログラムとほとんど内容は同じである。
なお、本節のプログラムは全て60FPSで設定されている。
図1 点Pと点P'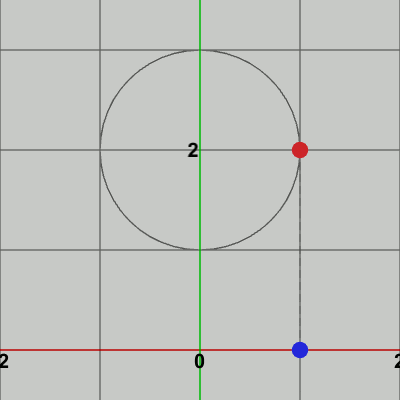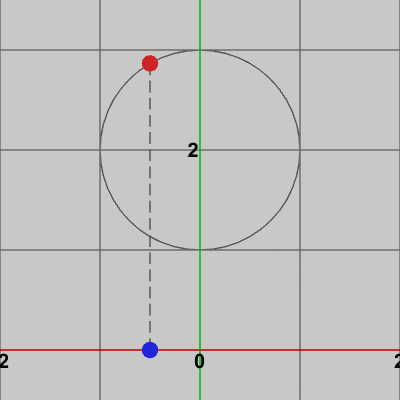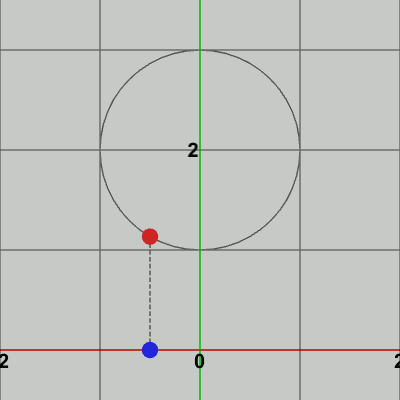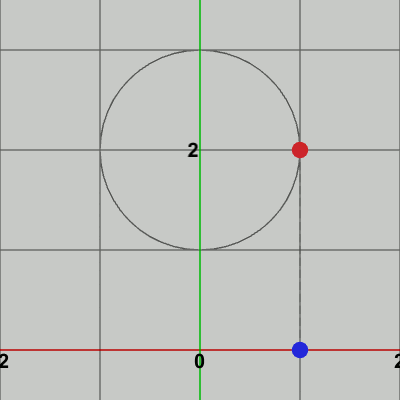 
図2 単振動
図1は半径$1$の円で、その中心がy軸上$(0, 2)$に置かれている。円周上には点$P$があるが、点$P$からx軸上に下ろした垂線とx軸との交点を$P'$とする (1-3節で述べた「射影」という語を用いれば、点$P$からx軸上に射影したときの像が点$P'$)。図2は円周上における点$P$の等速円運動と、点$P'$のx軸上での往復運動の様子である。点$P$が円周上を$1$周する間に($360^\circ$回転する間に)、点$P'$はx軸上の原点を中心とする $x = -1$ から $x = 1$ の範囲を1往復する。
このように等速円運動を行っている点をある直線上に射影すると、射影したときの像はその直線上において往復運動を行うが、この直線上の往復運動のことを単振動(Simple Harmonic Motion)という。
上の例では点$P'$がx軸上の $x = -1$ から $x = 1$ の区間で単振動を行っているのである。
単振動は次の公式で表される。\[ x = A\sin{(\omega t)} \]$A$は振幅と呼ばれ単振動の範囲を表す。この公式の場合は、単振動の範囲が $x = -A$ から $x = A$ の往復運動になる。$\omega$は角速度と呼ばれ単振動の速度(一定時間に何度進むか)を表し、プログラム中では1フレームあたりの角度の増加量の決定に使われる。$t$は時間を表し、文章中では$0$から始まり増加する変数であるとする。
この公式における $x$は、$\sin$関数の引数$\omega t$が$360$°増加する間に、$-A$から $A$の間を1往復するのである。
では実際に、x軸上の単振動を実装していくが、上の単振動の公式はプログラムで使用するには記述がやや'重い'ので、次のように簡略化する。
このコードは以降のプログラムにおいて頻繁に使用される単振動の計算処理である。1行目の i_shmは単振動の公式における$\omega t$に相当し、単振動軌道上($-A$から $A$の間)の何度の位置にいるかを示すfloat型のインスタンス変数である。上でも述べたように、単振動では$\omega t$が$360$°増加する間に $x$が $-A$から $A$の間を1往復する。このコードでは i_shmは毎フレーム $1$ずつ増加するので、$360$増加するまでに360フレームかかるわけである。つまり、このコードの場合 $x$の値は $-A$から $A$の間を1往復するのに360フレームかかることになる (60FPSならば1往復に6秒かかる)。もし、i_shmの毎フレームの増加量を $2$とした場合は、$360$増加するまでに180フレームかかるので、$-A$から $A$の間を1往復するのに180フレームかかることになる (60FPSならば1往復3秒である)。
2行目の Mathf.Sin はUnityに用意されている $\sin$関数である (Mathfは数学用の関数をまとめて扱っている構造体)。引数が i_shm * Mathf.Deg2Rad となっているのは、Mathf.Sinの引数に指定する角度は度数法($90$°、$180$°、$360$°など)ではなく、弧度法($\pi / 2$、$\pi$、$2\pi$ などで単位はラジアン)で表されている必要があるためである。
i_shm * Mathf.Deg2Radは度数法で表されている角度i_shmを弧度法の角度に変換するための記述である (Mathf.Deg2Rad は float型の定数値で、その値は $2\pi / 360$ である)。
図3に示されるオブジェクト Pointが、x軸上の $x = -1$ から $x = 1$ の間で単振動を行うプログラムを以下に示す (Pointの初期の位置は原点である)。
[Code1] (実行結果 図4)
図3 Point (初期の位置は原点) 
図4 Code1 実行結果
毎フレーム2行目で、そのフレームにおける移動位置xを計算して、3行目において その位置に平行移動させる行列Tを取得する。4行目でオブジェクト Pointに Tを実行することにより、Pointが毎フレーム 初期位置である原点から xまで移動することになる。この平行移動の移動先は3行目に示されるように (x, 0) であるが、xの値が毎フレーム異なるので、結果的に Pointによる単振動軌道上の往復運動になるのである。
プログラム2行目の1.0は振幅を表し、単振動の範囲は $x = -1$ から $x = 1$ の間で行われる。1行目の i_shmは単振動軌道上の位置を計算するために使われる角度であり、毎フレーム$1$ずつ増加する。60FPSの設定であるから1秒間で$60$増加する。これは、この単振動が1秒で$60$°分の距離を進むことを意味し、1往復するには($360$°分の距離進むには)6秒かかることを意味する (1往復に何秒かかるかはあくまで理論値である。文章中のアニメーションGIFでの運動は理論値と多少のずれがある)。
i_shmの1フレームあたりの増加量を変えて実行した結果を以下に示す。左から毎フレーム $0.5$ずつ増加させた場合、$2$ずつ増加させた場合、$6$ずつ増加させた場合である (プログラム1行目の右辺の値を 0.5f、2、6 に変更した場合の実行結果)。
i_shmの1フレームあたりの増加量は左から $0.5$, $2$, $6$であるから、1秒(60フレーム)ではそれぞれ $30$, $120$, $360$増加することになる。これは単振動のスピードが1秒間あたり、図4では$30$°分進み、図5では$120$°分進み、図6では$360$°分進むことを意味している。1往復にかかる時間は図4では12秒、図5では3秒、図6では1秒である。
$\cos$関数による単振動の公式を以下に示す。\[ x = A\cos{(\omega t)} \]上記の$\sin$の公式との違いは$\sin$が$\cos$に変わっただけで、各変数$A$, $\omega$, $t$の意味は同じである。 $\sin$による単振動と$\cos$による単振動の違いは開始する位置にある。$\sin$の場合は、単振動を行う範囲の中央からの開始であるのに対し、$cos$の場合は範囲の端からの開始になる。具体的には、\[ x = 2\cos{(\omega t)} \]の場合は、x軸上の$(2, 0)$から単振動が始まり、$(-2, 0)$から$(2, 0)$の間を往復する ($t$は$0$から増加する変数である。以下でも同様)。\[ x = -2\cos{(\omega t)} \]の場合は、x軸上の$(-2, 0)$から単振動が始まり、$(-2, 0)$から$(2, 0)$の間を往復する。\[ x = 2\sin{(\omega t)} \]の場合は、x軸上の原点$(0, 0)$から単振動が始まり、$(-2, 0)$から$(2, 0)$の間を往復する。
開始位置が異なるだけで、いずれの場合でも単振動を行う範囲は同じであり、運動自体も同じである。
$cos$関数による単振動の計算も$sin$の場合と同じように、プログラムでは次のように簡略化した形で使用する (Mathf.Sin が Mathf.Cos に変わっただけである)。
[Code2] (実行結果 図8)
Code1との違いは 1行目の i_shmの1フレームあたりの増加量が2になっていることと、2行目の Sinの部分が Cosに変わったことだけである (使用するオブジェクトが赤い点に変わっているが、プログラムではCode1と同じく「Point」という名前を使用する。Pointの初期の位置は このプログラムでも原点である)。2行目で そのフレームにおける単振動軌道上の移動位置を計算し、3行目で その位置へ移動する平行移動行列を取得し、4行目で その平行移動行列を Pointに実行する。Pointは毎フレーム 初期の位置である原点から計算された位置へ移動を行う。
2行目の 1.0fは この$cos$関数の単振動の振幅であるが、この振幅の値を変えて実行した結果を以下に示す。左から 振幅$1.0$、振幅$2.0$、振幅$4.0$で、全てのケースで i_shmは毎フレーム $2$ずつ増加する (このプログラムも60FPSの設定なので、いずれの場合も1往復にかかる時間は3秒である)。
上の3つのアニメーションから、単振動の振幅が変化しても i_shmの1フレームあたりの増加量が同じならば、1往復あたりにかかる時間は変わらないことが分かるであろう (i_shmの増加量が同じであるとは、上の公式 $x = A\cos{(\omega t)}$ における角速度$\omega$が同じであることを意味する)。 また、$\sin$関数の単振動と比べて運動自体は同じであることも分かるであろう(開始位置の違いは、これらのアニメーションからでは分からないが)。
振幅$A$の大きさを半分の$A/2$にしたときのx軸上の、$x = 0$ から $x = A$ までの範囲を往復する単振動は次のように求められる。\[ x = \frac{1}{2}A\sin{(\omega t)} + \frac{1}{2}A = \frac{1}{2}A(\sin{(\omega t)} + 1) \]この単振動は $x = 0$ と $x = A$ の中間にある $x = A/2$ を開始点とする。
$x = 0$ を開始点とする単振動は、上で見たように$\cos$関数を使えばよい。\[ x = -\frac{1}{2}A\cos{(\omega t)} + \frac{1}{2}A = \frac{1}{2}A(-\cos{(\omega t)} + 1) \]($\cos$の前にあるマイナス符号をとると、$x = A$が開始点になる)。
それぞれプログラム中では次のように簡略化される。
$x = 0$ から $x = A$ までの範囲を往復する$sin$の単振動 (開始点は $x = A/2$)。
$x = 0$ から $x = A$ までの範囲を往復する$cos$の単振動 (開始点は $x = 0$)。
以下のプログラムは$\cos$関数による $x = 0$ から $x = A$ までの範囲の単振動のプログラムである。
[Code3] (実行結果 図11)
図11 A = 5.0f 
図12 A = -5.0f
図11はプログラム2行目の振幅を表す変数Aを5.0fで実行した結果であり、単振動は $0$から $5$の間の往復運動となる。図12は A = -5.0f で実行した結果であり、単振動の往復範囲は $0$から $-5$となる。
単振動の記述がやや長くなったが、単振動はこの先非常に多く使用されるので、ここでしっかりと理解をしてほしい。
なお、プログラムで使用する場合には$sin$の単振動であったり、$cos$の単振動であったりするが深い意味はない。
オブジェクトDiskが何の変換も受けていない状態で図13に示される状態であるとする (Diskの中心は原点に置かれている)。このオブジェクトに対して原点周りの回転を実行するプログラムを以下に示す。
[Code4] (実行結果 図14)
1行目の i_degree は Diskの回転角度を表すfloat型のインスタンス変数で、このプログラムでは毎フレーム $1$ずつ増加する。これは Diskが毎フレーム $1$°ずつ回転することを意味する。したがって、Diskが$360$°回転するには360フレームかかることになる。i_degreeの1フレームあたりの増加量を $3$にすれば、Diskは毎フレーム $3$°ずつ回転することになり、$360$°回転するまでに120フレームかかることになる。
図14が i_degree = 1.0 の場合の実行結果であり、図15が i_degree = 3.0 の場合の実行結果である (60FPSの設定なので1回転にかかる時間は図14では6秒、図15では2秒である。ただし GIFアニメーションでは多少のずれがある)。
連続的な拡大縮小を実装するにあたって、再び単振動を用いる。
オブジェクトを$1$倍から$2$倍の間で拡大縮小させるには、倍率を$1$から$2$の範囲で往復させればよい。Code3において、$0$から$A$までの範囲を往復する単振動は、$\cos$関数を使う場合 次のように表された。\[ x = \frac{1}{2}A(-\cos{(\omega t)} + 1) \]範囲を$0$から$1$までにする場合は、上の$A$を$1$にすればよいから\[ x = \frac{1}{2}(-\cos{(\omega t)} + 1) \]となる。範囲を$1$から$2$までにする場合は、上の式に$1$を加算すればよい。
\[ x = \frac{1}{2}(-\cos{(\omega t)} + 1) + 1 \]では、$0.5$倍から$2.5$倍の間で拡大縮小させる場合を考えてみよう。倍率が$0.5$倍から$2.5$倍の範囲を往復する場合、往復の範囲長は $2.5 - 0.5 = 2$ である。$0$から$2$までの範囲を往復する単振動は上式の$A$を$2$として、\[ x = \frac{1}{2}\cdot2(-\cos{(\omega t)} + 1) \]と表されるから、範囲を$0.5$から$2.5$までにする場合は、上の式に$0.5$を加算すればよい。
\[ x = \frac{1}{2}\cdot2(-\cos{(\omega t)} + 1) + 0.5 \]以上の手続きを一般化すると次のようになる。
$min$から$max$までの範囲を往復する単振動\[ x = \frac{1}{2}(max - min)(-\cos{(\omega t)} + 1) + min \]これは$0$から$A$までの範囲の単振動の式において、$A = max - min$とし、さらに$min$を最後に加算したものに等しい。
以上をもとに、オブジェクトを連続的に拡大縮小するプログラムを以下に示す。
使用するオブジェクトは半径$2$の円形オブジェクトCircle(図16)で、何も変換を受けていない状態ではオブジェクトの中心が原点に置かれている。
[Code5] (実行結果 図17)
図17はプログラム中のmin、maxの値を min = 1.0、max = 2.0 と設定した場合の結果である。倍率$1$倍から$2$倍の範囲の拡大縮小になる。Circleの半径は$2$なので、半径が$2$から$4$の間を往復する。
図18は min = 0.5、max = 2.5 と設定した場合の結果である。倍率が$0.5$倍から$2.5$倍の範囲の拡大縮小になるので、Circleの半径は$1$から$5$の間を往復する。
いずれの場合においても単振動の角度i_shmは毎フレーム$2$ずつ増加する設定である。
平行移動、回転、スケールの3つの運動を扱うが、いずれも単純な構成であり今までの'静止映像'のプログラムとほとんど内容は同じである。
なお、本節のプログラムは全て60FPSで設定されている。
# Code1
第1のプログラムは平行移動による運動である。 図1は半径$1$の円で、その中心がy軸上$(0, 2)$に置かれている。円周上には点$P$があるが、点$P$からx軸上に下ろした垂線とx軸との交点を$P'$とする (1-3節で述べた「射影」という語を用いれば、点$P$からx軸上に射影したときの像が点$P'$)。図2は円周上における点$P$の等速円運動と、点$P'$のx軸上での往復運動の様子である。点$P$が円周上を$1$周する間に($360^\circ$回転する間に)、点$P'$はx軸上の原点を中心とする $x = -1$ から $x = 1$ の範囲を1往復する。
このように等速円運動を行っている点をある直線上に射影すると、射影したときの像はその直線上において往復運動を行うが、この直線上の往復運動のことを単振動(Simple Harmonic Motion)という。
上の例では点$P'$がx軸上の $x = -1$ から $x = 1$ の区間で単振動を行っているのである。
単振動は次の公式で表される。\[ x = A\sin{(\omega t)} \]$A$は振幅と呼ばれ単振動の範囲を表す。この公式の場合は、単振動の範囲が $x = -A$ から $x = A$ の往復運動になる。$\omega$は角速度と呼ばれ単振動の速度(一定時間に何度進むか)を表し、プログラム中では1フレームあたりの角度の増加量の決定に使われる。$t$は時間を表し、文章中では$0$から始まり増加する変数であるとする。
この公式における $x$は、$\sin$関数の引数$\omega t$が$360$°増加する間に、$-A$から $A$の間を1往復するのである。
では実際に、x軸上の単振動を実装していくが、上の単振動の公式はプログラムで使用するには記述がやや'重い'ので、次のように簡略化する。
i_shm += 1; float x = A * Mathf.Sin(i_shm * Mathf.Deg2Rad);
このコードは以降のプログラムにおいて頻繁に使用される単振動の計算処理である。1行目の i_shmは単振動の公式における$\omega t$に相当し、単振動軌道上($-A$から $A$の間)の何度の位置にいるかを示すfloat型のインスタンス変数である。上でも述べたように、単振動では$\omega t$が$360$°増加する間に $x$が $-A$から $A$の間を1往復する。このコードでは i_shmは毎フレーム $1$ずつ増加するので、$360$増加するまでに360フレームかかるわけである。つまり、このコードの場合 $x$の値は $-A$から $A$の間を1往復するのに360フレームかかることになる (60FPSならば1往復に6秒かかる)。もし、i_shmの毎フレームの増加量を $2$とした場合は、$360$増加するまでに180フレームかかるので、$-A$から $A$の間を1往復するのに180フレームかかることになる (60FPSならば1往復3秒である)。
2行目の Mathf.Sin はUnityに用意されている $\sin$関数である (Mathfは数学用の関数をまとめて扱っている構造体)。引数が i_shm * Mathf.Deg2Rad となっているのは、Mathf.Sinの引数に指定する角度は度数法($90$°、$180$°、$360$°など)ではなく、弧度法($\pi / 2$、$\pi$、$2\pi$ などで単位はラジアン)で表されている必要があるためである。
i_shm * Mathf.Deg2Radは度数法で表されている角度i_shmを弧度法の角度に変換するための記述である (Mathf.Deg2Rad は float型の定数値で、その値は $2\pi / 360$ である)。
図3に示されるオブジェクト Pointが、x軸上の $x = -1$ から $x = 1$ の間で単振動を行うプログラムを以下に示す (Pointの初期の位置は原点である)。
[Code1] (実行結果 図4)
i_shm += 1; float x = 1.0f * Mathf.Sin(i_shm * Mathf.Deg2Rad); THMatrix3x3 T = TH2DMath.GetTranslation3x3(x, 0); Point.SetMatrix(T);
毎フレーム2行目で、そのフレームにおける移動位置xを計算して、3行目において その位置に平行移動させる行列Tを取得する。4行目でオブジェクト Pointに Tを実行することにより、Pointが毎フレーム 初期位置である原点から xまで移動することになる。この平行移動の移動先は3行目に示されるように (x, 0) であるが、xの値が毎フレーム異なるので、結果的に Pointによる単振動軌道上の往復運動になるのである。
プログラム2行目の1.0は振幅を表し、単振動の範囲は $x = -1$ から $x = 1$ の間で行われる。1行目の i_shmは単振動軌道上の位置を計算するために使われる角度であり、毎フレーム$1$ずつ増加する。60FPSの設定であるから1秒間で$60$増加する。これは、この単振動が1秒で$60$°分の距離を進むことを意味し、1往復するには($360$°分の距離進むには)6秒かかることを意味する (1往復に何秒かかるかはあくまで理論値である。文章中のアニメーションGIFでの運動は理論値と多少のずれがある)。
i_shmの1フレームあたりの増加量を変えて実行した結果を以下に示す。左から毎フレーム $0.5$ずつ増加させた場合、$2$ずつ増加させた場合、$6$ずつ増加させた場合である (プログラム1行目の右辺の値を 0.5f、2、6 に変更した場合の実行結果)。
-
図5 i_shmを毎フレーム 0.5ずつ増加させた場合 -
図6 i_shmを毎フレーム 2ずつ増加させた場合 -
図7 i_shmを毎フレーム 6ずつ増加させた場合
i_shmの1フレームあたりの増加量は左から $0.5$, $2$, $6$であるから、1秒(60フレーム)ではそれぞれ $30$, $120$, $360$増加することになる。これは単振動のスピードが1秒間あたり、図4では$30$°分進み、図5では$120$°分進み、図6では$360$°分進むことを意味している。1往復にかかる時間は図4では12秒、図5では3秒、図6では1秒である。
# Code2
Code1の単振動では$\sin$関数を使っていたが、ここでは$\cos$関数による単振動を扱う。$\cos$関数による単振動の公式を以下に示す。\[ x = A\cos{(\omega t)} \]上記の$\sin$の公式との違いは$\sin$が$\cos$に変わっただけで、各変数$A$, $\omega$, $t$の意味は同じである。 $\sin$による単振動と$\cos$による単振動の違いは開始する位置にある。$\sin$の場合は、単振動を行う範囲の中央からの開始であるのに対し、$cos$の場合は範囲の端からの開始になる。具体的には、\[ x = 2\cos{(\omega t)} \]の場合は、x軸上の$(2, 0)$から単振動が始まり、$(-2, 0)$から$(2, 0)$の間を往復する ($t$は$0$から増加する変数である。以下でも同様)。\[ x = -2\cos{(\omega t)} \]の場合は、x軸上の$(-2, 0)$から単振動が始まり、$(-2, 0)$から$(2, 0)$の間を往復する。\[ x = 2\sin{(\omega t)} \]の場合は、x軸上の原点$(0, 0)$から単振動が始まり、$(-2, 0)$から$(2, 0)$の間を往復する。
開始位置が異なるだけで、いずれの場合でも単振動を行う範囲は同じであり、運動自体も同じである。
$cos$関数による単振動の計算も$sin$の場合と同じように、プログラムでは次のように簡略化した形で使用する (Mathf.Sin が Mathf.Cos に変わっただけである)。
i_shm += 1; float x = A * Mathf.Cos(i_shm * Mathf.Deg2Rad);
[Code2] (実行結果 図8)
i_shm += 2; float x = 1.0f * Mathf.Cos(i_shm * Mathf.Deg2Rad); THMatrix3x3 T = TH2DMath.GetTranslation3x3(x, 0); Point.SetMatrix(T);
Code1との違いは 1行目の i_shmの1フレームあたりの増加量が2になっていることと、2行目の Sinの部分が Cosに変わったことだけである (使用するオブジェクトが赤い点に変わっているが、プログラムではCode1と同じく「Point」という名前を使用する。Pointの初期の位置は このプログラムでも原点である)。2行目で そのフレームにおける単振動軌道上の移動位置を計算し、3行目で その位置へ移動する平行移動行列を取得し、4行目で その平行移動行列を Pointに実行する。Pointは毎フレーム 初期の位置である原点から計算された位置へ移動を行う。
2行目の 1.0fは この$cos$関数の単振動の振幅であるが、この振幅の値を変えて実行した結果を以下に示す。左から 振幅$1.0$、振幅$2.0$、振幅$4.0$で、全てのケースで i_shmは毎フレーム $2$ずつ増加する (このプログラムも60FPSの設定なので、いずれの場合も1往復にかかる時間は3秒である)。
-
図8 振幅1.0 -
図9 振幅2.0 -
図10 振幅4.0
上の3つのアニメーションから、単振動の振幅が変化しても i_shmの1フレームあたりの増加量が同じならば、1往復あたりにかかる時間は変わらないことが分かるであろう (i_shmの増加量が同じであるとは、上の公式 $x = A\cos{(\omega t)}$ における角速度$\omega$が同じであることを意味する)。 また、$\sin$関数の単振動と比べて運動自体は同じであることも分かるであろう(開始位置の違いは、これらのアニメーションからでは分からないが)。
# Code3
今までの単振動は振幅を$A$とすれば、$-A$から$A$までの範囲の往復運動であった。ここでは振幅$A$が指定された場合に、振幅の大きさを半分にして$0$から$A$までの範囲を往復するプログラムを作成する。振幅$A$の大きさを半分の$A/2$にしたときのx軸上の、$x = 0$ から $x = A$ までの範囲を往復する単振動は次のように求められる。\[ x = \frac{1}{2}A\sin{(\omega t)} + \frac{1}{2}A = \frac{1}{2}A(\sin{(\omega t)} + 1) \]この単振動は $x = 0$ と $x = A$ の中間にある $x = A/2$ を開始点とする。
$x = 0$ を開始点とする単振動は、上で見たように$\cos$関数を使えばよい。\[ x = -\frac{1}{2}A\cos{(\omega t)} + \frac{1}{2}A = \frac{1}{2}A(-\cos{(\omega t)} + 1) \]($\cos$の前にあるマイナス符号をとると、$x = A$が開始点になる)。
それぞれプログラム中では次のように簡略化される。
$x = 0$ から $x = A$ までの範囲を往復する$sin$の単振動 (開始点は $x = A/2$)。
i_shm += 1; float x = 0.5f * A * ( Mathf.Sin(i_shm * Mathf.Deg2Rad) + 1.0f);
$x = 0$ から $x = A$ までの範囲を往復する$cos$の単振動 (開始点は $x = 0$)。
i_shm += 1; float x = 0.5f * A * (-Mathf.Cos(i_shm * Mathf.Deg2Rad) + 1.0f);
以下のプログラムは$\cos$関数による $x = 0$ から $x = A$ までの範囲の単振動のプログラムである。
[Code3] (実行結果 図11)
i_shm += 2; float A = 5.0f; float x = 0.5f * A * (-Mathf.Cos(i_shm * Mathf.Deg2Rad) + 1.0f); THMatrix3x3 T = TH2DMath.GetTranslation3x3(x, 0); Point.SetMatrix(T);
図11はプログラム2行目の振幅を表す変数Aを5.0fで実行した結果であり、単振動は $0$から $5$の間の往復運動となる。図12は A = -5.0f で実行した結果であり、単振動の往復範囲は $0$から $-5$となる。
単振動の記述がやや長くなったが、単振動はこの先非常に多く使用されるので、ここでしっかりと理解をしてほしい。
なお、プログラムで使用する場合には$sin$の単振動であったり、$cos$の単振動であったりするが深い意味はない。
# Code4
次はオブジェクトの回転である。-
図13 Disk (何も変換を受けていない状態。Diskの中心は原点に置かれている) -
図14 Code4 実行結果 (毎フレーム1°ずつ回転) -
図15 Code4 実行結果 (毎フレーム3°ずつ回転)
オブジェクトDiskが何の変換も受けていない状態で図13に示される状態であるとする (Diskの中心は原点に置かれている)。このオブジェクトに対して原点周りの回転を実行するプログラムを以下に示す。
[Code4] (実行結果 図14)
i_degree += 1; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degree); Disk.SetMatrix(R);
1行目の i_degree は Diskの回転角度を表すfloat型のインスタンス変数で、このプログラムでは毎フレーム $1$ずつ増加する。これは Diskが毎フレーム $1$°ずつ回転することを意味する。したがって、Diskが$360$°回転するには360フレームかかることになる。i_degreeの1フレームあたりの増加量を $3$にすれば、Diskは毎フレーム $3$°ずつ回転することになり、$360$°回転するまでに120フレームかかることになる。
図14が i_degree = 1.0 の場合の実行結果であり、図15が i_degree = 3.0 の場合の実行結果である (60FPSの設定なので1回転にかかる時間は図14では6秒、図15では2秒である。ただし GIFアニメーションでは多少のずれがある)。
# Code5
最後はオブジェクトの拡大縮小を連続的に行ってみよう。連続的な拡大縮小を実装するにあたって、再び単振動を用いる。
オブジェクトを$1$倍から$2$倍の間で拡大縮小させるには、倍率を$1$から$2$の範囲で往復させればよい。Code3において、$0$から$A$までの範囲を往復する単振動は、$\cos$関数を使う場合 次のように表された。\[ x = \frac{1}{2}A(-\cos{(\omega t)} + 1) \]範囲を$0$から$1$までにする場合は、上の$A$を$1$にすればよいから\[ x = \frac{1}{2}(-\cos{(\omega t)} + 1) \]となる。範囲を$1$から$2$までにする場合は、上の式に$1$を加算すればよい。
\[ x = \frac{1}{2}(-\cos{(\omega t)} + 1) + 1 \]では、$0.5$倍から$2.5$倍の間で拡大縮小させる場合を考えてみよう。倍率が$0.5$倍から$2.5$倍の範囲を往復する場合、往復の範囲長は $2.5 - 0.5 = 2$ である。$0$から$2$までの範囲を往復する単振動は上式の$A$を$2$として、\[ x = \frac{1}{2}\cdot2(-\cos{(\omega t)} + 1) \]と表されるから、範囲を$0.5$から$2.5$までにする場合は、上の式に$0.5$を加算すればよい。
\[ x = \frac{1}{2}\cdot2(-\cos{(\omega t)} + 1) + 0.5 \]以上の手続きを一般化すると次のようになる。
$min$から$max$までの範囲を往復する単振動\[ x = \frac{1}{2}(max - min)(-\cos{(\omega t)} + 1) + min \]これは$0$から$A$までの範囲の単振動の式において、$A = max - min$とし、さらに$min$を最後に加算したものに等しい。
以上をもとに、オブジェクトを連続的に拡大縮小するプログラムを以下に示す。
使用するオブジェクトは半径$2$の円形オブジェクトCircle(図16)で、何も変換を受けていない状態ではオブジェクトの中心が原点に置かれている。
[Code5] (実行結果 図17)
i_shm += 2; float min = 1.0f; float max = 2.0f; float A = max - min; float scale = 0.5f * A * (-Mathf.Cos(i_shm * Mathf.Deg2Rad) + 1.0f) + min; THMatrix3x3 S = TH2DMath.GetScale3x3(scale); Circle.SetMatrix(S);
-
図16 Circle (何も変換を受けていない状態。Circleの中心は原点に置かれている) -
図17 Code5 実行結果 (倍率1倍から2倍の間の拡大縮小) -
図18 Code5 実行結果 (倍率0.5倍から2.5倍の間の拡大縮小)
図17はプログラム中のmin、maxの値を min = 1.0、max = 2.0 と設定した場合の結果である。倍率$1$倍から$2$倍の範囲の拡大縮小になる。Circleの半径は$2$なので、半径が$2$から$4$の間を往復する。
図18は min = 0.5、max = 2.5 と設定した場合の結果である。倍率が$0.5$倍から$2.5$倍の範囲の拡大縮小になるので、Circleの半径は$1$から$5$の間を往復する。
いずれの場合においても単振動の角度i_shmは毎フレーム$2$ずつ増加する設定である。
© 2020-2024 Redpoll's 60 (All rights reserved)