Redpoll's 60

第1章 2D空間の基礎

$§$1-1 点とベクトル	$§$1-6 行列による回転
$§$1-2 ベクトルによる平行移動	$§$1-7 行列によるスケール
$§$1-3 単位ベクトル	$§$1-8 変換行列の積
$§$1-4 行列	$§$1-9 フレームとフレームレート
$§$1-5 行列による平行移動	$§$1-10 オブジェクトの基本的な運動 (往復運動と回転)

$§$1-3 単位ベクトル

A) 単位ベクトル

ベクトルの大きさを1にすることを正規化(Normalization)という。正規化された大きさ1のベクトルを単位ベクトル(Unit Vector)という。
任意のベクトルを正規化して単位ベクトルにすると、その単位ベクトルの始点が原点にあるものとすれば終点は半径1の円周上のいずれかの点を指している。
図１にベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{\mathsf{v_2}}}$、図2にそれらを正規化した単位ベクトル$\boldsymbol{u_1}$、$\boldsymbol{u_2}$を示す。

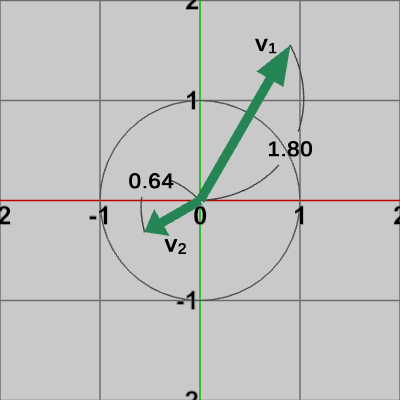
単位ベクトル$\boldsymbol{u_1}$は、ベクトル$\boldsymbol{\mathsf{v_1}}$を$\boldsymbol{\mathsf{v_1}}$の方向に縮めて大きさを$1$にしたものである。
単位ベクトル$\boldsymbol{u_2}$は、ベクトル$\boldsymbol{\mathsf{v_2}}$を$\boldsymbol{\mathsf{v_2}}$の方向に伸ばして大きさを$1$にしたものである。
$\boldsymbol{u_1}$と$\boldsymbol{\mathsf{v_1}}$、そして$\boldsymbol{u_2}$と$\boldsymbol{\mathsf{v_2}}$は大きさは異なるが方向は同じである。

B) 単位ベクトルの算出

単位ベクトルは、ベクトルの各成分をベクトルの大きさで割ることで求められる。

ベクトル$\boldsymbol{\mathsf{v}} = (x, y)$ の正規化 ($\boldsymbol{\mathsf{v}}$の大きさを$|\boldsymbol{\mathsf{v}}|$とする)\[\frac{\boldsymbol{\mathsf{v}}}{|\boldsymbol{\mathsf{v}}|}=\left(\frac{x}{|\boldsymbol{\mathsf{v}}|}, \frac{y}{|\boldsymbol{\mathsf{v}}|}\right) =\left(\frac{x}{\sqrt{x^2 + y^2}}, \frac{y}{\sqrt{x^2 + y^2}}\right) \]実際に大きさが1であることを確認しよう。

\begin{align*}\left|\frac{\boldsymbol{\mathsf{v}}}{|\boldsymbol{\mathsf{v}}|}\right|& =\sqrt{\left(\frac{x}{\sqrt{x^2 + y^2}}\right)^2 + \left(\frac{y}{\sqrt{x^2 + y^2}}\right)^2}= \sqrt{\frac{x^2}{\left(\sqrt{x^2 + y^2}\right)^2} + \frac{y^2}{\left(\sqrt{x^2 + y^2}\right)^2}} \\& = \sqrt{\frac{x^2 + y^2}{\left(\sqrt{x^2 + y^2}\right)^2}} = \sqrt{\frac{x^2 + y^2}{x^2 + y^2}} = 1\end{align*}

(計算例) ベクトル$\boldsymbol{\mathsf{v_1}} = (2, 4)$ の正規化

\begin{align*}|\boldsymbol{\mathsf{v_1}}| &= \sqrt{2^2 + 4^2} = \sqrt{4 + 16} = \sqrt{20} = 2\sqrt{5} \\\\\frac{\boldsymbol{\mathsf{v_1}}}{|\boldsymbol{\mathsf{v_1}}|} &= \left(\frac{2}{|\boldsymbol{\mathsf{v_1}}|}, \frac{4}{|\boldsymbol{\mathsf{v_1}}|}\right) = \left(\frac{2}{2\sqrt{5}},\ \frac{4}{2\sqrt{5}}\right) = \left(\frac{1}{\sqrt{5}},\ \frac{2}{\sqrt{5}}\right) \end{align*}

大きさを計算すると

\begin{align*}\left|\frac{\boldsymbol{\mathsf{v_1}}}{|\boldsymbol{\mathsf{v_1}}|}\right|&= \sqrt{\left(\frac{1}{\sqrt{5}}\right)^2 + \left(\frac{2}{\sqrt{5}}\right)^2}= \sqrt{\frac{1^2}{\left(\sqrt{5}\right)^2} + \frac{2^2}{\left(\sqrt{5}\right)^2}} \\&= \sqrt{\frac{1 + 4}{5}} = 1\end{align*}

確かに大きさは1になっていることが分かる。

C) 単位ベクトルを使った平行移動

コンピューターグラフィックスにおいて方向を扱う場合、単位ベクトルが非常に多く用いられる。平行移動を例に取ってそれを見てみよう。

(例1) XY平面上の点$P$をベクトル$\boldsymbol{\mathsf{v}}$の方向に距離3だけ移動させる問題を考える。
ここでは、$P = (-1, 1)$、$\boldsymbol{\mathsf{v}} = (3, 2)$ とする。

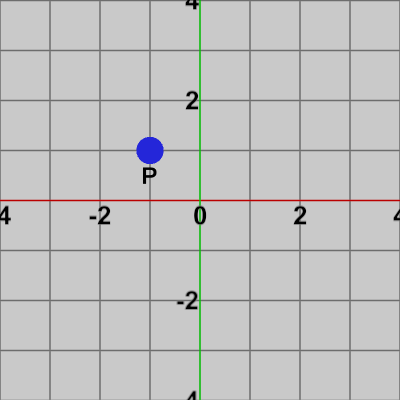図3 点P=(-1, 1)
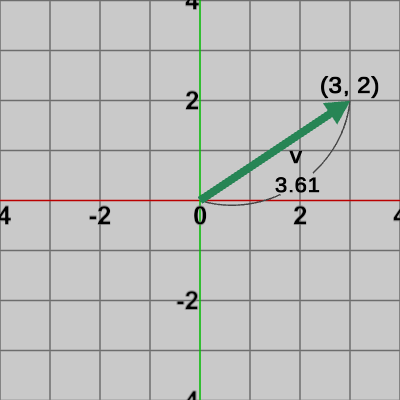図4 ベクトルv=(3, 2)
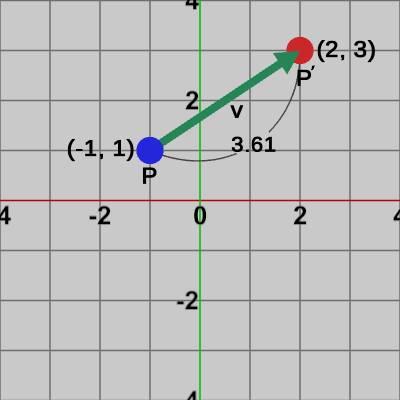図5 点Pをベクトルvによって移動させる

今までのようにベクトル$\boldsymbol{\mathsf{v}}$を単純に加算する場合を見てみよう(図5)。$P$の移動後の点を$P'$とする(図5における赤い点)。\[P + \boldsymbol{\mathsf{v}} = \begin{pmatrix}-1 \\1 \end{pmatrix} +\begin{pmatrix}3 \\2 \end{pmatrix} =\begin{pmatrix}2 \\3 \end{pmatrix} = P'\] $P$と$P'$の距離は1-1節で見たとおり、始点を$P$、終点を$P'$とするベクトル$(P'-P)$の大きさである。ベクトル$(P'-P)$とはもちろんこの場合ベクトル$\boldsymbol{\mathsf{v}}$に一致するので$P$と$P'$の距離は
\begin{align*}P'- P &=\begin{pmatrix}2 \\3 \end{pmatrix} -\begin{pmatrix}-1 \\1 \end{pmatrix} =\begin{pmatrix}3 \\2 \end{pmatrix} = \boldsymbol{\mathsf{v}} \\|P'- P|&= |\boldsymbol{\mathsf{v}}| = \sqrt{3^2 + 2^2} = \sqrt{13} \risingdotseq 3.61 \neq 3\end{align*}ベクトル$\boldsymbol{\mathsf{v}}$をそのまま加算して移動させる場合には、上の計算から分かるように$P$の移動距離は約$3.61$である。今回求めたい移動後の点は、点$P$からの距離が$3$でなければならないから明らかにただ$\boldsymbol{\mathsf{v}}$を加算するだけでは正しい答えは出ない。
そこでベクトル$\boldsymbol{\mathsf{v}}$の単位ベクトルを使ってこの問題を解決してみよう。単位ベクトルを$3$倍したベクトルの大きさは$3$であるから(1-1節参照)、この$3$倍したベクトルを点$P$に加算すれば点$P$はベクトル$\boldsymbol{\mathsf{v}}$の方向に距離$3$だけ移動することになる。

まず、ベクトル$\boldsymbol{\mathsf{v}}$の単位ベクトル$\boldsymbol{u}$をもとめる。\[\boldsymbol{u}=\frac{\boldsymbol{\mathsf{v}}}{|\boldsymbol{\mathsf{v}}|}=\left(\frac{3}{|\boldsymbol{\mathsf{v}}|}, \frac{2}{|\boldsymbol{\mathsf{v}}|}\right) =\left(\frac{3}{\sqrt{13}}, \frac{2}{\sqrt{13}}\right) \]単位ベクトル$\boldsymbol{u}$を$3$倍したベクトルを$3\boldsymbol{u}$とし、それを$P$に加算する。

\begin{align*}P + 3\boldsymbol{u}&=(-1, 1) + 3\left(\frac{3}{\sqrt{13}}, \frac{2}{\sqrt{13}}\right) \\&= (-1, 1) + \left(\frac{9}{\sqrt{13}}, \frac{6}{\sqrt{13}}\right)\risingdotseq(-1, 1) + (2.50,\ 1.66)\\&=(1.50,\ 2.66) = P'\end{align*}

ここで算出された点$P'$が本来求めるべき$P$の移動後の位置である。
以上の手順を図6、図7に示す。

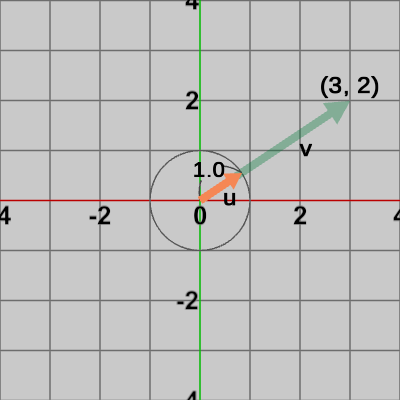
図７は点$P$にベクトル$3\boldsymbol{u}$を加算することにより、ベクトル$\boldsymbol{\mathsf{v}}$の方向に距離$3$だけ移動する様子を示している。

(例2) 図８に示される位置に点$P$、点$Q$が置かれている。線分$PQ$の$Q$側の延長上に$Q$を動かして、2点間の距離を$5$にする問題について考えよう。

手順は次の通り。
(1) $P$を始点、$Q$を終点とするベクトルを$\boldsymbol{\mathsf{v}}$とする。\begin{align*}\boldsymbol{\mathsf{v}} &= Q - P = (1, 3) - (-2, 2) = (3, 1) \\|\boldsymbol{\mathsf{v}}| &= \sqrt{3^2 + 1^2} = \sqrt{10}\end{align*}(2) $\boldsymbol{\mathsf{v}}$の単位ベクトルを$\boldsymbol{u}$とし、$\boldsymbol{u}$を求める。
\[\boldsymbol{u}=\frac{\boldsymbol{\mathsf{v}}}{|\boldsymbol{\mathsf{v}}|}=\left(\frac{3}{|\boldsymbol{\mathsf{v}}|}, \frac{1}{|\boldsymbol{\mathsf{v}}|}\right) =\left(\frac{3}{\sqrt{10}}, \frac{1}{\sqrt{10}}\right) \](3) 単位ベクトル$\boldsymbol{u}$を$5$倍したベクトル$5\boldsymbol{u}$を$P$に加算する(この位置に$Q$を移動させる)。

\begin{align*}P + 5\boldsymbol{u} &=(-2, 2) + 5\left(\frac{3}{\sqrt{10}}, \frac{1}{\sqrt{10}}\right) \\&= (-2, 2) + \left(\frac{15}{\sqrt{10}}, \frac{5}{\sqrt{10}}\right)\risingdotseq(-2, 2) + (4.74,\ 1.58)\\&=(2.74,\ 3.58)\end{align*}

これらの手順を以下の図に示す(図11のベクトル$\boldsymbol{\mathsf{v}}$、単位ベクトル$\boldsymbol{u}$はそれぞれ始点を原点に移したものである)。

図10 PQを結ぶベクトルv
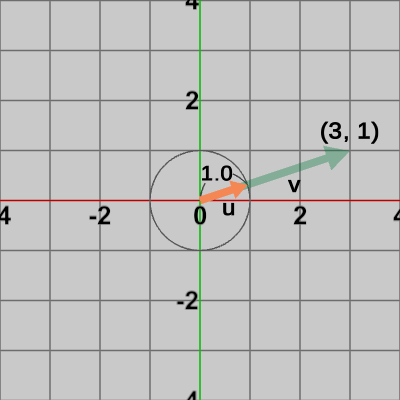図11 vを正規化した単位ベクトルu
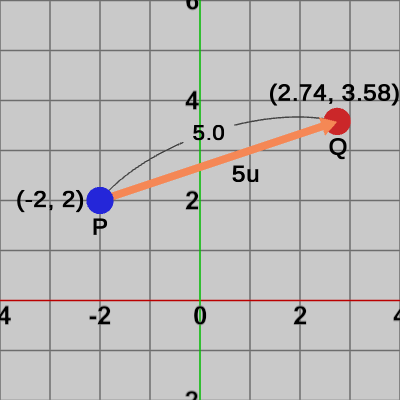図12 PQ間の距離を5にする

D) 単位ベクトルと内積

1-1節で見たように2つのベクトル $\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ の内積 $\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}}$ と、それらのなす角の余弦との間には次の関係式が成り立つのであった ($\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$のなす角を $\theta$ とし、$0^\circ \leq \theta \leq 180^\circ$ であるとする)。
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = |\boldsymbol{\mathsf{v_1}}||\boldsymbol{\mathsf{v_2}}|cos\theta\]もし、2つのベクトルの大きさが $1$ であるとき、すなわち 2つのベクトルが単位ベクトルである場合には、$|\boldsymbol{\mathsf{v_1}}| = 1$、$|\boldsymbol{\mathsf{v_2}}| = 1$ であるから、その内積は\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = |\boldsymbol{\mathsf{v_1}}||\boldsymbol{\mathsf{v_2}}|cos\theta = cos\theta\]となる。
つまり、2つのベクトル $\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ が単位ベクトルで、それらのなす角を $\theta$ とするとき、\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = cos\theta\]である。

以下では $cos\theta$ が簡単に求められる3つの場合を例にとって、単位ベクトルの内積について見ていく。
下の図における2つのベクトル $\boldsymbol{u}$、$\boldsymbol{\mathsf{v}}$ はいずれも大きさ $1$ の単位ベクトルである。

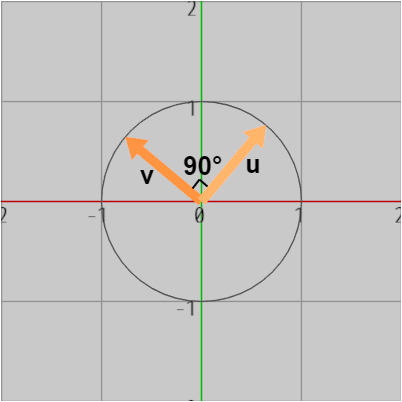図13 なす角が 90°
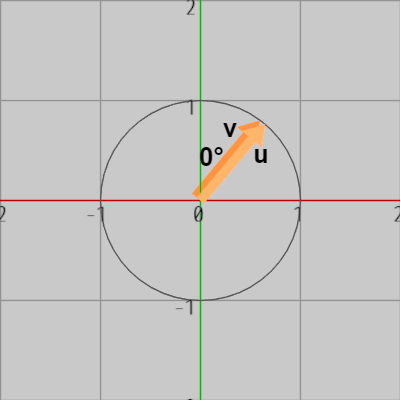図14 なす角が 0°
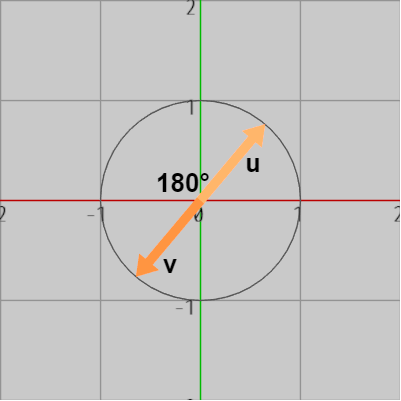図15 なす角が 180°

図13においては、2つのベクトルのなす角は $90^\circ$ である。
$cos90^\circ = 0$ であるから、\[ \boldsymbol{u}\cdot\boldsymbol{\mathsf{v}} = cos90^\circ = 0\]すなわち、2つのベクトルのなす角が $90^\circ$ であるとき、それらの内積は $0$ である。

図14では 2つのベクトルが重なっているが、このときのなす角は $0^\circ$ である。
$cos0^\circ = 1$ であるから、\[ \boldsymbol{u}\cdot\boldsymbol{\mathsf{v}} = cos0^\circ = 1\]すなわち、2つのベクトルのなす角が $0^\circ$ であるとき、それらの内積は $1$ である。

図15においては、2つのベクトルのなす角は $180^\circ$ である。
$cos180^\circ = -1$ であるから、\[ \boldsymbol{u}\cdot\boldsymbol{\mathsf{v}} = cos180^\circ = -1\]すなわち、2つのベクトルのなす角が $180^\circ$ であるとき、それらの内積は $-1$ である。

コンピューターグラフィックスでは2つのベクトルが直交しているか(なす角が $90^\circ$)、あるいは平行であるか(なす角が $0^\circ$ または $180^\circ$)を調べるためにまず内積の計算を行う。今見てきたように、内積が $0$ であれば2つのベクトルは直交しており、$1$ あるいは $-1$ であれば平行であると分かる。

E) 射影

「射影」という言葉は数学ではいくつかの意味で使われるが、この講義の2D空間の解説においては「射影」は主に、ある点からある直線上へ垂線を下すことを意味する (注)。また、長方形などの各頂点をある直線上に射影することを簡単に「長方形を射影する」といったりもする。

(注 : 高校数学などでは、ある点からある直線上へ下した垂線の足のことを射影または正射影と呼ぶが、この講義における射影は射影幾何学の「平行射影」の意味での射影である。具体的には、ある直線や平面に直交する方向への平行射影である)

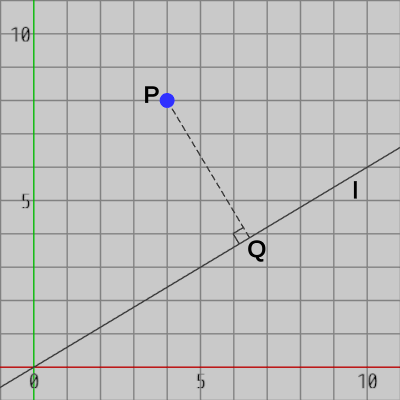
例えば下図16は、点Pを原点を通る直線 $l$ へ射影したときのものである。点Qは点Pを直線 $l$ 上へ射影したときの像である。
図17は長方形の各頂点を直線 $l$ 上へ射影したときのものであるが、4つの点 $Q_0$、$Q_1$、$Q_2$、$Q_3$ は長方形の各頂点 $P_0$、$P_1$、$P_2$、$P_3$ を直線 $l$ 上へ射影したときの像である。

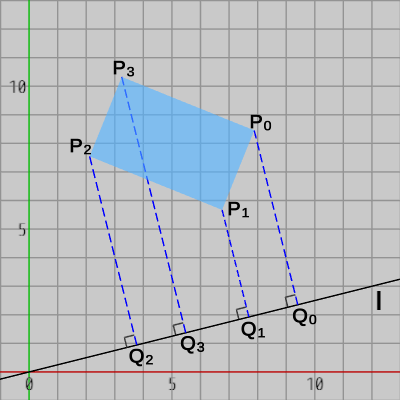
以降「直線への射影」といえば常に、その直線と直交する方向への射影を意味するものとする (直線や平面に直交する方向への射影は、詳しくは正射影という)。

以下では、図16における点Qが直線 $l$ 上で原点からどれだけ離れているかを単位ベクトルと内積を用いて計算する。
原点Oと点Pを結ぶベクトルを $\boldsymbol{\mathsf{v}}$ とし、直線 $l$ の方向を表す単位ベクトルを $\boldsymbol{u}$ とし、さらに 2つのベクトルのなす角を $\theta$ とする (図18)。
このとき、$|OP| = |\boldsymbol{\mathsf{v}}|$ であり、図18に示されるように点P、Q 及び原点Oは直角三角形をなすから、直線 $l$ 上における原点OからQまでの長さ$|OQ|$は以下のように求められる。\begin{align*}|OQ| &= |OP|cos\theta \\\\&= |\boldsymbol{\mathsf{v}}|cos\theta = \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u}\end{align*}
点や図形の直線上への射影については、第2章における図形同士の衝突判定において多用される。しかし、そこで用いられる計算は上記で示した原点とある点を結ぶベクトルとある直線の方向を表す単位ベクトルとの内積に過ぎない。

では最後に、単位ベクトルに関連したプログラムをいくつか作成する。

# Code1

Unityの Vector2、Vector3構造体には、単位ベクトルを取得するために normalized というプロパティが用意されている。最初のプログラムは、いくつかの適当なベクトルの単位ベクトル、及びその大きさを出力するプログラムである。

[Code1] (実行結果図19)

Vector2 v1 = new Vector2(8, 10);
Vector2 u1 = v1.normalized;
//Debug.Log(u1 + " : mag " + u1.magnitude);
Debug.Log("(" + u1.x + ", " + u1.y + ")" + " : mag " + u1.magnitude);

Vector2 v2 = new Vector2(12.536f, -7.033f);
Vector2 u2 = v2.normalized;
Debug.Log("(" + u2.x + ", " + u2.y + ")" + " : mag " + u2.magnitude);

Vector3 v3 = new Vector3(0.52f, -20.12f, 4.605f);
Vector3 u3 = v3.normalized;
Debug.Log("(" + u3.x + ", " + u3.y + ", " + u3.z + ")" + " : mag " + u3.magnitude);

Vector3 u4 = new Vector3(-2.4f, 1.8f, 8.9f).normalized;
Debug.Log("(" + u4.x + ", " + u4.y + ", " + u4.z + ")" + " : mag " + u4.magnitude);

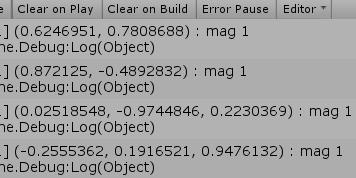
単位ベクトルを取得するためには、Vector2、Vector3型インスタンスの normalizedプロパティにアクセスすればよい。例えば、1行目の Vector2型インスタンス v1の単位ベクトルを取得するためには、2行目のように v1.normalized とすればよい。
なお、このプログラムではベクトルの内容を表示するための Debug.Log(..) の引数に、Vector2、Vector3型のインスタンスを渡さずに、それらのプロパティである x, y, z を直接渡している (つまり、3行目のように u1 を渡すのではなく、4行目のように u1.x、u1.y を渡している)。これは、Debug.Log(..)に対して Vector2、Vector3型のインスタンスを渡すと、出力される数値が四捨五入された小数第1位までの表示となってしまうためである (1-1節 Code1参照)。
また、14行目では new Vector3(..) から直接 normalized にアクセスしているが、こういった記述も可能である。
実行結果(図19)に示されるように、normalizedで取得された各ベクトルの大きさは、いずれも $1$である。

# Code2

次に、上の(例1)をプログラムで実装してみよう。
その内容は、XY平面上の点$P = (-1, 1)$ をベクトル$\boldsymbol{\mathsf{v}} = (3, 2)$ の方向に距離3だけ移動させるというものである (図7参照)。

[Code2] (実行結果図20)

Vector2 P = new Vector2(-1, 1);
Vector2 v = new Vector2(3, 2);
Vector2 u = v.normalized;

Vector2 P1 = P + 3 * u;
Debug.Log("(" + P1.x + ", " + P1.y + ")");
Debug.Log("|3u| : " + (3 * u).magnitude);

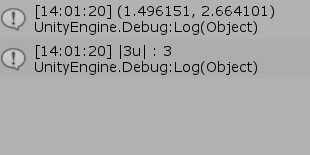
1行目が点P、2行目が移動方向を表すベクトルv、3行目が vを正規化した単位ベクトルu である。
5行目において、P を vの方向に$3$だけ移動させる計算を行い、結果を P1にセットしている。
図20に出力されている結果も、四捨五入して小数第2位までの表示にすれば上記(例1)で求めた結果と一致する。また、7行目に示されるように、単位ベクトルの3倍の大きさは $3$である。

# Code3

上と同様に、本節の(例2)をプログラムで実装する。
(例2)の内容は、点$P = (-2, 2)$、点$Q = (1, 3)$を結ぶ線分$PQ$の$Q$側の延長上に$Q$を動かして、2点間の距離を$5$にするというものである (図12参照)。

[Code3] (実行結果図21)

Vector2 P = new Vector2(-2, 2);
Vector2 Q = new Vector2(1, 3);
Vector2 v = Q - P;
Vector2 u = v.normalized;
// Vector2 u = (Q - P).normalized;

Vector2 Q1 = P + 5 * u;
Debug.Log("(" + Q1.x + ", " + Q1.y + ")");

3行目においてPを始点、Qを終点とするベクトルv を求め、4行目においてそれを正規化して uにセットしている。
7行目では、Pからu方向に$5$だけ離れた位置を計算し、Q1へセットしている。
実行結果(図21)から、四捨五入して小数第2位までの表示にすれば上記(例2)で求めた結果と一致することが確かめられる。
なお、Vector2、Vector3型のインスタンスのプロパティには、インスタンス同士の加算、減算結果から直接アクセスできる。具体的には、3行目においてVector2型インスタンスP、Qの減算結果を vへセットし、4行目では vを経由して単位ベクトルを取得しているが、5行目に書かれているように (Q - P).normalized として、直接P、Qを結ぶベクトルの単位ベクトルを取得することもできる。

# Code4

2D空間上に点$P$ 及び直線 $l$ が置かれている (図22)。図に示されるように点$P$の座標は $(6, 6)$ であり、直線 $l$ は原点$O$と $(8, 2)$ を通る直線である。点$P$を直線 $l$ に射影したときの像を点$Q$とするとき、直線 $l$ 上における原点$O$から点$Q$までの距離をプログラムで求めてみよう。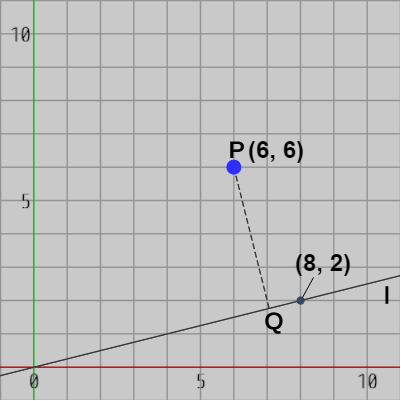

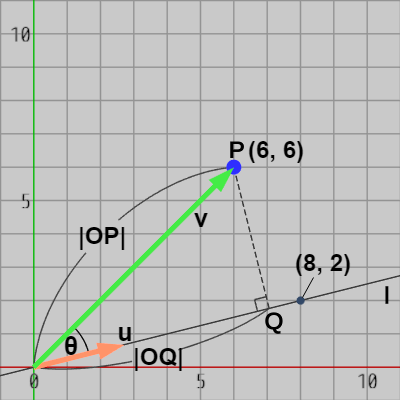
上で解説した方法と全く同様に求めればよい。すなわち、図23のように原点$O$と点$P$を結ぶベクトルを $\boldsymbol{\mathsf{v}}$ とし、直線 $l$ の方向を表す単位ベクトルを $\boldsymbol{u}$ とする。さらに、この2つのベクトルのなす角を $\theta$ とすれば、原点$O$から点$Q$までの距離$|OQ|$は\[ |OQ| = |OP|cos{\theta} = |v|cos{\theta} \]であるが、$\boldsymbol{\mathsf{v}}\cdot\boldsymbol{u} = |v|cos{\theta}$ であるから、結局\[ |OQ| = \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u} \]である。

プログラムは以下のとおり。
[Code4] (実行結果図24)

Vector2 v = new Vector2(6, 6);
Vector2 u = (new Vector2(8, 2)).normalized;
float OQ = Vector2.Dot(v, u);

Debug.Log("|OQ| = "+OQ);

1行目、2行目の v、u は上図23の $\boldsymbol{\mathsf{v}}$、$\boldsymbol{u}$ と同じである。3行目で v と u の内積を計算し $|OQ|$ を求めている。
実行結果(図24)に示されるように $|OQ|\risingdotseq7.3$ である。

<< 1-2
ベクトルによる平行移動

1-4 >>
行列