Redpoll's 60
Home / 3Dプログラミング入門 / 第1章 $§$1-8
第1章 2D空間の基礎
| $§$1-1 点とベクトル | $§$1-6 回転行列 |
| $§$1-2 ベクトルによる平行移動 | $§$1-7 スケール行列 |
| $§$1-3 単位ベクトル | $§$1-8 変換行列の積 |
| $§$1-4 行列の基礎 | $§$1-9 フレームとフレームレート |
| $§$1-5 平行移動行列 | $§$1-10 オブジェクトの基本的な運動 (往復運動と回転) |
$§$1-8 変換行列の積
1-5、1-6、1-7の3節では平行移動、回転、スケールなどの変換は、変換行列として行列の形で表されることを見た。本節では、複数の変換の合成を変換行列の積として1つの行列で表し、その積をオブジェクトに実行することは合成されるさまざまな変換を1つ1つ順番にオブジェクトに実行する場合と同じ結果になることについて具体的に見ていく。

図1 Disk (何も変換を行っていない状態) 図1は Diskという名前の半径$1$の円形オブジェクトで、その中心が原点に置かれている。この Diskに対し、次の変換を実行する。
(1) $45$°回転 (この回転を表す行列を$R_{45}$とする)
(2) y軸方向に$4$平行移動 (この平行移動を表す行列を$T$とする)
今回の変換を変換行列の積として表すと次のようになる (変換行列の積を $M$とする)。\[ TR_{45} = M \]行列の積は右から左へ進むので、最初の変換である$R_{45}$を右に、次の変換である$T$を左に記述する。
この変換を実行するプログラムを以下に示す。プログラム内で使用されるメソッドは、今までに使われてきたものであるから特に解説は不要であろう。
[Code1] (実行結果 図4)
変換過程及び、実行結果を以下に示す。
何も変換を受けていない状態の Disk(図1)に対して、$45$°の回転を実行した結果が図2である。さらに、回転を行った後の Diskに対して、y軸方向に$4$の平行移動を実行した結果が図3である。プログラム3行目の$3\times3$行列Mは、この2つの変換を1つにまとめたもので、図4は 何も変換を受けていない状態の Diskに対して Mを実行した結果である。つまり、図1の状態の Diskに変換を1つ1つ順番に実行した結果が図3であり、2つの変換を1つの変換行列にまとめ、それを(何も変換を受けていない状態の)Diskに実行した結果が図4である。どちらの場合でも結果は同じである。
1-4節でも述べたが、行列の積は可換ではない。つまり、行列の積の順序は交換可能ではない。2つの行列$A$、$B$があり、$A$と$B$の間で乗算が可能であるとき、$AB = BA$ が常に成り立つとは限らないということである (成り立つ場合もある)。
今回の例でいえば、回転行列$R_{45}$と平行移動行列$T$の具体的な内容は、\[R_{45} =\begin{pmatrix}0.707 &-0.707 &0 \\0.707 &0.707 &0 \\0 &0 &1\end{pmatrix}\qquad T =\begin{pmatrix}1 &0 &0\\0 &1 &4\\0 &0 &1\end{pmatrix}\]である (ただし、小数点以下は小数第4位を四捨五入して第3位までの表示にしてある)。
実際に、2つの積 $TR_{45}$ と $R_{45}T$ を計算すると、
なお、上の例において Diskに実行する変換行列の積を $TR_{45}$ ではなく、積の順序を逆にした $R_{45}T$ で変換を実行した場合は次のような結果になる (プログラムでは3行目を M = R45 * T とした場合)。
この場合では、何も変換を行っていない Disk(図1)に対して、まず y軸方向に$4$の平行移動が実行される(図5)。そして、その移動後の位置から次の変換である$45$°の回転が実行される (平行移動を行った後のDiskの中心位置は$(0, 4)$である。この位置から$45$°回転させることは、原点中心の半径$4$の円周上を Diskの中心が$(0, 4)$から$45$°回転することになる)。最終的には図6に示される結果になる。
(1) $45$°回転 ($R_{45}$)
(2) y軸方向に$4$平行移動 ($T$)
(3) $90$°回転 (この回転を表す行列を $R_{90}$ とする)
今回の変換を変換行列の積として表すと次のようになる (ここでも変換行列の積を $M$ とする)。\[ R_{90}TR_{45} = M\]この変換を実行するプログラムを以下に示す。
[Code2] (実行結果 図8)
では以下に、最初の2つの変換を実行した後の Diskに第3の変換を実行した結果と、このプログラムの実行結果を示す。
図4は Code1実行後の Diskであり、最初の2つの変換が終わった状態である。この状態の Diskに対して第3の変換である$90$°の回転を実行した結果が図7である (Code1実行後のDiskの中心位置は$(0, 4)$である。この位置から$90$°回転させることは、原点中心の半径$4$の円周上をDiskの中心が$(0, 4)$から$90$°回転することになる)。プログラム4行目の$3\times3$行列Mは、今回の3つの変換を1つの変換行列にまとめたもので、図8は 何も変換を受けていない状態の Diskに対して Mを実行した結果である。つまり、図1の状態の Diskに変換を1つ1つ順番に実行した結果が図7であり、3つの変換を1つの変換行列にまとめ、それを(何も変換を受けていない状態の)Diskに実行した結果が図8である。どちらの場合でも結果は同じである。
実行する変換は次の通り。
(1) x軸方向、y軸方向ともに$2$倍拡大 (このスケールを表す行列を $S$ とする)
(2) $225$°回転 (この回転を表す行列を $R$ とする)
(3) $(-4, -4)$だけ平行移動 (この平行移動を表す行列を $T$ とする)
今回の変換を変換行列の積として表すと次のようになる (変換行列の積を $M$ とする)。\[ TRS = M\]この変換を実行するプログラムを以下に示す。
[Code3] (実行結果 図12)
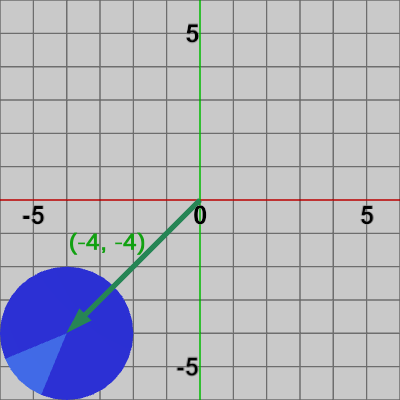
図11 (-4, -4) 平行移動(第3の変換) 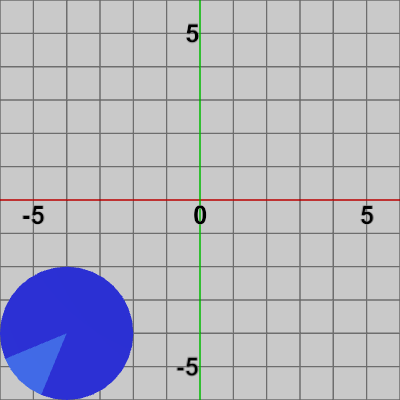
図12 Code3 実行結果
何も変換を行っていない状態の Diskに対して、第1の変換である$2$倍の拡大を実行した結果が図9である。拡大後の Diskに対して、第2の変換である$225$°の回転を実行した結果が図10であり、その回転後の Diskに第3の変換である $(-4, -4)$の平行移動を実行した結果が図11である。プログラム4行目の M はこの3つの変換を1つの変換行列にまとめたものであり、(何も変換を行っていない状態の)Diskに対して Mを実行した結果が図12である。
この場合でも、3つの変換を順番に実行した場合(図9、図10、図11)と、それらの変換を合成した行列を実行した場合(図12)とで、やはり結果は同じである。
1-4節では行列の逆行列について簡単に触れた。ある$3\times3$行列$M$に対して、$M$の逆行列$M^{-1}$を掛けると、算出される行列は単位行列になるのであった。\[ MM^{-1} = M^{-1}M = I \]たとえば、Code1では Diskに対して、$45$°の回転、y軸方向に$4$の平行移動をこの順序で実行したが、それぞれの変換を表す行列を $R_{45}$、$T$ とし、その積を $M$ とすれば、Diskに実行された変換行列は\[ TR_{45} = M \]であった。ここで、$M$に対して、その逆行列$M^{-1}$を掛け、その積を $M_1$ とする。\[ M^{-1}M = M_1 \]上で述べたことから、$M_1$ は単位行列である。オブジェクトに対して単位行列を実行すると、そのオブジェクトは何も変換が実行されていない初期の状態になる。このことは1-4節のプログラムでも確認したが、ここでも簡単に確認してみよう。
Code1を次のように変更する。
[Code1 変更版] (実行結果 図13)
変更部分は4行目、5行目である。M.inverse は変換行列 M の逆行列のことである (inverseは逆行列を表すTHMatrix3x3構造体のプロパティ)。4行目の M1 は上で述べたように単位行列である。5行目では Diskに対してこの M1 を実行しているが、その実行結果は図13に示されている通り、Diskは何の変換も受けていない初期の状態に戻っている。
同様のことを Code3でも行ってみよう。
Code3では Diskに対して、x軸方向、y軸方向に$2$倍の拡大、$225$°の回転、$(-4, -4)$の平行移動をこの順序で実行するものであった。それぞれの変換を表す行列を $S$、$R$、$T$ とし、その積 $TRS = M$ が Diskに実行された変換行列であった。ここでも、変換行列$M$に対して、その逆行列$M^{-1}$を掛け、その積を $M^{-1}M = M_1$ とし、この $M_1$ を Diskに実行する。
[Code3 変更版] (実行結果 図14)
Code3からの変更部分は5行目、6行目である (変換行列Mとその逆行列の積をM1にセットし、Diskに対しM1を実行する)。実行結果(図14)に示されるように、ここでも Diskは何も変換を受けていない初期の状態に戻っている。

図13 Code1変更版の実行結果(Diskは何の変換も受けていない初期の状態) 
図14 Code3変更版の実行結果(Diskは何の変換も受けていない初期の状態)
本節では複数の変換の合成は、複数の変換行列の積としてただ1つの行列で表されることを見た。例えばCode3においては、$2$倍のスケール、$225$°の回転、$(-4, -4)$の平行移動の3つの変換の合成は、$S$, $R$, $T$という3つの変換行列の積として$TRS$で表された。$TRS = M$とすれば、$M$はこの3つの変換を1つの行列にまとめたものになっており、$M$をオブジェクトに実行することは、3つの変換を1つ1つ順番にオブジェクトに実行する場合と同じ結果になるのであった。
このことは、合成する変換の数が増えても変わらない。例えば非常に多くの平行移動、回転、スケールを適当な順序で合成するとしよう。平行移動を表す行列を $T_1, T_2, \ldots , T_n$、回転を表す行列を $R_1, R_2, \ldots , R_n$、スケールを表す行列を $S_1, S_2, \ldots , S_n$ とし、これらの変換の合成が次のような積で表されるものとする。\[T_nS_nR_n\cdots R_2S_2T_2R_1T_1S_1 = M \]このときの積$M$は、この非常に多い変換を1つの行列にまとめたものになっており、$M$をオブジェクトに実行した結果は、合成されるさまざまな変換を1つ1つ順番にオブジェクトに実行していった場合と同じ結果になるのである。
最後のプログラムCode3においてはスケール、回転、平行移動をこの順序で合成した。そして、この合成はそれらの変換を表す変換行列 $S$、$R$、$T$ の積として次のように表された。\[ TRS = M \]スケール、回転、平行移動をこの順序でオブジェクトに実行することは、オブジェクトに対して行う変換のうち、最も基本的なものである。例えば、上記の非常に多くの変換の合成の場合も、実際にはただ1つのスケール行列$S$と、ただ1つの回転行列$R$、及びただ1つの平行移動行列$T$によって次のように表すことができるのである。\[T_nS_nR_n\cdots R_2S_2T_2R_1T_1S_1 = TRS\]これは、オブジェクトをある状態にするために多くの変換を実行した場合でも、実際にはオブジェクトをその状態にするためにはただ1つのスケールと、ただ1つの回転、及びただ1つの平行移動をこの順序で実行することだけが必要であることを示している。
このことについては4-6節で扱う。
# Code1
1-5節、1-6節で既に複数の変換の合成を変換行列の積として表した。例えば1-5節では $(3,0)$だけ平行移動させる行列$T_1$、$(−5,4)$だけ平行移動させる行列$T_2$、$(−2,−2)$だけ平行移動させる行列$T_3$の積を $M_2$とした。\[ T_3T_2T_1 = M_2 \]この$M_2$は、まず $(3, 0)$の平行移動、次に $(-5, 4)$の平行移動、最後に $(-2, -2)$の平行移動を行う行列であると述べた。しかし、平行移動という同じ種類の変換を合成することは、複数の変換を合成するという点であまり効果がない。そこで、今回は回転と平行移動という異なる種類の変換を合成し、それをオブジェクトに実行する。
(1) $45$°回転 (この回転を表す行列を$R_{45}$とする)
(2) y軸方向に$4$平行移動 (この平行移動を表す行列を$T$とする)
今回の変換を変換行列の積として表すと次のようになる (変換行列の積を $M$とする)。\[ TR_{45} = M \]行列の積は右から左へ進むので、最初の変換である$R_{45}$を右に、次の変換である$T$を左に記述する。
この変換を実行するプログラムを以下に示す。プログラム内で使用されるメソッドは、今までに使われてきたものであるから特に解説は不要であろう。
[Code1] (実行結果 図4)
THMatrix3x3 R45 = TH2DMath.GetRotation3x3(45); THMatrix3x3 T = TH2DMath.GetTranslation3x3(0, 4); THMatrix3x3 M = T * R45; Disk.SetMatrix(M);
変換過程及び、実行結果を以下に示す。
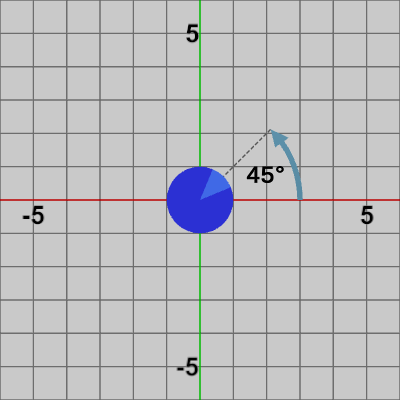 図2 45°の回転を実行した結果
図2 45°の回転を実行した結果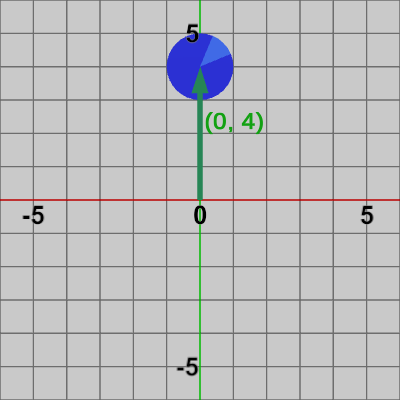 図3 y軸方向に4の平行移動を実行した結果
図3 y軸方向に4の平行移動を実行した結果 図4 Code1 実行結果
図4 Code1 実行結果
何も変換を受けていない状態の Disk(図1)に対して、$45$°の回転を実行した結果が図2である。さらに、回転を行った後の Diskに対して、y軸方向に$4$の平行移動を実行した結果が図3である。プログラム3行目の$3\times3$行列Mは、この2つの変換を1つにまとめたもので、図4は 何も変換を受けていない状態の Diskに対して Mを実行した結果である。つまり、図1の状態の Diskに変換を1つ1つ順番に実行した結果が図3であり、2つの変換を1つの変換行列にまとめ、それを(何も変換を受けていない状態の)Diskに実行した結果が図4である。どちらの場合でも結果は同じである。
1-4節でも述べたが、行列の積は可換ではない。つまり、行列の積の順序は交換可能ではない。2つの行列$A$、$B$があり、$A$と$B$の間で乗算が可能であるとき、$AB = BA$ が常に成り立つとは限らないということである (成り立つ場合もある)。
今回の例でいえば、回転行列$R_{45}$と平行移動行列$T$の具体的な内容は、\[R_{45} =\begin{pmatrix}0.707 &-0.707 &0 \\0.707 &0.707 &0 \\0 &0 &1\end{pmatrix}\qquad T =\begin{pmatrix}1 &0 &0\\0 &1 &4\\0 &0 &1\end{pmatrix}\]である (ただし、小数点以下は小数第4位を四捨五入して第3位までの表示にしてある)。
実際に、2つの積 $TR_{45}$ と $R_{45}T$ を計算すると、
\begin{align*}&TR_{45} =\begin{pmatrix}1 &0 &0\\0 &1 &4\\0 &0 &1\end{pmatrix}\begin{pmatrix}0.707 &-0.707 &0 \\0.707 &0.707 &0 \\0 &0 &1\end{pmatrix}=\begin{pmatrix}0.707 &-0.707 &0 \\0.707 &0.707 &4 \\0 &0 &1\end{pmatrix}\\\\&R_{45}T =\begin{pmatrix}0.707 &-0.707 &0 \\0.707 &0.707 &0 \\0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &0\\0 &1 &4\\0 &0 &1\end{pmatrix}=\begin{pmatrix}0.707 &-0.707 &-2.828 \\0.707 &0.707 & 2.828 \\0 &0 &1\end{pmatrix}\end{align*}
となり、2つの積の結果が一致しないことが示される。なお、上の例において Diskに実行する変換行列の積を $TR_{45}$ ではなく、積の順序を逆にした $R_{45}T$ で変換を実行した場合は次のような結果になる (プログラムでは3行目を M = R45 * T とした場合)。
 図1 Disk (何も変換を行っていない状態)
図1 Disk (何も変換を行っていない状態)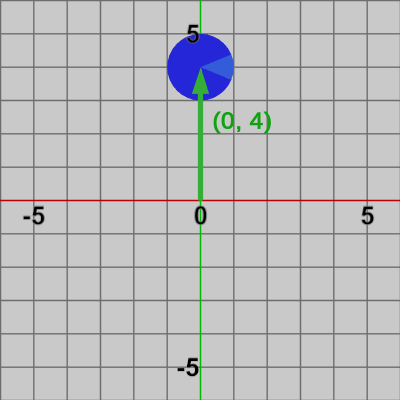 図5 y軸方向に4の平行移動を実行した結果
図5 y軸方向に4の平行移動を実行した結果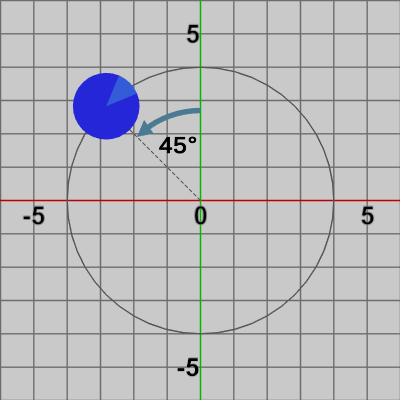 図6 45°の回転を実行した結果
図6 45°の回転を実行した結果
この場合では、何も変換を行っていない Disk(図1)に対して、まず y軸方向に$4$の平行移動が実行される(図5)。そして、その移動後の位置から次の変換である$45$°の回転が実行される (平行移動を行った後のDiskの中心位置は$(0, 4)$である。この位置から$45$°回転させることは、原点中心の半径$4$の円周上を Diskの中心が$(0, 4)$から$45$°回転することになる)。最終的には図6に示される結果になる。
# Code2
では次に、Code1の2つの変換後にさらに$90$°の回転を追加しよう。つまり全体では次の3つの変換が合成される。(1) $45$°回転 ($R_{45}$)
(2) y軸方向に$4$平行移動 ($T$)
(3) $90$°回転 (この回転を表す行列を $R_{90}$ とする)
今回の変換を変換行列の積として表すと次のようになる (ここでも変換行列の積を $M$ とする)。\[ R_{90}TR_{45} = M\]この変換を実行するプログラムを以下に示す。
[Code2] (実行結果 図8)
THMatrix3x3 R45 = TH2DMath.GetRotation3x3(45); THMatrix3x3 T = TH2DMath.GetTranslation3x3(0, 4); THMatrix3x3 R90 = TH2DMath.GetRotation3x3(90); THMatrix3x3 M = R90 * T * R45; Disk.SetMatrix(M);
では以下に、最初の2つの変換を実行した後の Diskに第3の変換を実行した結果と、このプログラムの実行結果を示す。
-
 図4 Code1 実行結果
図4 Code1 実行結果 -
 図7 90°の回転を実行した結果
図7 90°の回転を実行した結果 -
 図8 Code2 実行結果
図8 Code2 実行結果
図4は Code1実行後の Diskであり、最初の2つの変換が終わった状態である。この状態の Diskに対して第3の変換である$90$°の回転を実行した結果が図7である (Code1実行後のDiskの中心位置は$(0, 4)$である。この位置から$90$°回転させることは、原点中心の半径$4$の円周上をDiskの中心が$(0, 4)$から$90$°回転することになる)。プログラム4行目の$3\times3$行列Mは、今回の3つの変換を1つの変換行列にまとめたもので、図8は 何も変換を受けていない状態の Diskに対して Mを実行した結果である。つまり、図1の状態の Diskに変換を1つ1つ順番に実行した結果が図7であり、3つの変換を1つの変換行列にまとめ、それを(何も変換を受けていない状態の)Diskに実行した結果が図8である。どちらの場合でも結果は同じである。
# Code3
次の変換はスケール、回転、平行移動を合成した場合である。実行する変換は次の通り。
(1) x軸方向、y軸方向ともに$2$倍拡大 (このスケールを表す行列を $S$ とする)
(2) $225$°回転 (この回転を表す行列を $R$ とする)
(3) $(-4, -4)$だけ平行移動 (この平行移動を表す行列を $T$ とする)
今回の変換を変換行列の積として表すと次のようになる (変換行列の積を $M$ とする)。\[ TRS = M\]この変換を実行するプログラムを以下に示す。
[Code3] (実行結果 図12)
THMatrix3x3 S = TH2DMath.GetScale3x3(2, 2); THMatrix3x3 R = TH2DMath.GetRotation3x3(225); THMatrix3x3 T = TH2DMath.GetTranslation3x3(-4, -4); THMatrix3x3 M = T * R * S; Disk.SetMatrix(M);
-
 図1 Disk (何も変換を行っていない状態)
図1 Disk (何も変換を行っていない状態) -
 図9 2倍の拡大を実行した結果(第1の変換)
図9 2倍の拡大を実行した結果(第1の変換) -
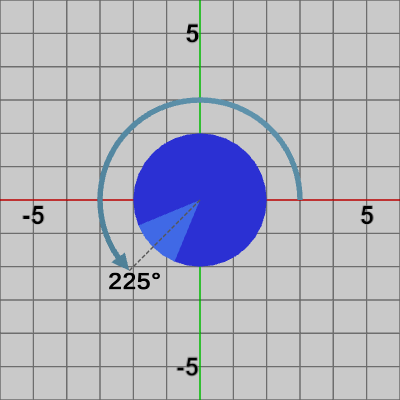 図10 225°の回転を実行した結果(第2の変換)
図10 225°の回転を実行した結果(第2の変換)


何も変換を行っていない状態の Diskに対して、第1の変換である$2$倍の拡大を実行した結果が図9である。拡大後の Diskに対して、第2の変換である$225$°の回転を実行した結果が図10であり、その回転後の Diskに第3の変換である $(-4, -4)$の平行移動を実行した結果が図11である。プログラム4行目の M はこの3つの変換を1つの変換行列にまとめたものであり、(何も変換を行っていない状態の)Diskに対して Mを実行した結果が図12である。
この場合でも、3つの変換を順番に実行した場合(図9、図10、図11)と、それらの変換を合成した行列を実行した場合(図12)とで、やはり結果は同じである。
1-4節では行列の逆行列について簡単に触れた。ある$3\times3$行列$M$に対して、$M$の逆行列$M^{-1}$を掛けると、算出される行列は単位行列になるのであった。\[ MM^{-1} = M^{-1}M = I \]たとえば、Code1では Diskに対して、$45$°の回転、y軸方向に$4$の平行移動をこの順序で実行したが、それぞれの変換を表す行列を $R_{45}$、$T$ とし、その積を $M$ とすれば、Diskに実行された変換行列は\[ TR_{45} = M \]であった。ここで、$M$に対して、その逆行列$M^{-1}$を掛け、その積を $M_1$ とする。\[ M^{-1}M = M_1 \]上で述べたことから、$M_1$ は単位行列である。オブジェクトに対して単位行列を実行すると、そのオブジェクトは何も変換が実行されていない初期の状態になる。このことは1-4節のプログラムでも確認したが、ここでも簡単に確認してみよう。
Code1を次のように変更する。
[Code1 変更版] (実行結果 図13)
THMatrix3x3 R45 = TH2DMath.GetRotation3x3(45); THMatrix3x3 T = TH2DMath.GetTranslation3x3(0, 4); THMatrix3x3 M = T * R45; THMatrix3x3 M1 = M.inverse * M; Disk.SetMatrix(M1);
変更部分は4行目、5行目である。
THMatrix3x3 M1 = M.inverse * M; Disk.SetMatrix(M1);
同様のことを Code3でも行ってみよう。
Code3では Diskに対して、x軸方向、y軸方向に$2$倍の拡大、$225$°の回転、$(-4, -4)$の平行移動をこの順序で実行するものであった。それぞれの変換を表す行列を $S$、$R$、$T$ とし、その積 $TRS = M$ が Diskに実行された変換行列であった。ここでも、変換行列$M$に対して、その逆行列$M^{-1}$を掛け、その積を $M^{-1}M = M_1$ とし、この $M_1$ を Diskに実行する。
[Code3 変更版] (実行結果 図14)
THMatrix3x3 S = TH2DMath.GetScale3x3(2, 2); THMatrix3x3 R = TH2DMath.GetRotation3x3(225); THMatrix3x3 T = TH2DMath.GetTranslation3x3(-4, -4); THMatrix3x3 M = T * R * S; THMatrix3x3 M1 = M.inverse * M; Disk.SetMatrix(M1);
Code3からの変更部分は5行目、6行目である (変換行列Mとその逆行列の積をM1にセットし、Diskに対しM1を実行する)。実行結果(図14)に示されるように、ここでも Diskは何も変換を受けていない初期の状態に戻っている。


本節では複数の変換の合成は、複数の変換行列の積としてただ1つの行列で表されることを見た。例えばCode3においては、$2$倍のスケール、$225$°の回転、$(-4, -4)$の平行移動の3つの変換の合成は、$S$, $R$, $T$という3つの変換行列の積として$TRS$で表された。$TRS = M$とすれば、$M$はこの3つの変換を1つの行列にまとめたものになっており、$M$をオブジェクトに実行することは、3つの変換を1つ1つ順番にオブジェクトに実行する場合と同じ結果になるのであった。
このことは、合成する変換の数が増えても変わらない。例えば非常に多くの平行移動、回転、スケールを適当な順序で合成するとしよう。平行移動を表す行列を $T_1, T_2, \ldots , T_n$、回転を表す行列を $R_1, R_2, \ldots , R_n$、スケールを表す行列を $S_1, S_2, \ldots , S_n$ とし、これらの変換の合成が次のような積で表されるものとする。\[T_nS_nR_n\cdots R_2S_2T_2R_1T_1S_1 = M \]このときの積$M$は、この非常に多い変換を1つの行列にまとめたものになっており、$M$をオブジェクトに実行した結果は、合成されるさまざまな変換を1つ1つ順番にオブジェクトに実行していった場合と同じ結果になるのである。
最後のプログラムCode3においてはスケール、回転、平行移動をこの順序で合成した。そして、この合成はそれらの変換を表す変換行列 $S$、$R$、$T$ の積として次のように表された。\[ TRS = M \]スケール、回転、平行移動をこの順序でオブジェクトに実行することは、オブジェクトに対して行う変換のうち、最も基本的なものである。例えば、上記の非常に多くの変換の合成の場合も、実際にはただ1つのスケール行列$S$と、ただ1つの回転行列$R$、及びただ1つの平行移動行列$T$によって次のように表すことができるのである。\[T_nS_nR_n\cdots R_2S_2T_2R_1T_1S_1 = TRS\]これは、オブジェクトをある状態にするために多くの変換を実行した場合でも、実際にはオブジェクトをその状態にするためにはただ1つのスケールと、ただ1つの回転、及びただ1つの平行移動をこの順序で実行することだけが必要であることを示している。
このことについては4-6節で扱う。
© 2020-2025 Redpoll's 60 (All rights reserved)