Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-1
第4章 3D空間におけるオブジェクトの運動
$§$4-1 自転と公転
本章からは、本格的に3D空間におけるオブジェクトの運動を扱う。3Dオブジェクトは2Dオブジェクトと比べてビジュアル的なインパクトが強い。平面的な世界では表現できないリアリティが、3D空間においては単純なオブジェクトからでも感じられる。その一方で3D空間のシーンをレンダリングするコストは、2D空間の場合に比べて非常に大きくなりやすい。
プログラミングの面からいえば、2Dオブジェクトを運動させるのも3Dオブジェクトを運動させるのも考え方に大きな違いはない。単純な構成のオブジェクトを使ってそれを示すために、本節では2-4節で扱った2D版の自転、公転を3D空間で実装する。
まずは このオブジェクトを、y軸を回転軸として$(3, 0, 0)$を通る半径3の円周上で回転させる。すなわち、Sphereの公転の実装である。

図1 Sphere 初期状態 
図2 Code1 実行結果
3-10節でも述べたように、3D空間においてオブジェクトを回転させる場合には回転角度のほかに回転軸を指定する必要がある。指定された軸の周りに指定された角度だけ回転させる行列を取得するために、前章でも用いた以下のカスタムライブラリのメソッドを使用する。
実際のプログラムは以下の通り。
[Code1] (実行結果 図2)
1行目の i_degRev は Sphereの公転角度を表すインスタンス変数であり、毎フレーム$1$ずつ増加する。これは、このプログラムにおいては Sphereは毎フレーム 円周上(公転軌道上)を$1$°ずつ進んでいくことを意味する。
2行目では回転行列revを取得しているが、今回はy軸周りなので回転軸を表す引数にはVector3.upが指定されている。この定数は前章でも出てきたが、Unityに標準で用意されている $(0, 1, 0)$ を表すVector3型の定数である。3行目では、そのフレームにおける半径$3$の円周上の移動先の位置npが計算される。回転行列revに $(3, 0, 0)$ の同次座標 $(3, 0, 0, 1)$ を掛けることで、半径$3$の円周上を $(3, 0, 0)$ から角度i_degRevだけ回転した位置が求められる。その位置に移動させるための平行移動行列が4行目で計算されるTであり、6行目で SphereにTを実行することで円周上への移動が行われる。
Sphereの自転軸は'北極'と'南極'を結ぶ軸とする(図1においては自転軸はy軸と一致する)。
[Code2] (実行結果 図3)
1行目で使われている変数i_degRotは Sphereの自転角度を表すインスタンス変数であり、毎フレーム $4$ ずつ増加する。つまり、Sphereは毎フレーム $4^\circ$ ずつ自転を行うことを意味する。公転角度i_degRevが毎フレーム $1$ ずつ増加するので、Sphereは毎フレーム $1^\circ$ ずつ公転し、$4^\circ$ ずつ自転を行う。すなわち、公転を1回する間に自転を4回することになる。Sphereが公転を1回する間に自転を10回させるようにするためには、i_degRot を毎フレーム $10$ ずつ増加させればよい。
2行目で計算される回転行列Rは、Sphereを自転させるための行列である。
4~7行目はCode1の1~4行目と同じである。
9行目の M = T * R は、まず初期状態の Sphereに対して自転を実行し(R)、次に公転軌道上の計算された位置に移動させる(T)という順序で2つの処理をまとめたものである。この行列を10行目で Sphereに実行することによって、Sphereは自転しながら公転することになる (図3のSphereを貫いている紫色の線は、Sphereの自転軸を表している)。
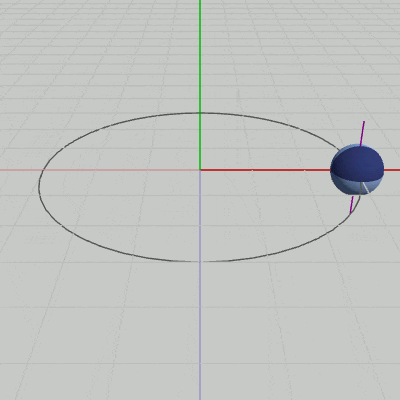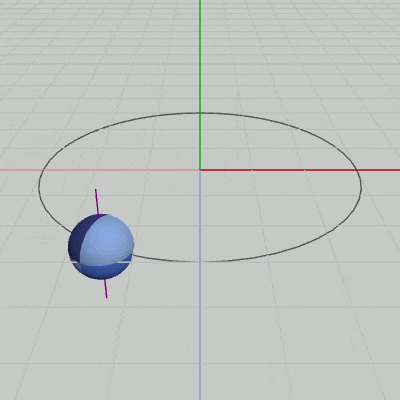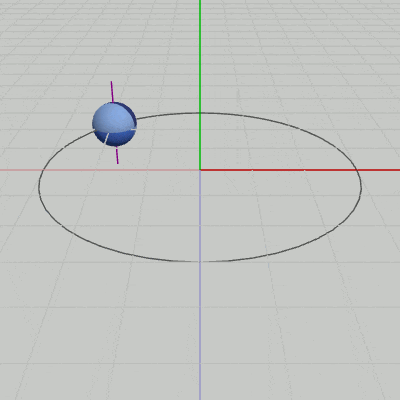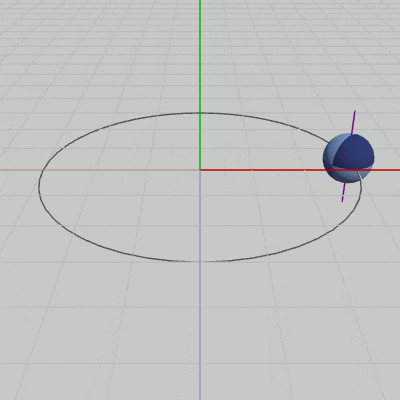
図3 Code3 実行結果 (紫色の線は自転軸を表している) 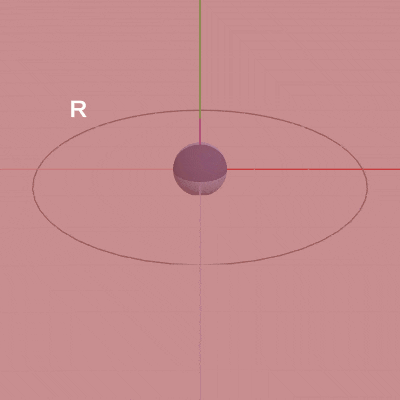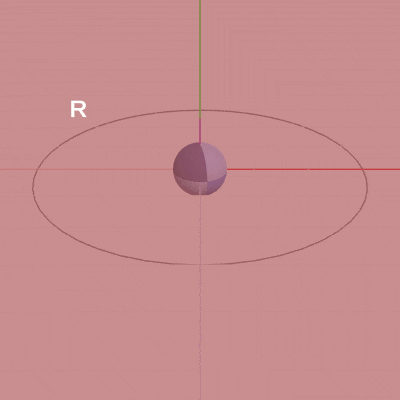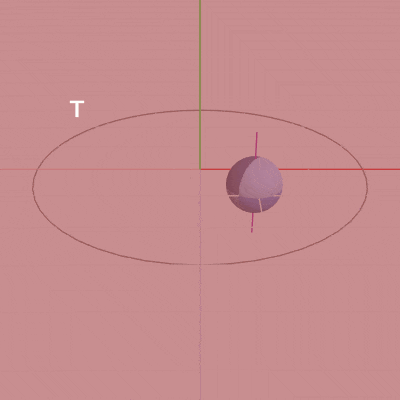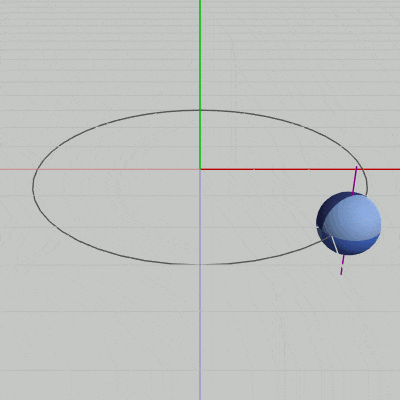
図4 いくつかのフレームにおける Sphereの変換過程 (赤いフィルターから通常色に切り替わった時点で フレーム描画が発生する)
図4は、最初の方のいくつかのフレームにおける Sphereの変換過程である。赤いフィルターで覆われた状態から通常の色に切り替わるが、通常色に切り替わった時点でフレーム描画が発生する。そして、それらのフレームを連続的に表示したものが図3である。

図5 Sphereをz軸周りに -20°回転させる(自転軸はy軸と20°の角度をなす) Code1、Code2は、2-4節のプログラムとほとんど変化がなかった。今回のプログラムでは多少の変化をつけて、Sphereの自転軸を傾ける問題を扱う。Sphereの自転軸とは先程も述べた通り、Sphereの'北極'、'南極'を貫く軸で図1においてはy軸に一致する。
ここでは、Sphereを図5に示されるように初期状態からz軸周りに $-20$°回転させて、紫色の線であらわされる自転軸がy軸と$20$°の角度をなすようにし、この傾いた軸の周りをSphereが(原点において)自転するプログラムを作成しよう (今回は自転のみの実装で公転は行わない)。
処理手順は次の通り。
(1) Sphereをy軸周りに自転させる
(2) Sphereをz軸周りに $-20$°回転させる
[Code3] (実行結果 図6)
2行目の rotY がy軸周りの自転を行う回転行列で、3行目の rotZ がz軸周りに $-20$°の回転を行って Sphere(及び 自転軸)を傾ける回転行列である。これらは上記の処理手順(1)、(2)に対応している。4行目の R = rotZ * rotY は、まずy軸周りの回転、次にz軸周りの回転という順序で2つの変換をまとめたものである。
重要なのはrotZである。rotYだけを行った段階ではy軸周りの自転にしかならない。そこからさらに、Sphereに対してrotZを実行することで、Sphereの自転がy軸と$20$°の角度をなす軸の周りで行われるようになるのである。
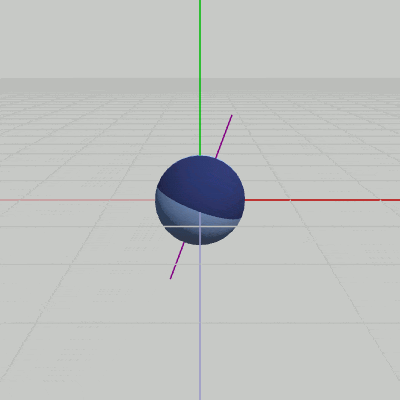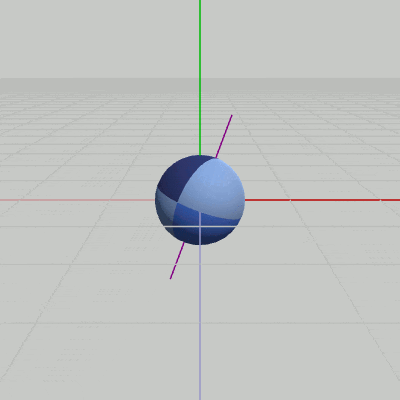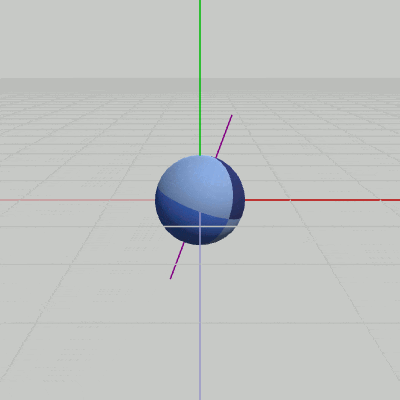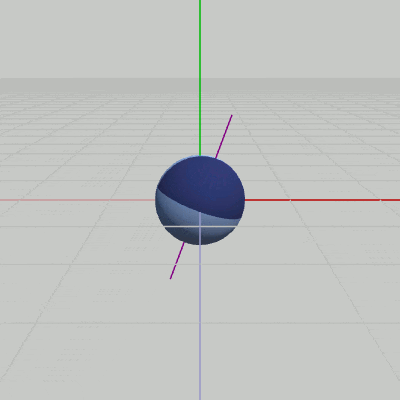
図6 Sphereの自転(自転軸はy軸と20°の角度をなす) 
図7 いくつかのフレームにおけるSphereの変換過程
図7は、図6のアニメーションの最初のいくつかのフレームにおける Sphereの変換過程である。赤いフィルターの状態から通常色に切り替わった時点でフレーム描画が発生するが、それらのフレームを連続的に表示したものが図6のアニメーションである。
処理手順は次の通り。
(1) Sphereをy軸周りに自転させる
(2) Sphereをz軸周りに $-20$°回転させる
(3) Sphereを公転軌道上へ移動させる
手順(1)、(2)は前回と同じであり、ここでは(3)の公転処理が追加されている。
[Code4] (実行結果 図8)
このプログラムはCode1とCode3を合わせた処理になっている。4行目まではCode3と同じであり、6~9行目はCode1の1~4行目と同じである。4行目の回転行列RはCode3で見たように、y軸と$20$°の角度をなす軸の周りで Sphereを自転させる行列であり、9行目の平行移動行列Tは、Sphereを公転軌道上に移動させる行列である。11行目の M = T * R は、まず(原点において)傾いた軸の周りでの自転を行い(R)、次に公転軌道上への移動を行う(T)という2つの変換をまとめたものである。
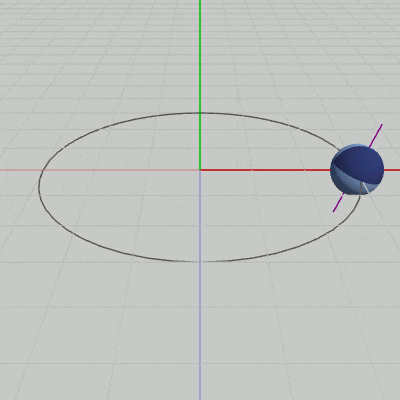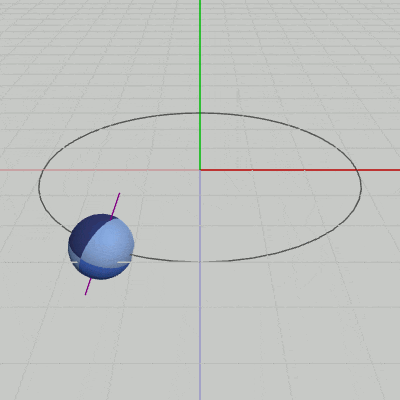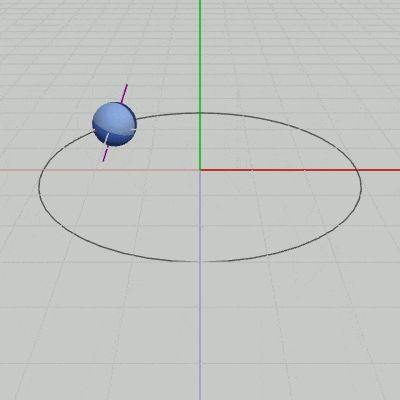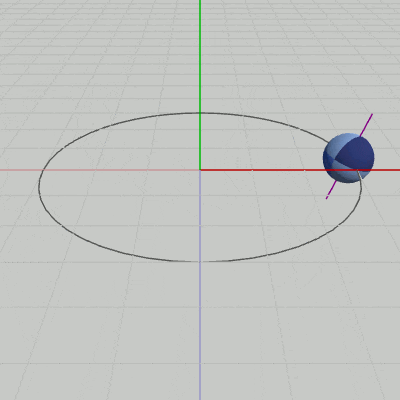
図8 Code4 実行結果(紫色の線は自転軸を表している) 
図9 いくつかのフレームにおけるSphereの変換過程
実行結果(図8)に見られるように、Sphereの運動は傾いた自転軸の周りを自転しながらの公転となっている。
図9は、図8の最初の方のいくつかのフレームにおける Sphereの変換過程である。赤いフィルターの状態から通常色に切り替わった時点でフレーム描画が発生するが、それらのフレームを連続的に表示したものが図9のアニメーションである。
図10には小さい球体が $(5,\ 3,-5)$ の位置に置かれている。今回作成するのは、この小さい球体を中心とする半径$3$の円周上を公転するプログラムである。ただし、公転面の法線はy軸に平行であるとする。つまり、今回の公転の中心は小さい球体であり、公転の回転軸は図には示されていないが、y軸に平行で小さい球体を通る軸である。また、自転についてはCode4と同じく、Sphereを原点に置いたときにy軸と$20$°の角度をなす軸を自転軸とする (図5参照)。
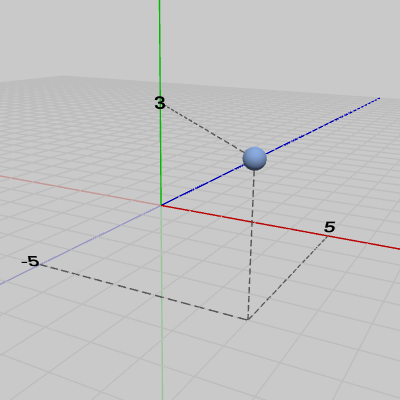
図10 (5, 3,-5)に置かれている小さな球 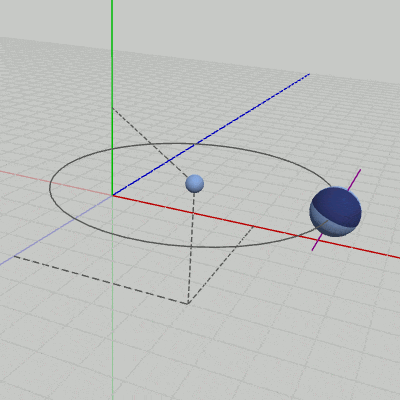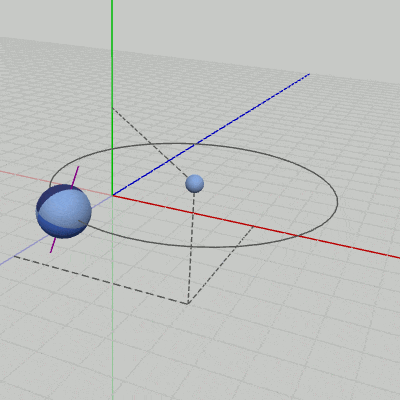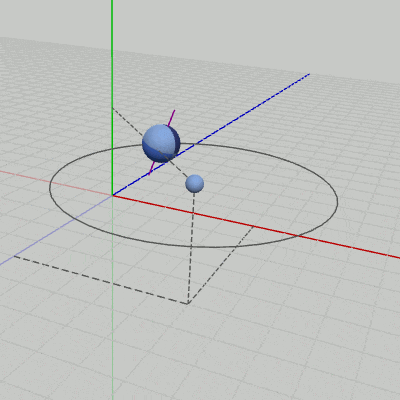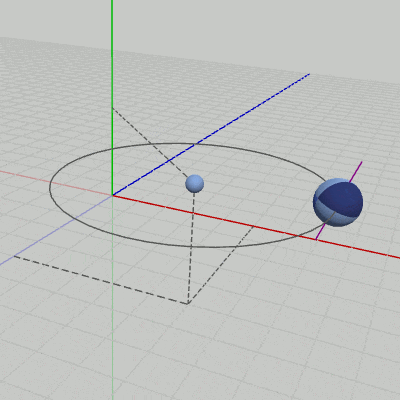
図11 Code5 実行結果
プログラムを以下に示す。
[Code5] (実行結果 図11)
このプログラムはCode4とほとんど同じである。違いが1点だけあり、それは9行目で np += c_centerPos という処理が追加されていることである。c_centerPosは、公転軌道の中心である $(5,\ 3,-5)$ (小さい球体の位置)を表すVector3型の定数である。8行目で計算される np は Sphereの移動先の位置であるが、それは原点を中心とする公転軌道上である。毎フレーム np に c_centerPos を加算することで、Sphereの移動先の位置は毎フレーム $(5,\ 3,-5)$ だけ余分にずれることになるが、これによって公転軌道が原点中心から $(5,\ 3,-5)$ 中心になるのである。
すなわち、Sphereは小さい球体を中心とする、y軸に平行で小さい球体を通る軸の周りを公転することになるのである。
プログラミングの面からいえば、2Dオブジェクトを運動させるのも3Dオブジェクトを運動させるのも考え方に大きな違いはない。単純な構成のオブジェクトを使ってそれを示すために、本節では2-4節で扱った2D版の自転、公転を3D空間で実装する。
# Code1
図1は、球体オブジェクトSphereの初期状態である(中心が原点に置かれている)。まずは このオブジェクトを、y軸を回転軸として$(3, 0, 0)$を通る半径3の円周上で回転させる。すなわち、Sphereの公転の実装である。


3-10節でも述べたように、3D空間においてオブジェクトを回転させる場合には回転角度のほかに回転軸を指定する必要がある。指定された軸の周りに指定された角度だけ回転させる行列を取得するために、前章でも用いた以下のカスタムライブラリのメソッドを使用する。
TH3DMath.GetRotation4x4(float degree, Vector3 axis)
: 回転軸axisの周りに角度degreeだけ回転させる行列を取得 (戻り値は Matrix4x4型)実際のプログラムは以下の通り。
[Code1] (実行結果 図2)
i_degRev += 1.0f; Matrix4x4 rev = TH3DMath.GetRotation4x4(i_degRev, Vector3.up); Vector3 np = rev * new Vector4(3.0f, 0.0f, 0.0f, 1.0f); Matrix4x4 T = TH3DMath.GetTranslation4x4(np); Sphere.SetMatrix(T);
1行目の i_degRev は Sphereの公転角度を表すインスタンス変数であり、毎フレーム$1$ずつ増加する。これは、このプログラムにおいては Sphereは毎フレーム 円周上(公転軌道上)を$1$°ずつ進んでいくことを意味する。
2行目では回転行列revを取得しているが、今回はy軸周りなので回転軸を表す引数にはVector3.upが指定されている。この定数は前章でも出てきたが、Unityに標準で用意されている $(0, 1, 0)$ を表すVector3型の定数である。3行目では、そのフレームにおける半径$3$の円周上の移動先の位置npが計算される。回転行列revに $(3, 0, 0)$ の同次座標 $(3, 0, 0, 1)$ を掛けることで、半径$3$の円周上を $(3, 0, 0)$ から角度i_degRevだけ回転した位置が求められる。その位置に移動させるための平行移動行列が4行目で計算されるTであり、6行目で SphereにTを実行することで円周上への移動が行われる。
# Code2
Code1はy軸周りの公転のみであったが、ここではさらに自転を加えた運動を実装してみよう。Sphereの自転軸は'北極'と'南極'を結ぶ軸とする(図1においては自転軸はy軸と一致する)。
[Code2] (実行結果 図3)
i_degRot += 4.0f; Matrix4x4 R = TH3DMath.GetRotation4x4(i_degRot, Vector3.up); i_degRev += 1.0f; Matrix4x4 rev = TH3DMath.GetRotation4x4(i_degRev, Vector3.up); Vector3 np = rev * new Vector4(3.0f, 0.0f, 0.0f, 1.0f); Matrix4x4 T = TH3DMath.GetTranslation4x4(np); Matrix4x4 M = T * R; Sphere.SetMatrix(M);
1行目で使われている変数i_degRotは Sphereの自転角度を表すインスタンス変数であり、毎フレーム $4$ ずつ増加する。つまり、Sphereは毎フレーム $4^\circ$ ずつ自転を行うことを意味する。公転角度i_degRevが毎フレーム $1$ ずつ増加するので、Sphereは毎フレーム $1^\circ$ ずつ公転し、$4^\circ$ ずつ自転を行う。すなわち、公転を1回する間に自転を4回することになる。Sphereが公転を1回する間に自転を10回させるようにするためには、i_degRot を毎フレーム $10$ ずつ増加させればよい。
2行目で計算される回転行列Rは、Sphereを自転させるための行列である。
4~7行目はCode1の1~4行目と同じである。
9行目の M = T * R は、まず初期状態の Sphereに対して自転を実行し(R)、次に公転軌道上の計算された位置に移動させる(T)という順序で2つの処理をまとめたものである。この行列を10行目で Sphereに実行することによって、Sphereは自転しながら公転することになる (図3のSphereを貫いている紫色の線は、Sphereの自転軸を表している)。


図4は、最初の方のいくつかのフレームにおける Sphereの変換過程である。赤いフィルターで覆われた状態から通常の色に切り替わるが、通常色に切り替わった時点でフレーム描画が発生する。そして、それらのフレームを連続的に表示したものが図3である。
# Code3

ここでは、Sphereを図5に示されるように初期状態からz軸周りに $-20$°回転させて、紫色の線であらわされる自転軸がy軸と$20$°の角度をなすようにし、この傾いた軸の周りをSphereが(原点において)自転するプログラムを作成しよう (今回は自転のみの実装で公転は行わない)。
処理手順は次の通り。
(1) Sphereをy軸周りに自転させる
(2) Sphereをz軸周りに $-20$°回転させる
[Code3] (実行結果 図6)
i_degRot += 4.0f; Matrix4x4 rotY = TH3DMath.GetRotation4x4(i_degRot, Vector3.up); Matrix4x4 rotZ = TH3DMath.GetRotation4x4(-20.0f, Vector3.forward); Matrix4x4 R = rotZ * rotY; Sphere.SetMatrix(R);
2行目の rotY がy軸周りの自転を行う回転行列で、3行目の rotZ がz軸周りに $-20$°の回転を行って Sphere(及び 自転軸)を傾ける回転行列である。これらは上記の処理手順(1)、(2)に対応している。4行目の R = rotZ * rotY は、まずy軸周りの回転、次にz軸周りの回転という順序で2つの変換をまとめたものである。
重要なのはrotZである。rotYだけを行った段階ではy軸周りの自転にしかならない。そこからさらに、Sphereに対してrotZを実行することで、Sphereの自転がy軸と$20$°の角度をなす軸の周りで行われるようになるのである。


図7は、図6のアニメーションの最初のいくつかのフレームにおける Sphereの変換過程である。赤いフィルターの状態から通常色に切り替わった時点でフレーム描画が発生するが、それらのフレームを連続的に表示したものが図6のアニメーションである。
# Code4
では上記のプログラムに公転処理を追加する。処理手順は次の通り。
(1) Sphereをy軸周りに自転させる
(2) Sphereをz軸周りに $-20$°回転させる
(3) Sphereを公転軌道上へ移動させる
手順(1)、(2)は前回と同じであり、ここでは(3)の公転処理が追加されている。
[Code4] (実行結果 図8)
i_degRot += 4.0f; Matrix4x4 rotY = TH3DMath.GetRotation4x4(i_degRot, Vector3.up); Matrix4x4 rotZ = TH3DMath.GetRotation4x4(-20.0f, Vector3.forward); Matrix4x4 R = rotZ * rotY; i_degRev += 1.0f; Matrix4x4 rev = TH3DMath.GetRotation4x4(i_degRev, Vector3.up); Vector3 np = rev * new Vector4(3.0f, 0.0f, 0.0f, 1.0f); Matrix4x4 T = TH3DMath.GetTranslation4x4(np); Matrix4x4 M = T * R; Sphere.SetMatrix(M);
このプログラムはCode1とCode3を合わせた処理になっている。4行目まではCode3と同じであり、6~9行目はCode1の1~4行目と同じである。4行目の回転行列RはCode3で見たように、y軸と$20$°の角度をなす軸の周りで Sphereを自転させる行列であり、9行目の平行移動行列Tは、Sphereを公転軌道上に移動させる行列である。11行目の M = T * R は、まず(原点において)傾いた軸の周りでの自転を行い(R)、次に公転軌道上への移動を行う(T)という2つの変換をまとめたものである。


実行結果(図8)に見られるように、Sphereの運動は傾いた自転軸の周りを自転しながらの公転となっている。
図9は、図8の最初の方のいくつかのフレームにおける Sphereの変換過程である。赤いフィルターの状態から通常色に切り替わった時点でフレーム描画が発生するが、それらのフレームを連続的に表示したものが図9のアニメーションである。
# Code5
本節における公転軌道は、すべて原点を中心とするy軸周りの軌道であった。ここでは、原点以外の点を中心とする公転軌道を公転するプログラムについて考える。図10には小さい球体が $(5,\ 3,-5)$ の位置に置かれている。今回作成するのは、この小さい球体を中心とする半径$3$の円周上を公転するプログラムである。ただし、公転面の法線はy軸に平行であるとする。つまり、今回の公転の中心は小さい球体であり、公転の回転軸は図には示されていないが、y軸に平行で小さい球体を通る軸である。また、自転についてはCode4と同じく、Sphereを原点に置いたときにy軸と$20$°の角度をなす軸を自転軸とする (図5参照)。


プログラムを以下に示す。
[Code5] (実行結果 図11)
i_degRot += 4.0f; Matrix4x4 rotY = TH3DMath.GetRotation4x4(i_degRot, Vector3.up); Matrix4x4 rotZ = TH3DMath.GetRotation4x4(-20.0f, Vector3.forward); Matrix4x4 R = rotZ * rotY; i_degRev += 1.0f; Matrix4x4 rev = TH3DMath.GetRotation4x4(i_degRev, Vector3.up); Vector3 np = rev * new Vector4(3.0f, 0.0f, 0.0f, 1.0f); np += c_centerPos; Matrix4x4 T = TH3DMath.GetTranslation4x4(np); Matrix4x4 M = T * R; Sphere.SetMatrix(M);
このプログラムはCode4とほとんど同じである。違いが1点だけあり、それは9行目で np += c_centerPos という処理が追加されていることである。c_centerPosは、公転軌道の中心である $(5,\ 3,-5)$ (小さい球体の位置)を表すVector3型の定数である。8行目で計算される np は Sphereの移動先の位置であるが、それは原点を中心とする公転軌道上である。毎フレーム np に c_centerPos を加算することで、Sphereの移動先の位置は毎フレーム $(5,\ 3,-5)$ だけ余分にずれることになるが、これによって公転軌道が原点中心から $(5,\ 3,-5)$ 中心になるのである。
すなわち、Sphereは小さい球体を中心とする、y軸に平行で小さい球体を通る軸の周りを公転することになるのである。
© 2020-2025 Redpoll's 60 (All rights reserved)