Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-15
第4章 3D空間におけるオブジェクトの運動
$§$4-15 一体化したオブジェクトの運動 6
小学校の算数では立体図形の展開や組み立てに関する問題がよく見られる。コンピューターグラフィックス的な観点でいえば、展開図から立体図形を組み立てることも、立体図形を展開することも階層構造に含まれる複数のオブジェクトによる一体化した運動である。立体図形の底面や側面の1つ1つがオブジェクトであり、それらのオブジェクトがある階層構造の中で親子関係を構成しているのである。
本節では基本的な立体図形を対象として、立体図形の展開や組み立てを実装する。
三角柱は上側、下側の2つの底面と3つの側面の計5つの面によって構成される。以下は各面 Face0 ~ Face4 の初期状態であり、下図において見えているのは各面の裏側である (注1)。プログラムではそれらの各面は Face[0] ~ Face[4] として配列の形で使われる。
なお、便宜上 以降の文章では三角柱の上側の底面を「上面」、下側の底面を単に「底面」と呼ぶことにする。
図1の Face0 は底面であり、図2の Face4 は上面である。上面、底面は初期状態では逆の方向を向いている (ここでは上面、底面にそれぞれ別のオブジェクトを使っているが、向きが逆なだけで大きさや形は同じであるから、これらの2つの面に全く同じオブジェクトを2つ使っても三角柱を構成することはできる。上面、底面のそれぞれに別のオブジェクトを使っているのはプログラムの内容を簡単にするため、また、本節のプログラムの内容を統一的なものにするためである)。
図3は側面であるが、3つの側面はいずれも大きさや形は同じであり、Face1 ~ Face3 には全く同じオブジェクトを3つ使っている。3つの側面はいずれも横の長さが $1.0$ 、高さは $1.2$ である。
下図4はこれらの Face から三角柱を組み立てた状態、図5は展開された状態、図6はこの5つのFaceの階層構造である (Face0(底面)が一番上の階層の親であり、Face4(上面)が一番下の階層の子である)。
図5の各Faceには番号が振られているが、これらは Face0 ~ Face4 を表している。
Face1 ~ Face3 は側面であるが、Face2をFace1にアタッチするには、下図7に示されるようにFace2の左端をFace1の右端まで平行移動させればよい。それは単に側面の横の長さ($1.0$)だけ x軸方向に移動させることを意味する。
Face3をFace2にアタッチする際の平行移動も全く同じである。


図8はFace4(上面)をFace3にアタッチしたときの状態であるが、これはFace4を初期状態の位置から側面の高さ($1.2$)だけ z軸方向に移動させればよい。
次のプログラムは図6に示される階層構造を持つFace0 ~ Face4を用いて、三角柱の展開図を構成するものである。
[Code1] (実行結果 図5)
上図1~3に示されるように各Faceは初期状態において裏側の面が見えている。したがって、展開された状態にするには各Faceの面の裏表を変える必要はなく、各Faceをそれぞれのアタッチポジションまで移動させればよい。
Face1は初期状態においてすでにFace0にアタッチされた状態になっているので動かす必要はない。また、Face0も特に動かす必要はないので、この2つのFaceのローカル行列は identity行列である。
側面のFace2、Face3はそれぞれ自身の左端を親オブジェクトの右端へ移動させるために x軸方向に $1$ だけ移動する(図7)。上面のFace4は自身の下端を親オブジェクトの上端へ移動させるために z軸方向に $1.2$ だけ移動する(図8)。
以上が各Faceのローカル行列の内容である (2~6行目)。
8行目以降は各Faceのワールド行列を計算して実行する処理であるが、これは以下の処理をfor文を使って書き直したに過ぎない (今までのプログラムでもそうであったが、ワールド行列の計算では無駄な計算が行われている。しかし、ワールド行列の計算を印象付けるためにしばらくはこのままの形を続ける)。
(注1 : 3-5節の法線ベクトルに関する解説の中で、Unityのデフォルトの設定では面の表側は表示されるが、裏側は表示されないと述べた。しかし、上記で使用している三角柱の各面を示す図では面の裏側が表示されている。例えば、以下の図9は三角柱の上面の裏側、図10は上面の表側である(図9の状態から $180^\circ$ 回転させて適当に位置を調整したもの)。両方とも表示されているのは単に面の表用と裏用に2つの三角形を使っているからである。言い換えれば、この上面は表用の三角形と裏用の三角形の2つを貼り合わせているだけである(下図11は貼り合わせた状態から開いた状態にしたもの)。
本節中で使われる立体図形の各面は三角形や長方形や円であるが、それらの面はすべて上記のように表用、裏用の2つを貼り合わせたものになっている。したがって「面の裏側」と記載されていても、それは実際には法線ベクトルの出ていない側が見えているというわけではない。)
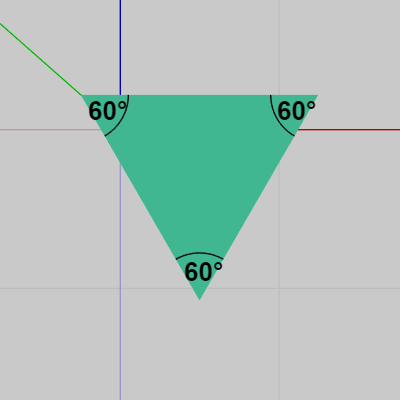
図12 この三角柱の上面(及び底面)は正三角形(真上から見たときのもの) 本節の三角柱はその底面が正三角形であり、したがって 各側面のなす角は図12に示されるように $60^\circ$ である (図12は組み立てられた三角柱を真上から見たときのもの)。
今回のプログラムでは三角柱の側面のみを組み立てる (簡単のため、側面Face1~Face3のみを使用する)。側面を組み立てるためには、3つのFaceが互いに $60^\circ$ の角をなすようにしなければならない。3つの側面は初期状態では上図3に示される状態であり、3つのFaceは完全に重なっているが、今回のプログラムにおいて Face2をFace1にアタッチする際には、2つのFaceのなす角が $60^\circ$ になるように、まず Face2に回転を行う必要がある。このときのFace2に実行する回転は z軸周りの $120^\circ$ の回転である ($60^\circ$ではない)。この回転を行ってからFace1の右端まで平行移動を行う。
プログラムにすると次のようになる。
[Beta2] (実行結果 図13)
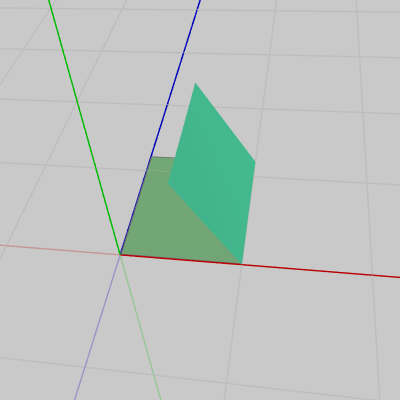
図13 Beta2 実行結果 Face2に実行される変換は、まず z軸周りの $120^\circ$ の回転を行い、さらにその回転後にアタッチポジションまでの平行移動を実行する、という2つの変換である。2行目の rotSide はこの変換における回転を表す回転行列であり、3行目の traSide はこの変換における平行移動を表す平行移動行列である。
Face3をFace2にアタッチする際の変換も同じである。まず z軸周りの $120^\circ$ の回転、次にアタッチポジションまでの平行移動の2つの変換である。
次のプログラムは Face1、Face2、Face3のうち、Face2、Face3を折り曲げて三角柱の側面を組み立てるものである。ここでは Face1に対しては何も変換は実行しないので、組み立てられた側面はXZ平面に横になったままの状態である。
[Code2] (実行結果 図14)
Face3に対する処理が追加されただけで、プログラム自体は上のBeta2とほとんど変わらない。
下図15は各Faceの変換過程をアニメーションにしたものである。まず、Face3が初期状態から(z軸周りに) $120^\circ$ 回転し、Face2にアタッチされる。次に、Face2が初期状態から $120^\circ$ 回転し、Face1にアタッチされる。
結果的に三角柱の側面が構成されるが、図に示されるようにまだXZ平面上に横になったままである。

図14 Code2 実行結果 
図15 各Faceの変換過程
(アニメーション中に「localFace3」「localFace2」が表示されている間は、Face3、Face2にlocalFace3、localFace2が実行されていることを意味している。それらのローカル行列は回転行列と平行移動行列の積であるが、アニメーション中に表示される「rotFace3」「rotFace2」はプログラム2行目のrotSideのことであり、「traFace3」「traFace2」はプログラム3行目のtraSideのことである。)
Code2は三角柱の側面を組み立てるものであったが、ここから追加する処理は側面を直立した状態にすること、そして三角柱の上側にフタをすることの2つの処理である。
側面を直立した状態にするためには、単に Face1に対して x軸周りの $-90^\circ$ 回転を行えばよい。具体的には次のコードになる。
[Beta3] (実行結果 図16)
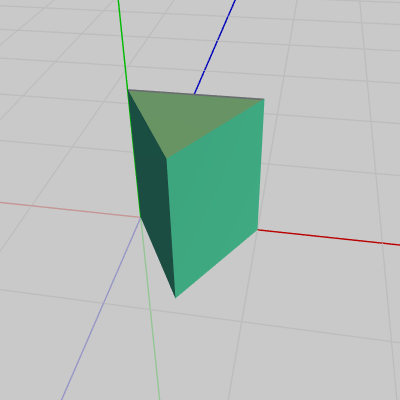
図16 Beta3 実行結果 Code2では、6行目のFace1のローカル行列の内容は identity行列であったが、ここではそれが x軸周りに $-90^\circ$ 回転させる行列になっている。変更点はそれだけである。ただし、このプログラムでは側面(Face1~Face3)しか使っていないため三角柱の上側が開いた状態になっている (図16)。
三角柱の上側にフタをするには、上面(Face4)をFace3にアタッチする際に、x軸周りに $-90^\circ$ 回転した状態でアタッチすればよい。そのようにすれば、組み立てた際に三角柱の上側が(Face4によって)フタをされた状態になる (この回転を行わないと三角柱の上側はフタが開いた状態ままである)。
次のプログラムはFace0~Face4を使って三角柱を組み立てた状態にするものである。
[Code3] (実行結果 図17)
2~3行目はFace4(上面)のローカル行列の計算である。x軸周りに $-90^\circ$ 回転させた状態で、アタッチポジションへの移動を行う。5~9行目は3つの側面 Face1~Face3のローカル行列の計算であるが、これは上記のBeta3と同じである。また、Face0は初期状態から動かさないので実行される行列は identity行列である。
13行目以降はワールド行列の計算及び実行であるが、この処理はCode1のものと同じである。
下図18は各Faceの変換過程をアニメーションにしたものである。Face2、Face3、Face4はアタッチポジションまでの平行移動を行うが、いずれのFaceも まず初期状態において回転してから、アタッチポジションまでの移動を行う。
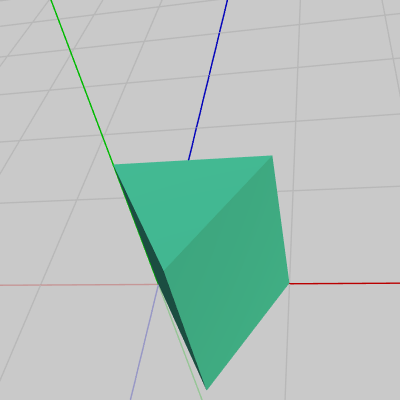
図17 Code3 実行結果 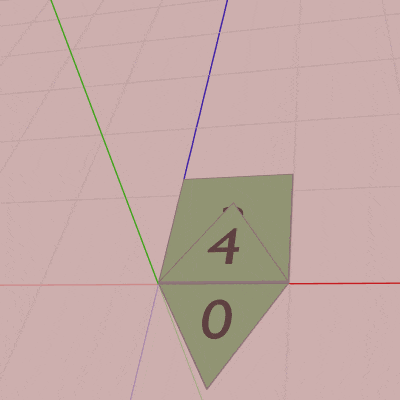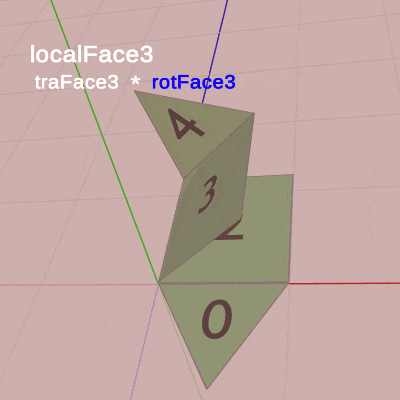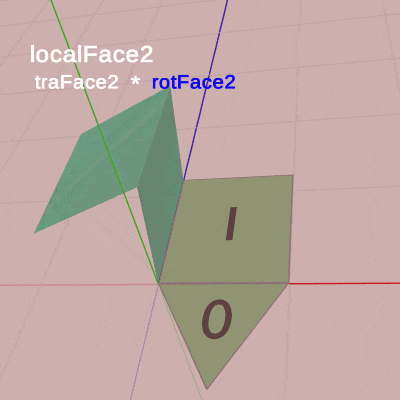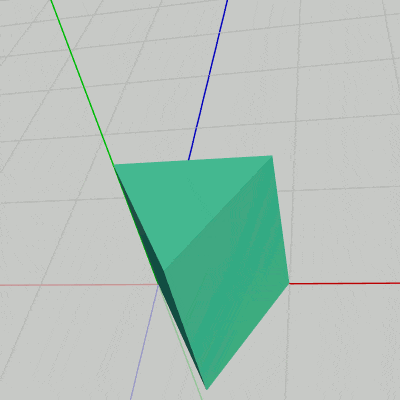
図18 変換過程のアニメーション
(このアニメーションにおいても「localFace#」と表示されている間は、Face1~Face4に対してその名前のローカル行列が実行されていることを意味している。Face2~Face4のローカル行列は回転行列と平行移動行列の積であるが、アニメーション中に表示される「traFace4」「rotFace4」は2~3行目の平行移動行列と回転行列であり、「rotFace3」「rotFace2」はプログラム5行目のrotSide、「traFace3」「traFace2」はプログラム6行目のtraSideのことである。)
展開された状態から組み立てられた状態へ(あるいはその逆へ)徐々に変化させるためには、上記のCode3において各Faceに実行される回転の回転角度を毎フレーム増減させればよい。
例えば、展開された状態から組み立てられた状態までの変化を180フレームかけて行うとしよう。その際、Face1の場合は180フレームかけて x軸周りに $-90^\circ$ 回転させればよいが、それはFace1に実行する回転の回転角度をその180フレームの間に $0^\circ$ から $-90^\circ$ に変化させることを意味する。
ここでは各Faceの回転用に以下のインスタンス変数を使用する (いずれも float型)。
次のプログラムは以下のキー操作によって、三角柱を展開された状態から組み立てられた状態へ、あるいはその逆へ変化させるものである (いずれも長押しに対応する)。
J : 三角柱を組み立てる。
K : 三角柱を展開する。
[Code4] (実行結果 図)
初期化ブロックではFaceの回転角度を表すインスタンス変数をすべて $0$ にセットしている。Faceに実行する回転角度が $0^\circ$ である場合、すべてのFaceをアタッチすると三角柱は展開された状態になる (このプログラムは展開された状態から始まる)。
6行目の i_motionCounter は三角柱の状態を変化させるために使われる int型のインスタンス変数である。このプログラムでは、展開された状態と組み立てられた状態の間を 180フレームかけて行き来するが、i_motionCounter は 180フレームかけて行われる変化の何フレーム目であるかを表す。プログラム開始時点では $0$ であり、このときには三角柱は展開された状態である (i_motionCounter の値を $180$ まで増加させると、三角柱は組み立てられた状態になる)。
12 ~ 21行目はキー操作の部分である。Jキーを押し続けると i_motionCounter が毎フレーム $1$ ずつ増加するが、その値が $180$ に達するとそれ以上は増加しない。Kキーを押し続けると i_motionCounter が毎フレーム $1$ ずつ減少するが、その値が $0$ まで下がるとそれ以上は減少しない。

図19 Code4 実行結果 24行目のfloat型ローカル変数 t は i_motionCounter の値によって $0$ から $1$ まで変化する。i_motionCounter が $0$ のときは t も $0$ であり、i_motionCounter が $180$ のときは t は $1$ である。
その下は各Faceの回転角度の計算であるが、ここでの計算では この t を使用している。したがって、i_motionCounter が $0$ から $180$ へ増加するにつれて、i_degPrimarySide、i_degTop は $0$ から $-90$ へ変化し、i_degSide は $0$ から $120$ へ変化する。i_motionCounter が $180$ から $0$ へ変化する場合は、それぞれの変化は逆方向(いずれも $0$)に向かう。
それ以降の処理についてはCode3と同じである。ただし、31行目、33行目、37行目の回転行列の計算において、ここではインスタンス変数が使われている (この部分はCode3では数値を直にセットしていた)。
今回のプログラムもCode4と内容自体は同じであり、キー操作によって2つの状態の間を行き来するものであるが、ここではその変化の過程を次の3段階に分ける。
(1) i_motionCounter の値が 0 から 60 の間に、展開された状態から側面を $90^\circ$ 回転させて直立させる。
(2) i_motionCounter の値が 60 から 180 の間に、側面を直立しただけの状態から底面に沿って折り曲げていく。
(3) i_motionCounter の値が 180 から 240 の間に、上面のフタをする。
プログラムは以下のとおり。
[Code5] (実行結果 図20)
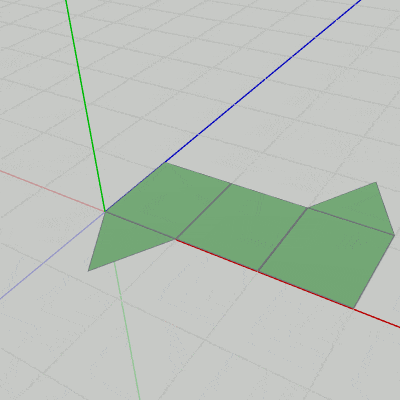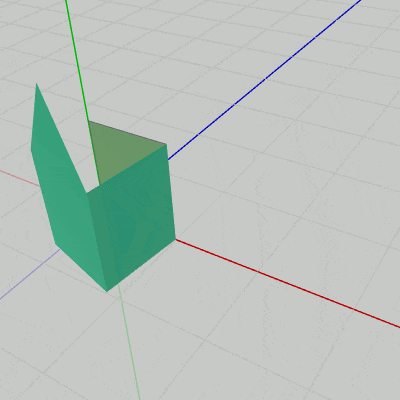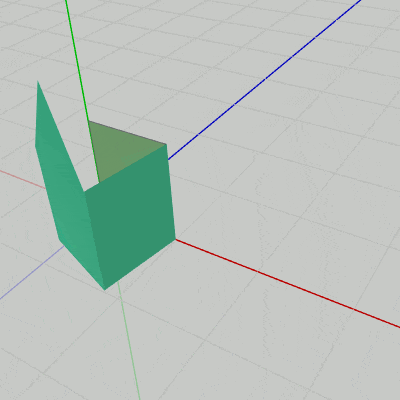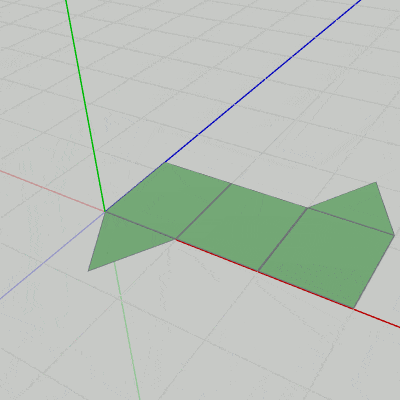
図20 Code5 実行結果 Code4との違いは2箇所で、1つ目は今回のプログラムでは一方の状態からもう一方の状態への変化が240フレームかけて行われるので、15行目の i_motionCounter の上限が $240$ に変わっていることである。
もう1つの違いは、その下の 24~38行目の部分で回転角度の計算が3段階に分かれている。
3つのifブロックがそれぞれの段階に対応している。処理内容に見られるように、それぞれの段階で行っていることは指定のFaceの回転角度を変化させているだけである。
最初のifブロック(24行目)は側面を直立させる処理に対応しており、Face1の回転角度 i_degPrimarySide を変化させている。次のifブロック(29行目)は底面に沿って側面を折り曲げる処理に対応しており、Face2、Face3の回転角度 i_degSide を変化させている。最後のifブロック(34行目)は上面にフタをする処理に対応しており、Face4の回転角度 i_degTop を変化させている。
それ以降の内容はCode4の29行目以降と同じものである。
立方体は6個の面で構成され、各面はいずれも正方形である。下図21は立方体を組み立てた状態、図22は立方体が展開された状態である (図22の各面の番号は三角柱の場合と同じく、ここで使用するFaceの番号である)。
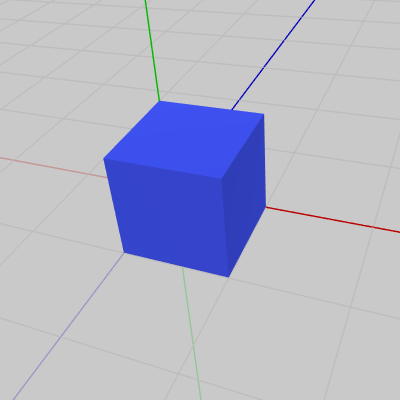
図21 立方体を組み立てた状態 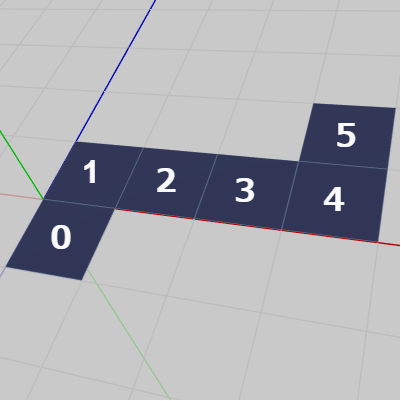
図22 展開された状態(展開図)
便宜上、以下では立方体の場合も上記の三角柱と同様に各面を「上面」「底面」「側面」で呼び分ける。
この立方体は2種類の正方形が使われており以下の図はそれぞれの初期状態である (この立方体の1辺の長さは $1$ であるため、正方形の1辺の長さも $1$ である)。
また、ここでも表示されているのは面の裏側である。
図23のFace0は立方体の底面に使う正方形であり、初期状態では x軸プラス側、z軸マイナス側に置かれている。
図24は5つのFaceに使われる正方形であり、初期状態では x軸プラス側、z軸プラス側に置かれている。Face1~Face4が側面、Face5が上面であり、これらすべてに図24の正方形を使う (6面すべてに同じ正方形を使って実装することもできるが、本節のプログラムの内容を統一するために初期状態で位置の異なる2種類の正方形を使用した)。
図25は各Faceの階層構造であり、Face0(底面)が一番上の親オブジェクト、Face5(上面)が一番下の子である。
次のプログラムは各Faceをそれぞれのアタッチポジションまで移動させて、立方体を展開された状態にするものである。
[Beta6] (実行結果 図22)
プログラムの内容はCode1とほとんど同じである。Code1は三角柱を展開された状態にするものであったが、そこでは Face1~Face3が側面として使われていた。今回は、側面の数が1つ増えているためFace1~Face4が側面であり、その分の記述が追加されているが、実際には各Faceをアタッチポジションまで平行移動させて一体化しているだけである (三角柱の場合と同じく、展開された状態ではFace0、Face1は初期状態のままである。Face1は初期状態においてアタッチされた状態であるためアタッチポジションまでの移動を行う必要はない)。
正方形の1辺の長さは $1$ であるため、アタッチポジションまでの移動の際は側面(Face2~Face4)の場合は x軸方向への $1$ の移動(3~5行目)、上面(Face5)の場合は z軸方向への $1$ の移動(2行目)となる。
続いて、立方体を組み立てた状態にする。プログラムは以下のとおり。
[Code6] (実行結果 図21)
このプログラムもまた実質的にはCode3と同じものである。Code3は三角柱を組み立てた状態にするものであったが、組み立てた状態にするためには各Faceをアタッチする際にまず指定の角度だけの回転を実行し、それからアタッチポジションまでの移動を行った。具体的には、Face1とFace4(上面)が x軸周りの $-90^\circ$ の回転、Face1以外の側面は z軸周りの $120^\circ$ の回転であった。
今回のプログラムは側面の数が1つ増えているだけで、その分の変更はあるが処理自体は同じである。各Faceにまず指定の角度だけの回転を実行し、アタッチポジションまでの移動である。
Face5(上面)の場合は初期状態において x軸周りに $-90^\circ$ の回転を行い、回転した状態でFace4の上端への移動(z軸方向への $1$ の移動)となる (2~3行目)。
Face1はアタッチポジションまでの移動を行う必要はないので x軸周りの $-90^\circ$ の回転だけである (10行目)。Face1以外の側面(Face2~Face4)は z軸周りの $90^\circ$ の回転であり、その回転を実行してからアタッチポジションまでの移動となる (5~9行目 ; 側面が4つになっているために回転角度が$90^\circ$に変わっている)。
J : 立方体を組み立てる。
K : 立方体を展開する。
しかし、その内容はCode5の三角柱の場合とほとんど同じである。
[Code7] (実行結果 図26)
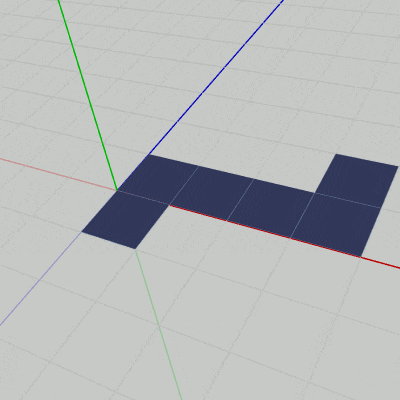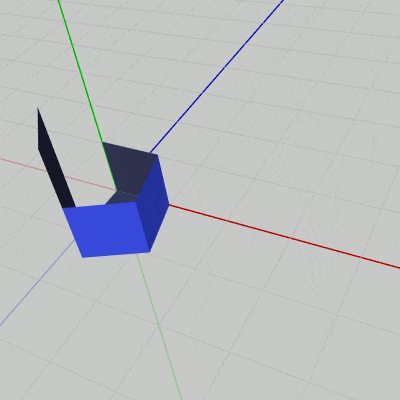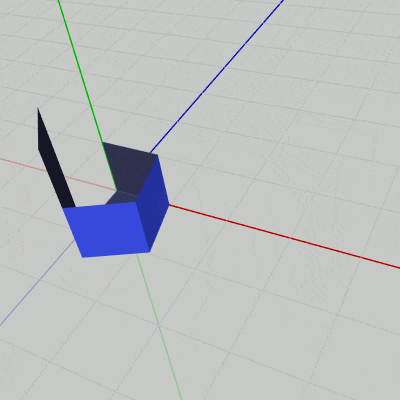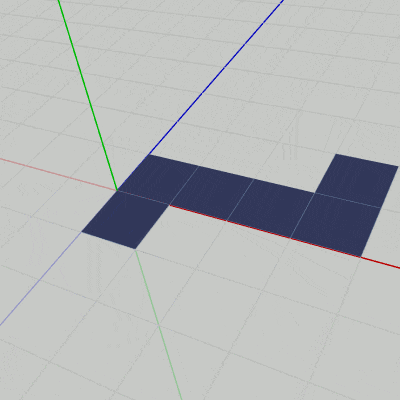
図26 Code7 実行結果 このプログラムで使われているインスタンス変数はCode5のものと同じであり、初期化ブロックの内容も同じである。i_degPrimarySide はFace1の回転角度、i_degSide はFace1以外の側面の回転角度、i_degTop はFace5(上面)の回転角度として使われる。
今回のプログラムも展開された状態から組み立てられた状態への変化(あるいはその逆への変化)が240フレームかけて行われる。i_motionCounter の役割もCode5と同じであり、その240フレームかけて行われる変化の何フレーム目であるかを表す。
それ以降の部分もCode5といくつかの点を除いては変わりはないが、簡単に触れておこう。
12~21行目はキー操作の部分であり、ここでも Jキーを押し続けることで展開された状態から組み立てられた状態へ変化し、Kキーを押し続けることでその逆の変化になる。
24~38行目は各Faceの回転角度の計算であり、i_motionCounter の値に応じて変化する。i_motionCounter が $0$ に近い程 回転角度は $0$ に近くなり、立方体は展開された状態になっていく。i_motionCounter が最大値である $240$ に近づくにつれて回転角度はそれぞれの最大値(あるいは最小値)に近づき、立方体は組み立てられた状態になっていく。
それ以降の処理は回転行列を算出する際の回転角度にインスタンス変数が使われている点(42、44、49行目)を除けばCode6と同じである。
Code5とCode7ではキー操作によって、三角柱 及び立方体を展開された状態から組み立てられた状態へ(あるいはその逆へ)変化させた。ここで作成するプログラムもまた同じくキー操作によって、立体図形の展開された状態と組み立てられた状態の間を行き来できるようにするものであるが、ここで課題となる図形は円柱である。
以下は今回使用する円柱の底面及び上面の初期状態である (今までと同様に「上面」「底面」「側面」で呼び分ける)。
図27のFace0は円柱の底面であり、図28のFace33は円柱の上面である (表示されているのは面の裏側)。三角柱や立方体の場合と同様に、底面と上面は形、大きさは同じであるが初期状態の位置だけが異なっている。そして、実際にはこれらの底面や上面は正確には円ではなく図29に示されるように多角形であり、図27の底面 及び図28の上面は具体的には正32角形である。図29は円柱の上面の表側を拡大したときのものであるが、上面(あるいは底面)の円周は正確には32個の長さの等しい辺によって構成されている。図中の cw は1辺の長さを表している。
下図30は円柱の側面の初期状態である。この円柱は正確には正32角柱であるため、側面の数は 32 であり、Face1~Face32が側面として使われる (図30の細長い長方形が32個ある)。側面は今までのものと同様に初期状態ではXZ平面に置かれており、表示されている面は面の裏側である。円柱の高さが $1.8$ なので図中の縦方向の長さは $1.8$ であり、側面の横幅は cw となっているが、これは上図29の cw と同じ値である。
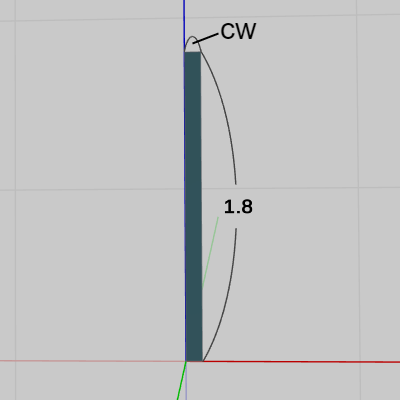
図30 Face1~Face32 初期状態 (側面 ; 側面を構成するFaceの数は32個である) 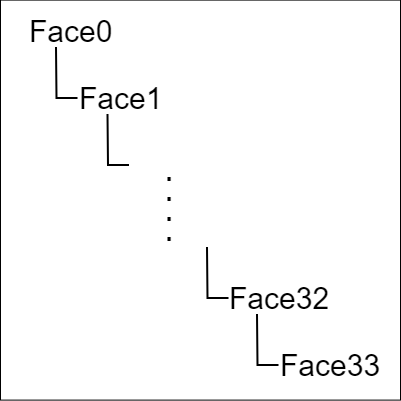
図31 オブジェクトの階層構造
図31はこの円柱を構成する全てのFaceの階層構造である。今回の階層構造は34階層であるが、その構造は三角柱や立方体の場合と同じである。底面(Face0)が一番上の親オブジェクトであり、上面(Face33)が一番下の子である。その他のFace(側面)については数字が小さい程 階層が上になっている。
上記の三角柱や立方体の場合でもそうであったが、今回の円柱の場合もその底面や上面は初期状態において、その中心が原点に置かれてはいない。このような配置になっているのはアタッチポジションまでの移動を簡単にするためである。
例えば、円柱の底面(Face0)は上図27に示されるように初期状態において z軸マイナス側に置かれている。以下の図32は底面(Face0)とFace1を表示したものであるが、両方とも初期状態のままである。図33はこの2つのFaceにカメラを近づけたときのものである (z軸は水色で表示してある)。
この図に示されるようにFace1の下側の辺は x軸上にあり、Face0の辺の1つも x軸上にある (この2つの辺の長さは両方とも同じであり、その値は上図29の cw である)。つまり、初期状態においてFace0の1つの辺とFace1の下側の辺が x軸上で重なった状態になっている。このため、Face1をFace0にアタッチする際はアタッチポジションまでの平行移動を行う必要がない。展開された状態や組み立てられた状態への変化の過程において、Face1は x軸周りの回転を行うがその回転は初期状態の位置で行えばよいのである。
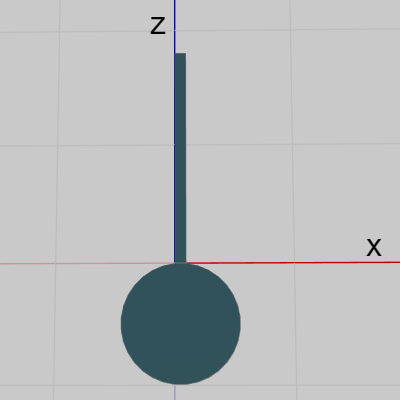
図32 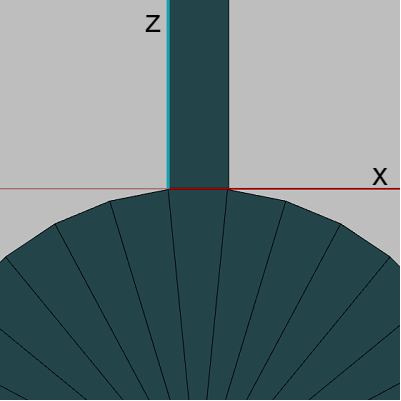
図33
円柱の上面(Face33)についても同様である。円柱の上面は上図28に示されるように初期状態において z軸プラス側に置かれている。以下の図34は上面(Face33)とFace32を表示したものであるが、この図ではFace33を z軸方向に円柱の高さ分($1.8$)だけ移動させている (Face33をFace32にアタッチした状態)。図35はこの2つのFaceにカメラを近づけたときのものである (ここでも z軸は水色で表示してある)。
この図に示されるように、Face32の上側の辺と上面(Face33)の辺の1つがちょうど重なった状態になっている。つまり、Face33をFace32にアタッチする際には、円柱の高さ分だけ z軸方向に平行移動させればよいのである。
底面や上面の配置が図27、28のようになっているのは、このような理由のためである。
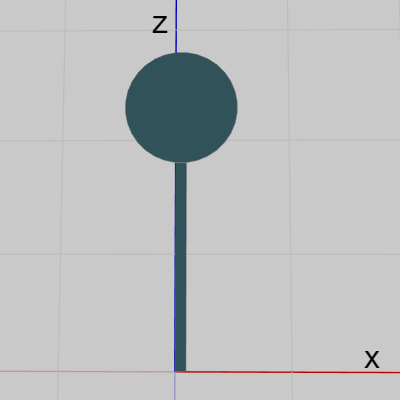
図34 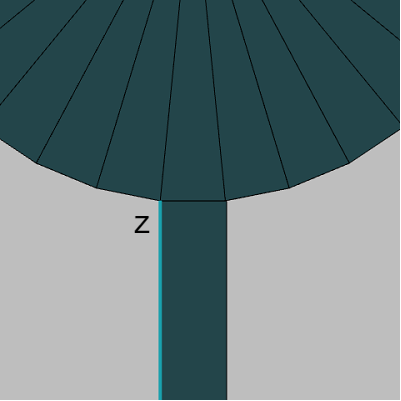
図35
プログラム中で用意されているインスタンス変数及び定数は以下のものである。
c_CylinderSideW 以外のインスタンス変数はCode5及びCode7で使われたものと同じである。すなわち、i_degPrimarySide、i_degSide、i_degTop はFaceの回転角度を表す3つのfloat型変数であり、i_motionCounter は展開された状態と組み立てられた状態の変化の過程で使われるint型変数である (これらの変数の役割についてもCode5やCode7の場合と同じである)。
プログラムは Sec415.cs内のCode8に作成するものとする。Code8は最初の段階では初期化ブロックのみが記述がされており、そのまま実行すると各オブジェクトが初期状態のまま重なって表示される。
今までのプログラムと同じように各Faceはプログラム中においては配列の形で使われるが、このプログラムで使用するのは Face[0] ~ Face[33] である。
また、三角柱や立方体の場合と同じく以下の2つのキーを使うものとする。
J : 円柱を組み立てる。
K : 円柱を展開する。
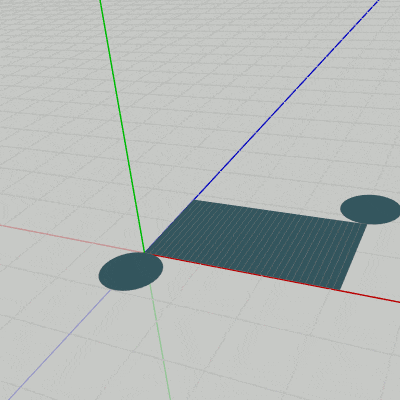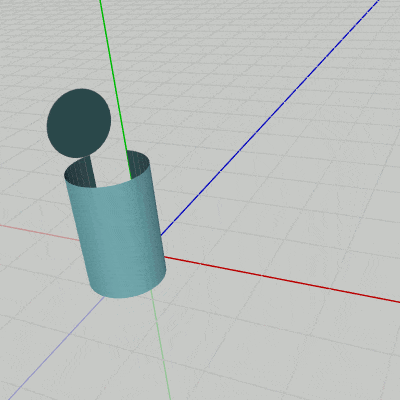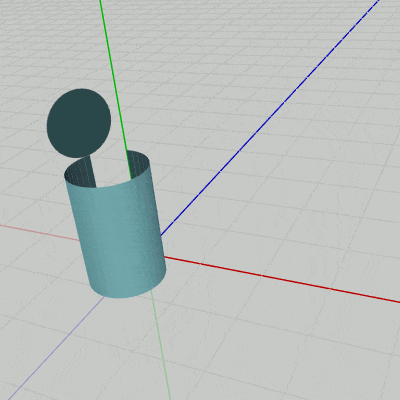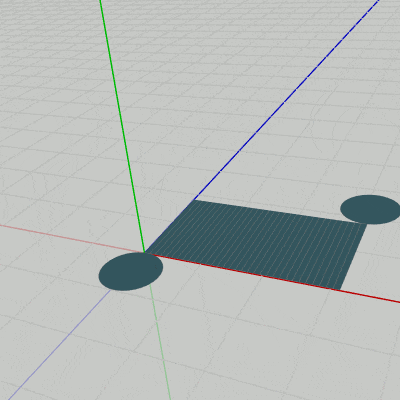
図36 Code8 実行結果 このプログラムは特に新しい処理を追加する必要はない。その内容はCode5やCode7と基本的には同じである。Code5は(正)三角柱であり、Code7は立方体、言い換えれば(正)四角柱である。今回の円柱は(正)32角柱である。三角柱は側面の数が 3、四角柱は側面の数が 4、32角柱は側面の数が 32である。このような見方をすれば、今回の円柱は三角柱や立方体と比べて側面の数に違いがあるに過ぎない。Code5やCode7と同じように作成すれば右図のような実行結果になる。
プログラムの解答例については Sec415_Ans.txt を参照 (Sec415_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
本節では基本的な立体図形を対象として、立体図形の展開や組み立てを実装する。
# Code1
まずは三角柱から始める (ここで使用する三角柱の底面は正三角形であるので詳しくは正三角柱である)。三角柱は上側、下側の2つの底面と3つの側面の計5つの面によって構成される。以下は各面 Face0 ~ Face4 の初期状態であり、下図において見えているのは各面の裏側である (注1)。プログラムではそれらの各面は Face[0] ~ Face[4] として配列の形で使われる。
なお、便宜上 以降の文章では三角柱の上側の底面を「上面」、下側の底面を単に「底面」と呼ぶことにする。
-
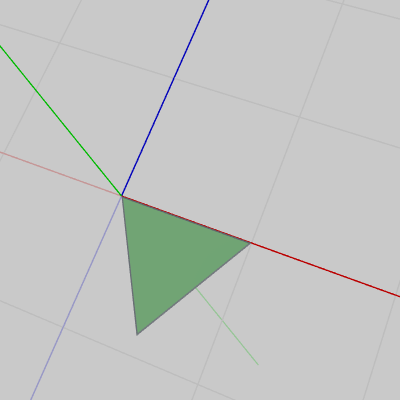 図1 Face0(底面)の初期状態
図1 Face0(底面)の初期状態 -
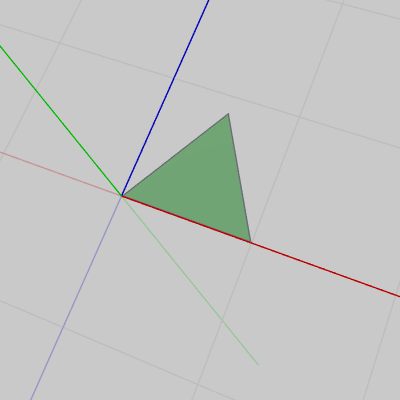 図2 Face4(上面)の初期状態
図2 Face4(上面)の初期状態 -
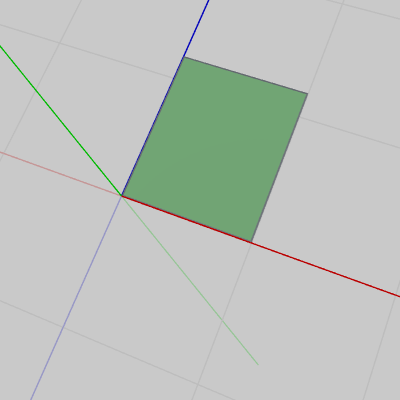 図3 Face1~Face3(側面)の初期状態 (3つの側面は形、大きさ いずれも同じ)
図3 Face1~Face3(側面)の初期状態 (3つの側面は形、大きさ いずれも同じ)
図1の Face0 は底面であり、図2の Face4 は上面である。上面、底面は初期状態では逆の方向を向いている (ここでは上面、底面にそれぞれ別のオブジェクトを使っているが、向きが逆なだけで大きさや形は同じであるから、これらの2つの面に全く同じオブジェクトを2つ使っても三角柱を構成することはできる。上面、底面のそれぞれに別のオブジェクトを使っているのはプログラムの内容を簡単にするため、また、本節のプログラムの内容を統一的なものにするためである)。
図3は側面であるが、3つの側面はいずれも大きさや形は同じであり、Face1 ~ Face3 には全く同じオブジェクトを3つ使っている。3つの側面はいずれも横の長さが $1.0$ 、高さは $1.2$ である。
下図4はこれらの Face から三角柱を組み立てた状態、図5は展開された状態、図6はこの5つのFaceの階層構造である (Face0(底面)が一番上の階層の親であり、Face4(上面)が一番下の階層の子である)。
-
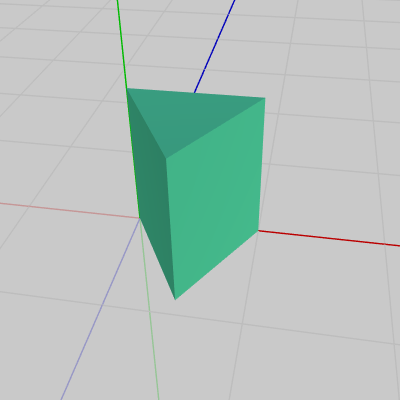 図4 三角柱を組み立てた状態
図4 三角柱を組み立てた状態 -
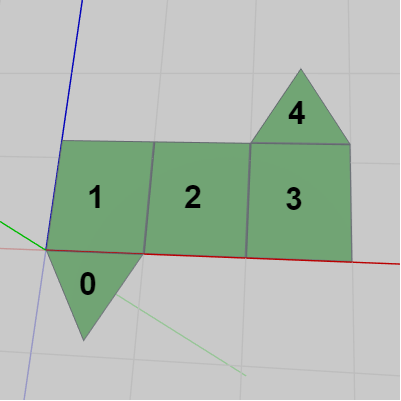 図5 展開された状態(展開図)
図5 展開された状態(展開図) -
 図6 オブジェクトの階層構造
図6 オブジェクトの階層構造
図5の各Faceには番号が振られているが、これらは Face0 ~ Face4 を表している。
Face1 ~ Face3 は側面であるが、Face2をFace1にアタッチするには、下図7に示されるようにFace2の左端をFace1の右端まで平行移動させればよい。それは単に側面の横の長さ($1.0$)だけ x軸方向に移動させることを意味する。
Face3をFace2にアタッチする際の平行移動も全く同じである。

図7 Face2をFace1にアタッチする (初期状態の位置から x軸方向に1.0移動)

図8 Face4をFace3にアタッチする (初期状態の位置から z軸方向に1.2移動)
図8はFace4(上面)をFace3にアタッチしたときの状態であるが、これはFace4を初期状態の位置から側面の高さ($1.2$)だけ z軸方向に移動させればよい。
次のプログラムは図6に示される階層構造を持つFace0 ~ Face4を用いて、三角柱の展開図を構成するものである。
[Code1] (実行結果 図5)
Matrix4x4[] localFace = new Matrix4x4[5];
localFace[4] = TH3DMath.GetTranslation4x4(0.0f, 0.0f, 1.2f);
localFace[3] = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f);
localFace[2] = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f);
localFace[1] = Matrix4x4.identity;
localFace[0] = Matrix4x4.identity;
for (int i = 4; i >= 0; i--)
{
Matrix4x4 worldM = localFace[0];
for (int j = 1; j <= i; j++)
{
worldM *= localFace[j];
}
Face[i].SetMatrix(worldM);
}
上図1~3に示されるように各Faceは初期状態において裏側の面が見えている。したがって、展開された状態にするには各Faceの面の裏表を変える必要はなく、各Faceをそれぞれのアタッチポジションまで移動させればよい。
Face1は初期状態においてすでにFace0にアタッチされた状態になっているので動かす必要はない。また、Face0も特に動かす必要はないので、この2つのFaceのローカル行列は identity行列である。
側面のFace2、Face3はそれぞれ自身の左端を親オブジェクトの右端へ移動させるために x軸方向に $1$ だけ移動する(図7)。上面のFace4は自身の下端を親オブジェクトの上端へ移動させるために z軸方向に $1.2$ だけ移動する(図8)。
以上が各Faceのローカル行列の内容である (2~6行目)。
8行目以降は各Faceのワールド行列を計算して実行する処理であるが、これは以下の処理をfor文を使って書き直したに過ぎない (今までのプログラムでもそうであったが、ワールド行列の計算では無駄な計算が行われている。しかし、ワールド行列の計算を印象付けるためにしばらくはこのままの形を続ける)。
worldFace[4] = localFace[0] * localFace[1] * localFace[2] * localFace[3] * localFace[4]; worldFace[3] = localFace[0] * localFace[1] * localFace[2] * localFace[3]; worldFace[2] = localFace[0] * localFace[1] * localFace[2]; worldFace[1] = localFace[0] * localFace[1]; worldFace[0] = localFace[0]; Face[4].SetMatrix(worldFace[4]); Face[3].SetMatrix(worldFace[3]); Face[2].SetMatrix(worldFace[2]); Face[1].SetMatrix(worldFace[1]); Face[0].SetMatrix(worldFace[0]);
(注1 : 3-5節の法線ベクトルに関する解説の中で、Unityのデフォルトの設定では面の表側は表示されるが、裏側は表示されないと述べた。しかし、上記で使用している三角柱の各面を示す図では面の裏側が表示されている。例えば、以下の図9は三角柱の上面の裏側、図10は上面の表側である(図9の状態から $180^\circ$ 回転させて適当に位置を調整したもの)。両方とも表示されているのは単に面の表用と裏用に2つの三角形を使っているからである。言い換えれば、この上面は表用の三角形と裏用の三角形の2つを貼り合わせているだけである(下図11は貼り合わせた状態から開いた状態にしたもの)。
-
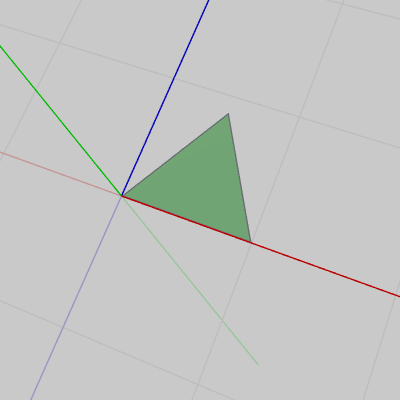 図9 上面の裏側
図9 上面の裏側 -
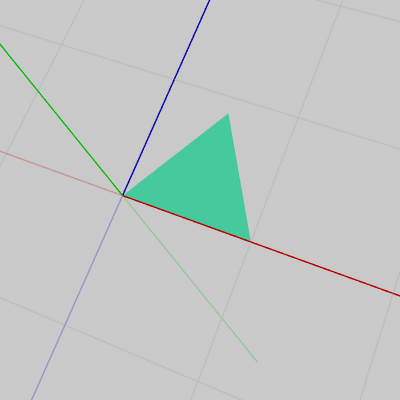 図10 上面の表側
図10 上面の表側 -
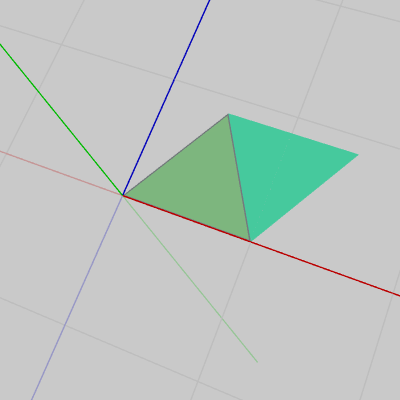 図11 2つの三角形を貼り合わせた状態から開いた状態にしたもの
図11 2つの三角形を貼り合わせた状態から開いた状態にしたもの
本節中で使われる立体図形の各面は三角形や長方形や円であるが、それらの面はすべて上記のように表用、裏用の2つを貼り合わせたものになっている。したがって「面の裏側」と記載されていても、それは実際には法線ベクトルの出ていない側が見えているというわけではない。)
# Code2

今回のプログラムでは三角柱の側面のみを組み立てる (簡単のため、側面Face1~Face3のみを使用する)。側面を組み立てるためには、3つのFaceが互いに $60^\circ$ の角をなすようにしなければならない。3つの側面は初期状態では上図3に示される状態であり、3つのFaceは完全に重なっているが、今回のプログラムにおいて Face2をFace1にアタッチする際には、2つのFaceのなす角が $60^\circ$ になるように、まず Face2に回転を行う必要がある。このときのFace2に実行する回転は z軸周りの $120^\circ$ の回転である ($60^\circ$ではない)。この回転を行ってからFace1の右端まで平行移動を行う。
プログラムにすると次のようになる。
[Beta2] (実行結果 図13)
Matrix4x4[] localFace = new Matrix4x4[5]; Matrix4x4 rotSide = TH3DMath.GetRotation4x4(120.0f, Vector3.forward); Matrix4x4 traSide = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f); localFace[2] = traSide * rotSide; localFace[1] = Matrix4x4.identity; Matrix4x4 worldFace2 = localFace[1] * localFace[2]; Matrix4x4 worldFace1 = localFace[1]; Face[2].SetMatrix(worldFace2); Face[1].SetMatrix(worldFace1);

Face3をFace2にアタッチする際の変換も同じである。まず z軸周りの $120^\circ$ の回転、次にアタッチポジションまでの平行移動の2つの変換である。
次のプログラムは Face1、Face2、Face3のうち、Face2、Face3を折り曲げて三角柱の側面を組み立てるものである。ここでは Face1に対しては何も変換は実行しないので、組み立てられた側面はXZ平面に横になったままの状態である。
[Code2] (実行結果 図14)
Matrix4x4[] localFace = new Matrix4x4[5]; Matrix4x4 rotSide = TH3DMath.GetRotation4x4(120.0f, Vector3.forward); Matrix4x4 traSide = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f); localFace[3] = traSide * rotSide; localFace[2] = traSide * rotSide; localFace[1] = Matrix4x4.identity; Matrix4x4 worldFace3 = localFace[1] * localFace[2] * localFace[3]; Matrix4x4 worldFace2 = localFace[1] * localFace[2]; Matrix4x4 worldFace1 = localFace[1]; Face[3].SetMatrix(worldFace3); Face[2].SetMatrix(worldFace2); Face[1].SetMatrix(worldFace1);
Face3に対する処理が追加されただけで、プログラム自体は上のBeta2とほとんど変わらない。
下図15は各Faceの変換過程をアニメーションにしたものである。まず、Face3が初期状態から(z軸周りに) $120^\circ$ 回転し、Face2にアタッチされる。次に、Face2が初期状態から $120^\circ$ 回転し、Face1にアタッチされる。
結果的に三角柱の側面が構成されるが、図に示されるようにまだXZ平面上に横になったままである。


(アニメーション中に「localFace3」「localFace2」が表示されている間は、Face3、Face2にlocalFace3、localFace2が実行されていることを意味している。それらのローカル行列は回転行列と平行移動行列の積であるが、アニメーション中に表示される「rotFace3」「rotFace2」はプログラム2行目のrotSideのことであり、「traFace3」「traFace2」はプログラム3行目のtraSideのことである。)
# Code3
続いて、三角柱を組み立てた状態にする。Code2は三角柱の側面を組み立てるものであったが、ここから追加する処理は側面を直立した状態にすること、そして三角柱の上側にフタをすることの2つの処理である。
側面を直立した状態にするためには、単に Face1に対して x軸周りの $-90^\circ$ 回転を行えばよい。具体的には次のコードになる。
[Beta3] (実行結果 図16)
Matrix4x4[] localFace = new Matrix4x4[5]; Matrix4x4 rotSide = TH3DMath.GetRotation4x4(120.0f, Vector3.forward); Matrix4x4 traSide = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f); localFace[3] = traSide * rotSide; localFace[2] = traSide * rotSide; localFace[1] = TH3DMath.GetRotation4x4(-90.0f, Vector3.right); Matrix4x4 worldFace3 = localFace[1] * localFace[2] * localFace[3]; Matrix4x4 worldFace2 = localFace[1] * localFace[2]; Matrix4x4 worldFace1 = localFace[1]; Face[3].SetMatrix(worldFace3); Face[2].SetMatrix(worldFace2); Face[1].SetMatrix(worldFace1);

三角柱の上側にフタをするには、上面(Face4)をFace3にアタッチする際に、x軸周りに $-90^\circ$ 回転した状態でアタッチすればよい。そのようにすれば、組み立てた際に三角柱の上側が(Face4によって)フタをされた状態になる (この回転を行わないと三角柱の上側はフタが開いた状態ままである)。
次のプログラムはFace0~Face4を使って三角柱を組み立てた状態にするものである。
[Code3] (実行結果 図17)
Matrix4x4[] localFace = new Matrix4x4[5];
localFace[4] = TH3DMath.GetTranslation4x4(0.0f, 0.0f, 1.2f) *
TH3DMath.GetRotation4x4(-90.0f, Vector3.right);
Matrix4x4 rotSide = TH3DMath.GetRotation4x4(120.0f, Vector3.forward);
Matrix4x4 traSide = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f);
localFace[3] = traSide * rotSide;
localFace[2] = traSide * rotSide;
localFace[1] = TH3DMath.GetRotation4x4(-90.0f, Vector3.right);
localFace[0] = Matrix4x4.identity;
for (int i = 4; i >= 0; i--)
{
Matrix4x4 worldM = localFace[0];
for (int j = 1; j <= i; j++)
{
worldM *= localFace[j];
}
Face[i].SetMatrix(worldM);
}
2~3行目はFace4(上面)のローカル行列の計算である。x軸周りに $-90^\circ$ 回転させた状態で、アタッチポジションへの移動を行う。5~9行目は3つの側面 Face1~Face3のローカル行列の計算であるが、これは上記のBeta3と同じである。また、Face0は初期状態から動かさないので実行される行列は identity行列である。
13行目以降はワールド行列の計算及び実行であるが、この処理はCode1のものと同じである。
下図18は各Faceの変換過程をアニメーションにしたものである。Face2、Face3、Face4はアタッチポジションまでの平行移動を行うが、いずれのFaceも まず初期状態において回転してから、アタッチポジションまでの移動を行う。


(このアニメーションにおいても「localFace#」と表示されている間は、Face1~Face4に対してその名前のローカル行列が実行されていることを意味している。Face2~Face4のローカル行列は回転行列と平行移動行列の積であるが、アニメーション中に表示される「traFace4」「rotFace4」は2~3行目の平行移動行列と回転行列であり、「rotFace3」「rotFace2」はプログラム5行目のrotSide、「traFace3」「traFace2」はプログラム6行目のtraSideのことである。)
# Code4
では続いて、三角柱を展開された状態から組み立てられた状態へ、あるいは組み立てられた状態から展開された状態へ、キー操作によって徐々に変化させるプログラムを作成する。展開された状態から組み立てられた状態へ(あるいはその逆へ)徐々に変化させるためには、上記のCode3において各Faceに実行される回転の回転角度を毎フレーム増減させればよい。
例えば、展開された状態から組み立てられた状態までの変化を180フレームかけて行うとしよう。その際、Face1の場合は180フレームかけて x軸周りに $-90^\circ$ 回転させればよいが、それはFace1に実行する回転の回転角度をその180フレームの間に $0^\circ$ から $-90^\circ$ に変化させることを意味する。
ここでは各Faceの回転用に以下のインスタンス変数を使用する (いずれも float型)。
i_degPrimarySide
: Face1の回転角度を表す変数であり、展開された状態から組み立てられた状態を行き来する際には、この変数の値を $0$ から $-90$ の間で変化させればよい。i_degSide
: Face2、Face3の回転角度を表す変数であり、展開された状態から組み立てられた状態を行き来する際には、この変数の値を $0$ から $120$ の間で変化させればよい。i_degTop
: Face4(上面)の回転角度を表す変数であり、展開された状態から組み立てられた状態を行き来する際には、この変数の値を $0$ から $-90$ の間で変化させればよい。次のプログラムは以下のキー操作によって、三角柱を展開された状態から組み立てられた状態へ、あるいはその逆へ変化させるものである (いずれも長押しに対応する)。
J : 三角柱を組み立てる。
K : 三角柱を展開する。
[Code4] (実行結果 図)
if (!i_INITIALIZED)
{
i_degPrimarySide = 0.0f;
i_degSide = 0.0f;
i_degTop = 0.0f;
i_motionCounter = 0;
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.J))
{
i_motionCounter++;
if (i_motionCounter > 180) { i_motionCounter = 180; }
}
else if (Input.GetKey(KeyCode.K))
{
i_motionCounter--;
if (i_motionCounter < 0) { i_motionCounter = 0; }
}
float t = i_motionCounter / 180.0f;
i_degPrimarySide = -90.0f * t;
i_degSide = 120.0f * t;
i_degTop = -90.0f * t;
Matrix4x4[] localFace = new Matrix4x4[5];
localFace[4] = TH3DMath.GetTranslation4x4(0.0f, 0.0f, 1.2f) *
TH3DMath.GetRotation4x4(i_degTop, Vector3.right);
Matrix4x4 rotSide = TH3DMath.GetRotation4x4(i_degSide, Vector3.forward);
Matrix4x4 traSide = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f);
localFace[3] = traSide * rotSide;
localFace[2] = traSide * rotSide;
localFace[1] = TH3DMath.GetRotation4x4(i_degPrimarySide, Vector3.right);
localFace[0] = Matrix4x4.identity;
for (int i = 4; i >= 0; i--)
{
Matrix4x4 worldM = localFace[0];
for (int j = 1; j <= i; j++)
{
worldM *= localFace[j];
}
Face[i].SetMatrix(worldM);
}
初期化ブロックではFaceの回転角度を表すインスタンス変数をすべて $0$ にセットしている。Faceに実行する回転角度が $0^\circ$ である場合、すべてのFaceをアタッチすると三角柱は展開された状態になる (このプログラムは展開された状態から始まる)。
6行目の i_motionCounter は三角柱の状態を変化させるために使われる int型のインスタンス変数である。このプログラムでは、展開された状態と組み立てられた状態の間を 180フレームかけて行き来するが、i_motionCounter は 180フレームかけて行われる変化の何フレーム目であるかを表す。プログラム開始時点では $0$ であり、このときには三角柱は展開された状態である (i_motionCounter の値を $180$ まで増加させると、三角柱は組み立てられた状態になる)。
12 ~ 21行目はキー操作の部分である。Jキーを押し続けると i_motionCounter が毎フレーム $1$ ずつ増加するが、その値が $180$ に達するとそれ以上は増加しない。Kキーを押し続けると i_motionCounter が毎フレーム $1$ ずつ減少するが、その値が $0$ まで下がるとそれ以上は減少しない。

その下は各Faceの回転角度の計算であるが、ここでの計算では この t を使用している。したがって、i_motionCounter が $0$ から $180$ へ増加するにつれて、i_degPrimarySide、i_degTop は $0$ から $-90$ へ変化し、i_degSide は $0$ から $120$ へ変化する。i_motionCounter が $180$ から $0$ へ変化する場合は、それぞれの変化は逆方向(いずれも $0$)に向かう。
それ以降の処理についてはCode3と同じである。ただし、31行目、33行目、37行目の回転行列の計算において、ここではインスタンス変数が使われている (この部分はCode3では数値を直にセットしていた)。
# Code5
Code4では展開された状態から組み立てられた状態へ変化する際(あるいはその逆の場合でも)、底面を除くすべてのFaceが同時に変化していた。一方の状態からもう一方の状態への変化は180フレームかけて行われたが、具体的には 各Faceが180フレームかけて指定の回転角度を回転するものであった。今回のプログラムもCode4と内容自体は同じであり、キー操作によって2つの状態の間を行き来するものであるが、ここではその変化の過程を次の3段階に分ける。
(1) i_motionCounter の値が 0 から 60 の間に、展開された状態から側面を $90^\circ$ 回転させて直立させる。
(2) i_motionCounter の値が 60 から 180 の間に、側面を直立しただけの状態から底面に沿って折り曲げていく。
(3) i_motionCounter の値が 180 から 240 の間に、上面のフタをする。
プログラムは以下のとおり。
[Code5] (実行結果 図20)
if (!i_INITIALIZED)
{
i_degPrimarySide = 0.0f;
i_degSide = 0.0f;
i_degTop = 0.0f;
i_motionCounter = 0;
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.J))
{
i_motionCounter++;
if (i_motionCounter > 240) { i_motionCounter = 240; }
}
else if (Input.GetKey(KeyCode.K))
{
i_motionCounter--;
if (i_motionCounter < 0) { i_motionCounter = 0; }
}
if (0 <= i_motionCounter && i_motionCounter <= 60)
{
float t = i_motionCounter / 60.0f;
i_degPrimarySide = -90.0f * t;
}
if (60 <= i_motionCounter && i_motionCounter <= 180)
{
float t = (i_motionCounter - 60) / 120.0f;
i_degSide = 120.0f * t;
}
if (180 <= i_motionCounter && i_motionCounter <= 240)
{
float t = (i_motionCounter - 180) / 60.0f;
i_degTop = -90.0f * t;
}
Matrix4x4[] localFace = new Matrix4x4[5];
localFace[4] = TH3DMath.GetTranslation4x4(0.0f, 0.0f, 1.2f) *
TH3DMath.GetRotation4x4(i_degTop, Vector3.right);
Matrix4x4 rotSide = TH3DMath.GetRotation4x4(i_degSide, Vector3.forward);
Matrix4x4 traSide = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f);
localFace[3] = traSide * rotSide;
localFace[2] = traSide * rotSide;
localFace[1] = TH3DMath.GetRotation4x4(i_degPrimarySide, Vector3.right);
localFace[0] = Matrix4x4.identity;
for (int i = 4; i >= 0; i--)
{
Matrix4x4 worldM = localFace[0];
for (int j = 1; j <= i; j++)
{
worldM *= localFace[j];
}
Face[i].SetMatrix(worldM);
}

もう1つの違いは、その下の 24~38行目の部分で回転角度の計算が3段階に分かれている。
3つのifブロックがそれぞれの段階に対応している。処理内容に見られるように、それぞれの段階で行っていることは指定のFaceの回転角度を変化させているだけである。
最初のifブロック(24行目)は側面を直立させる処理に対応しており、Face1の回転角度 i_degPrimarySide を変化させている。次のifブロック(29行目)は底面に沿って側面を折り曲げる処理に対応しており、Face2、Face3の回転角度 i_degSide を変化させている。最後のifブロック(34行目)は上面にフタをする処理に対応しており、Face4の回転角度 i_degTop を変化させている。
それ以降の内容はCode4の29行目以降と同じものである。
# Code6
続いては立方体である。立方体は6個の面で構成され、各面はいずれも正方形である。下図21は立方体を組み立てた状態、図22は立方体が展開された状態である (図22の各面の番号は三角柱の場合と同じく、ここで使用するFaceの番号である)。


便宜上、以下では立方体の場合も上記の三角柱と同様に各面を「上面」「底面」「側面」で呼び分ける。
この立方体は2種類の正方形が使われており以下の図はそれぞれの初期状態である (この立方体の1辺の長さは $1$ であるため、正方形の1辺の長さも $1$ である)。
また、ここでも表示されているのは面の裏側である。
-
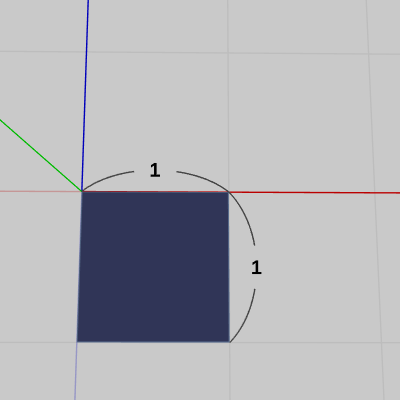 図23 Face0 初期状態 (底面)
図23 Face0 初期状態 (底面) -
 図24 Face1~Face5 初期状態 (側面及び上面)
図24 Face1~Face5 初期状態 (側面及び上面) -
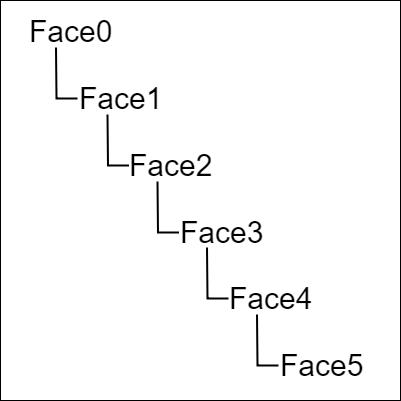 図25 オブジェクトの階層構造
図25 オブジェクトの階層構造
図23のFace0は立方体の底面に使う正方形であり、初期状態では x軸プラス側、z軸マイナス側に置かれている。
図24は5つのFaceに使われる正方形であり、初期状態では x軸プラス側、z軸プラス側に置かれている。Face1~Face4が側面、Face5が上面であり、これらすべてに図24の正方形を使う (6面すべてに同じ正方形を使って実装することもできるが、本節のプログラムの内容を統一するために初期状態で位置の異なる2種類の正方形を使用した)。
図25は各Faceの階層構造であり、Face0(底面)が一番上の親オブジェクト、Face5(上面)が一番下の子である。
次のプログラムは各Faceをそれぞれのアタッチポジションまで移動させて、立方体を展開された状態にするものである。
[Beta6] (実行結果 図22)
Matrix4x4[] localFace = new Matrix4x4[6];
localFace[5] = TH3DMath.GetTranslation4x4(0.0f, 0.0f, 1.0f);
localFace[4] = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f);
localFace[3] = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f);
localFace[2] = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f);
localFace[1] = Matrix4x4.identity;
localFace[0] = Matrix4x4.identity;
for (int i = 5; i >= 0; i--)
{
Matrix4x4 worldM = localFace[0];
for (int j = 1; j <= i; j++)
{
worldM *= localFace[j];
}
Face[i].SetMatrix(worldM);
}
プログラムの内容はCode1とほとんど同じである。Code1は三角柱を展開された状態にするものであったが、そこでは Face1~Face3が側面として使われていた。今回は、側面の数が1つ増えているためFace1~Face4が側面であり、その分の記述が追加されているが、実際には各Faceをアタッチポジションまで平行移動させて一体化しているだけである (三角柱の場合と同じく、展開された状態ではFace0、Face1は初期状態のままである。Face1は初期状態においてアタッチされた状態であるためアタッチポジションまでの移動を行う必要はない)。
正方形の1辺の長さは $1$ であるため、アタッチポジションまでの移動の際は側面(Face2~Face4)の場合は x軸方向への $1$ の移動(3~5行目)、上面(Face5)の場合は z軸方向への $1$ の移動(2行目)となる。
続いて、立方体を組み立てた状態にする。プログラムは以下のとおり。
[Code6] (実行結果 図21)
Matrix4x4[] localFace = new Matrix4x4[6];
localFace[5] = TH3DMath.GetTranslation4x4(0.0f, 0.0f, 1.0f) *
TH3DMath.GetRotation4x4(-90.0f, Vector3.right);
Matrix4x4 rotSide = TH3DMath.GetRotation4x4(90.0f, Vector3.forward);
Matrix4x4 traSide = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f);
localFace[4] = traSide * rotSide;
localFace[3] = traSide * rotSide;
localFace[2] = traSide * rotSide;
localFace[1] = TH3DMath.GetRotation4x4(-90.0f, Vector3.right);
localFace[0] = Matrix4x4.identity;
for (int i = 5; i >= 0; i--)
{
Matrix4x4 worldM = localFace[0];
for (int j = 1; j <= i; j++)
{
worldM *= localFace[j];
}
Face[i].SetMatrix(worldM);
}
このプログラムもまた実質的にはCode3と同じものである。Code3は三角柱を組み立てた状態にするものであったが、組み立てた状態にするためには各Faceをアタッチする際にまず指定の角度だけの回転を実行し、それからアタッチポジションまでの移動を行った。具体的には、Face1とFace4(上面)が x軸周りの $-90^\circ$ の回転、Face1以外の側面は z軸周りの $120^\circ$ の回転であった。
今回のプログラムは側面の数が1つ増えているだけで、その分の変更はあるが処理自体は同じである。各Faceにまず指定の角度だけの回転を実行し、アタッチポジションまでの移動である。
Face5(上面)の場合は初期状態において x軸周りに $-90^\circ$ の回転を行い、回転した状態でFace4の上端への移動(z軸方向への $1$ の移動)となる (2~3行目)。
Face1はアタッチポジションまでの移動を行う必要はないので x軸周りの $-90^\circ$ の回転だけである (10行目)。Face1以外の側面(Face2~Face4)は z軸周りの $90^\circ$ の回転であり、その回転を実行してからアタッチポジションまでの移動となる (5~9行目 ; 側面が4つになっているために回転角度が$90^\circ$に変わっている)。
# Code7
では次に、以下のキー操作によって立方体を展開された状態から組み立てられた状態へ(あるいはその逆へ)、徐々に変化させるプログラムを作成する。J : 立方体を組み立てる。
K : 立方体を展開する。
しかし、その内容はCode5の三角柱の場合とほとんど同じである。
[Code7] (実行結果 図26)
if (!i_INITIALIZED)
{
i_degPrimarySide = 0.0f;
i_degSide = 0.0f;
i_degTop = 0.0f;
i_motionCounter = 0;
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.J))
{
i_motionCounter++;
if (i_motionCounter > 240) { i_motionCounter = 240; }
}
else if (Input.GetKey(KeyCode.K))
{
i_motionCounter--;
if (i_motionCounter < 0) { i_motionCounter = 0; }
}
if (0 <= i_motionCounter && i_motionCounter <= 60)
{
float t = i_motionCounter / 60.0f;
i_degPrimarySide = -90.0f * t;
}
if (60 <= i_motionCounter && i_motionCounter <= 180)
{
float t = (i_motionCounter - 60) / 120.0f;
i_degSide = 90.0f * t;
}
if (180 <= i_motionCounter && i_motionCounter <= 240)
{
float t = (i_motionCounter - 180) / 60.0f;
i_degTop = -90.0f * t;
}
Matrix4x4[] localFace = new Matrix4x4[6];
localFace[5] = TH3DMath.GetTranslation4x4(0.0f, 0.0f, 1.0f) *
TH3DMath.GetRotation4x4(i_degTop, Vector3.right);
Matrix4x4 rotSide = TH3DMath.GetRotation4x4(i_degSide, Vector3.forward);
Matrix4x4 traSide = TH3DMath.GetTranslation4x4(1.0f, 0.0f, 0.0f);
localFace[4] = traSide * rotSide;
localFace[3] = traSide * rotSide;
localFace[2] = traSide * rotSide;
localFace[1] = TH3DMath.GetRotation4x4(i_degPrimarySide, Vector3.right);
localFace[0] = Matrix4x4.identity;
for (int i = 5; i >= 0; i--)
{
Matrix4x4 worldM = localFace[0];
for (int j = 1; j <= i; j++)
{
worldM *= localFace[j];
}
Face[i].SetMatrix(worldM);
}

今回のプログラムも展開された状態から組み立てられた状態への変化(あるいはその逆への変化)が240フレームかけて行われる。i_motionCounter の役割もCode5と同じであり、その240フレームかけて行われる変化の何フレーム目であるかを表す。
それ以降の部分もCode5といくつかの点を除いては変わりはないが、簡単に触れておこう。
12~21行目はキー操作の部分であり、ここでも Jキーを押し続けることで展開された状態から組み立てられた状態へ変化し、Kキーを押し続けることでその逆の変化になる。
24~38行目は各Faceの回転角度の計算であり、i_motionCounter の値に応じて変化する。i_motionCounter が $0$ に近い程 回転角度は $0$ に近くなり、立方体は展開された状態になっていく。i_motionCounter が最大値である $240$ に近づくにつれて回転角度はそれぞれの最大値(あるいは最小値)に近づき、立方体は組み立てられた状態になっていく。
それ以降の処理は回転行列を算出する際の回転角度にインスタンス変数が使われている点(42、44、49行目)を除けばCode6と同じである。
# Code8
最後のプログラムは読者用の課題である。Code5とCode7ではキー操作によって、三角柱 及び立方体を展開された状態から組み立てられた状態へ(あるいはその逆へ)変化させた。ここで作成するプログラムもまた同じくキー操作によって、立体図形の展開された状態と組み立てられた状態の間を行き来できるようにするものであるが、ここで課題となる図形は円柱である。
以下は今回使用する円柱の底面及び上面の初期状態である (今までと同様に「上面」「底面」「側面」で呼び分ける)。
-
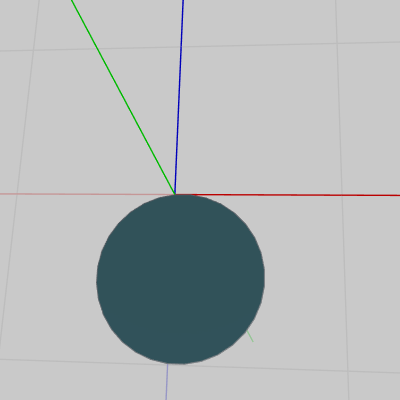 図27 Face0 初期状態 (底面)
図27 Face0 初期状態 (底面) -
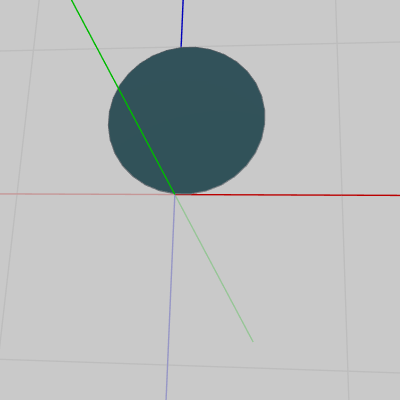 図28 Face33 初期状態 (上面)
図28 Face33 初期状態 (上面) -
 図29 ここで使用する円柱の底面や上面は正32角形
図29 ここで使用する円柱の底面や上面は正32角形
図27のFace0は円柱の底面であり、図28のFace33は円柱の上面である (表示されているのは面の裏側)。三角柱や立方体の場合と同様に、底面と上面は形、大きさは同じであるが初期状態の位置だけが異なっている。そして、実際にはこれらの底面や上面は正確には円ではなく図29に示されるように多角形であり、図27の底面 及び図28の上面は具体的には正32角形である。図29は円柱の上面の表側を拡大したときのものであるが、上面(あるいは底面)の円周は正確には32個の長さの等しい辺によって構成されている。図中の cw は1辺の長さを表している。
下図30は円柱の側面の初期状態である。この円柱は正確には正32角柱であるため、側面の数は 32 であり、Face1~Face32が側面として使われる (図30の細長い長方形が32個ある)。側面は今までのものと同様に初期状態ではXZ平面に置かれており、表示されている面は面の裏側である。円柱の高さが $1.8$ なので図中の縦方向の長さは $1.8$ であり、側面の横幅は cw となっているが、これは上図29の cw と同じ値である。


図31はこの円柱を構成する全てのFaceの階層構造である。今回の階層構造は34階層であるが、その構造は三角柱や立方体の場合と同じである。底面(Face0)が一番上の親オブジェクトであり、上面(Face33)が一番下の子である。その他のFace(側面)については数字が小さい程 階層が上になっている。
上記の三角柱や立方体の場合でもそうであったが、今回の円柱の場合もその底面や上面は初期状態において、その中心が原点に置かれてはいない。このような配置になっているのはアタッチポジションまでの移動を簡単にするためである。
例えば、円柱の底面(Face0)は上図27に示されるように初期状態において z軸マイナス側に置かれている。以下の図32は底面(Face0)とFace1を表示したものであるが、両方とも初期状態のままである。図33はこの2つのFaceにカメラを近づけたときのものである (z軸は水色で表示してある)。
この図に示されるようにFace1の下側の辺は x軸上にあり、Face0の辺の1つも x軸上にある (この2つの辺の長さは両方とも同じであり、その値は上図29の cw である)。つまり、初期状態においてFace0の1つの辺とFace1の下側の辺が x軸上で重なった状態になっている。このため、Face1をFace0にアタッチする際はアタッチポジションまでの平行移動を行う必要がない。展開された状態や組み立てられた状態への変化の過程において、Face1は x軸周りの回転を行うがその回転は初期状態の位置で行えばよいのである。


円柱の上面(Face33)についても同様である。円柱の上面は上図28に示されるように初期状態において z軸プラス側に置かれている。以下の図34は上面(Face33)とFace32を表示したものであるが、この図ではFace33を z軸方向に円柱の高さ分($1.8$)だけ移動させている (Face33をFace32にアタッチした状態)。図35はこの2つのFaceにカメラを近づけたときのものである (ここでも z軸は水色で表示してある)。
この図に示されるように、Face32の上側の辺と上面(Face33)の辺の1つがちょうど重なった状態になっている。つまり、Face33をFace32にアタッチする際には、円柱の高さ分だけ z軸方向に平行移動させればよいのである。
底面や上面の配置が図27、28のようになっているのは、このような理由のためである。


プログラム中で用意されているインスタンス変数及び定数は以下のものである。
c_CylinderSideW
: float型の定数で上記の図29や図30において円柱側面の横幅として使われている cw を表す。i_degPrimarySide, i_degSide, i_degTop, i_motionCounter
: これらのインスタンス変数の役割については上の解説で述べた通りである。c_CylinderSideW 以外のインスタンス変数はCode5及びCode7で使われたものと同じである。すなわち、i_degPrimarySide、i_degSide、i_degTop はFaceの回転角度を表す3つのfloat型変数であり、i_motionCounter は展開された状態と組み立てられた状態の変化の過程で使われるint型変数である (これらの変数の役割についてもCode5やCode7の場合と同じである)。
プログラムは Sec415.cs内のCode8に作成するものとする。Code8は最初の段階では初期化ブロックのみが記述がされており、そのまま実行すると各オブジェクトが初期状態のまま重なって表示される。
今までのプログラムと同じように各Faceはプログラム中においては配列の形で使われるが、このプログラムで使用するのは Face[0] ~ Face[33] である。
また、三角柱や立方体の場合と同じく以下の2つのキーを使うものとする。
J : 円柱を組み立てる。
K : 円柱を展開する。

プログラムの解答例については Sec415_Ans.txt を参照 (Sec415_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
© 2020-2025 Redpoll's 60 (All rights reserved)