Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-5
第4章 3D空間におけるオブジェクトの運動
$§$4-5 一体化したオブジェクトの運動 4
前節に引き続き、本節も読者用の課題である。
本節では、一体化するオブジェクトの階層は3階層であり、以下のオブジェクトを使用する。
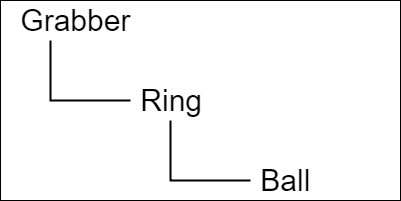
図4 オブジェクトの階層構造 図1の球体オブジェクト Ball、図2の環状オブジェクト Ringは、いずれも初期状態において その中心は原点である。また、図3の Grabberは初期状態では、x軸に関して線対称である。
これらのオブジェクトは図4に示される階層構造になっており、Ballの親オブジェクトが Ringであり、Ringの親オブジェクトが Grabberである。
一体化するオブジェクトの数が2つであれ、3つであれ、あるいはそれ以上であってもオブジェクトを一体化して運動させる際の原理は同じである。本節における課題も、今まで見てきたプログラムと本質的に変わるところはない。
[Beta1A] (実行結果 図5)
次に、Ringを Grabberにアタッチする。
[Beta1B] (実行結果 図6)
3つのオブジェクトを一体化したプログラムを以下に示す(各オブジェクトを親オブジェクトにアタッチしただけのもの)。ただし、結果を見やすくするために Grabberに $(0, 8, 0)$ の平行移動を実行している。
[Code1] (実行結果 図7)
Beta1Aの2行目の定数 c_attachPos_Ball は $(2, 0, 0)$ を表し、Ballは Ringにアタッチされる際に、この量だけ移動する。図5に示されるように、移動後(アタッチ後)の Ballの位置は、Ring上ではない。
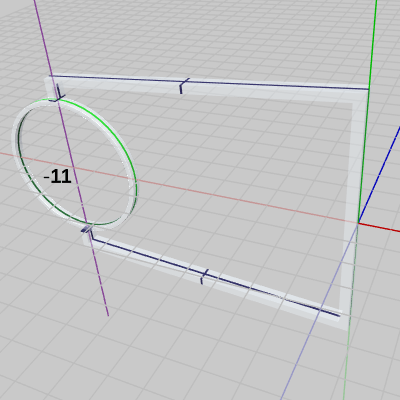
図8 Ringの中央を貫く紫色の軸 (y軸に平行で(-11, 0, 0)を通る) Beta1Bの2行目の定数 c_attachPos_Ring は $(-11,\ 0,\ 0)$ を表し、Ringは Grabberにアタッチされる際に、この量だけ移動する。図6に示されるように、この移動によって Ringは、Grabberの先端にアタッチされる。このとき、Grabberの先端では図8に示される紫色の軸が Ringを貫いている。この紫色の軸は $(-11,\ 0,\ 0)$ を通り、y軸に平行である。したがって、図2では y軸が Ringの中央を貫いているが、図8における紫色の軸も Ringの中央を貫いている。
図7は、Code1の実行結果であるが、これは3つのオブジェクトを一体化するだけのプログラムである。一番上の親オブジェクトである Grabberに対して $(0, 8, 0)$ の平行移動を実行しているので、Grabberの子オブジェクトである Ring、(さらにその子オブジェクトである)Ballも Grabberと一体化して同じだけ移動している。
まず、Ballがアタッチポジションである $(2, 0, 0)$ において、$1$倍から $1.5$倍の間で拡大縮小、さらに $(2, 0, 0)$ を通り、y軸に平行な軸(図9における水色の軸)の周りで自転を行うプログラムを作成する。
[Beta2] (実行結果 図9)
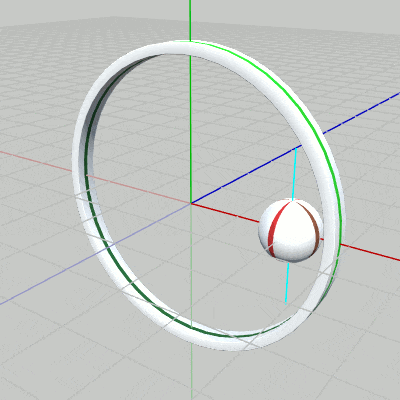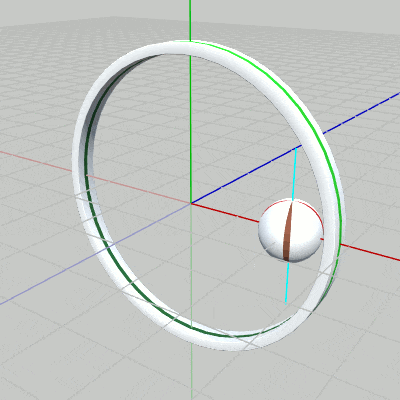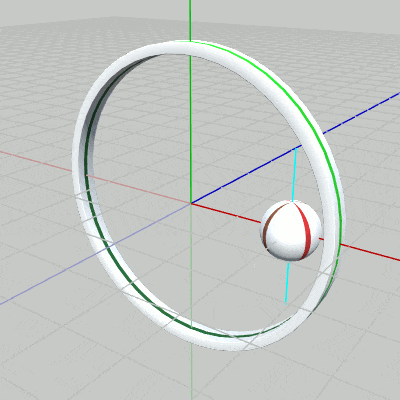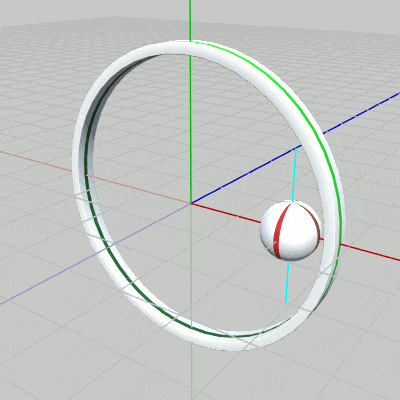
図9 Beta2 実行結果 2行目の i_shmBallは単振動の計算で使用されるfloat型インスタンス変数である。3行目の単振動計算によって scaleにセットされる値は、$1$から $1.5$の間を往復する。i_shmBallは毎フレーム $1.5$ずつ増加するので、$360 / 1.5 = 240$、すなわち 240フレームごとに $1$から $1.5$の間を往復する。5行目の i_degrotBallは、自転角度を表すfloat型インスタンス変数で、毎フレーム $1$ずつ増加するので、Ballの自転も毎フレーム $1$°ずつの回転となる。
実行順序としては、まず原点においてスケール(sclBall)、さらに自転(rotBall)を実行、そしてスケール、自転を行った状態の Ballに対してアタッチポジションへの平行移動(traBall)を実行する。毎フレームこの順序で変換を行うことで、Ballは 図9に示されるようにアタッチポジションにて拡大縮小しながら自転を行うようになる。
次に、Ballが上記の拡大縮小、及び 自転を行いながら、$(2, 0, 0)$ を通る半径 $2$の z軸周りの円周上を公転するプログラムを作成する。
[Code2] (実行結果 図10)

図10 Code2 実行結果 Beta2からの変更点は、Ballの平行移動行列 traBall の内容である。Beta2では、固定されたアタッチポジションへの移動だけであったが、ここでは $(2, 0, 0)$ を通る半径 $2$の円周上(公転軌道上)に、毎フレーム移動させなければならない。具体的には毎フレーム、8行目で その公転軌道上への移動位置を計算し、pos にセットする。詳しくは、$(2, 0, 0)$ から公転軌道上を角度 i_degrevBallだけ進んだ位置を求めて pos にセットする。ここで使われるfloat型インスタンス変数 i_degrevBallは Ballの公転角度のことで、毎フレーム $2$ずつ増加するので Ballの公転も毎フレーム $2$°ずつ進んでいく。
この例のように、オブジェクトに対して 平行移動、回転、スケールが行われる場合、実行順序は、スケール、回転、平行移動の順で実行するのが基本である(平行移動、回転の2つが行われる場合は、回転、平行移動の順で実行するのが基本である)。
Ringの運動は、Grabberの先端において 図8に示される紫色の軸の周りでの回転のみである。
[Code3] (実行結果 図11)
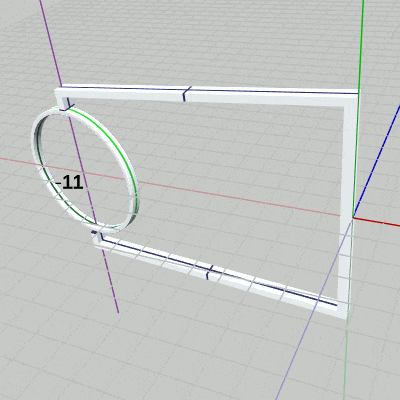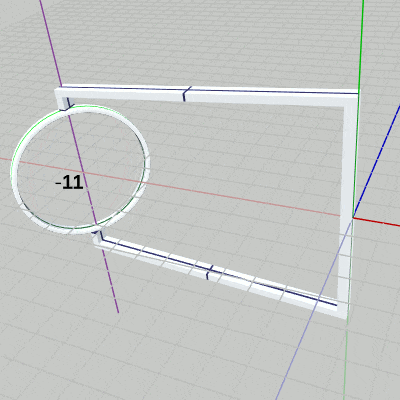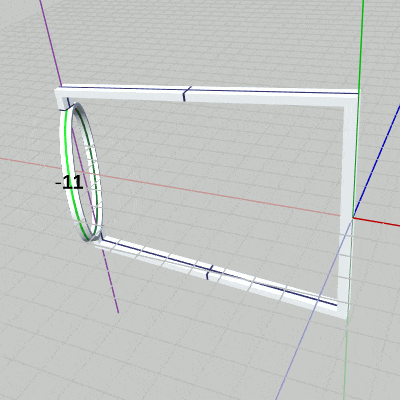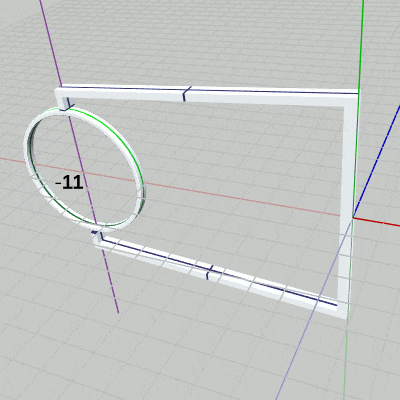
図11 Code3 実行結果 2行目の i_degRingは、Ringの回転角度を表すfloat型インスタンス変数である。ここでは、毎フレーム $1$ずつ増加しているので、Ringの回転も毎フレーム $1$°ずつの回転となる。
変換の実行順序は上記の Ballの場合と同様に、まず Ringを原点において y軸周りに i_degRingだけ回転させ(rotRing)、回転させた状態でアタッチポジションへの移動(traRing)を実行する。毎フレームこの順序で変換を実行することで、Ringはアタッチポジションにおいて回転を行うことになる。
なお、原点における回転は y軸周りで行っているので、アタッチポジションにおいて Ringは、y軸に平行な紫色の軸の周りで回転を行うことになる。
まず、Grabberを x軸に平行な軸の周りで回転させる。具体的には、上の図7(あるいは下図12)においてy軸上の $y=8$ から x軸に平行に伸びている点線の周りでの回転である。
[Beta4] (実行結果 図12)
2行目の i_degGrabber は、Grabberの回転角度を表すfloat型インスタンス変数である。ここでは毎フレーム $0.5$ずつ増加しているので Grabberも毎フレーム $0.5$°ずつの回転となる。Grabberの回転はx軸周りの回転ではなく、y軸上の $y=8$ を通りx軸に平行な軸の周りの回転であるから、Grabberを初期状態の位置でx軸周りに回転させてから、y軸プラス方向に$8$だけ平行移動させる必要がある (回転軸は図12において点線で示されている)。
3行目の GetRotation4x4(..)の回転角度の指定の部分で、i_degGrabber + 90 となっているため、Grabberの回転の始まりは $0$°からでなく $90$°回転した状態から始まる(回転のタイミングを調整するためだけの処理であり、深い意味はない ; また、3行目の Vector3.rightは、x軸プラス方向 $(1, 0, 0)$ を表す定数である)。
続いて、x軸に平行な軸周りの回転の他に y軸周りの回転を追加する。
[Code4] (実行結果 図13)
Beta4からの変更点は、3行目の rotGrabberの算出の際に、y軸周りの回転を追加している点のみである。Grabberに対する変換の実行順序は、まず初期状態の位置で x軸周りの回転、次に x軸周りに回転させた状態で y軸周りの回転。x軸周り、y軸周りに回転させた状態で $(0, 8, 0)$ の平行移動を実行。毎フレーム この順序で変換を実行することで、図13に示されるように $y = 8$ の位置で、Grabber自体がねじれるような回転を行いながら、y軸周りに回転するという結果になる。
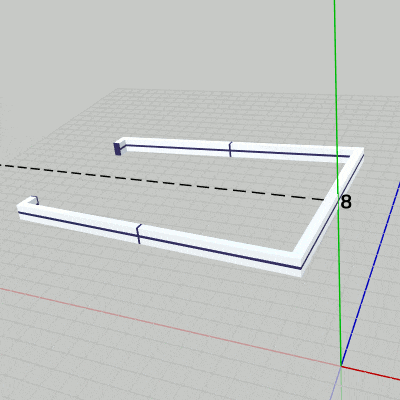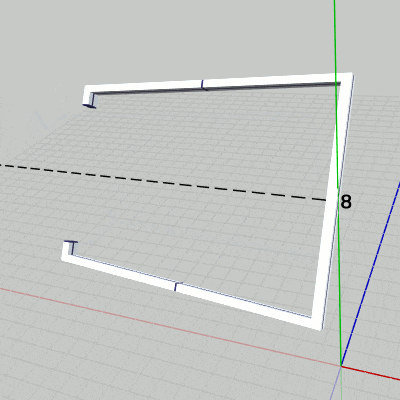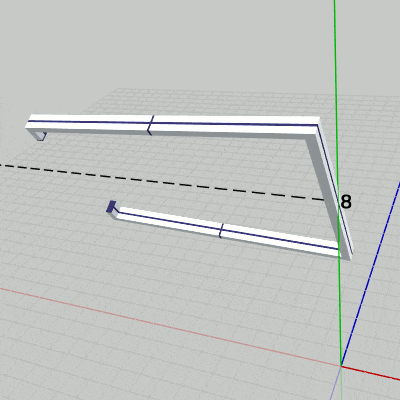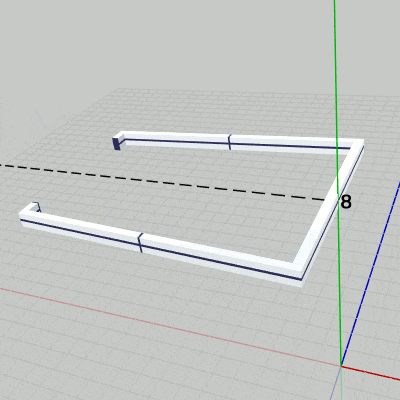
図12 Beta4 実行結果 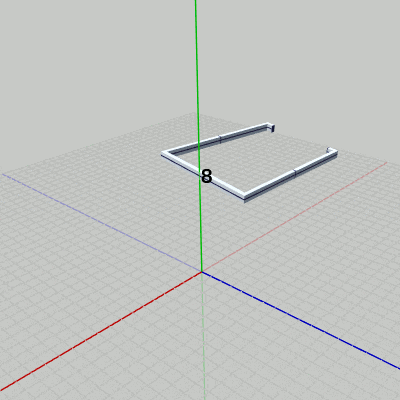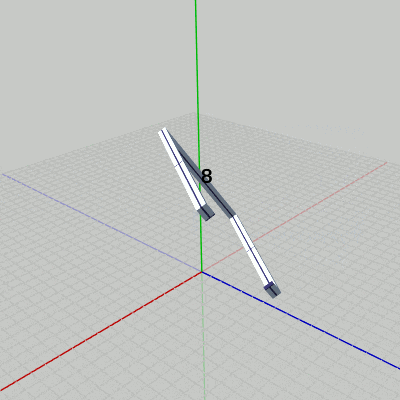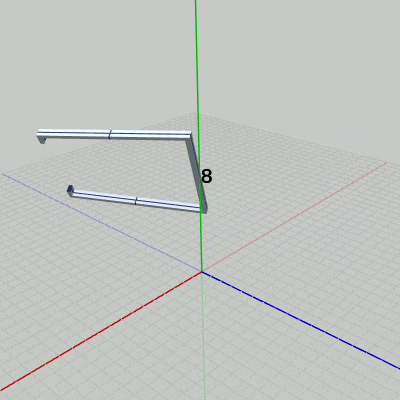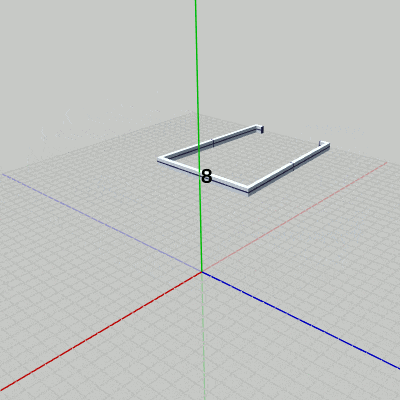
図13 Code4 実行結果
以下2つのプログラム作成は読者用の課題である。
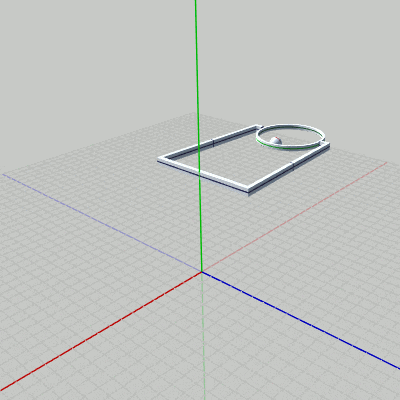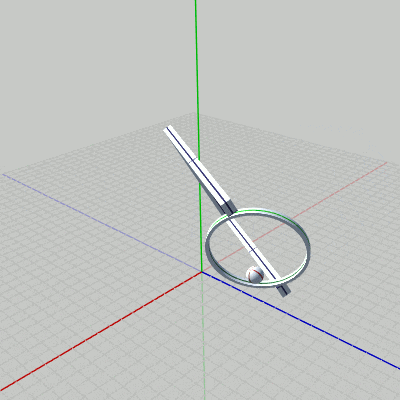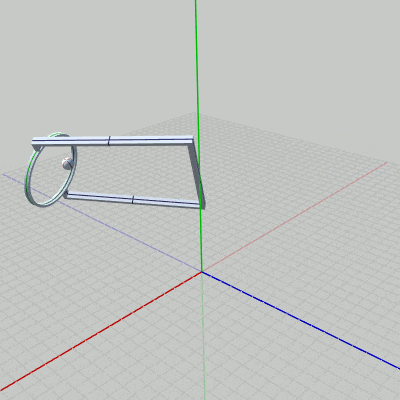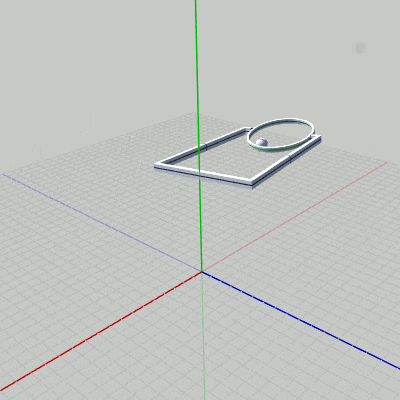
図14 Code5 実行結果 (3つのオブジェクトの一体化した運動) はじめのプログラムは、上で見てきた3つのオブジェクトの運動をすべて統合し、3つのオブジェクトが一体化して運動を行うようにすることである。
すなわち、一番上の親オブジェクトである Grabberは $y = 8$ の位置で、ねじれるような回転(x軸周りの回転)と y軸周りの回転を行っている。その Grabberの先端では、子オブジェクトの Ringが回転している。さらに、Ringの内側では、Ringの子オブジェクトの Ballが 拡大縮小、及び 自転をしながら、Ring内側の半径 $2$の円周上を公転している。
目的とする運動は、図14に示されるようなものになる。
今までのプログラムで使われてきたインスタンス変数を簡単に説明する (以下の変数の 1フレームあたりの値の増加量や スケール倍率の範囲などは あくまで目安であり、任意に変更して構わない)。
この課題は難しいものではない。本節で見てきたプログラムにおいて必要な部分を切り取ってつなげていけば、'自然に'完成する (解答例は、ソースファイル Sec405_Ans.txt 内のメソッド Code5() を参照)。
具体的には、次のキーを使って各オブジェクトの運動の実行/停止を切り替える。
H : Ballの拡大縮小と自転のスイッチ。
J : Ballの公転のスイッチ。
K : Ringの回転のスイッチ。
L : Grabberの回転のスイッチ。
例えば、3つのオブジェクトが運動しているときにLキーを押したとしよう。Lキーは Grabberの回転のスイッチであり、Grabberが回転しているときにこのキーを押すと Grabberの回転が停止する。さらに、Lキーに続いて Jキーを押した場合には、Ballの公転が停止する。
つまり、この時点では Ringが回転しており、その内側で Ballが拡大縮小、及び 自転しているだけの状態になる。
再び Lキーを押すと Grabberの回転が再開され、Jキーを押すと Ballの公転が再開される。
それぞれのスイッチのためのフラグとして以下の4つのbool型インスタンス変数が用意されている。
例えば、Hキーによって「Ballの拡大縮小と自転のスイッチ用のフラグ」である i_switch1_Ball の値を切り替えるには次のようなコードを書けばよい。
このコードによって、Hキーを押すたびに i_switch1_Ball の値がtrueになったりfalseになったりする。
以下の点を考慮してCode5に多少の追加及び 変更をすれば目的のプログラムは完成する。
各オブジェクトには、自身の拡大縮小や回転のためにインスタンス変数が用意されている。Ballの拡大縮小であれば i_shmBall、Ringの回転であれば i_degRing、Grabberの回転であれば i_degGrabberなどである。
指定のキーが押された際に、各スイッチ用のフラグの値を変更し、フラグの値がtrueのときにはそれらのインスタンス変数の値を更新し、falseのときには何も更新を行わないようにすれば、各オブジェクトは指定のキーが押されるたびに、その運動が実行したり停止したりすることになる (解答例は、ソースファイル Sec405_Ans.txt 内のメソッド Code6() を参照)。
本節では、一体化するオブジェクトの階層は3階層であり、以下のオブジェクトを使用する。
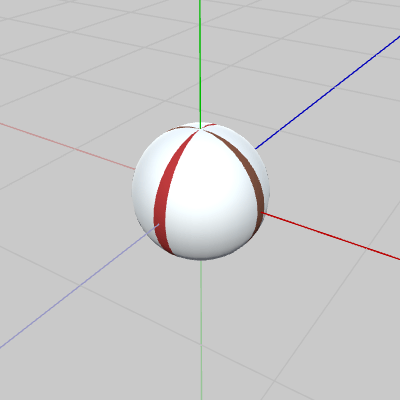 図1 Ball 初期状態
図1 Ball 初期状態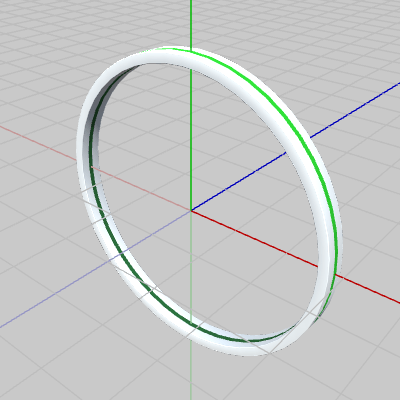 図2 Ring 初期状態
図2 Ring 初期状態 図3 Grabber 初期状態
図3 Grabber 初期状態

これらのオブジェクトは図4に示される階層構造になっており、Ballの親オブジェクトが Ringであり、Ringの親オブジェクトが Grabberである。
一体化するオブジェクトの数が2つであれ、3つであれ、あるいはそれ以上であってもオブジェクトを一体化して運動させる際の原理は同じである。本節における課題も、今まで見てきたプログラムと本質的に変わるところはない。
# Code1
まずは、Ballを Ringにアタッチするだけのプログラムである。[Beta1A] (実行結果 図5)
// Ball ; c_attachPos_Ball (2, 0, 0) Matrix4x4 localBall = TH3DMath.GetTranslation4x4(c_attachPos_Ball); // Ring Matrix4x4 localRing = Matrix4x4.identity; // world matrix Matrix4x4 worldBall = localRing * localBall; Matrix4x4 worldRing = localRing; Ball.SetMatrix(worldBall); Ring.SetMatrix(worldRing);
次に、Ringを Grabberにアタッチする。
[Beta1B] (実行結果 図6)
// Ring ; c_attachPos_Ring (-11, 0, 0) Matrix4x4 localRing = TH3DMath.GetTranslation4x4(c_attachPos_Ring); // Grabber Matrix4x4 localGrabber = Matrix4x4.identity; // world matrix Matrix4x4 worldRing = localGrabber * localRing; Matrix4x4 worldGrabber = localGrabber; Ring.SetMatrix(worldRing); Grabber.SetMatrix(worldGrabber);
3つのオブジェクトを一体化したプログラムを以下に示す(各オブジェクトを親オブジェクトにアタッチしただけのもの)。ただし、結果を見やすくするために Grabberに $(0, 8, 0)$ の平行移動を実行している。
[Code1] (実行結果 図7)
// Ball ; c_attachPos_Ball (2, 0, 0) Matrix4x4 localBall = TH3DMath.GetTranslation4x4(c_attachPos_Ball); // Ring ; c_attachPos_Ring (-11, 0, 0) Matrix4x4 localRing = TH3DMath.GetTranslation4x4(c_attachPos_Ring); // Grabber Matrix4x4 localGrabber = TH3DMath.GetTranslation4x4(0, 8, 0); // world matrix Matrix4x4 worldBall = localGrabber * localRing * localBall; Matrix4x4 worldRing = localGrabber * localRing; Matrix4x4 worldGrabber = localGrabber; Ball.SetMatrix(worldBall); Ring.SetMatrix(worldRing); Grabber.SetMatrix(worldGrabber);
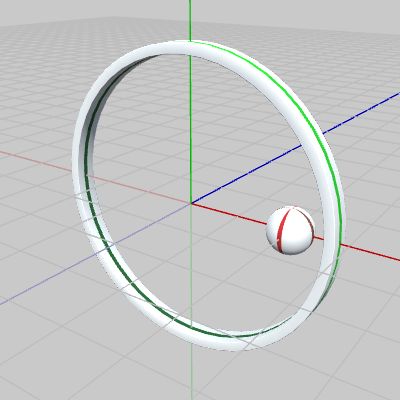 図5 Beta1A 実行結果
図5 Beta1A 実行結果 図6 Beta1B 実行結果
図6 Beta1B 実行結果 図7 Code1 実行結果
図7 Code1 実行結果
Beta1Aの2行目の定数 c_attachPos_Ball は $(2, 0, 0)$ を表し、Ballは Ringにアタッチされる際に、この量だけ移動する。図5に示されるように、移動後(アタッチ後)の Ballの位置は、Ring上ではない。

図7は、Code1の実行結果であるが、これは3つのオブジェクトを一体化するだけのプログラムである。一番上の親オブジェクトである Grabberに対して $(0, 8, 0)$ の平行移動を実行しているので、Grabberの子オブジェクトである Ring、(さらにその子オブジェクトである)Ballも Grabberと一体化して同じだけ移動している。
# Code2
次に、Ringにアタッチされている Ballの運動を実装する。まず、Ballがアタッチポジションである $(2, 0, 0)$ において、$1$倍から $1.5$倍の間で拡大縮小、さらに $(2, 0, 0)$ を通り、y軸に平行な軸(図9における水色の軸)の周りで自転を行うプログラムを作成する。
[Beta2] (実行結果 図9)
// Ball ; c_attachPos_Ball (2, 0, 0) i_shmBall += 1.5f; float scale = 0.25f * Mathf.Sin(i_shmBall * Mathf.Deg2Rad) + 1.25f; // 1 -- 1.5 Matrix4x4 sclBall = TH3DMath.GetScale4x4(scale); i_degrotBall += 1; Matrix4x4 rotBall = TH3DMath.GetRotation4x4(i_degrotBall, Vector3.up); Matrix4x4 traBall = TH3DMath.GetTranslation4x4(c_attachPos_Ball); Matrix4x4 localBall = traBall * rotBall * sclBall; // Ring Matrix4x4 localRing = Matrix4x4.identity; // world matrix Matrix4x4 worldBall = localRing * localBall; Matrix4x4 worldRing = localRing; Ball.SetMatrix(worldBall); Ring.SetMatrix(worldRing);

実行順序としては、まず原点においてスケール(sclBall)、さらに自転(rotBall)を実行、そしてスケール、自転を行った状態の Ballに対してアタッチポジションへの平行移動(traBall)を実行する。毎フレームこの順序で変換を行うことで、Ballは 図9に示されるようにアタッチポジションにて拡大縮小しながら自転を行うようになる。
次に、Ballが上記の拡大縮小、及び 自転を行いながら、$(2, 0, 0)$ を通る半径 $2$の z軸周りの円周上を公転するプログラムを作成する。
[Code2] (実行結果 図10)
// Ball ; c_attachPos_Ball (2, 0, 0) i_shmBall += 1.5f; float scale = 0.25f * Mathf.Sin(i_shmBall * Mathf.Deg2Rad) + 1.25f; // 1 -- 1.5 Matrix4x4 sclBall = TH3DMath.GetScale4x4(scale); i_degrotBall += 1; Matrix4x4 rotBall = TH3DMath.GetRotation4x4(i_degrotBall, Vector3.up); i_degrevBall += 2; Vector3 pos = TH3DMath.GetRotation4x4(i_degrevBall, Vector3.forward) * new Vector4(2, 0, 0, 1); Matrix4x4 traBall = TH3DMath.GetTranslation4x4(pos); Matrix4x4 localBall = traBall * rotBall * sclBall; // Ring Matrix4x4 localRing = Matrix4x4.identity; // world matrix Matrix4x4 worldBall = localRing * localBall; Matrix4x4 worldRing = localRing; Ball.SetMatrix(worldBall); Ring.SetMatrix(worldRing);

この例のように、オブジェクトに対して 平行移動、回転、スケールが行われる場合、実行順序は、スケール、回転、平行移動の順で実行するのが基本である(平行移動、回転の2つが行われる場合は、回転、平行移動の順で実行するのが基本である)。
# Code3
ここでは、Grabberにアタッチされている Ringの運動を実装する。Ringの運動は、Grabberの先端において 図8に示される紫色の軸の周りでの回転のみである。
[Code3] (実行結果 図11)
// Ring i_degRing += 1; Matrix4x4 rotRing = TH3DMath.GetRotation4x4(i_degRing, Vector3.up); Matrix4x4 traRing = TH3DMath.GetTranslation4x4(c_attachPos_Ring); // c_attachPos_Ring (-11, 0, 0) Matrix4x4 localRing = traRing * rotRing; // Grabber Matrix4x4 localGrabber = Matrix4x4.identity; // world matrix Matrix4x4 worldRing = localGrabber * localRing; Matrix4x4 worldGrabber = localGrabber; Ring.SetMatrix(worldRing); Grabber.SetMatrix(worldGrabber);

変換の実行順序は上記の Ballの場合と同様に、まず Ringを原点において y軸周りに i_degRingだけ回転させ(rotRing)、回転させた状態でアタッチポジションへの移動(traRing)を実行する。毎フレームこの順序で変換を実行することで、Ringはアタッチポジションにおいて回転を行うことになる。
なお、原点における回転は y軸周りで行っているので、アタッチポジションにおいて Ringは、y軸に平行な紫色の軸の周りで回転を行うことになる。
# Code4
では、一番上の親オブジェクトである Grabberの運動について見ていく。まず、Grabberを x軸に平行な軸の周りで回転させる。具体的には、上の図7(あるいは下図12)においてy軸上の $y=8$ から x軸に平行に伸びている点線の周りでの回転である。
[Beta4] (実行結果 図12)
// Grabber i_degGrabber += 0.5f; Matrix4x4 rotGrabber = TH3DMath.GetRotation4x4(i_degGrabber + 90, Vector3.right); Matrix4x4 traGrabber = TH3DMath.GetTranslation4x4(0, 8, 0); Matrix4x4 localGrabber = traGrabber * rotGrabber; Matrix4x4 worldGrabber = localGrabber; Grabber.SetMatrix(worldGrabber);
2行目の i_degGrabber は、Grabberの回転角度を表すfloat型インスタンス変数である。ここでは毎フレーム $0.5$ずつ増加しているので Grabberも毎フレーム $0.5$°ずつの回転となる。Grabberの回転はx軸周りの回転ではなく、y軸上の $y=8$ を通りx軸に平行な軸の周りの回転であるから、Grabberを初期状態の位置でx軸周りに回転させてから、y軸プラス方向に$8$だけ平行移動させる必要がある (回転軸は図12において点線で示されている)。
3行目の GetRotation4x4(..)の回転角度の指定の部分で、i_degGrabber + 90 となっているため、Grabberの回転の始まりは $0$°からでなく $90$°回転した状態から始まる(回転のタイミングを調整するためだけの処理であり、深い意味はない ; また、3行目の Vector3.rightは、x軸プラス方向 $(1, 0, 0)$ を表す定数である)。
続いて、x軸に平行な軸周りの回転の他に y軸周りの回転を追加する。
[Code4] (実行結果 図13)
// Grabber
i_degGrabber += 0.5f;
Matrix4x4 rotGrabber = TH3DMath.GetRotation4x4(i_degGrabber, Vector3.up) *
TH3DMath.GetRotation4x4(i_degGrabber + 90, Vector3.right);
Matrix4x4 traGrabber = TH3DMath.GetTranslation4x4(0, 8, 0);
Matrix4x4 localGrabber = traGrabber * rotGrabber;
Matrix4x4 worldGrabber = localGrabber;
Grabber.SetMatrix(worldGrabber);
Beta4からの変更点は、3行目の rotGrabberの算出の際に、y軸周りの回転を追加している点のみである。Grabberに対する変換の実行順序は、まず初期状態の位置で x軸周りの回転、次に x軸周りに回転させた状態で y軸周りの回転。x軸周り、y軸周りに回転させた状態で $(0, 8, 0)$ の平行移動を実行。毎フレーム この順序で変換を実行することで、図13に示されるように $y = 8$ の位置で、Grabber自体がねじれるような回転を行いながら、y軸周りに回転するという結果になる。


以下2つのプログラム作成は読者用の課題である。
# Code5

すなわち、一番上の親オブジェクトである Grabberは $y = 8$ の位置で、ねじれるような回転(x軸周りの回転)と y軸周りの回転を行っている。その Grabberの先端では、子オブジェクトの Ringが回転している。さらに、Ringの内側では、Ringの子オブジェクトの Ballが 拡大縮小、及び 自転をしながら、Ring内側の半径 $2$の円周上を公転している。
目的とする運動は、図14に示されるようなものになる。
今までのプログラムで使われてきたインスタンス変数を簡単に説明する (以下の変数の 1フレームあたりの値の増加量や スケール倍率の範囲などは あくまで目安であり、任意に変更して構わない)。
i_shmBall
: Ballのスケール倍率を求める際に、単振動による計算を行うが、その際に使用される角度。上のプログラムにおいては毎フレーム $1.5$ずつ増加(スケール倍率は $1$倍から $1.5$倍の間を往復 ; float型 初期値 $0$)。i_degrotBall
: Ballの自転角度。上のプログラムにおいては毎フレーム $1$ずつ増加 (float型 初期値 $0$)。i_degrevBall
: Ballの公転角度。上のプログラムにおいては毎フレーム $2$ずつ増加 (float型 初期値 $0$)。i_degRing
: Ringの回転角度。上のプログラムにおいては毎フレーム $1$ずつ増加 (float型 初期値 $0$)。i_degGrabber
: Grabberの回転角度。Grabberは x軸周りの回転(ねじれるような回転)と y軸周りの回転を行うが、どちらの回転でも この変数を使用する。上のプログラムにおいては毎フレーム $0.5$ずつ増加 (float型 初期値 $0$)。c_attachPos_Ring
: Ringのアタッチポジション(Grabberの先端)を表すVector3型定数で、その値は (-11, 0, 0) である (Ballのアタッチポジションを表す定数 c_attachPos_Ballもあるが、Ballは公転軌道上を公転しているので この課題プログラムにおいては特に使う必要はない)。この課題は難しいものではない。本節で見てきたプログラムにおいて必要な部分を切り取ってつなげていけば、'自然に'完成する (解答例は、ソースファイル Sec405_Ans.txt 内のメソッド Code5() を参照)。
# Code6
Code5においては3つのオブジェクトの運動はプログラム実行中不変であり、常に同じ運動を繰り返し続けるものであった。今回のプログラムでは、キー操作によって3つのオブジェクトそれぞれに運動の実行/停止のコントロールができるようにする。具体的には、次のキーを使って各オブジェクトの運動の実行/停止を切り替える。
H : Ballの拡大縮小と自転のスイッチ。
J : Ballの公転のスイッチ。
K : Ringの回転のスイッチ。
L : Grabberの回転のスイッチ。
例えば、3つのオブジェクトが運動しているときにLキーを押したとしよう。Lキーは Grabberの回転のスイッチであり、Grabberが回転しているときにこのキーを押すと Grabberの回転が停止する。さらに、Lキーに続いて Jキーを押した場合には、Ballの公転が停止する。
つまり、この時点では Ringが回転しており、その内側で Ballが拡大縮小、及び 自転しているだけの状態になる。
再び Lキーを押すと Grabberの回転が再開され、Jキーを押すと Ballの公転が再開される。
それぞれのスイッチのためのフラグとして以下の4つのbool型インスタンス変数が用意されている。
i_switch1_Ball
: Ballの拡大縮小と自転のスイッチ用のフラグ。i_switch2_Ball
: Ballの公転のスイッチ用のフラグ。i_switch_Ring
: Ringの回転のスイッチ用のフラグ。i_switch_Grabber
: Grabberの回転のスイッチ用のフラグ。例えば、Hキーによって「Ballの拡大縮小と自転のスイッチ用のフラグ」である i_switch1_Ball の値を切り替えるには次のようなコードを書けばよい。
if (Input.GetKeyDown(KeyCode.H))
{
i_switch1_Ball = !i_switch1_Ball;
}
以下の点を考慮してCode5に多少の追加及び 変更をすれば目的のプログラムは完成する。
各オブジェクトには、自身の拡大縮小や回転のためにインスタンス変数が用意されている。Ballの拡大縮小であれば i_shmBall、Ringの回転であれば i_degRing、Grabberの回転であれば i_degGrabberなどである。
指定のキーが押された際に、各スイッチ用のフラグの値を変更し、フラグの値がtrueのときにはそれらのインスタンス変数の値を更新し、falseのときには何も更新を行わないようにすれば、各オブジェクトは指定のキーが押されるたびに、その運動が実行したり停止したりすることになる (解答例は、ソースファイル Sec405_Ans.txt 内のメソッド Code6() を参照)。
© 2020-2025 Redpoll's 60 (All rights reserved)