Redpoll's 60
第4章 3D空間におけるオブジェクトの運動
§4-8 ローカル座標系とワールド座標系 1
今までに見てきたプログラムにおいて、一体化したオブジェクトの運動についての解説は、その運動の実装に焦点を当てたものであった。例えば、4-2節のプロペラ飛行機の運動についての解説では、まず始めにプロペラを初期状態の位置で回転させ、次にアタッチポジションに移動させ、最後に機体とプロペラを一体化して運動させる、といった内容のものが解説の主旨であった。
また、オブジェクトの一体化に関する記述の中では、親オブジェクト、子オブジェクトという呼び方を用いることはあっても、一体化によって発生するオブジェクトの階層構造については深く立ち入ることはなかった。
本節から4-11節までは、この階層構造に焦点を当て、一体化したオブジェクトの運動を解説する。そこでは、各オブジェクトが独自の座標系を持ち、それらの座標系は各オブジェクトの運動を表す変換行列と密接な関わりを持っていることが示される。
まずは、基本となる用語の説明から始めよう。
初期状態のオブジェクトもまた、何らかの座標系の中で定義されているわけであるが、初期状態のオブジェクトが定義されている座標系のことをローカル座標系(Local Coordinate System)という。ローカル座標系は、各オブジェクトが独自に持っている座標系である。
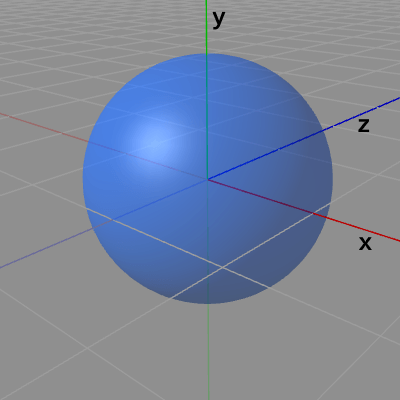
図1 ローカル座標系で定義された半径1の球体 例えば、図1はモデリングツールで作成された球体オブジェクトであり、このオブジェクトはこの状態で外部ファイルへ出力する。すなわち図1は、この球体オブジェクトの初期状態である。この球体の中心は原点で半径は1であるが、詳しくは、ローカル座標系の原点に球体の中心があり、ローカル座標系で測った場合に球体の半径が1なのである。
また、ローカル座標系においても赤色の軸を x軸、緑色の軸を y軸、青色の軸を z軸とする。
ローカル座標系は特殊な座標系であり、オブジェクトと一体化した座標系として考えることができる。例えば、オブジェクトに対し変換を実行して3D空間上で運動させる場合でも、オブジェクトが自身のローカル座標系の中を運動することはない。つまり、ローカル座標系の中でのオブジェクトの位置、向き、大きさなどの状態は、オブジェクトに対して実行される変換によって変わることはない。言い換えれば、ローカル座標系はオブジェクトと一体化して運動するのである。このことについては以降で説明していく。
オブジェクトを一体化して運動させる際には、あるオブジェクトを別のオブジェクトにアタッチする。このとき、アタッチされる側のオブジェクトが親オブジェクトであるが、親オブジェクトもローカル座標系を持っており、自身のローカル座標系の中で初期状態の位置、向き、大きさなどが定義されている。子オブジェクトから見たときの、親オブジェクトのローカル座標系を特に、親座標系(Parent's Coordinate System)という。
オブジェクトをアタッチする際には、オブジェクトを親オブジェクトの指定位置、あるいは指定領域へ移動させるが、詳しくは、オブジェクトのアタッチとは、オブジェクトを親座標系の指定位置、あるいは指定領域へ移動させることを意味する。
親オブジェクトを持つ子オブジェクトであれば、親座標系の中で運動を定義することはできるだろう。しかし、親子階層の最上位に位置する親オブジェクトや、どのオブジェクトとも親子関係のない単独のオブジェクトは親オブジェクトを持っていない。こういった、親オブジェクトを持っていないオブジェクトの場合、「親座標系の中で運動を定義する」ことはどのようにして行われるのだろうか。
実際には、そのような 親オブジェクトを持たないオブジェクト の運動を定義するための座標系が存在する。コンピューターグラフィックスの世界では、この特別な座標系をワールド座標系(World Coordinate System)という。

図2 ワールド座標系の中でのオブジェクトの運動 ワールド座標系はすべてのオブジェクトを包含する座標系である。これは、すべてのローカル座標系を包含することを意味している。したがって、ワールド座標系を最上位の親座標系として考えることができる。つまり、親オブジェクトを持たないオブジェクトも、ワールド座標系の中で運動を定義することで、「親座標系の中で運動を定義する」ことになるわけである。
ワールド座標系は既に何度も使われてきている。たとえば 今までのプログラムの実行中に表示されていた座標系は、すべてワールド座標系である。図2のアニメーションでは、2つのオブジェクトが y軸の周りを回転しているが、詳しくは、ワールド座標系の y軸の周りを回転しているのである。
本節から4-11節においては「オブジェクトに定義された運動」や「オブジェクトに定義された変換」といった表現が多く使われるが、どちらも同じ意味であり明確な違いはない (2-7節などでも、親子関係にあるオブジェクトの解説の中で「オブジェクトの独自の運動」といった表現が使われているが、これもまた同じ意味である)。
「オブジェクトに定義された運動」(あるいは「オブジェクトに定義された変換」) は今までのプログラムで何度も見ているものである。
今までのプログラムはすべて上の形で記述されていた。このプログラムの場合は3つのオブジェクト Obj1、Obj2、Obj3の一体化した運動の記述である。
「オブジェクトに定義された運動(あるいは変換)」とは、プログラムにおける変換行列 local### によって表される変換のことである。このプログラムの場合では、Obj1に定義された運動(あるいは変換)は localObj1 によって表される変換であり、Obj2、Obj3に定義された運動(あるいは変換)は localObj2、localObj3 によって表される変換である。
また、文章中において「ローカル行列」とあれば、それはプログラムにおいては変換行列 local### のことであり、「ワールド行列」とあれば、それはプログラムにおいては変換行列 world### のことである。例えば上のプログラムでは、Obj1のローカル行列は localObj1 であり、ワールド行列は worldObj1 である。
では、ここからは2つのオブジェクトの一体化した運動を、各階層の座標系に焦点を当てて見ていく。図3、図4は、今回使用するオブジェクト Sphere、Arm の初期状態である。Sphereは球体オブジェクトで、初期状態において、その中心は原点にあり、半径は 1である。
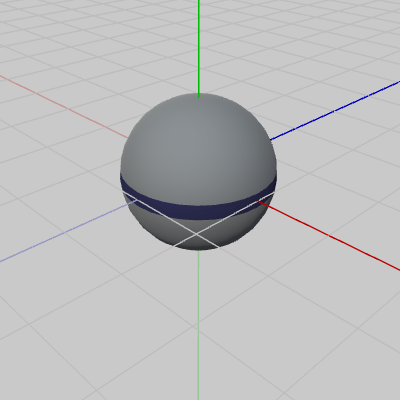
図3 Sphere 初期状態 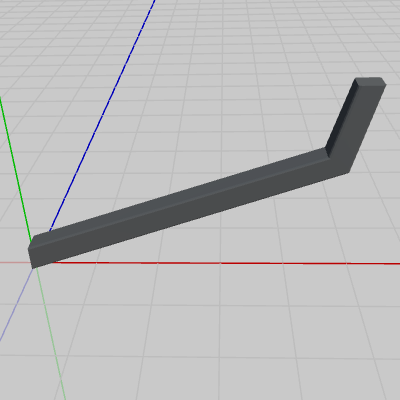
図4 Arm 初期状態
オブジェクトの初期状態に関して1つ補足しておこう。
今までにも、使用してきたオブジェクトについては初期状態の図を表示したが、これらの図はオブジェクトのローカル座標系での表示であるということである。例えば、上の図3、図4においても Sphere、Arm の置かれている座標系はそれぞれのローカル座標系である。
また、本節から4-12節までは複数の座標系が使われるが、その点について違いを明らかにしておこう。
図5は、2つのオブジェクト Sphereと Armが、ワールド座標系に置かれた様子を示している。図から分かるように、表示されている座標系はワールド座標系のみである。また、このときのカメラはワールド座標系に置かれている。
図6は、ワールド座標系に置かれた Sphereと Armのそれぞれに、ローカル座標系を表示したものである。ワールド座標系と区別するために、ローカル座標系では各軸の太さがやや太くなっている。また、Sphere、Armのローカル座標系は、どちらも座標軸のプラス側のみの表示であり、グリッドは省略してある。図中のラベルの意味は、x、y、zがワールド座標系のx軸、y軸、z軸を表し、S-x、S-y、S-zが Sphereのローカル座標系におけるx軸、y軸、z軸を表し、A-x、A-y、A-zが Armのローカル座標系におけるx軸、y軸、z軸を表している。図5と同様に、図6においてもカメラはワールド座標系に置かれている。
図7は、カメラを Armのローカル座標系に置いたときの2つのオブジェクトの表示である。表示内容を明確にするためにワールド座標系は描画していない。図中のラベルの意味は図6と同様である。Armのローカル座標系では、グリッドが部分的に表示されているが(XZ平面の第1象限のみ)、 Sphereのローカル座標系はここでも座標軸のみの表示とし、グリッドは省略してある。
簡単に述べると、この講義においてはワールド座標系は常に各軸が細い線で描画されている。座標系の各軸が太く描画されていれば、それはローカル座標系である。そして、そのとき表示されているのは各軸のプラス側のみである。また、ローカル座標系のグリッドは、表示する場合もあれば、していない場合もあり、グリッドを表示する場合は一部の例を除き XZ平面の第1象限のみの表示となる。
ただし、先にも述べたが図3、図4のようなオブジェクトの初期状態で使われる座標系は、ローカル座標系であるが、そのときの各軸は細い線で描画される。
では、実際にプログラムを作成していくが、冒頭でも述べたように本節から4-11節で使われるプログラムは、運動の実装方法の解説を目的とするものではない。また、その内容は今までに作成してきたものと同様のものであるので、プログラムについての解説は省略する。
[Code1] (実行結果 図8、図9)
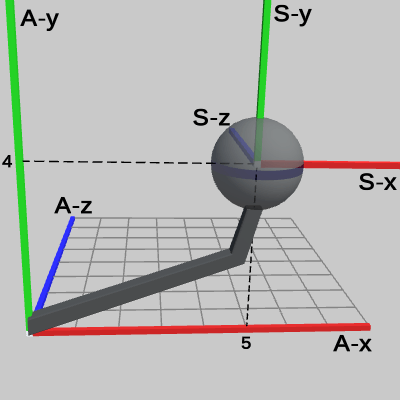
図8 Code1 実行結果 (Arm座標系から見たときの様子) 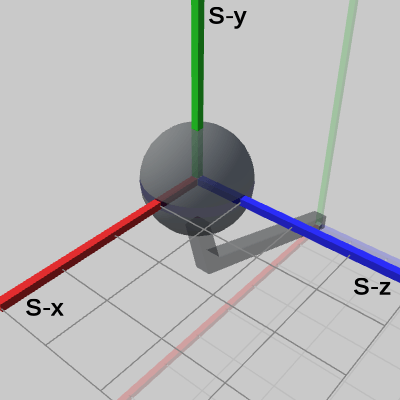
図9 Code1 実行結果 (Sphere座標系から見たときの様子)
プログラム2行目の c_attachPos_Sphereは、Sphereのアタッチポジションを表す Vector3型の定数で、その値は (5, 4, 0) である。
図8は、プログラムの実行結果を Armのローカル座標系から見たものであり、図からわかるように Sphereの中心は、Arm座標系において (5, 4, 0) に移動している。この移動は、Sphereを Armの先端にアタッチする処理であるが、詳しくは Sphereを、親座標系である Arm座標系の (5, 4, 0) にアタッチしているのである。
また、Sphereのローカル座標系の原点も同じく、(5, 4, 0)に移動しているが、このことは、Sphere座標系が Sphereと同じだけ移動していることを意味する。すなわち、Sphereは 自身のローカル座標系と一体化して移動しているのである。
図9は、実行結果を Sphereのローカル座標系から見たものであるが、Sphereは 自身のローカル座標系の中では全く動いていないことが分かるだろう。つまり、Sphereの中心は Sphere座標系の原点に置かれており、Sphereの半径は 1、これは図3の初期状態と同じである。
上でも述べたように、オブジェクトに変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクトの状態(位置、向き、大きさ)は変化しないのである。
言い換えれば、オブジェクトにどのような変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクト上の任意の位置における座標は変わらない。このことについて、以下の例で見ていこう。
次の図は Sphere上の2つの位置の座標を Sphere座標系、Arm座標系で表示したものである。それら2つの位置は、図中では黄色い点と水色の点で表されている。図において、A(##, ##, ##) となっているのは Arm座標系における座標値を表し、S(##, ##, ##) となっているのは Sphere座標系における座標値を表している。
図10は、Sphere及び、Sphere座標系のみを表示したもので、Sphereの中心は原点にあり、黄色い点は Sphere上の (1, 0, 0) の位置を示し、水色の点は Sphere上の (0.707, 0.707, 0.0) の位置を示している。これらの座標値はいずれも Sphere座標系での値である。
図11は、この2つの位置をCode1実行後の Arm座標系で表示したものである。Arm座標系においては Sphereの中心は (5, 4, 0) に移動しているため、2つの位置の座標値もその分だけ移動した結果になっている。これらの座標値はいずれも Arm座標系での値である。
図12は、この2つの位置をCode1実行後の Sphere座標系で表示したものである。図における座標値は Sphere座標系での値であり、図10のものと同じである。何らかの変換によってオブジェクトを動かす場合でも、オブジェクトとそのオブジェクトのローカル座標系は一体となって動くためこのような結果になるのである。
繰り返せば、オブジェクトにどのような変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクト上の任意の位置における座標は変わらないのである。
[Code2] (実行結果 図13、14)
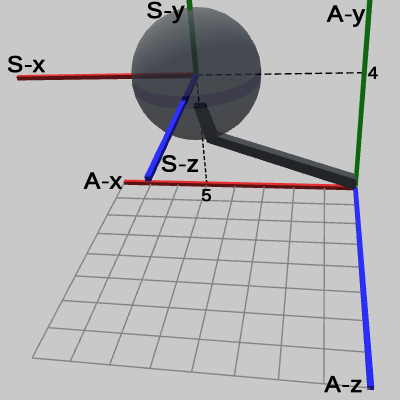
図13 Code2 実行結果 (Arm座標系から見たときの様子) 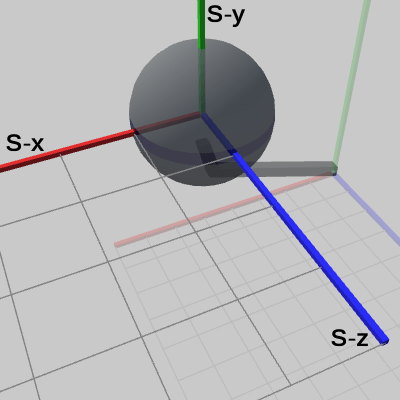
図14 Code2 実行結果 (Sphere座標系から見たときの様子)
図13は、Code2の実行結果を Arm座標系から見たときの様子である。Code1の場合と同様に、Sphereの中心が (5, 4, 0) に移動している。図14は、Code2の実行結果を Sphere座標系から見たときの様子である。Sphere座標系では、やはり Sphereの中心は原点に位置しており、Sphereの半径は 1であることがわかる。
だが、今回の Sphereの拡大によって、Sphereがやや大きく表示されている ということ以外には、これらの図から得られる情報はない。今回の拡大によって、2つの座標系の間で発生した違いを明確にするために、Sphereを Arm座標系の原点に移動させた場合の図を用意する。
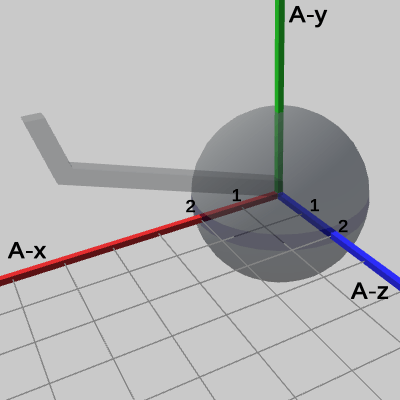
図15 2倍に拡大されたSphereを Arm座標系から見たときの様子 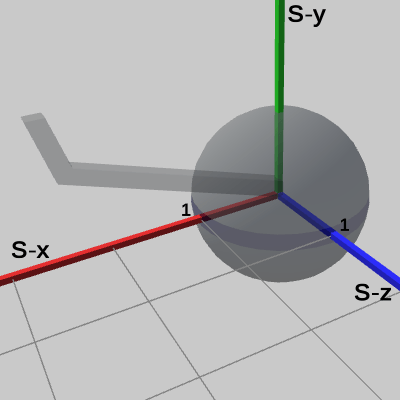
図16 2倍に拡大されたSphereを Sphere座標系から見たときの様子
図15は、2倍に拡大されたSphereを Arm座標系の原点に移動させ、Arm座標系のみを表示したときの様子である。図からわかるとおり、2倍に拡大されたSphereの中心は原点にあるが、半径は Arm座標系では 1ではなく、2になっている。
図16は、図15の状態から Arm座標系を非表示にし、Sphere座標系のみを表示したときの様子である。Sphere座標系においては、今までと同様に Sphereの中心は原点にあり、半径は 1である。これは、Code2によって Sphereは 2倍に拡大されるが、Sphere座標系自体も2倍に拡大するので、Sphere座標系で測ったときの半径は拡大前と後で変化はないのである。
実際に、図15と図16の座標系を見比べれば、グリッドの間隔が Arm座標系よりも Sphere座標系の方が明らかに広いことが分かるだろう(正確には2倍の間隔になっている)。
では、ここでも上の例で見たように、Code2実行後の Sphere上の2つの位置の座標を Arm座標系、Sphere座標系で表示してみよう(上の場合と同様に、A(##, ##, ##) は Arm座標系での座標値を、S(##, ##, ##) は Sphere座標系での座標値を表している)。
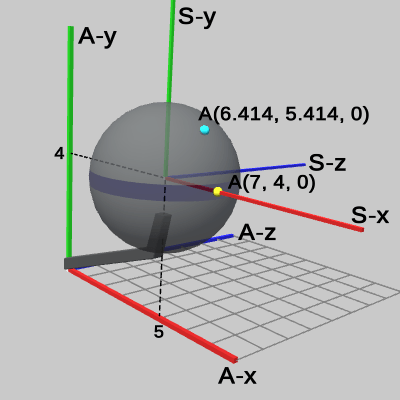
図17 2つの位置の Arm座標系における座標値(Code2実行後) 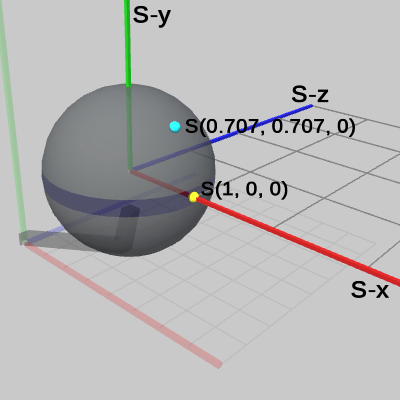
図18 2つの位置の Sphere座標系における座標値(Code2実行後)
図17は、この2つの位置をCode2実行後の Arm座標系で表示したものである。Sphereの中心が (5, 4, 0) であることは今までと同じである。しかし上記の図11とは異なり、ここでの Sphereの半径は Arm座標系において 2である。
そのため黄色い点の座標は (7, 4, 0) となっているが、これは以下のようにして求められる。 2 * (1, 0, 0) + (5, 4, 0) = (7, 4, 0) Code2の実行手順では、Sphereは初期状態から2倍拡大後にアタッチポジションへ アタッチされる。したがって、Code2実行後における Sphere上の各点の位置を計算する場合も、各位置の座標を2倍拡大後にアタッチ(平行移動)という順序で計算すればよい。水色の点の座標を求める場合も同様である。
図18は、この2つの位置をCode2実行後の Sphere座標系で表示したものである。Sphere座標系での2つの位置の座標は、図12のものと同じである。図12の Sphereには拡大は行われていないが、ここでは Sphereに対して 2倍の拡大が実行されている。それでも、Sphere座標系で見たときには Sphere上の水色と黄色の点の座標は、図12と図18の場合で変化はないのである。これは先ほども述べたように、Sphereに拡大が実行される場合、Sphereのローカル座標系にも同じ拡大が実行されるためである。
オブジェクトに対して何らかの変換を実行した場合、そのオブジェクトのローカル座標系にも同じ変換が実行される。オブジェクトが平行移動をすれば、ローカル座標系も同じだけ平行移動をし、オブジェクトが回転をすれば、ローカル座標系も同じだけの回転をする。そして、オブジェクトが拡大縮小すれば、ローカル座標系も同じだけの拡大縮小をすることになる。つまり、オブジェクトのローカル座標系は、オブジェクトと一体化して運動するのである。
[Code3] (実行結果 図19、図20)
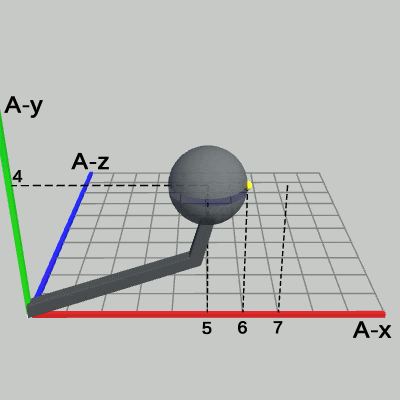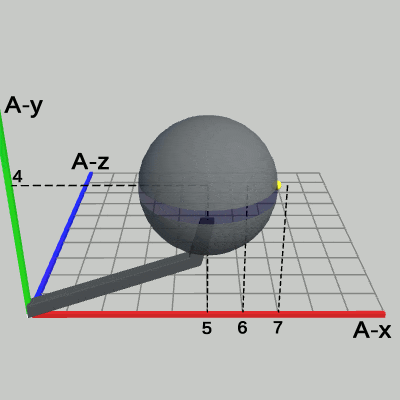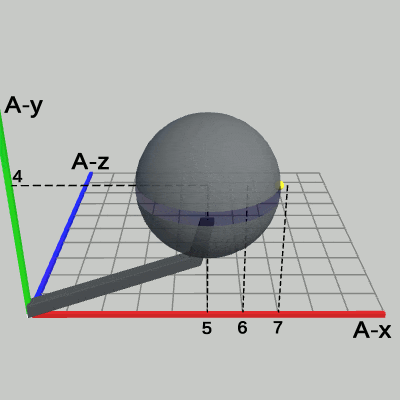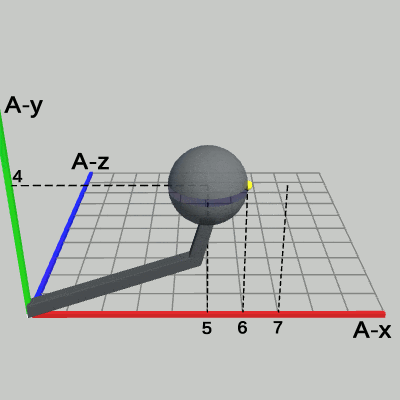
図19 Code3 実行結果 (Arm座標系から見たときの様子) 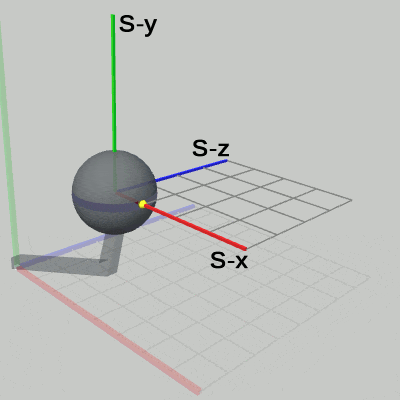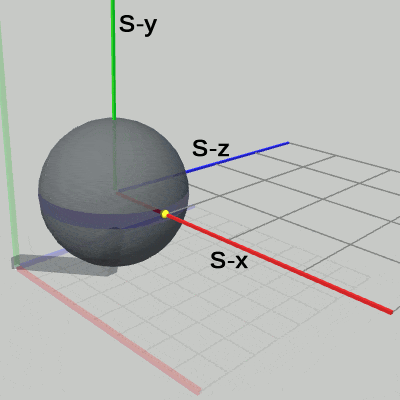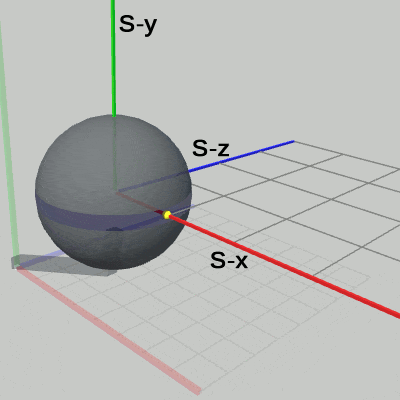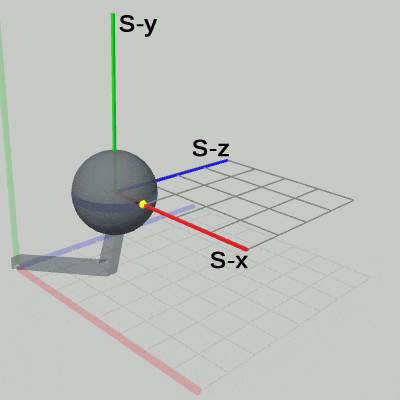
図20 Code3 実行結果 (Sphere座標系から見たときの様子)
1行目、2行目において拡大縮小の倍率を単振動によって計算している。i_shmSphereは単振動の計算で用いられる角度で、このプログラムでは毎フレーム 1ずつ増加する。また、この計算によって scaleは 1から 2の間を往復する。
図19は、Code3の実行結果を Arm座標系から見たときの様子である(ただし、図19では Sphere座標系は表示していない)。Arm座標系における Sphereの半径は 1から 2の間を往復する。また、Sphere右側の黄色い点の位置は、Arm座標系において、(6, 4, 0) から (7, 4, 0) の間を往復する。Sphereの中心の位置は、拡大縮小が行われている間でも (5, 4, 0) から変化しない。
図20は、Code3の実行結果を Sphere座標系から見たときの様子である。アニメーションからわかるように、Sphereの拡大縮小に連動して、Sphere座標系も Sphereと同じだけ拡大縮小している。そのため、Sphere座標系における Sphereの半径は、この運動中 常に初期状態と同じ 1のままなのである。また、Sphere上の黄色い点の位置は、Sphere座標系において、この運動中 常に(1, 0, 0) である。
つまり、「オブジェクトにどのような変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクト上の任意の位置における座標は変わらない」のである。
また、オブジェクトの一体化に関する記述の中では、親オブジェクト、子オブジェクトという呼び方を用いることはあっても、一体化によって発生するオブジェクトの階層構造については深く立ち入ることはなかった。
本節から4-11節までは、この階層構造に焦点を当て、一体化したオブジェクトの運動を解説する。そこでは、各オブジェクトが独自の座標系を持ち、それらの座標系は各オブジェクトの運動を表す変換行列と密接な関わりを持っていることが示される。
まずは、基本となる用語の説明から始めよう。
A) ローカル座標系と親座標系
モデリングツールなどでオブジェクトを作成し、FBXファイルやOBJファイルなどの外部ファイルに出力する。作成されたオブジェクトをゲームエンジンなどのツールで使う場合には、この出力された外部ファイルをロードして使用するわけだが、外部ファイルに出力された時のオブジェクトの状態を、この講義では「オブジェクトの初期状態」と呼んでいる。このことについては、2-1節で述べた。初期状態のオブジェクトもまた、何らかの座標系の中で定義されているわけであるが、初期状態のオブジェクトが定義されている座標系のことをローカル座標系(Local Coordinate System)という。ローカル座標系は、各オブジェクトが独自に持っている座標系である。

また、ローカル座標系においても赤色の軸を x軸、緑色の軸を y軸、青色の軸を z軸とする。
ローカル座標系は特殊な座標系であり、オブジェクトと一体化した座標系として考えることができる。例えば、オブジェクトに対し変換を実行して3D空間上で運動させる場合でも、オブジェクトが自身のローカル座標系の中を運動することはない。つまり、ローカル座標系の中でのオブジェクトの位置、向き、大きさなどの状態は、オブジェクトに対して実行される変換によって変わることはない。言い換えれば、ローカル座標系はオブジェクトと一体化して運動するのである。このことについては以降で説明していく。
オブジェクトを一体化して運動させる際には、あるオブジェクトを別のオブジェクトにアタッチする。このとき、アタッチされる側のオブジェクトが親オブジェクトであるが、親オブジェクトもローカル座標系を持っており、自身のローカル座標系の中で初期状態の位置、向き、大きさなどが定義されている。子オブジェクトから見たときの、親オブジェクトのローカル座標系を特に、親座標系(Parent's Coordinate System)という。
オブジェクトをアタッチする際には、オブジェクトを親オブジェクトの指定位置、あるいは指定領域へ移動させるが、詳しくは、オブジェクトのアタッチとは、オブジェクトを親座標系の指定位置、あるいは指定領域へ移動させることを意味する。
B) ワールド座標系
オブジェクトに対して何らかの変換を実行し、運動させる場合には、オブジェクトの運動は、そのオブジェクトの親座標系の中で考えることが基本である。つまり、そのオブジェクトの親座標系の中で運動を定義するのである。親オブジェクトを持つ子オブジェクトであれば、親座標系の中で運動を定義することはできるだろう。しかし、親子階層の最上位に位置する親オブジェクトや、どのオブジェクトとも親子関係のない単独のオブジェクトは親オブジェクトを持っていない。こういった、親オブジェクトを持っていないオブジェクトの場合、「親座標系の中で運動を定義する」ことはどのようにして行われるのだろうか。
実際には、そのような 親オブジェクトを持たないオブジェクト の運動を定義するための座標系が存在する。コンピューターグラフィックスの世界では、この特別な座標系をワールド座標系(World Coordinate System)という。

ワールド座標系は既に何度も使われてきている。たとえば 今までのプログラムの実行中に表示されていた座標系は、すべてワールド座標系である。図2のアニメーションでは、2つのオブジェクトが y軸の周りを回転しているが、詳しくは、ワールド座標系の y軸の周りを回転しているのである。
本節から4-11節においては「オブジェクトに定義された運動」や「オブジェクトに定義された変換」といった表現が多く使われるが、どちらも同じ意味であり明確な違いはない (2-7節などでも、親子関係にあるオブジェクトの解説の中で「オブジェクトの独自の運動」といった表現が使われているが、これもまた同じ意味である)。
「オブジェクトに定義された運動」(あるいは「オブジェクトに定義された変換」) は今までのプログラムで何度も見ているものである。
- Matrix4x4 sclObj3 = ... ;
- Matrix4x4 rotObj3 = ... ;
- Matrix4x4 traObj3 = ... ;
- Matrix4x4 localObj3 = traObj3 * rotObj3 * sclObj3;
- Matrix4x4 sclObj2 = ... ;
- Matrix4x4 rotObj2 = ... ;
- Matrix4x4 traObj2 = ... ;
- Matrix4x4 localObj2 = traObj2 * rotObj2 * sclObj2;
- Matrix4x4 sclObj1 = ... ;
- Matrix4x4 rotObj1 = ... ;
- Matrix4x4 traObj1 = ... ;
- Matrix4x4 localObj1 = traObj1 * rotObj1 * sclObj1;
- Matrix4x4 worldObj3 = localObj1 * localObj2 * localObj3;
- Matrix4x4 worldObj2 = localObj1 * localObj2;
- Matrix4x4 worldObj1 = localObj1;
- Obj3.SetMatrix(worldObj3);
- Obj2.SetMatrix(worldObj2);
- Obj1.SetMatrix(worldObj1);
今までのプログラムはすべて上の形で記述されていた。このプログラムの場合は3つのオブジェクト Obj1、Obj2、Obj3の一体化した運動の記述である。
「オブジェクトに定義された運動(あるいは変換)」とは、プログラムにおける変換行列 local### によって表される変換のことである。このプログラムの場合では、Obj1に定義された運動(あるいは変換)は localObj1 によって表される変換であり、Obj2、Obj3に定義された運動(あるいは変換)は localObj2、localObj3 によって表される変換である。
また、文章中において「ローカル行列」とあれば、それはプログラムにおいては変換行列 local### のことであり、「ワールド行列」とあれば、それはプログラムにおいては変換行列 world### のことである。例えば上のプログラムでは、Obj1のローカル行列は localObj1 であり、ワールド行列は worldObj1 である。
では、ここからは2つのオブジェクトの一体化した運動を、各階層の座標系に焦点を当てて見ていく。図3、図4は、今回使用するオブジェクト Sphere、Arm の初期状態である。Sphereは球体オブジェクトで、初期状態において、その中心は原点にあり、半径は 1である。


オブジェクトの初期状態に関して1つ補足しておこう。
今までにも、使用してきたオブジェクトについては初期状態の図を表示したが、これらの図はオブジェクトのローカル座標系での表示であるということである。例えば、上の図3、図4においても Sphere、Arm の置かれている座標系はそれぞれのローカル座標系である。
また、本節から4-12節までは複数の座標系が使われるが、その点について違いを明らかにしておこう。
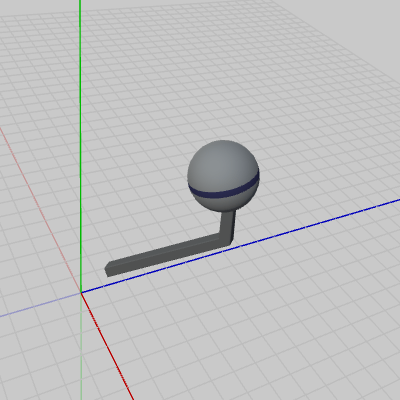 図5 ワールド座標系における2つのオブジェクト
図5 ワールド座標系における2つのオブジェクト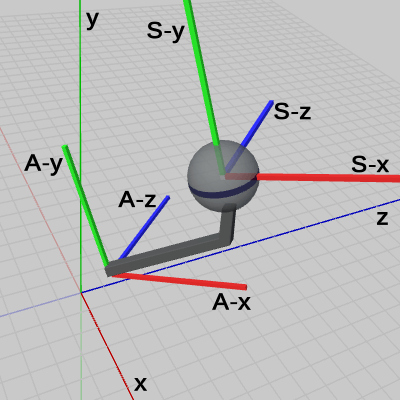 図6 ワールド座標系における2つのオブジェクト、及びそれらのローカル座標系
図6 ワールド座標系における2つのオブジェクト、及びそれらのローカル座標系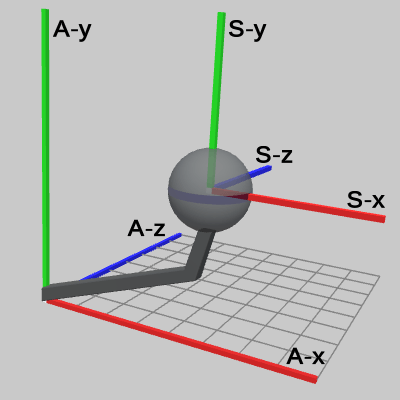 図7 Armのローカル座標系における2つのオブジェクト
図7 Armのローカル座標系における2つのオブジェクト
図5は、2つのオブジェクト Sphereと Armが、ワールド座標系に置かれた様子を示している。図から分かるように、表示されている座標系はワールド座標系のみである。また、このときのカメラはワールド座標系に置かれている。
図6は、ワールド座標系に置かれた Sphereと Armのそれぞれに、ローカル座標系を表示したものである。ワールド座標系と区別するために、ローカル座標系では各軸の太さがやや太くなっている。また、Sphere、Armのローカル座標系は、どちらも座標軸のプラス側のみの表示であり、グリッドは省略してある。図中のラベルの意味は、x、y、zがワールド座標系のx軸、y軸、z軸を表し、S-x、S-y、S-zが Sphereのローカル座標系におけるx軸、y軸、z軸を表し、A-x、A-y、A-zが Armのローカル座標系におけるx軸、y軸、z軸を表している。図5と同様に、図6においてもカメラはワールド座標系に置かれている。
図7は、カメラを Armのローカル座標系に置いたときの2つのオブジェクトの表示である。表示内容を明確にするためにワールド座標系は描画していない。図中のラベルの意味は図6と同様である。Armのローカル座標系では、グリッドが部分的に表示されているが(XZ平面の第1象限のみ)、 Sphereのローカル座標系はここでも座標軸のみの表示とし、グリッドは省略してある。
簡単に述べると、この講義においてはワールド座標系は常に各軸が細い線で描画されている。座標系の各軸が太く描画されていれば、それはローカル座標系である。そして、そのとき表示されているのは各軸のプラス側のみである。また、ローカル座標系のグリッドは、表示する場合もあれば、していない場合もあり、グリッドを表示する場合は一部の例を除き XZ平面の第1象限のみの表示となる。
ただし、先にも述べたが図3、図4のようなオブジェクトの初期状態で使われる座標系は、ローカル座標系であるが、そのときの各軸は細い線で描画される。
では、実際にプログラムを作成していくが、冒頭でも述べたように本節から4-11節で使われるプログラムは、運動の実装方法の解説を目的とするものではない。また、その内容は今までに作成してきたものと同様のものであるので、プログラムについての解説は省略する。
# Code1
まず始めに、SphereをArmにアタッチする。[Code1] (実行結果 図8、図9)
- // c_attachPos_Sphere : (5, 4, 0)
- Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere);
- Matrix4x4 localSphere = traSphere;
- Matrix4x4 localArm = Matrix4x4.identity;
- Matrix4x4 worldSphere = localArm * localSphere;
- Matrix4x4 worldArm = localArm;
- Sphere.SetMatrix(worldSphere);
- Arm.SetMatrix(worldArm);


プログラム2行目の c_attachPos_Sphereは、Sphereのアタッチポジションを表す Vector3型の定数で、その値は (5, 4, 0) である。
図8は、プログラムの実行結果を Armのローカル座標系から見たものであり、図からわかるように Sphereの中心は、Arm座標系において (5, 4, 0) に移動している。この移動は、Sphereを Armの先端にアタッチする処理であるが、詳しくは Sphereを、親座標系である Arm座標系の (5, 4, 0) にアタッチしているのである。
また、Sphereのローカル座標系の原点も同じく、(5, 4, 0)に移動しているが、このことは、Sphere座標系が Sphereと同じだけ移動していることを意味する。すなわち、Sphereは 自身のローカル座標系と一体化して移動しているのである。
図9は、実行結果を Sphereのローカル座標系から見たものであるが、Sphereは 自身のローカル座標系の中では全く動いていないことが分かるだろう。つまり、Sphereの中心は Sphere座標系の原点に置かれており、Sphereの半径は 1、これは図3の初期状態と同じである。
上でも述べたように、オブジェクトに変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクトの状態(位置、向き、大きさ)は変化しないのである。
言い換えれば、オブジェクトにどのような変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクト上の任意の位置における座標は変わらない。このことについて、以下の例で見ていこう。
次の図は Sphere上の2つの位置の座標を Sphere座標系、Arm座標系で表示したものである。それら2つの位置は、図中では黄色い点と水色の点で表されている。図において、A(##, ##, ##) となっているのは Arm座標系における座標値を表し、S(##, ##, ##) となっているのは Sphere座標系における座標値を表している。
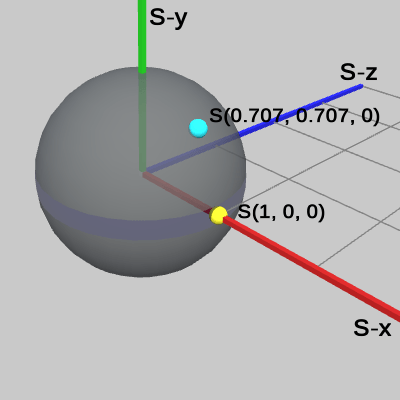 図10 2つの位置の Sphere座標系における座標値(Sphereと Sphere座標系のみの表示)
図10 2つの位置の Sphere座標系における座標値(Sphereと Sphere座標系のみの表示)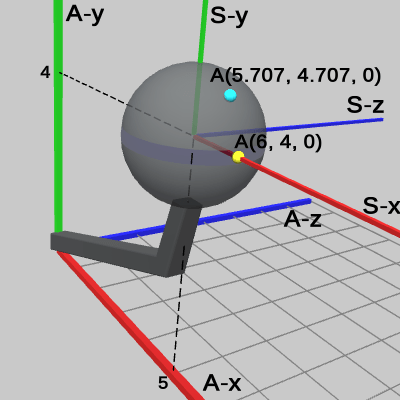 図11 2つの位置の Arm座標系における座標値(Code1実行後)
図11 2つの位置の Arm座標系における座標値(Code1実行後) 図12 2つの位置の Sphere座標系における座標値(Code1実行後)
図12 2つの位置の Sphere座標系における座標値(Code1実行後)
図10は、Sphere及び、Sphere座標系のみを表示したもので、Sphereの中心は原点にあり、黄色い点は Sphere上の (1, 0, 0) の位置を示し、水色の点は Sphere上の (0.707, 0.707, 0.0) の位置を示している。これらの座標値はいずれも Sphere座標系での値である。
図11は、この2つの位置をCode1実行後の Arm座標系で表示したものである。Arm座標系においては Sphereの中心は (5, 4, 0) に移動しているため、2つの位置の座標値もその分だけ移動した結果になっている。これらの座標値はいずれも Arm座標系での値である。
図12は、この2つの位置をCode1実行後の Sphere座標系で表示したものである。図における座標値は Sphere座標系での値であり、図10のものと同じである。何らかの変換によってオブジェクトを動かす場合でも、オブジェクトとそのオブジェクトのローカル座標系は一体となって動くためこのような結果になるのである。
繰り返せば、オブジェクトにどのような変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクト上の任意の位置における座標は変わらないのである。
# Code2
では、次に Sphereを Armにアタッチした状態で2倍に拡大する。[Code2] (実行結果 図13、14)
- Matrix4x4 sclSphere = TH3DMath.GetScale4x4(2.0f);
- Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); // c_attachPos_Sphere : (5, 4, 0)
- Matrix4x4 localSphere = traSphere * sclSphere;
- Matrix4x4 localArm = Matrix4x4.identity;
- Matrix4x4 worldSphere = localArm * localSphere;
- Matrix4x4 worldArm = localArm;
- Sphere.SetMatrix(worldSphere);
- Arm.SetMatrix(worldArm);


図13は、Code2の実行結果を Arm座標系から見たときの様子である。Code1の場合と同様に、Sphereの中心が (5, 4, 0) に移動している。図14は、Code2の実行結果を Sphere座標系から見たときの様子である。Sphere座標系では、やはり Sphereの中心は原点に位置しており、Sphereの半径は 1であることがわかる。
だが、今回の Sphereの拡大によって、Sphereがやや大きく表示されている ということ以外には、これらの図から得られる情報はない。今回の拡大によって、2つの座標系の間で発生した違いを明確にするために、Sphereを Arm座標系の原点に移動させた場合の図を用意する。


図15は、2倍に拡大されたSphereを Arm座標系の原点に移動させ、Arm座標系のみを表示したときの様子である。図からわかるとおり、2倍に拡大されたSphereの中心は原点にあるが、半径は Arm座標系では 1ではなく、2になっている。
図16は、図15の状態から Arm座標系を非表示にし、Sphere座標系のみを表示したときの様子である。Sphere座標系においては、今までと同様に Sphereの中心は原点にあり、半径は 1である。これは、Code2によって Sphereは 2倍に拡大されるが、Sphere座標系自体も2倍に拡大するので、Sphere座標系で測ったときの半径は拡大前と後で変化はないのである。
実際に、図15と図16の座標系を見比べれば、グリッドの間隔が Arm座標系よりも Sphere座標系の方が明らかに広いことが分かるだろう(正確には2倍の間隔になっている)。
では、ここでも上の例で見たように、Code2実行後の Sphere上の2つの位置の座標を Arm座標系、Sphere座標系で表示してみよう(上の場合と同様に、A(##, ##, ##) は Arm座標系での座標値を、S(##, ##, ##) は Sphere座標系での座標値を表している)。


図17は、この2つの位置をCode2実行後の Arm座標系で表示したものである。Sphereの中心が (5, 4, 0) であることは今までと同じである。しかし上記の図11とは異なり、ここでの Sphereの半径は Arm座標系において 2である。
そのため黄色い点の座標は (7, 4, 0) となっているが、これは以下のようにして求められる。 2 * (1, 0, 0) + (5, 4, 0) = (7, 4, 0) Code2の実行手順では、Sphereは初期状態から2倍拡大後にアタッチポジションへ アタッチされる。したがって、Code2実行後における Sphere上の各点の位置を計算する場合も、各位置の座標を2倍拡大後にアタッチ(平行移動)という順序で計算すればよい。水色の点の座標を求める場合も同様である。
図18は、この2つの位置をCode2実行後の Sphere座標系で表示したものである。Sphere座標系での2つの位置の座標は、図12のものと同じである。図12の Sphereには拡大は行われていないが、ここでは Sphereに対して 2倍の拡大が実行されている。それでも、Sphere座標系で見たときには Sphere上の水色と黄色の点の座標は、図12と図18の場合で変化はないのである。これは先ほども述べたように、Sphereに拡大が実行される場合、Sphereのローカル座標系にも同じ拡大が実行されるためである。
オブジェクトに対して何らかの変換を実行した場合、そのオブジェクトのローカル座標系にも同じ変換が実行される。オブジェクトが平行移動をすれば、ローカル座標系も同じだけ平行移動をし、オブジェクトが回転をすれば、ローカル座標系も同じだけの回転をする。そして、オブジェクトが拡大縮小すれば、ローカル座標系も同じだけの拡大縮小をすることになる。つまり、オブジェクトのローカル座標系は、オブジェクトと一体化して運動するのである。
# Code3
では本節の最後に、Sphereが Armの先端で拡大縮小を繰り返すプログラムを作成する(倍率は 1倍から 2倍)。[Code3] (実行結果 図19、図20)
- i_shmSphere += 1.0f; // 単振動計算で使われる角度
- float scale = 0.5f * Mathf.Sin(i_shmSphere * Mathf.Deg2Rad) + 1.5f; // 1から2の間を往復
- Matrix4x4 sclSphere = TH3DMath.GetScale4x4(scale);
- Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); // c_attachPos_Sphere : (5, 4, 0)
- Matrix4x4 localSphere = traSphere * sclSphere;
- Matrix4x4 localArm = Matrix4x4.identity;
- Matrix4x4 worldSphere = localArm * localSphere;
- Matrix4x4 worldArm = localArm;
- Sphere.SetMatrix(worldSphere);
- Arm.SetMatrix(worldArm);


1行目、2行目において拡大縮小の倍率を単振動によって計算している。i_shmSphereは単振動の計算で用いられる角度で、このプログラムでは毎フレーム 1ずつ増加する。また、この計算によって scaleは 1から 2の間を往復する。
図19は、Code3の実行結果を Arm座標系から見たときの様子である(ただし、図19では Sphere座標系は表示していない)。Arm座標系における Sphereの半径は 1から 2の間を往復する。また、Sphere右側の黄色い点の位置は、Arm座標系において、(6, 4, 0) から (7, 4, 0) の間を往復する。Sphereの中心の位置は、拡大縮小が行われている間でも (5, 4, 0) から変化しない。
図20は、Code3の実行結果を Sphere座標系から見たときの様子である。アニメーションからわかるように、Sphereの拡大縮小に連動して、Sphere座標系も Sphereと同じだけ拡大縮小している。そのため、Sphere座標系における Sphereの半径は、この運動中 常に初期状態と同じ 1のままなのである。また、Sphere上の黄色い点の位置は、Sphere座標系において、この運動中 常に(1, 0, 0) である。
つまり、「オブジェクトにどのような変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクト上の任意の位置における座標は変わらない」のである。
© 2020-2025 Redpoll's 60 (All rights reserved)