Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-11
第4章 3D空間におけるオブジェクトの運動
$§$4-11 ローカル座標系が表すオブジェクトの状態

結論から言うと、オブジェクトのローカル座標系は、そのオブジェクトの親座標系において、そのオブジェクトに定義される変換行列(オブジェクトのローカル行列)を可視化したものになっているのである。言い換えれば、親座標系における そのオブジェクトの現在の状態 (どれだけスケール、回転、平行移動が行われたか)を表しているのである。
本節においては、「ローカル座標系は、親座標系においてローカル行列を可視化したものになっている」という事実をいくつかの例を用いて示していくが、そこに展開される内容は いわば事実の確認に過ぎない。したがって、本節で解説される事柄については、その内容を文章や図とともに目で追っていく程度で構わない。
以下、2つのオブジェクトを一体化した場合、3つのオブジェクトを一体化した場合のそれぞれで、そのことについて見ていく。
使用するオブジェクトは前節に引き続き、以下の3つである。
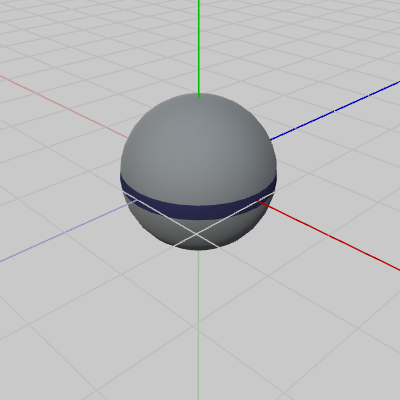 図2 Sphere 初期状態
図2 Sphere 初期状態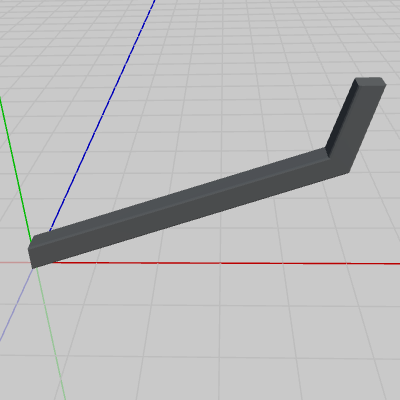 図3 Arm 初期状態
図3 Arm 初期状態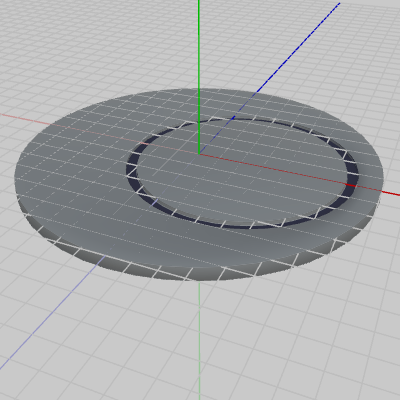 図4 Disk 初期状態
図4 Disk 初期状態
また、本節においても図の中では以下の略記が行われている。
D-x、D-y、D-z : Disk座標系のx軸、y軸、z軸
A-x、A-y、A-z : Arm座標系のx軸、y軸、z軸
S-x、S-y、S-z : Sphere座標系のx軸、y軸、z軸
W(##, ##, ##) : ワールド座標系における値
D(##, ##, ##) : Disk座標系における値
A(##, ##, ##) : Arm座標系における値
(本節で使用される図の中では、いくつかの位置について、各座標系における座標が表示されるが、それらの値の算出過程は特に解説はしていない。各座標系における座標の計算については次節で解説する。また、 本節では「オブジェクトに定義される変換行列」,「オブジェクトに実行される変換行列」といった表現が使われるが、「オブジェクトに定義される変換行列」とはオブジェクトのローカル行列のことであり、「オブジェクトに実行される変換行列」とはオブジェクトのワールド行列のことである)
A) 2つのオブジェクトの場合
まずは、Sphereと Armを一体化した場合である。[Beta1] (実行結果 図5~図16)
Matrix4x4 sclSphere = TH3DMath.GetScale4x4(2.0f); Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); // c_attachPos_Sphere : (5, 4, 0) Matrix4x4 localSphere = traSphere * sclSphere; Matrix4x4 rotArm = TH3DMath.GetRotation4x4(-60, Vector3.up); Matrix4x4 traArm = TH3DMath.GetTranslation4x4(3, 0, -3); Matrix4x4 localArm = traArm * rotArm; Matrix4x4 worldSphere = localArm * localSphere; Matrix4x4 worldArm = localArm; Sphere.SetMatrix(worldSphere); Arm.SetMatrix(worldArm);

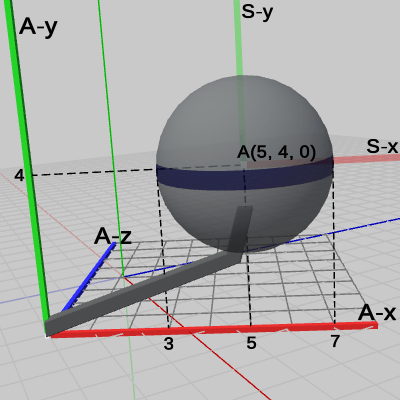
このプログラムは、4-9節の Code3と同じものである(実行結果の図5、図6も、4-9節の図11、図12と同じものである)。
ワールド座標系において Armを、$(3,0,−3)$ だけ移動させた状態で、Armの支点を通り、ワールド座標系のy軸に平行な軸の周りに、$−60$°の回転を実行する。Armの先端においては、Armにアタッチされている Sphereが $2$倍に拡大されている。
4-8節から 4-10節では、オブジェクトが親座標系の中でどのような運動を実行しているかについて見てきたが、本節における観察の対象はオブジェクトではなく、オブジェクトのローカル座標系である。
ここでは、プログラム実行後のローカル座標系について、さらに詳細な情報を追加した図を用いて観察を進めていく。
 図7
図7 図8
図8 図9
図9
図7、図8、図9はプログラムの実行結果をワールド座標系から見たものであり、図に示されている数値はすべてワールド座標系での値である。
図7は、Arm座標系の原点の座標の他に、Arm座標系の各軸の先端の座標が表示されている。A-x軸の先端は、ワールド座標系において $(7,\ 0,\ 3.93)$、同様に A-y軸、A-z軸の先端はワールド座標系において $(3, 8, -3)$、$(-3.93,\ 0,\ 1)$ である。
図8は、Arm座標系の各軸をベクトル表示したものである(緑色の数値)。A-x軸のベクトル表示は、Arm座標系の原点を始点とし、A-x軸の先端を終点とするベクトルのことで、その値は以下のように求められる。\[(7,\ 0,\ 3.93) - (3,\ 0, -3) = (4,\ 0,\ 6.93)\]同様に、A-y軸、A-z軸のベクトル表示は、\begin{align*}&(3,\ 8,\ -3) - (3,\ 0, -3) = (0,\ 8,\ 0) \\&(-3.93,\ 0,\ 1) - (3,\ 0, -3) = (-6.93,\ 0,\ 4)\end{align*}となる。さらに、図8には Arm座標系の各軸の長さが表示されており、各軸ともに $8$である(これは、上で求めたベクトルの大きさがワールド座標系において、すべて $8$であることを意味する)。
図9は、カメラを Arm座標系の原点付近へ移動させたときの図である。Arm座標系の各軸について、原点から Arm座標系のグリッド 1マス分の部分(以降、単位ベクトル部分と呼ぶ)を強調して太く表示してある。オレンジ色の数値は、図8の各軸のベクトル表示を単位ベクトル化したものである。
次に、Armに定義された変換を表す行列に焦点を当てる。
Armに定義された変換は、プログラムにおける5行目から7行目の部分で、
Matrix4x4 rotArm = TH3DMath.GetRotation4x4(-60, Vector3.up); Matrix4x4 traArm = TH3DMath.GetTranslation4x4(3, 0, -3); Matrix4x4 localArm = traArm * rotArm;
(注 : 本節においても行列の成分が小数である場合は、少数第3位を四捨五入して小数点以下第2位までの表示にしている。)
\begin{align*}traArm * rotArm &=\begin{pmatrix}1 &0 &0 &3 \\0 &1 &0 &0 \\ 0 &0 &1 &-3 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0.50 &0.00 &-0.87 &0.00 \\ 0.00 &1.00 &0.00 &0.00 \\ 0.87 &0.00 &0.50 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \\\\&= \begin{pmatrix}0.50 &0.00 &-0.87 &3.00 \\ 0.00 &1.00 &0.00 &0.00 \\ 0.87 &0.00 &0.50 &-3.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} = localArm\end{align*}
4-6節では変換行列に対し、次のような書き換えを行った。
\[M = \begin{pmatrix}m_{11} &m_{12} &m_{13} &m_{14} \\m_{21} &m_{22} &m_{23} &m_{24} \\m_{31} &m_{32} &m_{33} &m_{34} \\0 &0 &0 &1 \end{pmatrix} =\begin{pmatrix}s_x r_{11} &s_y r_{12} &s_z r_{13} &t_x \\s_x r_{21} &s_y r_{22} &s_z r_{23} &t_y \\s_x r_{31} &s_y r_{32} &s_z r_{33} &t_z \\0 &0 &0 &1 \end{pmatrix} \qquad(Ex1)\]
$s_x$、$s_y$、$s_z$は第1列目、第2列目、第3列目の大きさを表し、$(r_{11}, r_{21}, r_{31})$は、$(m_{11}, m_{21}, m_{31})$を $s_x$で割ったもの、$(r_{12}, r_{22}, r_{32})$、$(r_{13}, r_{23}, r_{33})$は、$(m_{12}, m_{22}, m_{32})$、$(m_{13}, m_{23}, m_{33})$を $s_y$、$s_z$で割ったもの、$t_x$、$t_y$、$t_z$は、$m_{14}$、$m_{24}$、$m_{34}$の値をそのままセットしたものである。
そして 4-6節によれば、$s_x$、$s_y$、$s_z$ を変換行列の「スケール成分」、$(r_{11}, r_{21}, r_{31})$、$(r_{12}, r_{22}, r_{32})$、$(r_{13}, r_{23}, r_{33})$ を変換行列の「回転成分」、$t_x$、$t_y$、$t_z$ を変換行列の「平行移動成分」と呼ぶのであった。
上で計算された $localArm$に対して、この書き換えを行うと次のようになる。
\[localArm =\begin{pmatrix}0.50 &0.00 &-0.87 &3.00 \\ 0.00 &1.00 &0.00 &0.00 \\ 0.87 &0.00 &0.50 &-3.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} = \begin{pmatrix}1\cdot 0.50 &1\cdot 0.00 &1\cdot (-0.87) &3.00 \\ 1\cdot 0.00 &1\cdot 1.00 &1\cdot 0.00 &0.00 \\ 1\cdot 0.87 &1\cdot 0.00 &1\cdot 0.50 &-3.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \]

$localArm$の第1列目、第2列目、第3列目(の3行目まで)に掛けられている係数はいずれも $1$であるが、これらは図における A-x軸、A-y軸、A-z軸の単位ベクトル部分(太くなっている部分)の長さに一致している (もし Armに対して、x軸方向にのみ $5$倍の拡大が実行されていれば、単位ベクトル部分の(ワールド座標系での)大きさは A-x軸のみ $5$になる。そのときは、$localArm$の各列に掛けられる係数は、第1列目のみ $5$になる)。
$localArm$の第1列目(の3行目まで)の係数以外の値は $(0.50, 0.00, 0.87)$ であるが、これは図9における A-x軸の単位ベクトル表示の値と同じものである。同様に第2列目、第3列目の係数以外の値は $(0.00, 1.00, 0.00)$、$(-0.87, 0.00, 0.50)$ であるが、これらは図9における A-y軸、A-z軸の単位ベクトル表示の値と同じものである。
$localArm$の第4列目(の3行目まで)の値は $(3.00, 0.00, -3.00)$ であるが、これは図9の Arm座標系の原点の座標に等しい。
つまり、図9のようにArmの親座標系であるワールド座標系において、Arm座標系の単位ベクトル部分のみを見た場合には、Arm座標系は、Armに定義された変換行列 localArmを ワールド座標系において可視化したものになっているのである。言い換えれば、Arm座標系は、親座標系であるワールド座標系において Armの現在の状態(どれだけスケール、回転、平行移動が行われたか)を表しているのである。

たとえば、図10は Arm座標系の単位ベクトル部分を Arm座標系において表示したものである(図中の数値はすべて Arm座標系での値である)。Arm座標系の各軸の単位ベクトル部分は、Armに対してどのような変換を実行しても、Arm座標系における単位ベクトル表示では常に、$(1, 0, 0)$、$(0, 1, 0)$、$(0, 0, 1)$ である。Arm座標系の原点も Arm座標系においては常に、$(0, 0, 0)$ である。これらの値と、上記に示される変換行列 $localArm$の内容との間には何のつながりも見られない。
前節や前々節では、オブジェクトに定義された変換は、そのオブジェクトの親座標系において'見える'ということについて解説してきたが、これと同様に、オブジェクトに定義された変換を表す行列は、そのオブジェクトの親座標系において、そのオブジェクトのローカル座標系によって可視化されるのである(より正確にはローカル座標系の単位ベクトル部分によって)。
続いて、Beta1実行後の Sphere座標系について見ていく。

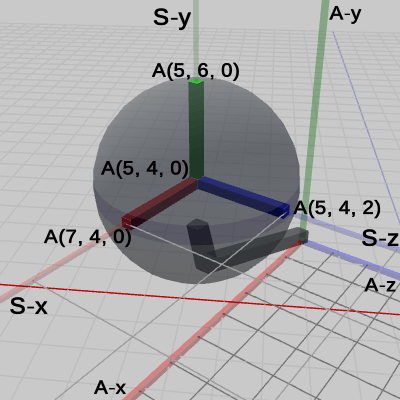
図11、図12はプログラムの実行結果を Arm座標系から見たものであり、図に示されている数値はすべて Arm座標系での値である。
図11は、Sphere座標系の原点座標 $(5, 4, 0)$ の他に、Sphere座標系の各軸の先端の座標が表示されている。S-x軸の先端は、Arm座標系において $(11, 4, 0)$、同様に S-y軸、S-z軸の先端は、Arm座標系において $(5, 10, 0)$、$(5, 4, 6)$ である。
図12は、カメラを Sphere座標系の原点付近へ移動させたときの図である。ここでも Arm座標系の場合と同様に、Sphere座標系の各軸について、原点から Sphere座標系のグリッド 1マス分の部分(単位ベクトル部分)を強調して表示してある。図12において Sphere座標系の原点座標の他に表示されているのは、各軸の単位ベクトル部分の先端の座標である。たとえば、S-z軸の単位ベクトル部分の先端は Arm座標系において $(5, 4, 2)$ である。

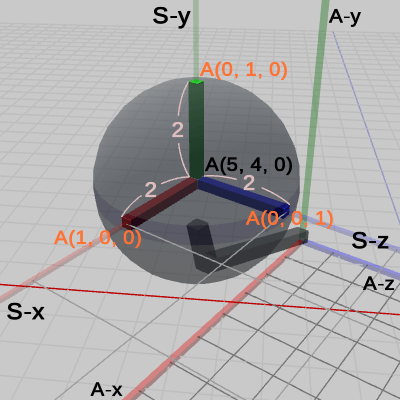
図13、図14も同様に プログラムの実行結果を Arm座標系から見たものであり、図に示されている数値はすべて Arm座標系での値である。
図13は、Sphere座標系の各軸の単位ベクトル部分をベクトル表示したものである(緑色の数値)。S-x軸の単位ベクトル部分のベクトル表示は、Sphere座標系の原点を始点とし、S-x軸の単位ベクトル部分の先端を終点とするベクトルのことで、その値は以下のように求められる。
\[(7,\ 4,\ 0) - (5,\ 4,\ 0) = (2,\ 0,\ 0)\]同様に、S-y軸、S-z軸の単位ベクトル部分のベクトル表示は、\begin{align*}&(5,\ 6,\ 0) - (5,\ 4,\ 0) = (0,\ 2,\ 0) \\&(5,\ 4,\ 2) - (5,\ 4,\ 0) = (0,\ 0,\ 2)\end{align*}となる。さらに、図13、図14には Sphere座標系の各軸の単位ベクトル部分の長さが表示されており、各軸ともに $2$である。Sphere座標系で測った場合は、Sphere座標系の各軸の単位ベクトル部分の長さは常に $1$である。しかし、Arm座標系においては、Sphereは $2$倍に拡大されているので、Sphere座標系の単位ベクトル部分の長さも Arm座標系では $2$倍の長さである $2$となるのである(4-8節 図15、図16参照)。
図14のオレンジ色の数値は、図13の 緑色で表された各軸のベクトル表示を単位ベクトル化したものである。
ではここで、Sphereに定義された変換を表す行列を見てみよう。
Sphereに定義された変換、プログラムにおける1行目から3行目の部分で、
Matrix4x4 sclSphere = TH3DMath.GetScale4x4(2.0f); Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); // c_attachPos_Sphere : (5, 4, 0) Matrix4x4 localSphere = traSphere * sclSphere;
\begin{align*}traSphere * sclSphere&=\begin{pmatrix}1 &0 &0 &5 \\0 &1 &0 &4 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}2 &0 &0 &0 \\ 0 &2 &0 &0 \\ 0 &0 &2 &0 \\ 0 &0 &0 &1\end{pmatrix} \\\\&= \begin{pmatrix}2 &0 &0 &5 \\ 0 &2 &0 &4 \\ 0 &0 &2 &0 \\ 0 &0 &0 &1\end{pmatrix} = localSphere\end{align*}
この $localSphere$に対して、先程と同じように$(Ex1)$の書き換えを行うと以下の結果になる。
\[localSphere =\begin{pmatrix}2 &0 &0 &5 \\ 0 &2 &0 &4 \\ 0 &0 &2 &0 \\ 0 &0 &0 &1\end{pmatrix} = \begin{pmatrix}2\cdot 1 &2\cdot 0 &2\cdot 0 &5 \\ 2\cdot 0 &2\cdot 1 &2\cdot 0 &4 \\ 2\cdot 0 &2\cdot 0 &2\cdot 1 &0 \\ 0 &0 &0 &1\end{pmatrix} \]

$localSphere$の第1列目、第2列目、第3列目(の3行目まで)に掛けられている係数はいずれも $2$であるが、これらは図における S-x軸、S-y軸、S-z軸の単位ベクトル部分(太くなっている部分)の長さに一致している。
$localSphere$ の第1列目(の3行目まで)の係数以外の値は $(1, 0, 0)$ であるが、これは図14における S-x軸の単位ベクトル表示の値と同じものである。同様に第2列目、第3列目の係数以外の値は $(0, 1, 0)$、$(0, 0, 1)$ であるが、これらは図14における S-y軸、S-z軸の単位ベクトル表示の値と同じものである。
$localSphere$の第4列目 (の3行目まで)の値は $(5, 4, 0)$ であるが、これは図14の Sphere座標系の原点の座標に等しい。
つまり、Sphere座標系の単位ベクトル部分は、Sphereに定義された変換行列 localSphereを、 Arm座標系において可視化したものになっているのである。言い換えれば、Sphere座標系は、Arm座標系において Sphereの現在の状態(どれだけスケール、回転、平行移動が行われたか)を表しているのである。
再度 繰り返すが、これらのことが成り立つのは Sphereの親座標系である Arm座標系においてのことである。Arm座標系で測ったときの Sphere座標系の各値が $localSphere$の各値に対応するのである。
たとえば 図15は、Sphere座標系の各軸の単位ベクトル部分の先端座標、及び 原点座標をワールド座標系において表示したものである。図16は、Sphere座標系の各軸の単位ベクトル部分を 単位ベクトル表示したものであるが、図中の数値はすべてワールド座標系で測ったときの値である。

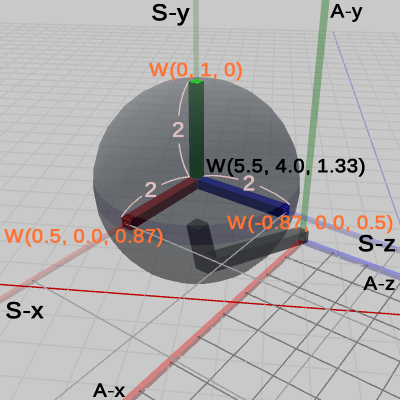
図16における各値と $localSphere$の内容との間には、上で示したような つながりは見られない(Sphereは Arm座標系の中で回転をしていないので、Sphere座標系の各軸の向きは、Arm座標系の各軸の向きと一致している。実際、図9と図16の各軸の単位ベクトル表示の値を比較すれば、確かに両者はワールド座標系において同じ値であることがわかる)。
B) 3つのオブジェクトの場合
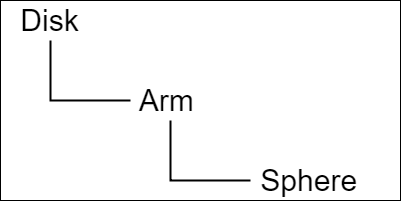
各オブジェクトには次のような変換が実行される。
Diskは、親座標系である ワールド座標系において x軸周りに $-15$°回転した状態で、$(0, 10, 0)$ へ平行移動。
Armは、親座標系である Disk座標系においてアタッチポジションである $(2, 0, 0)$ への平行移動、その位置では、Armの支点を通り Disk座標系の y軸に平行な軸の周りに $200$°の回転。
Sphereは、親座標系である Arm座標系においてアタッチポジションである $(5, 4, 0)$ への平行移動、その位置では、各軸の方向に $1.5$倍の拡大。
[Beta2] (実行結果 図18~図24)
Matrix4x4 sclSphere = TH3DMath.GetScale4x4(1.5f); Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); // c_attachPos_Sphere : (5, 4, 0) Matrix4x4 localSphere = traSphere * sclSphere; Matrix4x4 rotArm = TH3DMath.GetRotation4x4(200, Vector3.up); Matrix4x4 traArm = TH3DMath.GetTranslation4x4(c_attachPos_Arm); // c_attachPos_Arm : (2, 0, 0) Matrix4x4 localArm = traArm * rotArm; Matrix4x4 rotDisk = TH3DMath.GetRotation4x4(-15, Vector3.right); Matrix4x4 traDisk = TH3DMath.GetTranslation4x4(0, 10, 0); Matrix4x4 localDisk = traDisk * rotDisk; Matrix4x4 worldSphere = localDisk * localArm * localSphere; Matrix4x4 worldArm = localDisk * localArm; Matrix4x4 worldDisk = localDisk; Sphere.SetMatrix(worldSphere); Arm.SetMatrix(worldArm); Disk.SetMatrix(worldDisk);
 図18
図18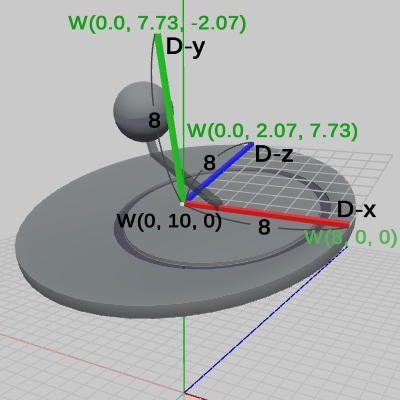 図19
図19 図20
図20
図18、図19、図20はプログラムの実行結果をワールド座標系から見たときの様子であり、観察の対象を Disk座標系に定めている。これらの図における数値は、すべてワールド座標系での値である。
図18には、Disk座標系の原点、及び、Disk座標系の各軸の先端の座標が表示されている。D-x軸、D-y軸、D-z軸の先端の座標は、それぞれ $(8, 10, 0)$、$(0.0,\ 17.73, -2.07)$、$(0.0,\ 12.07,\ 7.73)$ である。
図19は、Disk座標系の各軸をベクトル表示したものである(緑色の数値)。D-x軸のベクトル表示は、Disk座標系の原点を始点とし、D-x軸の先端を終点とするベクトルのことで、その値は以下のように求められる。\[(8, 10, 0) - (0, 10, 0) = (8, 0, 0)\]同様に、D-y軸、D-z軸のベクトル表示は、\begin{align*}&(0.0,\ 17.73, -2.07) - (0, 10, 0) = (0.0,\ 7.73, -2.07) \\&(0.0,\ 12.07,\ 7.73) - (0, 10, 0) = (0.0,\ 2.07,\ 7.73) \end{align*}となる。さらに、図19には Disk座標系の各軸の長さが表示されており、各軸ともに $8$である(これは、上で求めたベクトルの大きさがすべて $8$であることを意味する)。
図20は、カメラを Disk座標系の原点付近へ移動させたときの図である。Disk座標系の各軸について、原点から Disk座標系のグリッド 1マス分の部分(単位ベクトル部分)を強調して太く表示してある。Diskに対しては スケールを実行していないので、Disk座標系の単位ベクトル部分の長さは、ワールド座標系において各軸ともに $1$である。オレンジ色の数値は、図19の各軸のベクトル表示を単位ベクトル化したものである。
次に、Diskに定義された変換を表す行列について見ていこう。
Diskに定義された変換は、プログラムにおける9行目から11行目の部分で、
Matrix4x4 rotDisk = TH3DMath.GetRotation4x4(-15, Vector3.right); Matrix4x4 traDisk = TH3DMath.GetTranslation4x4(0, 10, 0); Matrix4x4 localDisk = traDisk * rotDisk;
\begin{align*}traDisk * rotDisk &=\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &10 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}1.00 &0.00 &0.00 &0.00 \\ 0.00 &0.97 &0.26 &0.00 \\ 0.00 &-0.26 &0.97 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \\\\&= \begin{pmatrix}1.00 &0.00 &0.00 &0.00 \\ 0.00 &0.97 &0.26 &10.00 \\ 0.00 &-0.26 &0.97 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} = localDisk\end{align*}
この $localDisk$に対して、上記 $(Ex1)$の書き換えを行ったものが以下である。\[localDisk =\begin{pmatrix}1.00 &0.00 &0.00 &0.00 \\ 0.00 &0.97 &0.26 &10.00 \\ 0.00 &-0.26 &0.97 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} = \begin{pmatrix}1\cdot 1.00 &1\cdot 0.00 &1\cdot 0.00 &0.00 \\ 1\cdot 0.00 &1\cdot 0.97 &1\cdot 0.26 &10.00 \\ 1\cdot 0.00 &1\cdot (-0.26) &1\cdot 0.97 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \]

$localDisk$の第1列目から第3列目に掛けられている係数は、各列ともすべて $1$であるが、Disk座標系の各軸の単位ベクトル部分の長さは、D-x軸、D-y軸、D-z軸いずれも $1$となっている。
$localDisk$の第1列目(の3行目まで)の係数以外の値は $(1.00,\ 0.00,\ 0.00)$ であるが、これは D-x軸の単位ベクトル表示の値に等しい。同様に、$localDisk$の第2列目、第3列目(の3行目まで)の係数以外の値は $(0.00,\ 0.97, -0.26)$、$(0.00,\ 0.26,\ 0.97)$ であるが、これらは D-y軸、D-z軸の単位ベクトル表示の値に等しい。
また、$localDisk$の第4列目(の3行目まで)の値は $(0.00, 10.00, 0.00)$ であるが、これは Disk座標系の原点座標に等しい。
続いて、観察の対象を Arm座標系、Sphere座標系に定めたときについて見ていくが、その内容については今までの解説と同様のものであるので、各座標系におけるプログラムの実行結果、及び、各オブジェクトのローカル行列のみを示し、それらの間の対応関係に関する解説は省略する。
Arm座標系、及び Armのローカル行列の対応について。
図21、図22はプログラムの実行結果を Disk座標系から見たときの様子である(数値はすべて Disk座標系での値である)。
図においては、D-x軸と A-x軸の一部が重なっており、違いを明らかにするため D-x軸を黄色い軸で表示している。また、ここにおいてのみ Disk座標系のグリッドは D-x軸、D-z軸のマイナス方向の領域も表示している (Arm座標系のグリッドを明らかにするために、グリッドの色を水色にしてある)。


図21は、Arm座標系の原点座標、及び 各軸の先端の座標が表示されている。
図22は、Arm座標系の原点座標の他に、Arm座標系の各軸の単位ベクトル表示の値が表示されている。また、Arm座標系の単位ベクトル部分を太く強調表示し、その部分の Disk座標系における長さも示されている。
次に、Armのローカル行列を以下に示す。Armのローカル行列は、プログラムにおける5行目から7行目までの部分で、
Matrix4x4 rotArm = TH3DMath.GetRotation4x4(200, Vector3.up); Matrix4x4 traArm = TH3DMath.GetTranslation4x4(c_attachPos_Arm); // c_attachPos_Arm : (2, 0, 0) Matrix4x4 localArm = traArm * rotArm;
\begin{align*}traArm * rotArm &=\begin{pmatrix}1 &0 &0 &2 \\0 &1 &0 &0 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}-0.94 &0.00 &-0.34 &0.00 \\ 0.00 &1.00 &0.00 &0.00 \\ 0.34 &0.00 &-0.94 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \\\\&= \begin{pmatrix}-0.94 &0.00 &-0.34 &2.00 \\ 0.00 &1.00 &0.00 &0.00 \\ 0.34 &0.00 &-0.94 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} =\begin{pmatrix}1\cdot(-0.94) &1\cdot 0.00 &1\cdot(-0.34) &2.00 \\ 1\cdot 0.00 &1\cdot 1.00 &1\cdot 0.00 &0.00 \\ 1\cdot 0.34 &1\cdot 0.00 &1\cdot(-0.94) &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} = localArm\end{align*}
Sphere座標系、及び Sphereのローカル行列の対応について。
図23、図24はプログラムの実行結果を Arm座標系から見たときの様子である(数値はすべて Arm座標系での値である)。
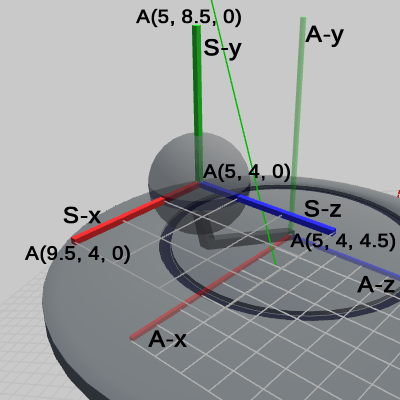
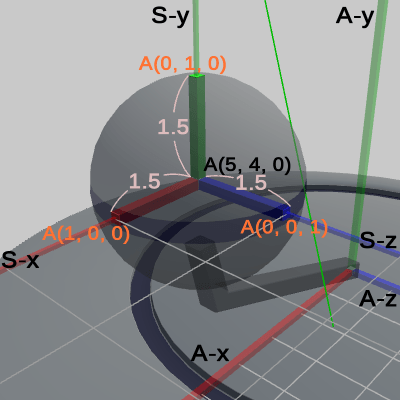
図23は、Sphere座標系の原点座標、及び 各軸の先端の座標が表示されている。
図24は、Sphere座標系の原点座標の他に、Sphere座標系の各軸の単位ベクトル表示の値が表示されている。また、Sphere座標系の単位ベクトル部分を太く強調表示し、その部分の Arm座標系における長さも示されている。
次に、Sphereのローカル行列を以下に示す。Sphereのローカル行列は、プログラムにおける1行目から3行目までの部分で、
Matrix4x4 sclSphere = TH3DMath.GetScale4x4(1.5f); Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); // c_attachPos_Sphere : (5, 4, 0) Matrix4x4 localSphere = traSphere * sclSphere;
\begin{align*}traSphere * sclSphere&=\begin{pmatrix}1 &0 &0 &5 \\0 &1 &0 &4 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}1.5 &0.0 &0.0 &0.0 \\ 0.0 &1.5 &0.0 &0.0 \\ 0.0 &0.0 &1.5 &0.0 \\ 0.0 &0.0 &0.0 &1.0\end{pmatrix} \\\\&= \begin{pmatrix}1.5 &0 &0 &5 \\ 0 &1.5 &0 &4 \\ 0 &0 &1.5 &0 \\ 0 &0 &0 &1\end{pmatrix} =\begin{pmatrix}1.5\cdot 1 &1.5\cdot 0 &1.5\cdot 0 &5 \\ 1.5\cdot 0 &1.5\cdot 1 &1.5\cdot 0 &4 \\ 1.5\cdot 0 &1.5\cdot 0 &1.5\cdot 1 &0 \\ 0 &0 &0 &1\end{pmatrix} = localSphere\end{align*}
C) 補足
これまでの内容では、ローカル座標系は親座標系において、オブジェクトのローカル行列を可視化したものになっている ということについて述べてきた。ここでは、そのことに関連して1つ補足する。それは、ワールド座標系における各オブジェクトのローカル座標系に関してである。
これまでの内容では、ローカル座標系は基本的に その親座標系の中で観察され、ローカル座標系の各軸の先端や原点の座標、各軸の単位ベクトル表示などは すべて親座標系での数値で表されていた。ここでは、それらのローカル座標系の各データをワールド座標系での数値で表し、オブジェクトのローカル座標系をワールド座標系の中で観察する。このように見方を変えることによって、観察対象であるローカル座標系が表す内容もまた 変化するのである。
結論を述べれば、オブジェクトのローカル座標系は、ワールド座標系においては、オブジェクトに実行される行列であるワールド行列を可視化したものになっているのである。
次のプログラムは上で使用した Beta2である。
以下では、Beta2の実行結果から Arm座標系、Sphere座標系をワールド座標系において見ていく。
[Beta2]
Matrix4x4 sclSphere = TH3DMath.GetScale4x4(1.5f); Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); // c_attachPos_Sphere : (5, 4, 0) Matrix4x4 localSphere = traSphere * sclSphere; Matrix4x4 rotArm = TH3DMath.GetRotation4x4(200, Vector3.up); Matrix4x4 traArm = TH3DMath.GetTranslation4x4(c_attachPos_Arm); // c_attachPos_Arm : (2, 0, 0) Matrix4x4 localArm = traArm * rotArm; Matrix4x4 rotDisk = TH3DMath.GetRotation4x4(-15, Vector3.right); Matrix4x4 traDisk = TH3DMath.GetTranslation4x4(0, 10, 0); Matrix4x4 localDisk = traDisk * rotDisk; Matrix4x4 worldSphere = localDisk * localArm * localSphere; Matrix4x4 worldArm = localDisk * localArm; Matrix4x4 worldDisk = localDisk; Sphere.SetMatrix(worldSphere); Arm.SetMatrix(worldArm); Disk.SetMatrix(worldDisk);
図25、図26は、観察の対象を Arm座標系に定めたものであり、図中の数値はすべてワールド座標系での値である。
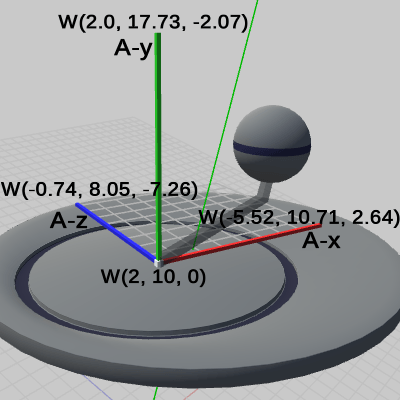
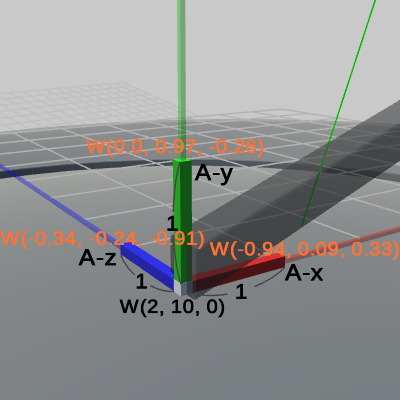
図25は、Arm座標系の原点座標、及び 各軸の先端の座標が表示されている。
図26は、Arm座標系の原点座標の他に、Arm座標系の各軸の単位ベクトル表示の値が表示されている。また、図に示されているように Arm座標系の単位ベクトル部分の長さは ワールド座標系においても $1$である。
次に、Armのワールド行列(worldArm)を以下に示す。Armのワールド行列は、プログラムにおける14行目で計算され、その内容は Armのローカル行列(localArm)と Diskのローカル行列(localDisk)の積である。
\begin{align*}localDisk * localArm &=\begin{pmatrix}1.00 &0.00 &0.00 &0.00 \\ 0.00 &0.97 &0.26 &10.00 \\ 0.00 &-0.26 &0.97 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix}\begin{pmatrix}-0.94 &0.00 &-0.34 &2.00 \\ 0.00 &1.00 &0.00 &0.00 \\ 0.34 &0.00 &-0.94 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \\\\&= \begin{pmatrix}-0.94 &0.00 &-0.34 &2.00 \\ 0.09 &0.97 &-0.24 &10.00 \\ 0.33 &-0.26 &-0.91 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} =\begin{pmatrix}1\cdot (-0.94) &1\cdot 0.00 &1\cdot (-0.34) &2.00 \\ 1\cdot 0.09 &1\cdot 0.97 &1\cdot (-0.24) &10.00 \\ 1\cdot 0.33 &1\cdot (-0.26) &1\cdot (-0.91) &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} = worldArm\end{align*}
この worldArmと、図26における各数値を比較すれば、上で見てきた対応関係が ここでも確認できるであろう。
次に、観察の対象を Sphere座標系に定めた場合について見ていく(図中の数値はすべて ワールド座標系での値である)。
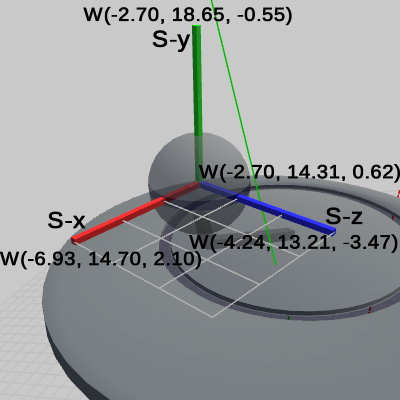
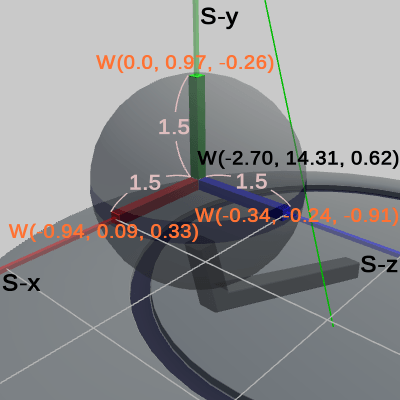
図27は、Sphere座標系の原点座標、及び 各軸の先端の座標が表示されている。
図28は、Sphere座標系の原点座標の他に、Sphere座標系の各軸の単位ベクトル表示の値が表示されている。また、Sphere座標系の単位ベクトル部分の長さは ワールド座標系においては $1.5$である。
次に、Sphereのワールド行列(worldSphere)を以下に示す。Sphereのワールド行列は、プログラムにおける13行目で計算され、その内容は Sphereのローカル行列(localSphere)、Armのローカル行列(localArm)、及び Diskのローカル行列(localDisk)の積である。
\begin{align*}localDisk * localArm * localSphere&=\begin{pmatrix}1.00 &0.00 &0.00 &0.00 \\ 0.00 &0.97 &0.26 &10.00 \\ 0.00 &-0.26 &0.97 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix}\begin{pmatrix}-0.94 &0.00 &-0.34 &2.00 \\ 0.00 &1.00 &0.00 &0.00 \\ 0.34 &0.00 &-0.94 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}1.5 &0 &0 &5 \\ 0 &1.5 &0 &4 \\ 0 &0 &1.5 &0 \\ 0 &0 &0 &1\end{pmatrix} \\\\&= \begin{pmatrix}-1.41 &0.00 &-0.51 &-2.70 \\ 0.13 &1.45 &-0.36 &14.31 \\ 0.50 &-0.39 &-1.36 &0.62 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} =\begin{pmatrix}1.5\cdot (-0.94) &1.5\cdot 0.00 &1.5\cdot (-0.34) &-2.70 \\ 1.5\cdot 0.09 &1.5\cdot 0.97 &1.5\cdot (-0.24) &14.31 \\ 1.5\cdot 0.33 &1.5\cdot (-0.26) &1.5\cdot (-0.91) &0.62 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} = worldSphere\end{align*}
ここで算出された worldSphereと、図28における各数値との間にも、やはり同様の対応関係が見られる。
オブジェクトのローカル座標系は、ワールド座標系において見た場合には、そのオブジェクトのワールド行列を可視化したものになっているのである。言い換えれば、ワールド座標系における オブジェクトの現在の状態(どれだけスケール、回転、平行移動が行われたか)を表しているのである。
© 2020-2025 Redpoll's 60 (All rights reserved)