Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-21
第4章 3D空間におけるオブジェクトの運動
$§$4-21 指定方向へのオブジェクトの移動 2
本節は読者用の課題である。
3-14節、3-15節におけるオイラー角の解説では球面上を緯度、経度で表したが、まずはそれについての復習から始める。
下図における球面は半径が $1$ であり、その中心が原点に置かれている。図中の黄色い点はこの球面と z軸マイナス側との交点であり、球面の半径が $1$ なのでその座標は $(0,\ 0, -1)$ である。
地球と同じく球面上の横方向の線を緯線、縦方向の線を経線とし、この黄色い点を起点 $0^\circ$ として球面上に緯度、経度を図1のように定める (下図においては経度が緑の数字、緯度が黒の数字である)。
すなわち 起点から経線上(縦方向の線)を上に進むにつれて緯度が増加し、下に進むにつれて緯度が減少する。同様に起点から緯線上(横方向の線)を左に進むにつれて経度が増加し、右に進むにつれて経度が減少する。ただし ここでは緯度、経度を東経、西経、北緯、南緯ではなく単にプラス、マイナスで表している。
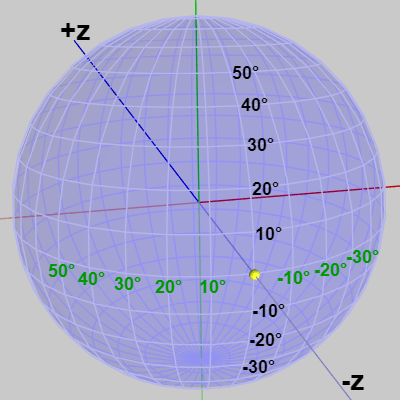
図1 球面上の緯度と経度 (黄色い点が起点 0° ; 黒い数字が緯度、緑の数字が経度を表している) 
図2 北極点(緯度90°)と南極点(緯度-90°)
そして地球と同様に緯度 $90^\circ$ の位置を「北極点」、緯度 $-90^\circ$ の位置を「南極点」と呼ぶことにする (図2 ; 図中の北極点の位置は $(0,\ 1,\ 0)$ であり、南極点の位置は $(0,-1,\ 0)$ である)。
では以上をふまえて本題に入る。
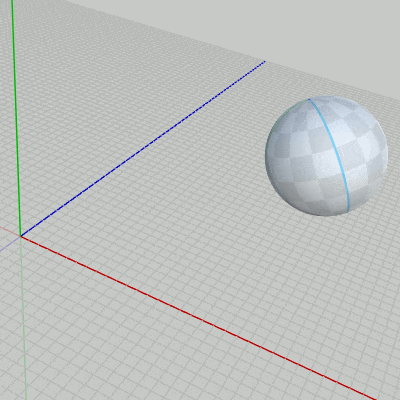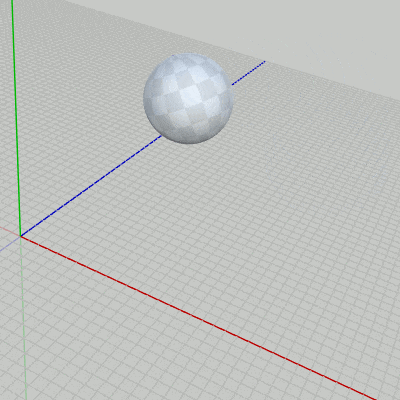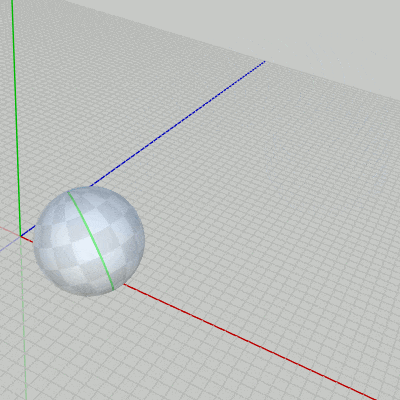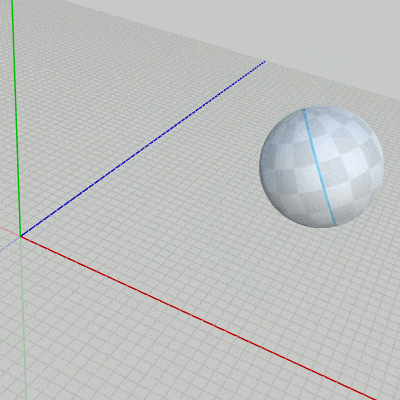
図3 
図4 Sphere 初期状態 (図中の黄色い点は起点 ; 青いラインは経度 0°の経線、緑のラインは経度 90°の経線)
下図5はオブジェクト Triangle の初期状態である。Triangleは厚みのある直角三角形で、初期状態では z軸マイナス方向を向いている。図6はTriangleを真横から見たときのものであるが、真横から見るとTriangleの垂直方向の辺は y軸プラス側に接しており、一番短い辺は z軸マイナス側に接している。
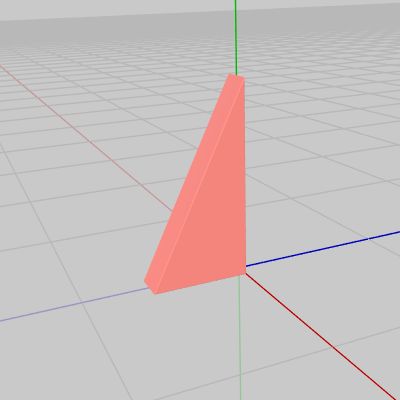
図5 Triangle 初期状態 (z軸マイナス方向を向いている) 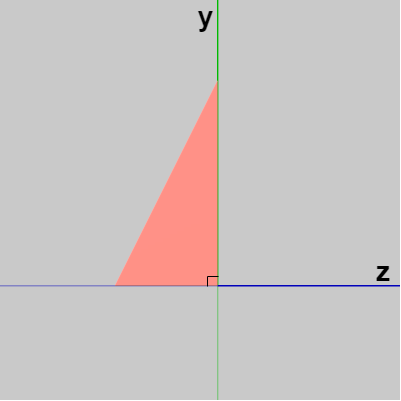
図6 Triangleを真横から見たときのもの (短い辺が z軸マイナス側に接している)
ここでの課題は図3のように回り続けるSphereの球面上において、上記のTriangleを指定の経路に沿って移動させることである。
Triangleの移動は次の順序で行うものとする。
(1) 北極点から青いラインを通って南極点まで移動する (1~600フレーム)。
(2) 南極点において進路を緑のラインに向ける (進路を $90^\circ$ 変える ; 601~900フレーム)。
(3) 南極点から緑のラインを通って北極点まで移動する (901~1500フレーム)。
Triangleは図5に示されるように初期状態では z軸マイナス方向を向いており、下側の短い辺が z軸マイナス側に接している。移動中においてはこの短い辺が常に移動経路の接線に接した状態(図10)で移動するものとする。それは具体的には図11のような移動になる。
また南極点において進路を変更する際には位置は移動させずに向きだけを緑のラインの方向に変えるものとする (図12)。青いラインは経度 $0^\circ$ の経線であり、緑のラインは経度 $90^\circ$ の経線であるから、この進路変更は南極点における $90^\circ$ の進路変更である。
さらに追加条件としてこの移動は指定された時間の間に等速度で行うものとする。上の移動順序にも記載されているが、具体的には
(1) 最初の600フレーム(1~600フレーム)において青いラインの移動を行う。
(2) 続く300フレーム(601~900フレーム)において南極点での進路変更を行う。
(3) 最後の600フレーム(901~1500フレーム)において緑のラインの移動を行う。
等速度で移動するためには1フレームあたりの移動量を同じにすればよい。青いライン、緑のラインはともに半円、すなわち円周の $180^\circ$ 分に相当する。各ラインの移動には600フレームが割り当てられているので、1フレームあたり $180^\circ \div 600 = 0.3^\circ$ ずつ移動すればよいということである (南極点における進路変更も毎フレーム $0.3^\circ$ ずつ行えばちょうど300フレームで $90^\circ$ の回転になる)。
今回のプログラムに用意されているインスタンス変数、定数を以下に示す。
なお今回のプログラムでは、あらかじめ用意されている以下の変数以外に必要なインスタンス変数などについては読者の側で用意するものとする。
また運動中のSphereに実行されている変換行列を取得するために GetSphereMatrix() というメソッドが用意されている。したがって毎フレーム Sphereのローカル行列を取得するためにはプログラム中で次のように記述すればよい (Sphereは単独のオブジェクトなのでローカル行列はワールド行列でもある)。
プログラムはCode1に作成するものとし、オブジェクトの移動は S キーを押すことにより開始されるものとする。Code1は始めの段階では以下のコードが記述されている。
[Code1]
さらに1点注意。
今回のプログラムでのカメラはTriangleの移動を追跡する形になっているが、カメラの位置はTriangleの位置には依存していない。その位置はフレームカウント(i_frameCountの値)によって決まる (つまりTriangleがどのような移動をしてもカメラは決まった時間に決まった位置にいる)。そのため、プログラム中の i_frameCount のインクリメント処理(上記16行目)を消してしまうとカメラの移動が行われなくなるので注意。
カメラは追跡型ではあるが全体の運動を離れた位置から見るように、V キーによって固定視点に切り替えることができる。追跡視点に戻すには再度 V キーを押せばよい。
なお今回使用しているSphereの北極点と南極点は次のように色分けされている (左図が北極点、右図が南極点)。

図13 北極点 (青) 
図14 南極点 (白)
すなわち 青い四角が北極点であり、白い四角が南極点である。初期状態では北極点は y軸プラス側にあり、その座標はSphereの半径を $c\_radSphere$ とすれば $(0,\ c\_radSphere,\ 0)$ である。
下図15はオブジェクト Wheel の初期状態であり、初期状態においてはその中心を x軸が貫いている。図16は初期状態のWheelを上から見下ろしたときのものであるが、図に示されるようにWheelには向きを表す矢印が付いており、この矢印はWheelの回転方向を表すものである (初期状態では z軸マイナス側を向いている)。
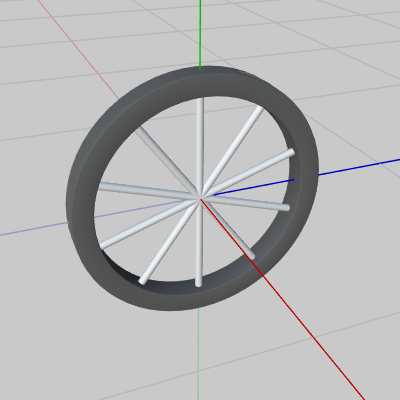
図15 Wheel 初期状態 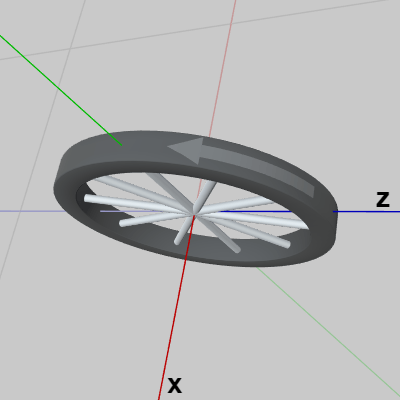
図16 Wheelに付いている矢印は回転方向を表す (初期状態では z軸マイナス側を向いている)
今回の課題は上記のWheelをCode1と全く同じ経路に沿って等速度で移動させることである。すなわち、
(1) 北極点から青いラインを通って南極点まで移動する (1~600フレーム)。
(2) 南極点において進路を緑のラインに向ける (進路を $90^\circ$ 変える ; 601~900フレーム)。
(3) 南極点から緑のラインを通って北極点まで移動する (901~1500フレーム)。
(移動時間などもCode1と同じであるので、等速度で移動させるためには各ライン上を毎フレーム $0.3^\circ$ 分ずつ移動させればよい)
ただし今回のWheelの場合はただ移動させるだけでなく、回転しながら移動させるものとする (下図17 ; オブジェクトの回転移動については 3-13節 Code6 を参照)。
南極点における進路変更はCode1と同じく向きだけを変えるようにすればよい (図18)。

図17 球面上におけるWheelの移動 
図18 南極点における進路変更
このプログラムに用意されているインスタンス変数、定数、メソッドはCode1でも使用した i_MOVE、i_frameCount、c_radSphere、GetSphereMatrix() の他に以下の定数が追加されている。
それ以外に必要なインスタンス変数などについては今回も読者の側で用意するものとする。
プログラムの作成はCode2に行うものとする。Code2は始めの段階では以下のコードが記述されているが、その内容は先程のCode1と同じである。
また今回もオブジェクトの移動は S キーを押すことで開始されるものとする。
[Code2]
(このプログラムにおいてもカメラ移動はオブジェクトの位置ではなくはフレームカウント(i_frameCountの値)に依存しているので注意。また今回も V キーによって追跡視点と固定視点の切り替えを行うことができる。解答例については Sec421_Ans.txt を参照)
3-14節、3-15節におけるオイラー角の解説では球面上を緯度、経度で表したが、まずはそれについての復習から始める。
下図における球面は半径が $1$ であり、その中心が原点に置かれている。図中の黄色い点はこの球面と z軸マイナス側との交点であり、球面の半径が $1$ なのでその座標は $(0,\ 0, -1)$ である。
地球と同じく球面上の横方向の線を緯線、縦方向の線を経線とし、この黄色い点を起点 $0^\circ$ として球面上に緯度、経度を図1のように定める (下図においては経度が緑の数字、緯度が黒の数字である)。
すなわち 起点から経線上(縦方向の線)を上に進むにつれて緯度が増加し、下に進むにつれて緯度が減少する。同様に起点から緯線上(横方向の線)を左に進むにつれて経度が増加し、右に進むにつれて経度が減少する。ただし ここでは緯度、経度を東経、西経、北緯、南緯ではなく単にプラス、マイナスで表している。


そして地球と同様に緯度 $90^\circ$ の位置を「北極点」、緯度 $-90^\circ$ の位置を「南極点」と呼ぶことにする (図2 ; 図中の北極点の位置は $(0,\ 1,\ 0)$ であり、南極点の位置は $(0,-1,\ 0)$ である)。
では以上をふまえて本題に入る。
# Code1
3D空間内のある軌道上を球体が自転しながら公転をしている (図3)。図4はこの球体オブジェクト Sphere の初期状態である (初期状態においてはその中心が原点に置かれている)。図に示されるようにSphereには青いラインと緑のラインが引かれており、この2つのラインはともに北極点と南極点を結ぶように引かれている。具体的には青いラインは北極点と南極点を結ぶ経度 $0^\circ$ の経線であり、緑のラインは北極点と南極点を結ぶ経度 $90^\circ$ の経線である (図4 ; 青いライン、緑のラインは北極点と南極点を結ぶ経線であり、Sphereの半径と同じ半径を持つ半円である)。

下図5はオブジェクト Triangle の初期状態である。Triangleは厚みのある直角三角形で、初期状態では z軸マイナス方向を向いている。図6はTriangleを真横から見たときのものであるが、真横から見るとTriangleの垂直方向の辺は y軸プラス側に接しており、一番短い辺は z軸マイナス側に接している。


ここでの課題は図3のように回り続けるSphereの球面上において、上記のTriangleを指定の経路に沿って移動させることである。
Triangleの移動は次の順序で行うものとする。
(1) 北極点から青いラインを通って南極点まで移動する (1~600フレーム)。
(2) 南極点において進路を緑のラインに向ける (進路を $90^\circ$ 変える ; 601~900フレーム)。
(3) 南極点から緑のラインを通って北極点まで移動する (901~1500フレーム)。
-
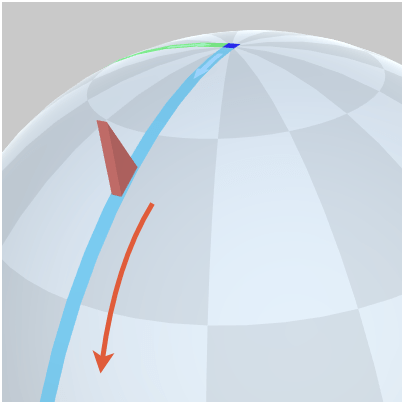 図7 青いラインを通って北極点から南極点まで移動
図7 青いラインを通って北極点から南極点まで移動 -
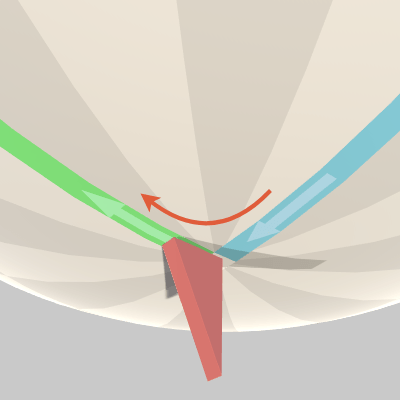 図8 南極点において進路を変える
図8 南極点において進路を変える -
 図9 緑のラインを通って南極点から北極点まで移動
図9 緑のラインを通って南極点から北極点まで移動
Triangleは図5に示されるように初期状態では z軸マイナス方向を向いており、下側の短い辺が z軸マイナス側に接している。移動中においてはこの短い辺が常に移動経路の接線に接した状態(図10)で移動するものとする。それは具体的には図11のような移動になる。
-
 図10 短い辺が常に移動経路の接線に接するように移動する
図10 短い辺が常に移動経路の接線に接するように移動する -
 図11 実際の移動の様子
図11 実際の移動の様子 -
 図12 南極点における進路変更
図12 南極点における進路変更
また南極点において進路を変更する際には位置は移動させずに向きだけを緑のラインの方向に変えるものとする (図12)。青いラインは経度 $0^\circ$ の経線であり、緑のラインは経度 $90^\circ$ の経線であるから、この進路変更は南極点における $90^\circ$ の進路変更である。
さらに追加条件としてこの移動は指定された時間の間に等速度で行うものとする。上の移動順序にも記載されているが、具体的には
(1) 最初の600フレーム(1~600フレーム)において青いラインの移動を行う。
(2) 続く300フレーム(601~900フレーム)において南極点での進路変更を行う。
(3) 最後の600フレーム(901~1500フレーム)において緑のラインの移動を行う。
等速度で移動するためには1フレームあたりの移動量を同じにすればよい。青いライン、緑のラインはともに半円、すなわち円周の $180^\circ$ 分に相当する。各ラインの移動には600フレームが割り当てられているので、1フレームあたり $180^\circ \div 600 = 0.3^\circ$ ずつ移動すればよいということである (南極点における進路変更も毎フレーム $0.3^\circ$ ずつ行えばちょうど300フレームで $90^\circ$ の回転になる)。
今回のプログラムに用意されているインスタンス変数、定数を以下に示す。
なお今回のプログラムでは、あらかじめ用意されている以下の変数以外に必要なインスタンス変数などについては読者の側で用意するものとする。
i_frameCount
: フレームカウント用のint型インスタンス変数。i_MOVE
: 移動/停止のスイッチの役割を務めるbool型インスタンス変数。c_radSphere
: Sphereの半径を表すfloat型インスタンス変数。また運動中のSphereに実行されている変換行列を取得するために GetSphereMatrix() というメソッドが用意されている。したがって毎フレーム Sphereのローカル行列を取得するためにはプログラム中で次のように記述すればよい (Sphereは単独のオブジェクトなのでローカル行列はワールド行列でもある)。
// Sphereのローカル行列を取得 Matrix4x4 localSphere = GetSphereMatrix();
プログラムはCode1に作成するものとし、オブジェクトの移動は S キーを押すことにより開始されるものとする。Code1は始めの段階では以下のコードが記述されている。
[Code1]
if (!i_INITIALIZED)
{
i_frameCount = 0;
i_MOVE = false;
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S))
{
i_MOVE = !i_MOVE;
}
if (i_MOVE)
{
i_frameCount++;
if (i_frameCount <= 600)
{
}
else if(i_frameCount <= 900)
{
}
else if(i_frameCount <= 1500)
{
}
}
さらに1点注意。
今回のプログラムでのカメラはTriangleの移動を追跡する形になっているが、カメラの位置はTriangleの位置には依存していない。その位置はフレームカウント(i_frameCountの値)によって決まる (つまりTriangleがどのような移動をしてもカメラは決まった時間に決まった位置にいる)。そのため、プログラム中の i_frameCount のインクリメント処理(上記16行目)を消してしまうとカメラの移動が行われなくなるので注意。
カメラは追跡型ではあるが全体の運動を離れた位置から見るように、V キーによって固定視点に切り替えることができる。追跡視点に戻すには再度 V キーを押せばよい。
なお今回使用しているSphereの北極点と南極点は次のように色分けされている (左図が北極点、右図が南極点)。


すなわち 青い四角が北極点であり、白い四角が南極点である。初期状態では北極点は y軸プラス側にあり、その座標はSphereの半径を $c\_radSphere$ とすれば $(0,\ c\_radSphere,\ 0)$ である。
# Code2
このプログラムもまた球面上の移動であるが、使用するオブジェクトが異なる。下図15はオブジェクト Wheel の初期状態であり、初期状態においてはその中心を x軸が貫いている。図16は初期状態のWheelを上から見下ろしたときのものであるが、図に示されるようにWheelには向きを表す矢印が付いており、この矢印はWheelの回転方向を表すものである (初期状態では z軸マイナス側を向いている)。


今回の課題は上記のWheelをCode1と全く同じ経路に沿って等速度で移動させることである。すなわち、
(1) 北極点から青いラインを通って南極点まで移動する (1~600フレーム)。
(2) 南極点において進路を緑のラインに向ける (進路を $90^\circ$ 変える ; 601~900フレーム)。
(3) 南極点から緑のラインを通って北極点まで移動する (901~1500フレーム)。
(移動時間などもCode1と同じであるので、等速度で移動させるためには各ライン上を毎フレーム $0.3^\circ$ 分ずつ移動させればよい)
ただし今回のWheelの場合はただ移動させるだけでなく、回転しながら移動させるものとする (下図17 ; オブジェクトの回転移動については 3-13節 Code6 を参照)。
南極点における進路変更はCode1と同じく向きだけを変えるようにすればよい (図18)。


このプログラムに用意されているインスタンス変数、定数、メソッドはCode1でも使用した i_MOVE、i_frameCount、c_radSphere、GetSphereMatrix() の他に以下の定数が追加されている。
c_radWheel
: Wheelの半径を表すfloat型インスタンス変数。それ以外に必要なインスタンス変数などについては今回も読者の側で用意するものとする。
プログラムの作成はCode2に行うものとする。Code2は始めの段階では以下のコードが記述されているが、その内容は先程のCode1と同じである。
また今回もオブジェクトの移動は S キーを押すことで開始されるものとする。
[Code2]
if (!i_INITIALIZED)
{
i_frameCount = 0;
i_MOVE = false;
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S))
{
i_MOVE = !i_MOVE;
}
if (i_MOVE)
{
i_frameCount++;
if (i_frameCount <= 600)
{
}
else if(i_frameCount <= 900)
{
}
else if(i_frameCount <= 1500)
{
}
}
(このプログラムにおいてもカメラ移動はオブジェクトの位置ではなくはフレームカウント(i_frameCountの値)に依存しているので注意。また今回も V キーによって追跡視点と固定視点の切り替えを行うことができる。解答例については Sec421_Ans.txt を参照)
© 2020-2025 Redpoll's 60 (All rights reserved)