Redpoll's 60
第4章 3D空間におけるオブジェクトの運動
§4-12 各階層における座標の計算 1
以下の図1から図3は、4-10節のCode4の実行結果である。
図1、図2、図3は、プログラムの実行結果をそれぞれ、ワールド座標系、Disk座標系、Arm座標系から見たときの様子である。
この運動中、Diskにアタッチされている Armは、Disk座標系の中では アタッチポジションである (2, 0, 0) から動いていない(図2)。また、Armにアタッチされている Sphereもこの運動の間、Arm座標系の中では アタッチポジションである (5, 4, 0) から動いていない(図3)。
しかし、図1から明らかなように、ワールド座標系の中では Diskは上下に運動しているので、Diskと一体となって運動している Armや Sphereの位置も、ワールド座標系の中では変化する。
ここで、必然的に生じる問題として、Armや Sphereの位置はワールド座標系の中では変化しているが、それらの位置はどのようにして求めるのか といったことが挙げられる。
本節では、親子関係にある複数のオブジェクトに関して、ある階層のオブジェクトの、ある位置の座標を、別階層の座標系における座標に変換する問題について扱う。今までのプログラムでは、オブジェクトを親オブジェクトにアタッチする場合には、そのオブジェクトに対してアタッチポジションへの平行移動を実行したが、そのアタッチポジションは正確には、親座標系での座標である。ここで問題とするのは、アタッチポジションのような1つ上の親座標系で表される座標の、さらに上の親座標系での座標、あるいは最上位の座標系であるワールド座標系での座標の算出である。
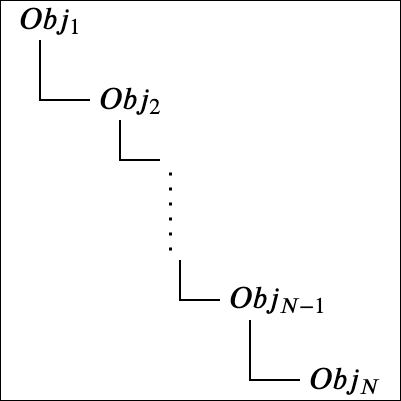
図4 N個のオブジェクト、Obj_1, Obj_2, .. Obj_N が親子関係にあるとする。図4に示されるように、Obj_1が最上位の親であり、Obj_Nが一番下の子である。
各オブジェクトのローカル座標系を、Obj_1座標系、Obj_2座標系、... Obj_N座標系とし、各オブジェクトのローカル行列を、localObj_1、localObj_2、... localObj_N とする。
Obj_Nの ある位置の座標を P_N とする。P_N は、Obj_N座標系での値である(以下の計算で使われる P_1、... P_N は同次座標化されているものとする。すなわち、(x, y, z, 1) の形)。
Obj_Nの親座標系である Obj_{N-1}座標系での、P_Nの値を P_{N-1} とすれば、P_{N-1} は次のように計算される。 P_{N-1} = localObj_{N} * P_{N} さらに1つ上の座標系である Obj_{N-2}座標系での、P_Nの値を P_{N-2} とすれば、P_{N-2} は次のように計算される。 P_{N-2} = localObj_{N-1} * localObj_{N} * P_{N} Obj_{N-3}座標系での、P_Nの値を P_{N-3} とすれば、P_{N-3} の計算も同様である。 P_{N-3} = localObj_{N-2} * localObj_{N-1} * localObj_{N} * P_{N} ワールド座標系での、P_Nの値を P_W とすれば、P_W は次のように計算される。

図5 具体的に、N = 3 の場合を以下に示す。
Obj_1、Obj_2、Obj_3が親子関係にあり、図5のような階層構造になっているとする(Obj_1が一番上の親である)。
Obj_1、Obj_2、Obj_3を一体化して運動させるプログラムを実装する場合は、以下のような記述になる。
[3つのオブジェクトを一体化して運動させる場合]
では、各階層における座標の計算について見ていこう。
Obj_3の ある位置の座標を P_3 とする。P_3はObj_3座標系での値である。
Obj_3の親座標系であるObj_2座標系での、P_3の値を P_2 とすれば、 P_{2} = localObj_{3} * P_{3} であり、Obj_1座標系での、P_3の値を P_1 とすれば、 P_{1} = localObj_{2} * localObj_{3} * P_{3} である。
ワールド座標系での、P_3の値を P_W とすれば、\begin{align*}P_{W} &= localObj_{1} * localObj_{2} * localObj_{3} * P_{3} \\\\&= worldObj_3 * P_3 \end{align*}である。
また、Obj_2の ある位置の座標を Q_2 とする。Q_2はObj_2座標系での値である。
Obj_1座標系での、Q_2の値を Q_1 とすれば、Q_{1} = localObj_{2} * Q_{2} であり、ワールド座標系での、Q_2の値を Q_W とすれば、\begin{align*}Q_{W} &= localObj_{1} * localObj_{2} * Q_{2} \\\\&= worldObj_2 * Q_2 \end{align*}である。
使用するオブジェクトは、以下の3つである。
図6から図8に示される四角錐形状のオブジェクト Tent1、Tent2、Tent3は、色が異なるのみで形、大きさはいずれも同じである。全頂点の内で 3つの頂点が赤、緑、青の小さな球になっており、それぞれの位置は初期状態で、赤 (2, 0, 0)、緑 (0, 2, 0)、青 (0, 0, 2) である。
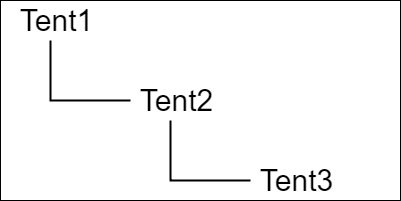
図9 オブジェクトの階層構造 これら3つのオブジェクトには親子関係があり、Tent3の親オブジェクトが Tent2、Tent2の親オブジェクトが Tent1である(図9)。
以下では、Tent1のローカル座標系を Tent1座標系、Tent1のローカル行列を localTent1 と表記する(Tent2、Tent3についても同様である)。
各オブジェクトに実行する変換は次の通り。
Tent3には親座標系である Tent2座標系において、z軸方向への 8の平行移動を実行する。
Tent2には親座標系である Tent1座標系において、y軸方向への 8の平行移動を実行する。
Tent1には親座標系である ワールド座標系において、x軸方向への 8の平行移動を実行する。
[Code1] (実行結果 図10、図11)

図10 Code1 実行結果 
図11 Code1 実行結果 (各オブジェクトのローカル座標系を表示)
図10、図11は、このプログラムの実行結果をワールド座標系から見たときの様子である。
Tent1、Tent2、Tent3の底面の中心が、(8, 0, 0)、(8, 8, 0)、(8, 8, 8) に移動している(底面の中心は、図10においては小さな白い球で表されている)。また、それらの位置は、各ローカル座標系の原点の位置でもある。図11には各オブジェクトのローカル座標系が表示されているが、Tent1座標系、Tent2座標系、Tent3座標系の原点の位置は、ワールド座標系において (8, 0, 0)、(8, 8, 0)、(8, 8, 8) にある。
なお、図中のラベル x1、y1、z1は、Tent1座標系の x軸、y軸、z軸を表している。同様に、x2、y2、z2、x3、y3、z3は、Tent2座標系、Tent3座標系の x軸、y軸、z軸を表している (ここでも W(##, ##, ##) はワールド座標系における値を表している)。
では、A) で解説した各階層における座標の計算方法を、今回のプログラムの場合に適用して、上の図と同じ結果になることを確認する。今回のプログラムの実行によって各オブジェクトの底面の中心が、ワールド座標系において どの位置に移ったか、つまり、各オブジェクトの底面の中心のワールド座標系における座標の計算である。
各オブジェクトのローカル行列は次の通り。
底面の中心は初期状態で (0, 0, 0) であるから、それぞれのオブジェクトの場合を計算すると次のようになる。
Tent1の底面の中心
3つとも図における数値と一致していることがわかる。
ただし、今回のようにローカル座標系の原点をワールド座標系などの他の親座標系での座標に変換するという場合には、上記のように、変換行列と 原点を同次座標化したベクトル の積を計算しなくても、目的の座標を取得できる。
たとえば、Tent3の底面の中心のワールド座標系における座標の場合、以下のようにローカル行列の積は、
であるが、この行列に対して原点を同次座標化したベクトル (0, 0, 0, 1) を掛けることは、ただ行列の第4列目を取得するに過ぎない。つまり、ローカル座標系の原点を他の親座標系での座標に変換する場合には、上記で行ったような変換行列と原点の積をしなくても、変換行列の第4列目(変換行列の平行移動成分 ; 4-6節参照)から目的の値を取得できるのである。
次に、Tent2の緑色の頂点、Tent3の青色の頂点のワールド座標系における座標を計算する。
それらの座標は以下の図12、図13に示されている。

図12 Tent2の緑色の頂点座標 
図13 Tent3の青色の頂点座標
緑色の頂点座標は初期状態で (0, 2, 0) であるから、プログラムの実行後のワールド座標系における Tent2の緑色の頂点座標は、
青色の頂点座標は初期状態で (0, 0, 2) であるから、プログラムの実行後のワールド座標系における Tent3の青色の頂点座標は、
次に、Tent2の緑色の頂点、Tent3の青色の頂点の Tent1座標系における座標を計算する。
それらの座標は以下の図14、図15に示されている(図における数値はすべて Tent1座標系での値であり、T1(##, ##, ##) はTent1座標系での値を表している)。
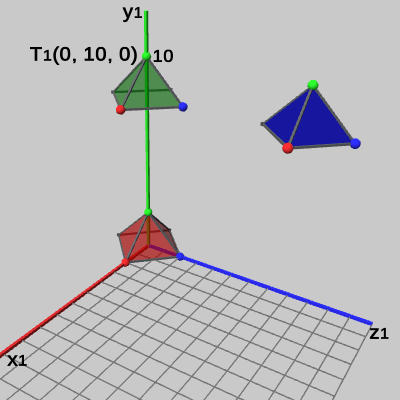
図14 Tent2の緑色の頂点座標 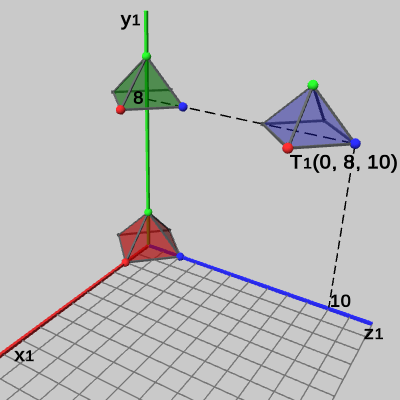
図15 Tent3の青色の頂点座標
プログラムの実行後の Tent1座標系における Tent2の緑色の頂点座標は、
プログラムの実行後の Tent1座標系における Tent3の青色の頂点座標は、
各オブジェクトに実行する変換は次の通り。
Tent3には親座標系である Tent2座標系において、y軸周りの 90°の回転、z軸方向への 8の平行移動をこの順序で実行する。
Tent2には親座標系である Tent1座標系において、z軸周りの 90°の回転、y軸周りの 90°の回転、y軸方向への 8の平行移動をこの順序で実行する。
Tent1には親座標系である ワールド座標系において、x軸周りの -90°の回転、x軸方向への 8の平行移動をこの順序で実行する。
[Code2] (実行結果 図16)

図16 Code2 実行結果 図16は、プログラムの実行結果をワールド座標系から見たときの様子である(図中における数値はすべてワールド座標系での値である)。
上の図10と同じように、表示されている座標はすべて各オブジェクトの底面の中心の座標である。各オブジェクトの底面の中心は、図においては小さな白い球で表されている。
Tent1の底面の中心の座標は (8, 0, 0)、Tent2は (8, 0, -8)、Tent3は (16, 0, -8) である。
まずは、Tent2の青色の頂点、Tent3の赤色の頂点のワールド座標系における座標を計算する。
それらの座標は以下の図17、図18に示されている。

図17 Tent2の青色の頂点座標 
図18 Tent3の赤色の頂点座標
各オブジェクトのローカル行列は次の通り。
座標計算に必要なローカル行列の積を以下に示す。
青色の頂点座標は初期状態で (0, 0, 2) であるから、プログラムの実行後のワールド座標系における Tent2の青色の頂点座標は、
赤色の頂点座標は初期状態で (2, 0, 0) であるから、プログラムの実行後のワールド座標系における Tent3の赤色の頂点座標は、
これらの結果は、確かに図17、図18に示される座標と一致している。
次に、Tent2の青色の頂点、Tent3の赤色の頂点の Tent1座標系における座標を計算する。
それらの座標は以下の図19、図20に示されている(図における数値はすべて Tent1座標系での値である)。
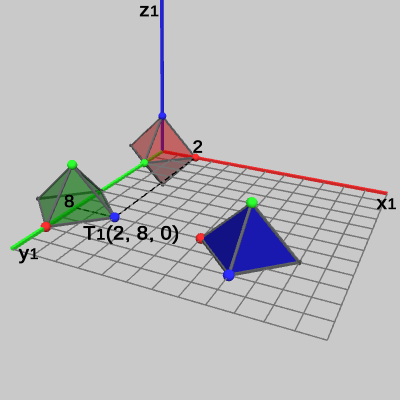
図19 Tent2の青色の頂点座標 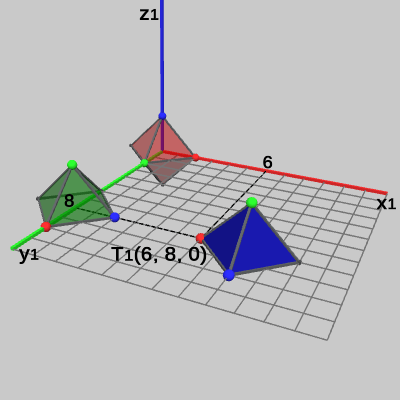
図20 Tent3の赤色の頂点座標
プログラムの実行後の Tent1座標系における Tent2の青色の頂点座標は、
プログラムの実行後の Tent1座標系における Tent3の赤色の頂点座標は、
前節では、プログラムの実行結果の図の中に、いくつかの位置については、各座標系での座標が表示されていたが、ここでは、それらの座標を実際に計算して求めてみよう。
以下のプログラムは、前節で使用した Beta2である。
[4-11節 Beta2] (実行結果 図21、図22)
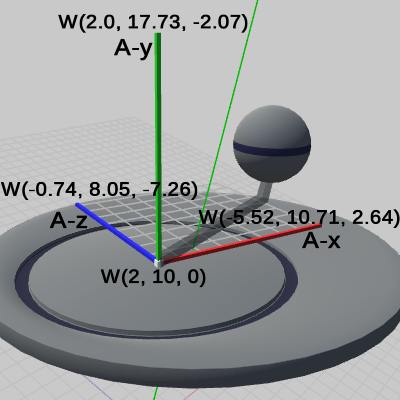
図21 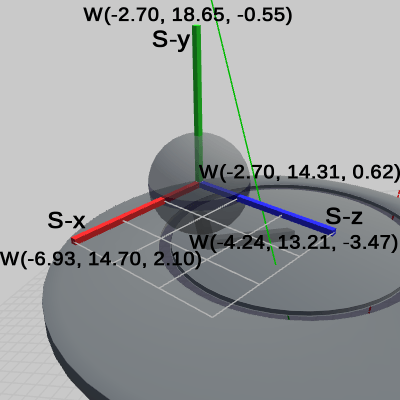
図22
図21、図22は、このプログラムの実行結果をワールド座標系から見たときの様子である(図中の数値は すべてワールド座標系での値である)。
図21には、オブジェクトの他に Arm座標系が表示されており、Arm座標系の各軸の長さは Arm座標系で測ったときに 8となる (Arm座標系に表示されているXZ平面は8\times8のグリッドである)。
図22には、オブジェクトの他に Sphere座標系が表示されており、Sphere座標系の各軸の長さは Sphere座標系で測ったときに 3となる (Sphere座標系に表示されているXZ平面は3\times3のグリッドである ; Sphere(及び Sphere座標系)は拡大されているのでワールド座標系で測ったときの各軸の長さは3ではない)。
ここで求めるのは、Arm座標系、Sphere座標系の各軸の先端座標のワールド座標系における値である (それらの値は図中にすでに表示されている)。
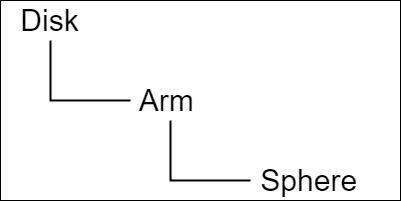
図23 オブジェクトの階層構造 まずは、Arm座標系の各軸について計算する。
Arm座標系の各軸の先端座標は Arm座標系において、A-x軸 (8, 0, 0)、A-y軸 (0, 8, 0)、A-z軸 (0, 0, 8) である。オブジェクトの階層構造は、図23の通りであるから、Arm座標系の親座標系が Disk座標系であり、Disk座標系の親座標系がワールド座標系である。
したがって、Arm座標系における 座標PA をワールド座標系の 座標PW に変換するためには、 localDisk * localArm * P_A = P_W を計算すればよい。
前節の終了部に示される計算結果から、
であるから、各軸の先端座標は以下のように求められる。
A-x軸
A-y軸
A-z軸
これらの結果は確かに、図21の各軸に示されている値と一致している。
続いて、Sphere座標系の各軸について計算する。
Sphere座標系の各軸の先端座標は Sphere座標系において、S-x軸 (3, 0, 0) 、S-y軸 (0, 3, 0) S-z軸 (0, 0, 3) である。Sphere座標系における 座標PS をワールド座標系の 座標PW に変換するためには、 localDisk * localArm * localSphere * P_S = P_W を計算すればよい。
前節の終了部に示される計算結果から、
であるから、各軸の先端座標は以下のように求められる。
S-x軸
S-y軸
S-z軸
やはり、これらの結果も 図22に示される各軸の数値に一致している。
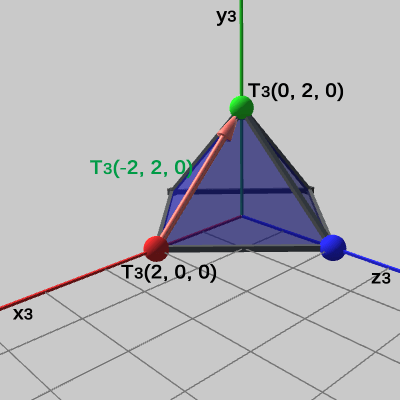
図24 Tent3座標系におけるベクトル (-2, 2, 0) 今までは、ある座標系における座標を他の座標系での座標に変換するということについて見てきた。言い換えれば、異なる座標系への点の変換である。ここでは、ある座標系におけるベクトルを他の座標系で表す問題について扱う。つまり、異なる座標系へのベクトルの変換である。
図24には Tent3の初期状態が表示されている。座標系は Tent3のローカル座標系である Tent3座標系であり、図中の数値はすべて Tent3座標系での値である。図には赤色の頂点から、緑色の頂点へのベクトルが表示されている。赤色の頂点座標は (2, 0, 0)、緑色の頂点座標は (0, 2, 0) なので、表示されているベクトルは \begin{pmatrix}0 \\2 \\0\end{pmatrix}-\begin{pmatrix}2 \\0 \\0\end{pmatrix}=\begin{pmatrix}-2 \\2 \\0\end{pmatrix}である(図中では緑色の数値で示されている)。
では、上で使用したプログラム Code2実行後の、このベクトルのワールド座標系での値を求めてみよう(すなわち、Tent3座標系からワールド座標系へのベクトルの変換である)。
以下の図は、Code2の実行結果をワールド座標系から見たときの様子である。

図25 
図26
図25は、Code2の実行結果を 3つのオブジェクトが見える位置にカメラを置いたときのものであり、図26は、Tent3にカメラを近づけて見たときのものである(図中の数値は すべてワールド座標系での値である)。図中に表示されている数値は、Tent3の赤色の頂点の座標が (14, 0, -8)、緑色の頂点の座標が (16, 2, -8) で、赤色の頂点を始点とし、緑色の頂点を終点とするベクトルが (2, 2, 0) であることを表している。
では実際に、計算によってそれらの値を求めてみよう。
上で述べたように、プログラム実行後のワールド座標系における Tent3の赤色の頂点座標は、
であり、同様の計算によって Tent3の緑色の頂点座標を計算すると、
今行った計算では、Tent3座標系における赤色の頂点座標、及び 緑色の頂点座標をワールド座標系における値に変換し、ワールド座標系における赤色の頂点座標と緑色の頂点座標から、目的のベクトルのワールド座標系における値を算出した。
具体的な計算式を示すと以下のようになる (計算結果の同次座標化されているベクトルの w値が 0であることに注意)。
この算出方法でも正しい答えは得られるが、行列の分配法則(3-7節)を使えば、より効率的に計算が行える。
分配法則によれば、3つの行列 A、B、Cについて次の等式が成り立つのであった (ただし 積AB、積AC は可能であるとする)。
A(B + C) = AB + AC したがって、ここでの例でいえば、上の計算式で使われている Tent3座標系の赤色、緑色の頂点座標を 4\times1行列として考えれば、この分配法則を適用して、次のように書き換えられる。
ただし、ベクトルの変換の場合は注意すべきことが1つある。
座標(あるいは点)の変換の場合は、その座標の同次座標化された値の w値は通常通り 1であるが、ベクトルの変換の場合には、そのベクトルを同次座標化した際の w値は 1ではなく 0になることである。すなわち、ベクトルを異なる座標系での値に変換するために、その座標系への変換行列とベクトルの積を実行する際には、同次座標化されたベクトルの w値は 0にして計算しなければならない。
その理由は、ベクトルの変換は結局のところ、2つの変換を行列の分配法則によって 1つの変換にまとめているためである。具体的には、上の数式の 1行目では、(2, 0, 0, 1)、(0, 2, 0, 1) の2つの座標に対する変換が記述されているが、これを分配法則によって 2行目(あるいは3行目)の記述では (-2, 2, 0, 0) の変換 1つにまとめている。この過程で 2つの座標の間で減算が行われているが、これが w値を 0にすることになるのである。
繰り返せば、座標(あるいは点)の変換の場合は、その座標の同次座標化された値の w値は通常通り 1であるが、ベクトルの変換の場合には、そのベクトルを同次座標化した際の w値は 1ではなく、0である。上の計算において、(-2, 2, 0, 0) ではなく (-2, 2, 0, 1) を掛けても正しい答えは得られない。
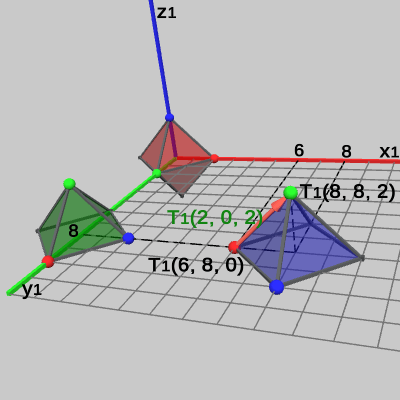
図27 続いて、この同じベクトル(図24に示される Tent3座標系のベクトル (-2, 2, 0) )を、Code2実行後の Tent1座標系における値に変換する。上で見てきたように、Tent3座標系の座標を Tent1座標系の座標に変換する行列は localTent2 * localTent3 である。また、先ほど述べた通り、ベクトルを他の座標系での値に変換する際には、目的の座標系へ変換する行列を直接ベクトルに掛ければ求める答えが得られる。
ここで、変換対象としているベクトルは Tent3座標系のベクトル (-2, 2, 0) で、Tent3座標系から Tent1座標系へ変換する行列は、localTent2 * localTent3 であるから、得られる結果は (上で述べたようにベクトルを変換する場合には同次座標化した際の w値は 0にする必要がある)、
異なる座標系へのベクトルの変換について、一般化した形で表現すると以下のようになる。
3D空間内の座標系L_1におけるベクトル \boldsymbol{\mathsf{v_1}} の値を L_1と異なる他の座標系L_2での値に変換する際、座標系L_1から座標系L_2への変換行列を M、Mの左上の3\times 3行列を M_{3\times 3}、\boldsymbol{\mathsf{v_1}} の変換後のL_2での値を \boldsymbol{\mathsf{v_2}} とすれば、 M_{3\times 3} * \boldsymbol{\mathsf{v_1}} = \boldsymbol{\mathsf{v_2}} である (\boldsymbol{\mathsf{v_1}}、\boldsymbol{\mathsf{v_2}} は同次座標化されていない 3次元ベクトルである)。
ただし、後の章で解説するが、法線ベクトルの変換については事情が異なる。
図1、図2、図3は、プログラムの実行結果をそれぞれ、ワールド座標系、Disk座標系、Arm座標系から見たときの様子である。
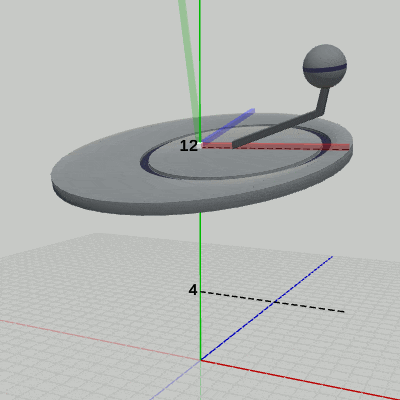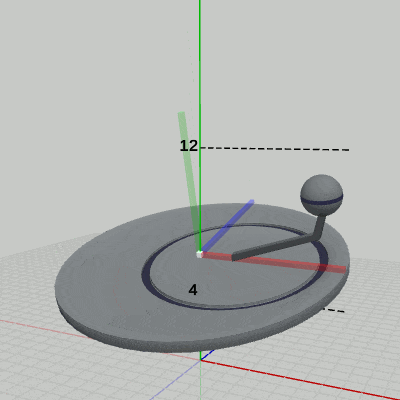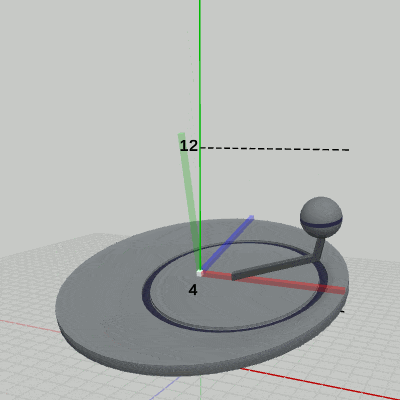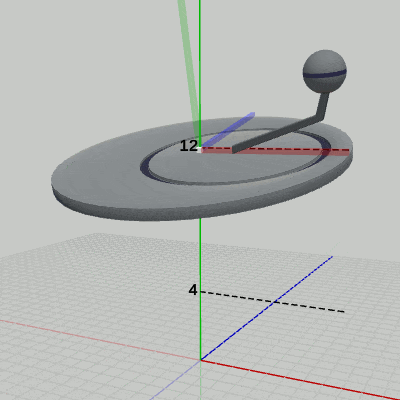 図1 4-10節 Code4 実行結果(ワールド座標系から見たときの様子)
図1 4-10節 Code4 実行結果(ワールド座標系から見たときの様子)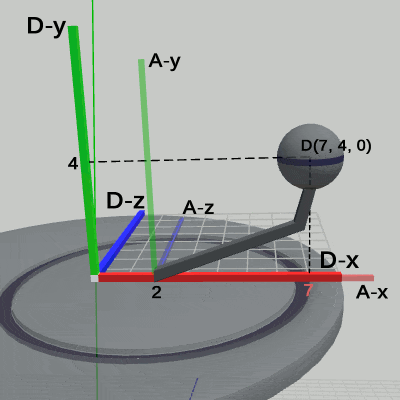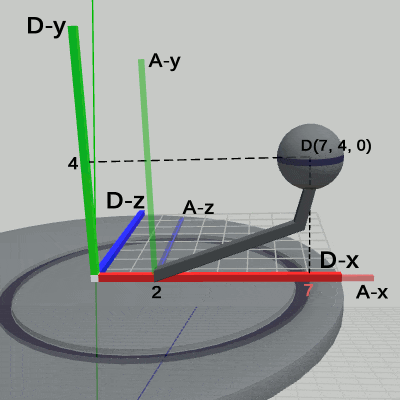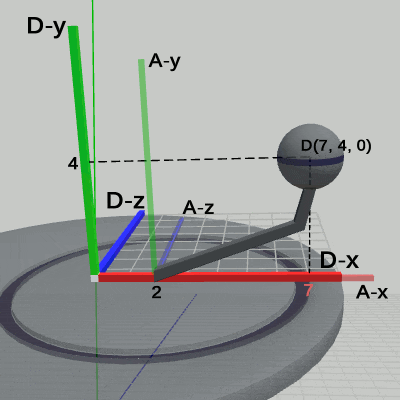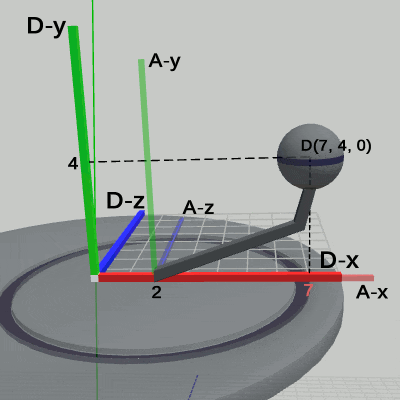 図2 4-10節 Code4 実行結果(Disk座標系から見たときの様子)
図2 4-10節 Code4 実行結果(Disk座標系から見たときの様子)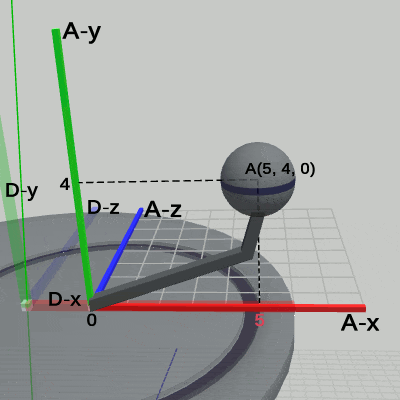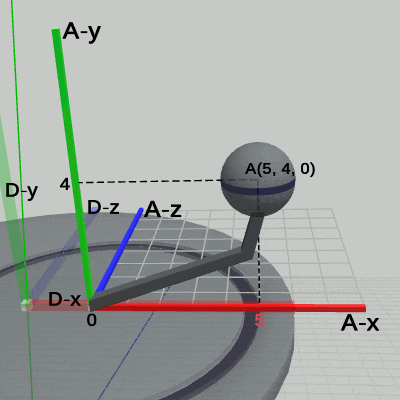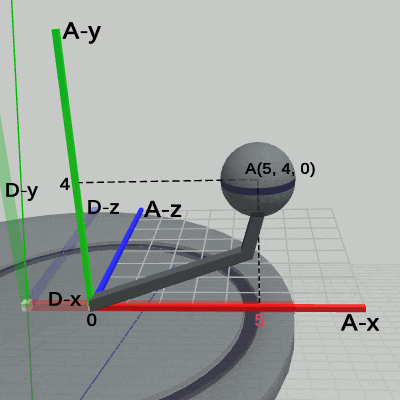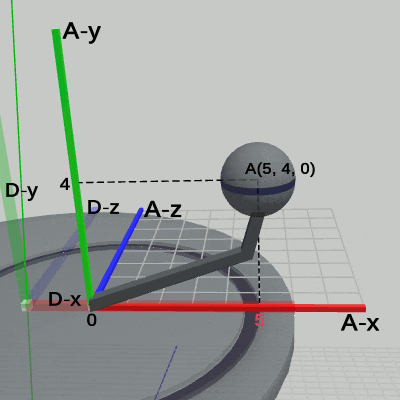 図3 4-10節 Code4 実行結果(Arm座標系から見たときの様子)
図3 4-10節 Code4 実行結果(Arm座標系から見たときの様子)
この運動中、Diskにアタッチされている Armは、Disk座標系の中では アタッチポジションである (2, 0, 0) から動いていない(図2)。また、Armにアタッチされている Sphereもこの運動の間、Arm座標系の中では アタッチポジションである (5, 4, 0) から動いていない(図3)。
しかし、図1から明らかなように、ワールド座標系の中では Diskは上下に運動しているので、Diskと一体となって運動している Armや Sphereの位置も、ワールド座標系の中では変化する。
ここで、必然的に生じる問題として、Armや Sphereの位置はワールド座標系の中では変化しているが、それらの位置はどのようにして求めるのか といったことが挙げられる。
本節では、親子関係にある複数のオブジェクトに関して、ある階層のオブジェクトの、ある位置の座標を、別階層の座標系における座標に変換する問題について扱う。今までのプログラムでは、オブジェクトを親オブジェクトにアタッチする場合には、そのオブジェクトに対してアタッチポジションへの平行移動を実行したが、そのアタッチポジションは正確には、親座標系での座標である。ここで問題とするのは、アタッチポジションのような1つ上の親座標系で表される座標の、さらに上の親座標系での座標、あるいは最上位の座標系であるワールド座標系での座標の算出である。
A) 各階層における座標の計算

各オブジェクトのローカル座標系を、Obj_1座標系、Obj_2座標系、... Obj_N座標系とし、各オブジェクトのローカル行列を、localObj_1、localObj_2、... localObj_N とする。
Obj_Nの ある位置の座標を P_N とする。P_N は、Obj_N座標系での値である(以下の計算で使われる P_1、... P_N は同次座標化されているものとする。すなわち、(x, y, z, 1) の形)。
Obj_Nの親座標系である Obj_{N-1}座標系での、P_Nの値を P_{N-1} とすれば、P_{N-1} は次のように計算される。 P_{N-1} = localObj_{N} * P_{N} さらに1つ上の座標系である Obj_{N-2}座標系での、P_Nの値を P_{N-2} とすれば、P_{N-2} は次のように計算される。 P_{N-2} = localObj_{N-1} * localObj_{N} * P_{N} Obj_{N-3}座標系での、P_Nの値を P_{N-3} とすれば、P_{N-3} の計算も同様である。 P_{N-3} = localObj_{N-2} * localObj_{N-1} * localObj_{N} * P_{N} ワールド座標系での、P_Nの値を P_W とすれば、P_W は次のように計算される。
P_{W} = localObj_ {1} * localObj_{2} * \cdots * localObj_{N-1} * localObj_{N} * P_{N}
Obj_Nのワールド行列を worldObj_N とすれば、 worldObj_N = localObj_ {1} * localObj_{2} * \cdots * localObj_{N-1} * localObj_{N}
であるから、結局 P_W は次のように計算される。 P_W = worldObj_N * P_N 
Obj_1、Obj_2、Obj_3が親子関係にあり、図5のような階層構造になっているとする(Obj_1が一番上の親である)。
Obj_1、Obj_2、Obj_3を一体化して運動させるプログラムを実装する場合は、以下のような記述になる。
[3つのオブジェクトを一体化して運動させる場合]
- Matrix4x4 localObj3 = ...; // Obj3に定義される変換
- Matrix4x4 localObj2 = ...; // Obj2に定義される変換
- Matrix4x4 localObj1 = ...; // Obj1に定義される変換
- Matrix4x4 worldObj3 = localObj1 * localObj2 * localObj3;
- Matrix4x4 worldObj2 = localObj1 * localObj2;
- Matrix4x4 worldObj1 = localObj1;
- Obj3.SetMatrix(worldObj3);
- Obj2.SetMatrix(worldObj2);
- Obj1.SetMatrix(worldObj1);
では、各階層における座標の計算について見ていこう。
Obj_3の ある位置の座標を P_3 とする。P_3はObj_3座標系での値である。
Obj_3の親座標系であるObj_2座標系での、P_3の値を P_2 とすれば、 P_{2} = localObj_{3} * P_{3} であり、Obj_1座標系での、P_3の値を P_1 とすれば、 P_{1} = localObj_{2} * localObj_{3} * P_{3} である。
ワールド座標系での、P_3の値を P_W とすれば、\begin{align*}P_{W} &= localObj_{1} * localObj_{2} * localObj_{3} * P_{3} \\\\&= worldObj_3 * P_3 \end{align*}である。
また、Obj_2の ある位置の座標を Q_2 とする。Q_2はObj_2座標系での値である。
Obj_1座標系での、Q_2の値を Q_1 とすれば、Q_{1} = localObj_{2} * Q_{2} であり、ワールド座標系での、Q_2の値を Q_W とすれば、\begin{align*}Q_{W} &= localObj_{1} * localObj_{2} * Q_{2} \\\\&= worldObj_2 * Q_2 \end{align*}である。
B) 具体例
では、実際にオブジェクトを用いて、各階層における座標の計算をしていこう。使用するオブジェクトは、以下の3つである。
 図6 Tent1 初期状態
図6 Tent1 初期状態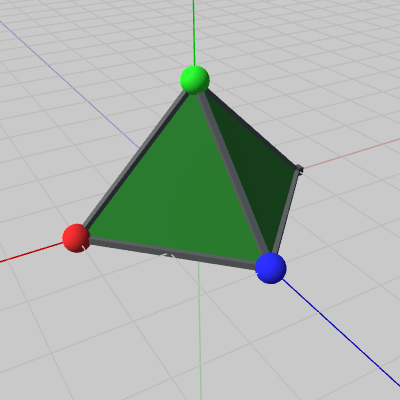 図7 Tent2 初期状態
図7 Tent2 初期状態 図8 Tent3 初期状態
図8 Tent3 初期状態
図6から図8に示される四角錐形状のオブジェクト Tent1、Tent2、Tent3は、色が異なるのみで形、大きさはいずれも同じである。全頂点の内で 3つの頂点が赤、緑、青の小さな球になっており、それぞれの位置は初期状態で、赤 (2, 0, 0)、緑 (0, 2, 0)、青 (0, 0, 2) である。

以下では、Tent1のローカル座標系を Tent1座標系、Tent1のローカル行列を localTent1 と表記する(Tent2、Tent3についても同様である)。
# Code1
まずは、3つのオブジェクトに平行移動だけを実行する単純なケースである。各オブジェクトに実行する変換は次の通り。
Tent3には親座標系である Tent2座標系において、z軸方向への 8の平行移動を実行する。
Tent2には親座標系である Tent1座標系において、y軸方向への 8の平行移動を実行する。
Tent1には親座標系である ワールド座標系において、x軸方向への 8の平行移動を実行する。
[Code1] (実行結果 図10、図11)
- Matrix4x4 localTent3 = TH3DMath.GetTranslation4x4(0, 0, 8);
- Matrix4x4 localTent2 = TH3DMath.GetTranslation4x4(0, 8, 0);
- Matrix4x4 localTent1 = TH3DMath.GetTranslation4x4(8, 0, 0);
- Matrix4x4 worldTent3 = localTent1 * localTent2 * localTent3;
- Matrix4x4 worldTent2 = localTent1 * localTent2;
- Matrix4x4 worldTent1 = localTent1;
- Tent3.SetMatrix(worldTent3);
- Tent2.SetMatrix(worldTent2);
- Tent1.SetMatrix(worldTent1);


図10、図11は、このプログラムの実行結果をワールド座標系から見たときの様子である。
Tent1、Tent2、Tent3の底面の中心が、(8, 0, 0)、(8, 8, 0)、(8, 8, 8) に移動している(底面の中心は、図10においては小さな白い球で表されている)。また、それらの位置は、各ローカル座標系の原点の位置でもある。図11には各オブジェクトのローカル座標系が表示されているが、Tent1座標系、Tent2座標系、Tent3座標系の原点の位置は、ワールド座標系において (8, 0, 0)、(8, 8, 0)、(8, 8, 8) にある。
なお、図中のラベル x1、y1、z1は、Tent1座標系の x軸、y軸、z軸を表している。同様に、x2、y2、z2、x3、y3、z3は、Tent2座標系、Tent3座標系の x軸、y軸、z軸を表している (ここでも W(##, ##, ##) はワールド座標系における値を表している)。
では、A) で解説した各階層における座標の計算方法を、今回のプログラムの場合に適用して、上の図と同じ結果になることを確認する。今回のプログラムの実行によって各オブジェクトの底面の中心が、ワールド座標系において どの位置に移ったか、つまり、各オブジェクトの底面の中心のワールド座標系における座標の計算である。
各オブジェクトのローカル行列は次の通り。
localTent1=\begin{pmatrix}1 &0 &0 &8 \\0 &1 &0 &0 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\qquad localTent2=\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &8 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\qquad localTent3=\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &0 \\ 0 &0 &1 &8 \\0 &0 &0 &1\end{pmatrix}
底面の中心は初期状態で (0, 0, 0) であるから、それぞれのオブジェクトの場合を計算すると次のようになる。
Tent1の底面の中心
localTent1 * \begin{pmatrix}0 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}1 &0 &0 &8 \\0 &1 &0 &0 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}8 \\0 \\ 0 \\1\end{pmatrix}
Tent2の底面の中心localTent1 * localTent2 * \begin{pmatrix}0 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}1 &0 &0 &8 \\0 &1 &0 &0 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &8 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}8 \\8 \\ 0 \\1\end{pmatrix}
Tent3の底面の中心localTent1 * localTent2 * localTent3 * \begin{pmatrix}0 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}1 &0 &0 &8 \\0 &1 &0 &0 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &8 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &0 \\ 0 &0 &1 &8 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}8 \\8 \\ 8 \\1\end{pmatrix}
3つとも図における数値と一致していることがわかる。
ただし、今回のようにローカル座標系の原点をワールド座標系などの他の親座標系での座標に変換するという場合には、上記のように、変換行列と 原点を同次座標化したベクトル の積を計算しなくても、目的の座標を取得できる。
たとえば、Tent3の底面の中心のワールド座標系における座標の場合、以下のようにローカル行列の積は、
localTent1 * localTent2 * localTent3 =\begin{pmatrix}1 &0 &0 &8 \\0 &1 &0 &0 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &8 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &0 \\ 0 &0 &1 &8 \\0 &0 &0 &1\end{pmatrix}=\begin{pmatrix}1 &0 &0 &8 \\0 &1 &0 &8 \\ 0 &0 &1 &8 \\0 &0 &0 &1\end{pmatrix}
であるが、この行列に対して原点を同次座標化したベクトル (0, 0, 0, 1) を掛けることは、ただ行列の第4列目を取得するに過ぎない。つまり、ローカル座標系の原点を他の親座標系での座標に変換する場合には、上記で行ったような変換行列と原点の積をしなくても、変換行列の第4列目(変換行列の平行移動成分 ; 4-6節参照)から目的の値を取得できるのである。
次に、Tent2の緑色の頂点、Tent3の青色の頂点のワールド座標系における座標を計算する。
それらの座標は以下の図12、図13に示されている。


緑色の頂点座標は初期状態で (0, 2, 0) であるから、プログラムの実行後のワールド座標系における Tent2の緑色の頂点座標は、
localTent1 * localTent2 * \begin{pmatrix}0 \\2 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}1 &0 &0 &8 \\0 &1 &0 &8 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 \\2 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}8 \\10 \\ 0 \\1\end{pmatrix}
となる (図12)。青色の頂点座標は初期状態で (0, 0, 2) であるから、プログラムの実行後のワールド座標系における Tent3の青色の頂点座標は、
localTent1 * localTent2 * localTent3 * \begin{pmatrix}0 \\0 \\ 2 \\1\end{pmatrix}=\begin{pmatrix}1 &0 &0 &8 \\0 &1 &0 &8 \\ 0 &0 &1 &8 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 \\0 \\ 2 \\1\end{pmatrix}=\begin{pmatrix}8 \\8 \\ 10 \\1\end{pmatrix}
となる (図13)。次に、Tent2の緑色の頂点、Tent3の青色の頂点の Tent1座標系における座標を計算する。
それらの座標は以下の図14、図15に示されている(図における数値はすべて Tent1座標系での値であり、T1(##, ##, ##) はTent1座標系での値を表している)。


プログラムの実行後の Tent1座標系における Tent2の緑色の頂点座標は、
localTent2 * \begin{pmatrix}0 \\2 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &8 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 \\2 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}0 \\10 \\ 0 \\1\end{pmatrix}
となる (図14)。プログラムの実行後の Tent1座標系における Tent3の青色の頂点座標は、
localTent2 * localTent3 * \begin{pmatrix}0 \\0 \\ 2 \\1\end{pmatrix}=\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &8 \\ 0 &0 &1 &8 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 \\0 \\ 2 \\1\end{pmatrix}=\begin{pmatrix}0 \\8 \\ 10 \\1\end{pmatrix}
となる (図15)。# Code2
続いて、実行する変換内容をもう少し複雑にした場合で見てみよう。各オブジェクトに実行する変換は次の通り。
Tent3には親座標系である Tent2座標系において、y軸周りの 90°の回転、z軸方向への 8の平行移動をこの順序で実行する。
Tent2には親座標系である Tent1座標系において、z軸周りの 90°の回転、y軸周りの 90°の回転、y軸方向への 8の平行移動をこの順序で実行する。
Tent1には親座標系である ワールド座標系において、x軸周りの -90°の回転、x軸方向への 8の平行移動をこの順序で実行する。
[Code2] (実行結果 図16)
- Matrix4x4 rotTent3 = TH3DMath.GetRotation4x4(90, Vector3.up);
- Matrix4x4 traTent3 = TH3DMath.GetTranslation4x4(0, 0, 8);
- Matrix4x4 localTent3 = traTent3 * rotTent3;
- Matrix4x4 rotTent2 = TH3DMath.GetRotation4x4(90, Vector3.up) *
- TH3DMath.GetRotation4x4(90, Vector3.forward);
- Matrix4x4 traTent2 = TH3DMath.GetTranslation4x4(0, 8, 0);
- Matrix4x4 localTent2 = traTent2 * rotTent2;
- Matrix4x4 rotTent1 = TH3DMath.GetRotation4x4(-90, Vector3.right);
- Matrix4x4 traTent1 = TH3DMath.GetTranslation4x4(8, 0, 0);
- Matrix4x4 localTent1 = traTent1 * rotTent1;
- Matrix4x4 worldTent3 = localTent1 * localTent2 * localTent3;
- Matrix4x4 worldTent2 = localTent1 * localTent2;
- Matrix4x4 worldTent1 = localTent1;
- Tent3.SetMatrix(worldTent3);
- Tent2.SetMatrix(worldTent2);
- Tent1.SetMatrix(worldTent1);

上の図10と同じように、表示されている座標はすべて各オブジェクトの底面の中心の座標である。各オブジェクトの底面の中心は、図においては小さな白い球で表されている。
Tent1の底面の中心の座標は (8, 0, 0)、Tent2は (8, 0, -8)、Tent3は (16, 0, -8) である。
まずは、Tent2の青色の頂点、Tent3の赤色の頂点のワールド座標系における座標を計算する。
それらの座標は以下の図17、図18に示されている。


各オブジェクトのローカル行列は次の通り。
localTent1 = traTent1 * rotTent1=\begin{pmatrix}1 &0 &0 &8 \\0 &1 &0 &0 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &0 &0 \\ 0 &0 &1 &0 \\ 0 &-1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}=\begin{pmatrix}1 &0 &0 &8 \\ 0 &0 &1 &0 \\ 0 &-1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}
localTent2 = traTent2 * rotTent2=\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &8 \\ 0 &0 &1 &0 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 &0 &1 &0 \\ 1 &0 &0 &0 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}=\begin{pmatrix}0 &0 &1 &0 \\ 1 &0 &0 &8 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}
localTent3 = traTent3 * rotTent3=\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &0 \\ 0 &0 &1 &8 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 &0 &1 &0 \\ 0 &1 &0 &0 \\ -1 &0 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}=\begin{pmatrix}0 &0 &1 &0 \\ 0 &1 &0 &0 \\ -1 &0 &0 &8 \\ 0 &0 &0 &1\end{pmatrix}
座標計算に必要なローカル行列の積を以下に示す。
localTent1 * localTent2=\begin{pmatrix}1 &0 &0 &8 \\ 0 &0 &1 &0 \\ 0 &-1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 &0 &1 &0 \\ 1 &0 &0 &8 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}=\begin{pmatrix}0 &0 &1 &8 \\ 0 &1 &0 &0 \\ -1 &0 &0 &-8 \\ 0 &0 &0 &1\end{pmatrix}
localTent2 * localTent3=\begin{pmatrix}0 &0 &1 &0 \\ 1 &0 &0 &8 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 &0 &1 &0 \\ 0 &1 &0 &0 \\ -1 &0 &0 &8 \\ 0 &0 &0 &1\end{pmatrix}=\begin{pmatrix}-1 &0 &0 &8 \\ 0 &0 &1 &8 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}
localTent1 * localTent2 * localTent3=\begin{pmatrix}1 &0 &0 &8 \\ 0 &0 &1 &0 \\ 0 &-1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 &0 &1 &0 \\ 1 &0 &0 &8 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 &0 &1 &0 \\ 0 &1 &0 &0 \\ -1 &0 &0 &8 \\ 0 &0 &0 &1\end{pmatrix}=\begin{pmatrix}-1 &0 &0 &16 \\ 0 &1 &0 &0 \\ 0 &0 &-1 &-8 \\ 0 &0 &0 &1\end{pmatrix}
青色の頂点座標は初期状態で (0, 0, 2) であるから、プログラムの実行後のワールド座標系における Tent2の青色の頂点座標は、
localTent1 * localTent2 * \begin{pmatrix}0 \\0 \\ 2 \\1\end{pmatrix}=\begin{pmatrix}0 &0 &1 &8 \\ 0 &1 &0 &0 \\ -1 &0 &0 &-8 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 \\0 \\ 2 \\1\end{pmatrix}=\begin{pmatrix}10 \\0 \\ -8 \\1\end{pmatrix}
となる。赤色の頂点座標は初期状態で (2, 0, 0) であるから、プログラムの実行後のワールド座標系における Tent3の赤色の頂点座標は、
localTent1 * localTent2 * localTent3 * \begin{pmatrix}2 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}-1 &0 &0 &16 \\ 0 &1 &0 &0 \\ 0 &0 &-1 &-8 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}2 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}14 \\0 \\ -8 \\1\end{pmatrix}
となる。これらの結果は、確かに図17、図18に示される座標と一致している。
次に、Tent2の青色の頂点、Tent3の赤色の頂点の Tent1座標系における座標を計算する。
それらの座標は以下の図19、図20に示されている(図における数値はすべて Tent1座標系での値である)。


プログラムの実行後の Tent1座標系における Tent2の青色の頂点座標は、
localTent2 * \begin{pmatrix}0 \\0 \\ 2 \\1\end{pmatrix}=\begin{pmatrix}0 &0 &1 &0 \\ 1 &0 &0 &8 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 \\0 \\ 2 \\1\end{pmatrix}=\begin{pmatrix}2 \\8 \\ 0 \\1\end{pmatrix}
となる。プログラムの実行後の Tent1座標系における Tent3の赤色の頂点座標は、
localTent2 * localTent3 * \begin{pmatrix}2 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}-1 &0 &0 &8 \\ 0 &0 &1 &8 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}2 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}6 \\8 \\ 0 \\1\end{pmatrix}
となる。前節では、プログラムの実行結果の図の中に、いくつかの位置については、各座標系での座標が表示されていたが、ここでは、それらの座標を実際に計算して求めてみよう。
以下のプログラムは、前節で使用した Beta2である。
[4-11節 Beta2] (実行結果 図21、図22)
- Matrix4x4 sclSphere = TH3DMath.GetScale4x4(1.5f);
- Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); // c_attachPos_Sphere : (5, 4, 0)
- Matrix4x4 localSphere = traSphere * sclSphere;
- Matrix4x4 rotArm = TH3DMath.GetRotation4x4(200, Vector3.up);
- Matrix4x4 traArm = TH3DMath.GetTranslation4x4(c_attachPos_Arm); // c_attachPos_Arm : (2, 0, 0)
- Matrix4x4 localArm = traArm * rotArm;
- Matrix4x4 rotDisk = TH3DMath.GetRotation4x4(-15, Vector3.right);
- Matrix4x4 traDisk = TH3DMath.GetTranslation4x4(0, 10, 0);
- Matrix4x4 localDisk = traDisk * rotDisk;
- Matrix4x4 worldSphere = localDisk * localArm * localSphere;
- Matrix4x4 worldArm = localDisk * localArm;
- Matrix4x4 worldDisk = localDisk;
- Sphere.SetMatrix(worldSphere);
- Arm.SetMatrix(worldArm);
- Disk.SetMatrix(worldDisk);


図21、図22は、このプログラムの実行結果をワールド座標系から見たときの様子である(図中の数値は すべてワールド座標系での値である)。
図21には、オブジェクトの他に Arm座標系が表示されており、Arm座標系の各軸の長さは Arm座標系で測ったときに 8となる (Arm座標系に表示されているXZ平面は8\times8のグリッドである)。
図22には、オブジェクトの他に Sphere座標系が表示されており、Sphere座標系の各軸の長さは Sphere座標系で測ったときに 3となる (Sphere座標系に表示されているXZ平面は3\times3のグリッドである ; Sphere(及び Sphere座標系)は拡大されているのでワールド座標系で測ったときの各軸の長さは3ではない)。
ここで求めるのは、Arm座標系、Sphere座標系の各軸の先端座標のワールド座標系における値である (それらの値は図中にすでに表示されている)。

Arm座標系の各軸の先端座標は Arm座標系において、A-x軸 (8, 0, 0)、A-y軸 (0, 8, 0)、A-z軸 (0, 0, 8) である。オブジェクトの階層構造は、図23の通りであるから、Arm座標系の親座標系が Disk座標系であり、Disk座標系の親座標系がワールド座標系である。
したがって、Arm座標系における 座標PA をワールド座標系の 座標PW に変換するためには、 localDisk * localArm * P_A = P_W を計算すればよい。
前節の終了部に示される計算結果から、
\begin{align*}localDisk * localArm =\begin{pmatrix}1.00 &0.00 &0.00 &0.00 \\ 0.00 &0.97 &0.26 &10.00 \\ 0.00 &-0.26 &0.97 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix}\begin{pmatrix}-0.94 &0.00 &-0.34 &2.00 \\ 0.00 &1.00 &0.00 &0.00 \\ 0.34 &0.00 &-0.94 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} = \begin{pmatrix}-0.94 &0.00 &-0.34 &2.00 \\ 0.09 &0.97 &-0.24 &10.00 \\ 0.33 &-0.26 &-0.91 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \end{align*}
であるから、各軸の先端座標は以下のように求められる。
A-x軸
localDisk * localArm * \begin{pmatrix}8 \\ 0 \\ 0 \\ 1\end{pmatrix} =\begin{pmatrix}-0.94 &0.00 &-0.34 &2.00 \\ 0.09 &0.97 &-0.24 &10.00 \\ 0.33 &-0.26 &-0.91 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}8 \\ 0 \\ 0 \\ 1\end{pmatrix} =\begin{pmatrix}-5.52 \\10.71 \\2.64 \\1.00\end{pmatrix}
A-y軸
localDisk * localArm * \begin{pmatrix}0 \\ 8 \\ 0 \\ 1\end{pmatrix} =\begin{pmatrix}-0.94 &0.00 &-0.34 &2.00 \\ 0.09 &0.97 &-0.24 &10.00 \\ 0.33 &-0.26 &-0.91 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}0 \\ 8 \\ 0 \\ 1\end{pmatrix} =\begin{pmatrix}2.00 \\17.73 \\-2.07 \\1.00\end{pmatrix}
A-z軸
localDisk * localArm * \begin{pmatrix}0 \\ 0 \\ 8 \\ 1\end{pmatrix} =\begin{pmatrix}-0.94 &0.00 &-0.34 &2.00 \\ 0.09 &0.97 &-0.24 &10.00 \\ 0.33 &-0.26 &-0.91 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}0 \\ 0 \\ 8 \\ 1\end{pmatrix} =\begin{pmatrix}-0.74 \\8.05 \\-7.26 \\1.00\end{pmatrix}
これらの結果は確かに、図21の各軸に示されている値と一致している。
続いて、Sphere座標系の各軸について計算する。
Sphere座標系の各軸の先端座標は Sphere座標系において、S-x軸 (3, 0, 0) 、S-y軸 (0, 3, 0) S-z軸 (0, 0, 3) である。Sphere座標系における 座標PS をワールド座標系の 座標PW に変換するためには、 localDisk * localArm * localSphere * P_S = P_W を計算すればよい。
前節の終了部に示される計算結果から、
\begin{align*}localDisk * localArm * localSphere&=\begin{pmatrix}1.00 &0.00 &0.00 &0.00 \\ 0.00 &0.97 &0.26 &10.00 \\ 0.00 &-0.26 &0.97 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix}\begin{pmatrix}-0.94 &0.00 &-0.34 &2.00 \\ 0.00 &1.00 &0.00 &0.00 \\ 0.34 &0.00 &-0.94 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}1.5 &0 &0 &5 \\ 0 &1.5 &0 &4 \\ 0 &0 &1.5 &0 \\ 0 &0 &0 &1\end{pmatrix} \\\\&= \begin{pmatrix}-1.41 &0.00 &-0.51 &-2.70 \\ 0.13 &1.45 &-0.36 &14.31 \\ 0.50 &-0.39 &-1.36 &0.62 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \end{align*}
であるから、各軸の先端座標は以下のように求められる。
S-x軸
localDisk * localArm * localSphere *\begin{pmatrix}3 \\ 0 \\ 0 \\ 1\end{pmatrix} =\begin{pmatrix}-1.41 &0.00 &-0.51 &-2.70 \\ 0.13 &1.45 &-0.36 &14.31 \\ 0.50 &-0.39 &-1.36 &0.62 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}3 \\ 0 \\ 0 \\ 1\end{pmatrix} =\begin{pmatrix}-6.93 \\14.70 \\2.10 \\1.00\end{pmatrix}
S-y軸
localDisk * localArm * localSphere *\begin{pmatrix}0 \\ 3 \\ 0 \\ 1\end{pmatrix} =\begin{pmatrix}-1.41 &0.00 &-0.51 &-2.70 \\ 0.13 &1.45 &-0.36 &14.31 \\ 0.50 &-0.39 &-1.36 &0.62 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}0 \\ 3 \\ 0 \\ 1\end{pmatrix} =\begin{pmatrix}-2.70 \\ 18.65 \\ -0.55 \\1.00\end{pmatrix}
S-z軸
localDisk * localArm * localSphere *\begin{pmatrix}0 \\ 0 \\ 3 \\ 1\end{pmatrix} =\begin{pmatrix}-1.41 &0.00 &-0.51 &-2.70 \\ 0.13 &1.45 &-0.36 &14.31 \\ 0.50 &-0.39 &-1.36 &0.62 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}0 \\ 0 \\ 3 \\ 1\end{pmatrix} =\begin{pmatrix}-4.24 \\13.21 \\-3.47 \\1.00\end{pmatrix}
やはり、これらの結果も 図22に示される各軸の数値に一致している。
C) 異なる座標系へのベクトルの変換

図24には Tent3の初期状態が表示されている。座標系は Tent3のローカル座標系である Tent3座標系であり、図中の数値はすべて Tent3座標系での値である。図には赤色の頂点から、緑色の頂点へのベクトルが表示されている。赤色の頂点座標は (2, 0, 0)、緑色の頂点座標は (0, 2, 0) なので、表示されているベクトルは \begin{pmatrix}0 \\2 \\0\end{pmatrix}-\begin{pmatrix}2 \\0 \\0\end{pmatrix}=\begin{pmatrix}-2 \\2 \\0\end{pmatrix}である(図中では緑色の数値で示されている)。
では、上で使用したプログラム Code2実行後の、このベクトルのワールド座標系での値を求めてみよう(すなわち、Tent3座標系からワールド座標系へのベクトルの変換である)。
以下の図は、Code2の実行結果をワールド座標系から見たときの様子である。


図25は、Code2の実行結果を 3つのオブジェクトが見える位置にカメラを置いたときのものであり、図26は、Tent3にカメラを近づけて見たときのものである(図中の数値は すべてワールド座標系での値である)。図中に表示されている数値は、Tent3の赤色の頂点の座標が (14, 0, -8)、緑色の頂点の座標が (16, 2, -8) で、赤色の頂点を始点とし、緑色の頂点を終点とするベクトルが (2, 2, 0) であることを表している。
では実際に、計算によってそれらの値を求めてみよう。
上で述べたように、プログラム実行後のワールド座標系における Tent3の赤色の頂点座標は、
localTent1 * localTent2 * localTent3 * \begin{pmatrix}2 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}-1 &0 &0 &16 \\ 0 &1 &0 &0 \\ 0 &0 &-1 &-8 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}2 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}14 \\0 \\ -8 \\1\end{pmatrix}
であり、同様の計算によって Tent3の緑色の頂点座標を計算すると、
localTent1 * localTent2 * localTent3 * \begin{pmatrix}0 \\2 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}-1 &0 &0 &16 \\ 0 &1 &0 &0 \\ 0 &0 &-1 &-8 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0 \\2 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}16 \\2 \\ -8 \\1\end{pmatrix}
となる。したがって、Tent3の赤色の頂点を始点とし、緑色の頂点を終点とするベクトルのワールド座標系における値は、 \begin{pmatrix}16 \\2 \\ -8 \\\end{pmatrix}-\begin{pmatrix}14 \\0 \\ -8 \\\end{pmatrix}=\begin{pmatrix}2 \\2 \\0\end{pmatrix}として求められる。今行った計算では、Tent3座標系における赤色の頂点座標、及び 緑色の頂点座標をワールド座標系における値に変換し、ワールド座標系における赤色の頂点座標と緑色の頂点座標から、目的のベクトルのワールド座標系における値を算出した。
具体的な計算式を示すと以下のようになる (計算結果の同次座標化されているベクトルの w値が 0であることに注意)。
localTent1 * localTent2 * localTent3 * \begin{pmatrix}0 \\2 \\ 0 \\1\end{pmatrix}-localTent1 * localTent2 * localTent3 * \begin{pmatrix}2 \\0 \\ 0 \\1\end{pmatrix}=\begin{pmatrix}16 \\2 \\ -8 \\1\end{pmatrix}-\begin{pmatrix}14 \\0 \\ -8 \\1\end{pmatrix}=\begin{pmatrix}2 \\2 \\ 0 \\0\end{pmatrix}
この算出方法でも正しい答えは得られるが、行列の分配法則(3-7節)を使えば、より効率的に計算が行える。
分配法則によれば、3つの行列 A、B、Cについて次の等式が成り立つのであった (ただし 積AB、積AC は可能であるとする)。
A(B + C) = AB + AC したがって、ここでの例でいえば、上の計算式で使われている Tent3座標系の赤色、緑色の頂点座標を 4\times1行列として考えれば、この分配法則を適用して、次のように書き換えられる。
\begin{align*}&localTent1 * localTent2 * localTent3 * \begin{pmatrix}0 \\2 \\ 0 \\1\end{pmatrix}-localTent1 * localTent2 * localTent3 * \begin{pmatrix}2 \\0 \\ 0 \\1\end{pmatrix} \\\\&= localTent1 * localTent2 * localTent3 * \left(\begin{pmatrix}0 \\2 \\ 0 \\1\end{pmatrix}-\begin{pmatrix}2 \\0 \\ 0 \\1\end{pmatrix} \right) \\\\&=localTent1 * localTent2 * localTent3 * \begin{pmatrix}0 - 2 \\2 - 0 \\ 0 - 0 \\1 - 1\end{pmatrix} \\\\&=localTent1 * localTent2 * localTent3 * \begin{pmatrix}-2 \\2 \\ 0 \\0\end{pmatrix} \\\\&=\begin{pmatrix}-1 &0 &0 &16 \\ 0 &1 &0 &0 \\ 0 &0 &-1 &-8 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}-2 \\2 \\ 0 \\0\end{pmatrix} =\begin{pmatrix}2 \\2 \\ 0 \\0\end{pmatrix} \end{align*}
この式は、Tent3座標系の座標をワールド座標系の座標に変換する行列(localTent1 * localTent2 * localTent3)を Tent3座標系の赤頂点と緑頂点を結ぶベクトルに直接 掛ければ、そのベクトルのワールド座標系における値が求められる ことを意味している。赤頂点、緑頂点のそれぞれを ワールド座標系の値に変換する必要はないのである。上の式に示されるように、赤頂点と緑頂点を結ぶベクトルを直接 Tent3座標系の値からワールド座標系における値に変換することが可能なのである。ただし、ベクトルの変換の場合は注意すべきことが1つある。
座標(あるいは点)の変換の場合は、その座標の同次座標化された値の w値は通常通り 1であるが、ベクトルの変換の場合には、そのベクトルを同次座標化した際の w値は 1ではなく 0になることである。すなわち、ベクトルを異なる座標系での値に変換するために、その座標系への変換行列とベクトルの積を実行する際には、同次座標化されたベクトルの w値は 0にして計算しなければならない。
その理由は、ベクトルの変換は結局のところ、2つの変換を行列の分配法則によって 1つの変換にまとめているためである。具体的には、上の数式の 1行目では、(2, 0, 0, 1)、(0, 2, 0, 1) の2つの座標に対する変換が記述されているが、これを分配法則によって 2行目(あるいは3行目)の記述では (-2, 2, 0, 0) の変換 1つにまとめている。この過程で 2つの座標の間で減算が行われているが、これが w値を 0にすることになるのである。
繰り返せば、座標(あるいは点)の変換の場合は、その座標の同次座標化された値の w値は通常通り 1であるが、ベクトルの変換の場合には、そのベクトルを同次座標化した際の w値は 1ではなく、0である。上の計算において、(-2, 2, 0, 0) ではなく (-2, 2, 0, 1) を掛けても正しい答えは得られない。

ここで、変換対象としているベクトルは Tent3座標系のベクトル (-2, 2, 0) で、Tent3座標系から Tent1座標系へ変換する行列は、localTent2 * localTent3 であるから、得られる結果は (上で述べたようにベクトルを変換する場合には同次座標化した際の w値は 0にする必要がある)、
localTent2 * localTent3 * \begin{pmatrix}-2 \\2 \\ 0 \\0\end{pmatrix}=\begin{pmatrix}-1 &0 &0 &8 \\ 0 &0 &1 &8 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1\end{pmatrix}\begin{pmatrix}-2 \\2 \\ 0 \\0\end{pmatrix}=\begin{pmatrix}2 \\0 \\ 2 \\0\end{pmatrix}
となる。すなわち、Tent1座標系では (2, 0, 2) という値になるが、この結果は図27に示される数値(緑色の数値)と確かに一致している。異なる座標系へのベクトルの変換について、一般化した形で表現すると以下のようになる。
3D空間内の座標系L_1におけるベクトル \boldsymbol{\mathsf{v_1}} の値を L_1と異なる他の座標系L_2での値に変換する際、座標系L_1から座標系L_2への変換行列を M、Mの左上の3\times 3行列を M_{3\times 3}、\boldsymbol{\mathsf{v_1}} の変換後のL_2での値を \boldsymbol{\mathsf{v_2}} とすれば、 M_{3\times 3} * \boldsymbol{\mathsf{v_1}} = \boldsymbol{\mathsf{v_2}} である (\boldsymbol{\mathsf{v_1}}、\boldsymbol{\mathsf{v_2}} は同次座標化されていない 3次元ベクトルである)。
ただし、後の章で解説するが、法線ベクトルの変換については事情が異なる。
© 2020-2025 Redpoll's 60 (All rights reserved)