Redpoll's 60
第4章 3D空間におけるオブジェクトの運動
§4-10 ローカル座標系とワールド座標系 3
4-8節、4‐9節では、2つのオブジェクトの一体化した運動を扱った。つまり、オブジェクトの階層は2階層であった。本節では、一体化するオブジェクトをもう1つ追加して、オブジェクトの階層を3階層にした運動を扱う。
使用するオブジェクトは以下の3つ。
今回、追加されるオブジェクトは図3の Diskである。Diskは厚みを持った円盤状のオブジェクトであり、内側に紺色の溝があり、その溝の内側に円形の領域がある。初期状態では、Diskの上面はローカル座標系の XZ平面と重なっている (つまり、Diskの上面は y = 0 の位置にある)。
4-8節、4-9節では一体化した2つのオブジェクトの各座標系における運動を見た。そこでは、オブジェクトにどのような変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクトは何も変化せず初期状態のままであるということ、さらに、オブジェクトに対して定義された変換は、そのオブジェクトの親座標系の中で実行されるということを学習した。本節においては、3つのオブジェクトの一体化した運動を通して、前2節で学習した それらの事柄について見ていく。本節は、3階層の親子関係にあるオブジェクトの運動を通しての、前2節の内容の復習である。
尚、本節においてもプログラムに関する解説は、使用する変数についての説明などの最低限のものに留める。
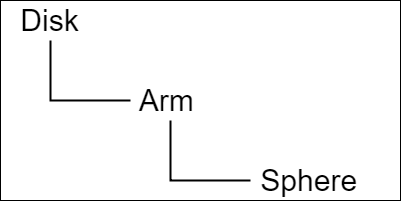
図4 オブジェクトの階層構造 まず初めに3つのオブジェクトを一体化する。
親子関係は図4に示される通りである。Diskには、Armがアタッチされ、Armに対しては、Sphereがアタッチされる。
前節までは、Armは親オブジェクトを持たなかったが、ここでは Diskが Armの親オブジェクトであり、Diskが一番上の階層に位置する (すなわち、Diskは親オブジェクトを持たない)。
[Code1] (実行結果 図5、図6、図7)
図中のラベルの意味は、x、y、zがワールド座標系の x軸、y軸、z軸を表し、D-x、D-y、D-zが Disk座標系の x軸、y軸、z軸を表し、A-x、A-y、A-zが Arm座標系の x軸、y軸、z軸を表し、S-x、S-y、S-zが Sphere座標系の x軸、y軸、z軸を表している。
図5は、プログラムの実行結果をワールド座標系から見たときの様子である。図中の数値はワールド座標系での値である。Diskは親オブジェクトを持たないので、Diskの親座標系はワールド座標系になる。Diskに定義されている変換は、プログラム9行目の記述で、その内容は identity行列、すなわち何も変換を実行しないというものである。したがって、Diskは親座標系であるワールド座標系の中では、全く動いていない (図5ではDisk座標系は表示されていないが、Disk座標系を表示した場合、Diskは動いていないのでワールド座標系と重なって表示される)。
図6は、プログラムの実行結果を Disk座標系から見たときの様子である(ワールド座標系は非表示にしてある)。図中の数値は Disk座標系での値である。Diskには Armがアタッチされるが、Armのアタッチポジションはプログラム中で定数 c_attachPos_Arm によって表され、その値は (2, 0, 0) である。つまり、Armは親座標系である Disk座標系の (2, 0, 0)にアタッチされる。実際、図6を見れば、Armの支点が Disk座標系の x軸上の 2の位置に移動していることがわかる。尚、図5のワールド座標系においても、Armの支点は (2, 0, 0) にあるが、これは Diskがワールド座標系の中で全く動いていないためである (たとえば、Diskをx軸方向に1だけ平行移動させた場合には、Armの支点はワールド座標系において(3, 0, 0)となる。Disk座標系では(2, 0, 0)のまま変わらない)。
図7は、プログラムの実行結果を Disk座標系において、図6よりも さらにカメラを近づけて見たときの様子である(ここでも、ワールド座標系は非表示にしてある)。図中の数値は Disk座標系での値である。ここでは、Disk座標系のほかに、Arm座標系、Sphere座標系も表示している。Arm座標系の原点は、Armの支点と同じ位置にあり、Disk座標系の (2, 0, 0) に置かれている。特に、ここでは回転をしているわけではないため Arm座標系の x軸と、Disk座標系の x軸が大部分重なってしまっている。
Sphereの中心の座標は、Arm座標系ではプログラム2行目の c_attachPos_Sphere の値と同じく (5, 4, 0) である。Disk座標系では (7, 4, 0) となるが、これは まず Sphereが Arm座標系の中で(5, 4, 0)に移動したときに、Armに平行移動が行われていない状態では Arm座標系も同じく平行移動が行われていない。この時点では Arm座標系と Disk座標系は重なっているので Sphereの中心座標は Disk座標系の中でも (5, 4, 0) である。そして、Armに対して(2, 0, 0)の平行移動が行われるとそれに連動して Arm座標系も同じだけ動き、その結果 Arm座標系の原点は Disk座標系の中では(2, 0, 0)に移動する(図7)。したがって、Arm座標系の中の(5, 4, 0)という位置は Disk座標系の中では (7, 4, 0) になるのである。
Arm座標系や、Sphere座標系から見たときの様子は、前節や前々節で見てきたものと背景を除いて同じであるためここでは省略する(例えば、4-8節 図8、図9を参照)。
Diskには、その上面の中心が、y軸上の y = 8 を中心とする振幅 4の単振動を実行する(つまり、y = 4 から y = 12 の間の往復)。
[Code2] (実行結果 図8)
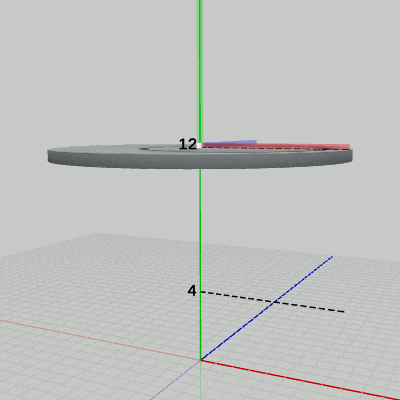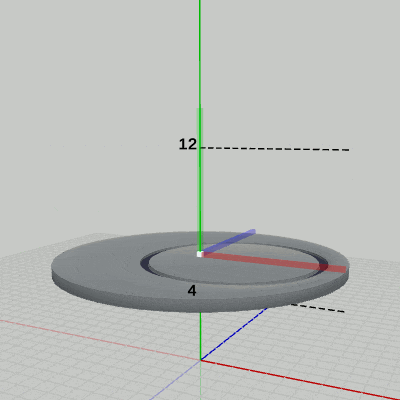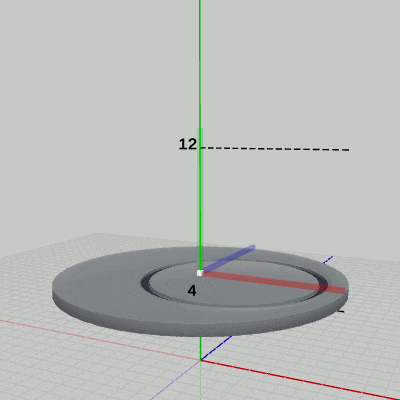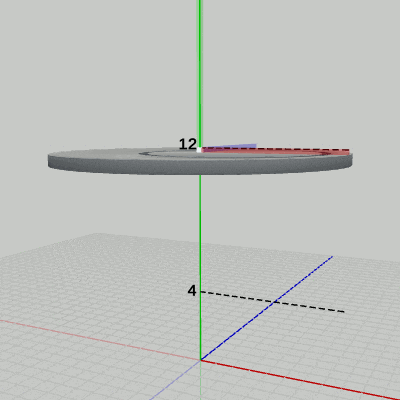
図8 Code2 実行結果(ワールド座標系から見たときの様子) 1行目の i_shmDiskは 2行目の単振動の計算で用いられる角度で、このプログラムでは毎フレーム 1ずつ増加する。また、この計算によって posYは 4から 12の間を往復する。
図8は、プログラムの実行結果をワールド座標系から見たときの様子である (図中の数値はワールド座標系での値である)。図に示されるように、Diskの上面の中心が y軸上の 4から 12の間を往復している。
また、図中には Diskのローカル座標系も表示されているが、やはり、ローカル座標系も Diskと一体となって単振動を行っている。
具体的には、図9に示されるように、Diskを初期状態から x軸周りに -15°回転させ、その状態で単振動を実行する。

図9 Diskをx軸周りに-15°回転させた状態 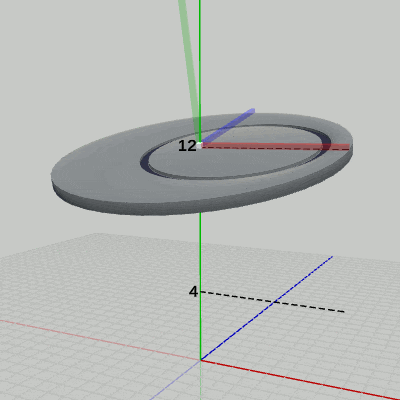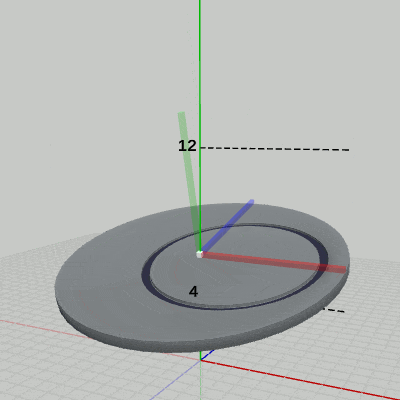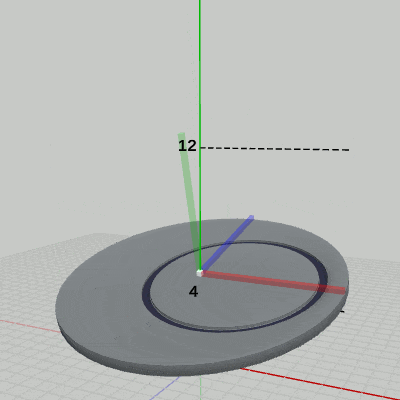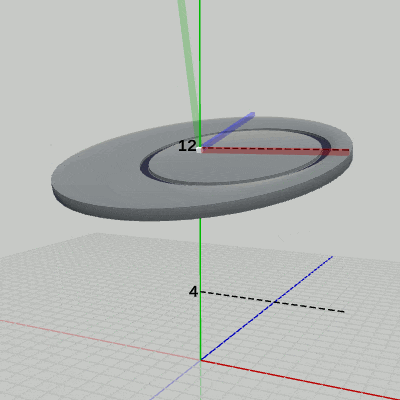
図10 Code3 実行結果(ワールド座標系から見たときの様子)
[Code3] (実行結果 図10)
上図10は、プログラムの実行結果をワールド座標系を見たときの様子である。
[Code4] (実行結果 図11、図12、図13)
このプログラムは、Code1の9行目の localDiskの定義の部分を、Code3の1行目から5行目の内容に変えただけのものである。
図11は、プログラムの実行結果をワールド座標系から見たときの様子である (図中の数値はワールド座標系での値である)。Diskに定義された運動は、プログラム中の9行目から13行目の記述で、その内容は、x軸周りに -15°傾けた状態で、y = 4からy = 12の区間において単振動を行うというものである。実際に図11から、この運動は Diskの親座標系であるワールド座標系において行われていることが分かる。
図12は、プログラムの実行結果を Disk座標系から見たときの様子である (図中の数値は Disk座標系での値である)。ワールド座標系の中では Diskは上下に単振動をしているので、この図の背景にあるワールド座標系も上下に動いている。Armに定義された運動は、このプログラムの6行目から7行目に記述されており、その内容は、アタッチポジションへ移動するために、(2, 0, 0)だけ平行移動するというものである。確かに、Armの親座標系である Disk座標系において、Armは (2, 0, 0)だけ移動しており、その結果、Armの支点が Disk座標系の x軸上の 2の位置に移動している。図11では、Diskの単振動のために、Armの位置は ワールド座標系の中では常に変動しているが、図12が示すように、Diskが単振動をしている間でも、Disk座標系の中における Armの位置は常に変わらない。毎フレーム、Armに定義された (2, 0, 0)だけ移動 という同じ変換が、親座標系である Disk座標系の中で実行されるためである。また、Armにアタッチされている Sphereの中心座標は Disk座標系においては (7, 4, 0) である。
図13は、プログラムの実行結果を Arm座標系から見たときの様子である (図中の数値は Arm座標系での値である)。この図においても、背景であるワールド座標系が上下に動いている。Sphereに定義された運動は、このプログラムの2行目から3行目に記述されており、その内容は、アタッチポジションへ移動するために、(5, 4, 0)だけ平行移動するというものである。確かに、Sphereの親座標系である Arm座標系において、Sphereは (5, 4, 0)だけ移動しており、その結果、Sphereの中心が Arm座標系の (5, 4, 0)に移動している。図11に示されるように、Diskの単振動に伴って、Sphereもワールド座標系の中における位置は常に変動する。しかし、図13が示すように、Diskが単振動をしている間でも、Arm座標系の中における Sphereの位置は常に変わらない。毎フレーム、Sphereに定義された (5, 4, 0)だけ移動 という同じ変換が、親座標系である Arm座標系の中で実行されるためである。
すなわち、ワールド座標系においては、Diskが x軸周りに -15°傾いた状態で、y = 4から y = 12の区間の単振動を行っており、Diskの上面にアタッチされている Armは、自身の支点を通り、Disk座標系の y軸に平行な軸の周りを回転している。そのとき、回転している Armの先端では、Armにアタッチされている Sphereが 1倍から2倍の拡大縮小を繰り返している。
[Code5] (実行結果 図14、図15、図16、図17)
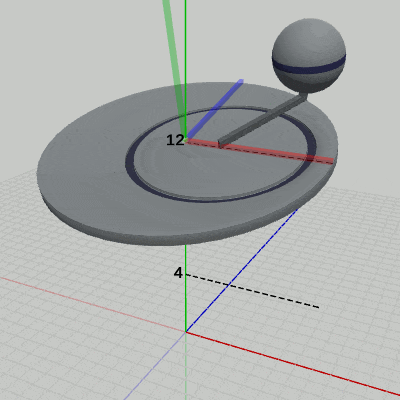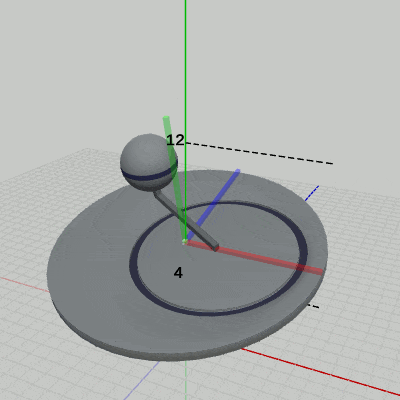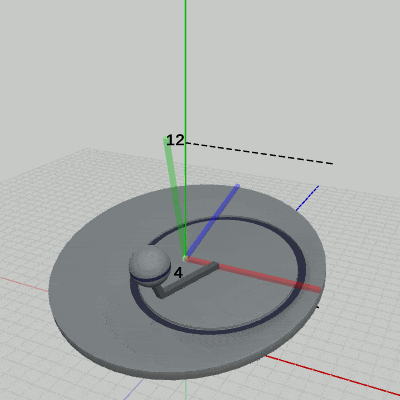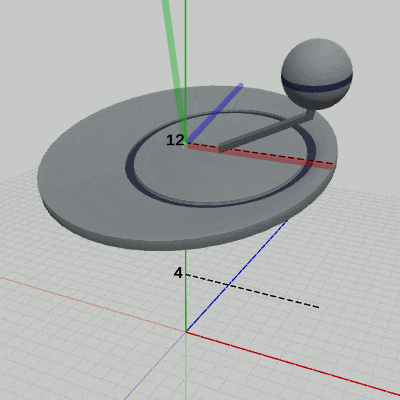
図14 Code5 実行結果(ワールド座標系から見たときの様子) 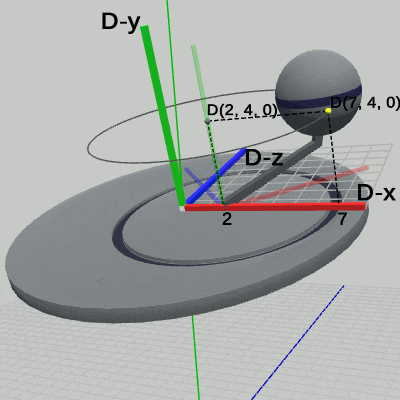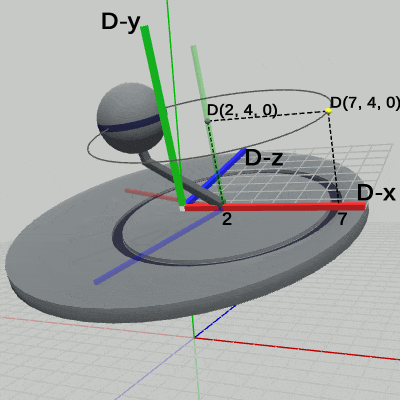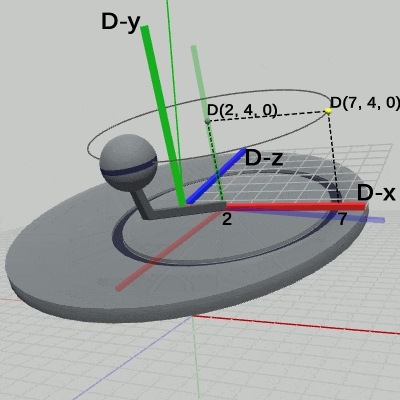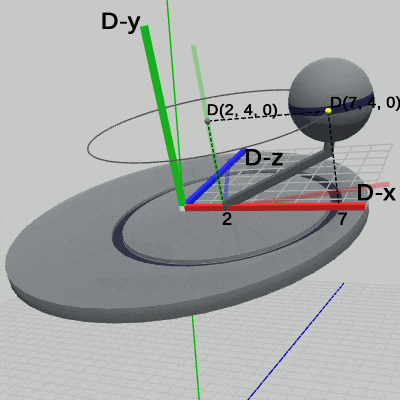
図15 Code5 実行結果(Disk座標系から見たときの様子)
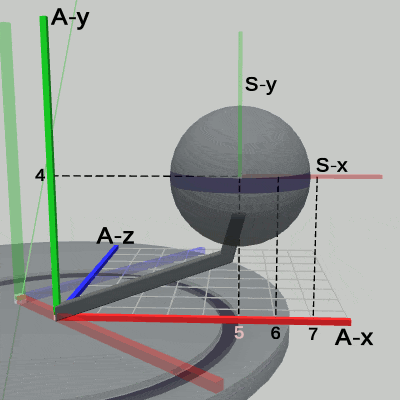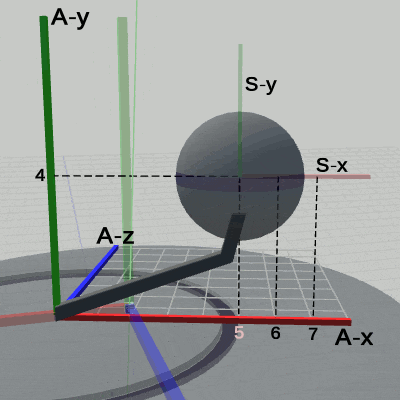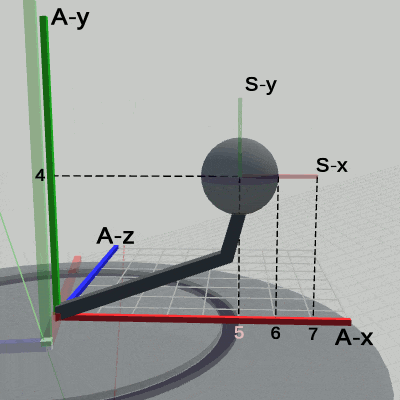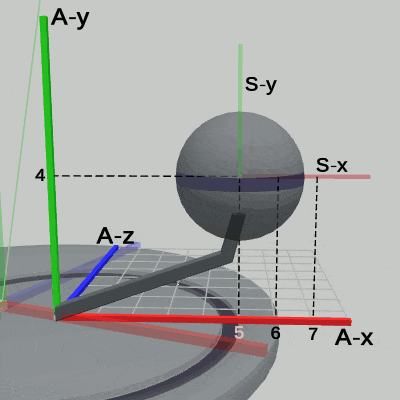
図16 Code5 実行結果(Arm座標系から見たときの様子) 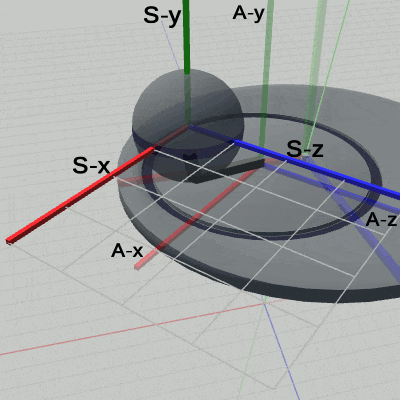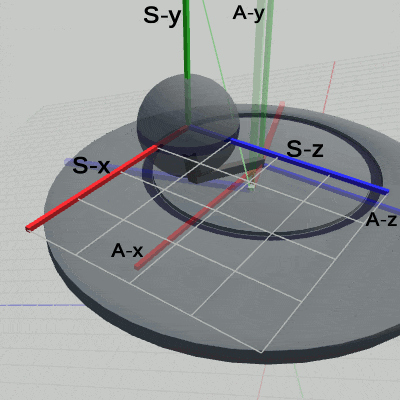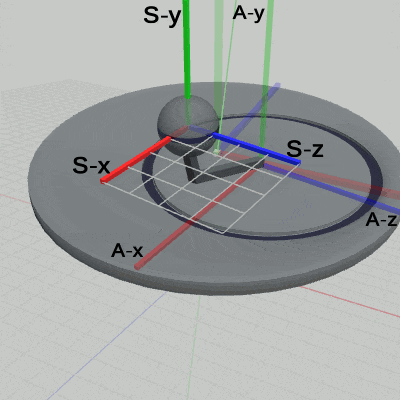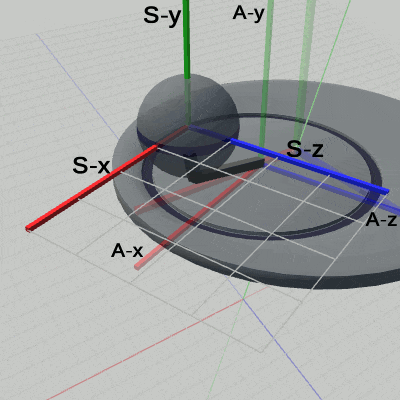
図17 Code5 実行結果(Sphere座標系から見たときの様子)
図14~図17は、プログラムの実行結果を各座標系から見たときのものであるが、図に示される それぞれの運動は、前節や本節において見てきたものと、背景を除いては同じものである。
以下、簡単に解説しよう。
図14は、プログラムの実行結果をワールド座標系から見たときの様子である (図中の数値はすべてワールド座標系での値である)。
3つのオブジェクトが一体化して運動しているが、この図においては、Diskの運動に焦点を当てる。Diskに定義された変換は、プログラム中の12行目から16行目の記述で、その内容は x軸周りに -15°傾けた状態で、y = 4からy = 12の区間において単振動を行うというものである。実際に図14から、この運動は Diskの親座標系であるワールド座標系において行われていることが分かる。
図15は、プログラムの実行結果を Disk座標系から見たときの様子である (図中の数値はすべて Disk座標系での値である)。カメラが Disk座標系に固定されているため、背景であるワールド座標系が上下に動いている。
Armの運動に焦点を当てると、Armは Disk座標系において、その支点が (2, 0, 0) にあり、支点を通り、Disk座標系の y軸に平行な軸の周りに回転をしている。それらの運動は、プログラム中の 7行目から10行目までに記述されているが、実際に、そこで定義された運動が親座標系である Disk座標系で行われていることは、図15が示す通りである。
図16は、プログラムの実行結果を Arm座標系から見たときの様子である (図中の数値はすべて Arm座標系での値である)。
ここでは、Sphereの運動に焦点を当てる。Arm座標系においては、Sphereは その中心が常に (5, 4, 0) にあり、その位置で拡大縮小を繰り返している。Sphereの運動は、プログラム中では1行目から5行目に記述されているが、実際に、プログラムに定義された通りの運動が親座標系である Arm座標系で行われていることが図16からわかる (例えば、他の座標系 Disk座標系やワールド座標系からでは、Sphereに定義された運動を確認することはできない。図15のDisk座標系では、Sphereは (2, 4, 0) を中心とし、(7, 4, 0) を通る円周上を回転している。図14のワールド座標系では、さらに上下運動が加わるので、Sphereの運動はすでに単純な円周上の回転ですらなくなっている。これらの運動は、プログラムの1行目から5行目において定義された運動とは何のつながりもないものである)。
図17は、プログラムの実行結果を Sphere座標系から見たときの様子である (図中の数値はすべて Sphere座標系での値である)。
Sphereは、常にその中心が Sphere座標系の原点にあり、拡大縮小を繰り返しているが、Sphere座標系も同様に拡大縮小をしているのでSphere座標系においては、Sphereの大きさは変化しない。つまり、Sphereは Sphere座標系においては常に 位置、向き、大きさは同じであり、初期状態から変化しない。このことは、Disk座標系において Diskを見た場合、Arm座標系において Armを見た場合にも同じことがいえる。何度か述べているように、オブジェクトにどのような変換を実行しても、オブジェクトは、自身のローカル座標系の中では初期状態から変化しないのである。
以上からわかるように、オブジェクトに定義された運動 (それはプログラム中ではオブジェクトのローカル行列によって表される)は、そのオブジェクトの親座標系の中で見えるのである。ワールド座標系において複数のオブジェクトが一体化して運動をしている場合でも、個々のオブジェクトについて焦点を当てれば、それらの階層構造にあるオブジェクトは、その親座標系の中で自身に定義された運動をしているのである。
使用するオブジェクトは以下の3つ。
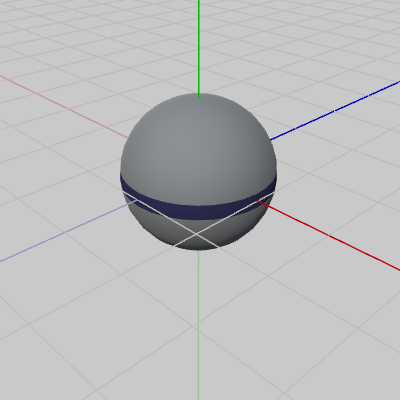 図1 Sphere 初期状態
図1 Sphere 初期状態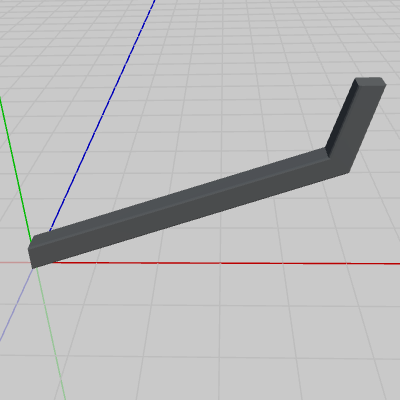 図2 Arm 初期状態
図2 Arm 初期状態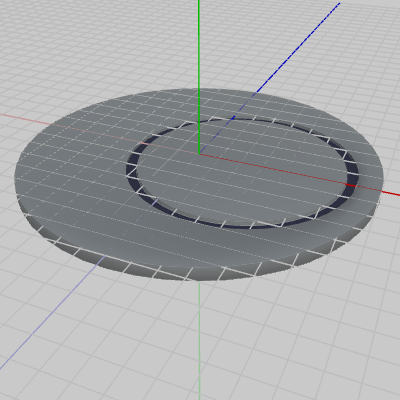 図3 Disk 初期状態
図3 Disk 初期状態
今回、追加されるオブジェクトは図3の Diskである。Diskは厚みを持った円盤状のオブジェクトであり、内側に紺色の溝があり、その溝の内側に円形の領域がある。初期状態では、Diskの上面はローカル座標系の XZ平面と重なっている (つまり、Diskの上面は y = 0 の位置にある)。
4-8節、4-9節では一体化した2つのオブジェクトの各座標系における運動を見た。そこでは、オブジェクトにどのような変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクトは何も変化せず初期状態のままであるということ、さらに、オブジェクトに対して定義された変換は、そのオブジェクトの親座標系の中で実行されるということを学習した。本節においては、3つのオブジェクトの一体化した運動を通して、前2節で学習した それらの事柄について見ていく。本節は、3階層の親子関係にあるオブジェクトの運動を通しての、前2節の内容の復習である。
尚、本節においてもプログラムに関する解説は、使用する変数についての説明などの最低限のものに留める。
# Code1

親子関係は図4に示される通りである。Diskには、Armがアタッチされ、Armに対しては、Sphereがアタッチされる。
前節までは、Armは親オブジェクトを持たなかったが、ここでは Diskが Armの親オブジェクトであり、Diskが一番上の階層に位置する (すなわち、Diskは親オブジェクトを持たない)。
[Code1] (実行結果 図5、図6、図7)
- // c_attachPos_Sphere : (5, 4, 0)
- Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere);
- Matrix4x4 localSphere = traSphere;
- // c_attachPos_Arm : (2, 0, 0)
- Matrix4x4 traArm = TH3DMath.GetTranslation4x4(c_attachPos_Arm);
- Matrix4x4 localArm = traArm;
- Matrix4x4 localDisk = Matrix4x4.identity;
- Matrix4x4 worldSphere = localDisk * localArm * localSphere;
- Matrix4x4 worldArm = localDisk * localArm;
- Matrix4x4 worldDisk = localDisk;
- Sphere.SetMatrix(worldSphere);
- Arm.SetMatrix(worldArm);
- Disk.SetMatrix(worldDisk);
図中のラベルの意味は、x、y、zがワールド座標系の x軸、y軸、z軸を表し、D-x、D-y、D-zが Disk座標系の x軸、y軸、z軸を表し、A-x、A-y、A-zが Arm座標系の x軸、y軸、z軸を表し、S-x、S-y、S-zが Sphere座標系の x軸、y軸、z軸を表している。
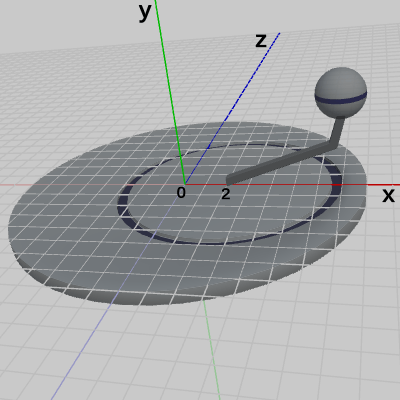 図5 Code1 実行結果(ワールド座標系から見たときの様子)
図5 Code1 実行結果(ワールド座標系から見たときの様子)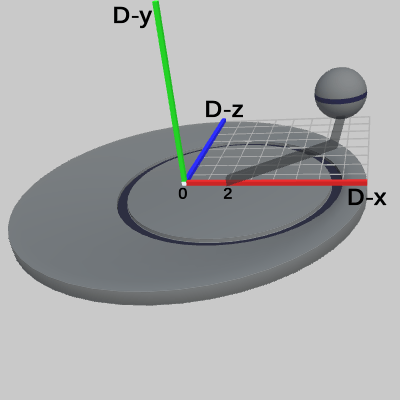 図6 Code1 実行結果(Disk座標系から見たときの様子)
図6 Code1 実行結果(Disk座標系から見たときの様子)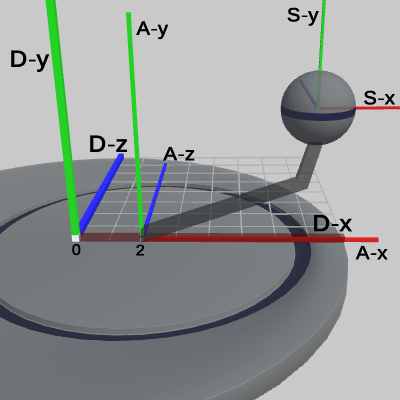 図7 Code1 実行結果(Disk座標系から見たときの様子 ; 3つのオブジェクトのローカル座標系を表示している)
図7 Code1 実行結果(Disk座標系から見たときの様子 ; 3つのオブジェクトのローカル座標系を表示している)
図5は、プログラムの実行結果をワールド座標系から見たときの様子である。図中の数値はワールド座標系での値である。Diskは親オブジェクトを持たないので、Diskの親座標系はワールド座標系になる。Diskに定義されている変換は、プログラム9行目の記述で、その内容は identity行列、すなわち何も変換を実行しないというものである。したがって、Diskは親座標系であるワールド座標系の中では、全く動いていない (図5ではDisk座標系は表示されていないが、Disk座標系を表示した場合、Diskは動いていないのでワールド座標系と重なって表示される)。
図6は、プログラムの実行結果を Disk座標系から見たときの様子である(ワールド座標系は非表示にしてある)。図中の数値は Disk座標系での値である。Diskには Armがアタッチされるが、Armのアタッチポジションはプログラム中で定数 c_attachPos_Arm によって表され、その値は (2, 0, 0) である。つまり、Armは親座標系である Disk座標系の (2, 0, 0)にアタッチされる。実際、図6を見れば、Armの支点が Disk座標系の x軸上の 2の位置に移動していることがわかる。尚、図5のワールド座標系においても、Armの支点は (2, 0, 0) にあるが、これは Diskがワールド座標系の中で全く動いていないためである (たとえば、Diskをx軸方向に1だけ平行移動させた場合には、Armの支点はワールド座標系において(3, 0, 0)となる。Disk座標系では(2, 0, 0)のまま変わらない)。
図7は、プログラムの実行結果を Disk座標系において、図6よりも さらにカメラを近づけて見たときの様子である(ここでも、ワールド座標系は非表示にしてある)。図中の数値は Disk座標系での値である。ここでは、Disk座標系のほかに、Arm座標系、Sphere座標系も表示している。Arm座標系の原点は、Armの支点と同じ位置にあり、Disk座標系の (2, 0, 0) に置かれている。特に、ここでは回転をしているわけではないため Arm座標系の x軸と、Disk座標系の x軸が大部分重なってしまっている。
Sphereの中心の座標は、Arm座標系ではプログラム2行目の c_attachPos_Sphere の値と同じく (5, 4, 0) である。Disk座標系では (7, 4, 0) となるが、これは まず Sphereが Arm座標系の中で(5, 4, 0)に移動したときに、Armに平行移動が行われていない状態では Arm座標系も同じく平行移動が行われていない。この時点では Arm座標系と Disk座標系は重なっているので Sphereの中心座標は Disk座標系の中でも (5, 4, 0) である。そして、Armに対して(2, 0, 0)の平行移動が行われるとそれに連動して Arm座標系も同じだけ動き、その結果 Arm座標系の原点は Disk座標系の中では(2, 0, 0)に移動する(図7)。したがって、Arm座標系の中の(5, 4, 0)という位置は Disk座標系の中では (7, 4, 0) になるのである。
Arm座標系や、Sphere座標系から見たときの様子は、前節や前々節で見てきたものと背景を除いて同じであるためここでは省略する(例えば、4-8節 図8、図9を参照)。
# Code2
ここでは、Diskの運動を定義する。Diskには、その上面の中心が、y軸上の y = 8 を中心とする振幅 4の単振動を実行する(つまり、y = 4 から y = 12 の間の往復)。
[Code2] (実行結果 図8)
- i_shmDisk += 1.0f;
- float posY = 4.0f * Mathf.Sin(i_shmDisk * Mathf.Deg2Rad) + 8.0f; // 4から12の間の往復
- Matrix4x4 traDisk = TH3DMath.GetTranslation4x4(0.0f, posY, 0.0f);
- Matrix4x4 localDisk = traDisk;
- Matrix4x4 worldDisk = localDisk;
- Disk.SetMatrix(worldDisk);

図8は、プログラムの実行結果をワールド座標系から見たときの様子である (図中の数値はワールド座標系での値である)。図に示されるように、Diskの上面の中心が y軸上の 4から 12の間を往復している。
また、図中には Diskのローカル座標系も表示されているが、やはり、ローカル座標系も Diskと一体となって単振動を行っている。
# Code3
次に、Diskをやや傾けた状態で、先程と同じ区間の単振動を実行する。具体的には、図9に示されるように、Diskを初期状態から x軸周りに -15°回転させ、その状態で単振動を実行する。


[Code3] (実行結果 図10)
- i_shmDisk += 1.0f;
- float posY = 4.0f * Mathf.Sin(i_shmDisk * Mathf.Deg2Rad) + 8.0f; // 4 -- 12の間を往復
- Matrix4x4 rotDisk = TH3DMath.GetRotation4x4(-15.0f, Vector3.right);
- Matrix4x4 traDisk = TH3DMath.GetTranslation4x4(0.0f, posY, 0.0f);
- Matrix4x4 localDisk = traDisk * rotDisk;
- Matrix4x4 worldDisk = localDisk;
- Disk.SetMatrix(worldDisk);
上図10は、プログラムの実行結果をワールド座標系を見たときの様子である。
# Code4
次に、3つのオブジェクトを一体化した状態で、Diskに単振動を実行する(Diskの単振動は、Code3と同じく やや傾けた状態で行う)。ここでは、3つのオブジェクトのうちで運動をしているのは、Diskだけで、Arm、Sphereに対しては、指定の位置へのアタッチ以外の変換は実行しない。[Code4] (実行結果 図11、図12、図13)
- // c_attachPos_Sphere : (5, 4, 0)
- Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere);
- Matrix4x4 localSphere = traSphere;
- // c_attachPos_Arm : (2, 0, 0)
- Matrix4x4 traArm = TH3DMath.GetTranslation4x4(c_attachPos_Arm);
- Matrix4x4 localArm = traArm;
- i_shmDisk += 1.0f;
- float posY = 4.0f * Mathf.Sin(i_shmDisk * Mathf.Deg2Rad) + 8.0f; // 4 -- 12の間を往復
- Matrix4x4 rotDisk = TH3DMath.GetRotation4x4(-15.0f, Vector3.right);
- Matrix4x4 traDisk = TH3DMath.GetTranslation4x4(0.0f, posY, 0.0f);
- Matrix4x4 localDisk = traDisk * rotDisk;
- Matrix4x4 worldSphere = localDisk * localArm * localSphere;
- Matrix4x4 worldArm = localDisk * localArm;
- Matrix4x4 worldDisk = localDisk;
- Sphere.SetMatrix(worldSphere);
- Arm.SetMatrix(worldArm);
- Disk.SetMatrix(worldDisk);
このプログラムは、Code1の9行目の localDiskの定義の部分を、Code3の1行目から5行目の内容に変えただけのものである。
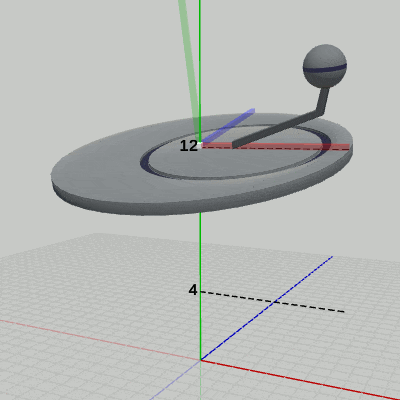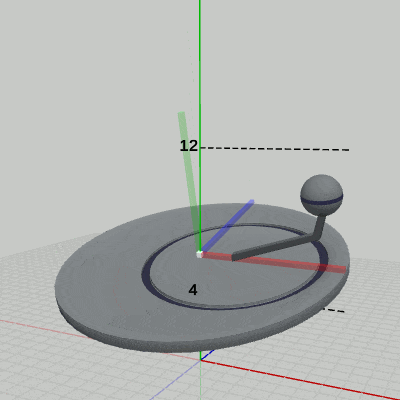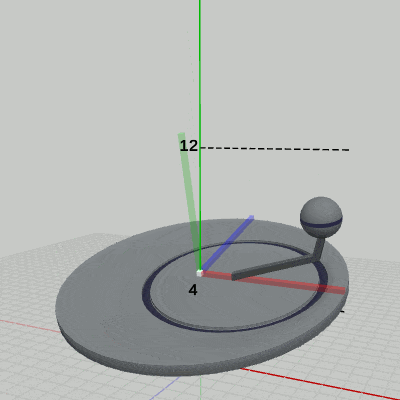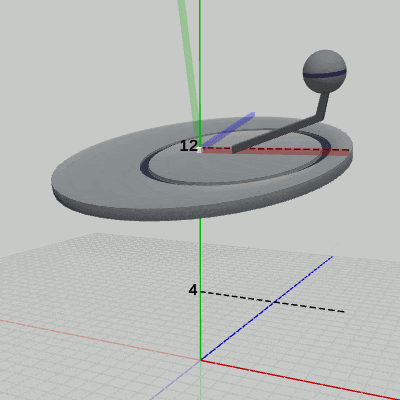 図11 Code4 実行結果(ワールド座標系から見たときの様子)
図11 Code4 実行結果(ワールド座標系から見たときの様子)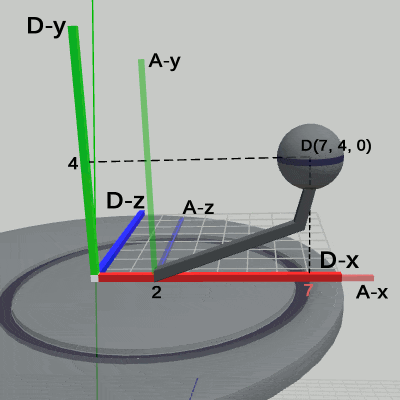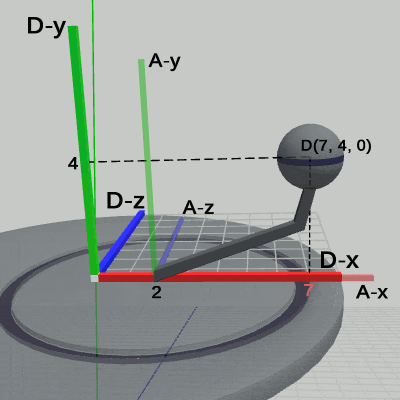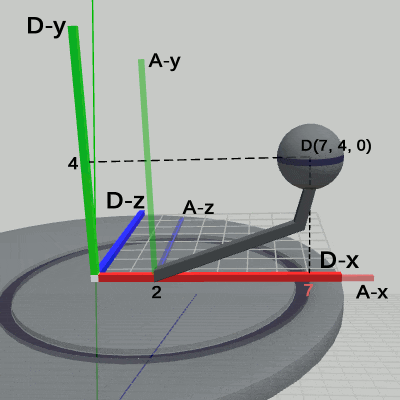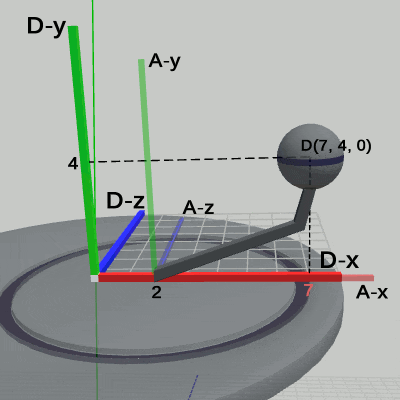 図12 Code4 実行結果(Disk座標系から見たときの様子)
図12 Code4 実行結果(Disk座標系から見たときの様子) 図13 Code4 実行結果(Arm座標系から見たときの様子)
図13 Code4 実行結果(Arm座標系から見たときの様子)
図11は、プログラムの実行結果をワールド座標系から見たときの様子である (図中の数値はワールド座標系での値である)。Diskに定義された運動は、プログラム中の9行目から13行目の記述で、その内容は、x軸周りに -15°傾けた状態で、y = 4からy = 12の区間において単振動を行うというものである。実際に図11から、この運動は Diskの親座標系であるワールド座標系において行われていることが分かる。
図12は、プログラムの実行結果を Disk座標系から見たときの様子である (図中の数値は Disk座標系での値である)。ワールド座標系の中では Diskは上下に単振動をしているので、この図の背景にあるワールド座標系も上下に動いている。Armに定義された運動は、このプログラムの6行目から7行目に記述されており、その内容は、アタッチポジションへ移動するために、(2, 0, 0)だけ平行移動するというものである。確かに、Armの親座標系である Disk座標系において、Armは (2, 0, 0)だけ移動しており、その結果、Armの支点が Disk座標系の x軸上の 2の位置に移動している。図11では、Diskの単振動のために、Armの位置は ワールド座標系の中では常に変動しているが、図12が示すように、Diskが単振動をしている間でも、Disk座標系の中における Armの位置は常に変わらない。毎フレーム、Armに定義された (2, 0, 0)だけ移動 という同じ変換が、親座標系である Disk座標系の中で実行されるためである。また、Armにアタッチされている Sphereの中心座標は Disk座標系においては (7, 4, 0) である。
図13は、プログラムの実行結果を Arm座標系から見たときの様子である (図中の数値は Arm座標系での値である)。この図においても、背景であるワールド座標系が上下に動いている。Sphereに定義された運動は、このプログラムの2行目から3行目に記述されており、その内容は、アタッチポジションへ移動するために、(5, 4, 0)だけ平行移動するというものである。確かに、Sphereの親座標系である Arm座標系において、Sphereは (5, 4, 0)だけ移動しており、その結果、Sphereの中心が Arm座標系の (5, 4, 0)に移動している。図11に示されるように、Diskの単振動に伴って、Sphereもワールド座標系の中における位置は常に変動する。しかし、図13が示すように、Diskが単振動をしている間でも、Arm座標系の中における Sphereの位置は常に変わらない。毎フレーム、Sphereに定義された (5, 4, 0)だけ移動 という同じ変換が、親座標系である Arm座標系の中で実行されるためである。
# Code5
最後に、前節の運動と本節における運動をすべて統合する。すなわち、ワールド座標系においては、Diskが x軸周りに -15°傾いた状態で、y = 4から y = 12の区間の単振動を行っており、Diskの上面にアタッチされている Armは、自身の支点を通り、Disk座標系の y軸に平行な軸の周りを回転している。そのとき、回転している Armの先端では、Armにアタッチされている Sphereが 1倍から2倍の拡大縮小を繰り返している。
[Code5] (実行結果 図14、図15、図16、図17)
- i_shmSphere += 1.0f;
- float scale = 0.5f * Mathf.Sin(i_shmSphere * Mathf.Deg2Rad) + 1.5f; // 1から2の間を往復
- Matrix4x4 sclSphere = TH3DMath.GetScale4x4(scale, scale, scale);
- Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere);
- Matrix4x4 localSphere = traSphere * sclSphere;
- i_degArm--;
- Matrix4x4 rotArm = TH3DMath.GetRotation4x4(i_degArm, Vector3.up);
- Matrix4x4 traArm = TH3DMath.GetTranslation4x4(c_attachPos_Arm);
- Matrix4x4 localArm = traArm * rotArm;
- i_shmDisk += 1.0f;
- float posY = 4.0f * Mathf.Sin(i_shmDisk * Mathf.Deg2Rad) + 8.0f; // 4から12の間を往復
- Matrix4x4 rotDisk = TH3DMath.GetRotation4x4(-15.0f, Vector3.right);
- Matrix4x4 traDisk = TH3DMath.GetTranslation4x4(0.0f, posY, 0.0f);
- Matrix4x4 localDisk = traDisk * rotDisk;
- Matrix4x4 worldSphere = localDisk * localArm * localSphere;
- Matrix4x4 worldArm = localDisk * localArm;
- Matrix4x4 worldDisk = localDisk;
- Sphere.SetMatrix(worldSphere);
- Arm.SetMatrix(worldArm);
- Disk.SetMatrix(worldDisk);




図14~図17は、プログラムの実行結果を各座標系から見たときのものであるが、図に示される それぞれの運動は、前節や本節において見てきたものと、背景を除いては同じものである。
以下、簡単に解説しよう。
図14は、プログラムの実行結果をワールド座標系から見たときの様子である (図中の数値はすべてワールド座標系での値である)。
3つのオブジェクトが一体化して運動しているが、この図においては、Diskの運動に焦点を当てる。Diskに定義された変換は、プログラム中の12行目から16行目の記述で、その内容は x軸周りに -15°傾けた状態で、y = 4からy = 12の区間において単振動を行うというものである。実際に図14から、この運動は Diskの親座標系であるワールド座標系において行われていることが分かる。
図15は、プログラムの実行結果を Disk座標系から見たときの様子である (図中の数値はすべて Disk座標系での値である)。カメラが Disk座標系に固定されているため、背景であるワールド座標系が上下に動いている。
Armの運動に焦点を当てると、Armは Disk座標系において、その支点が (2, 0, 0) にあり、支点を通り、Disk座標系の y軸に平行な軸の周りに回転をしている。それらの運動は、プログラム中の 7行目から10行目までに記述されているが、実際に、そこで定義された運動が親座標系である Disk座標系で行われていることは、図15が示す通りである。
図16は、プログラムの実行結果を Arm座標系から見たときの様子である (図中の数値はすべて Arm座標系での値である)。
ここでは、Sphereの運動に焦点を当てる。Arm座標系においては、Sphereは その中心が常に (5, 4, 0) にあり、その位置で拡大縮小を繰り返している。Sphereの運動は、プログラム中では1行目から5行目に記述されているが、実際に、プログラムに定義された通りの運動が親座標系である Arm座標系で行われていることが図16からわかる (例えば、他の座標系 Disk座標系やワールド座標系からでは、Sphereに定義された運動を確認することはできない。図15のDisk座標系では、Sphereは (2, 4, 0) を中心とし、(7, 4, 0) を通る円周上を回転している。図14のワールド座標系では、さらに上下運動が加わるので、Sphereの運動はすでに単純な円周上の回転ですらなくなっている。これらの運動は、プログラムの1行目から5行目において定義された運動とは何のつながりもないものである)。
図17は、プログラムの実行結果を Sphere座標系から見たときの様子である (図中の数値はすべて Sphere座標系での値である)。
Sphereは、常にその中心が Sphere座標系の原点にあり、拡大縮小を繰り返しているが、Sphere座標系も同様に拡大縮小をしているのでSphere座標系においては、Sphereの大きさは変化しない。つまり、Sphereは Sphere座標系においては常に 位置、向き、大きさは同じであり、初期状態から変化しない。このことは、Disk座標系において Diskを見た場合、Arm座標系において Armを見た場合にも同じことがいえる。何度か述べているように、オブジェクトにどのような変換を実行しても、オブジェクトは、自身のローカル座標系の中では初期状態から変化しないのである。
以上からわかるように、オブジェクトに定義された運動 (それはプログラム中ではオブジェクトのローカル行列によって表される)は、そのオブジェクトの親座標系の中で見えるのである。ワールド座標系において複数のオブジェクトが一体化して運動をしている場合でも、個々のオブジェクトについて焦点を当てれば、それらの階層構造にあるオブジェクトは、その親座標系の中で自身に定義された運動をしているのである。
© 2020-2025 Redpoll's 60 (All rights reserved)