Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-22
第4章 3D空間におけるオブジェクトの運動
$§$4-22 衝突判定 1
本節から 4-24節までは単純形状の3Dオブジェクト同士の衝突判定について見ていく。
ここで扱う衝突判定は3Dオブジェクト同士の衝突判定ではあるが、オブジェクトの運動及び配置については多少の制限がある。具体的には以下の2つである。
これに関連して今回の衝突判定に使用するアルゴリズムは3Dオブジェクト用の衝突判定アルゴリズムではなく、2Dオブジェクト用のアルゴリズム、すなわち 第2章で学習した平面図形同士の衝突判定アルゴリズムを用いる。
(上記の制限に見られるように本節では「水平方向の移動」という用語を多く用いるが、これは XZ平面に平行な移動を意味する)
まずは簡単な例から見ていこう。
3D空間内に下図に示される2つの球が置かれている。それぞれの球の中心は $C_1$、$C_2$、半径は $r_1$、$r_2$ であり、2つの球の中心の高さは等しい(y座標が同じ)。
ここで適当に両者を動かして衝突させたとする (図2)。上の制限に従って移動の際には y軸方向の移動は行われていないので図3に示されるように、この場合には $C_1$ を中心とする半径 $r_1$ の円盤と $C_2$ を中心とする半径 $r_2$ の円盤が衝突することになる (図中の平面はXZ平面であり、2つの円盤はXZ平面に平行である)。
このときの状況を真上から見下ろしたときのものが以下の図である (ただし 以下の図では2つの球を簡略化して表示している)。この図に示されるように球を真上から見下ろした場合、その形状は円盤であり、この例でいえば2つの球はそれぞれ中心が $C_1$、$C_2$、半径が $r_1$、$r_2$ の円盤として見ることができる。
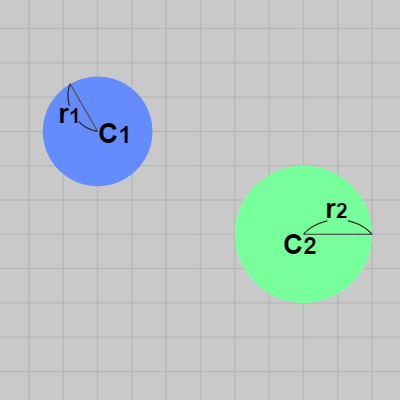
図4 衝突前の2つの球を真上から見下ろしたとき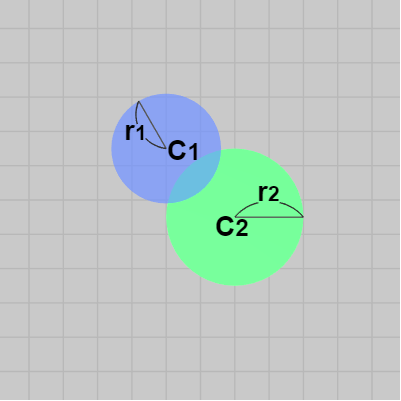 
図5 衝突後の2つの球を真上から見下ろしたとき
したがって この2つの球の衝突は真上から見下ろした場合には、中心 $C_1$、半径 $r_1$ の円盤と中心 $C_2$、半径 $r_2$ の円盤同士の衝突と見ることができる。
また別の例として次の直方体と球の場合を見てみよう。
下図の直方体はその上面と底面がXZ平面に平行であり、図に示されるように上面と底面の各辺の長さは $w$、$h$ である (図6)。また 球の中心は $C$、半径は $r$ であり、ここでも直方体の中心と球の中心の高さは同じ位置にある。
図7は両者を適当に動かして衝突させたときのものである。ここでも y軸方向の移動は行われていないので衝突時においても直方体の中心と球の中心は同じ高さにある。したがって 直方体の中心を $T$ とすれば、この衝突では図8に示されるように $T$ を中心とする各辺の長さ $w$、$h$ の長方形と $C$ を中心とする半径 $r$ の円盤が衝突することになる。
この場合にも直方体及び球を真上から見ると、直方体は中心 $T$、各辺の長さが $w$、$h$ の長方形であり、球は中心 $C$、半径 $r$ の円盤である。したがって この直方体と球の衝突は真上から見下ろした場合には、長方形と円盤の衝突として見ることができるわけである。
図9 衝突前の直方体と球を真上から見下ろしたとき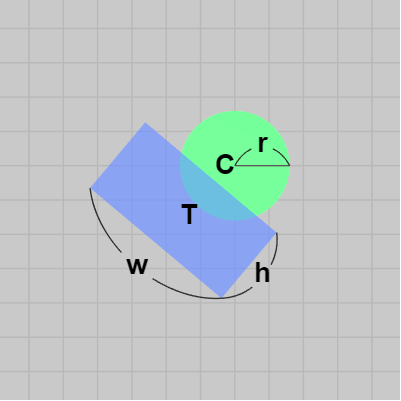 
図10 衝突後の直方体と球を真上から見下ろしたとき
上の例に示されるように、3Dオブジェクト同士の衝突判定も適当な制限のもとでは2つの平面図形の衝突判定として扱うことができる。以下3節で行われる衝突判定は全てこのパターンである。つまり 冒頭に述べた制限のもとで、3Dオブジェクト同士が衝突しているかどうかを2つの平面図形の衝突判定を通して調べるものである。
そのため、今回の衝突判定では各3Dオブジェクトには衝突判定用の平面図形が用いられるが、各オブジェクトに用いられるこの平面図形のことを以降「衝突モデル」と呼ぶことにする。
例えば上の例における球の衝突モデルは円盤であり、直方体の衝突モデルは長方形である。また上の制限にもあるようにオブジェクトの衝突モデルはXZ平面に平行である (そうなるようにオブジェクトは配置されている)。
上記の2つの球の衝突の例では2つの球の中心は同じ高さに配置されていた。そのため 2つの球が衝突する場合には上図3に示されるように2つの球の衝突モデルである中心 $C_1$、半径 $r_1$ の円盤と中心 $C_2$、半径 $r_2$ の円盤も必ず衝突することになる。
しかし、下図11のように2つの球の中心が異なる高さで配置されている場合にはこのようにはいかない。
図11の2つの球を水平方向に動かして下図12の状態になったとしよう。図12では明らかに両者は衝突していないが、この状況を真上から見下ろした場合には2つの円盤が重なっているように見えてしまう (図13)。つまり、この状況において2つの球の衝突モデルである図13の青い円盤と緑の円盤の衝突判定を行うと2つの円盤の衝突が検出されるが、それは正しい判定ではない。
今回の衝突判定は3Dオブジェクトの衝突モデル(平面図形)を用いた衝突判定であり、平面図形同士の衝突判定で衝突が検出されたならば3Dオブジェクト同士が衝突していなければならない。そのためにオブジェクトが衝突する際は、両者の衝突モデル同士が必ず衝突するようにあらかじめオブジェクトを配置しておく必要があるのである。
そのようにオブジェクトを配置することは難しくはない。基本的には各オブジェクトの衝突モデルが同じ高さに、すなわち同じ平面上に置かれるようにすればよいだけである。例えば下図14の星型オブジェクト Star と8面体オブジェクト Crystal の場合であれば、両者は真上から見下ろした場合には図15に示されるようにともに長方形である (Crystalは正確には正方形)。
図14 StarとCrystarl 
図15 StarとCrystalを真上から見下ろしたとき
したがってこの2つのオブジェクトの衝突モデルは長方形であるが(図16)、この2つのオブジェクトを3D空間内に配置する際には両者の衝突モデルである長方形が同じ平面上に含まれるように両者を配置する、具体的にはそれはCrystalとStarの衝突モデルの長方形が同じ高さに来るようにすればよい (図17 ; ただしここでは衝突モデルの長方形がXZ平面に平行になるようにオブジェクトが置かれていることを前提としている)。
図16 衝突モデルは長方形 
図17 衝突モデルの長方形は同じ平面上に含まれている(同じ高さにある)
2つのオブジェクトの衝突モデルが同じ平面上にあれば、水平方向に適当に平行移動させることによりオブジェクト同士が衝突するが(図18)、その際には必ず衝突モデルも衝突することになる (図19)。
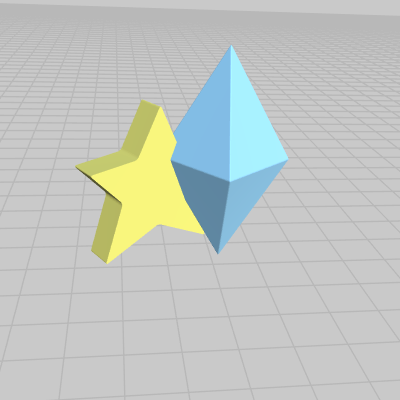
図18 
図19 衝突モデルが同じ平面上にあれば、2つのオブジェクトが衝突した際には必ず衝突モデルも衝突する
本節から 4-24節の衝突判定で使われるオブジェクトのほとんどはカスタムライブラリーの THAlphaObject3D クラスのインスタンスである。このクラスは今まで使用してきた THObject3D クラスのサブクラスであり、今回の衝突判定に必要となるいくつかのプロパティが定義されている。
例えば 以下のようなものである。
****XZ という名前のプロパティについて補足する。
下図20は球と直方体を配置したときのものである。球の中心は $C'$、半径は $r$、直方体の中心は $T'$ であり、直方体の上面及び底面の各辺の長さは $w$、$h$ である。また図中の $\boldsymbol{lx'}$、$\boldsymbol{lz'}$ は直方体のローカル座標系 x軸、z軸方向を表す単位ベクトルである。球の中心と直方体の中心は同じ高さにあるが、ここでは $y=3$ の位置にあるものとする。
球の衝突モデルである円盤と直方体の衝突モデルである長方形は同じ平面上($y=3$ の平面上)にあるので、球と直方体を水平方向に適当に動かして衝突させる場合には $y=3$ の平面上において円盤と長方形が衝突する。この $y=3$ の平面はXZ平面に平行であるから、結局 この例において球と直方体の衝突を考えることは、XZ平面上において2つのオブジェクトの衝突モデルである円盤と長方形の衝突を考えることと同じである。
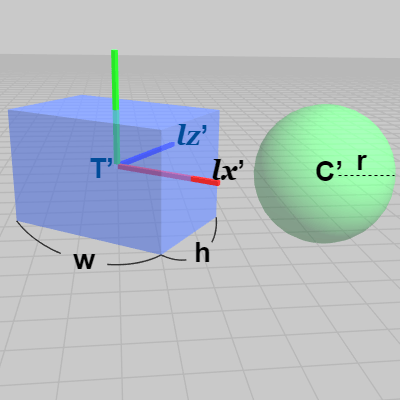
図20 球の中心 C' と直方体の中心 T' は同じ高さ(y=3)にある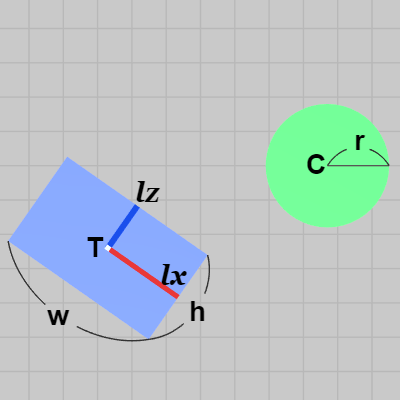 
図21 左図の球と直方体の衝突判定はXZ平面上における円盤と長方形の衝突判定に帰着する
図21は2つのオブジェクトを真上から見下ろしたときのものである。衝突モデルである円盤と長方形は実際には $y=3$ の平面上にあるが、衝突判定をするだけならばXZ平面上に置かれているものとして考えても問題はない。図中における $r$、$w$、$h$ は図20のものと同じであり、$C$、$T$、$\boldsymbol{lx}$、$\boldsymbol{lz}$ は図20の $C'$、$T'$、$\boldsymbol{lx'}$、$\boldsymbol{lz'}$ から y座標を取り除いた'xz座標'である (つまり x座標、z座標のみ)。
上にあげた ****XZ という名前のプロパティは図21における $C$ や $T$、あるいは $\boldsymbol{lx}$、$\boldsymbol{lz}$ などのことである。
具体的にはプログラムでは次のように使用する (プログラム中の Sphere、Box は上例の球、直方体を表すオブジェクトである)。
以下の C、T、lx、lz は上の解説における $C$、$T$、$\boldsymbol{lx}$、$\boldsymbol{lz}$ と同じものである。
実際には上のコードは以下の記述を簡略化したものに過ぎない。
ただし注意すべきは、これらの'xz座標'は上のコードに見られるようにVector2型のプロパティにセットされる点である。例えば上記におけるの場合 Sphereの'xz座標'を C にセットしているが、この C はVector2型なので z座標は存在しない。したがって Sphereの x座標が C.x に、z座標が C.y にセットされることになる。
つまり 今回の衝突判定はXZ平面上における衝突判定を前提としているが、実際の計算はXZ平面ではなくXY平面で行われるということである。XZ平面上の衝突判定をXY平面上の衝突判定として代替することは特に問題はない。それは次のような簡単な理由による。
下図22はXZ平面上において2つの長方形が衝突しているときのものである。2つの長方形はXZ平面上に置かれているので各頂点の座標はいずれも $(x, 0, z)$ という形である。ここでこの2つの長方形の各頂点の y座標と z座標を入れ替えたときのものが右図23である。この入れ替えによって各頂点の座標は $(x, 0, z)$ から $(x, z, 0)$ という形になるが、これは2つの長方形がXY平面上に置かれることを意味する。
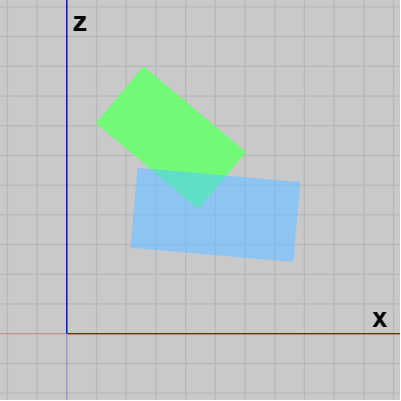
図22 XZ平面における衝突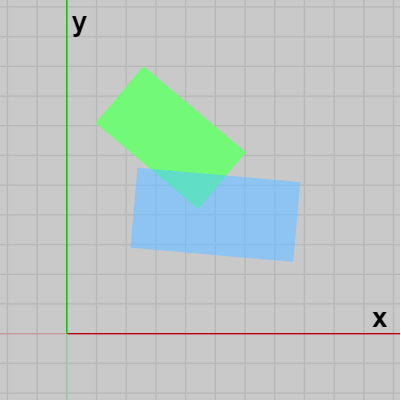 
図23 左図の長方形の各頂点の y座標と z座標を入れ替えると、XY平面における衝突になる
そして図に示されるように y座標と z座標の入れ替えによっても2つの長方形の相対的な位置関係は変わらない。つまり XZ平面上において2つの図形が衝突しているかどうかを調べるには y座標と z座標を入れ替えてXY平面上において衝突判定を行っても同じなのである (図22はXZ平面を y軸プラス側から見たときのもの。図23はXY平面を z軸マイナス側から見たときのもの)。
では実際に上で述べてきたことを実装していこう。
図24 BoxとSphere 
図25 BoxとSphereの衝突モデル
図26 BoxとSphereを真上から見下ろしたとき 
図27 Code1 実行結果 (衝突している場合には両者が赤く表示される)
キー操作は以下のとおり。
H、L : Sphereを x軸方向に移動させる。
J、K : Sphereを z軸方向に移動させる。
R : Boxを(ローカル座標系 y軸周りに)回転させる。
プログラムを以下に示す。
[Code1] (実行結果 図27)
初期化ブロックはSphere、Boxをそれぞれの開始時点での位置に配置するだけであるが、両者の中心位置の高さは同じである ($y=4$)。
このプログラムでは H、J、K、L キーによってSphereを水平方向に動かし(SphereMotion() ; 13行目)、R キーによってBoxをローカル座標系の y軸周りに回転させる(BoxMotion() ; 18行目)。共に y軸方向の移動はないので両者の中心の高さはプログラム実行中常に変わらない。したがって SphereとBoxの衝突は $y = 4$ の平面上において、両者の衝突モデルである円盤と長方形の衝突を調べることに帰着するが、この平面はXZ平面に平行な平面であるから上で述べたようにこの衝突判定は結局はXZ平面上での円盤と長方形の衝突判定を行うことと同じである。
25行目の CollisionTest_Disk_Rect(..) の引数について補足しておこう。このメソッドはメソッド名と引数の順序を除いては 2-20節の CollisionTest_Disk_OBB(..) と同じものである。第1、第2引数は円盤の中心及び半径であり、第3引数以降が長方形に関するデータである。
T は長方形の中心、w は長方形のローカル座標系 x軸方向の辺の長さ、h はローカル座標系 z軸方向の辺の長さであり、lx、lz はローカル座標系の x軸、z軸方向を表す単位ベクトルである。
しかし先程も述べたようにXZ平面の衝突判定を実際にはXY平面上で行うので C や T、lx、ly はVector2型(xy座標)である。
SphereとBoxが衝突している場合は CollisionTest_Disk_Rect(..) がtrueを返すが、26行目の補助メソッド ChangeObjectColor(..)の引数にtrueをセットすると、衝突していることを示すために両者が赤く表示される (図27)。
Standの円盤部分は厚みがあり、正確には円柱を横に寝かせたものであるが、衝突モデルの長方形はこの円盤部分を2等分する断面に相当する (図30の白い長方形)。
図31は今回使用する球体型の弾を表すオブジェクト Shell でありその衝突モデルは円盤である。Shellは図32のオブジェクト Cannon から発射される。
Shellの発射開始位置は、Standの円盤部分の中心と高さが同じになるように設定されている (図33 ; これによってShellの衝突モデルとStandの衝突モデルが同じ平面上に置かれることになる)。
次のプログラムは A キーを押すことでShellをStandの方向へ発射し、ShellをStandに衝突させるものである (Code4まではShellは1つのみであり、Shell発射後に A キーを押すとShellは発射開始位置に戻る。なお ここで使われるStandは1つだけであるが実際にはStandは複数個あり、プログラム中における Stand は要素数 5 の配列である。ここでは Stand[0] のみを使用している)。
[Code2] (実行結果 図34)
プログラム開始時点ではStandの衝突モデルと同じ高さになるようにCannonが配置されている (向きは初期状態と同じく z軸プラス方向)。A キーが押されると1行目のifブロックに入り、Shellを発射開始位置に移動させ(3行目)、Shellの発射方向をセットする(4行目)。c_initShootPosition はCannonの初期状態におけるShellの発射開始位置を表すVector4型定数で、Cannonの場合 発射開始位置は $(0,\ 0,\ 1.15)$ であるが c_initShootPosition を同次座標として使用するためその値は $(0,\ 0,\ 1.15,\ 1)$ である。
Shellは毎フレーム $0.075$ ずつ進んでいき(15行目)、毎フレーム ShellとStandの衝突判定が行われる (本節から4-24節で使用するShellは4-20節と同じく THShell3D クラスのインスタンスであり、position や direction という独自のプロパティを持っている)。
Shellの衝突モデルは円盤であり、Standの衝突モデルは長方形であるため、Code1と同じく今回の衝突判定もXZ平面上における円盤と長方形の衝突判定に帰着する。17~21行目のローカル変数については、C、r が円盤の中心 及び半径、T、w、h が長方形の中心 及びローカル座標系 x軸方向の長さ、z軸方向の長さである (図21)。
CollisionTest_Disk_Rect(..) の第6、第7引数には長方形のローカル座標系の x軸、z軸方向セットするが、今回のStandの衝突モデルの場合はそれは(ワールド座標系の) x軸プラス方向、z軸プラス方向である。しかし、上で述べたように XZ平面の衝突判定を実際にはXY平面上で行うので22行目では第7引数は z軸方向ではなく y軸方向を表す Vector2.up となっている。
図21 XZ平面上における円盤と長方形の衝突判定 
図34 Code2 実行結果
最後にリバウンド(跳ね返り処理)について簡単に説明しよう。衝突が発生した場合 24行目のifブロックに入るが、そこではリバウンドの際の方向と(1フレームあたりの)移動量を表すインスタンス変数 i_reboundVel に値をセットする。その値は 今までShellが進んできた方向とは反対の方向に適当な係数を掛けた値である (26行目)。また 次のフレームからShellがリバウンド状態になることを示すためにプロパティ rebound をtrue にする (27行目)。
リバウンド状態のShellは毎フレーム 8行目のifブロックに入るだけでそれ以降の処理には進まない。そのifブロックではShellの位置を毎フレーム i_reboundVel だけ移動させるだけである。i_reboundVel はこのifブロックでその y成分が減算されていくので、リバウンド状態のShellは実行結果(図34)に見られるようにStandに当たってからは反対の方向に落下していく (次第に落下速度は速くなる)。リバウンド処理とはただこれだけである。
図35 5個のStandを配置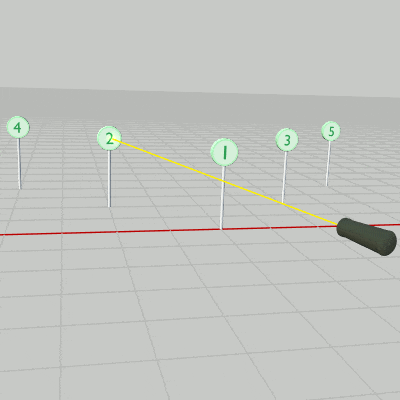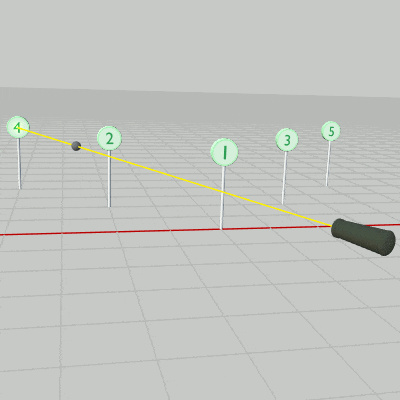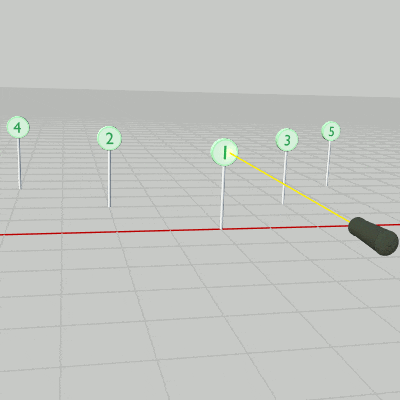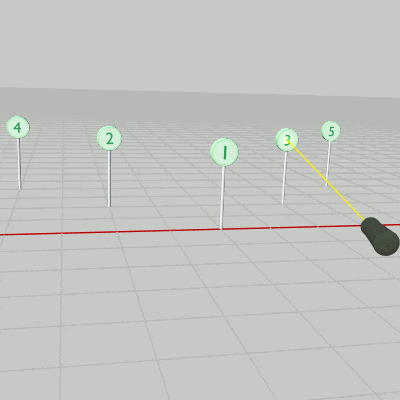 
図36 Code3 実行結果
プログラムは以下のとおり。
今回は H あるいは L キーによってShellの発射方向を変えられるようにしている。
[Code3] (実行結果 図36)
内容は先程のプログラムとほとんど同じである。主な違いとしては、今回はShellの発射方向が変化するために A キーを押した際のifブロックでそれを求める計算(11行目)を毎回行うことと、今回はStandが5個あるため衝突判定の部分がfor文になっており、あるStandとShellの衝突が検出された時点でリバウンド処理に切り替えることぐらいである (プログラム中の Stand は要素数 5 の配列であり、Stand[0]~Stand[4] は1~5の番号の付いたStandに対応する)。
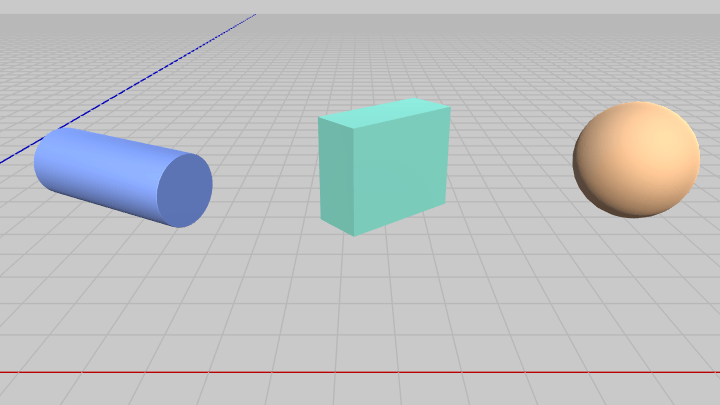
図37 Cylinder、Box、Sphere
それぞれの衝突モデルを以下に示す。今までと同じように各オブジェクトの衝突モデルがすべて同じ高さになるように、オブジェクトは配置されている。また Shellの発射開始位置も同じ高さである。
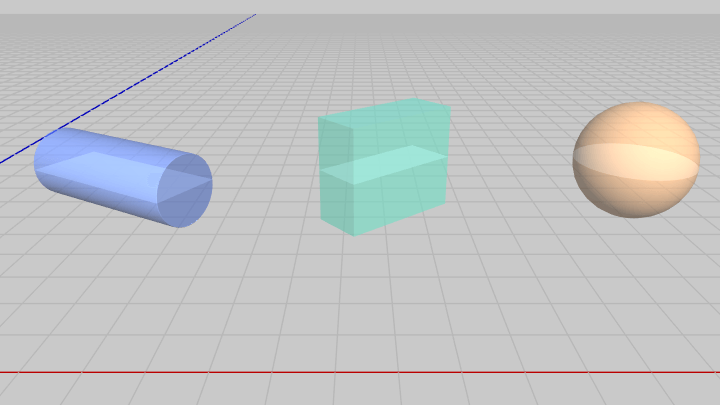
図38 各オブジェクトの衝突モデル (いずれもShellの発射開始位置と同じ高さにある)
プログラムを以下に示す。
[Code4] (実行結果 図39)
初期化ブロックでは今回の衝突対象の3つのオブジェクト Cylinder、Box、Sphere をインスタンス変数 i_targetObjects にセットしている。
プログラム実行中はオブジェクトは適当な運動を繰り返すがそれは14行目の ObjectMotion() に記述されている。
今回のプログラムではオブジェクトの衝突モデルが円盤と長方形の2種類であるため、衝突判定用のforeach文(36行目)では2つの衝突モデルでの場合分けが行われる。
Sphereの場合であれば43行目の「円盤 vs 円盤」用の衝突判定が行われ、CylinderあるいはBoxの場合であれば50行目の「円盤 vs 長方形」用の衝突判定が行われる (「円盤 vs 円盤」用の衝突判定メソッド CollisionTest_Disk_Disk(..) は 2-19節のものと同じである)。
それ以外の箇所については今までのプログラムと同じである。
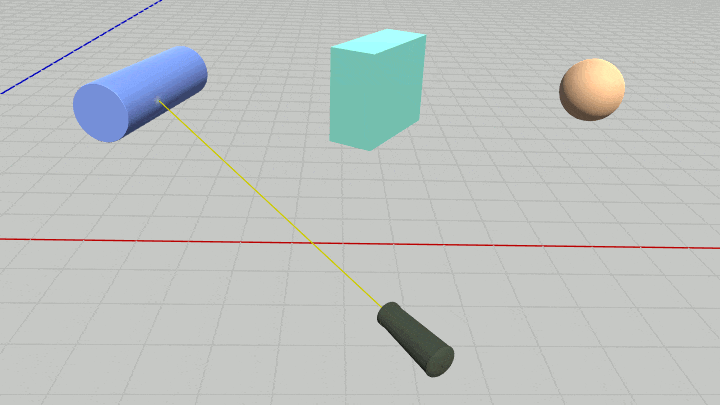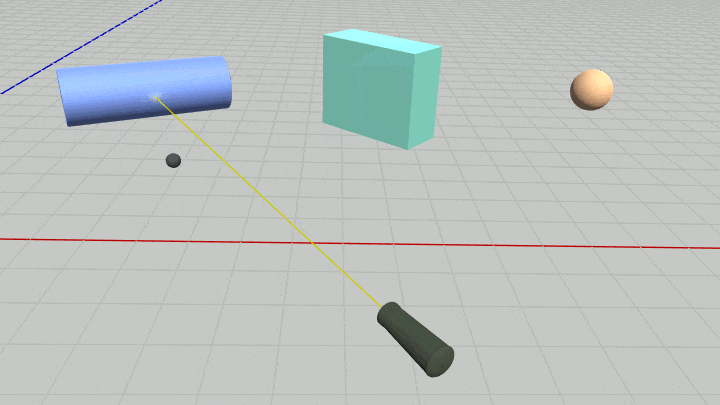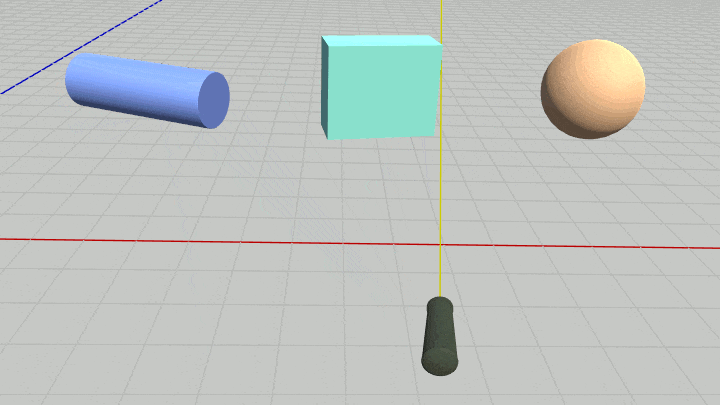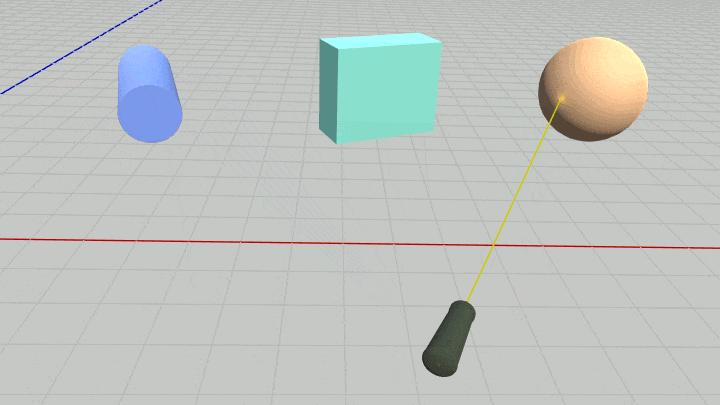
図39 Code4 実行結果
ここでは上記のCode4を連射版に書き換える。
プログラムを以下に示す。
[Code5]
連射の実装自体は 2-11節(あるいは 2-17節)のものと同じである。初期化ブロックは連射用の各プロパティの設定であり、lastShootFrame (int型)はShellを最後に発射したフレーム番号、shootInterval (int型)はShellの発射間隔、shellSpeed (float型)は毎フレームのShellの進行速度、initShootDirection (Vector4型)は初期状態における発射方向、initShootPosition(Vector4型)は初期状態におけるShellの発射開始位置を表す (5、6行目では Vector3 をセットしているが、自動的にその w座標は initShootDirection であれば $0$ が、initShootPosition であれば $1$ がセットされる)。
連射の実装部分は24~67行目であるが、この部分は第2章のコードと同じであるから解説については省略する (41行目のifブロックは飛行中のShellをactiveでないShellにするためのものであり、今回はShellがCannonから距離にして $60$ だけ離れた時点でactiveでないShellにし、適当な位置に移動させている)。
70行目以降の処理は発射された複数のShellのうちで(発射されたShellはプロパティ active がtrueになっている)、いずれかのオブジェクトと衝突しているものがあるかどうかを調べ、あるShellがあるオブジェクトと衝突しているのであればそのオブジェクトを赤く表示し、Shellの方はその時点で非activeにして見えない位置に移動させている (92行目のifブロック ; 今回は衝突時のShellのリバウンド処理は行わず、補助メソッド Hit(..) を実行して単にオブジェクトの色を変化させるだけである)。
先程のCode4では使用するShellは1つだけであったので1つのShellについてだけ衝突判定を行えばよかったが、今回は複数のShell(プログラム中ではUShellという配列として使われている)の1つ1つについて調べる必要があるので70行目のforeach文が追加されている。
ここでは以下の3つのオブジェクト Star、Torus、Crystal を使用する (図41)。
図41 Star、Torus、Crystal
Star、Crystal は上で見たようにその衝突モデルは長方形である。Torusは真上から見た場合には穴の開いた円盤であるが、Shellとの衝突は必ずTorusの外側において起こるので衝突モデルは円盤でも問題はない。これらのオブジェクトの衝突モデルを以下に示す。
図42 各オブジェクトの衝突モデル (いずれもShellの発射開始位置と同じ高さにある)
図43 Code6 実行結果
プログラムは以下のとおり
[Code6] (実行結果 図43)
22行目までは i_targetObjects (9行目)の内容を除いてはCode5と同じである。そして UShellMotion() はCode5の24~67行目をメソッド化したものであり、CollisionTest_ShellPhase(..) はCode5の70行目以降を(わずかな違いを除いて)メソッド化したものである。
具体的には以下のとおり。
[UShellMotion()]
[CollisionTest_ShellPhase(..)]
この UShellMotion(..)、CollisionTest_ShellPhase(..) の2つのメソッドは 4-24節で再び使われる。
ここで扱う衝突判定は3Dオブジェクト同士の衝突判定ではあるが、オブジェクトの運動及び配置については多少の制限がある。具体的には以下の2つである。
(1) オブジェクトが移動する際には水平方向(x軸、z軸方向)のみの移動とし、高さ方向(y軸方向)の移動は行わない。
(2) オブジェクトを配置する際には、オブジェクトの衝突モデルがXZ平面に平行になるように、さらに水平方向の移動によってオブジェクトの衝突モデル同士が必ず衝突するようにオブジェクトを配置する (「オブジェクトの衝突モデル」については後述する)。
(2) オブジェクトを配置する際には、オブジェクトの衝突モデルがXZ平面に平行になるように、さらに水平方向の移動によってオブジェクトの衝突モデル同士が必ず衝突するようにオブジェクトを配置する (「オブジェクトの衝突モデル」については後述する)。
これに関連して今回の衝突判定に使用するアルゴリズムは3Dオブジェクト用の衝突判定アルゴリズムではなく、2Dオブジェクト用のアルゴリズム、すなわち 第2章で学習した平面図形同士の衝突判定アルゴリズムを用いる。
(上記の制限に見られるように本節では「水平方向の移動」という用語を多く用いるが、これは XZ平面に平行な移動を意味する)
まずは簡単な例から見ていこう。
3D空間内に下図に示される2つの球が置かれている。それぞれの球の中心は $C_1$、$C_2$、半径は $r_1$、$r_2$ であり、2つの球の中心の高さは等しい(y座標が同じ)。
ここで適当に両者を動かして衝突させたとする (図2)。上の制限に従って移動の際には y軸方向の移動は行われていないので図3に示されるように、この場合には $C_1$ を中心とする半径 $r_1$ の円盤と $C_2$ を中心とする半径 $r_2$ の円盤が衝突することになる (図中の平面はXZ平面であり、2つの円盤はXZ平面に平行である)。
-
図1 2つの球 (球の中心C1とC2の高さは等しい) -
図2 2つの球の衝突 -
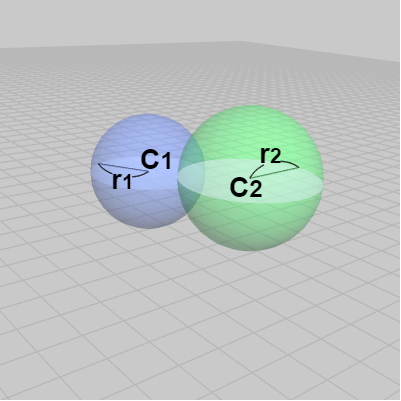図3
このときの状況を真上から見下ろしたときのものが以下の図である (ただし 以下の図では2つの球を簡略化して表示している)。この図に示されるように球を真上から見下ろした場合、その形状は円盤であり、この例でいえば2つの球はそれぞれ中心が $C_1$、$C_2$、半径が $r_1$、$r_2$ の円盤として見ることができる。
したがって この2つの球の衝突は真上から見下ろした場合には、中心 $C_1$、半径 $r_1$ の円盤と中心 $C_2$、半径 $r_2$ の円盤同士の衝突と見ることができる。
また別の例として次の直方体と球の場合を見てみよう。
下図の直方体はその上面と底面がXZ平面に平行であり、図に示されるように上面と底面の各辺の長さは $w$、$h$ である (図6)。また 球の中心は $C$、半径は $r$ であり、ここでも直方体の中心と球の中心の高さは同じ位置にある。
図7は両者を適当に動かして衝突させたときのものである。ここでも y軸方向の移動は行われていないので衝突時においても直方体の中心と球の中心は同じ高さにある。したがって 直方体の中心を $T$ とすれば、この衝突では図8に示されるように $T$ を中心とする各辺の長さ $w$、$h$ の長方形と $C$ を中心とする半径 $r$ の円盤が衝突することになる。
-
図6 直方体と球 -
図7 直方体と球の衝突 -
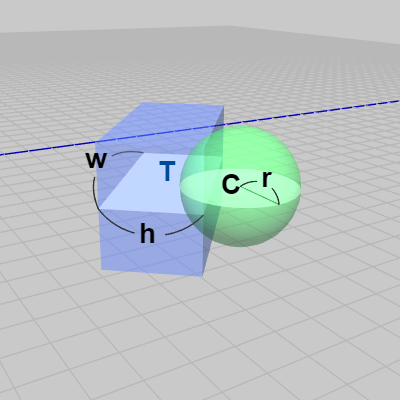図8
この場合にも直方体及び球を真上から見ると、直方体は中心 $T$、各辺の長さが $w$、$h$ の長方形であり、球は中心 $C$、半径 $r$ の円盤である。したがって この直方体と球の衝突は真上から見下ろした場合には、長方形と円盤の衝突として見ることができるわけである。
上の例に示されるように、3Dオブジェクト同士の衝突判定も適当な制限のもとでは2つの平面図形の衝突判定として扱うことができる。以下3節で行われる衝突判定は全てこのパターンである。つまり 冒頭に述べた制限のもとで、3Dオブジェクト同士が衝突しているかどうかを2つの平面図形の衝突判定を通して調べるものである。
そのため、今回の衝突判定では各3Dオブジェクトには衝突判定用の平面図形が用いられるが、各オブジェクトに用いられるこの平面図形のことを以降「衝突モデル」と呼ぶことにする。
例えば上の例における球の衝突モデルは円盤であり、直方体の衝突モデルは長方形である。また上の制限にもあるようにオブジェクトの衝突モデルはXZ平面に平行である (そうなるようにオブジェクトは配置されている)。
上記の2つの球の衝突の例では2つの球の中心は同じ高さに配置されていた。そのため 2つの球が衝突する場合には上図3に示されるように2つの球の衝突モデルである中心 $C_1$、半径 $r_1$ の円盤と中心 $C_2$、半径 $r_2$ の円盤も必ず衝突することになる。
しかし、下図11のように2つの球の中心が異なる高さで配置されている場合にはこのようにはいかない。
図11の2つの球を水平方向に動かして下図12の状態になったとしよう。図12では明らかに両者は衝突していないが、この状況を真上から見下ろした場合には2つの円盤が重なっているように見えてしまう (図13)。つまり、この状況において2つの球の衝突モデルである図13の青い円盤と緑の円盤の衝突判定を行うと2つの円盤の衝突が検出されるが、それは正しい判定ではない。
-
図11 -
図12 -
図13 左図12の状況を真上から見下ろしたとき。真上から見下ろした場合には衝突モデルの円盤同士が衝突しているように見えるが、実際には衝突していない。
今回の衝突判定は3Dオブジェクトの衝突モデル(平面図形)を用いた衝突判定であり、平面図形同士の衝突判定で衝突が検出されたならば3Dオブジェクト同士が衝突していなければならない。そのためにオブジェクトが衝突する際は、両者の衝突モデル同士が必ず衝突するようにあらかじめオブジェクトを配置しておく必要があるのである。
そのようにオブジェクトを配置することは難しくはない。基本的には各オブジェクトの衝突モデルが同じ高さに、すなわち同じ平面上に置かれるようにすればよいだけである。例えば下図14の星型オブジェクト Star と8面体オブジェクト Crystal の場合であれば、両者は真上から見下ろした場合には図15に示されるようにともに長方形である (Crystalは正確には正方形)。
したがってこの2つのオブジェクトの衝突モデルは長方形であるが(図16)、この2つのオブジェクトを3D空間内に配置する際には両者の衝突モデルである長方形が同じ平面上に含まれるように両者を配置する、具体的にはそれはCrystalとStarの衝突モデルの長方形が同じ高さに来るようにすればよい (図17 ; ただしここでは衝突モデルの長方形がXZ平面に平行になるようにオブジェクトが置かれていることを前提としている)。
2つのオブジェクトの衝突モデルが同じ平面上にあれば、水平方向に適当に平行移動させることによりオブジェクト同士が衝突するが(図18)、その際には必ず衝突モデルも衝突することになる (図19)。
本節から 4-24節の衝突判定で使われるオブジェクトのほとんどはカスタムライブラリーの THAlphaObject3D クラスのインスタンスである。このクラスは今まで使用してきた THObject3D クラスのサブクラスであり、今回の衝突判定に必要となるいくつかのプロパティが定義されている。
例えば 以下のようなものである。
type
: 衝突モデルのタイプ (円盤か長方形のいずれか)。radius
: 衝突モデルが円盤である場合、その半径 (float型)。width, height
: 衝突モデルが長方形である場合、各辺はそのオブジェクトのローカル座標系の x軸、z軸に平行であるが、width はローカル座標系の x軸に平行な辺の長さであり、height はローカル座標系の z軸に平行な辺の長さ (float型)。positionXZ
: 衝突モデルの中心位置の x座標、z座標がセットされたVector2型プロパティ (衝突モデルが円盤であっても長方形であってもこのプロパティにはその中心位置がセットされる)。rectVertsXZ
: 衝突モデルが長方形である場合、現時点におけるその長方形の4頂点の座標がセットされたプロパティ。このプロパティは要素数 4 のVector2[]型であり、配列の各要素には長方形の頂点座標がセットされるが、それらの頂点座標は具体的には x座標、z座標のみを含んだVector2型である (詳しくは次節を参照)。localAxisXZ
: 衝突モデルが長方形である場合、現時点におけるその長方形のローカル座標系の x軸方向、z軸方向がセットされたVector2[]型プロパティ。****XZ という名前のプロパティについて補足する。
下図20は球と直方体を配置したときのものである。球の中心は $C'$、半径は $r$、直方体の中心は $T'$ であり、直方体の上面及び底面の各辺の長さは $w$、$h$ である。また図中の $\boldsymbol{lx'}$、$\boldsymbol{lz'}$ は直方体のローカル座標系 x軸、z軸方向を表す単位ベクトルである。球の中心と直方体の中心は同じ高さにあるが、ここでは $y=3$ の位置にあるものとする。
球の衝突モデルである円盤と直方体の衝突モデルである長方形は同じ平面上($y=3$ の平面上)にあるので、球と直方体を水平方向に適当に動かして衝突させる場合には $y=3$ の平面上において円盤と長方形が衝突する。この $y=3$ の平面はXZ平面に平行であるから、結局 この例において球と直方体の衝突を考えることは、XZ平面上において2つのオブジェクトの衝突モデルである円盤と長方形の衝突を考えることと同じである。
図21は2つのオブジェクトを真上から見下ろしたときのものである。衝突モデルである円盤と長方形は実際には $y=3$ の平面上にあるが、衝突判定をするだけならばXZ平面上に置かれているものとして考えても問題はない。図中における $r$、$w$、$h$ は図20のものと同じであり、$C$、$T$、$\boldsymbol{lx}$、$\boldsymbol{lz}$ は図20の $C'$、$T'$、$\boldsymbol{lx'}$、$\boldsymbol{lz'}$ から y座標を取り除いた'xz座標'である (つまり x座標、z座標のみ)。
上にあげた ****XZ という名前のプロパティは図21における $C$ や $T$、あるいは $\boldsymbol{lx}$、$\boldsymbol{lz}$ などのことである。
具体的にはプログラムでは次のように使用する (プログラム中の Sphere、Box は上例の球、直方体を表すオブジェクトである)。
以下の C、T、lx、lz は上の解説における $C$、$T$、$\boldsymbol{lx}$、$\boldsymbol{lz}$ と同じものである。
Vector2 C = Sphere.positionXZ; Vector2 T = Box.positionXZ; Vector2 lx = Box.localAxisXZ[0]; Vector2 lz = Box.localAxisXZ[1];
実際には上のコードは以下の記述を簡略化したものに過ぎない。
Vector3 pos = Sphere.GetWorldPosition(); Vector2 C = new Vector2(pos.x, pos.z); pos = Box.GetWorldPosition(); Vector2 T = new Vector2(pos.x, pos.z); Matrix4x4 M = Box.GetMatrix(); Vector3 c0 = M.GetColumn(0); Vector3 c2 = M.GetColumn(2); Vector2 lx = new Vector2(c0.x, c0.z).normalized; Vector2 lz = new Vector2(c2.x, c2.z).normalized;
ただし注意すべきは、これらの'xz座標'は上のコードに見られるようにVector2型のプロパティにセットされる点である。例えば上記における
Vector2 C = Sphere.positionXZ;
つまり 今回の衝突判定はXZ平面上における衝突判定を前提としているが、実際の計算はXZ平面ではなくXY平面で行われるということである。XZ平面上の衝突判定をXY平面上の衝突判定として代替することは特に問題はない。それは次のような簡単な理由による。
下図22はXZ平面上において2つの長方形が衝突しているときのものである。2つの長方形はXZ平面上に置かれているので各頂点の座標はいずれも $(x, 0, z)$ という形である。ここでこの2つの長方形の各頂点の y座標と z座標を入れ替えたときのものが右図23である。この入れ替えによって各頂点の座標は $(x, 0, z)$ から $(x, z, 0)$ という形になるが、これは2つの長方形がXY平面上に置かれることを意味する。
そして図に示されるように y座標と z座標の入れ替えによっても2つの長方形の相対的な位置関係は変わらない。つまり XZ平面上において2つの図形が衝突しているかどうかを調べるには y座標と z座標を入れ替えてXY平面上において衝突判定を行っても同じなのである (図22はXZ平面を y軸プラス側から見たときのもの。図23はXY平面を z軸マイナス側から見たときのもの)。
では実際に上で述べてきたことを実装していこう。
# Code1
まずは直方体オブジェクト Box 球体オブジェクト Sphere のケースである。適当なキー操作によって両者を動かし、2つのオブジェクトを衝突させる。 キー操作は以下のとおり。
H、L : Sphereを x軸方向に移動させる。
J、K : Sphereを z軸方向に移動させる。
R : Boxを(ローカル座標系 y軸周りに)回転させる。
プログラムを以下に示す。
[Code1] (実行結果 図27)
if (!i_INITIALIZED)
{
Sphere.SetWorldPosition(12, 4, 0);
Box.SetWorldPosition(12, 4, 6);
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.J) ||
Input.GetKey(KeyCode.K) || Input.GetKey(KeyCode.L))
{
SphereMotion();
}
if (Input.GetKey(KeyCode.R))
{
BoxMotion();
}
Vector2 C = Sphere.positionXZ;
Vector2 T = Box.positionXZ;
Vector2 lx = Box.localAxisXZ[0];
Vector2 lz = Box.localAxisXZ[1];
bool bColl = CollisionTest_Disk_Rect(C, Sphere.radius, T, Box.width, Box.height, lx, lz);
ChangeObjectColor(bColl);
初期化ブロックはSphere、Boxをそれぞれの開始時点での位置に配置するだけであるが、両者の中心位置の高さは同じである ($y=4$)。
このプログラムでは H、J、K、L キーによってSphereを水平方向に動かし(SphereMotion() ; 13行目)、R キーによってBoxをローカル座標系の y軸周りに回転させる(BoxMotion() ; 18行目)。共に y軸方向の移動はないので両者の中心の高さはプログラム実行中常に変わらない。したがって SphereとBoxの衝突は $y = 4$ の平面上において、両者の衝突モデルである円盤と長方形の衝突を調べることに帰着するが、この平面はXZ平面に平行な平面であるから上で述べたようにこの衝突判定は結局はXZ平面上での円盤と長方形の衝突判定を行うことと同じである。
25行目の CollisionTest_Disk_Rect(..) の引数について補足しておこう。このメソッドはメソッド名と引数の順序を除いては 2-20節の CollisionTest_Disk_OBB(..) と同じものである。第1、第2引数は円盤の中心及び半径であり、第3引数以降が長方形に関するデータである。
bool CollisionTest_Disk_Rect(Vector2 C, float r,
Vector2 T, float w, float h, Vector2 lx, Vector2 lz)
しかし先程も述べたようにXZ平面の衝突判定を実際にはXY平面上で行うので C や T、lx、ly はVector2型(xy座標)である。
SphereとBoxが衝突している場合は CollisionTest_Disk_Rect(..) がtrueを返すが、26行目の補助メソッド ChangeObjectColor(..)の引数にtrueをセットすると、衝突していることを示すために両者が赤く表示される (図27)。
# Code2
続いて下図28のオブジェクト Stand に対して球体型の弾を当てて、簡単なリバウンド(跳ね返り処理)を実装する。Standは数字の付いた円盤部分と細長いポール部分で構成されている。図29はStandを真上から見下ろしたときのものであるが、真上から見た場合にはStandは長方形であるためStandの衝突モデルも長方形である (各辺は x軸、z軸に平行)。Standの円盤部分は厚みがあり、正確には円柱を横に寝かせたものであるが、衝突モデルの長方形はこの円盤部分を2等分する断面に相当する (図30の白い長方形)。
-
図28 Stand 初期状態 -
図29 Standを真上から見下ろしたとき (各辺が x軸、z軸に平行な長方形) -
図30 衝突モデルの長方形は円盤部分を2等分する断面に相当する
図31は今回使用する球体型の弾を表すオブジェクト Shell でありその衝突モデルは円盤である。Shellは図32のオブジェクト Cannon から発射される。
Shellの発射開始位置は、Standの円盤部分の中心と高さが同じになるように設定されている (図33 ; これによってShellの衝突モデルとStandの衝突モデルが同じ平面上に置かれることになる)。
-
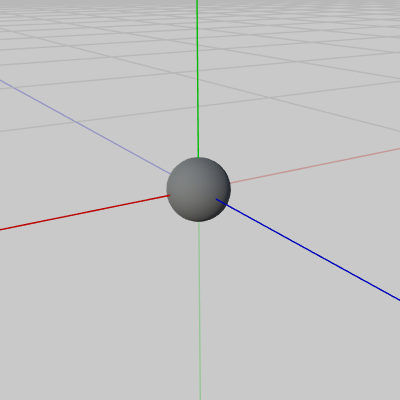図31 Shell 初期状態 -
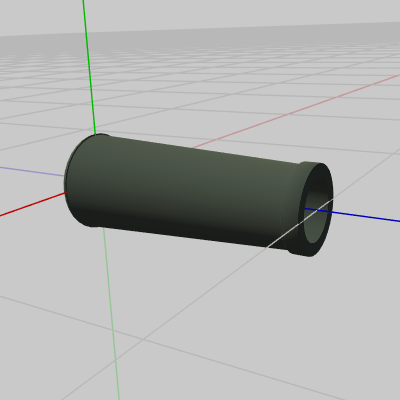図32 Cannon 初期状態 -
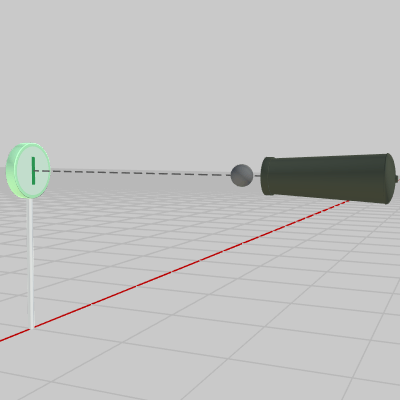図33 ShellとStandの衝突モデルが同じ高さになるように配置されている
次のプログラムは A キーを押すことでShellをStandの方向へ発射し、ShellをStandに衝突させるものである (Code4まではShellは1つのみであり、Shell発射後に A キーを押すとShellは発射開始位置に戻る。なお ここで使われるStandは1つだけであるが実際にはStandは複数個あり、プログラム中における Stand は要素数 5 の配列である。ここでは Stand[0] のみを使用している)。
[Code2] (実行結果 図34)
if (Input.GetKeyDown(KeyCode.A))
{
Shell.position = Cannon.GetMatrix() * c_initShootPosition;
Shell.direction = Vector3.forward;
Shell.rebound = false;
}
if (Shell.rebound)
{
i_reboundVel.y -= 0.002f;
Shell.position += i_reboundVel;
return;
}
Shell.position += 0.075f * Shell.direction;
Vector2 C = new Vector2(Shell.position.x, Shell.position.z);
float r = i_radShell;
Vector2 T = Stand[0].positionXZ;
float w = Stand[0].width;
float h = Stand[0].height;
bool bColl = CollisionTest_Disk_Rect(C, r, T, w, h, Vector2.right, Vector2.up);
if (bColl)
{
i_reboundVel = -0.016f * Shell.direction;
Shell.rebound = true;
}
プログラム開始時点ではStandの衝突モデルと同じ高さになるようにCannonが配置されている (向きは初期状態と同じく z軸プラス方向)。A キーが押されると1行目のifブロックに入り、Shellを発射開始位置に移動させ(3行目)、Shellの発射方向をセットする(4行目)。c_initShootPosition はCannonの初期状態におけるShellの発射開始位置を表すVector4型定数で、Cannonの場合 発射開始位置は $(0,\ 0,\ 1.15)$ であるが c_initShootPosition を同次座標として使用するためその値は $(0,\ 0,\ 1.15,\ 1)$ である。
Shellは毎フレーム $0.075$ ずつ進んでいき(15行目)、毎フレーム ShellとStandの衝突判定が行われる (本節から4-24節で使用するShellは4-20節と同じく THShell3D クラスのインスタンスであり、position や direction という独自のプロパティを持っている)。
Shellの衝突モデルは円盤であり、Standの衝突モデルは長方形であるため、Code1と同じく今回の衝突判定もXZ平面上における円盤と長方形の衝突判定に帰着する。17~21行目のローカル変数については、C、r が円盤の中心 及び半径、T、w、h が長方形の中心 及びローカル座標系 x軸方向の長さ、z軸方向の長さである (図21)。
CollisionTest_Disk_Rect(..) の第6、第7引数には長方形のローカル座標系の x軸、z軸方向セットするが、今回のStandの衝突モデルの場合はそれは(ワールド座標系の) x軸プラス方向、z軸プラス方向である。しかし、上で述べたように XZ平面の衝突判定を実際にはXY平面上で行うので22行目では第7引数は z軸方向ではなく y軸方向を表す Vector2.up となっている。
最後にリバウンド(跳ね返り処理)について簡単に説明しよう。衝突が発生した場合 24行目のifブロックに入るが、そこではリバウンドの際の方向と(1フレームあたりの)移動量を表すインスタンス変数 i_reboundVel に値をセットする。その値は 今までShellが進んできた方向とは反対の方向に適当な係数を掛けた値である (26行目)。また 次のフレームからShellがリバウンド状態になることを示すためにプロパティ rebound をtrue にする (27行目)。
リバウンド状態のShellは毎フレーム 8行目のifブロックに入るだけでそれ以降の処理には進まない。そのifブロックではShellの位置を毎フレーム i_reboundVel だけ移動させるだけである。i_reboundVel はこのifブロックでその y成分が減算されていくので、リバウンド状態のShellは実行結果(図34)に見られるようにStandに当たってからは反対の方向に落下していく (次第に落下速度は速くなる)。リバウンド処理とはただこれだけである。
# Code3
続いては上記のオブジェクトStandを5個にした場合である (図35)。各Standは適当な間隔で配置されており、どのStandも向きは変えていないのでその衝突モデルはCode2と同じく x軸、z軸に平行な長方形である。 プログラムは以下のとおり。
今回は H あるいは L キーによってShellの発射方向を変えられるようにしている。
[Code3] (実行結果 図36)
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.L))
{
ChangeDirection();
}
if (Input.GetKeyDown(KeyCode.A))
{
Matrix4x4 M = Cannon.GetMatrix();
Shell.position = M * c_initShootPosition;
Shell.direction = M * Vector3.forward;
Shell.rebound = false;
}
if (Shell.rebound)
{
i_reboundVel.y -= 0.002f;
Shell.position += i_reboundVel;
return;
}
Shell.position += 0.15f * Shell.direction;
Vector2 C = new Vector2(Shell.position.x, Shell.position.z);
float r = i_radShell;
float w = Stand[0].width;
float h = Stand[0].height;
for (int i = 0; i < Stand.Length; i++)
{
Vector2 T = Stand[i].positionXZ;
bool bColl = CollisionTest_Disk_Rect(C, r, T, w, h, Vector2.right, Vector2.up);
if (bColl)
{
i_reboundVel = -0.025f * Shell.direction;
Shell.rebound = true;
break;
}
}
内容は先程のプログラムとほとんど同じである。主な違いとしては、今回はShellの発射方向が変化するために A キーを押した際のifブロックでそれを求める計算(11行目)を毎回行うことと、今回はStandが5個あるため衝突判定の部分がfor文になっており、あるStandとShellの衝突が検出された時点でリバウンド処理に切り替えることぐらいである (プログラム中の Stand は要素数 5 の配列であり、Stand[0]~Stand[4] は1~5の番号の付いたStandに対応する)。
# Code4
続いては以下の3つのオブジェクト Cylinder、Box、Sphere を使用する (図37)。 それぞれの衝突モデルを以下に示す。今までと同じように各オブジェクトの衝突モデルがすべて同じ高さになるように、オブジェクトは配置されている。また Shellの発射開始位置も同じ高さである。
プログラムを以下に示す。
[Code4] (実行結果 図39)
if (!i_INITIALIZED)
{
i_targetObjects = new THAlphaObject3D[] { Cylinder, Box, Sphere };
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.L))
{
ChangeDirection();
}
ObjectMotion();
if (Input.GetKeyDown(KeyCode.A))
{
Matrix4x4 M = Cannon.GetMatrix();
Shell.position = M * c_initShootPosition;
Shell.direction = M * Vector3.forward;
Shell.rebound = false;
}
if (Shell.rebound)
{
i_reboundVel.y -= 0.002f;
Shell.position += i_reboundVel;
return;
}
Shell.position += 0.18f * Shell.direction;
Vector2 C = new Vector2(Shell.position.x, Shell.position.z);
float r = i_radShell;
foreach (var target in i_targetObjects)
{
Vector2 T = target.positionXZ;
bool bColl = false;
if (target.type == c_DISK)
{
bColl = CollisionTest_Disk_Disk(C, r, T, target.radius);
}
else if (target.type == c_RECT)
{
Vector2 lx = target.localAxisXZ[0];
Vector2 lz = target.localAxisXZ[1];
bColl = CollisionTest_Disk_Rect(C, r, T, target.width, target.height, lx, lz);
}
if (bColl)
{
i_reboundVel = -0.025f * Shell.direction;
Shell.rebound = true;
break;
}
}
初期化ブロックでは今回の衝突対象の3つのオブジェクト Cylinder、Box、Sphere をインスタンス変数 i_targetObjects にセットしている。
プログラム実行中はオブジェクトは適当な運動を繰り返すがそれは14行目の ObjectMotion() に記述されている。
今回のプログラムではオブジェクトの衝突モデルが円盤と長方形の2種類であるため、衝突判定用のforeach文(36行目)では2つの衝突モデルでの場合分けが行われる。
Sphereの場合であれば43行目の「円盤 vs 円盤」用の衝突判定が行われ、CylinderあるいはBoxの場合であれば50行目の「円盤 vs 長方形」用の衝突判定が行われる (「円盤 vs 円盤」用の衝突判定メソッド CollisionTest_Disk_Disk(..) は 2-19節のものと同じである)。
それ以外の箇所については今までのプログラムと同じである。
# Code5
以降のプログラムではShellの発射を連射として実装する。ここでは上記のCode4を連射版に書き換える。
プログラムを以下に示す。
[Code5]
if (!i_INITIALIZED)
{
Cannon.lastShootFrame = 0;
Cannon.shootInterval = 40;
Cannon.initShootDirection = Vector3.forward;
Cannon.initShootPosition = new Vector3(0.0f, 0.0f, 1.15f);
Cannon.shellSpeed = 0.2f;
i_targetObjects = new THAlphaObject3D[] { Cylinder, Box, Sphere };
i_frameCount = 0;
i_INITIALIZED = true;
}
i_frameCount++;
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.L))
{
ChangeDirection();
}
ObjectMotion();
bool bShoot = false;
if (Input.GetKey(KeyCode.A))
{
if (i_frameCount >= Cannon.lastShootFrame + Cannon.shootInterval)
{
Cannon.lastShootFrame = i_frameCount;
bShoot = true;
}
}
Vector3 posCannon = Cannon.GetWorldPosition();
foreach (var shell in UShell)
{
if (shell.active)
{
Vector3 newShellPos = shell.position + shell.speed * shell.direction;
if ((newShellPos - posCannon).magnitude >= 60.0f)
{
shell.active = false;
newShellPos = new Vector3(-1000, 0, 0);
}
shell.position = newShellPos;
}
else
{
if (bShoot)
{
Matrix4x4 M = Cannon.GetMatrix();
Vector3 startPos = M * Cannon.initShootPosition;
Vector3 shootDir = M * Cannon.initShootDirection;
shell.active = true;
shell.direction = shootDir.normalized;
shell.speed = Cannon.shellSpeed;
shell.position = startPos;
bShoot = false;
}
}
}
foreach (var shell in UShell)
{
if (!shell.active) { continue; }
Vector2 posShell = new Vector2(shell.position.x, shell.position.z);
foreach (var target in i_targetObjects)
{
Vector2 posTarget = target.positionXZ;
bool bColl = false;
if (target.type == c_DISK)
{
bColl = CollisionTest_Disk_Disk(posShell, i_radShell, posTarget, target.radius);
}
else if (target.type == c_RECT)
{
Vector2 lx = target.localAxisXZ[0];
Vector2 lz = target.localAxisXZ[1];
bColl = CollisionTest_Disk_Rect(posShell, i_radShell, posTarget, target.width, target.height, lx, lz);
}
if (bColl)
{
Hit(target);
shell.SetWorldPosition(-1000, 0, 0);
shell.active = false;
}
}
}
連射の実装自体は 2-11節(あるいは 2-17節)のものと同じである。初期化ブロックは連射用の各プロパティの設定であり、lastShootFrame (int型)はShellを最後に発射したフレーム番号、shootInterval (int型)はShellの発射間隔、shellSpeed (float型)は毎フレームのShellの進行速度、initShootDirection (Vector4型)は初期状態における発射方向、initShootPosition(Vector4型)は初期状態におけるShellの発射開始位置を表す (5、6行目では Vector3 をセットしているが、自動的にその w座標は initShootDirection であれば $0$ が、initShootPosition であれば $1$ がセットされる)。
連射の実装部分は24~67行目であるが、この部分は第2章のコードと同じであるから解説については省略する (41行目のifブロックは飛行中のShellをactiveでないShellにするためのものであり、今回はShellがCannonから距離にして $60$ だけ離れた時点でactiveでないShellにし、適当な位置に移動させている)。
70行目以降の処理は発射された複数のShellのうちで(発射されたShellはプロパティ active がtrueになっている)、いずれかのオブジェクトと衝突しているものがあるかどうかを調べ、あるShellがあるオブジェクトと衝突しているのであればそのオブジェクトを赤く表示し、Shellの方はその時点で非activeにして見えない位置に移動させている (92行目のifブロック ; 今回は衝突時のShellのリバウンド処理は行わず、補助メソッド Hit(..) を実行して単にオブジェクトの色を変化させるだけである)。
先程のCode4では使用するShellは1つだけであったので1つのShellについてだけ衝突判定を行えばよかったが、今回は複数のShell(プログラム中ではUShellという配列として使われている)の1つ1つについて調べる必要があるので70行目のforeach文が追加されている。
# Code6
では最後にCode5で使用した連射処理をメソッドとして独立させ、プログラムを簡潔に書き改めよう。ここでは以下の3つのオブジェクト Star、Torus、Crystal を使用する (図41)。
Star、Crystal は上で見たようにその衝突モデルは長方形である。Torusは真上から見た場合には穴の開いた円盤であるが、Shellとの衝突は必ずTorusの外側において起こるので衝突モデルは円盤でも問題はない。これらのオブジェクトの衝突モデルを以下に示す。
プログラムは以下のとおり
[Code6] (実行結果 図43)
if (!i_INITIALIZED)
{
Cannon.lastShootFrame = 0;
Cannon.shootInterval = 40;
Cannon.initShootDirection = Vector3.forward;
Cannon.initShootPosition = new Vector3(0.0f, 0.0f, 1.15f);
Cannon.shellSpeed = 0.2f;
i_targetObjects = new THAlphaObject3D[] { Star, Torus, Crystal };
i_frameCount = 0;
i_INITIALIZED = true;
}
i_frameCount++;
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.L))
{
ChangeDirection();
}
ObjectMotion();
UShellMotion();
CollisionTest_ShellPhase(UShell, i_targetObjects);
22行目までは i_targetObjects (9行目)の内容を除いてはCode5と同じである。そして UShellMotion() はCode5の24~67行目をメソッド化したものであり、CollisionTest_ShellPhase(..) はCode5の70行目以降を(わずかな違いを除いて)メソッド化したものである。
具体的には以下のとおり。
[UShellMotion()]
void UShellMotion()
{
bool bShoot = false;
if (Input.GetKey(KeyCode.A))
{
if (i_frameCount >= Cannon.lastShootFrame + Cannon.shootInterval)
{
Cannon.lastShootFrame = i_frameCount;
bShoot = true;
}
}
Vector3 posCannon = Cannon.GetWorldPosition();
foreach (var shell in UShell)
{
if (shell.active)
{
Vector3 newShellPos = shell.position + shell.speed * shell.direction;
if ((newShellPos - posCannon).magnitude >= 60.0f)
{
shell.active = false;
newShellPos = new Vector3(-1000, 0, 0);
}
shell.position = newShellPos;
}
else
{
if (bShoot)
{
Matrix4x4 M = Cannon.GetMatrix();
Vector3 startPos = M * Cannon.initShootPosition;
Vector3 shootDir = M * Cannon.initShootDirection;
shell.active = true;
shell.direction = shootDir.normalized;
shell.speed = Cannon.shellSpeed;
shell.position = startPos;
bShoot = false;
}
}
}
}
[CollisionTest_ShellPhase(..)]
void CollisionTest_ShellPhase(THShell3D[] shell_array, THAlphaObject3D[] target_array)
{
foreach (var shell in shell_array)
{
if (!shell.active) { continue; }
Vector2 posShell = new Vector2(shell.position.x, shell.position.z);
foreach (var target in target_array)
{
Vector2 posTarget = target.positionXZ;
bool bColl = false;
if (target.type == c_DISK)
{
bColl = CollisionTest_Disk_Disk(posShell, i_radShell, posTarget, target.radius);
}
else if (target.type == c_RECT)
{
Vector2 lx = target.localAxisXZ[0];
Vector2 lz = target.localAxisXZ[1];
bColl = CollisionTest_Disk_Rect(posShell, i_radShell, posTarget, target.width, target.height, lx, lz);
}
if (bColl)
{
Hit(target);
shell.SetWorldPosition(-1000, 0, 0);
shell.active = false;
}
} // shell_array
} // target_array
}
この UShellMotion(..)、CollisionTest_ShellPhase(..) の2つのメソッドは 4-24節で再び使われる。
© 2020-2024 Redpoll's 60 (All rights reserved)