Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-2
第4章 3D空間におけるオブジェクトの運動
$§$4-2 一体化したオブジェクトの運動 1
本節からは第2章と同様に複数のオブジェクトを階層的に構成し、それらを一体化して運動させるプログラムを実装する。
今回はプロペラの付いた飛行機の運動を扱う。
使用するオブジェクトは以下のBody(図1)、Propeller(図2)の2つであり、図に示されるようにそれぞれ初期状態ではz軸プラス方向を向いている (Propellerではz軸がその中心を貫いている)。
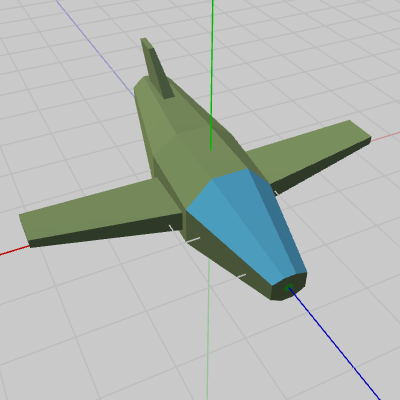
図1 Body 初期状態 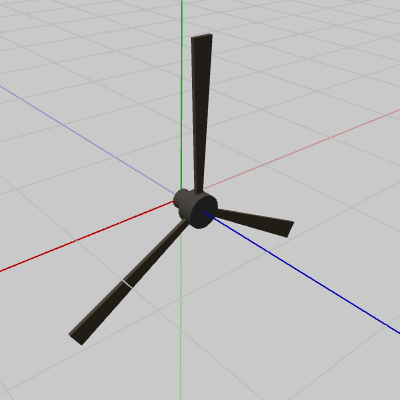
図2 Propeller 初期状態
次のプログラムは、PropellerをBodyの指定位置に移動させるだけの処理である。第2章で使用した用語を使えば、PropellerをBodyにアタッチするだけの処理である(2-5節参照)。ここでいう「Bodyの指定位置」とはBodyの先端部分のことで、プログラム内では1行目の定数c_attachPos_Propellerによって表されている。Bodyは初期状態のままでよいので、Bodyに実行する行列は identity行列になる。
[Beta1] (実行結果 図3)
第2章と同様に、ここからはオブジェクトに実行する行列にはlocalやworldといった単語が先頭に付く。これが何を意味するについては4-8節から4-11節で解説する(上記の場合は単に形式的な意味しか持たない)。
では実際にPropellerを回転させてみよう。プログラムは以下のようになる。
[Code1] (実行結果 図4)
1行目の i_degPropeller は Propellerの(そのフレームにおける)回転角度を表すint型インスタンス変数である。このプログラムでは毎フレーム$15$ずつ増加するので、Propellerは毎フレーム$15$°ずつ回転することになる。
2行目のrotPropは、Propellerを角度i_degPropellerだけz軸周りに回転させるための行列である。Vector3.forward はUnityに標準で用意されている定数で、z軸のプラス方向である$(0, 0, 1)$を表す。3行目のtraPropは、Propellerをアタッチポジション(ここでは Bodyの先端)にアタッチするための平行移動行列である。
4行目の localPropeller = traProp * rotProp は、まず Propellerを初期状態の位置でz軸周りにi_degPropellerだけ回転させ(rotProp)、次にアタッチポジションに移動させる(traProp)という2つの処理をまとめたものである。具体的には、Propellerを(初期状態の位置である)原点でi_degPropellerだけ回転させて、回転させた状態で Bodyの先端に移動させるという処理を毎フレーム行っているのである。
6行目以降は、Beta1の2行目以降と同じである。
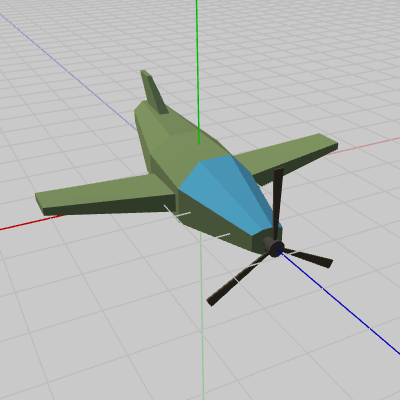
図3 Beta1 実行結果 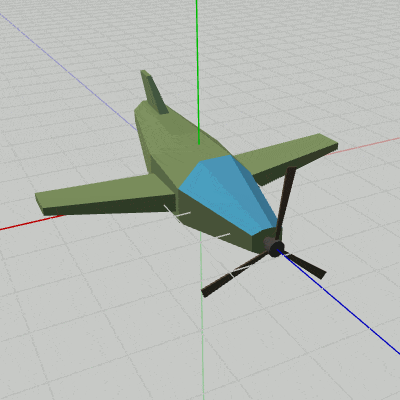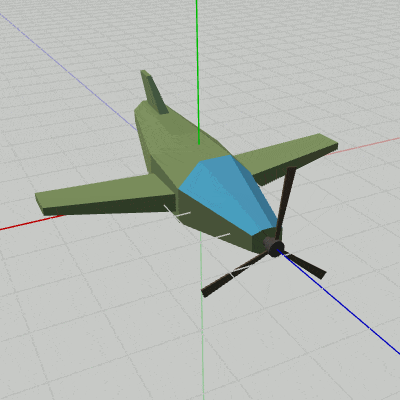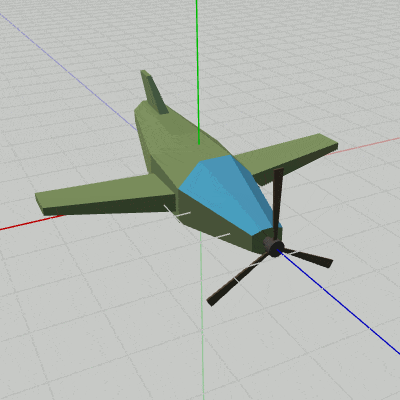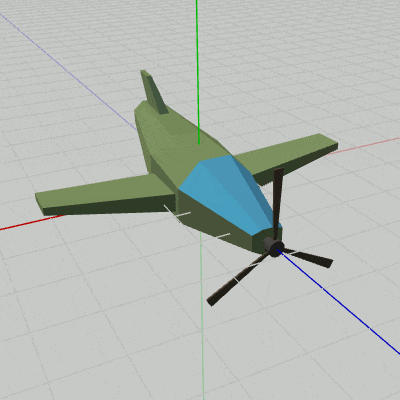
図4 Code1 実行結果
次のプログラムは Propellerを回転させている状態で、この円周上に Bodyと Propellerを移動させるだけの処理を実装したものである。
[Beta2] (実行結果 図6)
1~4行目はCode1の1~4行目と同じである (Propellerを回転させてアタッチする行列を求めている)。
この円周上での運動の開始位置は$(8,\ 10,\ 0)$で、図5に示される位置である。このとき、Bodyはz軸プラス方向を向いている。Code1と今回のプログラムの違いは、円周上への移動処理が加わったことである。
6行目のi_degBodyは運動の開始地点である$(8,\ 10,\ 0)$から円周上を何度進んだかを表すint型インスタンス変数である。i_degBodyは毎フレーム $2$ずつ減少するので、Bodyは毎フレーム 円周上を$-2$°ずつ進むことになる。「円周上を$-2$°ずつ進む」というのは、この運動を上から見た場合に、図6のように円周上を反時計周りに毎フレーム$2$°ずつ進むということである (i_degBodyが$2$ずつ増加する場合は、(上から見たときに)時計周りに$2$°ずつ進んでいく)。7行目でy軸周りにi_degBodyだけ回転させる回転行列 rotBody を取得し、それを8行目で開始位置を表す同次座標$(8,\ 10,\ 0,\ 1)$に掛けることで、そのフレームにおける円周上の移動位置を計算している。9行目の traBody は、その計算された位置へ移動させる平行移動行列である。
12行目の worldPropeller = localBody * localPropeller は、まず Propellerを初期位置である原点で回転させて、次に Bodyへアタッチする(localPropeller)、さらにそのアタッチした状態で円周上の移動位置へ移動させる(localBody)という処理をまとめたものである。
13行目の worldBody = localBody は、Bodyを円周上の移動位置へ移動させるだけの処理である。
結果的には、Bodyにも Propellerにも localBody が実行されることになるが、これによってこの2つのオブジェクトが一体化して円周上を運動することになるのである (実行結果 図6)。

図5 運動開始位置 (8, 10, 0) (飛行機はz軸プラス方向を向いている) 
図6 Beta2 実行結果
しかし、図6の運動は明らかに不自然である。確かに円周上を運動してはいるがオブジェクトに対して向きの設定をしていないために、運動中は常に初期方向であるz軸プラス方向を向いている。以下では、この点を修正していく。
図7は円周上の各点における接線を表示したアニメーションである(接線は緑色の矢印で表されている)。図8は、図7の運動する接線の始点を円周上から原点に固定したときのアニメーションである。
両方のアニメーションを比較すればわかるように、接線の始点を原点に固定した場合でも接線の向き自体は、円周上を運動している場合と変わらない。つまり、図7において運動開始位置から円周上を角度$\theta$だけ移動した位置での接線の方向は、図8における接線の初期方向(z軸プラス方向)から角度$\theta$だけ回転させた方向に等しい。
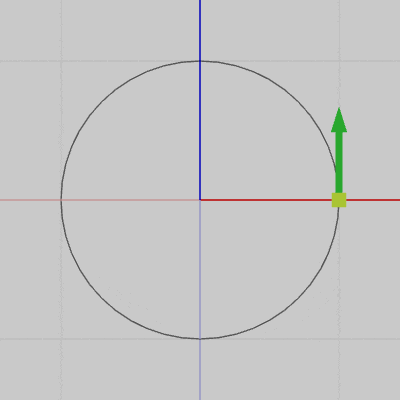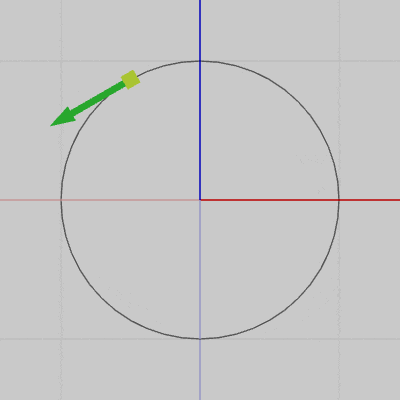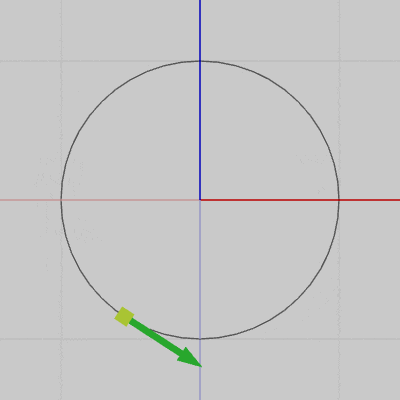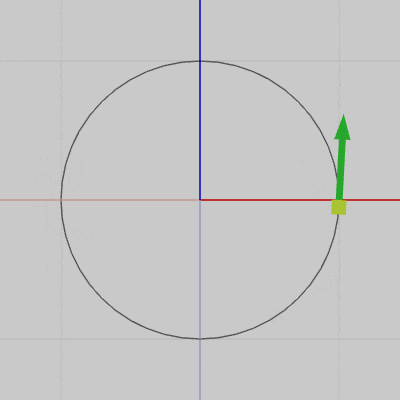
図7 円周上の接線 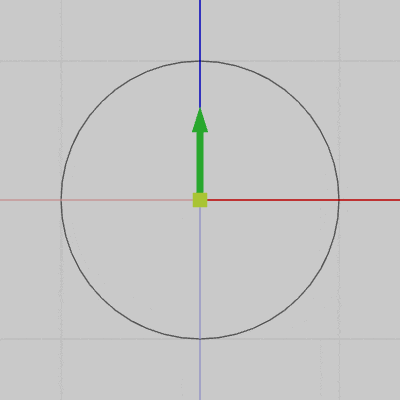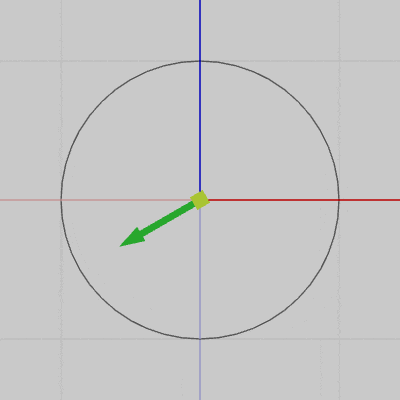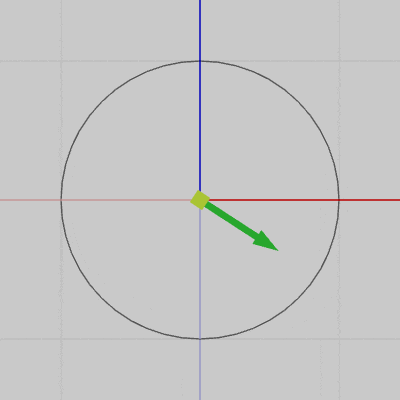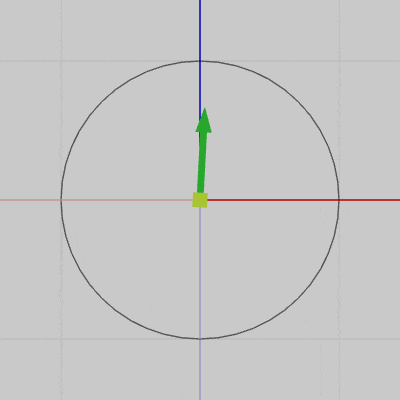
図8 接線の始点を原点に固定して表示
上のプログラムBeta2では、オブジェクトに対して向きの設定をしていなかった。今回使用している飛行機オブジェクトの運動は円周上であるので、ここでは図7に示されるように、円周上の各点での接線方向をオブジェクトの向きとして設定しよう。
具体的には、Bodyが円周上を開始位置から角度$\theta$だけ進んだ位置にいるときの向きを、Bodyの初期方向であるz軸プラス方向から角度$\theta$だけ回転させた方向とするのである。
[Code2] (実行結果 図9)
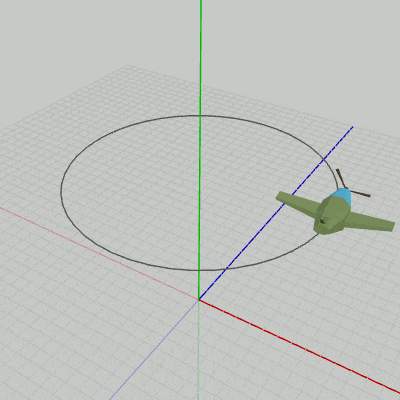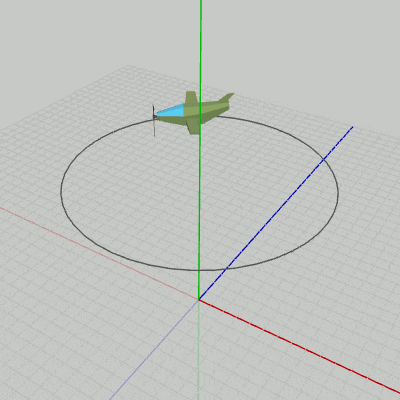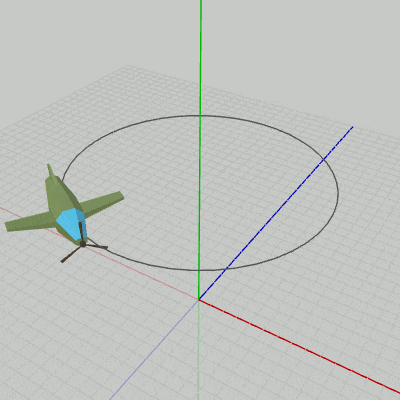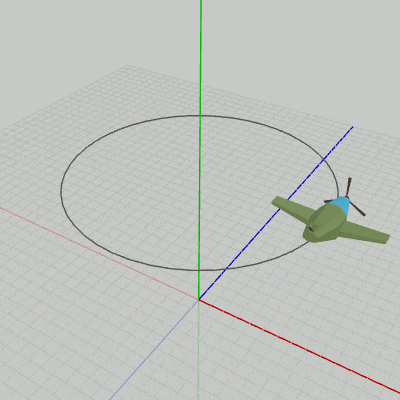
図9 Code2 実行結果 Beta2からの変更点は1箇所のみである。
それは10行目で、Beta2では localBody = traBody として円周上への移動のみであったのが、ここでは localBody = traBody * rotBody となっている。
7行目の rotBody はy軸周りに角度i_degBodyだけ回転させる行列であるが、Bodyが円周上の開始位置から角度i_degBodyだけ進んだ位置を求めるために、まず8行目において使われている。
上で述べたように、Bodyが円周上の開始位置から角度$\theta$だけ進んだ位置にいるときの向きは、z軸プラス方向から角度$\theta$だけ回転させた方向である。したがって、Bodyが円周上を角度i_degBodyだけ進んだ位置における向きは、z軸プラス方向から角度i_degBodyだけ回転させた方向ということになる。rotBodyはy軸周りに角度i_degBodyだけ回転させる行列であるから、これをこのまま(初期状態の)Bodyに実行すれば、Bodyは初期状態ではz軸プラス方向を向いているので、z軸プラス方向から角度i_degBodyだけ回転させた方向を向くことになる。
rotBodyによって向きを変えてからtraBodyによって円周上へ移動する、これがlocalBodyの内容である。
上記の変更によって12行目の worldPropeller = localBody * localPropeller の内容にも変更が生じる。localPropellerについては前のコードと同じく、初期状態で回転させてBodyの先端にアタッチするという処理である。アタッチした状態でlocalBodyを実行するが、前のコードではただ円周上に移動させるだけの処理であったのに対し、今回の処理は円周上への移動の前に上で述べた向きの設定が発生する。つまり、Bodyの先端にアタッチした状態で、Bodyとともに指定された向きになるように回転し、その状態で円周上への移動という処理になる。
繰り返しになるが、PropellerをBodyにアタッチした状態で両者に同じ行列(localBody)を実行するので、この2つのオブジェクトは一体化して運動するのである。
図10は、図9の最初のいくつかのフレームにおけるオブジェクトの変換過程である。赤いフィルターで覆われた状態から通常の色に切り替わるが、通常色に切り替わった状態でフレーム描画が発生する。図11は、それらの描画されたフレームをコマ送りで表示したものである (描画されたフレームを連続的に表示すれば図9のアニメーションになる)。
ただし、以下のアニメーションでは図6、図9とは異なり、便宜上、円周をXZ平面上に設置してある。

図10 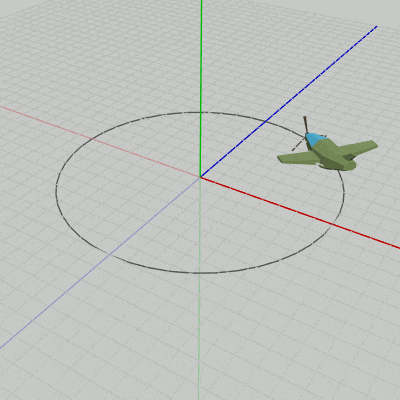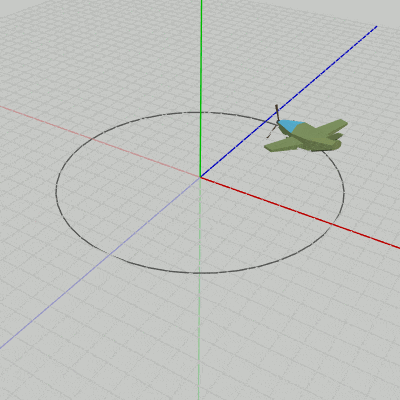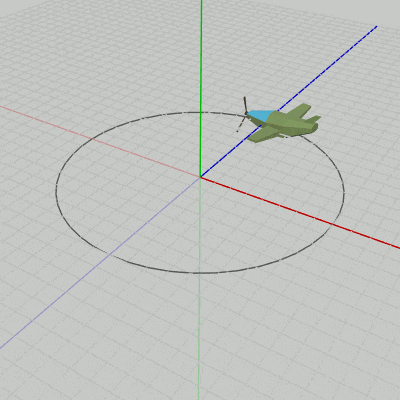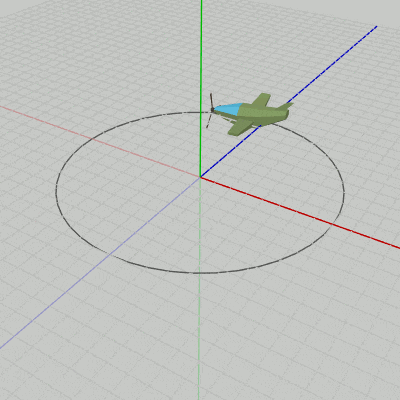
図11
3-9節ではオブジェクト原点というものを導入してオブジェクトの運動について述べたが、今回の例において、Bodyのオブジェクト原点を表示した場合を以下に示す。
図12の座標系原点にある黄色い点は、Bodyの初期状態におけるオブジェクト原点である(Propellerはアタッチした状態)。図13は、Bodyのオブジェクト原点を表示してCode2を実行した結果である。
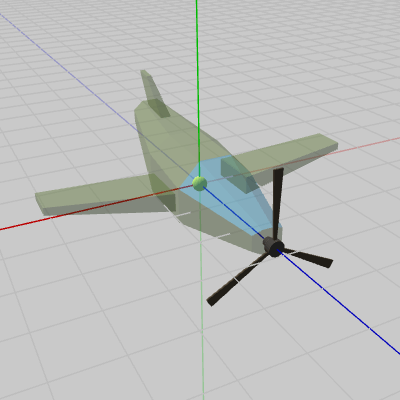
図12 Bodyのオブジェクト原点(Propellerはアタッチした状態) 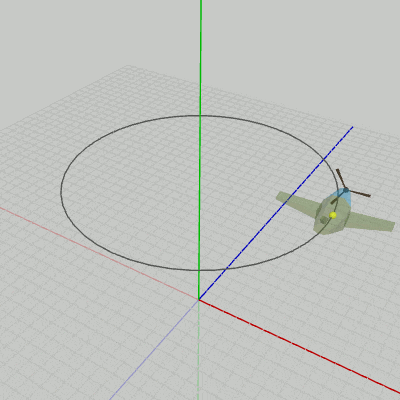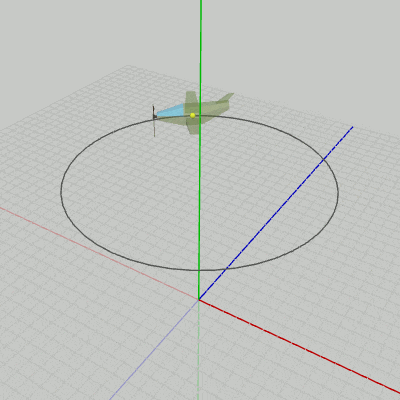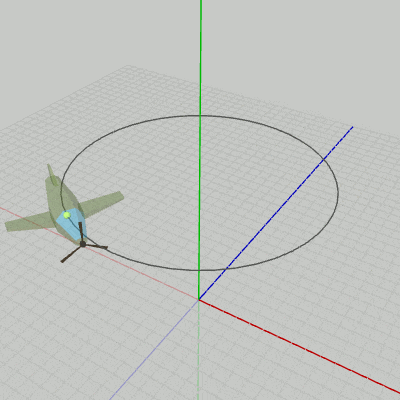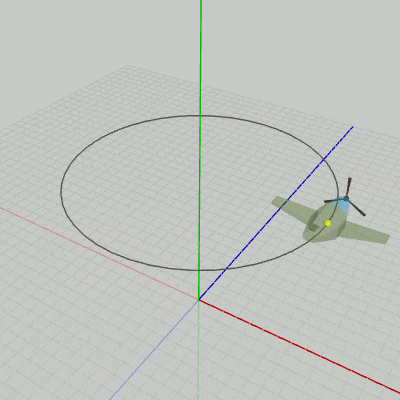
図13 Bodyのオブジェクト原点を表示した状態でのCode2の実行結果
毎フレームBodyに対して、$(0,\ 10,\ 0)$を中心とする半径$8$の円周上への移動が実行されるが、図13を見ればわかるように、実際にその円周上を運動しているのはBodyのオブジェクト原点である。
図14は Bodyに Propellerをアタッチした状態を示したもので、プログラムBeta1の視点をややずらして実行した結果である。図15はオイラー角によるオブジェクトの姿勢制御を可視化するために、3-15節のようにオブジェクトを覆う球面とオブジェクトの向きを示す水色のベクトルを表示したものである。向きを示すベクトルは、初期状態でBodyの初期方向であるz軸プラス方向を向いている。
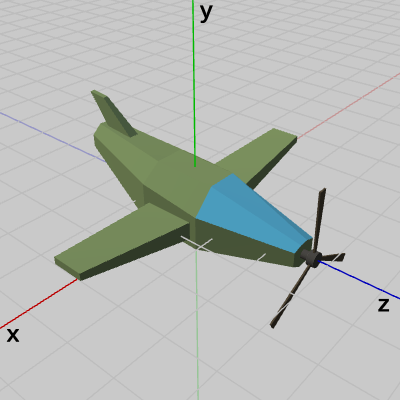
図14 BodyにPropellerをアタッチした状態(Beta1 実行結果) 
図15 水色のベクトルは、この飛行機の向きを示している
オイラー角経由でオブジェクトの向きを設定するために、次のキー操作を定義する。
H : オイラー角のy-角度を $1$減少させる。
J : オイラー角のx-角度を $1$増加させる。
K : オイラー角のx-角度を $1$減少させる。
L : オイラー角のy-角度を $1$増加させる。
オブジェクトの向きを示す水色のベクトルは、H、Lを押すことで球面上を横方向に動き、J、Kを押すことで球面上を縦方向に動く。
(x-角度、y-角度とは、オイラー角による回転でのx軸周りの回転角度、y軸周りの回転角度のことである ; 3-14節参照)
また、オイラー角による回転行列を取得するためにカスタムライブラリから次のメソッドを用いる。
実際のプログラムは次の通り。
[Code3] (実行結果 図16)

図16 Code3 実行結果 1~17行目はキー操作の部分で、i_eulerX、i_eulerYはオイラー角のx-角度、y-角度を表すfloat型インスタンス変数である(初期値は$0$)。19、20行目は今までのプログラムでも使われたコードで、Propellerを Bodyへアタッチする平行移動行列の算出である (今回は Propellerをアタッチするのみで回転は行わない)。
22行目でオイラー角による回転行列rotBodyを求めている。今回はx軸周りの回転、y軸周りの回転のみでz軸周りの回転は行わないのでz-角度の値は常に$0$である。Bodyに実行される行列はworldBodyであるが、その内容は実際には このrotBodyのみであり、rotBodyの回転は図16に示されるように Bodyの向きを変えるものである。具体的には、Bodyの先端が球面上の経線上、緯線上動くことになる (詳しくは3-15節参照)。
23行目の c_initDir は、Bodyの初期方向であるz軸プラス方向を表す定数であるが、同次座標化されているのでその値は $(0,\ 0,\ 1,\ 1)$ である。forwardDir は、Bodyの現在の方向(図中の水色のベクトルの方向)を表すVector3型のローカル変数であり、その値は初期方向であるz軸プラス方向から rotBody の表す回転を実行した結果が毎フレームセットされる。したがって、Bodyの向きを表す水色のベクトルはこの forwardDir を可視化したものであるといえる (大きさの違いを無視すれば)。ただし Code3では、forwardDir は23行目で算出されるだけでそれ以降使われることはない。
前回のプログラムでは、キー操作によってオブジェクトの向きを設定したが、ここではその設定された向きに進行するコードを追加してプロペラ飛行機の飛行を実装する。
操作方法は次の通り。
H、J、K、L : Code3と同様にオイラー角による回転でオブジェクトの向きを設定する。
S : 飛行の ON/OFF。
Sキーについて補足すると、この飛行機が静止しているときに、Sキーを押すとそのときのオブジェクトの方向(Bodyの先端の方向)に一定のスピードで進んでいく(飛行中に向きを変えると、変えられた方向に進んでいく)。飛行中にSキーを押すと静止状態になる(静止状態でも向きを変える操作はできる)。
[Code4] (実行結果 図17)

図17 Code4 実行結果 22行目までがキー操作の部分で、今回はBodyの旋回速度を上げるためにy-角度の増減を$2$にしてある(y-角度の数値を大きくすれば旋回速度は速くなる)。Sキーを押すことでbool型インスタンス変数i_MOVEの値が切り替わるが、これが飛行機の運動/停止の役目を果たしている(i_MOVEの初期値はfalseであり静止状態から始まる)。
25~28行目は Code1の1~4行目と同じであり、Propellerをアタッチポジションで回転させる行列 localPropeller の算出である。
31、32行目はオブジェクトを指定された向きに変えるための回転行列rotBody、及び その向き forwardDir を計算する部分である。
33~35行目が飛行の実装のために新たに追加された部分である。33行目の GetWorldPosition() はカスタムライブラリのメソッドで、オブジェクトの現在位置を取得するものである (上で述べたオブジェクト原点の座標が Vector3型で返される)。ここで取得されるオブジェクトの現在位置は前回のフレームでの Bodyの移動先の位置である。このプログラムでは Bodyは毎フレーム 34行目で算出されるnewPosへ移動するが、あるフレームにおいて33行目の Body.GetWorldPosition() で返される値は前回のフレームにおいて算出された newPos の値である (前回フレームにおけるBodyの移動先の位置が返されるようにするためには Body.GetWorldPosition() の位置が、43行目の Body.SetMatrix(worldBody) よりも前でなければならない)。
34行目では このフレームにおける Bodyの移動先の位置newPosを求めている。具体的には、Bodyの現在の位置(curPos)から 0.1f * forwardDir だけ進んだ位置が、Bodyの新しい位置(newPos)ということになる。つまり、i_MOVEがtrueであれば、Bodyは毎フレーム forwardDir の方向に $0.1$ずつ進んでいく。i_MOVEがfalseのときは、毎フレーム 34行目において newPos には Bodyの現在の位置curPosがそのままセットされる。これによって飛行機は静止状態になる。
今回はプロペラの付いた飛行機の運動を扱う。
使用するオブジェクトは以下のBody(図1)、Propeller(図2)の2つであり、図に示されるようにそれぞれ初期状態ではz軸プラス方向を向いている (Propellerではz軸がその中心を貫いている)。


# Code1
まず初めに、Bodyは初期状態のままでPropellerが指定位置で回転するプログラムを作成する。次のプログラムは、PropellerをBodyの指定位置に移動させるだけの処理である。第2章で使用した用語を使えば、PropellerをBodyにアタッチするだけの処理である(2-5節参照)。ここでいう「Bodyの指定位置」とはBodyの先端部分のことで、プログラム内では1行目の定数c_attachPos_Propellerによって表されている。Bodyは初期状態のままでよいので、Bodyに実行する行列は identity行列になる。
[Beta1] (実行結果 図3)
Matrix4x4 localPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller); Matrix4x4 localBody = Matrix4x4.identity; Matrix4x4 worldPropeller = localBody * localPropeller; Matrix4x4 worldBody = localBody; Propeller.SetMatrix(worldPropeller); Body.SetMatrix(worldBody);
第2章と同様に、ここからはオブジェクトに実行する行列にはlocalやworldといった単語が先頭に付く。これが何を意味するについては4-8節から4-11節で解説する(上記の場合は単に形式的な意味しか持たない)。
では実際にPropellerを回転させてみよう。プログラムは以下のようになる。
[Code1] (実行結果 図4)
i_degPropeller += 15; Matrix4x4 rotProp = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward); Matrix4x4 traProp = TH3DMath.GetTranslation4x4(c_attachPos_Propeller); Matrix4x4 localPropeller = traProp * rotProp; Matrix4x4 localBody = Matrix4x4.identity; Matrix4x4 worldPropeller = localBody * localPropeller; Matrix4x4 worldBody = localBody; Propeller.SetMatrix(worldPropeller); Body.SetMatrix(worldBody);
1行目の i_degPropeller は Propellerの(そのフレームにおける)回転角度を表すint型インスタンス変数である。このプログラムでは毎フレーム$15$ずつ増加するので、Propellerは毎フレーム$15$°ずつ回転することになる。
2行目のrotPropは、Propellerを角度i_degPropellerだけz軸周りに回転させるための行列である。Vector3.forward はUnityに標準で用意されている定数で、z軸のプラス方向である$(0, 0, 1)$を表す。3行目のtraPropは、Propellerをアタッチポジション(ここでは Bodyの先端)にアタッチするための平行移動行列である。
4行目の localPropeller = traProp * rotProp は、まず Propellerを初期状態の位置でz軸周りにi_degPropellerだけ回転させ(rotProp)、次にアタッチポジションに移動させる(traProp)という2つの処理をまとめたものである。具体的には、Propellerを(初期状態の位置である)原点でi_degPropellerだけ回転させて、回転させた状態で Bodyの先端に移動させるという処理を毎フレーム行っているのである。
6行目以降は、Beta1の2行目以降と同じである。


# Code2
Code1では飛行機自体は静止していたが、今回は Propellerの回転だけでなく飛行機自体の運動も実装する。具体的には、y軸を回転軸として反時計周りに、$(0,\ 10,\ 0)$を中心とする半径$8$の円周上でこのプロペラ飛行機を運動させてみよう。次のプログラムは Propellerを回転させている状態で、この円周上に Bodyと Propellerを移動させるだけの処理を実装したものである。
[Beta2] (実行結果 図6)
i_degPropeller += 15; Matrix4x4 rotProp = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward); Matrix4x4 traProp = TH3DMath.GetTranslation4x4(c_attachPos_Propeller); Matrix4x4 localPropeller = traProp * rotProp; i_degBody -= 2; Matrix4x4 rotBody = TH3DMath.GetRotation4x4(i_degBody, Vector3.up); Vector3 np = rotBody * new Vector4(8.0f, 10.0f, 0.0f, 1.0f); Matrix4x4 traBody = TH3DMath.GetTranslation4x4(np); Matrix4x4 localBody = traBody; Matrix4x4 worldPropeller = localBody * localPropeller; Matrix4x4 worldBody = localBody; Propeller.SetMatrix(worldPropeller); Body.SetMatrix(worldBody);
1~4行目はCode1の1~4行目と同じである (Propellerを回転させてアタッチする行列を求めている)。
この円周上での運動の開始位置は$(8,\ 10,\ 0)$で、図5に示される位置である。このとき、Bodyはz軸プラス方向を向いている。Code1と今回のプログラムの違いは、円周上への移動処理が加わったことである。
6行目のi_degBodyは運動の開始地点である$(8,\ 10,\ 0)$から円周上を何度進んだかを表すint型インスタンス変数である。i_degBodyは毎フレーム $2$ずつ減少するので、Bodyは毎フレーム 円周上を$-2$°ずつ進むことになる。「円周上を$-2$°ずつ進む」というのは、この運動を上から見た場合に、図6のように円周上を反時計周りに毎フレーム$2$°ずつ進むということである (i_degBodyが$2$ずつ増加する場合は、(上から見たときに)時計周りに$2$°ずつ進んでいく)。7行目でy軸周りにi_degBodyだけ回転させる回転行列 rotBody を取得し、それを8行目で開始位置を表す同次座標$(8,\ 10,\ 0,\ 1)$に掛けることで、そのフレームにおける円周上の移動位置を計算している。9行目の traBody は、その計算された位置へ移動させる平行移動行列である。
12行目の worldPropeller = localBody * localPropeller は、まず Propellerを初期位置である原点で回転させて、次に Bodyへアタッチする(localPropeller)、さらにそのアタッチした状態で円周上の移動位置へ移動させる(localBody)という処理をまとめたものである。
13行目の worldBody = localBody は、Bodyを円周上の移動位置へ移動させるだけの処理である。
結果的には、Bodyにも Propellerにも localBody が実行されることになるが、これによってこの2つのオブジェクトが一体化して円周上を運動することになるのである (実行結果 図6)。


しかし、図6の運動は明らかに不自然である。確かに円周上を運動してはいるがオブジェクトに対して向きの設定をしていないために、運動中は常に初期方向であるz軸プラス方向を向いている。以下では、この点を修正していく。
図7は円周上の各点における接線を表示したアニメーションである(接線は緑色の矢印で表されている)。図8は、図7の運動する接線の始点を円周上から原点に固定したときのアニメーションである。
両方のアニメーションを比較すればわかるように、接線の始点を原点に固定した場合でも接線の向き自体は、円周上を運動している場合と変わらない。つまり、図7において運動開始位置から円周上を角度$\theta$だけ移動した位置での接線の方向は、図8における接線の初期方向(z軸プラス方向)から角度$\theta$だけ回転させた方向に等しい。


上のプログラムBeta2では、オブジェクトに対して向きの設定をしていなかった。今回使用している飛行機オブジェクトの運動は円周上であるので、ここでは図7に示されるように、円周上の各点での接線方向をオブジェクトの向きとして設定しよう。
具体的には、Bodyが円周上を開始位置から角度$\theta$だけ進んだ位置にいるときの向きを、Bodyの初期方向であるz軸プラス方向から角度$\theta$だけ回転させた方向とするのである。
[Code2] (実行結果 図9)
i_degPropeller += 15; Matrix4x4 rotProp = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward); Matrix4x4 traProp = TH3DMath.GetTranslation4x4(c_attachPos_Propeller); Matrix4x4 localPropeller = traProp * rotProp; i_degBody -= 2; Matrix4x4 rotBody = TH3DMath.GetRotation4x4(i_degBody, Vector3.up); Vector3 np = rotBody * new Vector4(8.0f, 10.0f, 0.0f, 1.0f); Matrix4x4 traBody = TH3DMath.GetTranslation4x4(np); Matrix4x4 localBody = traBody * rotBody; Matrix4x4 worldPropeller = localBody * localPropeller; Matrix4x4 worldBody = localBody; Propeller.SetMatrix(worldPropeller); Body.SetMatrix(worldBody);

それは10行目で、Beta2では localBody = traBody として円周上への移動のみであったのが、ここでは localBody = traBody * rotBody となっている。
7行目の rotBody はy軸周りに角度i_degBodyだけ回転させる行列であるが、Bodyが円周上の開始位置から角度i_degBodyだけ進んだ位置を求めるために、まず8行目において使われている。
上で述べたように、Bodyが円周上の開始位置から角度$\theta$だけ進んだ位置にいるときの向きは、z軸プラス方向から角度$\theta$だけ回転させた方向である。したがって、Bodyが円周上を角度i_degBodyだけ進んだ位置における向きは、z軸プラス方向から角度i_degBodyだけ回転させた方向ということになる。rotBodyはy軸周りに角度i_degBodyだけ回転させる行列であるから、これをこのまま(初期状態の)Bodyに実行すれば、Bodyは初期状態ではz軸プラス方向を向いているので、z軸プラス方向から角度i_degBodyだけ回転させた方向を向くことになる。
rotBodyによって向きを変えてからtraBodyによって円周上へ移動する、これがlocalBodyの内容である。
上記の変更によって12行目の worldPropeller = localBody * localPropeller の内容にも変更が生じる。localPropellerについては前のコードと同じく、初期状態で回転させてBodyの先端にアタッチするという処理である。アタッチした状態でlocalBodyを実行するが、前のコードではただ円周上に移動させるだけの処理であったのに対し、今回の処理は円周上への移動の前に上で述べた向きの設定が発生する。つまり、Bodyの先端にアタッチした状態で、Bodyとともに指定された向きになるように回転し、その状態で円周上への移動という処理になる。
繰り返しになるが、PropellerをBodyにアタッチした状態で両者に同じ行列(localBody)を実行するので、この2つのオブジェクトは一体化して運動するのである。
図10は、図9の最初のいくつかのフレームにおけるオブジェクトの変換過程である。赤いフィルターで覆われた状態から通常の色に切り替わるが、通常色に切り替わった状態でフレーム描画が発生する。図11は、それらの描画されたフレームをコマ送りで表示したものである (描画されたフレームを連続的に表示すれば図9のアニメーションになる)。
ただし、以下のアニメーションでは図6、図9とは異なり、便宜上、円周をXZ平面上に設置してある。


3-9節ではオブジェクト原点というものを導入してオブジェクトの運動について述べたが、今回の例において、Bodyのオブジェクト原点を表示した場合を以下に示す。
図12の座標系原点にある黄色い点は、Bodyの初期状態におけるオブジェクト原点である(Propellerはアタッチした状態)。図13は、Bodyのオブジェクト原点を表示してCode2を実行した結果である。


毎フレームBodyに対して、$(0,\ 10,\ 0)$を中心とする半径$8$の円周上への移動が実行されるが、図13を見ればわかるように、実際にその円周上を運動しているのはBodyのオブジェクト原点である。
# Code3
次は、キー操作によってオブジェクトの向きを設定する。オブジェクトの向きの設定は今まで通り $4\times4$行列を使うが、その行列の算出はオイラー角経由で行う。3-15節ではオイラー角によるオブジェクトの姿勢制御を扱ったが、ここでも同じようにオイラー角経由でオブジェクトの向きを設定するプログラムを作成する。ただし、今回の実装はキー操作によってオブジェクトの向きを変えられるようにすることのみである(オブジェクト自体は移動しない)。図14は Bodyに Propellerをアタッチした状態を示したもので、プログラムBeta1の視点をややずらして実行した結果である。図15はオイラー角によるオブジェクトの姿勢制御を可視化するために、3-15節のようにオブジェクトを覆う球面とオブジェクトの向きを示す水色のベクトルを表示したものである。向きを示すベクトルは、初期状態でBodyの初期方向であるz軸プラス方向を向いている。


オイラー角経由でオブジェクトの向きを設定するために、次のキー操作を定義する。
H : オイラー角のy-角度を $1$減少させる。
J : オイラー角のx-角度を $1$増加させる。
K : オイラー角のx-角度を $1$減少させる。
L : オイラー角のy-角度を $1$増加させる。
オブジェクトの向きを示す水色のベクトルは、H、Lを押すことで球面上を横方向に動き、J、Kを押すことで球面上を縦方向に動く。
(x-角度、y-角度とは、オイラー角による回転でのx軸周りの回転角度、y軸周りの回転角度のことである ; 3-14節参照)
また、オイラー角による回転行列を取得するためにカスタムライブラリから次のメソッドを用いる。
TH3DMath.GetEulerRotation4x4(float degX, float degY, float degZ)
: オイラー角による回転行列を取得する。引数にはx軸周りの回転角度、y軸周りの回転角度、z軸周りの回転角度をこの順で指定する (戻り値は Matrix4x4型)。実際のプログラムは次の通り。
[Code3] (実行結果 図16)
if (Input.GetKey(KeyCode.J))
{
i_eulerX += 1;
}
else if (Input.GetKey(KeyCode.K))
{
i_eulerX -= 1;
}
if (Input.GetKey(KeyCode.H))
{
i_eulerY -= 1;
}
else if (Input.GetKey(KeyCode.L))
{
i_eulerY += 1;
}
Matrix4x4 traProp = TH3DMath.GetTranslation4x4(c_attachPos_Propeller);
Matrix4x4 localPropeller = traProp;
Matrix4x4 rotBody = TH3DMath.GetEulerRotation4x4(i_eulerX, i_eulerY, 0.0f);
Matrix4x4 localBody = rotBody;
Vector3 forwardDir = rotBody * c_initDir;
Matrix4x4 worldPropeller = localBody * localPropeller;
Matrix4x4 worldBody = localBody;
Propeller.SetMatrix(worldPropeller);
Body.SetMatrix(worldBody);

22行目でオイラー角による回転行列rotBodyを求めている。今回はx軸周りの回転、y軸周りの回転のみでz軸周りの回転は行わないのでz-角度の値は常に$0$である。Bodyに実行される行列はworldBodyであるが、その内容は実際には このrotBodyのみであり、rotBodyの回転は図16に示されるように Bodyの向きを変えるものである。具体的には、Bodyの先端が球面上の経線上、緯線上動くことになる (詳しくは3-15節参照)。
23行目の c_initDir は、Bodyの初期方向であるz軸プラス方向を表す定数であるが、同次座標化されているのでその値は $(0,\ 0,\ 1,\ 1)$ である。forwardDir は、Bodyの現在の方向(図中の水色のベクトルの方向)を表すVector3型のローカル変数であり、その値は初期方向であるz軸プラス方向から rotBody の表す回転を実行した結果が毎フレームセットされる。したがって、Bodyの向きを表す水色のベクトルはこの forwardDir を可視化したものであるといえる (大きさの違いを無視すれば)。ただし Code3では、forwardDir は23行目で算出されるだけでそれ以降使われることはない。
# Code4
では最後に、キー操作によってこのプロペラ飛行機を飛ばしてみよう。前回のプログラムでは、キー操作によってオブジェクトの向きを設定したが、ここではその設定された向きに進行するコードを追加してプロペラ飛行機の飛行を実装する。
操作方法は次の通り。
H、J、K、L : Code3と同様にオイラー角による回転でオブジェクトの向きを設定する。
S : 飛行の ON/OFF。
Sキーについて補足すると、この飛行機が静止しているときに、Sキーを押すとそのときのオブジェクトの方向(Bodyの先端の方向)に一定のスピードで進んでいく(飛行中に向きを変えると、変えられた方向に進んでいく)。飛行中にSキーを押すと静止状態になる(静止状態でも向きを変える操作はできる)。
[Code4] (実行結果 図17)
if (Input.GetKey(KeyCode.J))
{
i_eulerX += 1.0f;
}
else if (Input.GetKey(KeyCode.K))
{
i_eulerX -= 1.0f;
}
if (Input.GetKey(KeyCode.H))
{
i_eulerY -= 2.0f;
}
else if (Input.GetKey(KeyCode.L))
{
i_eulerY += 2.0f;
}
if (Input.GetKeyDown(KeyCode.S)) // 移動/停止
{
i_MOVE = !i_MOVE;
}
// localPropeller
i_degPropeller += 15;
Matrix4x4 rotProp = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward);
Matrix4x4 traProp = TH3DMath.GetTranslation4x4(c_attachPos_Propeller);
Matrix4x4 localPropeller = traProp * rotProp;
// localBody
Matrix4x4 rotBody = TH3DMath.GetEulerRotation4x4(i_eulerX, i_eulerY, 0.0f);
Vector3 forwardDir = rotBody * c_initDir;
Vector3 curPos = Body.GetWorldPosition();
Vector3 newPos = (i_MOVE) ? curPos + 0.1f * forwardDir : curPos;
Matrix4x4 traBody = TH3DMath.GetTranslation4x4(newPos);
Matrix4x4 localBody = traBody * rotBody;
// world matrix
Matrix4x4 worldPropeller = localBody * localPropeller;
Matrix4x4 worldBody = localBody;
Propeller.SetMatrix(worldPropeller);
Body.SetMatrix(worldBody);

25~28行目は Code1の1~4行目と同じであり、Propellerをアタッチポジションで回転させる行列 localPropeller の算出である。
31、32行目はオブジェクトを指定された向きに変えるための回転行列rotBody、及び その向き forwardDir を計算する部分である。
33~35行目が飛行の実装のために新たに追加された部分である。33行目の GetWorldPosition() はカスタムライブラリのメソッドで、オブジェクトの現在位置を取得するものである (上で述べたオブジェクト原点の座標が Vector3型で返される)。ここで取得されるオブジェクトの現在位置は前回のフレームでの Bodyの移動先の位置である。このプログラムでは Bodyは毎フレーム 34行目で算出されるnewPosへ移動するが、あるフレームにおいて33行目の Body.GetWorldPosition() で返される値は前回のフレームにおいて算出された newPos の値である (前回フレームにおけるBodyの移動先の位置が返されるようにするためには Body.GetWorldPosition() の位置が、43行目の Body.SetMatrix(worldBody) よりも前でなければならない)。
34行目では このフレームにおける Bodyの移動先の位置newPosを求めている。具体的には、Bodyの現在の位置(curPos)から 0.1f * forwardDir だけ進んだ位置が、Bodyの新しい位置(newPos)ということになる。つまり、i_MOVEがtrueであれば、Bodyは毎フレーム forwardDir の方向に $0.1$ずつ進んでいく。i_MOVEがfalseのときは、毎フレーム 34行目において newPos には Bodyの現在の位置curPosがそのままセットされる。これによって飛行機は静止状態になる。
© 2020-2025 Redpoll's 60 (All rights reserved)