Redpoll's 60
 Home / 3Dプログラミング入門 / 第4章 $§$4-7
第4章 3D空間におけるオブジェクトの運動
$§$4-1 自転と公転$§$4-13 各階層における座標の計算 2 (ローカル座標からワールド座標への変換 3D)
$§$4-2 一体化したオブジェクトの運動 1$§$4-14 一体化したオブジェクトの運動 5
$§$4-3 一体化したオブジェクトの運動 2$§$4-15 一体化したオブジェクトの運動 6
$§$4-4 一体化したオブジェクトの運動 3$§$4-16 一体化したオブジェクトの運動 7
$§$4-5 一体化したオブジェクトの運動 4$§$4-17 一体化したオブジェクトの運動 8
$§$4-6 変換行列の分解$§$4-18 一体化したオブジェクトの運動 9
$§$4-7 変換行列の可視化$§$4-19 一体化したオブジェクトの運動 10
$§$4-8 ローカル座標系とワールド座標系 1$§$4-20 指定方向へのオブジェクトの移動 1
$§$4-9 ローカル座標系とワールド座標系 2$§$4-21 指定方向へのオブジェクトの移動 2
$§$4-10 ローカル座標系とワールド座標系 3$§$4-22 衝突判定 1
$§$4-11 ローカル座標系が表すオブジェクトの状態$§$4-23 衝突判定 2
$§$4-12 各階層における座標の計算 1$§$4-24 衝突判定 3

$§$4-7 変換行列の可視化


図1 UCS 初期状態(各軸の長さは 1)
図1は、3D空間上に置かれている各軸の長さが $1$ の小さな座標系UCSである。UCSの赤い軸を U-x軸、緑の軸を U-y軸、青い軸を U-z軸、UCSの原点を U-原点 と呼ぶことにする。初期状態でU-x軸は、3D空間上のx軸と重なっており、U-y軸、U-z軸は3D空間上のy軸、z軸と重なっている。また、U-原点は初期状態で3D空間上の原点に位置している。
また、以下ではx軸、y軸、z軸による座標系をUCSと区別するために xyz座標系と呼ぶことにする。本節の図における座標値はすべて xyz座標系での値である。

初期状態においては、UCSの各軸の長さは $1$ であり、UCSの原点は xyz座標系の原点に一致しているので、UCSのU-x軸、U-y軸、U-z軸の先端の座標は、$(1,\ 0,\ 0)$、$(0,\ 1,\ 0)$、$(0,\ 0,\ 1)$ である(図2 ; UCSの各軸の先端は四角形であり「先端の座標」という表現はこの場合あまり適切ではないが、正確には四角形の中央の座標のことである)。
また、U-x軸をベクトルとしてみたとき、そのベクトルは、U-原点を始点とし、U-x軸の先端を終点とするベクトルであるが、初期状態ではそのベクトルの値は $(1,\ 0,\ 0)$である。このように、U-x軸を U-原点からU-x軸の先端までのベクトルとして表すことを「U-x軸のベクトル表示」と呼ぶことにする。U-y軸、U-z軸の場合も同様にしてベクトル表示を行う。図3は、初期状態における各軸のベクトル表示である。

図2 UCSの各軸の先端の座標(正確には先端の四角形の中央の座標)
図3 UCSの各軸のベクトル表示(緑色の数値はベクトルを表している)

図3では緑色の数値が使われているが、これは今までに何度か出てきたが、ベクトルを表すためのものである。この緑色の数値の組は、先端の座標ではなく各軸のベクトル表示を意味している。
図2と図3を見ればわかるように、各軸の先端の座標と各軸のベクトル表示の値は同じである。これは、UCSの原点(U-原点)が xyz座標系の原点と一致しているためである。

では、ここからUCSに対していくつかの変換を実行していく。
今のUCSは初期状態であり、これは何の変換も実行されていない状態であるが、このような状態を表す変換行列を identity行列というのであった (つまり、オブジェクトに identity行列をセットすると、オブジェクトは初期状態に戻る)。したがって、UCSの現在の状態を表す変換行列を $LocalMatrix$ とすれば、その内容は identity行列であるから以下のようになる。
\[LocalMatrix = \begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &0 \\0 &0 &1 &0 \\0 &0 &0 &1 \end{pmatrix} \]
(1)  第1の変換  ：  z軸方向に $2$倍拡大

この変換を表す行列を$S$とすれば、
\[S = \begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &0 \\0 &0 &2 &0 \\0 &0 &0 &1 \end{pmatrix} \]である。

これを初期状態のUCSに実行することは、行列計算では次のようになる。
\begin{align*}\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &0 \\0 &0 &2 &0 \\0 &0 &0 &1 \end{pmatrix} \begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &0 \\0 &0 &1 &0 \\0 &0 &0 &1 \end{pmatrix} &= \\\\\begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &0 \\0 &0 &2 &0 \\0 &0 &0 &1 \end{pmatrix} &= LocalMatrix\end{align*}UCSの状態を表す変換行列$LocalMatrix$の内容が、z軸方向に $2$倍拡大するものになった。
この変換後のUCSを図4、図5に示す。

図4 UCSの各軸の先端の座標(第1の変換後)
図5 UCSの各軸のベクトル表示(第1の変換後)

図4には各軸の先端の座標が示されている。この変換によって、z軸の長さが $2$倍になり、z軸の先端の座標が $(0,\ 0,\ 2)$になっている。
図5は各軸のベクトル表示である。xyz座標系の原点と U-原点が一致しているため、先端の座標と同じ値になっている。

(2)  第2の変換  ：  $(-2,\ 1,\ 1)$の方向を指し示す回転軸$m$の周りに$30$°回転

図6 回転軸 m (先端は (-2, 1, 1) を指している)
この変換を表す行列を$R$とすれば、
\[R = \begin{pmatrix}0.96 &-0.25 &0.16 &0.00 \\ 0.16 &0.89 &0.43 &0.00 \\ -0.25 &-0.39 &0.89 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \]である(任意軸周りの回転行列の取得については 3-11節参照)。

(注 : 本節においても、図中の数値や行列の成分が小数である場合は、少数第3位を四捨五入して小数点以下第2位までの表示にしている。)

この変換によって UCSの変換行列は、次のようになる。
\begin{align*}\begin{pmatrix}0.96 &-0.25 &0.16 &0.00 \\ 0.16 &0.89 &0.43 &0.00 \\ -0.25 &-0.39 &0.89 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &0 \\0 &0 &2 &0 \\0 &0 &0 &1 \end{pmatrix} &= \\\\\begin{pmatrix}0.96 &-0.25 &0.32 &0.00 \\ 0.16 &0.89 &0.86 &0.00 \\ -0.25 &-0.39 &1.78 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} &= LocalMatrix\end{align*}
この結果は、第1の変換後の$LocalMatrix$に、今回の変換行列$R$を掛けたものである。
この変換後のUCSを図7、図8に示す。

図7 UCSの各軸の先端の座標(第2の変換後 ; 正確には先端の四角形の中央の座標)
図8 UCSの各軸のベクトル表示(第2の変換後)

図7には第2の変換後の各軸の先端の座標が示されている。U-x軸の先端座標は $(0.96, 0.16, -0.25)$ であるが、これは以下のように求められる。
第2の変換前(回転前)のU-x軸の先端座標は $(1, 0, 0)$ であるから、今回の回転によって $(1, 0, 0)$ の移動先を計算すると
\[R\begin{pmatrix}1\\0\\0\\1\\\end{pmatrix}=\begin{pmatrix}0.96 &-0.25 &0.16 &0.00 \\ 0.16 &0.89 &0.43 &0.00 \\ -0.25 &-0.39 &0.89 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}1\\0\\0\\1\\\end{pmatrix}=\begin{pmatrix}0.96 \\0.16 \\-0.25 \\1.00\end{pmatrix} \]
となる。U-y軸、U-z軸の先端座標の求め方も同様である。
図8は各軸のベクトル表示である。ここでも、xyz座標系の原点と U-原点が一致しているため、先端の座標と同じ値になっている。

(3)  第3の変換  ：  $(3,\ 2, -2)$だけ平行移動

この変換を表す行列を$T$とすれば、
\[T = \begin{pmatrix}1 &0 &0 &3 \\ 0 &1 &0 &2 \\ 0 &0 &1 &-2 \\ 0 &0 &0 &1\end{pmatrix} \]である。

この変換によって UCSの変換行列は、次のようになる。
\begin{align*}\begin{pmatrix}1 &0 &0 &3 \\ 0 &1 &0 &2 \\ 0 &0 &1 &-2 \\ 0 &0 &0 &1\end{pmatrix} \begin{pmatrix}0.96 &-0.25 &0.32 &0.00 \\ 0.16 &0.89 &0.86 &0.00 \\ -0.25 &-0.39 &1.78 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} &= \\\\\begin{pmatrix}0.96 &-0.25 &0.32 &3.00 \\ 0.16 &0.89 &0.86 &2.00 \\ -0.25 &-0.39 &1.78 &-2.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} &= LocalMatrix\end{align*}
この結果は、第2の変換後の$LocalMatrix$に、今回の変換行列$T$を掛けたものである。
この変換後のUCSを図9、図10に示す。

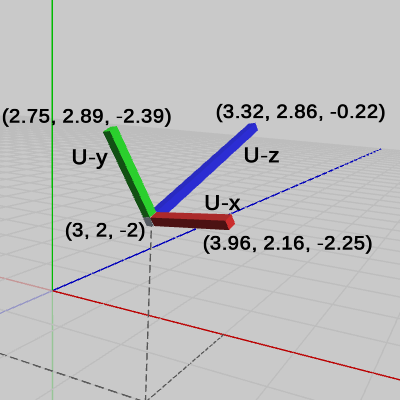
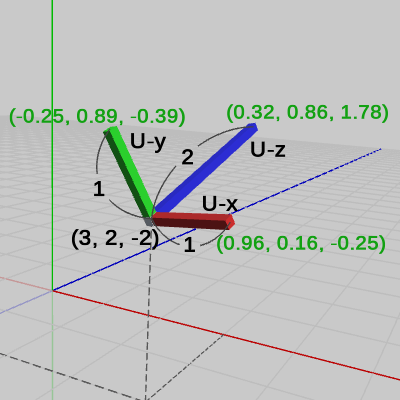
図9 UCSの各軸の先端の座標(第3の変換後 ; 正確には先端の四角形の中央の座標)
図10 UCSの各軸のベクトル表示(第3の変換後)

図9には第3の変換後の各軸の先端の座標、及び U-原点(UCSの原点)の座標が示されている。これらの座標は第2の変換後の各座標値に $(3,\ 2, -2)$ を加算しただけのものである。

この変換後の UCSの各軸のベクトル表示を求めてみよう。
U-原点は $(3,\ 2, -2)$に移動したので、その座標がベクトルの始点となる。したがって、各軸のベクトル表示は以下のように求められる。
        U-x  :  $(3.96, 2.16, -2.25) - (3, 2, -2) = (0.96, 0.16, -0.25)$
        U-y  :  $(2.75, 2.89, -2.39) - (3, 2, -2) = (-0.25, 0.89, -0.39)$
        U-z  :  $(3.32, 2.86, -0.22) - (3, 2, -2) = (0.32, 0.86, 1.78)$

この結果を図10に示す。
今回の変換では、U-原点が xyz座標系の原点から移動しているので、各軸の先端の座標と各軸のベクトル表示は同じではない。


前節では変換行列に対し、次のような書き換えを行った。
\[M = \begin{pmatrix}m_{11} &m_{12} &m_{13} &m_{14} \\m_{21} &m_{22} &m_{23} &m_{24} \\m_{31} &m_{32} &m_{33} &m_{34} \\0 &0 &0 &1 \end{pmatrix} =\begin{pmatrix}s_x r_{11} &s_y r_{12} &s_z r_{13} &t_x \\s_x r_{21} &s_y r_{22} &s_z r_{23} &t_y \\s_x r_{31} &s_y r_{32} &s_z r_{33} &t_z \\0 &0 &0 &1 \end{pmatrix} \qquad(Ex1)\]
($s_x$、$s_y$、$s_z$は第1列目、第2列目、第3列目の大きさを表している。したがって、$(r_{11}, r_{21}, r_{31})$、$(r_{12}, r_{22}, r_{32})$、$(r_{13}, r_{23}, r_{33})$は単位ベクトルになることに注意。)

第3の変換後の$LocalMatrix$に対して、同じように書き換えを行うと次のようになる。
\begin{align*}LocalMatrix &= \begin{pmatrix}0.96 &-0.25 &0.32 &3.00 \\ 0.16 &0.89 &0.86 &2.00 \\ -0.25 &-0.39 &1.78 &-2.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \\\\ &=\begin{pmatrix}1\cdot0.96 &1\cdot(-0.25) &2\cdot0.16 &3.00 \\ 1\cdot0.16 &1\cdot0.89 &2\cdot0.43 &2.00 \\ 1\cdot(-0.25) &1\cdot(-0.39) &2\cdot0.89 &-2.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \qquad(Ex2)\end{align*}

図11 UCSの各軸の単位ベクトル表示(第3の変換後)
図10では UCSの各軸をベクトル表示で示したが、このベクトル表示を単位ベクトルとして表示したものを図11に示す。つまり、図11におけるオレンジ色の数値は、各軸のベクトル表示を単位ベクトル化して表示したものである。
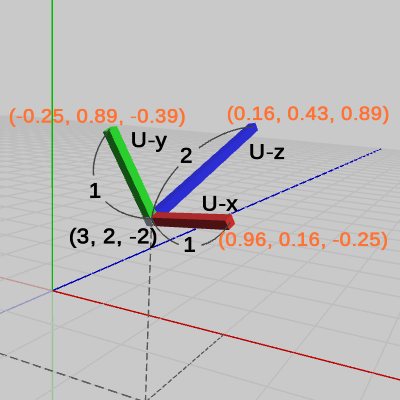
U-x軸、U-y軸については元々の長さが$1$であるので図11における数値は、図10の数値と変わりはない。U-z軸は長さが$2$であるため、単位ベクトル表示にすると、図10の数値とは同じではなくなる。

では、書き換えの行われた$LocalMatrix\ (Ex2)$と図11を見比べていこう。
$LocalMatrix$の第1列目の3行目までの成分には$1$が係数として掛けられている。第2列目も同様に3行目までの成分には$1$が係数として掛けられている。第3列目では、掛けられている係数が$2$になっている。前節で述べたが、この係数は $LocalMatrix$の第1列目、第2列目、第3列目の大きさを表している。
図11には各軸の長さが表示されている。U-x軸、U-y軸は長さ$1$であり、U-z軸は長さ$2$である。このことから容易に推測されるように、$LocalMatrix$の各列に掛けられている係数は、UCSの各軸の長さに等しいのである。つまり、$LocalMatrix$の第1列目に掛けられている係数はU-x軸の長さに等しく、第2列目に掛けられている係数はU-y軸の長さに等しく、第3列目に掛けられている係数はU-z軸の長さに等しい。そして、繰り返しになるが各列に掛けられている係数は $LocalMatrix$の各列の大きさを表しているのである。
次に、$LocalMatrix$の第1列目、第2列目、第3列目において係数の掛けられている方の成分について見ていこう。第1列目の3行目までの、係数を除いた成分は $(0.96, 0.16, -0.25)$である。この数値は、図11における U-x軸の単位ベクトル表示の数値と同じものである。第2列目の3行目までの、係数を除いた成分は $(-0.25, 0.89, -0.39)$であり、第3列目では、$(0.16, 0.43, 0.89)$である。これらの数値も第1列目の場合と同様に、図11における U-y軸、U-z軸の単位ベクトル表示の数値と同じである。実際には、$LocalMatrix$の第1列目、第2列目、第3列目を正規化した(3行目までの)数値は、UCSの U-x軸、U-y軸、U-z軸を正規化して表示したものと等しいのである。
$LocalMatrix$の第4列目の3行目までの成分は $(3, 2, -2)$である。この数値は、U-原点(UCSの原点)の現在の位置である。すなわち、$LocalMatrix$の第4列目は、UCSの原点の座標に等しいのである。

では、上に述べたことをプログラムを用いて再度、解説しよう。
[Beta1]
Matrix4x4 S = TH3DMath.GetScale4x4(1, 1, 2);  // 第1の変換
Matrix4x4 R = TH3DMath.GetRotation4x4(30.0f, new Vector(-2, 1, 1).normalized);  // 第2の変換
Matrix4x4 T = TH3DMath.GetTranslation4x4(3, 2, -2);  // 第3の変換
Matrix4x4 LocalMatrix = T * R * S;
UCS.SetMatrix(LocalMatrix);

このプログラムは、上記の3つの変換をUCSに実行するものであり、実行結果は 図11のようになる。
5行目でUCSに実行される変換行列LocalMatrixは、3つの変換行列 S、R、Tの積であり、その内容は、上記の$(Ex2)$に示されている。
図11の U-x軸、U-y軸、U-z軸の長さは、それぞれ $1$、$1$、$2$であるが、それらはLocalMatrixの第1列目、第2列目、第3列目の大きさに等しい。また、U-原点を始点、U-x軸の先端を終点とするベクトルを正規化したものは、LocalMatrixの第1列目を正規化したものに等しい。同様に、U-y軸、U-z軸を正規化したものは、LocalMatrixの第2列目、第3列目を正規化したものに等しい。
図11では U-原点の座標も示されており、その値は $(3, 2, -2)$であるが、それは LocalMatrixの第4列目(の3行目まで)の値に等しい。
つまり、このUCSという座標系は、この座標系に実行された変換行列LocalMatrixを可視化したものになっているのである。

さらに、前節で用いた「平行移動成分」「回転成分」「スケール成分」という用語を再度用いると以下のように述べられる。

UCSの各軸の長さがスケール成分を表し、UCSの各軸を正規化したものが回転成分を表し、UCSの原点が平行移動成分を表している。

このことは、$(Ex2)$の形の$LocalMatrix$を次のようにTRS分解したものと図11を見比べれば明らかである。
\begin{align*}LocalMatrix &= \begin{pmatrix}1\cdot0.96 &1\cdot(-0.25) &2\cdot0.16 &3.00 \\ 1\cdot0.16 &1\cdot0.89 &2\cdot0.43 &2.00 \\ 1\cdot(-0.25) &1\cdot(-0.39) &2\cdot0.89 &-2.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \\\\&=\begin{pmatrix}1 &0 &0 &3 \\0 &1 &0 &2 \\0 &0 &1 &-2 \\0 &0 &0 &1\end{pmatrix} \begin{pmatrix}0.96 &-0.25 &0.16 &0.00 \\ 0.16 &0.89 &0.43 &0.00 \\ -0.25 &-0.39 &0.89 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}1 &0 &0 &0 \\0 &1 &0 &0 \\0 &0 &2 &0 \\0 &0 &0 &1\end{pmatrix} \end{align*}



変換行列の可視化について、別の例を使って見てみよう。
[Beta2]
Matrix4x4 M1 = TH3DMath.GetTranslation4x4(3.0f, 4.0f, 5.0f);
Matrix4x4 M2 = TH3DMath.GetRotation4x4(-30.0f, Vector3.up);
Matrix4x4 M3 = TH3DMath.GetScale4x4(3.0f);
Matrix4x4 M4 = TH3DMath.GetRotation4x4(-45.0f, Vector3.right);
Matrix4x4 M5 = TH3DMath.GetTranslation4x4(2.0f, -20.0f, -1.0f);
Matrix4x4 LocalMatrix = M5 * M4 * M3 * M2 * M1;
UCS.SetMatrix(LocalMatrix);

このプログラムは、前節の B) の[例1]で使われた以下の5つの変換をUCSに実行したものである。
(1)  第1の変換  ：  $(3,\ 4,\ 5)$だけ平行移動
(2)  第2の変換  ：  y軸周りに $-30$°回転
(3)  第3の変換  ：  ｘ軸、ｙ軸、ｚ軸方向に$3$倍拡大
(4)  第4の変換  ：  x軸周りに $-45$°回転
(5)  第5の変換  ：  $(2, -20, -1)$だけ平行移動

行列計算の結果を以下に示す(小数第3位を四捨五入し、小数点以下第2位までの表示)。
\begin{align*}&M_5M_4M_3M_2M_1 \\\\&= \begin{pmatrix}1 &0 &0 &2 \\0 &1 &0 &-20 \\0 &0 &1 &-1 \\0 &0 &0 &1 \end{pmatrix} \begin{pmatrix}1.00 &0.00 &0.00 &0.00 \\ 0.00 &0.71 &0.71 &0.00 \\ 0.00 &-0.71 &0.71 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix}\begin{pmatrix}3 &0 &0 &0 \\0 &3 &0 &0 \\0 &0 &3 &0 \\0 &0 &0 &1 \end{pmatrix} \begin{pmatrix}0.87 &0.00 &-0.50 &0.00 \\ 0.00 &1.00 &0.00 &0.00 \\ 0.50 &0.00 &0.87 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix}\begin{pmatrix}1 &0 &0 &3 \\0 &1 &0 &4 \\0 &0 &1 &5 \\0 &0 &0 &1 \end{pmatrix} \\\\ &=\begin{pmatrix} 2.60 &0.00 &-1.50 &2.29 \\ 1.06 &2.12 &1.84 &0.85 \\ 1.06 &-2.12 &1.84 &2.88 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} = LocalMatrix\end{align*}

このプログラムの実行結果は次のようになる。

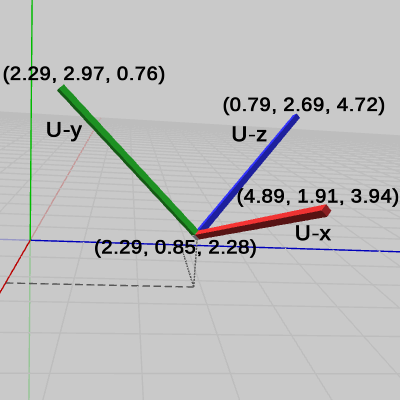
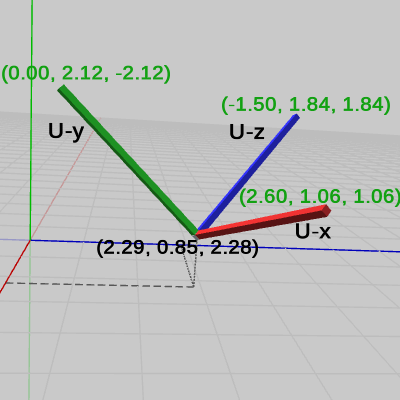
図12 UCSの各軸の先端の座標(正確には先端の四角形の中央の座標)
図13 UCSの各軸のベクトル表示

図12には、5つの変換を実行した後の各軸の先端座標、及び U-原点(UCSの原点)の座標が示されている(U-原点の座標は $(2.29, 0.85, 2.88)$ である)。変換実行後の各座標は次のように求められる (U-x軸の先端座標を例にとる)。
変換前のU-x軸の先端座標は $(1, 0, 0)$ であるから、上記の5つの変換を $(1, 0, 0)$ に実行すると
\begin{align*}M_5M_4M_3M_2M_1\begin{pmatrix} 1\\0\\0\\1\end{pmatrix} &= \begin{pmatrix} 2.60 &0.00 &-1.50 &2.29 \\ 1.06 &2.12 &1.84 &0.85 \\ 1.06 &-2.12 &1.84 &2.88 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix} 1\\0\\0\\1\end{pmatrix} \\\\&=\begin{pmatrix} 2.60\cdot1 + 2.29\cdot1 \\ 1.06\cdot1 + 0.85\cdot1 \\ 1.06\cdot1 + 2.88\cdot1 \\ 0.00\cdot1 + 1.00\cdot1\end{pmatrix} =\begin{pmatrix} 4.89\\1.91\\3.94\\1\end{pmatrix} \end{align*}
となる。U-y軸、U-z軸の先端座標、及び U-原点についても同様の計算で求められる。

図13は、この変換後の UCSの各軸のベクトル表示であるが、これは次のように求められる。
        U-x  :  $(4.89, 1.91, 3.94) - (2.29, 0.85, 2.88) = (2.60, 1.06, 1.06)$
        U-y  :  $(2.29, 2.97, 0.76) - (2.29, 0.85, 2.88) = (0.00, 2.12, -2.12)$
        U-z  :  $(0.79, 2.69, 4.72) - (2.29, 0.85, 2.88) = (-1.50, 1.84, 1.84)$

例によってここでも、上記$(Ex1)$に示される変換行列の書き換えを行う(小数点以下第2位までの表示なので以下の等式には、わずかな誤差が含まれている)。
\begin{align*}LocalMatrix &= \begin{pmatrix}2.60 &0.00 &-1.50 &2.29 \\ 1.06 &2.12 &1.84 &0.85 \\ 1.06 &-2.12 &1.84 &2.88 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \\\\ &=\begin{pmatrix}3\cdot0.87 &3\cdot0.00 &3\cdot(-0.50) &2.29 \\ 3\cdot0.35 &3\cdot0.71 &3\cdot0.61 &0.85 \\ 3\cdot0.35 &3\cdot(-0.71) &3\cdot0.61 &2.88 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \qquad(Ex3)\end{align*}

図14 UCSの各軸の単位ベクトル表示
図14は先程の例と同様に、各軸のベクトル表示を単位ベクトルとして表示したものである。
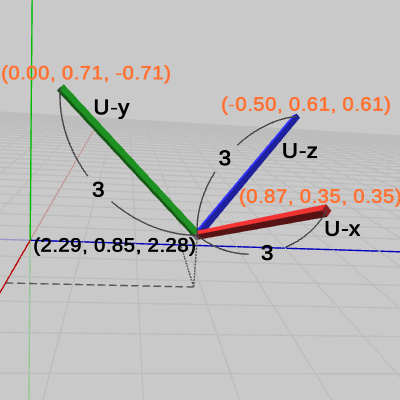
図14と上の$LocalMatrix\ (Ex3)$を見比べて、先程の例で述べたことを確認しよう。
今回の実行結果では、U-x軸、U-y軸、U-z軸の長さは$3$になっている。これらの長さは、$LocalMatrix$の第1列目、第2列目、第3列目の大きさに等しいのであった。実際、$(Ex3)$の第1列目から第3列目に掛けられている係数は、各軸の長さと同じ$3$である (この係数は、これらの列の大きさを表している)。
また、U-x軸、U-y軸、U-z軸のベクトル表示を単位ベクトルとして表示したものは、$LocalMatrix$の第1列目、第2列目、第3列目(の3行目まで)を単位ベクトル化したものと等しくなるのであった。実際、$(Ex3)$の第1列目から第3列目における係数$3$を除いて比較すれば、図14に表示されている数値と確かに一致している。
そして、今回のプログラムではU-原点は $(2.29, 0.85, 2.88)$ に移動しているが、この値は$LocalMatrix$の第4列目(の3行目まで)の値に一致するのであった。$(Ex3)$の第4列目を見ると確かにその値になっていることがわかる。
やはり、この例によっても UCSという座標系は、この座標系に実行された変換行列を可視化したものであるということが確認できる。

さらに、$LocalMatrix$を$(Ex3)$の形からTRS分解したものを以下に示す。
\begin{align*}LocalMatrix &= \begin{pmatrix}3\cdot0.87 &3\cdot0.00 &3\cdot(-0.50) &2.29 \\ 3\cdot0.35 &3\cdot0.71 &3\cdot0.61 &0.85 \\ 3\cdot0.35 &3\cdot(-0.71) &3\cdot0.61 &2.88 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \\\\&=\begin{pmatrix}1 &0 &0 &2.29 \\0 &1 &0 &0.85 \\0 &0 &1 &2.88 \\0 &0 &0 &1\end{pmatrix} \begin{pmatrix}0.87 &0.00 &-0.50 &0.00 \\ 0.35 &0.71 &0.61 &0.00 \\ 0.35 &-0.71 &0.61 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix} \begin{pmatrix}3 &0 &0 &0 \\0 &3 &0 &0 \\0 &0 &3 &0 \\0 &0 &0 &1\end{pmatrix} \end{align*}
先ほども述べたように、UCSの各軸の長さがスケール成分を表し、UCSの各軸を正規化したものが回転成分を表し、UCSの原点が平行移動成分を表している。
このことは、TRS分解と図14から明らかである。


ここからは、座標系UCSをオブジェクトに関連付けて見ていこう。
図15は、球体オブジェクトBallの初期状態である。さらに図16には、初期状態のBallとともに初期状態のUCSを追加して表示している。両者ともに初期状態であるから、Ball及び UCSにセットされている変換行列は identity行列である。
上で述べたように、UCSは自身に実行された変換行列を可視化したものである。そして、ここではBallとUCSには同じ変換行列が実行されているので、この時点でのUCSは Ballに実行された変換行列を可視化したもの としても見ることができる。

図15 Ball 初期状態
図16 この時点でのUCSは、Ballの初期状態(identity行列)を可視化したもの

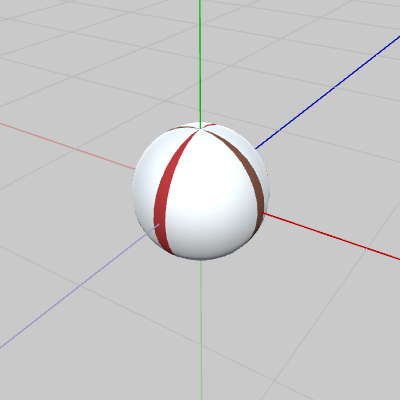
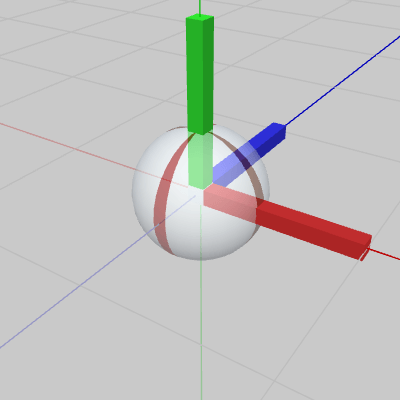
図17、図18は上のプログラムBeta1、Beta2をBallを使って実行したものである (各プログラム内の UCS.SetMatrix(..) の部分を Ball.SetMatrix(..) に変えたときの実行結果)。BallとともにUCSも表示されているが、上記の言い方を用いれば、ここでもUCSは Ballに実行された変換行列を可視化したもの として見ることができる (UCSにも同じ変換行列が実行されており、図17、図18のUCSはそれぞれ図11、図14と同じ状態)。

図17 Beta1 実行結果(Ballを使用した場合)
図18 Beta2 実行結果(Ballを使用した場合)

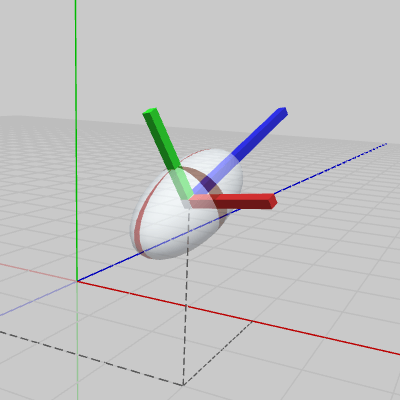
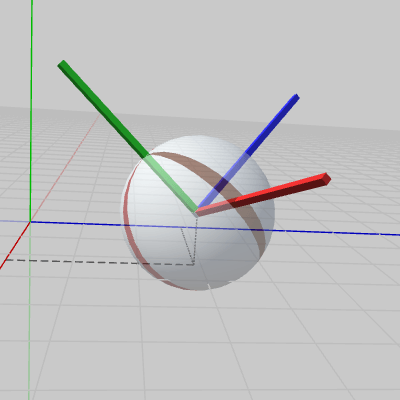
UCSにはBallと同じ変換行列が実行されているが、このようにUCSをオブジェクトと関連付けることによって、UCSの'存在価値'がより自然なものになるのである。
つまり、本節で見てきたUCSという座標系は、上の場合のようにオブジェクトと関連付けると、オブジェクトに実行された変換行列を可視化したものという意味を持つ。言い換えれば、UCSという座標系はオブジェクトの現在の状態を表しているのである。

本節において学習した内容は、この後の 4-11節において再び使われる。そこでは、UCSの代わりにオブジェクトのローカル座標系というものを対象にして、本節において行われたものと同様の議論がなされる。












<<  4-6
変換行列の分解
4-8  >>
ローカル座標系とワールド座標系 1
© 2020-2024 Redpoll's 60 (All rights reserved)