Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-17
第4章 3D空間におけるオブジェクトの運動
$§$4-17 一体化したオブジェクトの運動 8
本節は読者用の課題である。
本章で扱ってきた一体化運動においてはオブジェクトの間に親子関係があり、どのオブジェクトもあるオブジェクトの親オブジェクト、あるいは子オブジェクトとして階層構造に含まれていた。
しかし、複数のオブジェクトが一体化して運動する場合であっても、オブジェクトの間に親子関係を設定するべきではない場合がある。例えば、その代表的な例が惑星と衛星の運動である。
惑星が一定の周期で公転や自転をする際、衛星もまたその惑星の周りを一定の周期で公転し、自転する。以下の図1における青い円盤は惑星を表しており、緑の円盤は衛星を表している。また、ここでは簡単のため惑星は自転のみを行うものとする。
例えば、惑星が 10回自転する間に衛星が惑星の周りを 1回公転するとしよう。
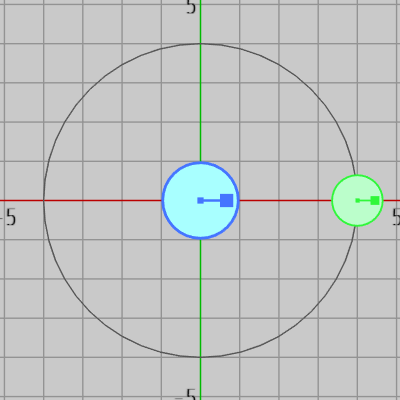
図1 惑星(青)と衛星(緑) 
図2
その場合、惑星が 10回自転する間に衛星は公転軌道上を $360^\circ$ 分進むのであるから、惑星が 1回自転する間には衛星は公転軌道上を $36^\circ$ 分だけ進むことになる。しかし、惑星が親オブジェクト、衛星がその子オブジェクとして惑星と衛星の間に親子関係が設定されていると、図2に示されるように惑星が 1回自転するたびに、惑星にアタッチされている衛星も自動的に 1回公転してしまうのである (子オブジェクトに対して何も変換を行わなくても親オブジェクトが1回自転をするたびに、子オブジェクトはアタッチポジションから1回公転する)。
したがって、惑星と衛星の間に親子関係が設定されている場合に衛星の運動を考える際は、親オブジェクトである惑星の自転の影響を差し引いて考えなければならない。また、衛星自身の自転までを考慮すると問題はさらに面倒になる。
結局、惑星と衛星の運動を考える際は両者には親子関係を設定せずに、2つの単独のオブジェクトの運動として考える方が簡単なのである。
本節の課題もまた、複数のオブジェクトによる一体化した運動であるが、オブジェクトの間に親子関係を設定するべきでない例の1つである。ここでの課題は観覧車である。
本節で使用する観覧車は以下の3種類のオブジェクトによって構成される。
いずれも初期状態であり、図3のSupportの底面は長方形で初期状態においてXZ平面に置かれており、各辺が x軸、z軸に平行である。また、Supportの底面の中心は原点に位置している。図4のWheelの初期状態における回転軸は z軸である。
オブジェクトは3種類であるが図5の Cabin は同じものが12個あり、プログラム中では Cabin[i] として配列の形で使われる (初期状態においてCabinは ほとんどの部分がXZ平面の下側、すなわち y軸マイナス側にある)。
そして、これらのオブジェクトの間で親子関係を設定するのは Support と Wheel のみであり、Supportが親で Wheelが子である。
各CabinはWheelに取り付けられた状態で回転するわけであるが、各CabinはWheelとの間に親子関係を設定しない(するべきではない)ということである。
次のプログラムはWheelをSupportにアタッチした状態で回転させるものである。
[BetaA] (実行結果 図6)

図6 BetaA 実行結果 1行目の i_degWheel はWheelの回転角度を表すインスタンス変数であり、ここでは毎フレーム $0.2^\circ$ ずつ増加させている。3行目の c_attachPos_Wheel はWheelのアタッチポジションを表すVector3型の定数であり、初期状態のWheelを c_attachPos_Wheel だけ平行移動させると図6に示される位置に移動する。
このプログラムではSupportには何も変換を実行しないので初期状態のままであり、Supportのローカル行列(及びワールド行列)は identity行列である。
実行結果(図6)に示されるように、Wheelが指定の位置で回転を行うようになるだけである。
Cabinは12個あり、それぞれWheel内の指定の位置に $30^\circ$ 間隔で配置される。
次のプログラムは初期状態のWheelに12個のCabinを配置するものである。
[BetaB] (実行結果 図7、図8)
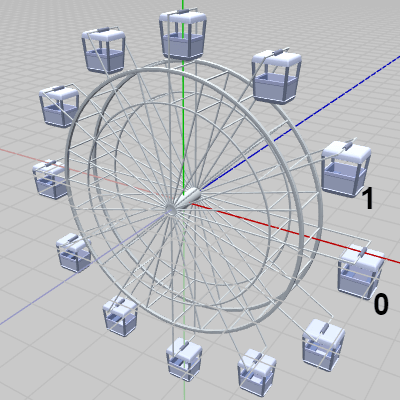
図7 BetaB 実行結果 (斜め上から見たときのもの) 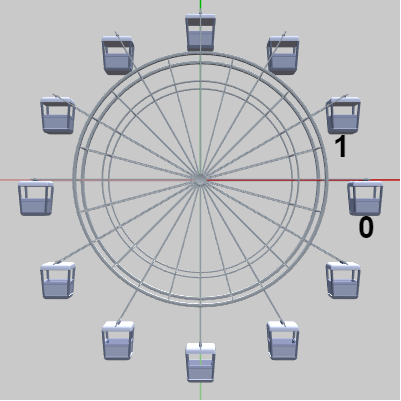
図8 BetaB 実行結果 (正面から見たときのもの)
上図7はプログラムの実行結果を斜め上から見たときのものであり、図8は正面から見たときのものである。プラス側の x軸上に配置されているのがCabin[0]であり、各Cabinはそこから $30^\circ$ 間隔で配置されている (図中の「0」「1」はCabin[0]、Cabin[1]を示している)。
5行目の c_initCabinPositions[i] は、各Cabinが配置されるWheel内の位置を示すVector3型の配列である。c_initCabinPositions[0] はCabin[0]の配置される位置であり、c_initCabinPositions[1] はCabin[1]の配置される位置である。
ただし、注意すべきは c_initCabinPositions[i] の表す位置は初期状態のWheel内の位置であるという点である。
つまり Wheelが初期状態であるときに、(初期状態の)Cabinに対して c_initCabinPositions[0] だけの平行移動を実行すれば上図に示される「0」の位置に配置され、c_initCabinPositions[1] だけの平行移動を実行すれば上図に示される「1」の位置に配置されるということである。
では以上をふまえて観覧車を回転させるプログラムを作成する。

図9 最初のプログラムにおいては、観覧車の回転は図9に示される青い長方形の上で行うものとする。図中の長方形はSupportの底面と全く同じ大きさであり、この長方形の各辺は x軸、z軸に平行である。また、長方形の中心の位置は $(12,\ 0,\ 8)$ である。
Supportの底面は初期状態において各辺が x軸、z軸に平行、そしてその中心が原点に置かれている。したがって、Supportをこの長方形の上に移動させるためには $(12,\ 0,\ 8)$ だけの平行移動を行えばよい。
使用するインスタンス変数や定数を以下に示す(これらはいずれも上記のプログラムで使われている)。
プログラムは Sec417.cs内のCode1に作成するものとする (Code1に何も記述しないまま実行すると図9の長方形が表示され、各オブジェクトは初期状態のまま原点付近で重なった状態になっている)。
この長方形はCode1と同様にSupportの底面と大きさは同じであり、長方形の中心は $(12,\ 0,\ 8)$ である。しかし、今回はその各辺が x軸、z軸に平行ではなく図11に示されるように x軸と $30^\circ$ の角をなしている。

図10 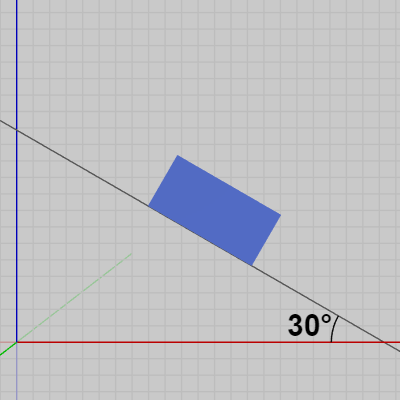
図11
プログラムは Sec417.cs内のCode2に作成するものとする (Code2に何も記述しないまま実行すると図10の長方形が表示され、各オブジェクトは初期状態のまま原点付近で重なった状態になっている)。
プログラムの解答例については Sec417_Ans.txt を参照 (Sec417_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
本章で扱ってきた一体化運動においてはオブジェクトの間に親子関係があり、どのオブジェクトもあるオブジェクトの親オブジェクト、あるいは子オブジェクトとして階層構造に含まれていた。
しかし、複数のオブジェクトが一体化して運動する場合であっても、オブジェクトの間に親子関係を設定するべきではない場合がある。例えば、その代表的な例が惑星と衛星の運動である。
惑星が一定の周期で公転や自転をする際、衛星もまたその惑星の周りを一定の周期で公転し、自転する。以下の図1における青い円盤は惑星を表しており、緑の円盤は衛星を表している。また、ここでは簡単のため惑星は自転のみを行うものとする。
例えば、惑星が 10回自転する間に衛星が惑星の周りを 1回公転するとしよう。


その場合、惑星が 10回自転する間に衛星は公転軌道上を $360^\circ$ 分進むのであるから、惑星が 1回自転する間には衛星は公転軌道上を $36^\circ$ 分だけ進むことになる。しかし、惑星が親オブジェクト、衛星がその子オブジェクとして惑星と衛星の間に親子関係が設定されていると、図2に示されるように惑星が 1回自転するたびに、惑星にアタッチされている衛星も自動的に 1回公転してしまうのである (子オブジェクトに対して何も変換を行わなくても親オブジェクトが1回自転をするたびに、子オブジェクトはアタッチポジションから1回公転する)。
したがって、惑星と衛星の間に親子関係が設定されている場合に衛星の運動を考える際は、親オブジェクトである惑星の自転の影響を差し引いて考えなければならない。また、衛星自身の自転までを考慮すると問題はさらに面倒になる。
結局、惑星と衛星の運動を考える際は両者には親子関係を設定せずに、2つの単独のオブジェクトの運動として考える方が簡単なのである。
本節の課題もまた、複数のオブジェクトによる一体化した運動であるが、オブジェクトの間に親子関係を設定するべきでない例の1つである。ここでの課題は観覧車である。
本節で使用する観覧車は以下の3種類のオブジェクトによって構成される。
-
 図3 Support 初期状態
図3 Support 初期状態 -
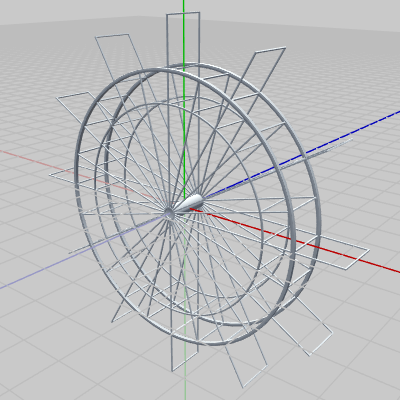 図4 Wheel 初期状態
図4 Wheel 初期状態 -
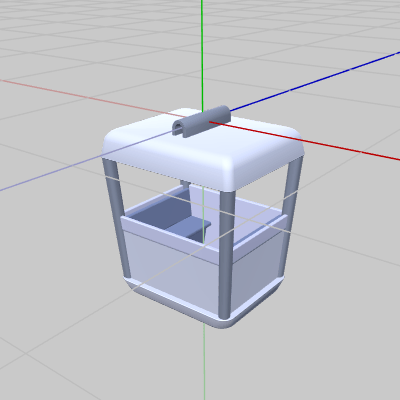 図5 Cabin 初期状態 (同じものが12個ありプログラム中ではCabin[0] ~ Cabin[11]として使われる)
図5 Cabin 初期状態 (同じものが12個ありプログラム中ではCabin[0] ~ Cabin[11]として使われる)
いずれも初期状態であり、図3のSupportの底面は長方形で初期状態においてXZ平面に置かれており、各辺が x軸、z軸に平行である。また、Supportの底面の中心は原点に位置している。図4のWheelの初期状態における回転軸は z軸である。
オブジェクトは3種類であるが図5の Cabin は同じものが12個あり、プログラム中では Cabin[i] として配列の形で使われる (初期状態においてCabinは ほとんどの部分がXZ平面の下側、すなわち y軸マイナス側にある)。
そして、これらのオブジェクトの間で親子関係を設定するのは Support と Wheel のみであり、Supportが親で Wheelが子である。
各CabinはWheelに取り付けられた状態で回転するわけであるが、各CabinはWheelとの間に親子関係を設定しない(するべきではない)ということである。
次のプログラムはWheelをSupportにアタッチした状態で回転させるものである。
[BetaA] (実行結果 図6)
i_degWheel += 0.2f; Matrix4x4 rotWheel = TH3DMath.GetRotation4x4(i_degWheel, Vector3.forward); Matrix4x4 traWheel = TH3DMath.GetTranslation4x4(c_attachPos_Wheel); Matrix4x4 localWheel = traWheel * rotWheel; Matrix4x4 localSupport = Matrix4x4.identity; Matrix4x4 worldWheel = localSupport * localWheel; Matrix4x4 worldSupport = localSupport; Wheel.SetMatrix(worldWheel); Support.SetMatrix(worldSupport);

このプログラムではSupportには何も変換を実行しないので初期状態のままであり、Supportのローカル行列(及びワールド行列)は identity行列である。
実行結果(図6)に示されるように、Wheelが指定の位置で回転を行うようになるだけである。
Cabinは12個あり、それぞれWheel内の指定の位置に $30^\circ$ 間隔で配置される。
次のプログラムは初期状態のWheelに12個のCabinを配置するものである。
[BetaB] (実行結果 図7、図8)
Wheel.SetMatrix(Matrix4x4.identity);
for (int i = 0; i < Cabin.Length; i++)
{
Matrix4x4 T = TH3DMath.GetTranslation4x4(c_initCabinPositions[i]);
Cabin[i].SetMatrix(T);
}


上図7はプログラムの実行結果を斜め上から見たときのものであり、図8は正面から見たときのものである。プラス側の x軸上に配置されているのがCabin[0]であり、各Cabinはそこから $30^\circ$ 間隔で配置されている (図中の「0」「1」はCabin[0]、Cabin[1]を示している)。
5行目の c_initCabinPositions[i] は、各Cabinが配置されるWheel内の位置を示すVector3型の配列である。c_initCabinPositions[0] はCabin[0]の配置される位置であり、c_initCabinPositions[1] はCabin[1]の配置される位置である。
ただし、注意すべきは c_initCabinPositions[i] の表す位置は初期状態のWheel内の位置であるという点である。
つまり Wheelが初期状態であるときに、(初期状態の)Cabinに対して c_initCabinPositions[0] だけの平行移動を実行すれば上図に示される「0」の位置に配置され、c_initCabinPositions[1] だけの平行移動を実行すれば上図に示される「1」の位置に配置されるということである。
では以上をふまえて観覧車を回転させるプログラムを作成する。
# Code1

Supportの底面は初期状態において各辺が x軸、z軸に平行、そしてその中心が原点に置かれている。したがって、Supportをこの長方形の上に移動させるためには $(12,\ 0,\ 8)$ だけの平行移動を行えばよい。
使用するインスタンス変数や定数を以下に示す(これらはいずれも上記のプログラムで使われている)。
i_degWheel
: Wheelの回転角度を表すfloat型インスタンス変数である。c_attachPos_Wheel
: Wheelのアタッチポジションを表すVector3型の定数である。c_initCabinPositions
: 12個のCabinの配置される位置を表すVector3型の定数配列である。それらの位置は初期状態におけるWheel内の位置である。プログラムは Sec417.cs内のCode1に作成するものとする (Code1に何も記述しないまま実行すると図9の長方形が表示され、各オブジェクトは初期状態のまま原点付近で重なった状態になっている)。
# Code2
このプログラムもまた観覧車を回転させるプログラムであるが、今回は観覧車を図10の青い長方形の上に置くものとする。この長方形はCode1と同様にSupportの底面と大きさは同じであり、長方形の中心は $(12,\ 0,\ 8)$ である。しかし、今回はその各辺が x軸、z軸に平行ではなく図11に示されるように x軸と $30^\circ$ の角をなしている。


プログラムは Sec417.cs内のCode2に作成するものとする (Code2に何も記述しないまま実行すると図10の長方形が表示され、各オブジェクトは初期状態のまま原点付近で重なった状態になっている)。
プログラムの解答例については Sec417_Ans.txt を参照 (Sec417_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
© 2020-2025 Redpoll's 60 (All rights reserved)