Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-14
第4章 3D空間におけるオブジェクトの運動
$§$4-14 一体化したオブジェクトの運動 4
本節からは再びオブジェクトの運動に焦点を当てる。
一体化するオブジェクトの数や階層構造に関しては今までのものより多少複雑になるが、実装の難易度が上がるわけではない。
本節で使用するオブジェクト及び その階層構造を以下に示す。
図1 Pole 初期状態 
図2 Arm0、Arm1、Arm2 初期状態
使用するオブジェクトは図1から図4の4種類のオブジェクトであるが、Arm(図2)、Box(図3)、Propeller(図4)は3つずつあり、それぞれ Arm0、Arm1、Arm2、Box0、Box1、Box2、Propeller0、Propeller1、Propeller2という名前で使われる (これらの複数あるオブジェクトは形、大きさ、初期状態 いずれも同じである)。図1の Poleは正六角形の柱である。
図5は全てのオブジェクトを一体化した際の階層構造である (一番上の親オブジェクトがPoleであり、Poleの直接の子が3つのArmである。3つのArmはそれぞれBoxを子オブジェクトとして持っており、それらのBoxも子オブジェクトとしてPropellerを持っている)。
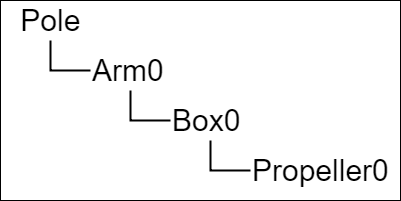
図6 オブジェクトの階層構造 Arm、Box、Propellerは3つずつあるが、まずは1組だけ(Propeller0、Box0、Arm0)を使った場合の運動を見ていく。
以下のプログラムは Propeller0、Box0、Arm0、Poleを一体化するだけの処理を記述したものである。
図6はこの一体化における階層構造である。
(プログラム中では Propeller、Box、Armは配列として使われているため、Propeller0、Box0、Arm0はプログラムにおいては Propeller[0]、Box[0]、Arm[0] である)
[Beta1] (実行結果 図8)
Poleは初期状態のままである。Arm0も同様に初期状態であるが、図7に示されるように Arm0は初期状態の位置がすでに Poleの1つの側面上に位置している。Box0、Propeller0に実行される変換はアタッチポジションへの平行移動のみである (1行目、2行目の定数 c_attachPos_Propeller、c_attachPos_Box は Propeller0、Box0のアタッチポジションを表しているが、これらの値はそれぞれのオブジェクトの親座標系での値である)。
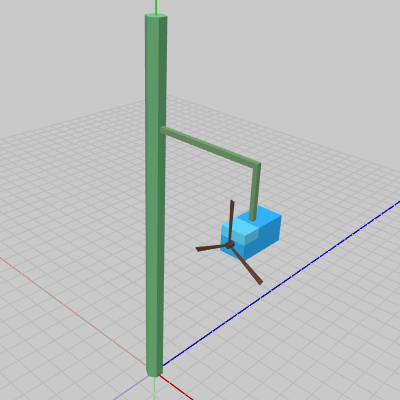
図7 Beta1 実行結果 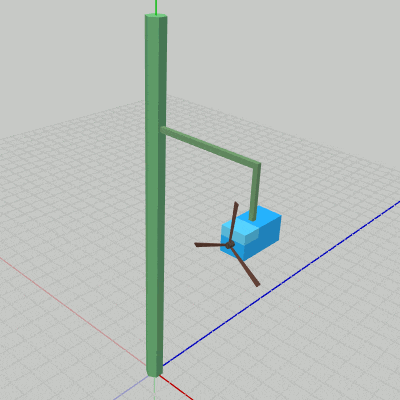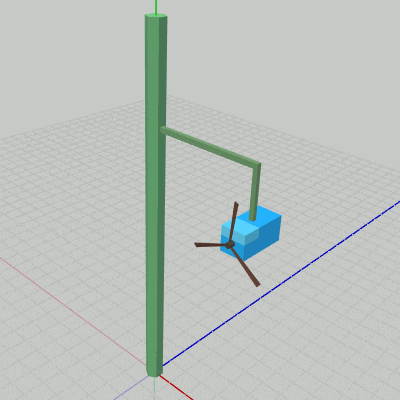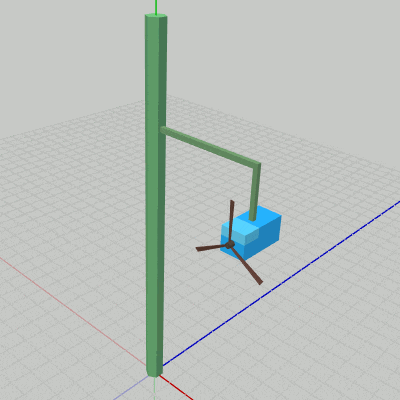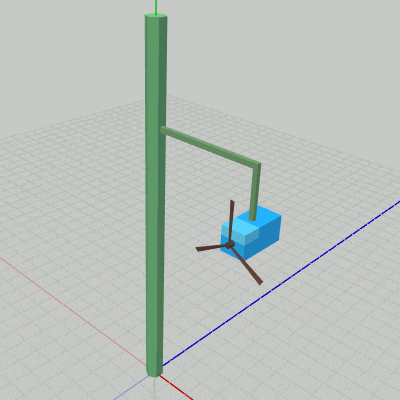
図8 Code1 実行結果
次に、この状態から Box0にアタッチされている Propeller0を回転させる。
[Code1] (実行結果 図8)
Beta1からの変更点は1箇所で、それは localPropeller の内容である(1~4行目)。Beta1ではアタッチポジションへの平行移動だけであったが、ここでは毎フレーム $-6$°ずつの回転を実行している。i_degPropeller は Propeller0の回転角度を表すインスタンス変数で、毎フレーム $6$ずつ減少する。localPropellerの内容は、Propeller0を初期状態の位置で角度i_degPropellerだけ回転させ、その状態でアタッチポジションへの平行移動を実行するという2つの処理をまとめたものである (Propellerは初期状態において z軸周りに回転を行うので、2行目のメソッドの第2引数は z軸プラス方向を表すVector3.forwardとなっている)。
これによって、図8に示されるように Propeller0は Box0にアタッチされている状態で回転を行うことになる。
Arm0の運動は単振動による上昇下降である。具体的には、初期状態の位置からy軸方向に振幅$3$の単振動を行う (単振動については1-10節参照)。
[Beta2] (実行結果 図9)
Code1からの変更点は1箇所で、それは localArm の内容である(11~13行目)。Code1では localArmは identity行列であったが、ここでは振幅$3$の単振動を実行する。11行目の i_shmArmは単振動の計算で使われる角度を表すインスタンス変数で、毎フレーム$1$ずつ増加するので Armは初期状態の位置から振幅$3$の上昇下降を$360$フレームかけて行うことになる (上昇下降の1往復に360フレームかかる)。12行目が実際の単振動の計算であり myの値は $-3$から $3$の間を往復する。
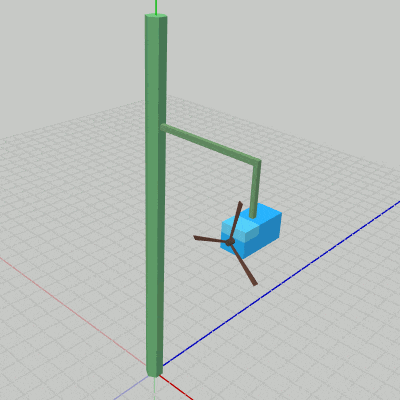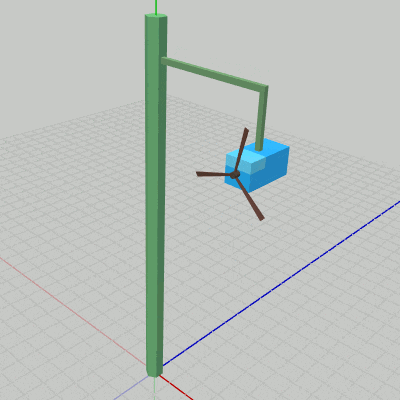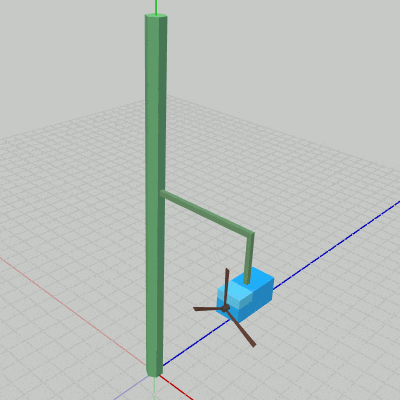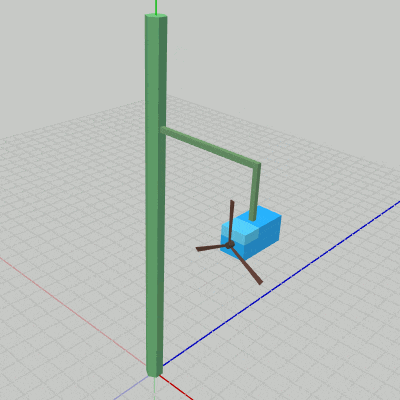
図9 Beta2 実行結果 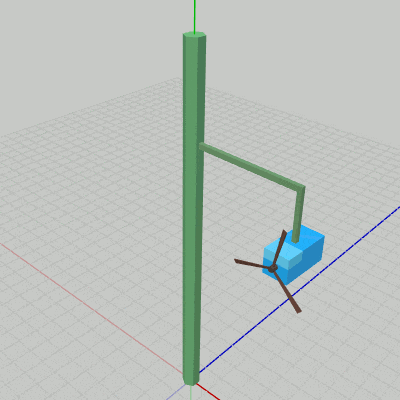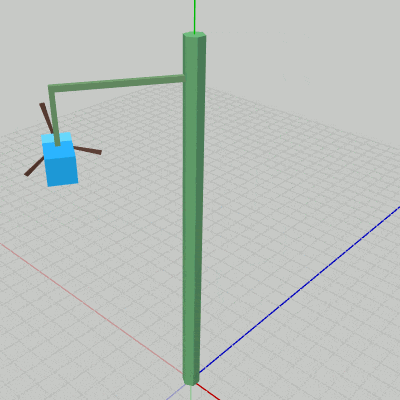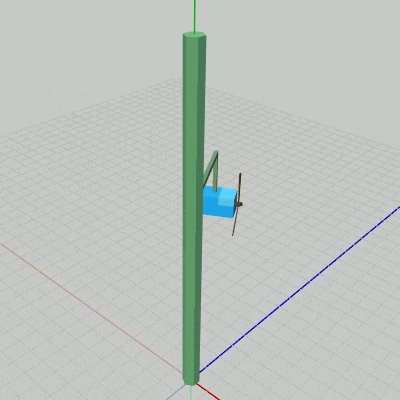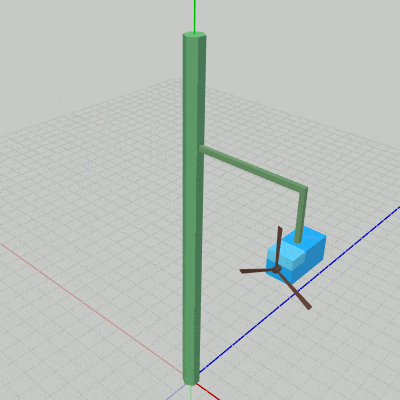
図10 Code2 実行結果
ではさらに、Poleの回転も追加しよう。Poleの回転は初期状態の位置において、y軸周りの回転を行うだけである。
[Code2] (実行結果 図10)
Beta2からの変更点は1箇所で、それは localPole の内容が identity行列からy軸周りに回転を行う回転行列に変わっている点のみである (16~17行目)。16行目の i_degPoleは、Poleの回転角度を表すインスタンス変数で毎フレーム$1$ずつ増加するので、Poleはy軸周りに毎フレーム$1$°ずつ回転を行う (図10)。
まずは、すべてのオブジェクトを一体化するプログラムから始める。
[Beta3] (実行結果 図11)
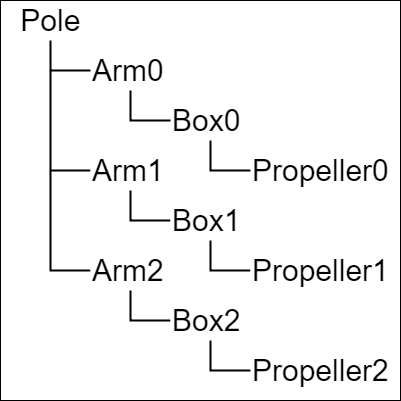
図5 オブジェクトの階層構造 
図11 Beta3 実行結果 (各Arm、Box、Propellerはずらして表示してある)
冒頭でも述べたように、Arm、Box、Propellerは3つずつあり、いずれも形、大きさ、初期状態が同じである (図5はすべてを一体化した際の階層構造)。
このプログラムは、すべてのオブジェクトを一体化するだけのものである。Arm、Box、Propellerについてはいずれも形、大きさ、初期状態だけでなく、ここではアタッチポジションも同じなので、実行すると3組は完全に重なって表示されてしまう。そのため実行結果の図11では3組をややずらして表示してある。
Beta3では3組すべてが同じ位置に置かれる結果となった。Poleは正六角形の柱であるが、次のプログラムではこのPoleの3つの面のそれぞれに1組ずつ配置されるように書き改めよう。
[Code3] (実行結果 図13)
Beta3では localArm の内容は、3つの Armいずれの場合も identity行列であったが、今回は各Armを Poleの3つの面に配置するために localArmの内容は回転行列になっている。図12は今回の実行結果を Poleの真上から見下ろしたときのものであるが、 この図に示されるように Arm0、Arm1、Arm2は$120$°の間隔で配置される。したがって、7行目の localArmの内容は Arm0のときは$0$°の回転、Arm1のときは$120$°の回転、Arm2のときは$240$°の回転となる。
各Box及びPropellerは各Armの子オブジェクトなので、たとえば Arm1を$120$°回転させるとその子オブジェクトであるBox1、Propeller1も同様に図11の位置から$120$°回転した位置に来る。Arm2を$240$°回転させた場合も同様に子オブジェクトであるBox2、Propeller2は図11の位置から$240$°回転した位置に来る。そして結果的には、3組のArm、Box、Propellerは図13に示されるようにPoleの3つの面に等間隔で配置されるようになる。
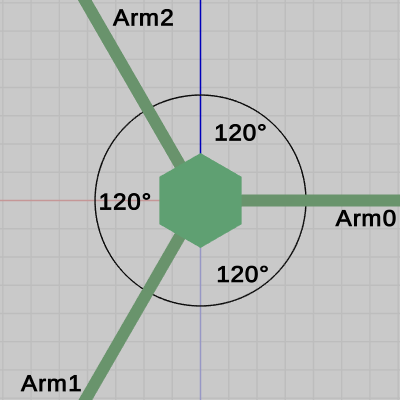
図12 Arm0、Arm1、Arm2をPoleの3つの面に配置する (Poleの真上から見下ろしたときの様子) 
図13 Code3 実行結果
3組のArm、Box、Propellerを図13のように等間隔に配置するために、Armのローカル行列である localArmの内容だけを変えていることに注意しよう。各Box及びPropellerのローカル行列 localBox、localPropellerの内容は3つのBox、3つのPropellerで同じものである (親オブジェクトにアタッチするための移動のみ)。
まず、3つのPropellerの回転から実装する。
[Beta4A] (実行結果 図14)

図14 Beta4A 実行結果 Code3からの変更点は1箇所で、それは localPropeller の内容である (2~5行目)。しかし、この localPropellerもCode1、Code2のものと内容は同じであり、毎フレーム$6$°ずつ Propellerを回転させるための回転行列である。
今回は Arm、Box、Propellerは3組あるが、3つのPropellerのローカル行列localPropellerの内容は同じであるので、実行結果である図14に示されるように3つのPropellerはいずれも各Boxの先端で毎フレーム$6$°ずつの回転を行うことになる。
実際に3つのPropellerに実行される行列は20行目の worldPropeller であるが、この worldPropellerは4つのローカル行列の積であり、その内容は3つのPropellerで異なる。具体的には、各Propellerにおける worldPropellerの計算では、localArmは先程のCode3と同じく回転行列であるが、それぞれの場合でその回転角度が異なっている。
もし、worldPropellerの計算において localArmの内容が3つのPropellerで同じ内容、たとえば identity行列ならば、その場合の実行結果は図11のように3組のArm、Box、Propellerが重なった状態で3つのPropellerが同じ速度で回転を行う結果になる。
続いて、3つのArmのそれぞれに単振動を実行する。
[Beta4B] (実行結果 図15)
上のBeta4Aからの変更点は1箇所で、それは localArm の内容である。Beta4Aでの localArmは、Poleの3つの面に配置するための回転行列であったが、ここでは Poleの各面に配置した後に単振動を実行する。
具体的には、20行目の rotArmが Poleの各面に配置するための回転行列であり、19行目の traArmがその配置された面において振幅$3$の単振動を行う平行移動行列である。この単振動はCode2のものとほとんど同じである。単振動の計算に使われる角度i_shmArmは毎フレーム$1$ずつ増加するので(14行目)、3つのArmは360フレームごとにy軸方向に$-3$から$3$の上昇下降を行う。
ただし、ここでは18行目の単振動の計算においてその角度が (i_shmArm + i * 60) となっているが、これは3つのArmの上昇下降をずらして行わせるための調整である。

図15 Beta4B 実行結果 
図16
プログラムの実行結果 図15に示されるように、3つのArmの単振動は上昇下降のタイミングが同じではない。これは、18行目の単振動の計算における角度が Arm0のときには (i_shmArm + 0)、Arm1のときには (i_shmArm + 60)、Arm2のときには (i_shmArm + 120) となるためである。つまり、この調整によって Arm1は Arm0に比べて常に$60$°分進んだ位置で単振動を行い、Arm2は Arm0に比べて常に$120$°分進んだ位置で単振動を行うことになる。
もし、18行目の単振動の計算における角度にこのような調整を行わずに、(i_shmArm + i * 60) をただ単に i_shmArm とした場合は図16のような実行結果になる。この場合には3つのArmの上昇下降のタイミングは同じになる。
ここで再度、Poleの回転を追加する。
[Code4] (実行結果 図17)

図17 Code4 実行結果 Beta4Bからの変更点は1箇所で、それは Poleのローカル行列 localPole の内容が identity行列からy軸周りの回転行列になった点である (12行目)。
繰り返しになるが、3組のArm、Box、Propellerが Poleの各面において、それぞれのタイミングで上昇下降を行うのは各組のArmのローカル行列localArmの内容が異なるからである。Boxのローカル行列は3つのBoxで共通であり、Propellerのローカル行列は3つのPropellerで共通である。もし、Arm0、Arm1、Arm2のローカル行列の内容が同じである場合には、3組のArm、Box、Propellerは完全に重なった状態になり、3組は重なった状態で Poleのある1つの面において上昇下降をすることになるが、このときの実行結果は1組のArm、Box、Propellerのみを運動させた場合の実行結果 Code2の図10と全く区別がつかないものになる。
使用するキー及びそれに対応する処理は以下のとおり。
J : Poleの回転の ON/OFF (長押し非対応)。
K : 3つの Armの単振動の ON/OFF (長押し非対応)。
L : Box0の回転 (長押しに対応する ; Shiftキーと同時押しで逆方向に回転)。
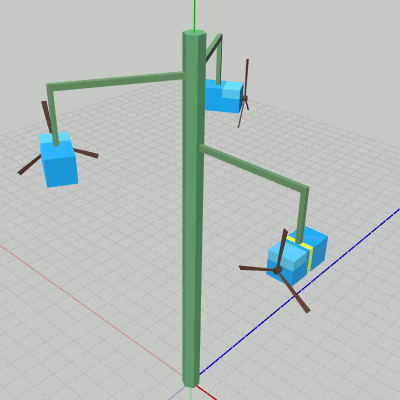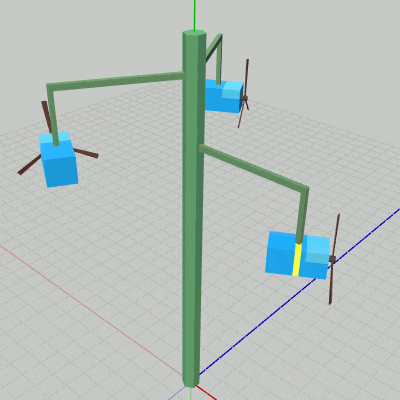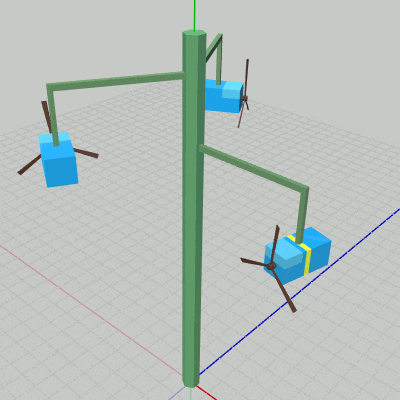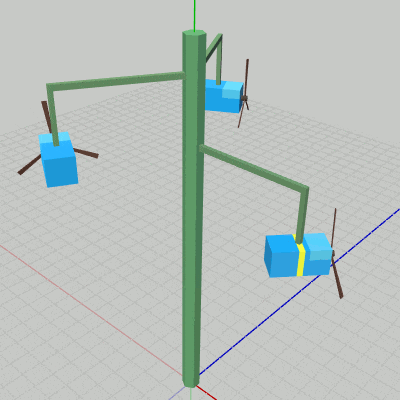
図18 Lキーを押しているときの動作 Jキーを押すと、Poleが回転中であれば停止し、停止していれば回転する。Kキーは3つのArmすべての 運動/停止 のスイッチで、3つのArmが上昇下降しているときに押すと3つのArmすべてが停止し、停止しているときに押すと3つのArmすべてが上昇下降を再開する。Lキーは1つのBoxの運動を操作するためものである。長押しに対応しており、具体的には Lキーを押している際は、Arm0の先端で Box0が自身の中心を貫通するy軸に平行な軸周りの回転を行うことになる。
図18はPoleとArmが停止している状態でLキーを押しているときの様子である。回転しているBoxがBox0であり、今回のプログラムではBox0にだけ他のBoxと区別するための黄色いラインが描かれている。
プログラムを以下に示す。
[Code5] (実行結果 図19)

図19 Code5 実行結果 1~12行目がキー操作のコードである。Jキーを押したとき、Kキーを押したときには i_switch_Pole、i_switch_Arm の値が更新されるが、この2つの変数は Pole、Armの 運動/停止 のためのbool型インスタンス変数である。Jキー、Kキーが押されるたびにこれらのbool型変数の値が反転する。
たとえば、i_switch_Poleの値がtrueであるときには29行目において i_degPoleの値が $1$ ずつ増加する。したがって、i_switch_Poleがtrueである間は毎フレーム Poleはy軸周りに $1^\circ$ ずつ回転することになる。i_switch_Poleの値がfalseのときには29行目において i_degPoleの値は変化しないので、結果的に Poleは停止状態になる。
i_switch_Armについても同様である。i_switch_Armがtrueである間は33行目において i_shmArmの値が $1$ ずつ増加するので、毎フレーム Armは $1^\circ$ 分ずつ単振動を行うが、i_switch_Armがfalseのときには33行目において i_shmArmの値が変化しないので、Armは停止状態になる (Code5においては、i_switch_Poleの初期値はfalse、i_switch_Armの初期値はtrueである)。
Lキーを押している間はBox0の回転角度を表すインスタンス変数 i_degBox0 が更新される (9~12行目)。Lキーだけを押している場合は i_degBox0は毎フレーム$2$ずつ増加し、Shiftキーと同時に押している場合は$2$ずつ減少する (11行目のTHUtil.IsShiftDown()はカスタムライブラリのメソッドでShiftキーが押されていればtrueを返す)。
このプログラムにおいては Box0だけは独自に回転を行う、そのため Box0のローカル行列は、Box1、Box2のローカル行列とは同じにはできない。したがって、23行目では Box1、Box2用のローカル行列 lcBox を求め、26行目で Box0用のローカル行列 lcBox0 を求めている。
lcBoxはArmの先端にアタッチするだけの平行移動行列であるが、lcBox0はまず初期状態の位置でy軸周りに角度i_degBox0だけ回転し、回転した状態でArmの先端にアタッチするという2つの変換をまとめたものである。
37行目の記述は
Box0のワールド行列を計算する際には lcBox0が使われるように、そして Box1、Box2のワールド行列を計算する際には lcBoxが使われるようにするためのものである。
なお、以前にも指摘したが プログラムにおけるワールド行列の計算には'無駄な'計算が含まれている。例えば、本節においても4つのオブジェクトのワールド行列計算は次のように記述されているが、
この計算において localPole * localArm などは3回書かれている。つまり、同じ計算を3回行っているのである。
このように敢えて'無駄な'処理を残しているのは、階層構造にあるオブジェクトのワールド行列の計算内容を印象付けるためであり、そのための形式的な記述として捉えていただきたい。
一体化するオブジェクトの数や階層構造に関しては今までのものより多少複雑になるが、実装の難易度が上がるわけではない。
本節で使用するオブジェクト及び その階層構造を以下に示す。


-
 図3 Box0、Box1、Box2 初期状態
図3 Box0、Box1、Box2 初期状態 -
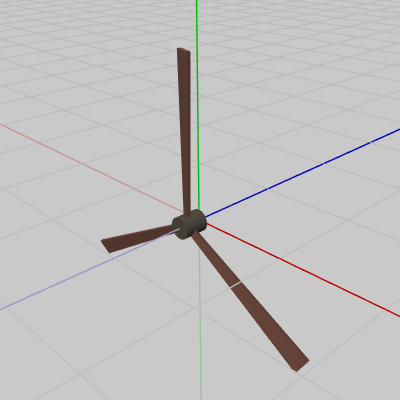 図4 Propeller0、Propeller1、Propeller2 初期状態
図4 Propeller0、Propeller1、Propeller2 初期状態 -
 図5 オブジェクトの階層構造
図5 オブジェクトの階層構造
使用するオブジェクトは図1から図4の4種類のオブジェクトであるが、Arm(図2)、Box(図3)、Propeller(図4)は3つずつあり、それぞれ Arm0、Arm1、Arm2、Box0、Box1、Box2、Propeller0、Propeller1、Propeller2という名前で使われる (これらの複数あるオブジェクトは形、大きさ、初期状態 いずれも同じである)。図1の Poleは正六角形の柱である。
図5は全てのオブジェクトを一体化した際の階層構造である (一番上の親オブジェクトがPoleであり、Poleの直接の子が3つのArmである。3つのArmはそれぞれBoxを子オブジェクトとして持っており、それらのBoxも子オブジェクトとしてPropellerを持っている)。
# Code1

以下のプログラムは Propeller0、Box0、Arm0、Poleを一体化するだけの処理を記述したものである。
図6はこの一体化における階層構造である。
(プログラム中では Propeller、Box、Armは配列として使われているため、Propeller0、Box0、Arm0はプログラムにおいては Propeller[0]、Box[0]、Arm[0] である)
[Beta1] (実行結果 図8)
Matrix4x4 localPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller); Matrix4x4 localBox = TH3DMath.GetTranslation4x4(c_attachPos_Box); Matrix4x4 localArm = Matrix4x4.identity; Matrix4x4 localPole = Matrix4x4.identity; Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller; Matrix4x4 worldBox = localPole * localArm * localBox; Matrix4x4 worldArm = localPole * localArm; Matrix4x4 worldPole = localPole; Propeller[0].SetMatrix(worldPropeller); Box[0].SetMatrix(worldBox); Arm[0].SetMatrix(worldArm); Pole.SetMatrix(worldPole);
Poleは初期状態のままである。Arm0も同様に初期状態であるが、図7に示されるように Arm0は初期状態の位置がすでに Poleの1つの側面上に位置している。Box0、Propeller0に実行される変換はアタッチポジションへの平行移動のみである (1行目、2行目の定数 c_attachPos_Propeller、c_attachPos_Box は Propeller0、Box0のアタッチポジションを表しているが、これらの値はそれぞれのオブジェクトの親座標系での値である)。


次に、この状態から Box0にアタッチされている Propeller0を回転させる。
[Code1] (実行結果 図8)
i_degPropeller -= 6; Matrix4x4 rotPropeller = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward); Matrix4x4 traPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller); Matrix4x4 localPropeller = traPropeller * rotPropeller; Matrix4x4 localBox = TH3DMath.GetTranslation4x4(c_attachPos_Box); Matrix4x4 localArm = Matrix4x4.identity; Matrix4x4 localPole = Matrix4x4.identity; Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller; Matrix4x4 worldBox = localPole * localArm * localBox; Matrix4x4 worldArm = localPole * localArm; Matrix4x4 worldPole = localPole; Propeller[0].SetMatrix(worldPropeller); Box[0].SetMatrix(worldBox); Arm[0].SetMatrix(worldArm); Pole.SetMatrix(worldPole);
Beta1からの変更点は1箇所で、それは localPropeller の内容である(1~4行目)。Beta1ではアタッチポジションへの平行移動だけであったが、ここでは毎フレーム $-6$°ずつの回転を実行している。i_degPropeller は Propeller0の回転角度を表すインスタンス変数で、毎フレーム $6$ずつ減少する。localPropellerの内容は、Propeller0を初期状態の位置で角度i_degPropellerだけ回転させ、その状態でアタッチポジションへの平行移動を実行するという2つの処理をまとめたものである (Propellerは初期状態において z軸周りに回転を行うので、2行目のメソッドの第2引数は z軸プラス方向を表すVector3.forwardとなっている)。
これによって、図8に示されるように Propeller0は Box0にアタッチされている状態で回転を行うことになる。
# Code2
続いて、Arm0及び Poleの運動を定義する。Arm0の運動は単振動による上昇下降である。具体的には、初期状態の位置からy軸方向に振幅$3$の単振動を行う (単振動については1-10節参照)。
[Beta2] (実行結果 図9)
// Propeller i_degPropeller -= 6; Matrix4x4 rotPropeller = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward); Matrix4x4 traPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller); Matrix4x4 localPropeller = traPropeller * rotPropeller; // Box Matrix4x4 localBox = TH3DMath.GetTranslation4x4(c_attachPos_Box); // Arm i_shmArm += 1; float my = 3.0f * Mathf.Sin(i_shmArm * Mathf.Deg2Rad); // -3.0 -- 3.0 Matrix4x4 localArm = TH3DMath.GetTranslation4x4(0.0f, my, 0.0f); // Pole Matrix4x4 localPole = Matrix4x4.identity; // world matrix Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller; Matrix4x4 worldBox = localPole * localArm * localBox; Matrix4x4 worldArm = localPole * localArm; Matrix4x4 worldPole = localPole; Propeller[0].SetMatrix(worldPropeller); Box[0].SetMatrix(worldBox); Arm[0].SetMatrix(worldArm); Pole.SetMatrix(worldPole);
Code1からの変更点は1箇所で、それは localArm の内容である(11~13行目)。Code1では localArmは identity行列であったが、ここでは振幅$3$の単振動を実行する。11行目の i_shmArmは単振動の計算で使われる角度を表すインスタンス変数で、毎フレーム$1$ずつ増加するので Armは初期状態の位置から振幅$3$の上昇下降を$360$フレームかけて行うことになる (上昇下降の1往復に360フレームかかる)。12行目が実際の単振動の計算であり myの値は $-3$から $3$の間を往復する。


ではさらに、Poleの回転も追加しよう。Poleの回転は初期状態の位置において、y軸周りの回転を行うだけである。
[Code2] (実行結果 図10)
// Propeller i_degPropeller -= 6; Matrix4x4 rotPropeller = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward); Matrix4x4 traPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller); Matrix4x4 localPropeller = traPropeller * rotPropeller; // Box Matrix4x4 localBox = TH3DMath.GetTranslation4x4(c_attachPos_Box); // Arm i_shmArm += 1; float my = 3.0f * Mathf.Sin(i_shmArm * Mathf.Deg2Rad); // -3.0 -- 3.0 Matrix4x4 localArm = TH3DMath.GetTranslation4x4(0.0f, my, 0.0f); // Pole i_degPole += 1; Matrix4x4 localPole = TH3DMath.GetRotation4x4(i_degPole, Vector3.up); // world matrix Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller; Matrix4x4 worldBox = localPole * localArm * localBox; Matrix4x4 worldArm = localPole * localArm; Matrix4x4 worldPole = localPole; Propeller[0].SetMatrix(worldPropeller); Box[0].SetMatrix(worldBox); Arm[0].SetMatrix(worldArm); Pole.SetMatrix(worldPole);
Beta2からの変更点は1箇所で、それは localPole の内容が identity行列からy軸周りに回転を行う回転行列に変わっている点のみである (16~17行目)。16行目の i_degPoleは、Poleの回転角度を表すインスタンス変数で毎フレーム$1$ずつ増加するので、Poleはy軸周りに毎フレーム$1$°ずつ回転を行う (図10)。
# Code3
今までのプログラムでは、Arm、Box、Propellerは1組のみを使っていたが、ここからは3組すべてを使用する。まずは、すべてのオブジェクトを一体化するプログラムから始める。
[Beta3] (実行結果 図11)
Matrix4x4 localPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller);
Matrix4x4 localBox = TH3DMath.GetTranslation4x4(c_attachPos_Box);
Matrix4x4 localArm = Matrix4x4.identity;
Matrix4x4 localPole = Matrix4x4.identity;
for (int i = 0; i < 3; i++)
{
Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller;
Matrix4x4 worldBox = localPole * localArm * localBox;
Matrix4x4 worldArm = localPole * localArm;
Propeller[i].SetMatrix(worldPropeller);
Box[i].SetMatrix(worldBox);
Arm[i].SetMatrix(worldArm);
}
Matrix4x4 worldPole = localPole;
Pole.SetMatrix(worldPole);


冒頭でも述べたように、Arm、Box、Propellerは3つずつあり、いずれも形、大きさ、初期状態が同じである (図5はすべてを一体化した際の階層構造)。
このプログラムは、すべてのオブジェクトを一体化するだけのものである。Arm、Box、Propellerについてはいずれも形、大きさ、初期状態だけでなく、ここではアタッチポジションも同じなので、実行すると3組は完全に重なって表示されてしまう。そのため実行結果の図11では3組をややずらして表示してある。
Beta3では3組すべてが同じ位置に置かれる結果となった。Poleは正六角形の柱であるが、次のプログラムではこのPoleの3つの面のそれぞれに1組ずつ配置されるように書き改めよう。
[Code3] (実行結果 図13)
Matrix4x4 localPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller);
Matrix4x4 localBox = TH3DMath.GetTranslation4x4(c_attachPos_Box);
Matrix4x4 localPole = Matrix4x4.identity;
for (int i = 0; i < 3; i++)
{
Matrix4x4 localArm = TH3DMath.GetRotation4x4(i * 120, Vector3.up);
Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller;
Matrix4x4 worldBox = localPole * localArm * localBox;
Matrix4x4 worldArm = localPole * localArm;
Propeller[i].SetMatrix(worldPropeller);
Box[i].SetMatrix(worldBox);
Arm[i].SetMatrix(worldArm);
}
Matrix4x4 worldPole = localPole;
Pole.SetMatrix(worldPole);
Beta3では localArm の内容は、3つの Armいずれの場合も identity行列であったが、今回は各Armを Poleの3つの面に配置するために localArmの内容は回転行列になっている。図12は今回の実行結果を Poleの真上から見下ろしたときのものであるが、 この図に示されるように Arm0、Arm1、Arm2は$120$°の間隔で配置される。したがって、7行目の localArmの内容は Arm0のときは$0$°の回転、Arm1のときは$120$°の回転、Arm2のときは$240$°の回転となる。
各Box及びPropellerは各Armの子オブジェクトなので、たとえば Arm1を$120$°回転させるとその子オブジェクトであるBox1、Propeller1も同様に図11の位置から$120$°回転した位置に来る。Arm2を$240$°回転させた場合も同様に子オブジェクトであるBox2、Propeller2は図11の位置から$240$°回転した位置に来る。そして結果的には、3組のArm、Box、Propellerは図13に示されるようにPoleの3つの面に等間隔で配置されるようになる。


3組のArm、Box、Propellerを図13のように等間隔に配置するために、Armのローカル行列である localArmの内容だけを変えていることに注意しよう。各Box及びPropellerのローカル行列 localBox、localPropellerの内容は3つのBox、3つのPropellerで同じものである (親オブジェクトにアタッチするための移動のみ)。
# Code4
Code2では1組のArm、Box、Propellerが運動するプログラムを作成したが、ここでは3組のArm、Box、Propellerすべてが運動するようにしてみよう。まず、3つのPropellerの回転から実装する。
[Beta4A] (実行結果 図14)
// Propeller
i_degPropeller -= 6;
Matrix4x4 rotPropeller = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward);
Matrix4x4 traPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller);
Matrix4x4 localPropeller = traPropeller * rotPropeller;
// Box
Matrix4x4 localBox = TH3DMath.GetTranslation4x4(c_attachPos_Box);
// Pole
Matrix4x4 localPole = Matrix4x4.identity;
for (int i = 0; i < 3; i++)
{
// Arm
Matrix4x4 localArm = TH3DMath.GetRotation4x4(i * 120, Vector3.up);
// world matrix : Propeller, Box, Arm
Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller;
Matrix4x4 worldBox = localPole * localArm * localBox;
Matrix4x4 worldArm = localPole * localArm;
Propeller[i].SetMatrix(worldPropeller);
Box[i].SetMatrix(worldBox);
Arm[i].SetMatrix(worldArm);
}
// world matrix : Pole
Matrix4x4 worldPole = localPole;
Pole.SetMatrix(worldPole);

今回は Arm、Box、Propellerは3組あるが、3つのPropellerのローカル行列localPropellerの内容は同じであるので、実行結果である図14に示されるように3つのPropellerはいずれも各Boxの先端で毎フレーム$6$°ずつの回転を行うことになる。
実際に3つのPropellerに実行される行列は20行目の worldPropeller であるが、この worldPropellerは4つのローカル行列の積であり、その内容は3つのPropellerで異なる。具体的には、各Propellerにおける worldPropellerの計算では、localArmは先程のCode3と同じく回転行列であるが、それぞれの場合でその回転角度が異なっている。
もし、worldPropellerの計算において localArmの内容が3つのPropellerで同じ内容、たとえば identity行列ならば、その場合の実行結果は図11のように3組のArm、Box、Propellerが重なった状態で3つのPropellerが同じ速度で回転を行う結果になる。
続いて、3つのArmのそれぞれに単振動を実行する。
[Beta4B] (実行結果 図15)
// Propeller
i_degPropeller -= 6;
Matrix4x4 rotPropeller = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward);
Matrix4x4 traPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller);
Matrix4x4 localPropeller = traPropeller * rotPropeller;
// Box
Matrix4x4 localBox = TH3DMath.GetTranslation4x4(c_attachPos_Box);
// Pole
Matrix4x4 localPole = Matrix4x4.identity;
i_shmArm += 1;
for (int i = 0; i < 3; i++)
{
// Arm
float my = 3.0f * Mathf.Sin((i_shmArm + i * 60) * Mathf.Deg2Rad); // -3.0 -- 3.0
Matrix4x4 traArm = TH3DMath.GetTranslation4x4(0.0f, my, 0.0f);
Matrix4x4 rotArm = TH3DMath.GetRotation4x4(i * 120, Vector3.up);
Matrix4x4 localArm = traArm * rotArm;
// world matrix : Propeller, Box, Arm
Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller;
Matrix4x4 worldBox = localPole * localArm * localBox;
Matrix4x4 worldArm = localPole * localArm;
Propeller[i].SetMatrix(worldPropeller);
Box[i].SetMatrix(worldBox);
Arm[i].SetMatrix(worldArm);
}
// world matrix : Pole
Matrix4x4 worldPole = localPole;
Pole.SetMatrix(worldPole);
上のBeta4Aからの変更点は1箇所で、それは localArm の内容である。Beta4Aでの localArmは、Poleの3つの面に配置するための回転行列であったが、ここでは Poleの各面に配置した後に単振動を実行する。
具体的には、20行目の rotArmが Poleの各面に配置するための回転行列であり、19行目の traArmがその配置された面において振幅$3$の単振動を行う平行移動行列である。この単振動はCode2のものとほとんど同じである。単振動の計算に使われる角度i_shmArmは毎フレーム$1$ずつ増加するので(14行目)、3つのArmは360フレームごとにy軸方向に$-3$から$3$の上昇下降を行う。
ただし、ここでは18行目の単振動の計算においてその角度が (i_shmArm + i * 60) となっているが、これは3つのArmの上昇下降をずらして行わせるための調整である。


プログラムの実行結果 図15に示されるように、3つのArmの単振動は上昇下降のタイミングが同じではない。これは、18行目の単振動の計算における角度が Arm0のときには (i_shmArm + 0)、Arm1のときには (i_shmArm + 60)、Arm2のときには (i_shmArm + 120) となるためである。つまり、この調整によって Arm1は Arm0に比べて常に$60$°分進んだ位置で単振動を行い、Arm2は Arm0に比べて常に$120$°分進んだ位置で単振動を行うことになる。
もし、18行目の単振動の計算における角度にこのような調整を行わずに、(i_shmArm + i * 60) をただ単に i_shmArm とした場合は図16のような実行結果になる。この場合には3つのArmの上昇下降のタイミングは同じになる。
ここで再度、Poleの回転を追加する。
[Code4] (実行結果 図17)
// Propeller
i_degPropeller -= 6;
Matrix4x4 rotPropeller = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward);
Matrix4x4 traPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller);
Matrix4x4 localPropeller = traPropeller * rotPropeller;
// Box
Matrix4x4 localBox = TH3DMath.GetTranslation4x4(c_attachPos_Box);
// Pole
i_degPole += 1;
Matrix4x4 localPole = TH3DMath.GetRotation4x4(i_degPole, Vector3.up);
i_shmArm += 1;
for (int i = 0; i < 3; i++)
{
// Arm
float my = 3.0f * Mathf.Sin((i_shmArm + i * 60) * Mathf.Deg2Rad); // -3.0 -- 3.0
Matrix4x4 traArm = TH3DMath.GetTranslation4x4(0.0f, my, 0.0f);
Matrix4x4 rotArm = TH3DMath.GetRotation4x4(i * 120, Vector3.up);
Matrix4x4 localArm = traArm * rotArm;
// world matrix : Propeller, Box, Arm
Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller;
Matrix4x4 worldBox = localPole * localArm * localBox;
Matrix4x4 worldArm = localPole * localArm;
Propeller[i].SetMatrix(worldPropeller);
Box[i].SetMatrix(worldBox);
Arm[i].SetMatrix(worldArm);
}
// world matrix : Pole
Matrix4x4 worldPole = localPole;
Pole.SetMatrix(worldPole);

繰り返しになるが、3組のArm、Box、Propellerが Poleの各面において、それぞれのタイミングで上昇下降を行うのは各組のArmのローカル行列localArmの内容が異なるからである。Boxのローカル行列は3つのBoxで共通であり、Propellerのローカル行列は3つのPropellerで共通である。もし、Arm0、Arm1、Arm2のローカル行列の内容が同じである場合には、3組のArm、Box、Propellerは完全に重なった状態になり、3組は重なった状態で Poleのある1つの面において上昇下降をすることになるが、このときの実行結果は1組のArm、Box、Propellerのみを運動させた場合の実行結果 Code2の図10と全く区別がつかないものになる。
# Code5
今までのプログラムでは実行中にオブジェクトの運動をコントロールすることはできなかったが、最後にいくつかのキー操作によって各オブジェクトの 運動/停止 をコントロールできるようにしよう。使用するキー及びそれに対応する処理は以下のとおり。
J : Poleの回転の ON/OFF (長押し非対応)。
K : 3つの Armの単振動の ON/OFF (長押し非対応)。
L : Box0の回転 (長押しに対応する ; Shiftキーと同時押しで逆方向に回転)。

図18はPoleとArmが停止している状態でLキーを押しているときの様子である。回転しているBoxがBox0であり、今回のプログラムではBox0にだけ他のBoxと区別するための黄色いラインが描かれている。
プログラムを以下に示す。
[Code5] (実行結果 図19)
if (Input.GetKeyDown(KeyCode.J))
{
i_switch_Pole = !i_switch_Pole;
}
else if(Input.GetKeyDown(KeyCode.K))
{
i_switch_Arm = !i_switch_Arm;
}
else if(Input.GetKey(KeyCode.L)) // 長押しに対応
{
i_degBox0 = THUtil.IsShiftDown() ? i_degBox0 - 2 : i_degBox0 + 2;
}
// Propeller
i_degPropeller -= 6;
Matrix4x4 rotPropeller = TH3DMath.GetRotation4x4(i_degPropeller, Vector3.forward);
Matrix4x4 traPropeller = TH3DMath.GetTranslation4x4(c_attachPos_Propeller);
Matrix4x4 localPropeller = traPropeller * rotPropeller;
// Box
Matrix4x4 traBox = TH3DMath.GetTranslation4x4(c_attachPos_Box);
Matrix4x4 lcBox = traBox; // Box1, Box2用のローカル行列
Matrix4x4 rotBox0 = TH3DMath.GetRotation4x4(i_degBox0, Vector3.up);
Matrix4x4 lcBox0 = traBox * rotBox0; // Box0用のローカル行列
// Pole
i_degPole = (i_switch_Pole) ? i_degPole + 1 : i_degPole;
Matrix4x4 localPole = TH3DMath.GetRotation4x4(i_degPole, Vector3.up);
i_shmArm = (i_switch_Arm) ? i_shmArm + 1 : i_shmArm;
for (int i = 0; i < 3; i++)
{
// Box
Matrix4x4 localBox = (i == 0) ? lcBox0 : lcBox;
// Arm
float my = 3.0f * Mathf.Sin((i_shmArm + i * 60) * Mathf.Deg2Rad); // -3.0 -- 3.0
Matrix4x4 traArm = TH3DMath.GetTranslation4x4(0.0f, my, 0.0f);
Matrix4x4 rotArm = TH3DMath.GetRotation4x4(i * 120, Vector3.up);
Matrix4x4 localArm = traArm * rotArm;
// world matrix : Propeller, Box, Arm
Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller;
Matrix4x4 worldBox = localPole * localArm * localBox;
Matrix4x4 worldArm = localPole * localArm;
Propeller[i].SetMatrix(worldPropeller);
Box[i].SetMatrix(worldBox);
Arm[i].SetMatrix(worldArm);
}
// world matrix : Pole
Matrix4x4 worldPole = localPole;
Pole.SetMatrix(worldPole);

たとえば、i_switch_Poleの値がtrueであるときには29行目において i_degPoleの値が $1$ ずつ増加する。したがって、i_switch_Poleがtrueである間は毎フレーム Poleはy軸周りに $1^\circ$ ずつ回転することになる。i_switch_Poleの値がfalseのときには29行目において i_degPoleの値は変化しないので、結果的に Poleは停止状態になる。
i_switch_Armについても同様である。i_switch_Armがtrueである間は33行目において i_shmArmの値が $1$ ずつ増加するので、毎フレーム Armは $1^\circ$ 分ずつ単振動を行うが、i_switch_Armがfalseのときには33行目において i_shmArmの値が変化しないので、Armは停止状態になる (Code5においては、i_switch_Poleの初期値はfalse、i_switch_Armの初期値はtrueである)。
Lキーを押している間はBox0の回転角度を表すインスタンス変数 i_degBox0 が更新される (9~12行目)。Lキーだけを押している場合は i_degBox0は毎フレーム$2$ずつ増加し、Shiftキーと同時に押している場合は$2$ずつ減少する (11行目のTHUtil.IsShiftDown()はカスタムライブラリのメソッドでShiftキーが押されていればtrueを返す)。
このプログラムにおいては Box0だけは独自に回転を行う、そのため Box0のローカル行列は、Box1、Box2のローカル行列とは同じにはできない。したがって、23行目では Box1、Box2用のローカル行列 lcBox を求め、26行目で Box0用のローカル行列 lcBox0 を求めている。
lcBoxはArmの先端にアタッチするだけの平行移動行列であるが、lcBox0はまず初期状態の位置でy軸周りに角度i_degBox0だけ回転し、回転した状態でArmの先端にアタッチするという2つの変換をまとめたものである。
37行目の記述は
Matrix4x4 localBox = (i == 0) ? lcBox0 : lcBox;
なお、以前にも指摘したが プログラムにおけるワールド行列の計算には'無駄な'計算が含まれている。例えば、本節においても4つのオブジェクトのワールド行列計算は次のように記述されているが、
// world matrix Matrix4x4 worldPropeller = localPole * localArm * localBox * localPropeller; Matrix4x4 worldBox = localPole * localArm * localBox; Matrix4x4 worldArm = localPole * localArm; Matrix4x4 worldPole = localPole;
このように敢えて'無駄な'処理を残しているのは、階層構造にあるオブジェクトのワールド行列の計算内容を印象付けるためであり、そのための形式的な記述として捉えていただきたい。
© 2020-2025 Redpoll's 60 (All rights reserved)