Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-3
第4章 3D空間におけるオブジェクトの運動
$§$4-3 一体化したオブジェクトの運動 2
本節では以下の3つのオブジェクト Body、WingL、WingR を使って、簡易化された鳥の運動を実装する。
[Code1] (実行結果 図4)

図4 Code1 実行結果 このプログラムは、WingL、WingRをBodyにアタッチするだけの処理である。Bodyは初期状態のまま動かさないので、6行目の localBody には identity行列がセットされている。
1行目の定数c_attachPos_wingLは、WingLを Bodyにアタッチする位置を表し、traWingLは その位置に移動させる平行移動行列である。この平行移動によって、WingLは Bodyの左側にアタッチされることになる。同様に、3行目の定数c_attachPos_wingR、及び 平行移動行列traWingRは、WingRを Bodyの右側にアタッチするためのものである。
例によって、localやworldという接頭辞のついた変数に代入して使用しているのはここでは冗長ではあるが、形式的なものと捉えて頂きたい。
具体的には、WingL、WingRを初期状態の位置でz軸周りに回転させ、回転させた状態で Bodyにアタッチするという手順であるが、まずは、WingRだけを用いてz軸周りの回転の部分のみを実装する。
[Beta2A] (実行結果 図5)

図5 Beta2A 実行結果 (WingRのz軸周りの回転。-45°から45°の間を往復している) このプログラムは初期状態の WingR(図3)に対して、z軸周りの回転行列を実行するものである。
実行されるz軸周りの回転は、$-45$°から$+45$°の間を往復する。この$-45$から$+45$までの区間を往復する値の算出には単振動を使っている (1~2行目 ; 単振動については1-10節参照)。1行目の i_shm は現在の単振動の角度を表すint型インスタンス変数であり、毎フレーム $3$ずつ増加する。60FPSであれば1秒あたりi_shmは$180$増加するので、$360$増加するまでに2秒かかることになる。これは、WingRがz軸周りに $-45$°から$+45$°の間を1往復するのに(60FPSであれば)2秒かかることを意味している。毎フレームのi_shmの増加量を上げれば単振動の往復運動が速くなる。これはすなわち、翼のはばたきのスピードが速くなることを意味する。3行目では、z軸周りに角度degWingだけ回転させる行列を取得している。GetRotation4x4の第2引数に指定されているVector3.forwardは、Unityに標準で用意されている定数で、その値はz軸プラス方向を表す$(0,\ 0,\ 1)$である。
実行結果(図5)を見ればわかるように、WingRのz軸周りの回転を$-45$°から$+45$°の範囲で往復させることで、単純ではあるが翼のはばたきを表現することができる。
では次に、WingRをBodyにアタッチした状態で、この はばたきを実装する。
[Beta2B] (実行結果 図6)
3行目まではBeta2Aと同じである。Beta2Aからの主な追加は、4行目、5行目の WingRのアタッチに関する部分である。
4行目の traWingR は、Code1においても使われているが、これは WingRを Bodyの右側にアタッチするための平行移動行列である。
5行目の localWingR = traWingR * rotWingR は、まず初期状態の WingRをz軸周りに回転させ(rotWingR)、その状態から Bodyの右側にアタッチする(traWingR)という順で変換が行われる。この実行順序によって、WingRが Bodyの右側にアタッチされた状態ではばたくようになるのである。
ここでも Bodyは動かさないので、Bodyに実行される行列は identity行列である。
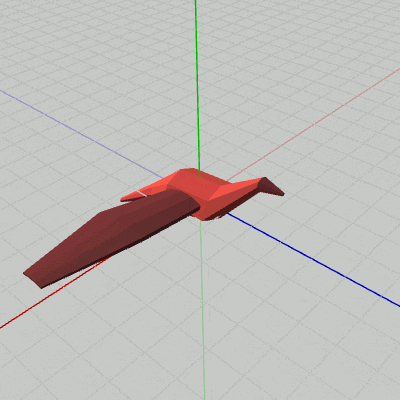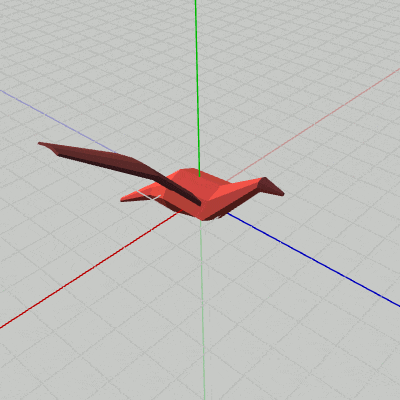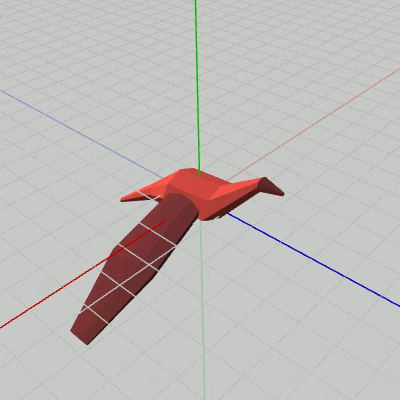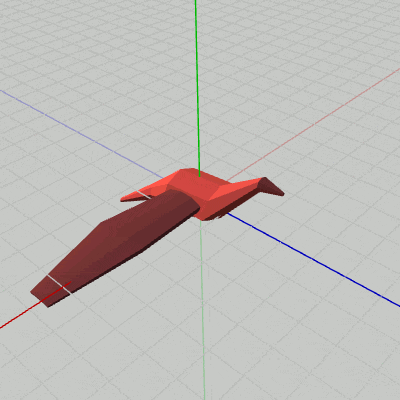
図6 Beta2B 実行結果 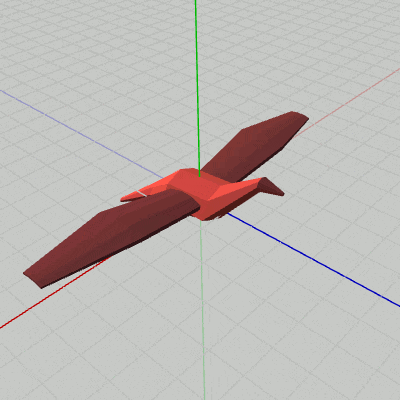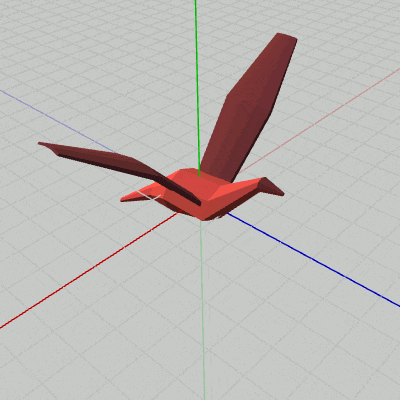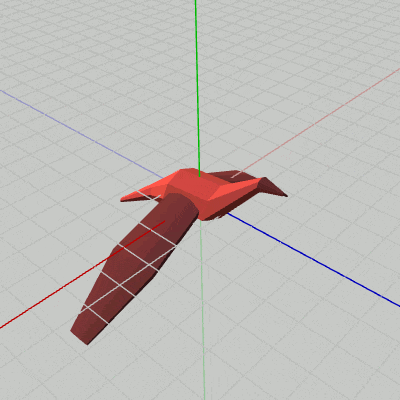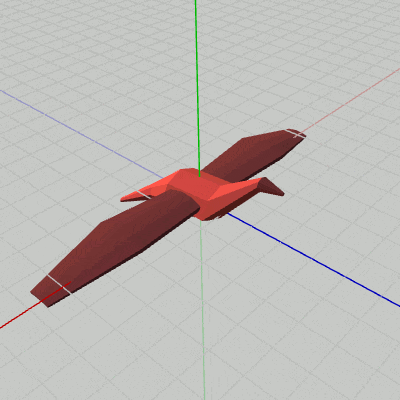
図7 Code2 実行結果
両方の翼 WingL、WingRをはばたかせるプログラムは以下のようになる。
WingLに関するコードが追加されただけで、Beta2Bとほとんど内容は同じである。ただ1箇所注意すべき点は、WingLのz軸周りの回転は WingRとは逆になるという点である。具体的には回転角度のプラス、マイナスのことで、WingRをz軸周りに角度 degWingだけ回転させるときは、WingLのz軸周りの回転角度は -degWingにする必要がある(以下の5行目、10行目)。
[Code2] (実行結果 図7)
図8は WingL、WingRを Bodyにアタッチした状態で、Code1を実行した結果と同じものであるが、前節と同様にオブジェクトの向きを表す水色のベクトルを表示してある。図に示されるように、初期方向はz軸プラス方向を向いている。
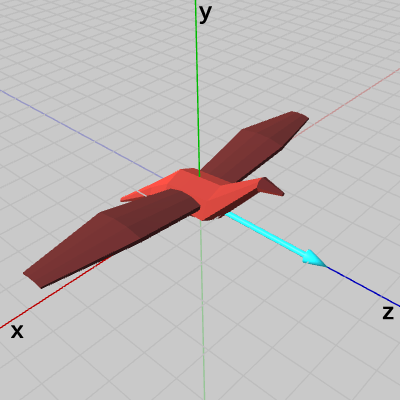
図8 オブジェクトの向きを示す水色のベクトル 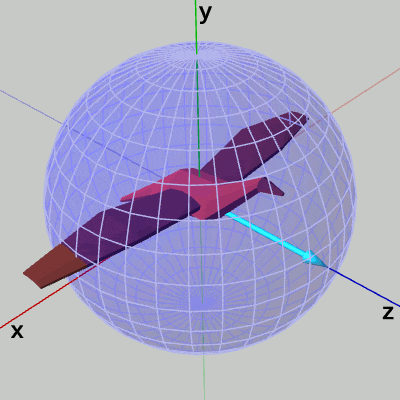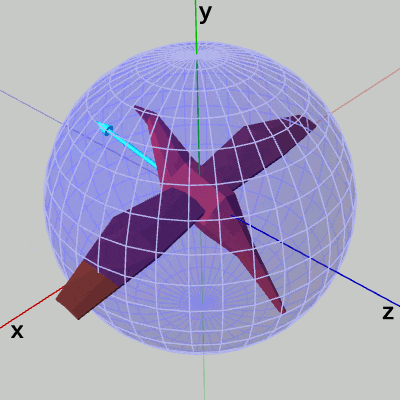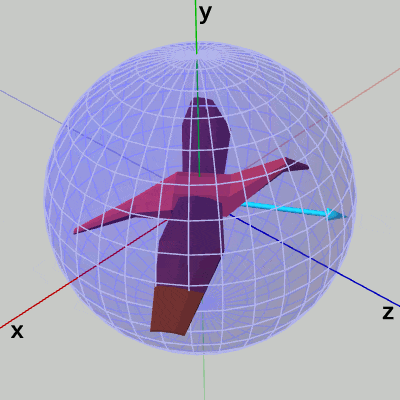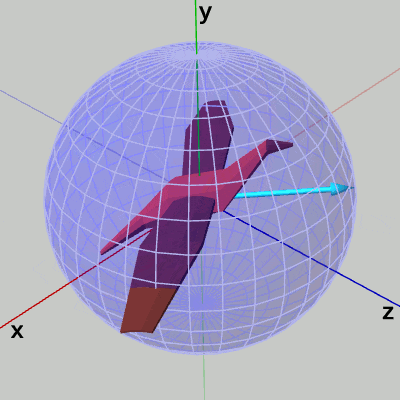
図9 Code3 実行結果
キー操作の内容は前節と同じである。
H : オイラー角のy-角度を $1$減少させる。
J : オイラー角のx-角度を $1$増加させる。
K : オイラー角のx-角度を $1$減少させる。
L : オイラー角のy-角度を $1$増加させる。
オブジェクトの向きを示す水色のベクトルは、H、Lを押すことで球面上を横方向に動き、J、Kを押すことで球面上を縦方向に動く。
[Code3] (実行結果 図9)
(以下では「オブジェクトの向き」と同じ意味で「Bodyの向き」という表現を主に使用する)
17行目までは前節のCode3と同じであり、24~26行目のrotBody、forwardDirの計算も前節のものと同じである。オイラー角のx-角度、y-角度を表すfloat型インスタンス変数i_eulerX、i_eulerYの値をキー操作によって変えていき、それらを引数としてオイラー角による回転行列rotBodyを24行目で取得する。rotBodyは、Bodyの向きを設定するための回転行列で、Bodyに最終的に実行される34行目の行列worldBodyの内容はこのrotBodyである。Bodyの向きとは図9の水色のベクトルの方向のことで、H、Lキーによってy-角度を変化させると横方向に動き、J、Kキーによってx-角度を変化させると縦方向に動く。
26行目のforwardDirは、Bodyの現在の向きを表すVector3型のローカル変数で、初期方向のz軸プラス方向からrotBodyが表す回転を実行した結果が毎フレームセットされる(定数c_initDirは z軸プラス方向を表す同次座標である)。簡単に言えば forwardDirの値は、Bodyの向き(図9の水色のベクトルの方向)と常に一致する。ただしCode3では、forwardDirは26行目で算出されるだけでそれ以降使われることはない。
19~22行目は、2つのWingをBodyにアタッチする平行移動行列を算出する部分である。
28行目 worldWingL = localBody * localWingL は、まず、WingLをBodyの左側にアタッチし(localWingL)、次にアタッチされたその位置から、Bodyとともに指定の向きになるように回転を実行する(localBody)という2つの変換をまとめたものである。
localBodyという行列は30行目でworldBodyにセットされて、最終的にBodyにも実行される。Bodyの回転時に、WingLやWingRがBodyと一体化して回転するのは、この3つのオブジェクトにlocalBodyという同じ行列が実行されるからである。WingL、WingRの場合は、localWing#によってBodyの指定位置にアタッチされてからこのlocalBodyが実行されるが、この実行順序によってBodyと2つのWingが一体化して運動をするのである。
実装方法は前節と同じく、キー操作によって設定されたBodyの向きに、毎フレーム指定された量だけ、Bodyが進んでいく処理を追加するだけである。
操作方法は次の通り。
H、J、K、L : Code3と同様にオイラー角による回転でオブジェクトの向きを設定する。
S : 飛行の ON/OFF。
[Code4] (実行結果 図10)

図10 Code4 実行結果 22行目までは前節のCode4と同じである (オイラー角の1フレーム当たりの変化量が若干異なる)。それ以降についても、localBodyを計算する部分を除いては本節のCode2と同じであり、localBodyを計算する部分(37~43行目)は前節のCode4の30~36行目と同じである。
キー操作の部分については上で述べた通りである。38行目のrotBodyや39行目のforwardDirなどもCode3で解説した通りである。
40行目ではBodyの現在位置を取得し、curPosにセットしている。Sキーによってbool型インスタンス変数i_MOVEがtrueになると、41行目のnewPosにはBodyの新しい移動先の位置が計算されるが、この値は現在のBodyの位置からforwardDirの方向に$0.1$だけ進んだ位置である。したがって、i_MOVEがtrueである限りBodyは毎フレームforwardDirの方向に$0.1$ずつ進んでいくことになる。i_MOVEがfalseの場合は、newPosにはBodyの現在位置であるcurPosがセットされるので、この場合にはBodyの位置に変化はない。つまり、再びSキーが押されるまで、今現在いる場所にとどまり続けることになる (その場合でも、向きを変える操作はできる)。42行目のtraBodyは、BodyをnewPosへ移動させる平行移動行列である。
43行目の localBody = traBody * rotBody は、まず初期状態のBodyに対しrotBodyを実行し、その向きがz軸プラス方向からforwardDirで示される方向になるようにし、forwardDirの方向を向いた状態のBodyに対してtraBodyを実行する。この処理によって、「Bodyが向いている方向に」進んでいくことになる。
Bodyの向いている方向へ進ませるといった処理は、2-9節の戦車、2-10節のヘリコプター、及び 前節の飛行機のプログラムにおいて実装してきたものであるが、いずれのプログラムにおいても記述内容はほとんど同じである。ある時点でのBodyの向きを単位ベクトル化したものは、2D空間においては単位円上のいずれかの点を指しており、3D空間においては単位球面上のいずれかの点を指すことになる。
 図1 Body 初期状態
図1 Body 初期状態 図2 WingL 初期状態
図2 WingL 初期状態 図3 WingR 初期状態
図3 WingR 初期状態
# Code1
上の図はオブジェクトの初期状態での配置である。ここでは、まずこれらの3つのオブジェクトを一体化させるプログラムから始める。[Code1] (実行結果 図4)
Matrix4x4 traWingL = TH3DMath.GetTranslation4x4(c_attachPos_wingL); Matrix4x4 localWingL = traWingL; Matrix4x4 traWingR = TH3DMath.GetTranslation4x4(c_attachPos_wingR); Matrix4x4 localWingR = traWingR; Matrix4x4 localBody = Matrix4x4.identity; Matrix4x4 worldWingL = localBody * localWingL; Matrix4x4 worldWingR = localBody * localWingR; Matrix4x4 worldBody = localBody; WingL.SetMatrix(worldWingL); WingR.SetMatrix(worldWingR); Body.SetMatrix(worldBody);

1行目の定数c_attachPos_wingLは、WingLを Bodyにアタッチする位置を表し、traWingLは その位置に移動させる平行移動行列である。この平行移動によって、WingLは Bodyの左側にアタッチされることになる。同様に、3行目の定数c_attachPos_wingR、及び 平行移動行列traWingRは、WingRを Bodyの右側にアタッチするためのものである。
例によって、localやworldという接頭辞のついた変数に代入して使用しているのはここでは冗長ではあるが、形式的なものと捉えて頂きたい。
# Code2
次に、この鳥の両方の翼 WingL、WingRを運動させる。具体的には、WingL、WingRを初期状態の位置でz軸周りに回転させ、回転させた状態で Bodyにアタッチするという手順であるが、まずは、WingRだけを用いてz軸周りの回転の部分のみを実装する。
[Beta2A] (実行結果 図5)
i_shm += 3; float degWing = 45.0f * Mathf.Sin(i_shm * Mathf.Deg2Rad); // -45 -- 45 Matrix4x4 rotWingR = TH3DMath.GetRotation4x4(degWing, Vector3.forward); Matrix4x4 localWingR = rotWingR; Matrix4x4 worldWingR = localWingR; WingR.SetMatrix(worldWingR);

実行されるz軸周りの回転は、$-45$°から$+45$°の間を往復する。この$-45$から$+45$までの区間を往復する値の算出には単振動を使っている (1~2行目 ; 単振動については1-10節参照)。1行目の i_shm は現在の単振動の角度を表すint型インスタンス変数であり、毎フレーム $3$ずつ増加する。60FPSであれば1秒あたりi_shmは$180$増加するので、$360$増加するまでに2秒かかることになる。これは、WingRがz軸周りに $-45$°から$+45$°の間を1往復するのに(60FPSであれば)2秒かかることを意味している。毎フレームのi_shmの増加量を上げれば単振動の往復運動が速くなる。これはすなわち、翼のはばたきのスピードが速くなることを意味する。3行目では、z軸周りに角度degWingだけ回転させる行列を取得している。GetRotation4x4の第2引数に指定されているVector3.forwardは、Unityに標準で用意されている定数で、その値はz軸プラス方向を表す$(0,\ 0,\ 1)$である。
実行結果(図5)を見ればわかるように、WingRのz軸周りの回転を$-45$°から$+45$°の範囲で往復させることで、単純ではあるが翼のはばたきを表現することができる。
では次に、WingRをBodyにアタッチした状態で、この はばたきを実装する。
[Beta2B] (実行結果 図6)
i_shm += 3; float degWing = 45.0f * Mathf.Sin(i_shm * Mathf.Deg2Rad); Matrix4x4 rotWingR = TH3DMath.GetRotation4x4(degWing, Vector3.forward); Matrix4x4 traWingR = TH3DMath.GetTranslation4x4(c_attachPos_wingR); Matrix4x4 localWingR = traWingR * rotWingR; Matrix4x4 localBody = Matrix4x4.identity; Matrix4x4 worldWingR = localBody * localWingR; Matrix4x4 worldBody = localBody; WingR.SetMatrix(worldWingR); Body.SetMatrix(worldBody);
3行目まではBeta2Aと同じである。Beta2Aからの主な追加は、4行目、5行目の WingRのアタッチに関する部分である。
4行目の traWingR は、Code1においても使われているが、これは WingRを Bodyの右側にアタッチするための平行移動行列である。
5行目の localWingR = traWingR * rotWingR は、まず初期状態の WingRをz軸周りに回転させ(rotWingR)、その状態から Bodyの右側にアタッチする(traWingR)という順で変換が行われる。この実行順序によって、WingRが Bodyの右側にアタッチされた状態ではばたくようになるのである。
ここでも Bodyは動かさないので、Bodyに実行される行列は identity行列である。


両方の翼 WingL、WingRをはばたかせるプログラムは以下のようになる。
WingLに関するコードが追加されただけで、Beta2Bとほとんど内容は同じである。ただ1箇所注意すべき点は、WingLのz軸周りの回転は WingRとは逆になるという点である。具体的には回転角度のプラス、マイナスのことで、WingRをz軸周りに角度 degWingだけ回転させるときは、WingLのz軸周りの回転角度は -degWingにする必要がある(以下の5行目、10行目)。
[Code2] (実行結果 図7)
i_shm += 3; float degWing = 45.0f * Mathf.Sin(i_shm * Mathf.Deg2Rad); // localWingL Matrix4x4 rotWingL = TH3DMath.GetRotation4x4(-degWing, Vector3.forward); Matrix4x4 traWingL = TH3DMath.GetTranslation4x4(c_attachPos_wingL); Matrix4x4 localWingL = traWingL * rotWingL; // localWingR Matrix4x4 rotWingR = TH3DMath.GetRotation4x4(degWing, Vector3.forward); Matrix4x4 traWingR = TH3DMath.GetTranslation4x4(c_attachPos_wingR); Matrix4x4 localWingR = traWingR * rotWingR; // localBody Matrix4x4 localBody = Matrix4x4.identity; // world matrix Matrix4x4 worldWingL = localBody * localWingL; Matrix4x4 worldWingR = localBody * localWingR; Matrix4x4 worldBody = localBody; WingL.SetMatrix(worldWingL); WingR.SetMatrix(worldWingR); Body.SetMatrix(worldBody);
# Code3
次は、前節と同じくキー操作によって、オイラー角経由でオブジェクトの向きを設定する。図8は WingL、WingRを Bodyにアタッチした状態で、Code1を実行した結果と同じものであるが、前節と同様にオブジェクトの向きを表す水色のベクトルを表示してある。図に示されるように、初期方向はz軸プラス方向を向いている。


キー操作の内容は前節と同じである。
H : オイラー角のy-角度を $1$減少させる。
J : オイラー角のx-角度を $1$増加させる。
K : オイラー角のx-角度を $1$減少させる。
L : オイラー角のy-角度を $1$増加させる。
オブジェクトの向きを示す水色のベクトルは、H、Lを押すことで球面上を横方向に動き、J、Kを押すことで球面上を縦方向に動く。
[Code3] (実行結果 図9)
if (Input.GetKey(KeyCode.H))
{
i_eulerY -= 1;
}
else if (Input.GetKey(KeyCode.L))
{
i_eulerY += 1;
}
if (Input.GetKey(KeyCode.J))
{
i_eulerX += 1;
}
else if (Input.GetKey(KeyCode.K))
{
i_eulerX -= 1;
}
Matrix4x4 traWingL = TH3DMath.GetTranslation4x4(c_attachPos_wingL);
Matrix4x4 localWingL = traWingL;
Matrix4x4 traWingR = TH3DMath.GetTranslation4x4(c_attachPos_wingR);
Matrix4x4 localWingR = traWingR;
Matrix4x4 rotBody = TH3DMath.GetEulerRotation4x4(i_eulerX, i_eulerY, 0);
Matrix4x4 localBody = rotBody;
Vector3 forwardDir = rotBody * c_initDir;
Matrix4x4 worldWingL = localBody * localWingL;
Matrix4x4 worldWingR = localBody * localWingR;
Matrix4x4 worldBody = localBody;
WingL.SetMatrix(worldWingL);
WingR.SetMatrix(worldWingR);
Body.SetMatrix(worldBody);
(以下では「オブジェクトの向き」と同じ意味で「Bodyの向き」という表現を主に使用する)
17行目までは前節のCode3と同じであり、24~26行目のrotBody、forwardDirの計算も前節のものと同じである。オイラー角のx-角度、y-角度を表すfloat型インスタンス変数i_eulerX、i_eulerYの値をキー操作によって変えていき、それらを引数としてオイラー角による回転行列rotBodyを24行目で取得する。rotBodyは、Bodyの向きを設定するための回転行列で、Bodyに最終的に実行される34行目の行列worldBodyの内容はこのrotBodyである。Bodyの向きとは図9の水色のベクトルの方向のことで、H、Lキーによってy-角度を変化させると横方向に動き、J、Kキーによってx-角度を変化させると縦方向に動く。
26行目のforwardDirは、Bodyの現在の向きを表すVector3型のローカル変数で、初期方向のz軸プラス方向からrotBodyが表す回転を実行した結果が毎フレームセットされる(定数c_initDirは z軸プラス方向を表す同次座標である)。簡単に言えば forwardDirの値は、Bodyの向き(図9の水色のベクトルの方向)と常に一致する。ただしCode3では、forwardDirは26行目で算出されるだけでそれ以降使われることはない。
19~22行目は、2つのWingをBodyにアタッチする平行移動行列を算出する部分である。
28行目 worldWingL = localBody * localWingL は、まず、WingLをBodyの左側にアタッチし(localWingL)、次にアタッチされたその位置から、Bodyとともに指定の向きになるように回転を実行する(localBody)という2つの変換をまとめたものである。
localBodyという行列は30行目でworldBodyにセットされて、最終的にBodyにも実行される。Bodyの回転時に、WingLやWingRがBodyと一体化して回転するのは、この3つのオブジェクトにlocalBodyという同じ行列が実行されるからである。WingL、WingRの場合は、localWing#によってBodyの指定位置にアタッチされてからこのlocalBodyが実行されるが、この実行順序によってBodyと2つのWingが一体化して運動をするのである。
# Code4
では最後に、キー操作によってこの鳥を飛ばしてみよう。実装方法は前節と同じく、キー操作によって設定されたBodyの向きに、毎フレーム指定された量だけ、Bodyが進んでいく処理を追加するだけである。
操作方法は次の通り。
H、J、K、L : Code3と同様にオイラー角による回転でオブジェクトの向きを設定する。
S : 飛行の ON/OFF。
[Code4] (実行結果 図10)
if (Input.GetKey(KeyCode.H))
{
i_eulerY -= 1;
}
else if (Input.GetKey(KeyCode.L))
{
i_eulerY += 1;
}
if (Input.GetKey(KeyCode.J))
{
i_eulerX += 0.5f;
}
else if (Input.GetKey(KeyCode.K))
{
i_eulerX -= 0.5f;
}
if (Input.GetKeyDown(KeyCode.S))
{
i_MOVE = !i_MOVE;
}
i_shm += 3;
float degWing = 45.0f * Mathf.Sin(i_shm * Mathf.Deg2Rad);
// localWingL
Matrix4x4 rotWingL = TH3DMath.GetRotation4x4(-degWing, Vector3.forward);
Matrix4x4 traWingL = TH3DMath.GetTranslation4x4(c_attachPos_wingL);
Matrix4x4 localWingL = traWingL * rotWingL;
// localWingR
Matrix4x4 rotWingR = TH3DMath.GetRotation4x4(degWing, Vector3.forward);
Matrix4x4 traWingR = TH3DMath.GetTranslation4x4(c_attachPos_wingR);
Matrix4x4 localWingR = traWingR * rotWingR;
// localBody
Matrix4x4 rotBody = TH3DMath.GetEulerRotation4x4(i_eulerX, i_eulerY, 0.0f);
Vector3 forwardDir = rotBody * c_initDir;
Vector3 curPos = Body.GetWorldPosition();
Vector3 newPos = (i_MOVE) ? curPos + 0.1f * forwardDir : curPos;
Matrix4x4 traBody = TH3DMath.GetTranslation4x4(newPos);
Matrix4x4 localBody = traBody * rotBody;
// world matrix
Matrix4x4 worldWingL = localBody * localWingL;
Matrix4x4 worldWingR = localBody * localWingR;
Matrix4x4 worldBody = localBody;
WingL.SetMatrix(worldWingL);
WingR.SetMatrix(worldWingR);
Body.SetMatrix(worldBody);

キー操作の部分については上で述べた通りである。38行目のrotBodyや39行目のforwardDirなどもCode3で解説した通りである。
40行目ではBodyの現在位置を取得し、curPosにセットしている。Sキーによってbool型インスタンス変数i_MOVEがtrueになると、41行目のnewPosにはBodyの新しい移動先の位置が計算されるが、この値は現在のBodyの位置からforwardDirの方向に$0.1$だけ進んだ位置である。したがって、i_MOVEがtrueである限りBodyは毎フレームforwardDirの方向に$0.1$ずつ進んでいくことになる。i_MOVEがfalseの場合は、newPosにはBodyの現在位置であるcurPosがセットされるので、この場合にはBodyの位置に変化はない。つまり、再びSキーが押されるまで、今現在いる場所にとどまり続けることになる (その場合でも、向きを変える操作はできる)。42行目のtraBodyは、BodyをnewPosへ移動させる平行移動行列である。
43行目の localBody = traBody * rotBody は、まず初期状態のBodyに対しrotBodyを実行し、その向きがz軸プラス方向からforwardDirで示される方向になるようにし、forwardDirの方向を向いた状態のBodyに対してtraBodyを実行する。この処理によって、「Bodyが向いている方向に」進んでいくことになる。
Bodyの向いている方向へ進ませるといった処理は、2-9節の戦車、2-10節のヘリコプター、及び 前節の飛行機のプログラムにおいて実装してきたものであるが、いずれのプログラムにおいても記述内容はほとんど同じである。ある時点でのBodyの向きを単位ベクトル化したものは、2D空間においては単位円上のいずれかの点を指しており、3D空間においては単位球面上のいずれかの点を指すことになる。
© 2020-2025 Redpoll's 60 (All rights reserved)