Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-4
第2章 2D空間におけるオブジェクトの運動
$§$2-4 自転と公転
オブジェクトの運動は、オブジェクトに対して平行移動、回転、スケールを実行することによって実現される。スケールを必要としない場合は多いが、オブジェクトを運動させる際には平行移動や回転の使用頻度は高い。本節では平行移動と回転を組み合わせた運動のうちで最も基本的なものの1つである自転(Rotation)と公転(Revolution)について扱う。
図1 Disk 初期状態 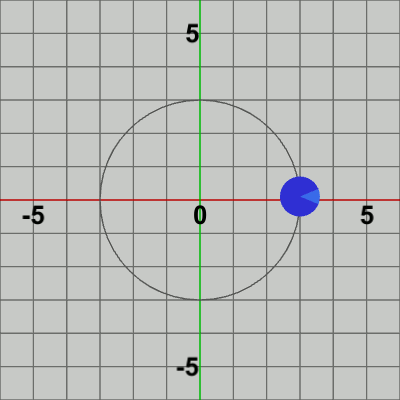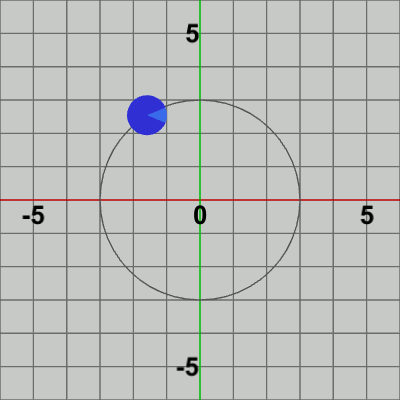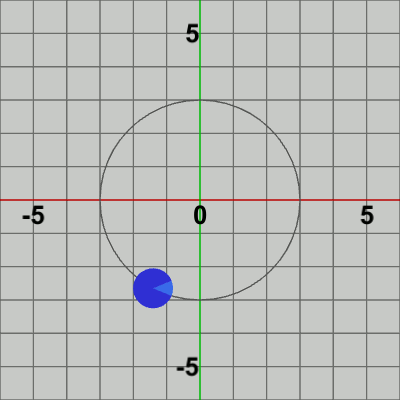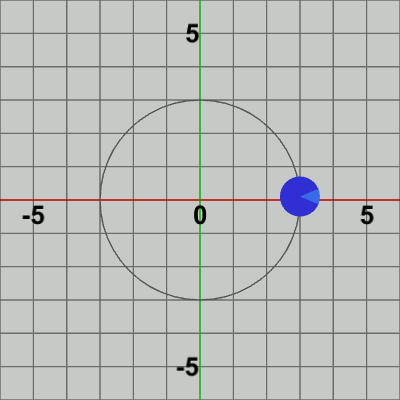
図2 Code1 実行結果
[Code1] (実行結果 図2)
1行目の i_degRev はDiskの公転角度を表すインスタンス変数である。毎フレーム 1行目において公転角度i_degRevを更新し、2行目で角度i_degRevだけ回転させる回転行列Revを取得する。Diskの公転は $(3,\ 0)$ から始まる。c_initPosはDiskの公転運動の開始位置を表す定数であるが、同次座標であるため その値は $(3, 0, 1)$ である。3行目の pos = Rev * c_initPos によって、そのフレームにおける移動位置を算出する。i_degRevが$3$ずつ増加するので Diskも毎フレーム$3$°ずつ公転軌道上を進んでいく (最初のフレームでのDiskの移動先は$(3,\ 0)$である。そのために、i_degRevの初期値は$0$ではなく$-3$に設定してある)。
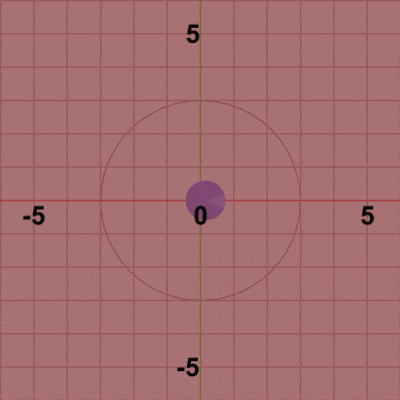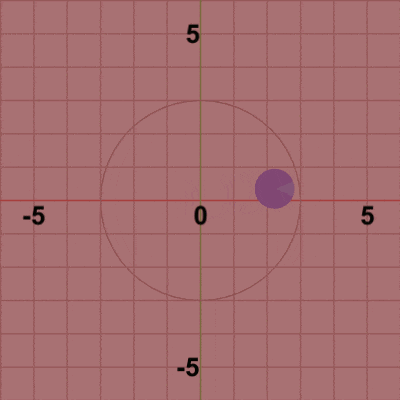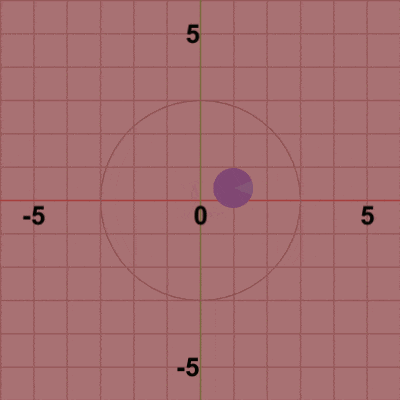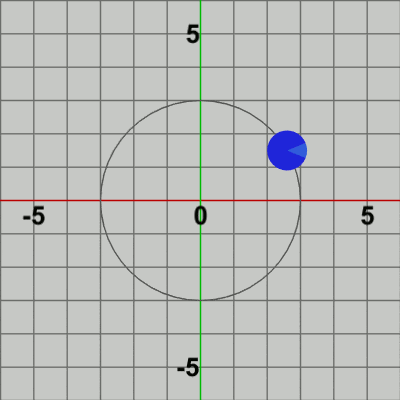
図3 公転の開始位置$(3, 0)$をフレーム1とすれば、フレーム2で開始位置から原点周りに$3$°回転した位置に移動、フレーム3で開始位置から$6$°回転した位置に移動、フレーム4で ... といった具合に進行する。この pos だけ移動させる平行移動行列Tを4行目で取得し Diskに実行するが、このTの実行によりDiskは毎フレーム (初期状態の位置である原点から)公転軌道上の指定された位置に移動することになる。
図3は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターの状態のかかっている状態は、Diskに実行される変換行列(T)の実行過程であり、通常色の状態は変換行列が実行された実行結果の状態である。赤いフィルターの状態から通常色に切り替わった時点でフレーム描画が発生する。描画されたフレームを連続的に表示すれば図2のアニメーションになる。
実行結果を見ればわかるように、このDiskの運動は公転のみである(Disk自体は回転していない)。次のプログラムからは公転に加えて、Disk自体の回転である自転の実装について考えていく。
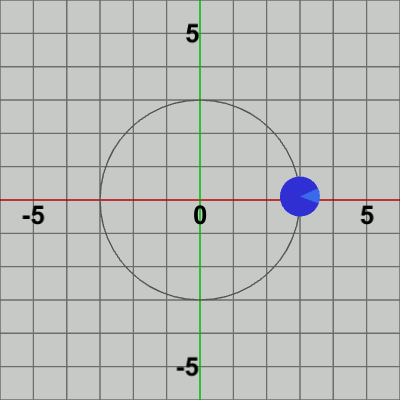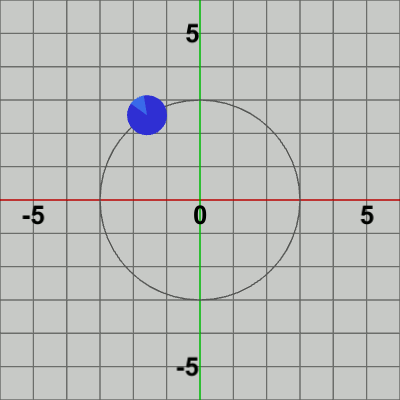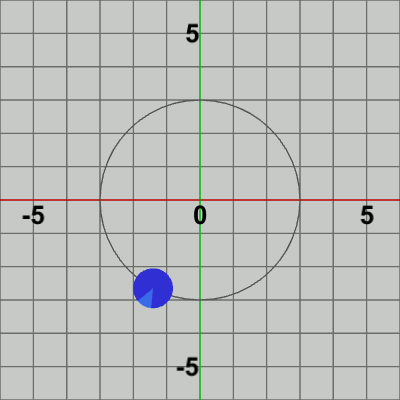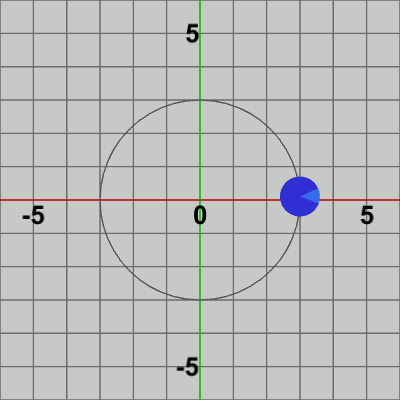
図4 Code2 実行結果 Code1で実装した公転は、具体的には毎フレーム平行移動行列を使ってDiskを指定位置に移動させる処理である。つまり、平行移動行列によってDiskの位置(Position)を毎フレーム更新しているのである。
Diskの自転を実装するにあたって必要となるのは、Diskの向き(Rotation あるいは Orientation ; 1-6節)の更新である。
ここでは、Diskが公転を1回する間に自転を1回するプログラムを作成する。使用するインスタンス変数は上でも使用した公転角度を表す i_degRev の他に、自転角度を表す i_degRot が追加される。
実行手順
(1) i_degRotを更新する。
(2) i_degRotだけ回転させる行列Rを取得する。
(3) i_degRevを更新する。
(4) i_degRevだけ回転させる行列を取得し、それを公転開始位置を表す定数c_initPosに掛けて、公転軌道上の移動位置を算出し posにセット。
(5) posだけ平行移動させる行列Tを取得する。
(6) RとTの積 M = T * R をDiskに実行。
プログラムは次の通り。
[Code2] (実行結果 図4)
1フレームあたりの公転角度i_degRevの増加量と、1フレームあたりの自転角度i_degRotの増加量が等しいので (毎フレームそれぞれ$3$°ずつ増加)、Diskが1回公転する間に1回自転する結果になる。i_degRot、i_degRevともに初期値は$-3$であり、最初のフレームで$0$になる。
9行目の M = T * R は、まず原点(Diskの初期状態の位置)において R によって自転を行い、次に T によって公転軌道上の指定位置に移動するという2つの変換をまとめたものである。
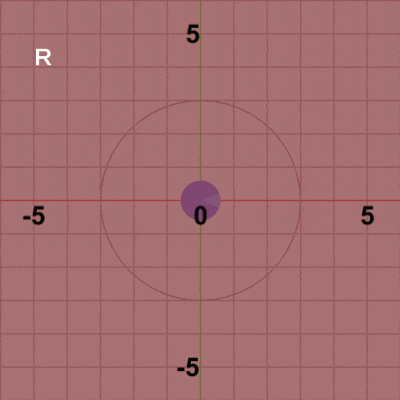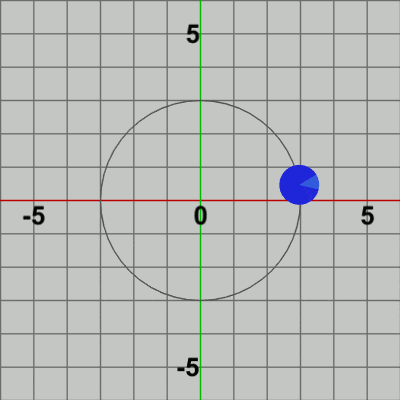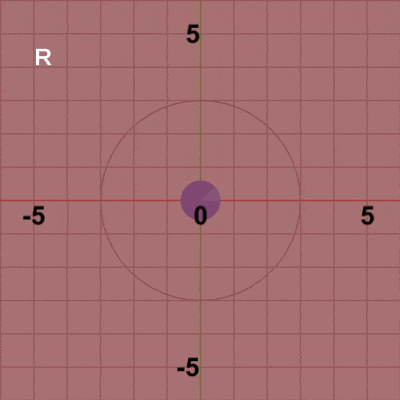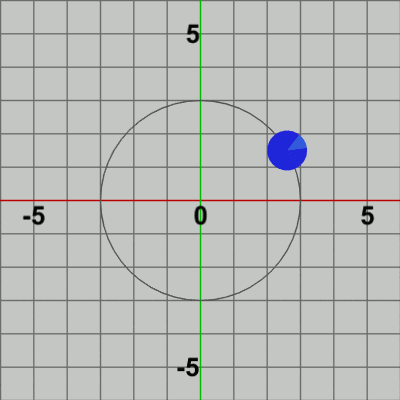
図5 図5はCode2の最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものであるが、図中に表示される白文字 R、T は回転行列R、平行移動行列Tを意味している。Diskの変換は初期状態から始まるが、まず原点において回転行列Rを実行する。これによって、Diskは角度i_degRotだけ回転し、回転した状態で次の変換である平行移動行列Tが実行される。表示されている白文字がRであるときは回転行列Rが実行されていることを意味しており、Tが表示されていれば平行移動行列Tが実行されていることを意味している。
平行移動が終わった時点で赤いフィルターの状態から通常色へ変換するが、この瞬間にフレーム描画が発生する。このプログラムでは、最初のフレームで i_degRot、i_degRev の値は$0$になるので (それぞれの初期値は$-3$)、最初のフレームでは Diskは初期状態の向きのまま、公転開始位置$(3,\ 0)$へ移動し、そこでフレーム描画が発生する。次のフレームでは、i_degRot、i_degRev の値は$3$になるので、Diskは初期状態の向きから$3$°回転し、$3$°回転した状態で公転開始位置から$3$°進んだ位置へ移動する。そこでフレーム描画が発生する。それ以降のフレームにおいても処理手順は同様である。描画されたフレームを連続的に表示すれば図4のアニメーションになる。
このプログラムは公転1回につき自転を1回する。自転周期を変えて実行することを以下で考えよう。プログラムの変更点は1箇所のみである。Code1では、1フレームあたりの公転角度の増加量と、自転角度の増加量がともに同じであった (それぞれ$3$ずつ増加した)。この設定によって、公転回数と自転回数が等しくなったのである。したがって、例えば公転1回につき自転を2回するという場合は単に、自転角度i_degRotの増加量を公転角度i_degRevの増加量の2倍の値にすればよいのである。
以下の図は左からそれぞれ、自転角度i_degRotの増加量を $6$、$9$、$12$としたものである (すなわち 1行目の右辺の値を $6$、$9$、$12$とした場合)。公転角度i_degRevの増加量はいずれの場合も$3$なので、公転1回につき自転回数はそれぞれ2回、3回、4回となる。
2-3節Code2で見たように、公転の中心を $(a, b)$ に移動させるには、公転軌道全体を $(a, b)$ だけずらせばよい。具体的には、今までのプログラムにおける Diskの公転軌道は原点を中心とする半径$3$の円周上であるから、その円周上の各位置を $(a, b)$だけずらせば、公転軌道は $(a, b)$を中心とする半径$3$の円周上になるわけである。
[Code3] (実行結果 図9)

図9 Code3 実行結果 (公転の中心座標は(1, 2)) 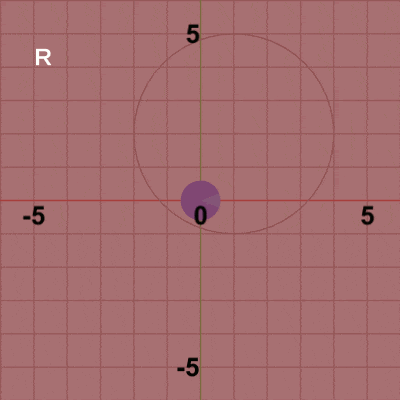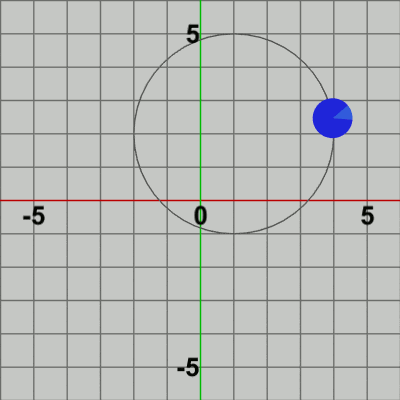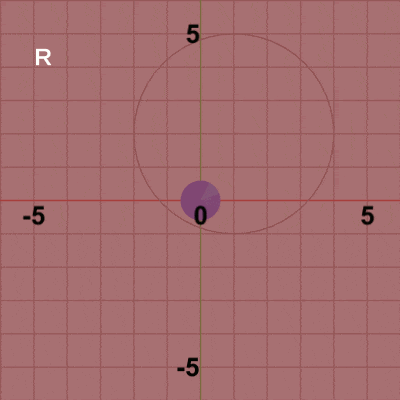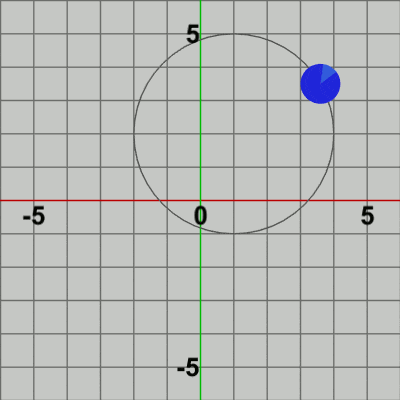
図10
このプログラムはCode2に1行追加しただけのものである。それは、7行目でローカル変数posに $(1, 2)$ だけ加算代入する処理である。6行目で算出されるposは、原点中心の半径$3$の円周上の点であるが、7行目でそのposに $(1, 2)$ 加算すると、posは原点中心ではなく$(1, 2)$中心の円周上の点を表すようになる。
実行結果(図9)に見られるように、Diskは原点ではなく $(1, 2)$ を中心とする半径$3$の円周上を公転している。7行目の処理を追加したことによって、Diskの移動先がCode2の場合と比べて毎フレーム $(1, 2)$ だけずれるので、公転軌道全体が $(1, 2)$ だけずれる結果になるのである (また、今回はi_degRotの毎フレームの増加量$6$はi_degRevの増加量$3$ の2倍の値になっている、そのため公転1回につき自転を2回行うことになる。 i_degRev、i_degRotの初期値は $-6$、$-3$ であり、最初のフレームで両方とも $0$ になる)。
図10はCode3の最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。今回の公転開始位置は $(3, 0)$ から $(1, 2)$ だけ移動した位置 $(4, 2)$ である。最初のフレームでは自転角度$0$°、移動先の位置は$(4, 2)$である。次のフレームでは自転角度$6$°、移動先の位置は$(4, 2)$から公転軌道上を$3$°進んだ位置である。さらに次のフレームでは自転角度$12$°、移動先の位置は$(4, 2)$から公転軌道上を$6$°進んだ位置である。それ以降のフレームにおいても同様である。
赤いフィルターの状態から通常色の状態に切り替わった時点でフレーム描画が発生する。それらの描画されたフレームを連続的に表示すると図9に示されるアニメーションになる。
# Code1
図1に示されるDiskを、原点中心の半径$3$の円周上で回転させる運動、すなわち原点周りの公転を実装するプログラムを以下に示す。

[Code1] (実行結果 図2)
i_degRev += 3; THMatrix3x3 Rev = TH2DMath.GetRotation3x3(i_degRev); Vector2 pos = Rev * c_initPos; THMatrix3x3 T = TH2DMath.GetTranslation3x3(pos); Disk.SetMatrix(T);
1行目の i_degRev はDiskの公転角度を表すインスタンス変数である。毎フレーム 1行目において公転角度i_degRevを更新し、2行目で角度i_degRevだけ回転させる回転行列Revを取得する。Diskの公転は $(3,\ 0)$ から始まる。c_initPosはDiskの公転運動の開始位置を表す定数であるが、同次座標であるため その値は $(3, 0, 1)$ である。3行目の pos = Rev * c_initPos によって、そのフレームにおける移動位置を算出する。i_degRevが$3$ずつ増加するので Diskも毎フレーム$3$°ずつ公転軌道上を進んでいく (最初のフレームでのDiskの移動先は$(3,\ 0)$である。そのために、i_degRevの初期値は$0$ではなく$-3$に設定してある)。

図3は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターの状態のかかっている状態は、Diskに実行される変換行列(T)の実行過程であり、通常色の状態は変換行列が実行された実行結果の状態である。赤いフィルターの状態から通常色に切り替わった時点でフレーム描画が発生する。描画されたフレームを連続的に表示すれば図2のアニメーションになる。
実行結果を見ればわかるように、このDiskの運動は公転のみである(Disk自体は回転していない)。次のプログラムからは公転に加えて、Disk自体の回転である自転の実装について考えていく。
# Code2

Diskの自転を実装するにあたって必要となるのは、Diskの向き(Rotation あるいは Orientation ; 1-6節)の更新である。
ここでは、Diskが公転を1回する間に自転を1回するプログラムを作成する。使用するインスタンス変数は上でも使用した公転角度を表す i_degRev の他に、自転角度を表す i_degRot が追加される。
実行手順
(1) i_degRotを更新する。
(2) i_degRotだけ回転させる行列Rを取得する。
(3) i_degRevを更新する。
(4) i_degRevだけ回転させる行列を取得し、それを公転開始位置を表す定数c_initPosに掛けて、公転軌道上の移動位置を算出し posにセット。
(5) posだけ平行移動させる行列Tを取得する。
(6) RとTの積 M = T * R をDiskに実行。
プログラムは次の通り。
[Code2] (実行結果 図4)
i_degRot += 3; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degRot); i_degRev += 3; THMatrix3x3 Rev = TH2DMath.GetRotation3x3(i_degRev); Vector2 pos = Rev * c_initPos; THMatrix3x3 T = TH2DMath.GetTranslation3x3(pos); THMatrix3x3 M = T * R; Disk.SetMatrix(M);
1フレームあたりの公転角度i_degRevの増加量と、1フレームあたりの自転角度i_degRotの増加量が等しいので (毎フレームそれぞれ$3$°ずつ増加)、Diskが1回公転する間に1回自転する結果になる。i_degRot、i_degRevともに初期値は$-3$であり、最初のフレームで$0$になる。
9行目の M = T * R は、まず原点(Diskの初期状態の位置)において R によって自転を行い、次に T によって公転軌道上の指定位置に移動するという2つの変換をまとめたものである。

平行移動が終わった時点で赤いフィルターの状態から通常色へ変換するが、この瞬間にフレーム描画が発生する。このプログラムでは、最初のフレームで i_degRot、i_degRev の値は$0$になるので (それぞれの初期値は$-3$)、最初のフレームでは Diskは初期状態の向きのまま、公転開始位置$(3,\ 0)$へ移動し、そこでフレーム描画が発生する。次のフレームでは、i_degRot、i_degRev の値は$3$になるので、Diskは初期状態の向きから$3$°回転し、$3$°回転した状態で公転開始位置から$3$°進んだ位置へ移動する。そこでフレーム描画が発生する。それ以降のフレームにおいても処理手順は同様である。描画されたフレームを連続的に表示すれば図4のアニメーションになる。
このプログラムは公転1回につき自転を1回する。自転周期を変えて実行することを以下で考えよう。プログラムの変更点は1箇所のみである。Code1では、1フレームあたりの公転角度の増加量と、自転角度の増加量がともに同じであった (それぞれ$3$ずつ増加した)。この設定によって、公転回数と自転回数が等しくなったのである。したがって、例えば公転1回につき自転を2回するという場合は単に、自転角度i_degRotの増加量を公転角度i_degRevの増加量の2倍の値にすればよいのである。
以下の図は左からそれぞれ、自転角度i_degRotの増加量を $6$、$9$、$12$としたものである (すなわち 1行目の右辺の値を $6$、$9$、$12$とした場合)。公転角度i_degRevの増加量はいずれの場合も$3$なので、公転1回につき自転回数はそれぞれ2回、3回、4回となる。
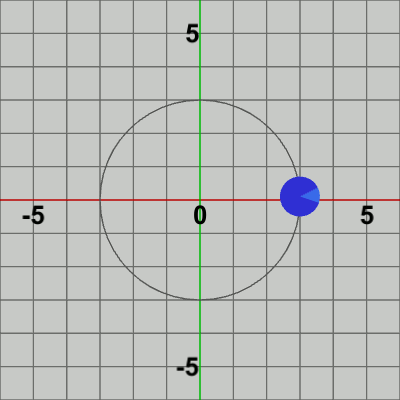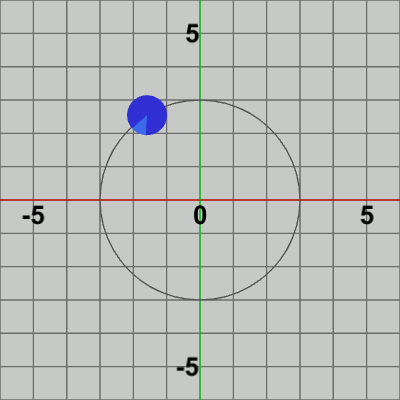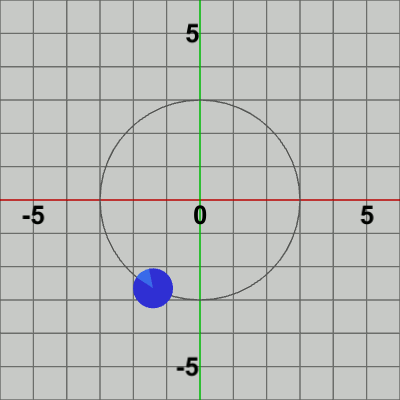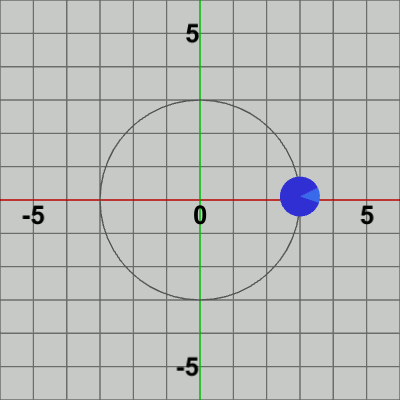 図6 公転1回につき自転2回
図6 公転1回につき自転2回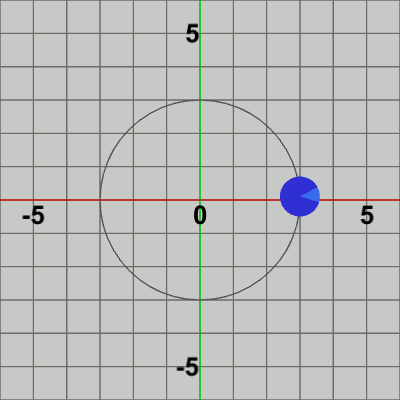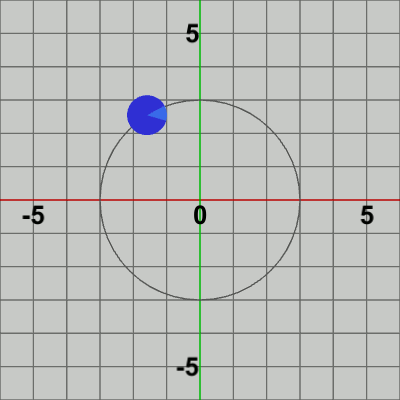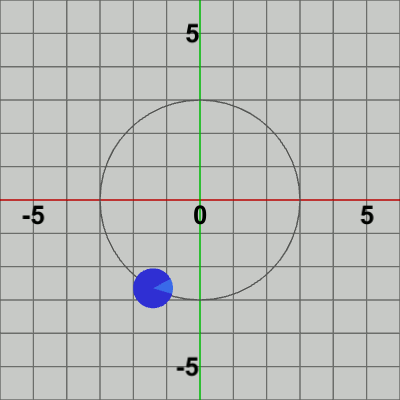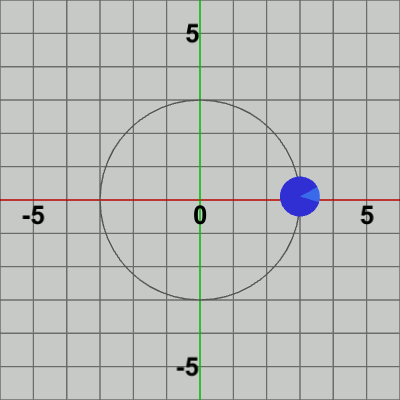 図7 公転1回につき自転3回
図7 公転1回につき自転3回 図8 公転1回につき自転4回
図8 公転1回につき自転4回
# Code3
上のプログラムでは Diskの公転の中心は原点であったが、ここでは原点以外の位置を公転の中心とするプログラムを作成する。2-3節Code2で見たように、公転の中心を $(a, b)$ に移動させるには、公転軌道全体を $(a, b)$ だけずらせばよい。具体的には、今までのプログラムにおける Diskの公転軌道は原点を中心とする半径$3$の円周上であるから、その円周上の各位置を $(a, b)$だけずらせば、公転軌道は $(a, b)$を中心とする半径$3$の円周上になるわけである。
[Code3] (実行結果 図9)
i_degRot += 6; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degRot); i_degRev += 3; THMatrix3x3 Rev = TH2DMath.GetRotation3x3(i_degRev); Vector2 pos = Rev * c_initPos; pos += new Vector2(1, 2); THMatrix3x3 T = TH2DMath.GetTranslation3x3(pos); THMatrix3x3 M = T * R; Disk.SetMatrix(M);


このプログラムはCode2に1行追加しただけのものである。それは、7行目でローカル変数posに $(1, 2)$ だけ加算代入する処理である。6行目で算出されるposは、原点中心の半径$3$の円周上の点であるが、7行目でそのposに $(1, 2)$ 加算すると、posは原点中心ではなく$(1, 2)$中心の円周上の点を表すようになる。
実行結果(図9)に見られるように、Diskは原点ではなく $(1, 2)$ を中心とする半径$3$の円周上を公転している。7行目の処理を追加したことによって、Diskの移動先がCode2の場合と比べて毎フレーム $(1, 2)$ だけずれるので、公転軌道全体が $(1, 2)$ だけずれる結果になるのである (また、今回はi_degRotの毎フレームの増加量$6$はi_degRevの増加量$3$ の2倍の値になっている、そのため公転1回につき自転を2回行うことになる。 i_degRev、i_degRotの初期値は $-6$、$-3$ であり、最初のフレームで両方とも $0$ になる)。
図10はCode3の最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。今回の公転開始位置は $(3, 0)$ から $(1, 2)$ だけ移動した位置 $(4, 2)$ である。最初のフレームでは自転角度$0$°、移動先の位置は$(4, 2)$である。次のフレームでは自転角度$6$°、移動先の位置は$(4, 2)$から公転軌道上を$3$°進んだ位置である。さらに次のフレームでは自転角度$12$°、移動先の位置は$(4, 2)$から公転軌道上を$6$°進んだ位置である。それ以降のフレームにおいても同様である。
赤いフィルターの状態から通常色の状態に切り替わった時点でフレーム描画が発生する。それらの描画されたフレームを連続的に表示すると図9に示されるアニメーションになる。
© 2020-2025 Redpoll's 60 (All rights reserved)