Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-21
第2章 2D空間におけるオブジェクトの運動
$§$2-21 衝突判定 8 (回転した長方形同士の衝突)
本節では傾きのある長方形同士の衝突判定について考える。
2-19節では軸平行な長方形同士の衝突判定を扱ったが、そこでは分離直線及び分離軸というものが使われた。傾きのある長方形の場合にも同様に分離直線と分離軸が使われる。しかし、軸平行な長方形の場合のように単純に x軸、y軸だけで解決することはできない。まずはその点から見ていくことにしよう。
上の図には2つの軸平行な長方形が互いに重なっていない(衝突していない)状態で置かれている。2つの長方形の各頂点を x軸または y軸に射影した際に、それらの軸上にできる有限の範囲を2-19節では射影区間と呼んだ。図1は2つの長方形を x軸へ射影したときのもので、図2は両者を y軸へ射影したときのものである。
そして、上図のように2つの軸平行な長方形が重なっていない場合、x軸またはy軸上の両者の射影区間の間には必ずギャップ(間隔)が存在するのであった。上の例では y軸上の2つの射影区間の間にギャップが見られる。
2つの長方形をある直線上に射影したときに、両者の射影区間の間にこのようなギャップが存在する直線のことを分離軸というのであった (上記の例ではy軸が分離軸である)。さらに、分離軸が存在するとき、この分離軸上のギャップを通り分離軸に垂直で2つの長方形のどちらとも交わることのない直線を(2つの長方形の間に)引くことができるが、この直線を分離直線と呼んだ。これらのことはいずれも図3に表記されている通りである。
では、軸平行でない長方形、すなわち傾きのある長方形同士の場合について見てみよう。
例えば、下図に示される2つの長方形はいずれも x軸、y軸に平行ではない、さらにこの2つの長方形は重なっている部分がない。つまり、2つの傾きのある長方形が衝突していない状態である。
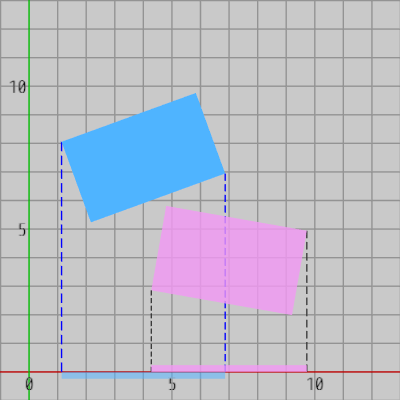
図4 x軸上への射影 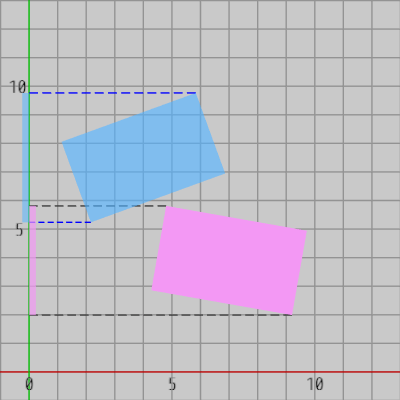
図5 y軸上への射影
図4、図5はこの2つの長方形の各頂点を x軸、y軸に射影したときの結果である。
今回の場合、2つの長方形自体は重なってはいないが、2つの長方形の射影区間は x軸上においてもy軸上においても重なっている。つまり、この例では2つの長方形を x軸、y軸に射影してもその射影区間による判定では、2つの長方形自体は重なっていないこと が分からないのである。
このように、傾きのある長方形同士の場合(正確にはどちらか一方が傾いている場合)には、2つの長方形が重なっていないときでも x軸、y軸上の両者の射影区間は重なっている(射影区間の間にギャップが存在しない)場合がある。言い換えれば、傾きのある長方形同士が衝突していないことを調べる際に、常に x軸、y軸を分離軸として使うことはできないということである。
では当然ここで考えるべき問題として傾きのある長方形同士の衝突判定においては、(両者が衝突していない場合に)どのような直線が分離軸となり得るかという問題が生じるわけである。
2-19節では、長方形の衝突判定は以下の2つの命題を調べることに帰着すると述べた。
(1) ある直線が分離軸になるならば、2つの長方形は重なっていない (衝突していない)。
(2) どのような直線も分離軸にならないならば、2つの長方形は重なっている (衝突している)。
そして、(1) については2-19節の終わりに簡単に解説したが、(2) の命題についてはその概要を述べただけであった。以下ではこの (2) の命題が成り立つことについて解説するが、具体的には (2) の対偶である
「2つの長方形が重なっていないならば、ある直線が分離軸になる」
ことを示す。
1つの長方形は2組の平行な辺によって構成される。したがって、長方形は辺を4つ持っているが各辺の向きはすべて異なるわけではなく、辺の向きは2つしかないわけである。そして長方形であるから、その2つの辺の向きは直交している。
結論から言うと、傾きのある長方形同士の衝突判定において分離軸となり得る直線は、2つの長方形の各辺の向きに平行な直線である。1つの長方形は2つの辺の向きしか持たないから、分離軸となり得る直線は4つあるわけである。
このことは次のようにして導かれる。
任意の2つの長方形を任意の位置、任意の向き、さらに 両者が重ならないように配置したとき、それらのうち少なくとも一方の長方形をもう一方の長方形に衝突しないように、その長方形の1つの辺の向きに沿って(両方向に)無限に引き伸ばすことができる。
図6、図7では両者が衝突しないように無限に引き延ばせるのは片方の長方形だけであるが、図8のように2つの長方形が平行である場合には両方の長方形を無限に引き延ばしても両者は衝突しない。
この事実を使えば、2つの傾きのある長方形同士が衝突していない場合、それらの長方形を分離する分離直線を次のように引くことができる。
図9には2つの長方形$A$、$B$ が衝突していない状態で置かれている。図から明らかなように長方形$A$の辺$PQ$に沿った方向に$A$を(両方向に)無限に引き伸ばしても長方形$B$とは衝突しない。したがって、$PQ$を通る直線も$B$とは衝突しない。
このとき、図10に示されるように$PQ$を通る黒い直線と適当な間隔を置いて、その黒い直線に平行な黄色い直線を $A$ と $B$ の間に置くことができるが、この黄色い直線は2つの長方形と交わることのない分離直線である。
分離軸は分離直線と直交する直線であるから、この場合、図11において黄色い直線と直交している直線が2つの長方形$A$と$B$の分離軸になる。
例えば、先程の図4の場合における分離軸をこの方法で求めてみよう (便宜上ここでも2つの長方形を$A$、$B$とし、$A$の2つの頂点を$P$、$Q$としている)。
図13に示されるように、長方形$A$を辺$PQ$に沿って無限に引き伸ばせるので$PQ$を通る直線は長方形$B$とは衝突しない。また、$PQ$を通る黒い直線からわずかな距離を置いて その黒い直線に平行な黄色い直線を2つの長方形の間に置くことができるが、この黄色い直線は分離直線である (図13)。
したがって、図14に示されるように分離直線(黄色い直線)に直交する直線が分離軸になる。実際、その直線上にある2つの長方形の射影区間の間にはギャップが存在している。
繰り返しになるが、2つの長方形が重なっていないならば、2つの長方形のいずれかの辺に平行な直線は必ず分離直線になる。分離直線と分離軸は一方が存在すればもう一方も存在し(2-19節)、分離軸と分離直線は直交しているので、「2つの長方形が重なっていないならば、2つの長方形のいずれかの辺に平行な直線は必ず分離軸になる」ともいえるわけである。言い換えれば、2つの長方形の辺に平行な直線がどれも分離軸にならないならば、2つの長方形は重なっているのである。
そして、これが上記の 2-19節 (2) の主張なのである。
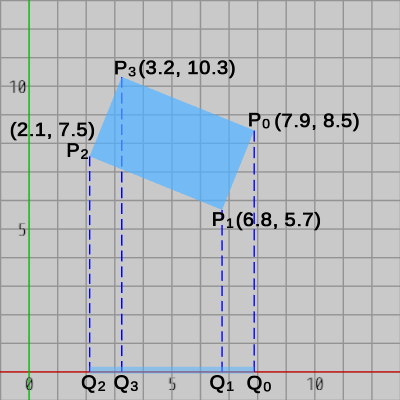
図15 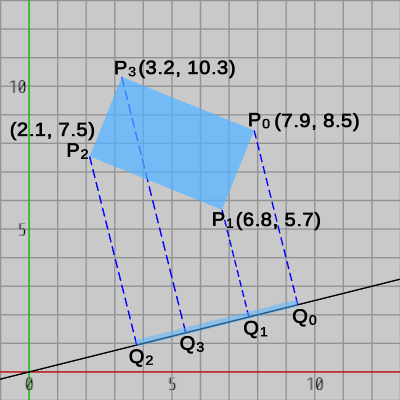
図16
図15は長方形を x軸上に射影したときのものであるが、このとき一番左の頂点$P_2$を射影したときの像$Q_2$が射影区間の最小値であり、一番右の頂点$P_0$を射影したときの像$Q_0$が射影区間の最大値である。
具体的には x軸上において $Q_2 = 2.1$、$Q_0 = 7.9$ であるので、射影区間は $2.1$ から $7.9$ までということになる(図15)。
射影したときの像は、射影する直線上において原点からどれだけ離れているかを表している。図15において長方形の4つの頂点$P_0$~$P_3$を x軸上に射影したときの各像は点$Q_0$~$Q_3$であるが、それらの値は小さい順に $Q_2 = 2.1$、$Q_3 = 3.2$、$Q_1 = 6.8$、$Q_0 = 7.9$ である。この値は x軸上において各像が原点からどれだけ離れているかを表す距離である。最小値、最大値は直線上における 原点からの距離 で決まるのである。
射影する直線が x軸であれば、射影区間を求めることは容易である。長方形の4つの頂点を x軸上に射影したときの像は、各頂点の x座標と同じ値になるので各頂点の x座標を比較すればよい。
しかし、射影する直線が x軸や y軸ではなく、図16に示されるような傾きのある直線の場合、射影区間はこのように単純には求めることはできない。傾きのある直線上における射影区間を求めるには、1-3節で扱った単位ベクトルによる内積を使うことになる。
例えば 上の図16では長方形の射影区間は黒い直線上の $Q_2$ から $Q_0$ であるが、この直線上における原点から$Q_2$までの距離、及び原点から$Q_0$までの距離は以下のように求められる。
長方形の点$P_2$を黒い直線へ射影したときの像が$Q_2$であるから、原点$O$と$P_2$を結ぶベクトルを $\overrightarrow{OP_2}$ 、黒い直線の方向を表す単位ベクトルを $\boldsymbol{u}$ とすれば、原点$O$から$Q_2$までの距離$|OQ_2|$は次のように計算される (図17の緑のベクトルが $\overrightarrow{OP_2}$、オレンジのベクトルが $\boldsymbol{u}$ である)。
\[\overrightarrow{OP_2}\cdot \boldsymbol{u} = |OQ_2|\]$\overrightarrow{OP_2}$ 及び $\boldsymbol{u}$ に図17に示される各値を代入して計算すると、\[|OQ_2| = \overrightarrow{OP_2}\cdot \boldsymbol{u} = (2.1,\ 7.5) \cdot (0.97,\ 0.24) \risingdotseq 3.9\]となるが、この値が黒い直線上における原点から$Q_2$までの距離である。
同様にして、図18における原点$O$から$Q_0$までの距離$|OQ_0|$は次のように計算される (図18の緑のベクトルが $\overrightarrow{OP_0}$、オレンジのベクトルが $\boldsymbol{u}$ である)。
\[|OQ_0| = \overrightarrow{OP_0}\cdot \boldsymbol{u} = (7.9,\ 8.5) \cdot (0.97,\ 0.24) \risingdotseq 9.7\]
すなわち、黒い直線上における長方形の射影区間は $3.9$ から $9.7$ である (図19)。
以下のメソッド CollisionTest_OBB_OBB(..) は傾きのある長方形同士の衝突判定を実装したものである。
[CollisionTest_OBB_OBB(..)]
メソッドに送られてくる引数 vertsA、vertsB は2つの長方形$A$、$B$の頂点座標の配列であり、要素数はいずれも $4$ である。4行目の Vector2[]型のローカル変数 sideDirs には2つの長方形の4つの辺の方向がセットされる (4つの辺の方向は単位ベクトルとしてセットされる)。上で述べたように、分離軸の候補となる直線は2つの長方形のいずれかの辺に平行な直線であり、2つの長方形の辺の方向は多くて4つであるから、それらをすべて sideDirs にセットしている。
9行目の foreachブロックは、分離軸候補となる4つの直線のそれぞれで2つの長方形の射影区間の比較を行う部分である。ここで使われる変数 u は、分離軸候補の各直線の方向を表す単位ベクトルである。先程、直線上の射影区間を求める計算を行ったが、そこで使われた単位ベクトル $\boldsymbol{u}$ と役割は同じである。
まず2つの長方形$A$、$B$の射影区間を求める必要があるが、17行目の forブロックがその処理である。4つの float型変数 minA、maxA、minB、maxB には最終的には2つの長方形の射影区間を表す最小値、最大値がセットされる。
19行目で計算される projA は、長方形$A$の各頂点を直線上に射影したときの 各像の原点からの距離である。その下の2つのifブロックにおいて各像の原点からの距離を比較し最大値、最小値を決定する。23行目以降では長方形$B$について同様のことを行っている。
17行目の forブロックが終了する時点(27行目)では、ある直線についての2つの長方形の射影区間が算出されているので、28行目の ifブロックでその直線において2つの射影区間の間にギャップが存在するかを調べ、存在するならば衝突していないことを表す false を返す。
4つの分離軸候補の直線のすべての場合で、この28行目の ifブロックに入らないときは、分離軸候補のどの直線にもギャップが存在しないということであり、それは2つの長方形が衝突していることを意味する。その場合は、このメソッドの最後で衝突を表す true を返す。
ただ実際には上のメソッド内で使われている sideDirs の各要素を正規化する必要はない。この配列の各要素には2つの長方形の各辺の方向を表す単位ベクトルがセットされているが、2つの射影区間の間にギャップがあるかどうかを調べるだけならば各辺の方向を単位ベクトルにしてもしなくても結果は変わらないためである。つまり 4行目の sideDirs は次のようにセットしても結果は同じである。
では最後に、本節で述べた内容に関するプログラムを作成する。
青い長方形のキー操作
H : 左へ移動
J : 下へ移動
K : 上へ移動
L : 右へ移動
R : 反時計周りに回転(Shiftと同時押しで逆回転)
緑の長方形のキー操作
Q : 反時計周りに回転(Shiftと同時押しで逆回転)
なお、本節でもプログラム内では青い長方形、緑の長方形は Blue、Green として使われている。
[Code1] (実行結果 図21)
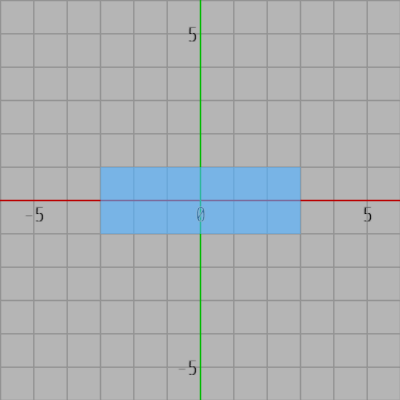
図20 初期状態における長方形(横の長さは 6、縦の長さは 2) 
図21 Code1 実行結果
1行目のifブロックは初期化ブロックであり、i_initVertsBlue、i_initVertsGreen はVector2[]型のインスタンス変数で、初期状態における Blue、Greenの頂点座標がセットされる (2つの長方形はともに図20に示される大きさで 横の長さが $6$、縦の長さは $2$ である)。i_degBlue、i_degGreen は Blue、Greenの回転角度を表すインスタンス変数である。
Qキーを押すと Greenが所定の位置において回転を行うが、14行目のifブロックはその処理が記述されている。
22行目から49行目まではBlueをキー操作によって動かす部分であるが上で述べたとおり、H、J、K、L が上下左右の移動であり、Rキーによって回転する。
52行目以降が衝突判定処理の部分である。
傾きのある長方形同士の衝突判定用メソッド CollisionTest_OBB_OBB(..) の引数には、その時点における2つの長方形の各頂点座標をセットする必要があるが、2つの長方形の頂点座標は56行目のfor文において計算される。何度か述べたように、ある時点におけるオブジェクト上のある位置$P$の座標は、その時点においてオブジェクトに実行されている変換行列と初期状態における$P$の座標との積によって求めることができる。そして、その際には初期状態における$P$の座標を同次座標化し z成分を $1$ にする必要がある (2-13節参照)。
ここで求めるのは、衝突判定を行う時点での2つの長方形の各頂点座標である。したがって、ここではその時点において長方形に実行されている変換行列と初期状態における長方形の各頂点座標を同次座標化したものの積を計算すればよい。
56行目のfor文内で使われている mtxB や mtxG は Blue、Greenに実行されている変換行列であり、i_initVertsBlue[i] や i_initVertsGreen[i] は初期状態のBlue、Greenの各頂点座標であり、ToVector3(..) は引数の2次元ベクトルを同次座標化して返すカスタムライブラリーのメソッドである (z成分が $1$ の同次座標が返される)。
プログラムを実行すると緑の長方形が適当な運動を行っているが、キー操作によって青い長方形を動かし2つの長方形同士の衝突を検出する。
キー操作は青い長方形についてはCode1と同じであり、H、J、K、L によって上下左右の移動、R によって回転を行う。
また、ここでは Sキーによって緑の長方形の運動を停止/再開させることができる。
[Code2] (実行結果 図22)
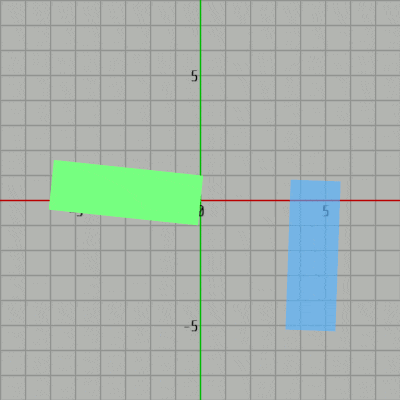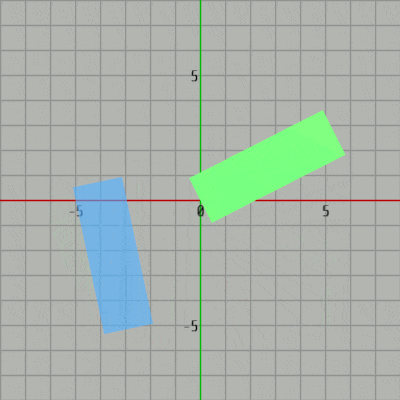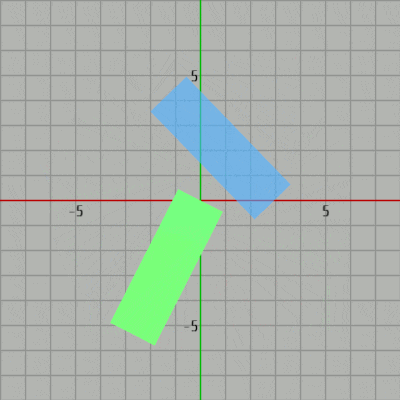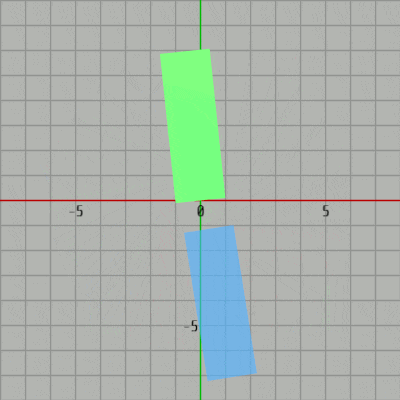
図22 Code2 実行結果 Code1との違いは Code1では QキーによってGreenを回転させていたが、その部分の代わりにGreenの運動用のメソッド GreenMotion(..) が実行されるようになっている (14行目から22行目)。このメソッドの引数が $0$ のときは Greenは単振動を行い、$1$ のときは原点周りの回転を行う。Sキーによってその運動を停止/再開させることができる。
それ以外の部分はCode1と同じである。
2-19節では軸平行な長方形同士の衝突判定を扱ったが、そこでは分離直線及び分離軸というものが使われた。傾きのある長方形の場合にも同様に分離直線と分離軸が使われる。しかし、軸平行な長方形の場合のように単純に x軸、y軸だけで解決することはできない。まずはその点から見ていくことにしよう。
A) ある反例
まず、2-19節で述べた分離直線、分離軸、射影区間について簡単に復習する。-
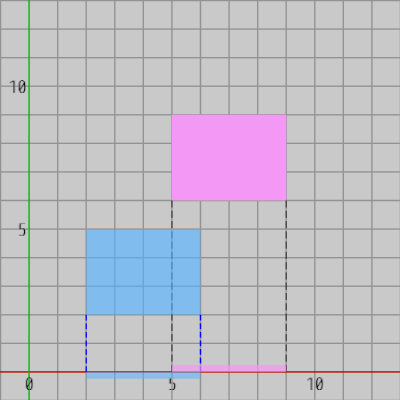 図1 x軸上への射影(2つの射影区間は重なっている)
図1 x軸上への射影(2つの射影区間は重なっている) -
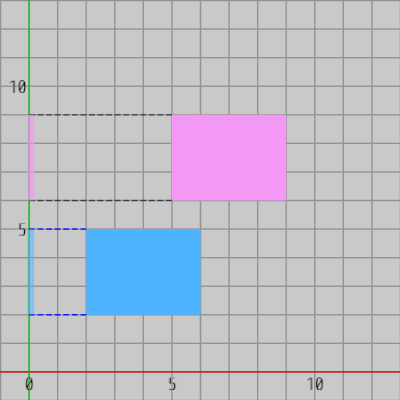 図2 y軸上への射影(2つの射影区間の間にギャップが存在する)
図2 y軸上への射影(2つの射影区間の間にギャップが存在する) -
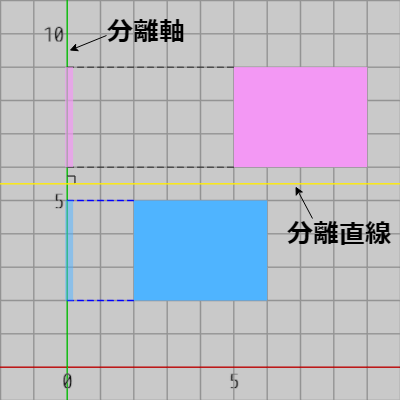 図3 分離軸と分離直線
図3 分離軸と分離直線
上の図には2つの軸平行な長方形が互いに重なっていない(衝突していない)状態で置かれている。2つの長方形の各頂点を x軸または y軸に射影した際に、それらの軸上にできる有限の範囲を2-19節では射影区間と呼んだ。図1は2つの長方形を x軸へ射影したときのもので、図2は両者を y軸へ射影したときのものである。
そして、上図のように2つの軸平行な長方形が重なっていない場合、x軸またはy軸上の両者の射影区間の間には必ずギャップ(間隔)が存在するのであった。上の例では y軸上の2つの射影区間の間にギャップが見られる。
2つの長方形をある直線上に射影したときに、両者の射影区間の間にこのようなギャップが存在する直線のことを分離軸というのであった (上記の例ではy軸が分離軸である)。さらに、分離軸が存在するとき、この分離軸上のギャップを通り分離軸に垂直で2つの長方形のどちらとも交わることのない直線を(2つの長方形の間に)引くことができるが、この直線を分離直線と呼んだ。これらのことはいずれも図3に表記されている通りである。
では、軸平行でない長方形、すなわち傾きのある長方形同士の場合について見てみよう。
例えば、下図に示される2つの長方形はいずれも x軸、y軸に平行ではない、さらにこの2つの長方形は重なっている部分がない。つまり、2つの傾きのある長方形が衝突していない状態である。


図4、図5はこの2つの長方形の各頂点を x軸、y軸に射影したときの結果である。
今回の場合、2つの長方形自体は重なってはいないが、2つの長方形の射影区間は x軸上においてもy軸上においても重なっている。つまり、この例では2つの長方形を x軸、y軸に射影してもその射影区間による判定では、2つの長方形自体は重なっていないこと が分からないのである。
このように、傾きのある長方形同士の場合(正確にはどちらか一方が傾いている場合)には、2つの長方形が重なっていないときでも x軸、y軸上の両者の射影区間は重なっている(射影区間の間にギャップが存在しない)場合がある。言い換えれば、傾きのある長方形同士が衝突していないことを調べる際に、常に x軸、y軸を分離軸として使うことはできないということである。
では当然ここで考えるべき問題として傾きのある長方形同士の衝突判定においては、(両者が衝突していない場合に)どのような直線が分離軸となり得るかという問題が生じるわけである。
B) 傾きのある長方形同士の衝突判定における分離軸
ここで考えるべき問題は「傾きのある長方形同士の場合(正確にはどちらか一方が傾いている場合)の衝突判定においては、(両者が衝突していない場合に)どのような直線が分離軸となり得るか」というものであるが、この問題を考えることは以下に示す 2-19節の (2) の命題を考えることと同じである。2-19節では、長方形の衝突判定は以下の2つの命題を調べることに帰着すると述べた。
(1) ある直線が分離軸になるならば、2つの長方形は重なっていない (衝突していない)。
(2) どのような直線も分離軸にならないならば、2つの長方形は重なっている (衝突している)。
そして、(1) については2-19節の終わりに簡単に解説したが、(2) の命題についてはその概要を述べただけであった。以下ではこの (2) の命題が成り立つことについて解説するが、具体的には (2) の対偶である
「2つの長方形が重なっていないならば、ある直線が分離軸になる」
ことを示す。
1つの長方形は2組の平行な辺によって構成される。したがって、長方形は辺を4つ持っているが各辺の向きはすべて異なるわけではなく、辺の向きは2つしかないわけである。そして長方形であるから、その2つの辺の向きは直交している。
結論から言うと、傾きのある長方形同士の衝突判定において分離軸となり得る直線は、2つの長方形の各辺の向きに平行な直線である。1つの長方形は2つの辺の向きしか持たないから、分離軸となり得る直線は4つあるわけである。
このことは次のようにして導かれる。
任意の2つの長方形を任意の位置、任意の向き、さらに 両者が重ならないように配置したとき、それらのうち少なくとも一方の長方形をもう一方の長方形に衝突しないように、その長方形の1つの辺の向きに沿って(両方向に)無限に引き伸ばすことができる。
-
 図6
図6 -
 図7
図7 -
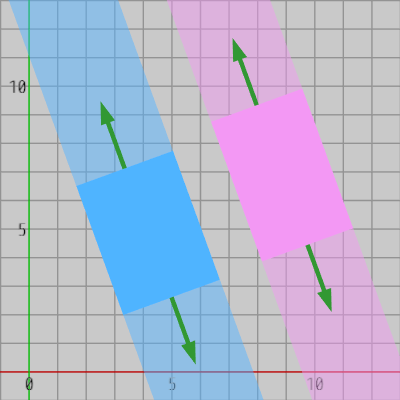 図8
図8
図6、図7では両者が衝突しないように無限に引き延ばせるのは片方の長方形だけであるが、図8のように2つの長方形が平行である場合には両方の長方形を無限に引き延ばしても両者は衝突しない。
この事実を使えば、2つの傾きのある長方形同士が衝突していない場合、それらの長方形を分離する分離直線を次のように引くことができる。
-
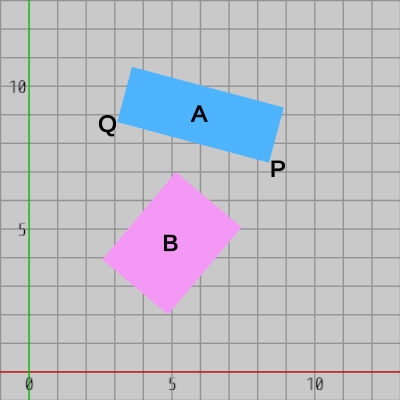 図9 2つの長方形 A、B は衝突していない
図9 2つの長方形 A、B は衝突していない -
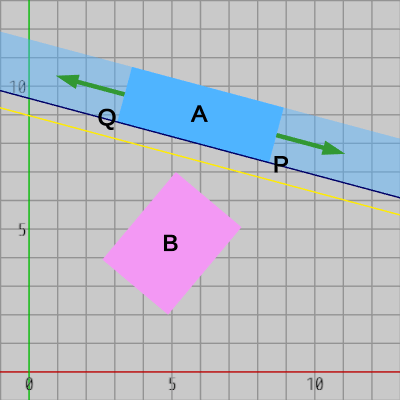 図10 黄色い直線は、辺PQを通る直線に平行であり、2つの長方形と交わらないので 分離直線である
図10 黄色い直線は、辺PQを通る直線に平行であり、2つの長方形と交わらないので 分離直線である -
 図11 分離直線に直交する直線が分離軸
図11 分離直線に直交する直線が分離軸
図9には2つの長方形$A$、$B$ が衝突していない状態で置かれている。図から明らかなように長方形$A$の辺$PQ$に沿った方向に$A$を(両方向に)無限に引き伸ばしても長方形$B$とは衝突しない。したがって、$PQ$を通る直線も$B$とは衝突しない。
このとき、図10に示されるように$PQ$を通る黒い直線と適当な間隔を置いて、その黒い直線に平行な黄色い直線を $A$ と $B$ の間に置くことができるが、この黄色い直線は2つの長方形と交わることのない分離直線である。
分離軸は分離直線と直交する直線であるから、この場合、図11において黄色い直線と直交している直線が2つの長方形$A$と$B$の分離軸になる。
例えば、先程の図4の場合における分離軸をこの方法で求めてみよう (便宜上ここでも2つの長方形を$A$、$B$とし、$A$の2つの頂点を$P$、$Q$としている)。
-
 図12
図12 -
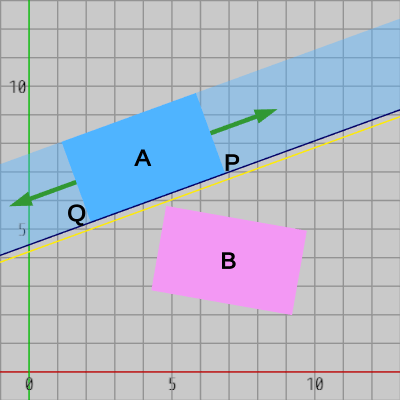 図13 PQを通る黒い直線に平行な黄色い直線は分離直線
図13 PQを通る黒い直線に平行な黄色い直線は分離直線 -
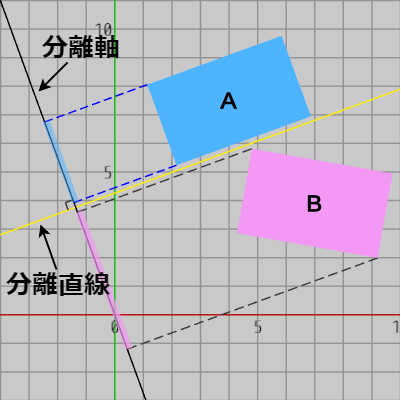 図14 分離直線に直交する分離軸
図14 分離直線に直交する分離軸
図13に示されるように、長方形$A$を辺$PQ$に沿って無限に引き伸ばせるので$PQ$を通る直線は長方形$B$とは衝突しない。また、$PQ$を通る黒い直線からわずかな距離を置いて その黒い直線に平行な黄色い直線を2つの長方形の間に置くことができるが、この黄色い直線は分離直線である (図13)。
したがって、図14に示されるように分離直線(黄色い直線)に直交する直線が分離軸になる。実際、その直線上にある2つの長方形の射影区間の間にはギャップが存在している。
繰り返しになるが、2つの長方形が重なっていないならば、2つの長方形のいずれかの辺に平行な直線は必ず分離直線になる。分離直線と分離軸は一方が存在すればもう一方も存在し(2-19節)、分離軸と分離直線は直交しているので、「2つの長方形が重なっていないならば、2つの長方形のいずれかの辺に平行な直線は必ず分離軸になる」ともいえるわけである。言い換えれば、2つの長方形の辺に平行な直線がどれも分離軸にならないならば、2つの長方形は重なっているのである。
そして、これが上記の 2-19節 (2) の主張なのである。
C) 直線上の射影区間の求め方
ある直線上に長方形を射影したときにできる射影区間とは、長方形の4つの頂点を射影したときの各像の最小値と最大値の間の区間のことである (最小値、最大値は原点からの距離に関しての値である)。

図15は長方形を x軸上に射影したときのものであるが、このとき一番左の頂点$P_2$を射影したときの像$Q_2$が射影区間の最小値であり、一番右の頂点$P_0$を射影したときの像$Q_0$が射影区間の最大値である。
具体的には x軸上において $Q_2 = 2.1$、$Q_0 = 7.9$ であるので、射影区間は $2.1$ から $7.9$ までということになる(図15)。
射影したときの像は、射影する直線上において原点からどれだけ離れているかを表している。図15において長方形の4つの頂点$P_0$~$P_3$を x軸上に射影したときの各像は点$Q_0$~$Q_3$であるが、それらの値は小さい順に $Q_2 = 2.1$、$Q_3 = 3.2$、$Q_1 = 6.8$、$Q_0 = 7.9$ である。この値は x軸上において各像が原点からどれだけ離れているかを表す距離である。最小値、最大値は直線上における 原点からの距離 で決まるのである。
射影する直線が x軸であれば、射影区間を求めることは容易である。長方形の4つの頂点を x軸上に射影したときの像は、各頂点の x座標と同じ値になるので各頂点の x座標を比較すればよい。
しかし、射影する直線が x軸や y軸ではなく、図16に示されるような傾きのある直線の場合、射影区間はこのように単純には求めることはできない。傾きのある直線上における射影区間を求めるには、1-3節で扱った単位ベクトルによる内積を使うことになる。
例えば 上の図16では長方形の射影区間は黒い直線上の $Q_2$ から $Q_0$ であるが、この直線上における原点から$Q_2$までの距離、及び原点から$Q_0$までの距離は以下のように求められる。
-
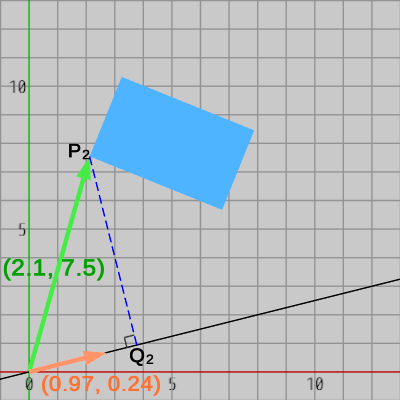 図17
図17 -
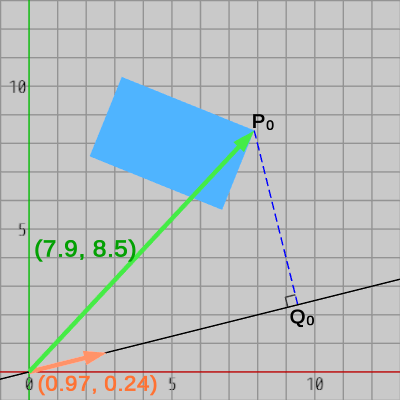 図18
図18 -
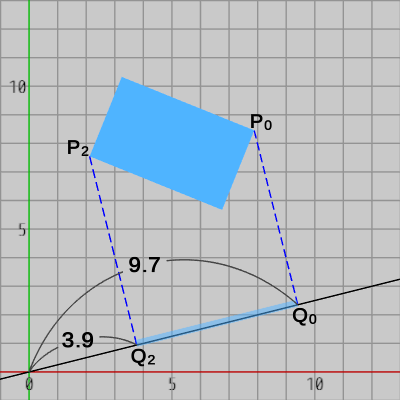 図19
図19
長方形の点$P_2$を黒い直線へ射影したときの像が$Q_2$であるから、原点$O$と$P_2$を結ぶベクトルを $\overrightarrow{OP_2}$ 、黒い直線の方向を表す単位ベクトルを $\boldsymbol{u}$ とすれば、原点$O$から$Q_2$までの距離$|OQ_2|$は次のように計算される (図17の緑のベクトルが $\overrightarrow{OP_2}$、オレンジのベクトルが $\boldsymbol{u}$ である)。
\[\overrightarrow{OP_2}\cdot \boldsymbol{u} = |OQ_2|\]$\overrightarrow{OP_2}$ 及び $\boldsymbol{u}$ に図17に示される各値を代入して計算すると、\[|OQ_2| = \overrightarrow{OP_2}\cdot \boldsymbol{u} = (2.1,\ 7.5) \cdot (0.97,\ 0.24) \risingdotseq 3.9\]となるが、この値が黒い直線上における原点から$Q_2$までの距離である。
同様にして、図18における原点$O$から$Q_0$までの距離$|OQ_0|$は次のように計算される (図18の緑のベクトルが $\overrightarrow{OP_0}$、オレンジのベクトルが $\boldsymbol{u}$ である)。
\[|OQ_0| = \overrightarrow{OP_0}\cdot \boldsymbol{u} = (7.9,\ 8.5) \cdot (0.97,\ 0.24) \risingdotseq 9.7\]
すなわち、黒い直線上における長方形の射影区間は $3.9$ から $9.7$ である (図19)。
以下のメソッド CollisionTest_OBB_OBB(..) は傾きのある長方形同士の衝突判定を実装したものである。
[CollisionTest_OBB_OBB(..)]
// OBB vs OBB
bool CollisionTest_OBB_OBB(Vector2[] vertsA, Vector2[] vertsB)
{
Vector2[] sideDirs =
{
(vertsA[0] - vertsA[1]).normalized, (vertsA[1] - vertsA[2]).normalized,
(vertsB[0] - vertsB[1]).normalized, (vertsB[1] - vertsB[2]).normalized
};
foreach (var u in sideDirs)
{
float minA = Vector2.Dot(vertsA[0], u);
float maxA = minA;
float minB = Vector2.Dot(vertsB[0], u);
float maxB = minB;
for (int i = 1; i < 4; i++)
{
float projA = Vector2.Dot(vertsA[i], u);
if (projA < minA) { minA = projA; }
else if (projA > maxA) { maxA = projA; }
float projB = Vector2.Dot(vertsB[i], u);
if (projB < minB) { minB = projB; }
else if (projB > maxB) { maxB = projB; }
}
if (maxB < minA || maxA < minB)
{
return false;
}
}
return true;
}
メソッドに送られてくる引数 vertsA、vertsB は2つの長方形$A$、$B$の頂点座標の配列であり、要素数はいずれも $4$ である。4行目の Vector2[]型のローカル変数 sideDirs には2つの長方形の4つの辺の方向がセットされる (4つの辺の方向は単位ベクトルとしてセットされる)。上で述べたように、分離軸の候補となる直線は2つの長方形のいずれかの辺に平行な直線であり、2つの長方形の辺の方向は多くて4つであるから、それらをすべて sideDirs にセットしている。
9行目の foreachブロックは、分離軸候補となる4つの直線のそれぞれで2つの長方形の射影区間の比較を行う部分である。ここで使われる変数 u は、分離軸候補の各直線の方向を表す単位ベクトルである。先程、直線上の射影区間を求める計算を行ったが、そこで使われた単位ベクトル $\boldsymbol{u}$ と役割は同じである。
まず2つの長方形$A$、$B$の射影区間を求める必要があるが、17行目の forブロックがその処理である。4つの float型変数 minA、maxA、minB、maxB には最終的には2つの長方形の射影区間を表す最小値、最大値がセットされる。
19行目で計算される projA は、長方形$A$の各頂点を直線上に射影したときの 各像の原点からの距離である。その下の2つのifブロックにおいて各像の原点からの距離を比較し最大値、最小値を決定する。23行目以降では長方形$B$について同様のことを行っている。
17行目の forブロックが終了する時点(27行目)では、ある直線についての2つの長方形の射影区間が算出されているので、28行目の ifブロックでその直線において2つの射影区間の間にギャップが存在するかを調べ、存在するならば衝突していないことを表す false を返す。
4つの分離軸候補の直線のすべての場合で、この28行目の ifブロックに入らないときは、分離軸候補のどの直線にもギャップが存在しないということであり、それは2つの長方形が衝突していることを意味する。その場合は、このメソッドの最後で衝突を表す true を返す。
ただ実際には上のメソッド内で使われている sideDirs の各要素を正規化する必要はない。この配列の各要素には2つの長方形の各辺の方向を表す単位ベクトルがセットされているが、2つの射影区間の間にギャップがあるかどうかを調べるだけならば各辺の方向を単位ベクトルにしてもしなくても結果は変わらないためである。つまり 4行目の sideDirs は次のようにセットしても結果は同じである。
Vector2[] sideDirs =
{
vertsA[0] - vertsA[1], vertsA[1] - vertsA[2],
vertsB[0] - vertsB[1], vertsB[1] - vertsB[2]
};
では最後に、本節で述べた内容に関するプログラムを作成する。
# Code1
最初のプログラムでは2つの長方形を以下のキー操作によって動かし、上記の CollisionTest_OBB_OBB(..) を用いて衝突判定を行う。青い長方形のキー操作
H : 左へ移動
J : 下へ移動
K : 上へ移動
L : 右へ移動
R : 反時計周りに回転(Shiftと同時押しで逆回転)
緑の長方形のキー操作
Q : 反時計周りに回転(Shiftと同時押しで逆回転)
なお、本節でもプログラム内では青い長方形、緑の長方形は Blue、Green として使われている。
[Code1] (実行結果 図21)
if (!i_INITIALIZED)
{
i_initVertsBlue = new Vector2[] { new Vector2(3, 1), new Vector2(-3, 1),
new Vector2(-3, -1), new Vector2(3, -1), };
i_initVertsGreen = new Vector2[] { new Vector2(3, 1), new Vector2(-3, 1),
new Vector2(-3, -1), new Vector2(3, -1), };
i_degBlue = 0;
i_degGreen = 0;
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.Q))
{
i_degGreen = (THUtil.IsShiftDown()) ? i_degGreen - 1 : i_degGreen + 1;
THMatrix3x3 mtx = TH2DMath.GetTranslation3x3(0, 5) * TH2DMath.GetRotation3x3(i_degGreen);
Green.SetMatrix(mtx);
}
Vector2 posB = Blue.GetPosition();
float speed = 0.10f;
if (Input.GetKey(KeyCode.H))
{
posB.x -= speed;
}
else if (Input.GetKey(KeyCode.L))
{
posB.x += speed;
}
if (Input.GetKey(KeyCode.J))
{
posB.y -= speed;
}
else if (Input.GetKey(KeyCode.K))
{
posB.y += speed;
}
if (Input.GetKey(KeyCode.R))
{
i_degBlue = (THUtil.IsShiftDown()) ? i_degBlue - 1 : i_degBlue + 1;
}
THMatrix3x3 M = TH2DMath.GetTranslation3x3(posB) * TH2DMath.GetRotation3x3(i_degBlue);
Blue.SetMatrix(M);
Vector2[] vertsB = new Vector2[4];
Vector2[] vertsG = new Vector2[4];
THMatrix3x3 mtxB = Blue.GetMatrix();
THMatrix3x3 mtxG = Green.GetMatrix();
for (int i = 0; i < 4; i++)
{
vertsB[i] = mtxB * TH2DMath.ToVector3(i_initVertsBlue[i]);
vertsG[i] = mtxG * TH2DMath.ToVector3(i_initVertsGreen[i]);
}
bool bColl = CollisionTest_OBB_OBB(vertsB, vertsG);
Hit(bColl);


1行目のifブロックは初期化ブロックであり、i_initVertsBlue、i_initVertsGreen はVector2[]型のインスタンス変数で、初期状態における Blue、Greenの頂点座標がセットされる (2つの長方形はともに図20に示される大きさで 横の長さが $6$、縦の長さは $2$ である)。i_degBlue、i_degGreen は Blue、Greenの回転角度を表すインスタンス変数である。
Qキーを押すと Greenが所定の位置において回転を行うが、14行目のifブロックはその処理が記述されている。
22行目から49行目まではBlueをキー操作によって動かす部分であるが上で述べたとおり、H、J、K、L が上下左右の移動であり、Rキーによって回転する。
52行目以降が衝突判定処理の部分である。
傾きのある長方形同士の衝突判定用メソッド CollisionTest_OBB_OBB(..) の引数には、その時点における2つの長方形の各頂点座標をセットする必要があるが、2つの長方形の頂点座標は56行目のfor文において計算される。何度か述べたように、ある時点におけるオブジェクト上のある位置$P$の座標は、その時点においてオブジェクトに実行されている変換行列と初期状態における$P$の座標との積によって求めることができる。そして、その際には初期状態における$P$の座標を同次座標化し z成分を $1$ にする必要がある (2-13節参照)。
ここで求めるのは、衝突判定を行う時点での2つの長方形の各頂点座標である。したがって、ここではその時点において長方形に実行されている変換行列と初期状態における長方形の各頂点座標を同次座標化したものの積を計算すればよい。
56行目のfor文内で使われている mtxB や mtxG は Blue、Greenに実行されている変換行列であり、i_initVertsBlue[i] や i_initVertsGreen[i] は初期状態のBlue、Greenの各頂点座標であり、ToVector3(..) は引数の2次元ベクトルを同次座標化して返すカスタムライブラリーのメソッドである (z成分が $1$ の同次座標が返される)。
# Code2
次のプログラムはCode1とほとんど同じものである。プログラムを実行すると緑の長方形が適当な運動を行っているが、キー操作によって青い長方形を動かし2つの長方形同士の衝突を検出する。
キー操作は青い長方形についてはCode1と同じであり、H、J、K、L によって上下左右の移動、R によって回転を行う。
また、ここでは Sキーによって緑の長方形の運動を停止/再開させることができる。
[Code2] (実行結果 図22)
if (!i_INITIALIZED)
{
i_initVertsGreen = new Vector2[] { new Vector2(3, 1), new Vector2(-3, 1),
new Vector2(-3, -1), new Vector2(3, -1), };
i_initVertsBlue = new Vector2[] { new Vector2(3, 1), new Vector2(-3, 1),
new Vector2(-3, -1), new Vector2(3, -1), };
i_degBlue = 0;
i_MOVE = true;
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S))
{
i_MOVE = !i_MOVE;
}
if (i_MOVE)
{
GreenMotion(0); // Greenの運動 (0 単振動 ; 1 回転)
}
Vector2 posB = Blue.GetPosition();
float speed = 0.10f;
if (Input.GetKey(KeyCode.H))
{
posB.x -= speed;
}
else if (Input.GetKey(KeyCode.L))
{
posB.x += speed;
}
if (Input.GetKey(KeyCode.J))
{
posB.y -= speed;
}
else if (Input.GetKey(KeyCode.K))
{
posB.y += speed;
}
if (Input.GetKey(KeyCode.R))
{
i_degBlue = (THUtil.IsShiftDown()) ? i_degBlue - 1 : i_degBlue + 1;
}
THMatrix3x3 M = TH2DMath.GetTranslation3x3(posB) * TH2DMath.GetRotation3x3(i_degBlue);
Blue.SetMatrix(M);
Vector2[] vertsB = new Vector2[4];
Vector2[] vertsG = new Vector2[4];
THMatrix3x3 mtxB = Blue.GetMatrix();
THMatrix3x3 mtxG = Green.GetMatrix();
for (int i = 0; i < 4; i++)
{
vertsB[i] = mtxB * TH2DMath.ToVector3(i_initVertsBlue[i]);
vertsG[i] = mtxG * TH2DMath.ToVector3(i_initVertsGreen[i]);
}
bool bColl = CollisionTest_OBB_OBB(vertsB, vertsG);
Hit(bColl);

それ以外の部分はCode1と同じである。
© 2020-2025 Redpoll's 60 (All rights reserved)