$§$2-13 衝突判定 1 (点 vs 円盤、長方形 ; ローカル座標からワールド座標への変換 2D)

本節から2-24節までは2D空間における衝突判定について見ていく。2D空間においても衝突判定の種類はいろいろあるが、ここで扱う内容は円や長方形、あるいは三角形の集合としての多角形に関連した基本的なもののみであり、深入りはしない。

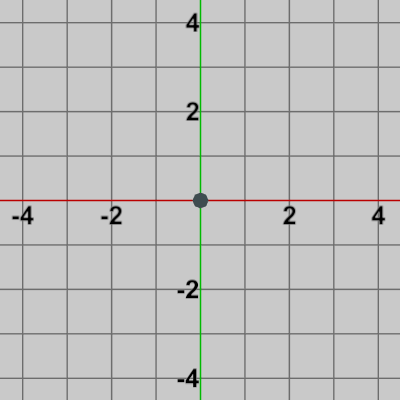
前節や前々節では図1に示される小さな円形オブジェクトShellを戦車やヘリコプターから発射させた。そこでは、Shellは2D空間内を等速に直線運動するものであったが、2-17節までに扱う衝突判定ではこの等速直線運動を行うShellと2D空間内のオブジェクトとの衝突が対象となる。
衝突判定において使用される Shellは、点(あるいは粒子)として扱い、その大きさについては考えないものとする。

A) 点 対 円盤 (Point vs Disk)

最も簡単なケースである。
下の図2はShellが2D空間内を等速直線運動しているときのもので、緑色の矢印の方向に進んでいることを意味している。図3は図2の状態から一定時間が経過したときのもので、運動中のShellが円盤オブジェクトに衝突した瞬間である。


Shellと円盤との衝突判定は次のように行われる。


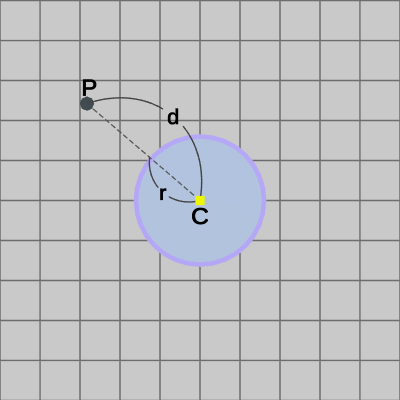
円盤の中心の座標を$C$、半径を$r$、Shellの座標を$P$とする (正確にはShellの中心座標)。Shellから円の中心$C$までの距離を$d$とする。
このとき、Shellから円盤の中心までの距離$d$が円盤の半径$r$以下であれば衝突とし(図4)、Shellから円盤の中心までの距離$d$が円盤の半径$r$より大きければ衝突していないものとする(図5)。
つまり、\[ r \geq d \]ならば Shellと円盤は衝突しているということである。

以下のメソッド CollisionTest_Point_Disk(..) は、Shellと円盤との衝突を実装したものである。
[CollisionTest_Point_Disk(..)]
メソッド内で使われている変数 C、r、P、d は上で述べたものと同じで、円盤の中心座標、円盤の半径、Shellの座標、Shellから円盤の中心までの距離を意味している。

B) 点 対 長方形 (Point vs AABB, OBB)

次に長方形との衝突判定について考える。
図6はある長方形の初期状態であり、長方形の各辺はx軸、y軸に平行である。図7はその長方形にShellが衝突したときの様子である (ここではShellを明確にするために水色にしてある)。図中の $A$、$B$ は初期状態の長方形の左下隅の頂点、右上隅の頂点を表し、$P$ はShellの位置を表している。


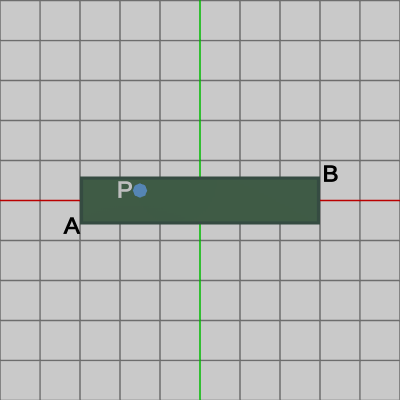
このとき、Shellと長方形が次の条件\[ A.x \leq P.x \leq B.x \quad \&\& \quad A.y \leq P.y \leq B.y \]を満たすとき、Shellと長方形は衝突しているものとする (式中の $\&\&$ はプログラミングにおける論理演算子 && と同じ意味で論理積ANDを意味する)。

プログラムに記述すると以下のようになる。

たとえば、上図7は Shellと長方形が衝突しているときのものであるが、このときのShellは そのx座標が$A$のx座標と$B$のx座標の間にあり、かつ、y座標が$A$のy座標と$B$のy座標の間にあるので、確かに上記の衝突の条件を満たしている。
これは長方形との衝突判定での最も簡単な場合である。2D空間上に配置されている長方形は平行移動や回転、スケールによってさまざまな位置にさまざまな状態で置かれているので、上記の初期状態の場合の衝突判定はそのままでは使えない。しかし、ごく簡単な処理によってすべての長方形に対し、上記の初期状態での衝突判定を用いることができる。
以下では、そのことについて見ていこう。

2D空間に配置される長方形は大別して、軸平行な長方形(Axis Aligned Bounding Box : AABB)と傾きのある長方形(Oriented Bounding Box : OBB)の2つに分けられるが、上で見てきた例は軸平行な長方形の例である。ここでは傾きのある長方形の衝突判定を通して、すべての長方形の場合における衝突判定メソッドを作成する (軸平行な長方形の場合でもメソッドは同じものになる)。


「傾きのある長方形」とは図9に示されるように長方形の各辺がx軸、y軸に対して平行でない長方形、すなわち 軸平行でない長方形のことである。


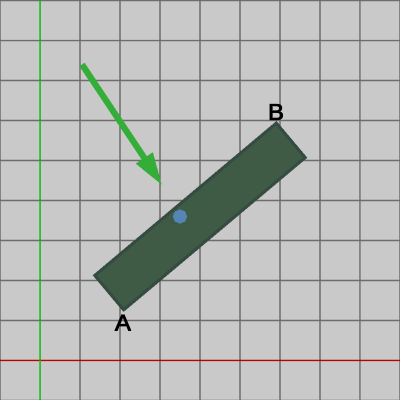
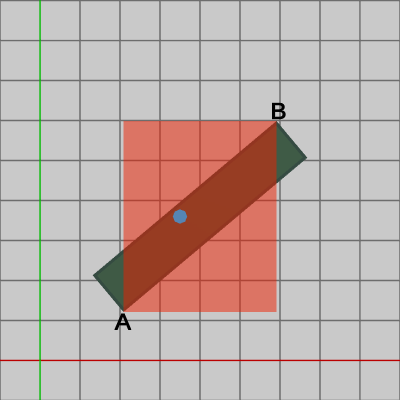
図10は、2D空間を進んできたShellが傾きのある長方形に衝突したときの様子である ($A$、$B$はこの長方形の左下隅、右上隅の頂点である)。Shellとこの長方形が衝突したかを判定するために、上記の軸平行な長方形に対して使用した方法はここでは使えない。軸平行な長方形に対して使用した方法は、具体的には2つの点$A$、$B$を左下隅、右上隅とする軸平行な長方形の中にShellが含まれるかどうかの判定である。今問題としている長方形の場合、2点$A$、$B$を左下隅、右上隅とする軸平行な長方形は図11における赤いエリアになる。そして、この赤いエリアに Shellがある場合は全て衝突としてみなされてしまう。


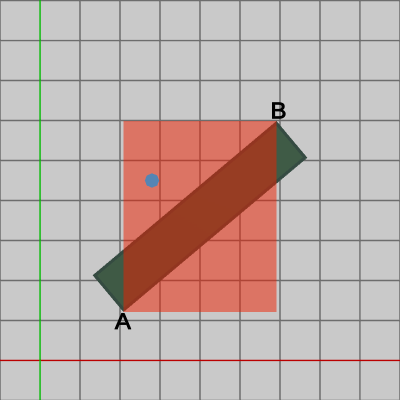
例えば、図12では Shellは長方形に衝突しているわけではないが、赤いエリアに含まれるので衝突としたものとして扱われる。また、図13においては Shellは長方形と衝突しているが赤いエリアに含まれていないので、この場合の衝突は検出されない。
これらの問題点に対する解決策は簡単である。1-4節や1-8節では逆行列について少し触れたが、何らかの変換行列が実行されているオブジェクトに対して、その変換行列の逆行列をオブジェクトに実行すると、オブジェクトは何の変換も受けていない初期状態に戻るのであった。傾きのある長方形の場合も、その長方形に実行されている変換行列の逆行列を実行すれば(軸平行な)初期状態に戻るので、その状態において上記の軸平行な長方形の場合のメソッドを使えばよいのである。ただし、以下の議論は傾きのある長方形の初期状態が軸平行であることを前提としている。


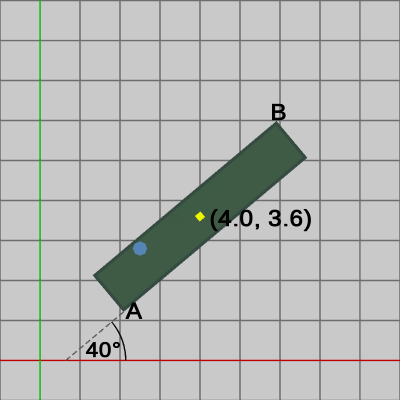
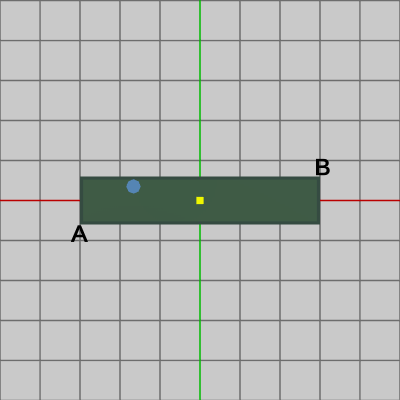
たとえば、図14は傾きのある長方形にShellが衝突した状態であるが、この傾きのある長方形には、$40$°の回転、$(4.0, 3.6)$の平行移動がこの順で実行されている (図中の黄色い印は長方形の中心を表し、その位置は $(4.0, 3.6)$ である)。したがって、この長方形に実行された変換行列の逆行列を実行すると初期状態に戻るが、このとき その逆行列を Shellに対しても実行すると、Shellは長方形と同じ変換を受けることになり、図15に示されるように Shellは初期状態の長方形に衝突した状態になる。したがって、図15の状態の長方形とShellを使えば軸平行な場合の方法による衝突判定が可能になるわけである。
この長方形に実行された変換行列の逆行列を具体的に示そう。$40$°の回転を $R$、$(4.0, 3.6)$の平行移動を $T$、その積を $M = TR$ とすれば、$M$ の逆行列 $M^{-1}$ は、\[ M^{-1} = (TR)^{-1} = R^{-1}T^{-1}\]となる。$T^{-1}$ は $(-4.0, -3.6)$ の平行移動を表し、$R^{-1}$ は $-40$°の回転を表す。したがって、逆行列 $M^{-1} = R^{-1}T^{-1}$ の具体的な内容は、$(-4.0, -3.6)$ の平行移動、$-40$°の回転をこの順序で実行するというものである。以下の図16は、図14の状態から $(-4.0, -3.6)$ の平行移動が実行された状態である。図14では長方形の中心(図中の黄色い印)が $(4.0, 3.6)$ であったが、この平行移動によって図16では長方形の中心が原点に移動している。図17はその状態からさらに $-40$°の回転を実行したときのもので、図17では長方形が初期状態に戻っている。また、この逆行列は同時に Shellにも実行されているので図17に示されるように、逆行列実行後においては Shellは初期状態の長方形に衝突した状態になっている。

• 
  図14
• 
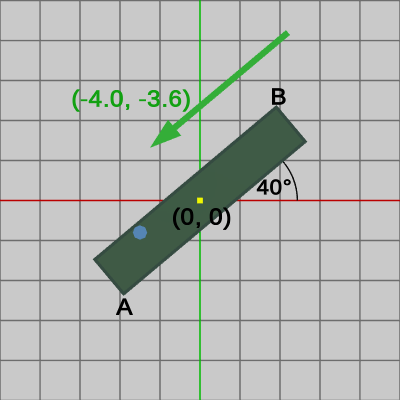  図16
• 
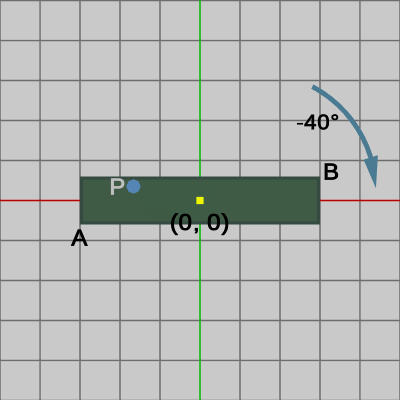  図17

以下のメソッド CollisionTest_Point_AABB(..) は軸平行な長方形とShellとの間における衝突判定メソッドである。第1引数の P はShellの位置を表し、第2引数の minmax は、軸平行な長方形の左下隅の頂点座標、右上隅の頂点座標がセットされた配列である (以下のメソッドではローカル変数 min、max が左下隅、右上隅の頂点として使われている)。
[CollisionTest_Point_AABB(..)]


この長方形用の衝突判定メソッドは、プログラムから次のように利用することで Shellと(任意の)長方形との間の衝突判定を行うことが可能になる。

1行目の shell_pos は Shellの現在位置を表している。2行目の Rectは長方形オブジェクトのことで、ここでは GetMatrix() によって Rectに実行された変換行列を取得している。3行目では、Rectに実行された変換行列 mtx の逆行列 mtx.inverse を、同次座標化した shell_pos に掛けることで、Rectを初期状態に戻した状態における Shellの位置 P を計算している (inverseは逆行列を表すTHMatrix3x3構造体のプロパティ)。なお、3行目の ToVector3(..) はカスタムライブラリーの TH2DMathクラスのstaticメソッドで、引数の Vector2型の値を同次座標化して Vector3型の値で返すものである (例えば、$(a, b)$ ならば $(a, b, 1)$ が返される)。
上で見てきた例でいえば、1行目の shell_pos が図14のShellの位置のことであり、3行目の P が図17のShellの位置のことである。
4行目の initRectBounds は、Rectの初期状態における左下隅、右上隅の頂点座標を取得するためのプロパティで、配列の形で返される。上の例の長方形でいえば、initRectBounds によって返される配列の中身は図17の $A$、$B$ (の座標)である。

ここでは長方形の衝突判定について、傾きのある長方形の場合で解説してきたが、傾きのない長方形、すなわち軸平行な長方形の場合でも上記と同じ方法で衝突判定を行えることは明らかであろう。さらに、長方形に対して平行移動、回転の他にスケールが実行されている場合でもこの方法、すなわち、逆行列によって長方形を初期状態に戻した状態で衝突判定を行うという方法が適用できる。
しかし、上で見てきたように実際にはプログラム中で逆行列が長方形に実行されることはない。逆行列が使われるのは、長方形を初期状態に戻した状態でのShellの位置を求めるときにのみ使われる。初期状態における長方形の左下隅、右上隅の頂点座標はあらかじめプロパティとして保持しているので逆行列によって計算する必要はないのである。
逆行列によって初期状態に戻した状態で衝突判定を行うという方法は長方形に留まらず、より一般のオブジェクトに対しても適用できるが、そのことについては 2-15節において扱う。

C) オブジェクトの頂点座標の計算

オブジェクトとの衝突判定に関連して、プログラム実行中におけるオブジェクトの頂点座標の求め方について簡単に述べておこう。具体的には、何らかの変換を実行した際のオブジェクトの頂点座標の計算であり、いわゆるローカル座標からワールド座標への変換である (ローカル座標やワールド座標については4-8節を参照)。

まず長方形を例にとる。図18はある長方形の初期状態であり、図19はこの初期状態の長方形に対して $60$°の回転、$(-3.2,\ 2.5)$ の平行移動をこの順で実行した結果である。


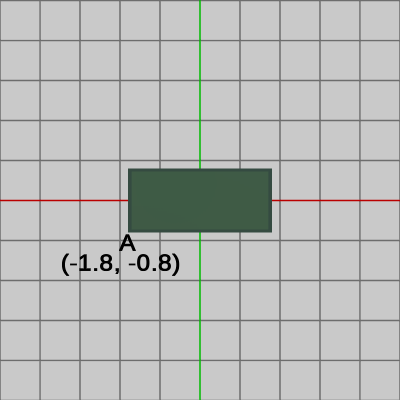
図中の点 $A$ は長方形の左下隅の頂点であり変換実行前の位置は $(-1.8, -0.8)$、変換実行後の位置は $(-3.41,\ 0.54)$ である (ただし、小数第3位を四捨五入し小数第2位までを表示)。
この変換の過程を順に示したのが以下の図20、図21である。図20は初期状態の長方形に第1の変換である$60$°の回転を実行したときの様子であり、図21は回転実行後の長方形に対して第2の変換である $(-3.2,\ 2.5)$ の平行移動を実行したときの様子である。

• 
  図18
• 
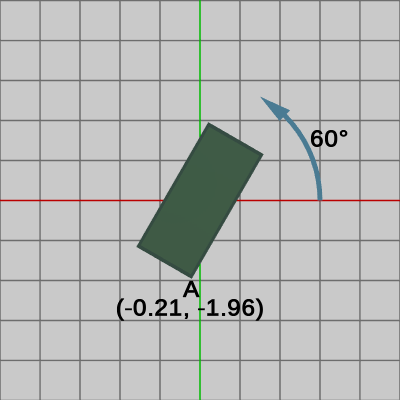  図20
• 
  図21

長方形に対して実行した変換は、もちろん長方形の左下隅の点$A$に対しても実行されるので、点$A$は初期状態の位置である $(-1.8,\ 0.8)$ から、$60$°回転し、次に $(-3.2,\ 2.5)$ だけの平行移動が実行される。$60$°の回転を表す行列を $R$、$(-3.2,\ 2.5)$ の平行移動を表す行列を $T$ とする。この $R$、$T$ を使って、2つの変換後の点$A$の座標を以下で計算しよう (以下の計算では $A$ は同次座標化されて $A = (-1.8, -0.8,\ 1)$ として使われている。また、計算中の数値は小数第3位を四捨五入して小数第2位までの表示にしている)。
1行目の数式 $RA$ は第1の変換である$60$°の回転を $A$ に実行したときの結果であり、この変換によって $A$ は $(-0.21,-1.96)$ に移動する (図20)。2行目の数式は、移動後の位置 $(-0.21, -1.96)$ からさらに $(-3.2,\ 2.5)$ だけの平行移動を行うものであり、その結果 $A$ は最終的に $(-3.41,\ 0.54)$ に移動する (図21)。

今回、長方形に実行された変換は回転、平行移動の順であるが、$R$ と $T$ の積を $M$ とすれば 2つの変換を1つの行列にまとめたものが変換行列$M$であるから、初期状態の長方形(図18)に対して変換行列 $M$ を実行しても同じ結果(図21)になる。同様のことが点$A$についてもいえるから、上記の計算は次のように表せる。これは、変換実行後の長方形の左下隅の点$A$の座標は、長方形に実行された変換行列と同じものを初期状態の点$A$(の同次座標)に掛ければ求められるということを意味している。

このことは長方形だけでなく一般のオブジェクトに対しても成り立つ。
すなわち、変換実行後のオブジェクト上のある点$P$の座標は、そのオブジェクトに実行された変換行列と同じものを初期状態のオブジェクト上の点$P$(の同次座標)に掛ければ求められるということである。


では、他のオブジェクトを用いて、変換が実行されたオブジェクト上のある位置の座標計算をしてみよう。
次の図22は月の形をしたオブジェクトMoonの初期状態である。図23はMoonに対し、y軸方向に $0.6$倍の縮小、次に $45$°の回転、さらに $(3.4,\ 3.2)$ の平行移動をこの順序で結果である。


プログラムでは次のように記述される。

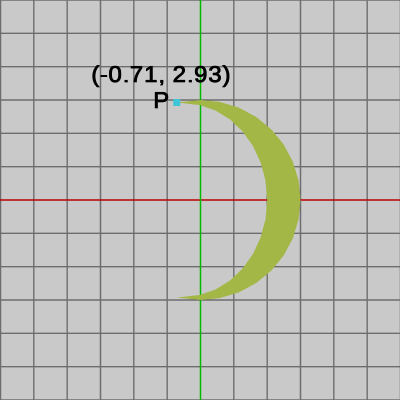
Moon上の点$P$の位置は初期状態では $(-0.71,\ 2.93)$ である (図22)。y軸方向に $0.6$倍縮小するスケール行列を$S$、$45$°の回転を実行する回転行列を$R$、$(3.4,\ 3.2)$ の平行移動を実行する平行移動行列を$T$とし、これら3つの行列の積を $M = TRS$ とすると (以下では小数第3位を四捨五入し小数第2位までの表示)、であり、初期状態の点$P$と変換行列$M$の積を計算すると、
(以下では$P$は同次座標化され $(-0.71,\ 2.93,\ 1)$ として表されている)\[MP = \begin{pmatrix}0.71 &-0.42 &3.40 \\ 0.71 &0.42 &3.20 \\ 0.00 &0.00 &1.00\end{pmatrix}\begin{pmatrix}-0.71\\2.93\\1\end{pmatrix}=\begin{pmatrix}1.65\\ 3.94\\1\end{pmatrix}\]となり、確かに図23(あるいは下図26)に示される変換実行後の点$P$の座標に一致している。

以下の図は上記の3つの変換を1つずつ実行したときの点$P$の座標を表示したものである。

• 
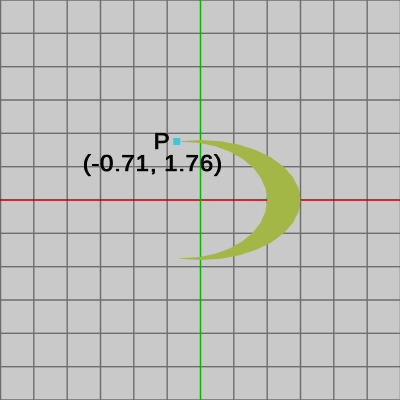  図24
• 
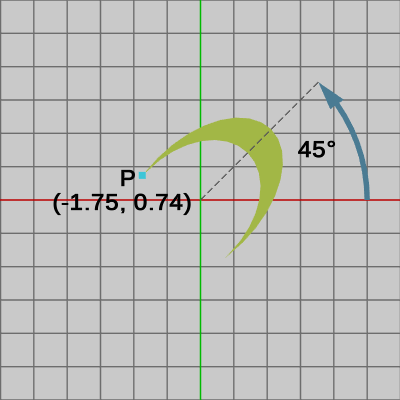  図25
• 
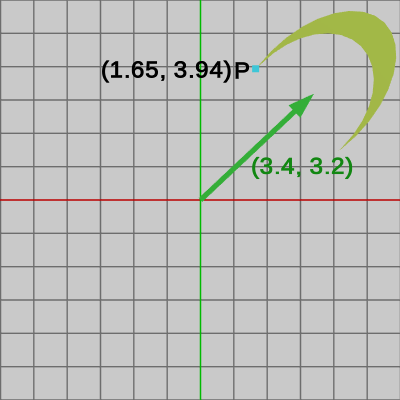  図26

図24は第1の変換であるスケール行列$S$を実行したときのものであり、このときの点$P$は初期状態の位置からy軸方向に $0.6$倍縮小した位置に移動しており、その位置は次のように求められる。\[SP = \begin{pmatrix}1.00 &0.00 &0.00 \\ 0.00 &0.60 &0.00 \\ 0.00 &0.00 &1.00\end{pmatrix}\begin{pmatrix}-0.71\\2.93\\1\end{pmatrix}=\begin{pmatrix}-0.71\\ 1.76\\1\end{pmatrix}\]図25は第1の変換後に 第2の変換である回転行列$R$を実行したときのものであり、このときの点$P$は初期状態の位置からy軸方向に $0.6$倍縮小した位置に移動し、そこからさらに $45$°回転した位置に移動している。したがって、第2の変換後の位置は次のように求められる。
図26はすべての変換を実行したときのものであり、位置の算出についてはすでに上で示されている。

以上のことは次のように要約される。
初期状態におけるオブジェクト上の点$P$の位置が $(x, y)$ であるとする。そのオブジェクトに対し変換行列 $M$ が実行されたとき、変換行列実行後のオブジェクト上の点$P$の位置を $(x', y')$ とすれば、$(x', y')$ は変換行列 $M$ に初期状態の点$P=(x, y)$ の同次座標でz成分を $1$ にしたものを掛けることで求められる。つまり、\[ M\begin{pmatrix}x \\y \\1\end{pmatrix}=\begin{pmatrix}x' \\y' \\1\end{pmatrix}\]である。

D) オブジェクトの方向の計算

2-11節、2-12節ではヘリコプター及び戦車からShellを発射するプログラムを作成した。そこでは Shellを発射する際に、ヘリコプターであれば Bodyの向き、戦車であれば Barrelの向きを事前に計算し、それらの方向へ Shellを発射するのであった。
ここで扱う内容も、ある時点でのオブジェクトの向きを求めるというものだが、2-11節、2-12節とは算出方法が異なる。2-11節、2-12節では Bodyや Barrelの向きを求めるにあたって、それらの回転角度を用いたが ここでは回転角度を使わずに、まずはオブジェクト上のいくつかの座標からその時点でのオブジェクトの方向を計算する。オブジェクト上の座標を求めるには上で述べた方法を使用する。そして、それを元にして ある時点でのオブジェクトの方向 をより一般的な形で計算する。
なお、ここでも図中及び計算式中における数値は、小数第3位を四捨五入し、小数第2位までの表示となっている。

下図27は星型オブジェクト Starの初期状態である。Star上部の先端は赤色が使われており、Starの左下の先端には青色が使われている。図28には、赤い先端部分の点$A$ 及び 青い先端部分の点$B$の座標が表示されている。また、中央に黄色い印があるが、この印は Starの中心位置 $O$ を示しており、初期状態では原点に一致する。

• 
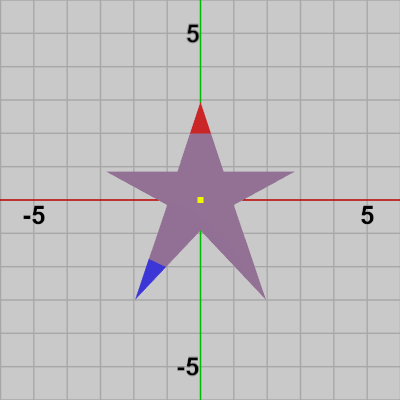  図27
• 
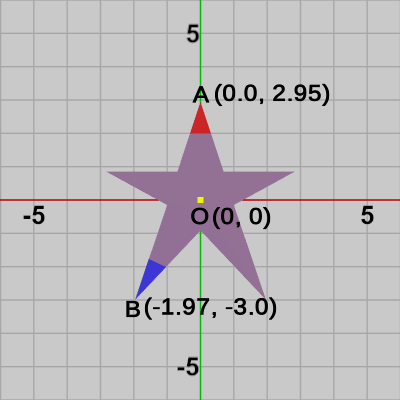  図28
• 
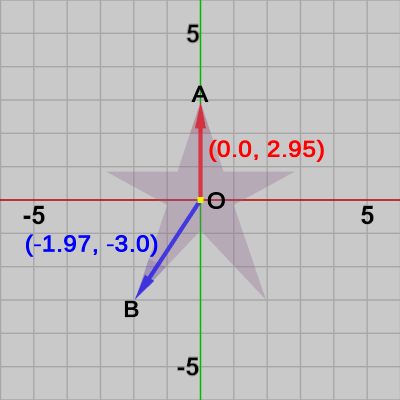  図29

以下では便宜上、Starの中心$O$から赤い先端部分の点$A$への方向を「赤の方向」と呼び、中心$O$から青い先端部分の点$B$への方向を「青の方向」と呼ぶ。具体的には、「赤の方向」とは図29における赤い矢印の方向のことで、Starの中心$O$から点$A$を結ぶベクトル$\vec{OA}$のことである。同様に、「青の方向」とは図29における青い矢印の方向のことで、Starの中心$O$から点$B$を結ぶベクトル$\vec{OB}$のことである。
図29の $(0.0,\ 2.95)$、$(-1.97, -3.0)$ はそれぞれ赤の方向を表すベクトル$\vec{OA}$、青の方向を表すベクトル$\vec{OB}$の内容である (今までは図中においてベクトルの内容を表す数値は緑色のフォントが使われていたが、ここでは一時的に赤、青のフォントで代用する)。

ここで、ある変換を Starに実行し、その結果 Starが図30の状態になったとする。この変換後の Starの赤の方向、青の方向を求めることについて以下では考えていこう。


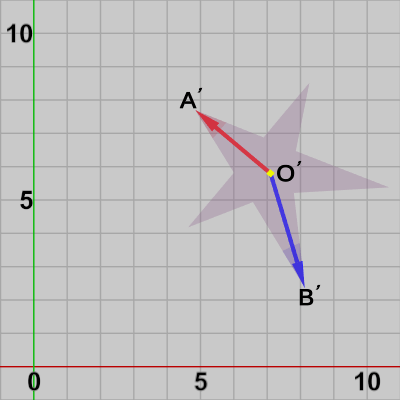
変換実行前(図28)のStar上の各点$O$、$A$、$B$の変換後の位置を $O'$、$A'$、$B'$とする(図30)。
変換後における赤の方向とは、$O'$から$A'$への方向のことであり、変換後の青の方向とは $O'$から$B'$への方向のことである。図31にはそれらの方向が、赤い矢印、青い矢印で表示されている。
したがって、変換後の赤の方向、青の方向を求めるには、変換後の各点 $O'$、$A'$、$B'$ の位置がわかればよいわけである。ある時点におけるオブジェクト上のある位置の計算については上で解説したので、ここではその手続きを使用して $O'$、$A'$、$B'$ を計算しよう。

Starに実行された変換は具体的には、$50$°の回転、$(7.1,\ 5.8)$ の平行移動がこの順序で行われている。回転を表す行列を $R$、平行移動を表す行列を $T$ とし、それらの積を $M = TR$ とする。
上で見てきたように、ある時点におけるオブジェクト上の各位置の座標は、その時点でオブジェクトに実行されている変換行列を初期状態のオブジェクト上の各位置の座標に掛けることで求められる。この例でいえば、図30におけるStar上の $O'$、$A'$、$B'$ の座標は、Starに実行されている変換行列 $M$ を初期状態のStar上の $O = (0, 0)$、$A = (0.0,\ 2.95)$、$B = (-1.97, -3.0)$ に掛けることで求められるということである (ただし、計算においてはこれらの座標は同次座標化されて使われる)。

実際には次のように計算される (以下計算では小数第3位を四捨五入しているため、わずかの誤差を含んでいる)。ここで求められた値を以下の図32に表示する。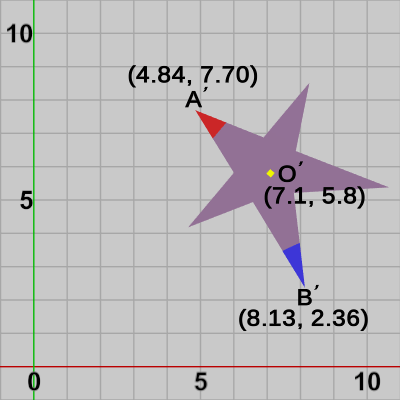


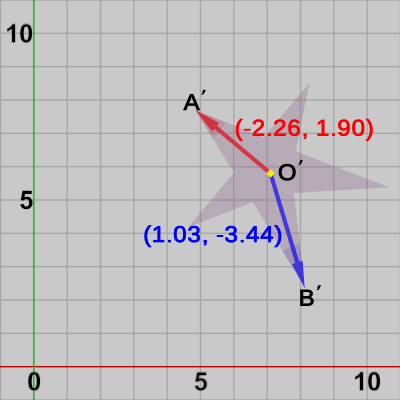
3点 $O'$、$A'$、$B'$ の座標が分かったので、変換後のStarの赤の方向、青の方向を計算しよう。
ここで求める 赤の方向とは $O'$を始点とし、$A'$を終点とするベクトル$\vec{O'A'}$のことであり、青の方向は $O'$を始点とし、$B'$を終点とするベクトル$\vec{O'B'}$のことであるから、それぞれ\begin{align*}\vec{O'A'} = \begin{pmatrix}4.84 \\7.70 \end{pmatrix}-\begin{pmatrix}7.1 \\5.8 \end{pmatrix}=\begin{pmatrix}-2.26 \\1.90 \end{pmatrix}\\\\\vec{O'B'} = \begin{pmatrix}8.13 \\2.36 \end{pmatrix}-\begin{pmatrix}7.1 \\5.8 \end{pmatrix}=\begin{pmatrix}1.03 \\-3.44 \end{pmatrix}\end{align*}となる (図33)。

今行ってきた計算を行列の分配法則(1-4節参照)を使って、より簡潔な形にしよう。
行列の分配法則では、行列 $A$、$B$、$C$ があるとき (ここでは $A$、$B$、$C$ の間で積が可能であるとする)、\[ A(B \pm C) = AB \pm AC \]が成り立つのであった。
また、$A$を $3\times 3$行列、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ を3次元ベクトルとすると、1-4節で見てきたように $3\times 3$行列と3次元ベクトルとの積は行列同士の積として扱えるから、$A$、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ の間にも、\[ A(\boldsymbol{\mathsf{v}} \pm \boldsymbol{\mathsf{w}}) = A\boldsymbol{\mathsf{v}} \pm A\boldsymbol{\mathsf{w}} \]が成り立つ。

上で求めた $O'$、$A'$、$B'$ は $3\times 3$行列 $M$ と同次座標化された3次元ベクトル $O = (0, 0, 1)$、$A = (0.0,\ 2.95,\ 1)$、$B = (-1.97, -3.0,\ 1)$ との積であり、具体的には、$O' = MO$、$A' = MA$、$B' = MB$ と計算された。
ここで、分配法則を用いて変換後の赤の方向であるベクトル$\vec{O'A'}$を求めてみよう。
\begin{align*}\vec{O'A'} &= A' - O' = MA - MO = M(A-O) \\\\&=\begin{pmatrix}0.64 &-0.77 &7.10 \\ 0.77 &0.64 &5.80 \\ 0.00 &0.00 &1.00\end{pmatrix}\left(\begin{pmatrix}0.0 \\2.95 \\1\end{pmatrix}-\begin{pmatrix}0 \\0 \\1\end{pmatrix}\right)\\\\&=\begin{pmatrix}0.64 &-0.77 &7.10 \\ 0.77 &0.64 &5.80 \\ 0.00 &0.00 &1.00\end{pmatrix}\begin{pmatrix}0.0 \\2.95 \\0\end{pmatrix}=\begin{pmatrix}-2.26 \\1.90 \\0\end{pmatrix}\end{align*}最後の行の積では変換行列 $M$ に同次座標 $(0.0,\ 2.95,\ 0)$ が掛けられている。ここで注意すべきは、この同次座標のz成分が $1$ ではなく、$0$ になっていることである。今までは、行列と同次座標化された3次元ベクトルの計算においては、同次座標のz成分は常に $1$ であった。しかし、上記の分配法則を使う計算では最終的に同次座標のz成分は $0$ になってしまい、z成分が $0$ の同次座標と行列の積を計算することになる。
また、$(0.0,\ 2.95)$ は初期状態におけるStarの赤の方向であり、ベクトル$\vec{OA}$のことである。つまり $(0.0,\ 2.95,\ 0)$ は、初期状態におけるベクトル$\vec{OA}$を同次座標化する際に、z成分を $0$ にしたものである。したがって、Starに変換行列 $M$ を実行した後の赤の方向、すなわち ベクトル$\vec{O'A'}$は、変換行列 $M$ と初期状態におけるベクトル$\vec{OA}$の同次座標でz成分を $0$ にしたものとの積によって求められるわけである。
変換行列 $M$ 実行後の青の方向であるベクトル$\vec{O'B'}$の計算も同様である。
\begin{align*}\vec{O'B'} &= B' - O' = MB - MO = M(B-O) \\\\&=\begin{pmatrix}0.64 &-0.77 &7.10 \\ 0.77 &0.64 &5.80 \\ 0.00 &0.00 &1.00\end{pmatrix}\left(\begin{pmatrix}-1.97 \\-3.0 \\1\end{pmatrix}-\begin{pmatrix}0 \\0 \\1\end{pmatrix}\right)\\\\&=\begin{pmatrix}0.64 &-0.77 &7.10 \\ 0.77 &0.64 &5.80 \\ 0.00 &0.00 &1.00\end{pmatrix}\begin{pmatrix}-1.97 \\-3.0 \\0\end{pmatrix}=\begin{pmatrix}1.03 \\-3.44 \\0\end{pmatrix}\end{align*}初期状態におけるStarの青の方向、すなわちベクトル$\vec{OB}$は $(-1.97,-3.0)$ である。したがって、上記の計算は変換行列 $M$ を実行した後の青の方向、すなわち ベクトル$\vec{O'B'}$は、変換行列 $M$ と初期状態におけるベクトル$\vec{OB}$の同次座標でz成分を $0$ にしたものとの積によって求められることを意味している。

今述べてきたことをより一般的な形で言い表そう。
初期状態におけるオブジェクトの方向が $(x, y)$ であるとする。そのオブジェクトに対し、変換行列 $M$ が実行されたとき、変換行列実行後のオブジェクトの方向 $(x', y')$ は、変換行列 $M$ に、初期状態におけるオブジェクトの方向 $(x, y)$ の同次座標でz成分を $0$ にしたものを掛けることで求められる。つまり、\[ M\begin{pmatrix}x \\y \\0\end{pmatrix}=\begin{pmatrix}x' \\y' \\0\end{pmatrix}\]である。


要約すると、ある時点におけるオブジェクトの位置を求めるには、オブジェクトに実行された変換行列 と 同次座標で表されたオブジェクトの初期状態における位置 の積を計算する。そして、位置の場合は同次座標のz成分は $1$ である。ある時点におけるオブジェクトの向きを求めるには、オブジェクトに実行された変換行列 と 同次座標で表されたオブジェクトの初期状態における向き の積を計算する。そして、向きの場合は同次座標のz成分は $0$ である。


最後に1点補足しておこう。
2-8節 Code5 ではオブジェクトの向きを求める際には次のような計算を行った。
ここで使われている変数 R は回転行列であり、(0, 1, 1) は初期状態におけるオブジェクトの向き $(0, 1)$ を同次座標化したものである。
2-8節から2-12節にかけては、ある時点におけるオブジェクトの方向を求める際には同様の計算が行われている。たとえば、2-11節 Code3 においても次のような記述が見られる。
これは、ある時点における Bodyの向きを算出するコードであるが、上記と同様に変数 rotBody は回転行列であり、(0, 1, 1) は初期状態における Bodyの向きである $(0, 1)$ を同次座標化したものである。
先程の解説の中では、オブジェクトの向きを計算する際にはその計算で使用する同次座標のz成分は $0$ にする必要がある と述べた。しかし、今挙げた例ではオブジェクトの向きを計算する際に使われている同次座標のz成分は $0$ ではなく、$1$ となっている。
結論からいえば、ある時点におけるオブジェクトの向きを求めるにあたって、オブジェクトに実行されている変換行列と初期状態のオブジェクトの向きを同次座標化したものの積を計算するが、その計算で使われる同次座標のz成分は $0$ にする必要がある。しかし、z成分を $1$ にして計算した場合でも正しい答えが算出されることがある。どのような場合かというと、いくつかのケースがあるがその1つとしてオブジェクトに実行されている変換行列が回転行列のみの場合があげられる。
ある時点においてオブジェクトに実行されている変換行列が回転行列のみの場合には、その時点でのオブジェクトの向きを求める計算で使われる同次座標のz成分が $0$ であっても、$1$ であっても算出される方向は同じ値になる (つまり計算結果においてz成分が $0$、$1$ と異なるが、x、y成分は同じ値になる)。しかし、オブジェクトに実行されている変換行列が回転行列だけでなく、平行移動行列やスケール行列との合成になっている場合、つまり、回転と回転以外の変換を複数まとめたものになっている場合には、オブジェクトの向きを求める際に同次座標のz成分を $1$ として計算すると一般には正しい答えにはならない。
上記の 2-8節 Code5 や 2-11節 Code3 の計算において、オブジェクトの初期状態の方向を表す同次座標が (0, 1, 1) として使われていても正しい答えが算出されるのは、その計算が回転行列との積になっているからである (もちろん、(0, 1, 0) で計算しても正しい答えにはなる)。