Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-29
第2章 2D空間におけるオブジェクトの運動
$§$2-29 その他の重要事項 3 (スクリーン座標からワールド座標への変換 2D; スクリーンショットの撮影範囲)
本節では2D空間におけるテキストの表示、マウスを用いたインタラクティブな操作(マウスによるオブジェクトの選択、マウスドラッグによるオブジェクトの移動など)、そして最後にスクリーンショットを撮影する際の撮影範囲について扱う。
前節でもそうであったが、本節においてもカメラの投影モードが「Perspective」、Field of View が「$60^\circ$」、画面のアスペクト比が「$16:9$」であることを前提としている (これらの設定については前節冒頭を参照)。
下図1はテキストを貼り付けるオブジェクト CharRect の初期状態であり、このオブジェクトは初期状態においては1辺の長さが $1$ の正方形で、左下隅が原点に位置している。1つのCharRectに1つの文字を貼り付けるので、例えば10個の文字列であればCharRectが10個必要になるわけである。
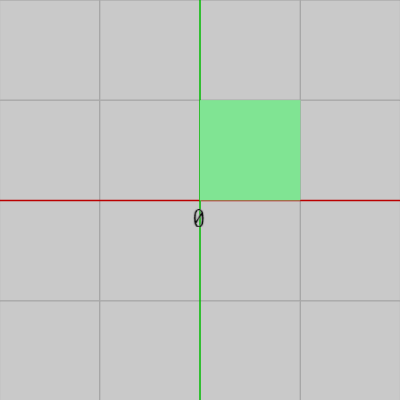
図1 CharRect 初期状態 (1辺の長さ 1 の正方形。初期状態においては左下隅が原点に位置している) 
図2 テキスト用のテクスチャ「sample_letters_2.png」(テクスチャのサイズは 512x512 であり、プログラムで表示できるのは赤い長方形で囲まれている文字のみ)
図2は今回使用するテキスト用のテクスチャであり、いわゆる Bitmap Font と呼ばれるものである。Bitmap Font を用いたテキスト表示は、テクスチャ内の一部の領域を長方形に貼り付ける形で文字を表示するだけであり、近年よく見られる SDF Font (Signed Distance Field Font) などと異なり文字の回転や拡大などを行うとジャギー(ギザギザ)が現れやすいという欠点があるが、作成が簡単であり文字表示の方法も単純であるため今回はこの方法で進めていく (図2のテクスチャのサイズは $512 \times 512$ pix であり、テクスチャのファイルパス(Resourcesフォルダからのファイルパス)は「Resources/images/sample_letters_2.png」である)。
まず1文字分の長方形の大きさを $0.4 \times 1.2$ とする (図3 ; これは単にCharRectを x軸方向に $0.4$ 倍、y軸方向に $1.2$ 倍すればよい)。そして画面上に表示する文字数を8文字とし、文字列領域の左下隅の位置を $(12,\ 8)$ とする (図4)。図の設定では z座標を $-0.02$ としているが、これは前節と同じく文字列が常に画面の手前に表示されるようにするための設定である。
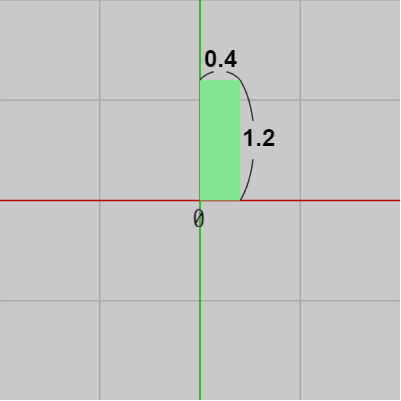
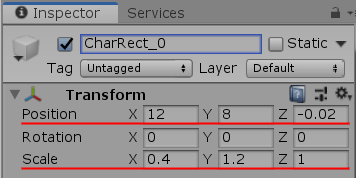
図4
下図に示されるように、この設定によって8個のCharRectが画面右上に配置される (各CharRectの大きさはすべて同じ)。図中の $V_0$ は文字列領域の左下隅を表し、その座標は $(12,\ 8)$ である。
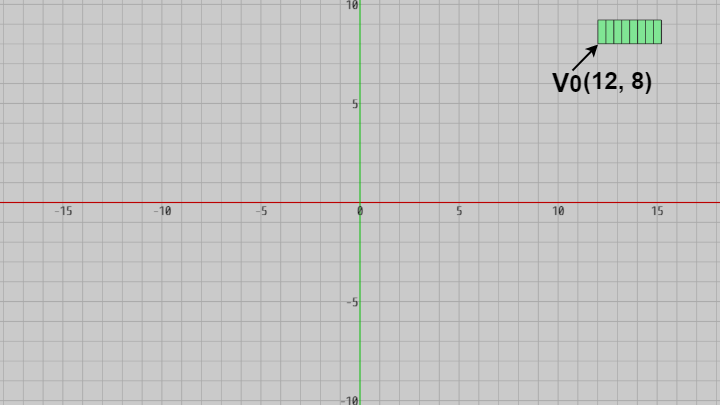
図5 8個のCharRectが画面右上に表示される
以下のプログラムは上で定められた文字列領域に適当な文字列を表示するものである。
[Beta1] (実行結果 図6)
冒頭のローカル変数 RW、RH はCharRect 1つ分の大きさ、すなわち1文分の長方形の大きさであり、V0 は文字列領域の左下隅の位置を表す。
8行目のfor文は8個のCharRectを配置し、各CharRectに指定の文字を表示させる処理である。各CharRectは上図に示されるようにすき間なく隣り合っているので、その位置は V0 から(x軸方向に) RW ずつずらしていけばよい (10行目 ; LL は各CharRectの左下隅の位置)。また各CharRectはすべて同じ大きさであり、その倍率は x軸方向、y軸方向に RW、RH である (13行目)。
各CharRectの位置を定める際のプロパティとして localPosition が使われているが、ここではCharRectは親子関係のない独立したオブジェクトであるのでプロパティを position としても結果は同じである。
今回使用しているテキスト表示用のオブジェクト CharRect はカスタムライブラリーの THComponentObject クラスのインスタンスである。このクラスにはテキスト用として使うテクスチャをセットするメソッド SetTexture(..)、及びそのテクスチャ内においてどの部分を長方形に貼り付けるかを指定するためのメソッド SetUVs(..) が用意されている。
今回はどのCharRectも同じテクスチャ(上図2のテクスチャ)を使用するので SetTexture(..) の引数にはこのテクスチャのファイルパス "images/sample_letters_2" をセットすればよい (「Resources」フォルダを含める必要はない)。
上図2のテクスチャのうち一部の文字は赤い長方形に囲まれているが、この長方形に囲まれた領域がテクスチャ内における各文字の領域であり、SetUVs(..) の引数にはこの領域を指定する。具体的にはこの小さな長方形の4つの頂点座標を引数にセットする (例えば文字 'a' なら 'a' を囲む小さな長方形の各頂点座標をセットする)。
しかしプログラムに見られるように実際には GetUVs(..) という補助メソッドが用意されており、各文字の領域情報はこのメソッドを通して簡単に取得することができる。例えば文字 'a' ならば GetUVs('a')、文字 '1' ならば GetUVs('1') のようにすれば、このメソッドからは指定された文字のテクスチャ内での領域情報(その文字を囲む長方形の各頂点座標)が返される。
(注 : 本節のテキスト表示においては、表示する文字としてASCIIコードのみを前提としている。そのため上記の補助メソッド GetUVs(..) の引数にセットするchar型の文字はアルファベットや数字であり、ひらがなや漢字をセットすることはできない。具体的には、表示できる文字は上図2において赤い長方形で囲まれている文字のみである)
プログラム 7行目では表示する文字列を "ABCD1234" としているが、これによって上で指定した領域にこの文字列が適切に配置されることになる (図6)。

図6 Beta1 実行結果
以下のプログラムは上記と同じ領域に現在時刻をデジタル表示するものである。現在時刻は「hh:mm:ss」の形で表示するため、使用する文字数は8個であり、上の設定をそのまま使うことができる。
[Code1] (実行結果 図7)
初期化ブロックはわずかな違いを除いて先程のBeta1と同じである。今回は初期化ブロックにおいては各CharRectの位置及び大きさ、使用するテクスチャのみを設定している。
19行目以降は現在時刻をデジタル表示するための処理であり23~25行目の sH、sM、sS にはそれぞれ 時、分、秒が2ケタの文字列でセットされる。例えば現在時刻が 19時23分5秒 ならば sH には "19"、sM には "23"、sS には "05" がセットされる (数字が1ケタの場合は "0#" の形でセットされる)。
なお上の設定では各CharRectの z座標を $-0.02$ としたので下図の実行結果に示されるように、XY平面上のオブジェクトよりも手前に表示されるようになる。

図7 Code1 実行結果
下図8は今回吹き出しとして使用するオブジェクト Bubble の初期状態であり、Bubbleは初期状態において原点を指している。Bubbleの中にテキストを表示するためには、先程のCharRectを適当な大きさに変えてBubble内の白い領域に必要な数だけ並べればよい。今回はCharRectの大きさを $0.32 \times 0.94$ とし、使用する文字数を 16、Bubble内に定める文字列領域の左下隅の位置を $(1.4,\ 1.5)$ とする (図9 ; これらの数値の決定も実際には初期状態のBubbleを表示し、CharRectの位置や大きさが適切な値になるように、プログラム実行中にInspectorで調整を行う)。
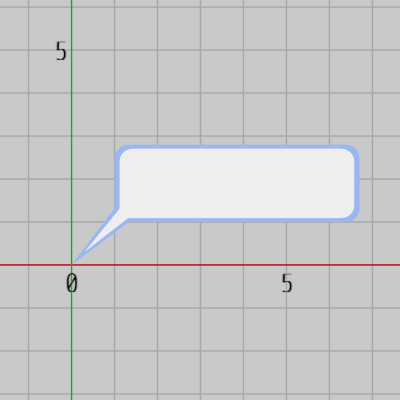
図8 Bubble 初期状態 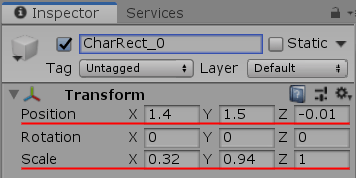
図9
この設定によって16個のCharRectはBubble内に下図10のように配置される (図中の $V_0$ は文字列領域の左下隅を表しその位置は $(1.4,\ 1.5)$ である)。上の設定では各CharRectの z座標を $-0.01$ としているので、すべてのCharRectがBubbleよりも手前に表示されている (Bubbleの z座標は初期状態では $0$ )。
そして今回のプログラムではプログラム実行中にオブジェクトを動かし、その現在地をBubbleに表示する。具体的には図11に示されるように、オブジェクトの現在地(x座標、y座標)を "x_###.#__y_###.#" の形で小数第1位まで表示する (左記における '_' は空白)。今回の文字列領域は16個分であるが、そのすべてが使われることもあるが、使われない場合には左から文字を詰めていき右側の余る部分には空白を表示する。
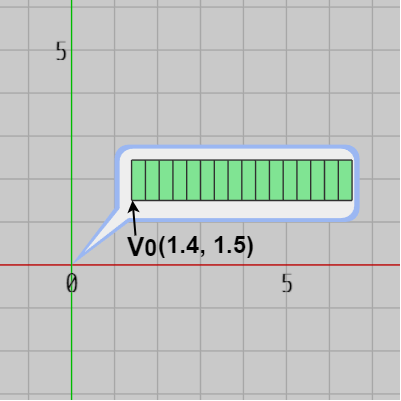
図10 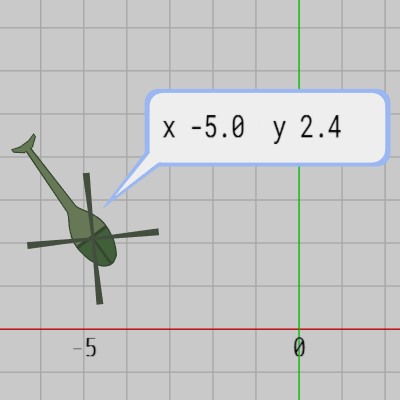
図11
以下のプログラムはキー操作によってオブジェクトを動かし、Bubbleにオブジェクトの現在地を表示するものである。
H : 左へ旋回
L : 右へ旋回
S : オブジェクトの移動/停止用スイッチ
[Code2] (実行結果 図12)
初期化ブロックの内容はCode1と同じく各CharRectを指定の位置に指定の大きさで配置するものであるが、今回はBubbleを親オブジェクト、各CharRectを子オブジェクトとして親子関係を設定している (11行目)。Bubbleに置かれる文字列領域は動くことはないので初期化ブロックにおいて1度だけ設定すればよい。
21行目の HelicopterMotion() はプログラムで使用しているヘリコプターをキー操作によって動かすためのメソッドであるが、その内容は 2-10節 Code4 と同じである。
23行目ではヘリコプターの現在地を取得している。Bubbleはその現在地からわずかに離れた位置に置かれるが、具体的にはヘリコプターの現在地から x軸方向、y軸方向に $0.4$ だけ離れた位置に置かれるので、Bubbleは常にヘリコプターのやや右上に表示されることになる。なお23行目の設定では z座標を $-0.03$ としているが、これはBubbleがヘリコプターよりも手前に表示されるようにするためのものである (Bubbleの子オブジェクトである各CharRectの z座標はBubbleよりも $0.01$ だけ z軸マイナス側に置かれているので、各CharRectの実際の z座標は $-0.04$ である)。
各CharRectとBubbleには親子関係が設定されているので、Bubbleの位置を動かすだけで自動的にCharRectも同じだけ移動する。そのためBubbleがどのように動いても、Bubble内における文字列領域の位置は常に同じである。
28行目以降はヘリコプターの現在地の x座標、y座標を文字列化してCharRectに貼り付ける処理である。その処理は、まずすべてのCharRectの内容を空白によってクリアし(28行目のfor文)、その後に現在地を文字列化して各CharRectに貼り付けるという手順で行われる (33~37行目)。
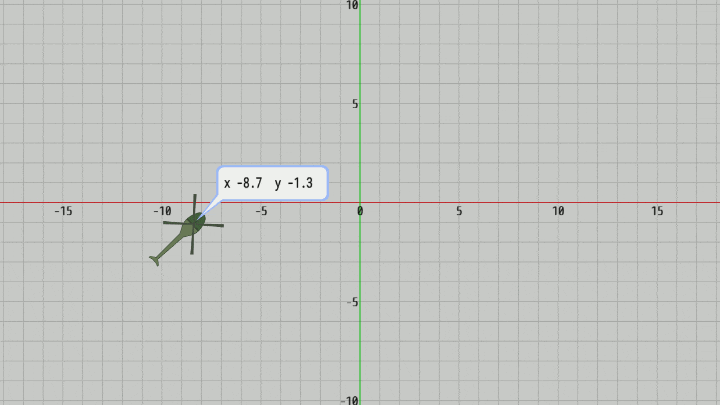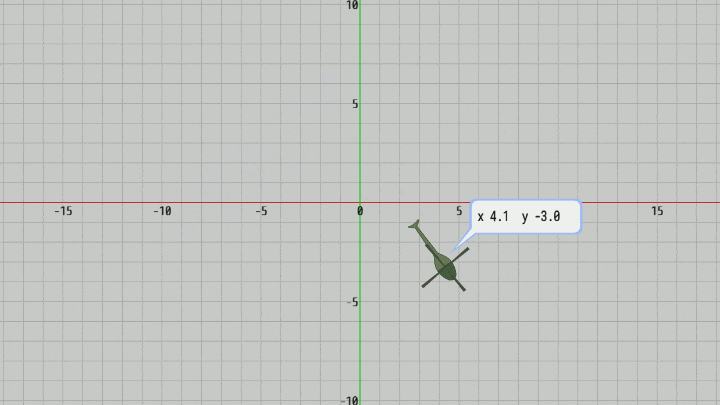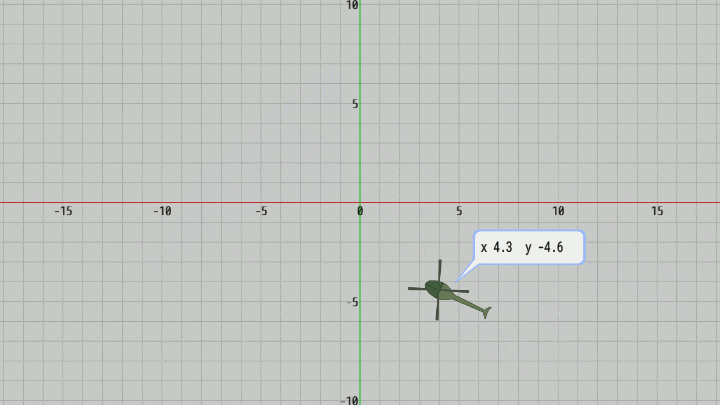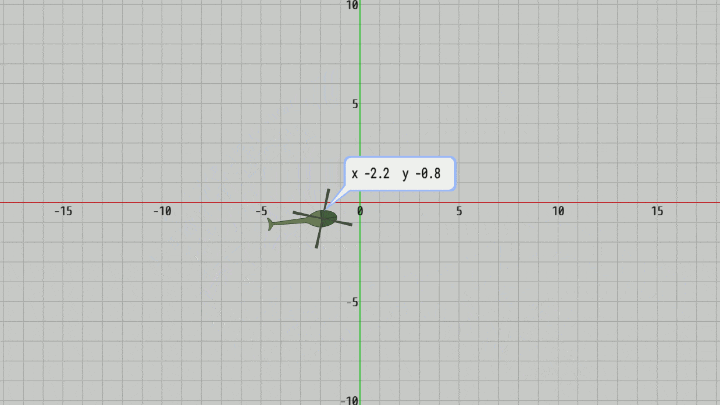
図12 Code2 実行結果
しかしその前に、まずはスクリーン座標とワールド座標の変換について簡単に復習する。
(以下では前節と同じくスクリーン座標の単位を「pix」、ワールド座標の単位(XY平面上の単位)を「wld」と表記する)
画面中心のスクリーン座標を $P'(cx,\ cy)$ とする。画面の横方向の長さを $w$、縦方向の長さを $h$ とすれば、横半分の長さは $w/2$、縦半分の長さは $h/2$ であるが、Unityではスクリーン座標の起点 $(0,\ 0)$ は左下隅であるから結局、画面中心のスクリーン座標 $P'$ は $(cx,\ cy) = (w/2,\ h/2)$ である (図13)。
また $P'$ から横方向に $dx$、縦方向に $dy$ だけ離れた位置を $M'(mx,\ my)$ とするとき ($dx, dy > 0$)、$mx - cx = dx$、$my - cy = dy$ である (以上すべて単位は pix)。
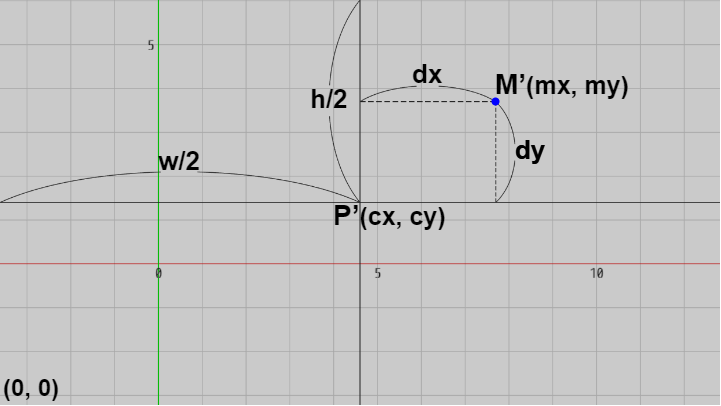
図13
スクリーン座標 $P'$ に対応するワールド座標を $P$、スクリーン座標 $M'$ に対応するワールド座標を $M$ とする (図14)。またワールド座標系で測った実行画面の横の長さを $W$、縦の長さを $H$ とし、上記のスクリーン座標系での長さ $w/2$、$h/2$、$dx$、$dy$ に対応するワールド座標系の長さを $W/2$、$H/2$、$s$、$t$ とする (これらの単位は wld)。
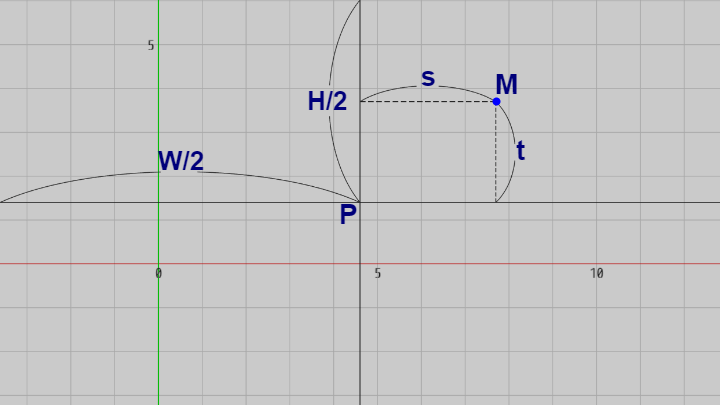
図14
これらを元にしてスクリーン座標からワールド座標への変換は次のように行われる。
カメラの位置を $(E.\!x,\ E.\!y,\ E.\!z)$ とし、XY平面からカメラまでの距離を $d$ とする (このとき $d = -E.\!z$ である)。またFOVの半分の角度を $\theta$ とする。
このとき、ワールド座標系で測ったときの画面縦半分の長さ $H/2$ は\[d\tan\theta = H/2\]である。
画面縦半分はスクリーン座標系で測ると $h/2$ pix であるが、これが $H/2$ wld に相当するということであるから、スクリーン座標系の 1 pix がワールド座標系において何wldであるかを表す変数を $WldPerPix$ とすれば\[ (H/2)/(h/2) = H/h = WldPerPix \]である。
カメラの位置が $(E.\!x,\ E.\!y,\ E.\!z)$ であるから、画面中心のワールド座標 $P$ は $(E.\!x,\ E.\!y)$ である (2-27節)。
スクリーン座標 $M'$ に対応するワールド座標 $M$ は、$P$ から x軸方向に $s$、y軸方向に $t$ だけ離れた位置にあるから、結局 $M = (P.\!x + s\ P.\!y + t)$ となり、$s$ 及び $t$ がわかればよいわけである。
$s$、$t$ はスクリーン座標系での長さ $dx$、$dy$ に対応するワールド座標系の長さであるから、上記の $WldPerPix$ を使えば簡単に\begin{align*}&dx \cdot WldPerPix = s \\ \\&dy \cdot WldPerPix = t \\ \\\end{align*}として求められる。
次のメソッド ConvertScreenToWorld(..) は引数にセットされたスクリーン座標をワールド座標(XY座標)に変換するものであり、今述べてきたことを実装したものである (メソッド内で使われている変数は上の解説のものと意味は同じである)。
[ConvertScreenToWorld(..)]
上記のオーバーロード版として以下のものも使用する。
ただし上のメソッドにおいて計算されるいくつかの変数については、カメラの位置やFOV及び画面の大きさが変わらなければ、算出される値は毎回同じである (例えば WldPerPix や cx、cy)。したがって、カメラの位置やFOV及び画面の大きさが変わらないことがあらかじめわかっている場合には、それらの変数をインスタンス変数などとして使う方が実用的であろう。
では上で述べたことを応用して画面上の指定の位置に指定の大きさでテキストを表示するが、今回の文字列領域はスクリーン座標によって設定する。それは単に文字列領域の左下隅のスクリーン座標を $M'(mx,\ my)$ として上の手続きを繰り返すだけである (図15)。
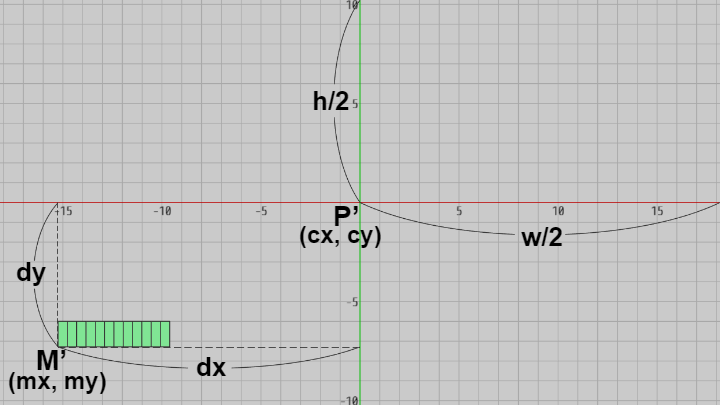
図15
次のプログラムは画面上の $(100,\ 100)$ の位置にテキストを表示するものである (文字列領域の左下隅が $(100,\ 100)$ )。今回の文字数は12で、文字1つの画面上での大きさは $16 \times 44$ pix である (ここでは上記の ConvertScreenToWorld(..) は使っていない)。
[Code3] (実行結果 図16)
18~19行目の rw、rh はスクリーン座標系における1文字分の大きさ($16 \times 44$ pix)、RW、RH はワールド座標系における1文字分の大きさである。すなわちスクリーン座標系における長さ rw、rh をワールド座標系での長さに変換したものが RW、RH であり、これは各CharRectに設定する大きさでもある (34行目)。
16~17行目の mx、my はその初期値として $100$、$100$ がセットされているが、これは文字列領域の左下隅のスクリーン座標を表している。しかしこの後のfor文内で mx の値は rw ずつ($16$ pix ずつ)加算されるので、このプログラムにおける mx、my は実際には各文字の左下隅のスクリーン座標として使われる。
25行目のfor文は12個のCharRectを指定の位置に指定の大きさで配置し、それぞれに指定の文字を貼り付ける(テクスチャの指定の部分を貼り付ける)処理である。ここで使われている cx、cy は画面中心のスクリーン座標、M (31行目)は各文字の左下隅のワールド座標、P は画面中心のワールド座標である (今回は画面中心に原点が来るので P の値は $(0,\ 0)$ )。
各文字はスクリーン座標系で測ると rw ずつ横にずらして置かれているので、先程述べたようにこのfor文ではループ1回ごとに mx の値が rw ずつ加算される (38行目)。
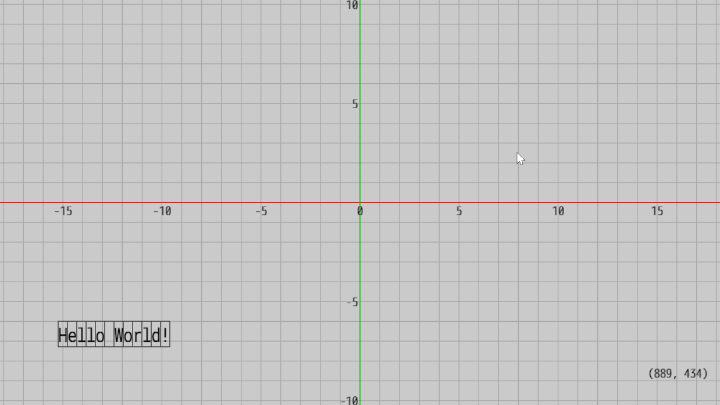
図16 Code3 実行結果
実行結果の画面右下に表示される1組の数字は、マウスカーソルの指すスクリーン座標である。カーソルを文字列領域の適当な位置に置けば、実際に文字列領域の左下隅のスクリーン座標が $(100,\ 100)$ であるか、あるいは各文字の大きさが $16 \times 44$ pix であるかなどを調べることができる (もちろんラスターグラフィックスではないので、1 pix 前後の誤差はある)。
具体的にはマウスクリックした位置にオブジェクトを置いたり、あるいはマウスクリックによるオブジェクトの選択、またはマウスドラッグによるオブジェクトの移動といったものである。
なお以降のプログラムではマウス操作の際に、カスタムライブラリーで用意されている以下のメソッドを使用する (以下のメソッドの戻り値はいずれもbool型である)。

図17 Code4 実行結果 (クリックした位置にDotが置かれる)
次のプログラムはマウスクリックした位置にDotを置くものである。
[Code4] (実行結果 図17)
プログラムは簡単である。このプログラムではマウスの左ボタンが押されるとifブロックに入るが、そこでは単にマウスのスクリーン座標(mx、my)を取得し、そのスクリーン座標をワールド座標に変換して、Dotをその位置に移動させるだけである。
5行目の ConvertScreenToWorld(..) は上で解説したものであり、引数にセットされたスクリーン座標をワールド座標(XY座標)に変換するメソッドである。
ワールド座標とはここではXY平面上の点であるから、具体的にいえばマウスの位置に対応するXY平面上の点が円盤や長方形、あるいは三角形に含まれているかを調べ、含まれていればそのオブジェクトを選択されたものとして処理を進めればよい。
ここでは選択対象として長方形、実際には下図に示されるトランプのカードを使用する。
そしてマウスクリックによってあるカードが選択されたと判定された場合には、選択されたことを示すためにそのカードを裏返す処理を入れている。
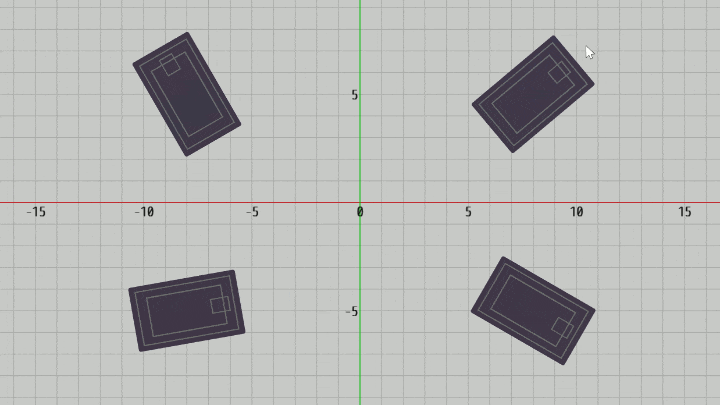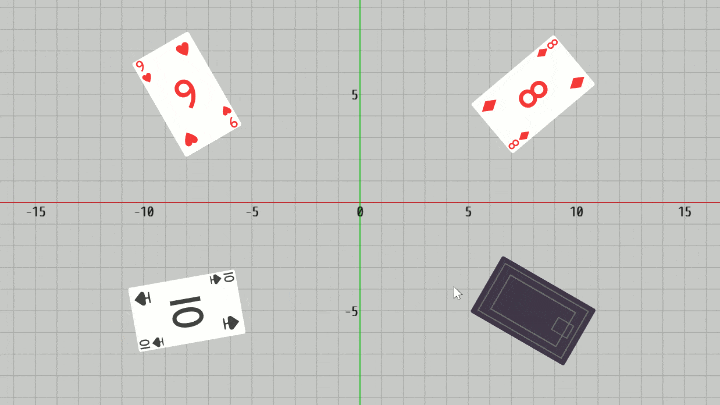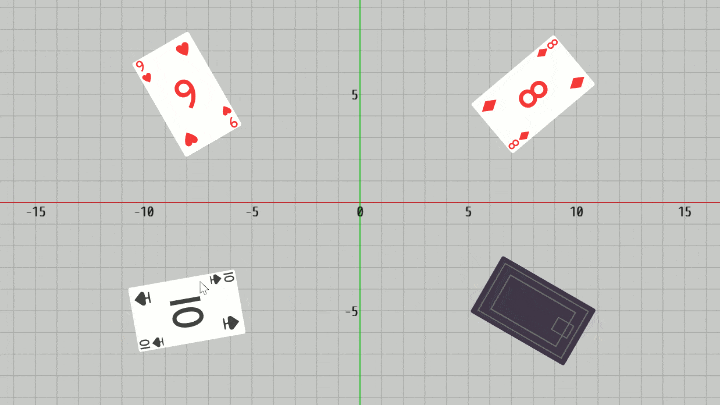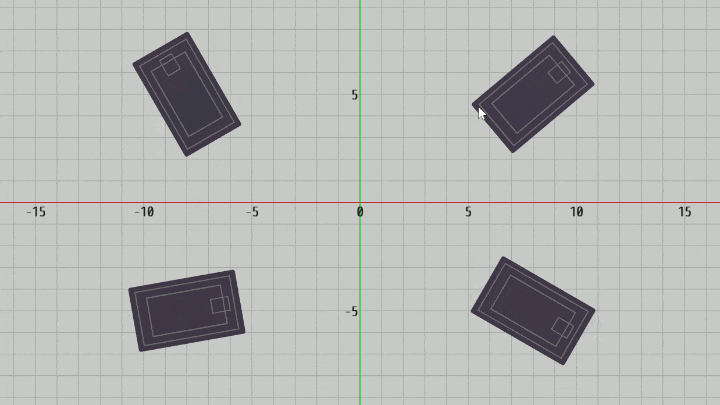
図18 Code5 実行結果
プログラムは以下のとおり。
[Code5] (実行結果 図18)
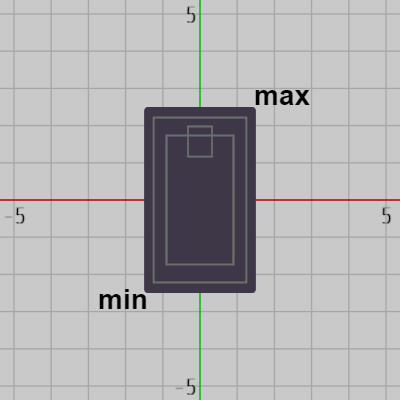
図19 Card 初期状態 右図はここで使用している長方形オブジェクト Card の初期状態である。初期状態ではCardの各辺は x軸、y軸に平行、その中心は原点に置かれており、カードは裏を向いた状態になっている。図中の $min$、$max$ は初期状態におけるCardの左下の頂点、右上の頂点を表している。
プログラム中ではCardは配列として使われており(要素数 4)、初期化ブロックにおいてそれぞれ適当な位置に適当な向きで配置される (3~10行目)。
処理の手順は、まずマウスクリック時のスクリーン座標(Md)を取得し、そのスクリーン座標(Md)をワールド座標(M)に変換する (19~20行目)。そしてそのワールド座標が4枚のCardのいずれかに含まれているかを調べ、もしあるCardに含まれているならば、そのCardをマウスによって選択されたCardとみなして次のフレームから裏返す処理を実行する (23行目のfor文)。
スクリーン座標から変換されたワールド座標が4枚のCardのいずれかに含まれているかを調べる処理(23行目のfor文)は、簡単にいえばXY平面上のある点が4つの長方形のいずれかに含まれているかを調べているだけであり、この処理は2-13~2-14節で扱った長方形と点の衝突判定と同じである (26行目の c_CardMinMax は初期状態におけるCardの左下、右上の頂点(図19における $min$、$max$)がセットされた配列)。
プログラム中で使われている i_turnCardIndex は選択されたCardのインデックスをセットするためのインスタンス変数である (int型)。あるCardが選択されるとこのインスタンス変数にそのCardのインデックスがセットされ(30行目)、次のフレームから一定の時間そのCardを裏返す処理が行われる。その裏返す処理が終わると自動的にこのインスタンス変数には $-1$ がセットされ、次に他のCardが選択されるまでは $-1$ のままである (ほとんどの状況においてはこのインスタンス変数の値は $-1$ であり、Cardが選択されてから裏返す処理が終わるまでの間だけ選択されたCardのインデックスがセットされている)。Cardを裏返す処理の解説については省略する。
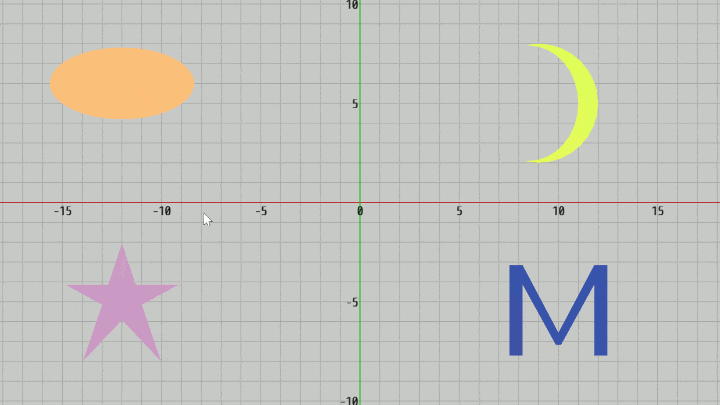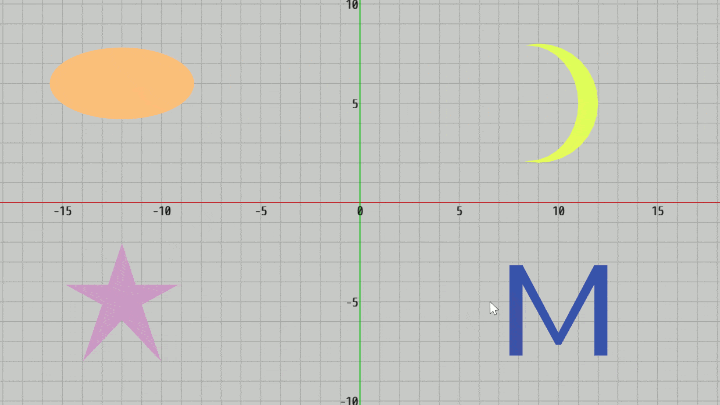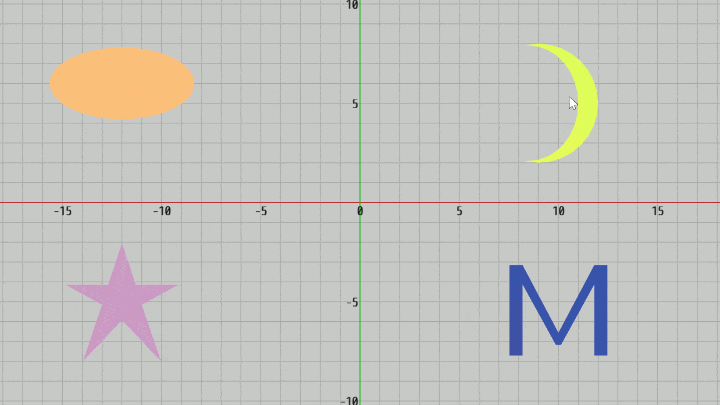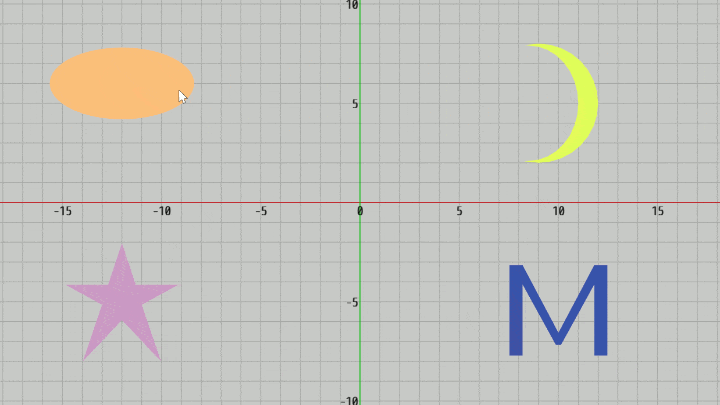
図20 Code6 実行結果 (4つのオブジェクトは右上から反時計周りに Moon、Ellipse、Star、Letter)
プログラムは以下のとおり。
[Code6] (実行結果 図20)
今回は4つのオブジェクト Moon、Ellipse、Star、Letter が適当な位置にそれぞれ置かれている。いずれのオブジェクトも三角形の集合であり、そのオブジェクトを構成するすべての三角形の頂点配列を取得するために initTriangleCoords というVector2[]型のプロパティが用意されている(2-15節参照)。
マウスがクリックされると、まずその位置をスクリーン座標(Md)からワールド座標(M)に変換する (13~14行目)。そしてそのワールド座標が4つのオブジェクトのいずれかに含まれているかを調べ(16行目のforeach文)、あるオブジェクトに含まれていればそのオブジェクトが選択されたことを示すために、今回はオブジェクトの色を一時的に変化させる (23行目の SelectObject(..) は引数にセットされたオブジェクトの色を一時的に変化させるための補助メソッド)。
マウスの位置に対応するワールド座標がオブジェクトに含まれているかを調べる処理は18~20行目で行われるが、この処理はXY平面上のある点が三角形の集合に含まれているかを調べることと同じである (2-15節参照)。
オブジェクトの形状は円盤、長方形、三角形の集合と分かれているが処理自体は同じであり、マウスでクリックした位置にオブジェクトがあれば、そのオブジェクトを選択されたオブジェクトとし、さらにその後にマウスドラッグが行われればそのオブジェクトをドラッグした分だけ移動させるだけである。
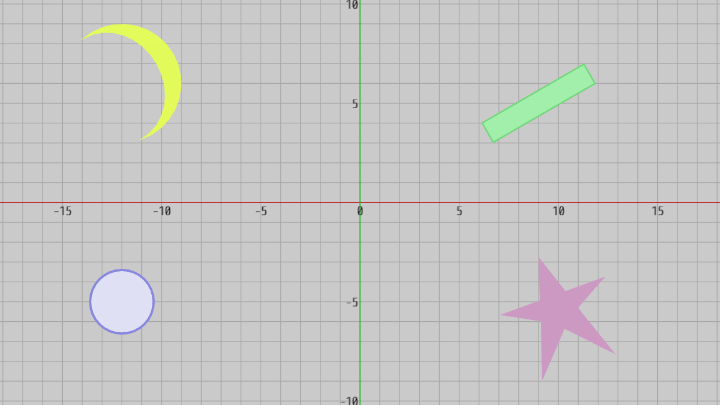
図21 4つのオブジェクトが適当な位置に置かれている (右上から反時計周りに Block、Moon、Disk、Star)
ここで重要なのがマウスドラッグ時のオブジェクトの移動量であるが、これは次のように求められる。
下図22の円盤をマウスでクリックしたときのワールド座標を $M_1$ とし、その位置からマウスを右下にドラッグしたときのマウスの位置(ワールド座標)を $M_2$ とする。すなわち $M_1$ がドラッグ前のワールド座標、$M_2$ がドラッグ後のワールド座標である ($M_1$、$M_2$ はワールド座標である。スクリーン座標ではない)。
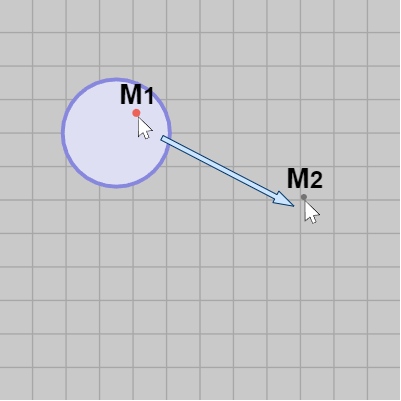
図22 
図23
図22に示されるようにドラッグ前のマウスカーソルは円盤上の赤い点 $M_1$ を指しているが、マウスドラッグによってオブジェクトを移動させる場合にはドラッグ後においてもマウスカーソルがオブジェクトの同じ位置を指していることが望ましい。つまり、この場合にはドラッグ後においてもマウスカーソルが円盤上の赤い点を指すようにするということである。
マウスドラッグ後のマウスカーソルは点 $M_2$ を指しているので、ドラッグ後においてもマウスカーソルが円盤上の赤い点を指した状態にするためには、マウスドラッグ後に円盤上の赤い点の位置が $M_2$ に来ていればよいわけである。
このとき図23に示されるように円盤上の赤い点は $M_1$ から $M_2$ に移動することになるから、結局このマウスドラッグでは円盤を $M_2 - M_1$ だけ移動させれば目的が達せられることになる。
以下のプログラムは上記の4つのオブジェクトをマウスドラッグによって移動させるものである。
[Code7] (実行結果 図24)
初期化ブロックにおけるインスタンス変数 i_selectObject はマウスクリックした位置にオブジェクトがあれば、そのオブジェクトがこのインスタンス変数にセットされ、マウスリリース(マウスボタンが離される)までこの変数にはそのオブジェクトがセットされた状態になる。つまりクリック後にマウスドラッグが続いて起これば、マウスドラッグ中もこのインスタンス変数には選択されたオブジェクトがセットされたままである。マウスリリースの時点で null になる。
13行目はマウスクリック時の処理であるが、これは上で見てきたプログラムと同じである。ただしここではマウスクリックした位置にオブジェクトがあれば21行目のifブロック内で、まずオブジェクトの色を変え(SelectObject(..))、次に2つのインスタンス変数 i_selectObject、i_M1 の値を更新する。i_selectObject は上で述べたものであり、i_M1 はマウスクリックした位置のワールド座標を表すインスタンス変数で、これは上記解説中の $M_1$ と同じである (ドラッグ前のマウスのワールド座標)。
インスタンス変数 i_selectObject が null でない場合には(オブジェクトが選択されている場合には)、32行目のifブロックに処理が進むが、このときにマウスドラッグが行われていればオブジェクトの移動処理が行われる。それは34行目のifブロックで、この部分では上で述べた、オブジェクトを $M_2 - M_1$ だけ移動させるという処理を行っている (プログラム中の M2 は上記解説中の $M_2$ と同じで、ドラッグ後のマウスのワールド座標)。
i_selectObject がnullでない状態で、マウスドラッグが続く場合には毎フレームこの34行目のifブロックに入り続ける (ドラッグ中は13行目のifブロックには入らない)。そのため、ドラッグ前の位置を表すインスタンス変数 i_M1 を毎フレーム更新する必要があるが、それは単にそのフレームにおけるドラッグ後の位置 $M_2$ を次のフレームにおけるドラッグ前の位置として使えばよい (41行目)。
(なお、このプログラムではマウスがオブジェクトの上空に入った時点でオブジェクトの色を変える処理を裏側で行っている)
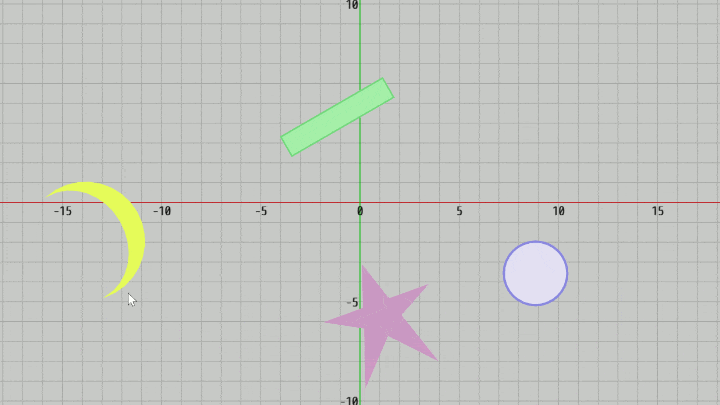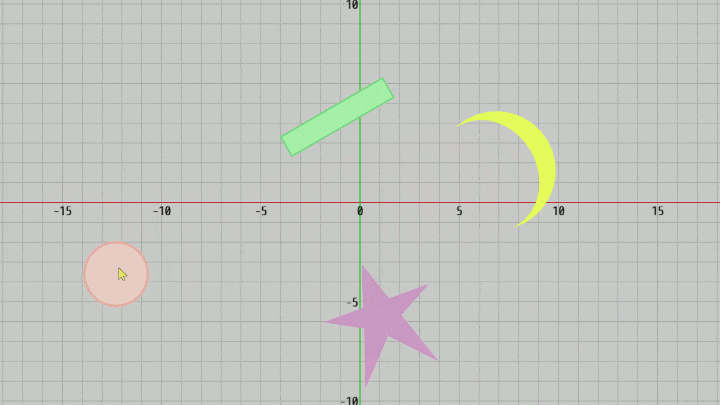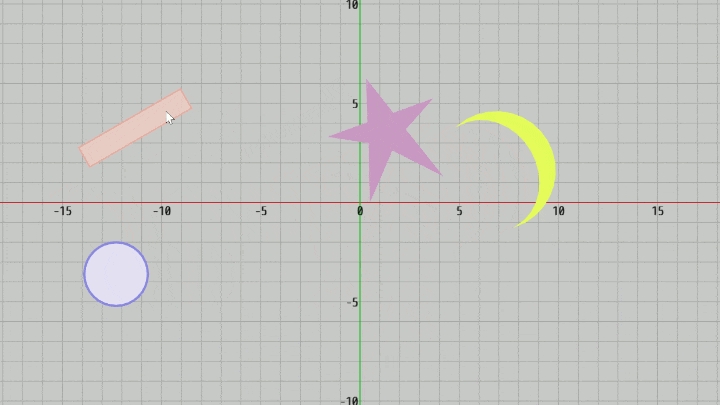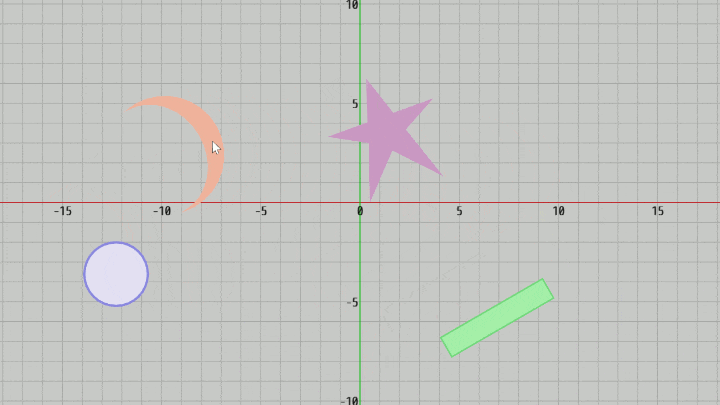
図24 Code7 実行結果
以下のプログラムにおいてはスクリーンショットを撮影するために MakeScreenshot(..) という補助的なメソッドが使われる。このメソッドの引数にはファイル名及び画像のサイズを指定するが、出力される画像ファイル(PNGファイル)の中心には必ず画面の中心が来る。
例えば実行画面が以下の内容であるとしよう。青い長方形のスクリーン座標系での大きさは $400 \times 300$ pix、図中の点 $P$ は長方形の中心であり、画面の中心でもある。
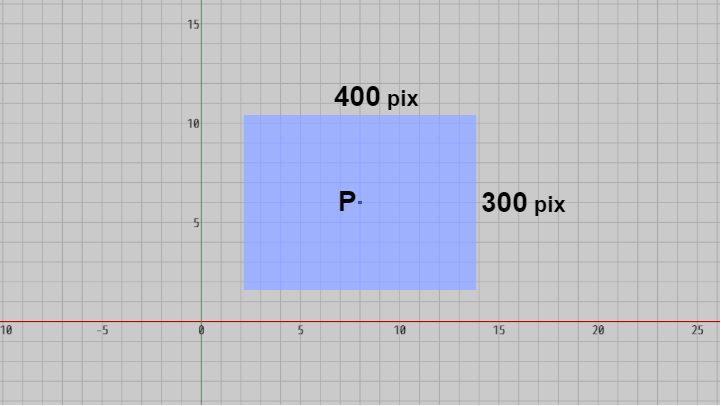
図25
このときスクリーンショットを撮影するために MakeScreenshot(..) を次のように実行したとき、出力される画像は $400 \times 300$ pix の大きさで、図の青い長方形のみが写ったものとなり、画像の中心には上記の点 $P$ が来る。すなわち、ちょうど上図25における青い長方形の領域だけを切り取ったものが画像として出力されるわけである。
ここからはXY平面上における指定の領域を指定の大きさの画像として出力することについて考えていく。
(引き続き以降の文章中においても、XY座標(XY平面上の座標)の代わりに「ワールド座標」、XY平面の代わりに「ワールド座標系」という語を用いる。同様にスクリーン座標系の単位を「pix」、ワールド座標系の単位を「wld」として進める)。
下図における青い枠の大きさはワールド座標系において $RW \times RH$ wld であり、青い枠の中心 $P$ は画面の中心でもある ($P$ はワールド座標)。先程と同様にワールド座標系で測ったときの画面の横の長さ、縦の長さを $W$、$H$ とし、横半分、縦半分の長さそれぞれ $W/2$、$H/2$ で表す (図26)。
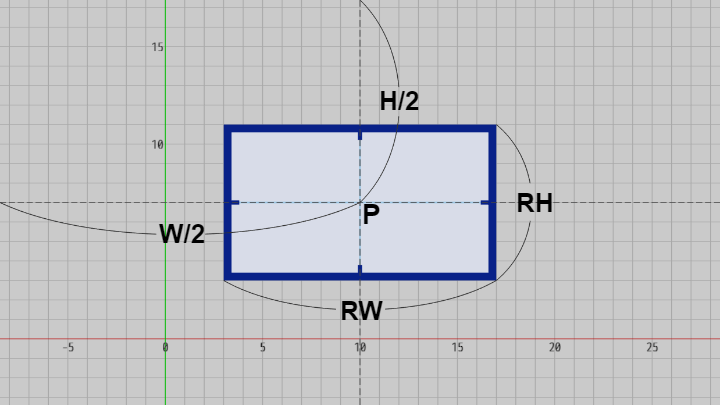
図26
ここで、図の青い枠に囲まれた領域を $rw \times rh$ pix のスクリーンショットとして出力するとしよう。以下の解説においては、撮影対象の領域(ここでは青い枠)のアスペクト比とスクリーンショットのアスペクト比が等しいことを前提として進める。つまり、以下では $RW : RH = rw : rh$ であることが前提である。
この例の場合ではすでに青い枠の中心 $P$ は画面の中心であるので、出力される画像の中心には $P$ が来る。したがってカメラの x座標、y座標を変える必要はないが、もし $P$ が画面の中心でない場合にはまず出力される画像の中心に $P$ が来るようにカメラの位置を合わせる必要がある。しかし、それは単にカメラの x座標、y座標を $P.\!x$、$P.\!y$ とすればよい (2-27節)。カメラの x座標、y座標をこのように定めたときに画面中心には確かに $P$ が来るが、ここで問題となるのがスクリーン座標系で測ったときの青い枠の大きさである。
2-28節で見たように画面に表示されるオブジェクトの大きさは、カメラをXY平面に近づければ大きくなり、カメラがXY平面から離れていくにしたがって小さくなる。すなわち画面上における青い枠の大きさはカメラのXY平面からの距離で決まるので、画面上における青い枠の大きさを $rw \times rh$ pix にするためには、XY平面からの適切な距離を求める必要があるわけである。
しかしこの問題も結局は、スクリーン座標とワールド座標の変換の応用に過ぎない。
スクリーン座標系における青い枠の大きさが $rw \times rh$ であるとき、その縦の長さは $rh$ pix である。そしてこの青い枠はワールド座標系では $RW \times RH$ であるから、その縦の長さは $RH$ wld である。すなわちこの場合には、スクリーン座標系における $rh$ pix がワールド座標系では $RH$ wld に相当するわけである。
したがって、ここでも 1 pix が何 wld に相当するかを表す変数を $WldPerPix$ とすれば、\[ RH/rh = WldPerPix \]である。
スクリーン座標系で測ったときの画面の縦方向の長さを $h$ とし、縦半分の長さを $h/2$ とするとき、この $h/2$ pix に対応するワールド座標系の長さは上図26の $H/2$ wld であるが、$H/2$ は $WldPerPix$ を使って簡単に\[ h/2 \cdot WldPerPix = H/2 \]として求められる。
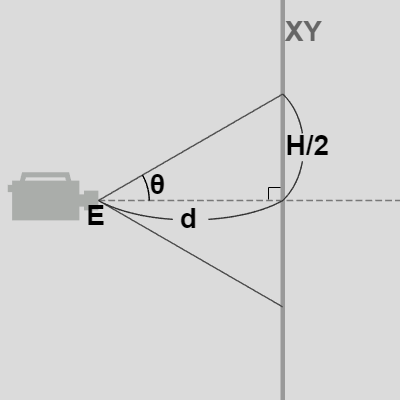
図27 カメラは z軸マイナス側に置かれ z軸プラス方向を向いている (図中の太い縦線はXY平面) さらに前節で見たようにXY平面からカメラまでの距離を $d$、FOVの半分の角度を $\theta$ とするとき、画面縦半分のワールド座標系での長さ $H/2$ は\[d\tan{\theta} = H/2\]として求められるから、結局 $d$ は\[(H/2) / \tan{\theta} = d\]となる (右図においてカメラの位置 $E$ は z軸マイナス側に置かれ、カメラは z軸プラス方向を向いている。図中の太い縦線はXY平面を表している)。
すなわち、XY平面からカメラまでの距離 $d$ を上のように求めたときに、カメラをXY平面から $d$ だけ離れた位置に置いて撮影すると、実行結果の画面においては $rh$ pix が $RH$ wld に相当するのである。
したがって、カメラの位置を $(P.\!x,\ P.\!y,\ -d)$ とすれば目的のスクリーンショットを撮影できるわけである。
下図に示されるようにXY平面上には青い領域があるが、この青い領域の中心は原点に置かれ、青い領域の中心と画面中心は一致する。またこの領域の横の長さと縦の長さの比は $4 : 3$ である。
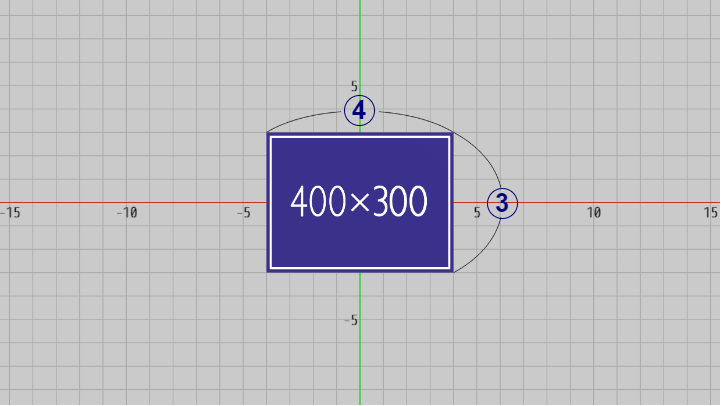
図28
今回はこの青い領域を $400 \times 300$ pix のスクリーンショットとして撮影する。その際以下のキー操作を用いる。
V : カメラの位置の変更
T : スクリーンショットの撮影
(注意 : T キーを押してスクリーンショットを撮影する際、上記のメソッド MakeScreenshot(..) が実行されるがこのメソッドの第1引数には出力される画像のファイルパスを指定しなければならない。例えば Windows において C ドライブ直下に "image.png" という名前でスクリーンショットを作成する場合はファイルパスを "C:/image.png" とする必要がある。以下のプログラムではデフォルトのファイルパスとして "screenshot1.png" としてあるため、スクリーンショットの出力先はUnityの現在のプロジェクトフォルダである)
プログラムは以下のとおり。
[Code8]
プログラム開始時点ではカメラはXY平面からやや離れた位置に置かれているので、その位置で T キーを押してスクリーンショットを撮影しても出力される画像には青い領域の周りも入ってしまう (下図29はプログラム開始時点における実行画面であり、赤い枠の大きさは $400 \times 300$ pix)。
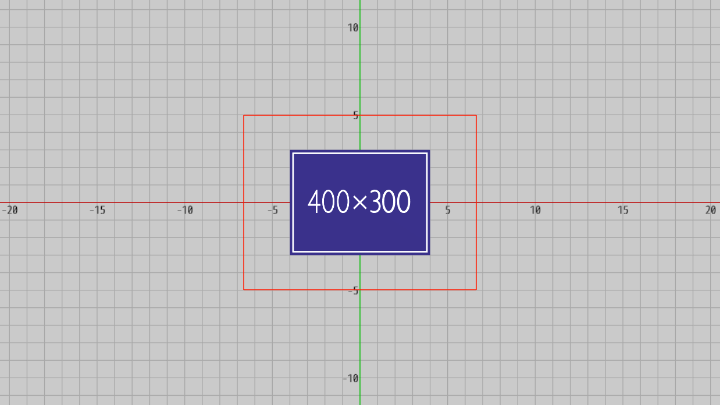
図29 プログラム開始時点における実行画面 (この時点ではカメラの位置はやや離れた位置に置かれているため、スクリーンショットを撮影すると下図31に見られるように青い領域の周りも画像に入ってしまう ; 図中央の赤枠の大きさは 400 x 300 pix)
上図の状態から V キーを押すとインスタンス変数 i_SET_VIEW がtrueになり、6行目のifブロックに処理が進む。このブロックは上で述べたことを実装したものであり、ここで使われている各変数 P、RW、RH、rw、rh などは上記の $P$、$RW$、$RH$、$rw$、$rh$ と同じである。
また c_BoardCenter (8行目)は青い領域の中心を表す定数(ここでは原点)、c_BoardW、c_BoardH はワールド座標系で測った青い領域の横の長さ、縦の長さである (float型定数)。
この6行目のifブロックによってカメラは適切な位置に置かれるが、下図はそのときの実行画面である。この場合には青い領域の大きさは $400 \times 300$ pix になっているので、ここで T キーを押してスクリーンショットを撮影すると目的のスクリーンショットが得られる。

図30 カメラを適切な位置に置いたときの実行画面 (ちょうど赤枠と青い領域が同じ大きさになっている)

図31 プログラム開始時点で撮影したスクリーンショット 
図32 カメラを適切な位置に置いて撮影したスクリーンショット
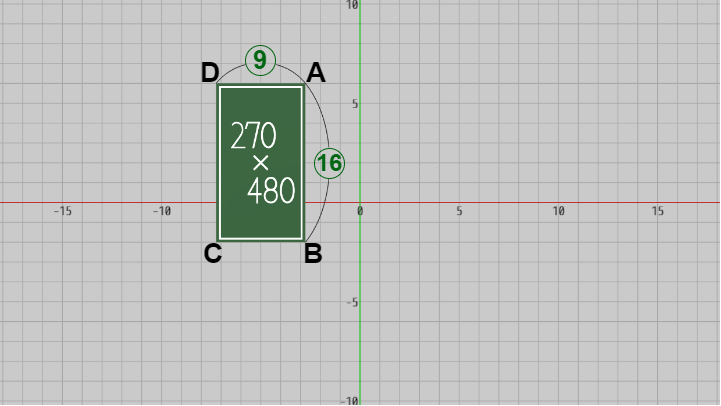
図33
今回はこの緑の領域を $270 \times 480$ pix のスクリーンショットとして撮影する。
使用するキーは前回と同じである。
V : カメラの位置の変更
T : スクリーンショットの撮影
(注意 : このプログラムでもスクリーンショットのファイルパスはデフォルトでは "screenshot2.png" となっているため、ファイルパスを書き換えずに撮影すると、スクリーンショットはUnityのプロジェクトフォルダに作成される)
プログラムを以下に示す。
[Code9]
プログラムの内容はわずかな違いを除いてCode8と同じである。今回は画面の中心 $P$ を緑の領域の2つの頂点 $A$、$C$ から計算し(8行目)、緑の領域の縦横の長さも同様に緑の領域の各頂点から計算している (12~13行目)。違いはその点だけである。
前回と同じくプログラム開始時点ではカメラの位置は調整されていないので、この時点でスクリーンショットを撮影しても画像には緑の領域がほとんど入ることはない (下図34はプログラム開始時点における実行画面であり、赤い枠の大きさは $270 \times 480$ pix)。
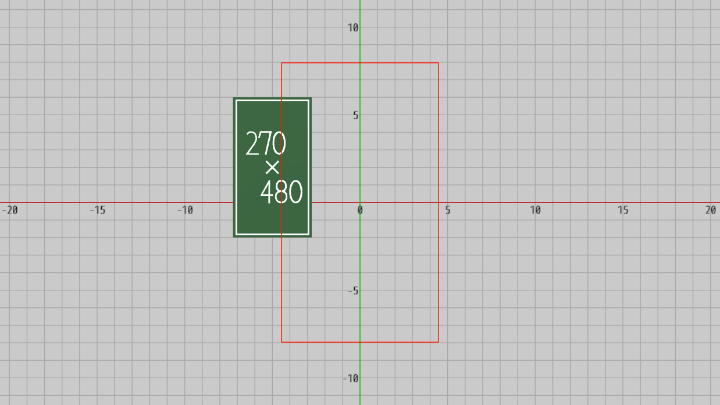
図34 プログラム開始時点における実行画面 (この時点ではカメラの位置は調整されていないため、スクリーンショットを撮影すると下図36のようになる ; 図中央の赤枠の大きさは 270 x 480 pix)
上図の状態から V キーを押すとインスタンス変数 i_SET_VIEW がtrueになり、6行目のifブロック内での処理によってカメラは適切な位置に置かれるが、下図はそのときの実行画面である。この場合には緑の領域の大きさは $270 \times 480$ pix になっているので、ここで T キーを押してスクリーンショットを撮影すると目的のスクリーンショットが得られる。

図35 カメラを適切な位置に置いたときの実行画面 (ちょうど赤枠と緑の領域が同じ大きさになっている)
下図36はプログラム開始時点において撮影したときの結果であり、図37は V キーを押してカメラの位置を調整した後の撮影結果である。
図36 
図37
前節でもそうであったが、本節においてもカメラの投影モードが「Perspective」、Field of View が「$60^\circ$」、画面のアスペクト比が「$16:9$」であることを前提としている (これらの設定については前節冒頭を参照)。
A) テキストの表示
テキストの表示は第7章においても扱うが、この講義における画面上のテキストは最も単純な方法、すなわちテキスト用のテクスチャ(の一部)を長方形に貼り付けるという形で実装されている。下図1はテキストを貼り付けるオブジェクト CharRect の初期状態であり、このオブジェクトは初期状態においては1辺の長さが $1$ の正方形で、左下隅が原点に位置している。1つのCharRectに1つの文字を貼り付けるので、例えば10個の文字列であればCharRectが10個必要になるわけである。


図2は今回使用するテキスト用のテクスチャであり、いわゆる Bitmap Font と呼ばれるものである。Bitmap Font を用いたテキスト表示は、テクスチャ内の一部の領域を長方形に貼り付ける形で文字を表示するだけであり、近年よく見られる SDF Font (Signed Distance Field Font) などと異なり文字の回転や拡大などを行うとジャギー(ギザギザ)が現れやすいという欠点があるが、作成が簡単であり文字表示の方法も単純であるため今回はこの方法で進めていく (図2のテクスチャのサイズは $512 \times 512$ pix であり、テクスチャのファイルパス(Resourcesフォルダからのファイルパス)は「Resources/images/sample_letters_2.png」である)。
# Code1
最初の2つのプログラムではテキストの表示領域をXY平面上の座標を用いて設定するが、ここで行うことは前節の終わりで見たミニマップに対する設定と同じである。すなわち Inspector上で上記のCharRectの大きさ及び位置を設定していく (以降しばらくはカメラは z軸上に置かれる。そのためXY平面上の原点が画面中心に来る)。まず1文字分の長方形の大きさを $0.4 \times 1.2$ とする (図3 ; これは単にCharRectを x軸方向に $0.4$ 倍、y軸方向に $1.2$ 倍すればよい)。そして画面上に表示する文字数を8文字とし、文字列領域の左下隅の位置を $(12,\ 8)$ とする (図4)。図の設定では z座標を $-0.02$ としているが、これは前節と同じく文字列が常に画面の手前に表示されるようにするための設定である。

図3 1文字分の長方形に使うために大きさを変更

下図に示されるように、この設定によって8個のCharRectが画面右上に配置される (各CharRectの大きさはすべて同じ)。図中の $V_0$ は文字列領域の左下隅を表し、その座標は $(12,\ 8)$ である。

以下のプログラムは上で定められた文字列領域に適当な文字列を表示するものである。
[Beta1] (実行結果 図6)
if (!i_INITIALIZED)
{
float RW = 0.4f;
float RH = 1.2f;
Vector3 V0 = new Vector3(12, 8, -0.02f);
string ss = "ABCD1234";
for (int i = 0; i < ss.Length; i++)
{
Vector3 LL = V0 + new Vector3(i * RW, 0, 0);
CharRect[i].transform.localPosition = LL;
CharRect[i].transform.localScale = new Vector3(RW, RH, 1);
CharRect[i].SetTexture("images/sample_letters_2");
CharRect[i].SetUVs(GetUVs(ss[i]));
}
i_INITIALIZED = true;
}
冒頭のローカル変数 RW、RH はCharRect 1つ分の大きさ、すなわち1文分の長方形の大きさであり、V0 は文字列領域の左下隅の位置を表す。
8行目のfor文は8個のCharRectを配置し、各CharRectに指定の文字を表示させる処理である。各CharRectは上図に示されるようにすき間なく隣り合っているので、その位置は V0 から(x軸方向に) RW ずつずらしていけばよい (10行目 ; LL は各CharRectの左下隅の位置)。また各CharRectはすべて同じ大きさであり、その倍率は x軸方向、y軸方向に RW、RH である (13行目)。
各CharRectの位置を定める際のプロパティとして localPosition が使われているが、ここではCharRectは親子関係のない独立したオブジェクトであるのでプロパティを position としても結果は同じである。
今回使用しているテキスト表示用のオブジェクト CharRect はカスタムライブラリーの THComponentObject クラスのインスタンスである。このクラスにはテキスト用として使うテクスチャをセットするメソッド SetTexture(..)、及びそのテクスチャ内においてどの部分を長方形に貼り付けるかを指定するためのメソッド SetUVs(..) が用意されている。
今回はどのCharRectも同じテクスチャ(上図2のテクスチャ)を使用するので SetTexture(..) の引数にはこのテクスチャのファイルパス "images/sample_letters_2" をセットすればよい (「Resources」フォルダを含める必要はない)。
上図2のテクスチャのうち一部の文字は赤い長方形に囲まれているが、この長方形に囲まれた領域がテクスチャ内における各文字の領域であり、SetUVs(..) の引数にはこの領域を指定する。具体的にはこの小さな長方形の4つの頂点座標を引数にセットする (例えば文字 'a' なら 'a' を囲む小さな長方形の各頂点座標をセットする)。
しかしプログラムに見られるように実際には GetUVs(..) という補助メソッドが用意されており、各文字の領域情報はこのメソッドを通して簡単に取得することができる。例えば文字 'a' ならば GetUVs('a')、文字 '1' ならば GetUVs('1') のようにすれば、このメソッドからは指定された文字のテクスチャ内での領域情報(その文字を囲む長方形の各頂点座標)が返される。
(注 : 本節のテキスト表示においては、表示する文字としてASCIIコードのみを前提としている。そのため上記の補助メソッド GetUVs(..) の引数にセットするchar型の文字はアルファベットや数字であり、ひらがなや漢字をセットすることはできない。具体的には、表示できる文字は上図2において赤い長方形で囲まれている文字のみである)
プログラム 7行目では表示する文字列を "ABCD1234" としているが、これによって上で指定した領域にこの文字列が適切に配置されることになる (図6)。

以下のプログラムは上記と同じ領域に現在時刻をデジタル表示するものである。現在時刻は「hh:mm:ss」の形で表示するため、使用する文字数は8個であり、上の設定をそのまま使うことができる。
[Code1] (実行結果 図7)
if (!i_INITIALIZED)
{
float RW = 0.4f;
float RH = 1.2f;
Vector3 V0 = new Vector3(12, 8, -0.02f);
for (int i = 0; i < 8; i++)
{
Vector3 LL = V0 + new Vector3(i * RW, 0, 0);
CharRect[i].transform.localPosition = LL;
CharRect[i].transform.localScale = new Vector3(RW, RH, 1);
CharRect[i].SetTexture("images/sample_letters_2");
}
i_INITIALIZED = true;
}
System.DateTime time = System.DateTime.Now;
int hour = time.Hour; // 0--23
int min = time.Minute;
int sec = time.Second;
string sH = (hour < 10) ? "0" + hour : "" + hour;
string sM = (min < 10) ? "0" + min : "" + min;
string sS = (sec < 10) ? "0" + sec : "" + sec;
string str = sH + ":" + sM + ":" + sS;
for (int i = 0; i < str.Length; i++)
{
CharRect[i].SetUVs(GetUVs(str[i]));
}
初期化ブロックはわずかな違いを除いて先程のBeta1と同じである。今回は初期化ブロックにおいては各CharRectの位置及び大きさ、使用するテクスチャのみを設定している。
19行目以降は現在時刻をデジタル表示するための処理であり23~25行目の sH、sM、sS にはそれぞれ 時、分、秒が2ケタの文字列でセットされる。例えば現在時刻が 19時23分5秒 ならば sH には "19"、sM には "23"、sS には "05" がセットされる (数字が1ケタの場合は "0#" の形でセットされる)。
なお上の設定では各CharRectの z座標を $-0.02$ としたので下図の実行結果に示されるように、XY平面上のオブジェクトよりも手前に表示されるようになる。

# Code2
続いては、いわゆる吹き出しの実装である。下図8は今回吹き出しとして使用するオブジェクト Bubble の初期状態であり、Bubbleは初期状態において原点を指している。Bubbleの中にテキストを表示するためには、先程のCharRectを適当な大きさに変えてBubble内の白い領域に必要な数だけ並べればよい。今回はCharRectの大きさを $0.32 \times 0.94$ とし、使用する文字数を 16、Bubble内に定める文字列領域の左下隅の位置を $(1.4,\ 1.5)$ とする (図9 ; これらの数値の決定も実際には初期状態のBubbleを表示し、CharRectの位置や大きさが適切な値になるように、プログラム実行中にInspectorで調整を行う)。


この設定によって16個のCharRectはBubble内に下図10のように配置される (図中の $V_0$ は文字列領域の左下隅を表しその位置は $(1.4,\ 1.5)$ である)。上の設定では各CharRectの z座標を $-0.01$ としているので、すべてのCharRectがBubbleよりも手前に表示されている (Bubbleの z座標は初期状態では $0$ )。
そして今回のプログラムではプログラム実行中にオブジェクトを動かし、その現在地をBubbleに表示する。具体的には図11に示されるように、オブジェクトの現在地(x座標、y座標)を "x_###.#__y_###.#" の形で小数第1位まで表示する (左記における '_' は空白)。今回の文字列領域は16個分であるが、そのすべてが使われることもあるが、使われない場合には左から文字を詰めていき右側の余る部分には空白を表示する。


以下のプログラムはキー操作によってオブジェクトを動かし、Bubbleにオブジェクトの現在地を表示するものである。
H : 左へ旋回
L : 右へ旋回
S : オブジェクトの移動/停止用スイッチ
[Code2] (実行結果 図12)
if (!i_INITIALIZED)
{
float RW = 0.32f;
float RH = 0.94f;
Vector3 V0 = new Vector3(1.4f, 1.5f, -0.01f);
for (int i = 0; i < 16; i++)
{
Vector3 LL = V0 + new Vector3(i * RW, 0, 0);
CharRect[i].transform.SetParent(Bubble.transform);
CharRect[i].transform.localPosition = LL;
CharRect[i].transform.localScale = new Vector3(RW, RH, 1);
CharRect[i].SetTexture("images/sample_letters_2");
}
i_INITIALIZED = true;
}
HelicopterMotion();
Vector2 pos = Body.GetPosition();
Vector3 posBubble = new Vector3(pos.x + 0.4f, pos.y + 0.4f, -0.03f);
Bubble.transform.localPosition = posBubble;
for (int i = 0; i < CharRect.Length; i++) // Clear
{
CharRect[i].SetUVs(GetUVs(' '));
}
string str = string.Format("x {0:f1} y {1:f1}", pos.x, pos.y);
for (int i = 0; i < str.Length; i++)
{
CharRect[i].SetUVs(GetUVs(str[i]));
}
初期化ブロックの内容はCode1と同じく各CharRectを指定の位置に指定の大きさで配置するものであるが、今回はBubbleを親オブジェクト、各CharRectを子オブジェクトとして親子関係を設定している (11行目)。Bubbleに置かれる文字列領域は動くことはないので初期化ブロックにおいて1度だけ設定すればよい。
21行目の HelicopterMotion() はプログラムで使用しているヘリコプターをキー操作によって動かすためのメソッドであるが、その内容は 2-10節 Code4 と同じである。
23行目ではヘリコプターの現在地を取得している。Bubbleはその現在地からわずかに離れた位置に置かれるが、具体的にはヘリコプターの現在地から x軸方向、y軸方向に $0.4$ だけ離れた位置に置かれるので、Bubbleは常にヘリコプターのやや右上に表示されることになる。なお23行目の設定では z座標を $-0.03$ としているが、これはBubbleがヘリコプターよりも手前に表示されるようにするためのものである (Bubbleの子オブジェクトである各CharRectの z座標はBubbleよりも $0.01$ だけ z軸マイナス側に置かれているので、各CharRectの実際の z座標は $-0.04$ である)。
各CharRectとBubbleには親子関係が設定されているので、Bubbleの位置を動かすだけで自動的にCharRectも同じだけ移動する。そのためBubbleがどのように動いても、Bubble内における文字列領域の位置は常に同じである。
28行目以降はヘリコプターの現在地の x座標、y座標を文字列化してCharRectに貼り付ける処理である。その処理は、まずすべてのCharRectの内容を空白によってクリアし(28行目のfor文)、その後に現在地を文字列化して各CharRectに貼り付けるという手順で行われる (33~37行目)。

# Code3
前節のCode4及びCode5ではスクリーン座標をワールド座標に変換する処理について扱ったが、今回のプログラムでは表示するテキストの領域(文字列領域)を、ピクセルを単位とするスクリーン座標によって定める。前節と同じくここでも「ワールド座標」といえばXY座標(XY平面上の座標)のことであり、「ワールド座標系」といえばXY平面のことである (これらの語は単にXY座標、XY平面の代わりに使っているに過ぎない)。しかしその前に、まずはスクリーン座標とワールド座標の変換について簡単に復習する。
(以下では前節と同じくスクリーン座標の単位を「pix」、ワールド座標の単位(XY平面上の単位)を「wld」と表記する)
画面中心のスクリーン座標を $P'(cx,\ cy)$ とする。画面の横方向の長さを $w$、縦方向の長さを $h$ とすれば、横半分の長さは $w/2$、縦半分の長さは $h/2$ であるが、Unityではスクリーン座標の起点 $(0,\ 0)$ は左下隅であるから結局、画面中心のスクリーン座標 $P'$ は $(cx,\ cy) = (w/2,\ h/2)$ である (図13)。
また $P'$ から横方向に $dx$、縦方向に $dy$ だけ離れた位置を $M'(mx,\ my)$ とするとき ($dx, dy > 0$)、$mx - cx = dx$、$my - cy = dy$ である (以上すべて単位は pix)。
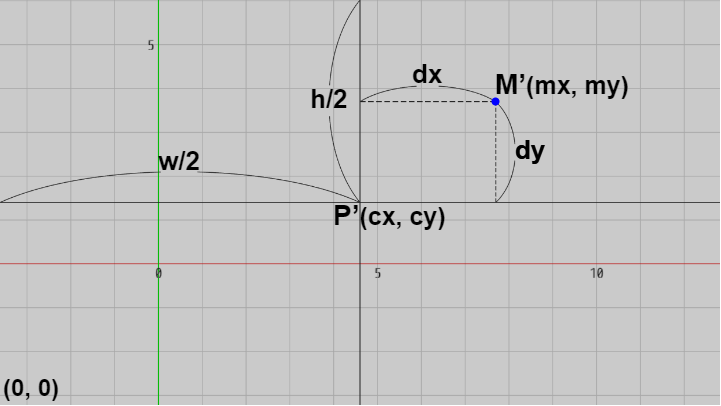
スクリーン座標 $P'$ に対応するワールド座標を $P$、スクリーン座標 $M'$ に対応するワールド座標を $M$ とする (図14)。またワールド座標系で測った実行画面の横の長さを $W$、縦の長さを $H$ とし、上記のスクリーン座標系での長さ $w/2$、$h/2$、$dx$、$dy$ に対応するワールド座標系の長さを $W/2$、$H/2$、$s$、$t$ とする (これらの単位は wld)。

これらを元にしてスクリーン座標からワールド座標への変換は次のように行われる。
カメラの位置を $(E.\!x,\ E.\!y,\ E.\!z)$ とし、XY平面からカメラまでの距離を $d$ とする (このとき $d = -E.\!z$ である)。またFOVの半分の角度を $\theta$ とする。
このとき、ワールド座標系で測ったときの画面縦半分の長さ $H/2$ は\[d\tan\theta = H/2\]である。
画面縦半分はスクリーン座標系で測ると $h/2$ pix であるが、これが $H/2$ wld に相当するということであるから、スクリーン座標系の 1 pix がワールド座標系において何wldであるかを表す変数を $WldPerPix$ とすれば\[ (H/2)/(h/2) = H/h = WldPerPix \]である。
カメラの位置が $(E.\!x,\ E.\!y,\ E.\!z)$ であるから、画面中心のワールド座標 $P$ は $(E.\!x,\ E.\!y)$ である (2-27節)。
スクリーン座標 $M'$ に対応するワールド座標 $M$ は、$P$ から x軸方向に $s$、y軸方向に $t$ だけ離れた位置にあるから、結局 $M = (P.\!x + s\ P.\!y + t)$ となり、$s$ 及び $t$ がわかればよいわけである。
$s$、$t$ はスクリーン座標系での長さ $dx$、$dy$ に対応するワールド座標系の長さであるから、上記の $WldPerPix$ を使えば簡単に\begin{align*}&dx \cdot WldPerPix = s \\ \\&dy \cdot WldPerPix = t \\ \\\end{align*}として求められる。
次のメソッド ConvertScreenToWorld(..) は引数にセットされたスクリーン座標をワールド座標(XY座標)に変換するものであり、今述べてきたことを実装したものである (メソッド内で使われている変数は上の解説のものと意味は同じである)。
[ConvertScreenToWorld(..)]
Vector2 ConvertScreenToWorld(float mx, float my)
{
Vector3 E = MainCamera.transform.position;
float d = -E.z;
float FOV = 60.0f;
float theta = FOV * 0.5f * Mathf.Deg2Rad;
float w2 = Screen.width * 0.5f;
float h2 = Screen.height * 0.5f;
float cx = w2;
float cy = h2;
float H2 = d * Mathf.Tan(theta);
float WldPerPix = H2 / h2;
float s = (mx - cx) * WldPerPix;
float t = (my - cy) * WldPerPix;
Vector2 P = E;
Vector2 pos = P + new Vector2(s, t);
return pos;
}
上記のオーバーロード版として以下のものも使用する。
Vector2 ConvertScreenToWorld(Vector2 Md)
{
return ConvertScreenToWorld(Md.x, Md.y);
}
ただし上のメソッドにおいて計算されるいくつかの変数については、カメラの位置やFOV及び画面の大きさが変わらなければ、算出される値は毎回同じである (例えば WldPerPix や cx、cy)。したがって、カメラの位置やFOV及び画面の大きさが変わらないことがあらかじめわかっている場合には、それらの変数をインスタンス変数などとして使う方が実用的であろう。
では上で述べたことを応用して画面上の指定の位置に指定の大きさでテキストを表示するが、今回の文字列領域はスクリーン座標によって設定する。それは単に文字列領域の左下隅のスクリーン座標を $M'(mx,\ my)$ として上の手続きを繰り返すだけである (図15)。
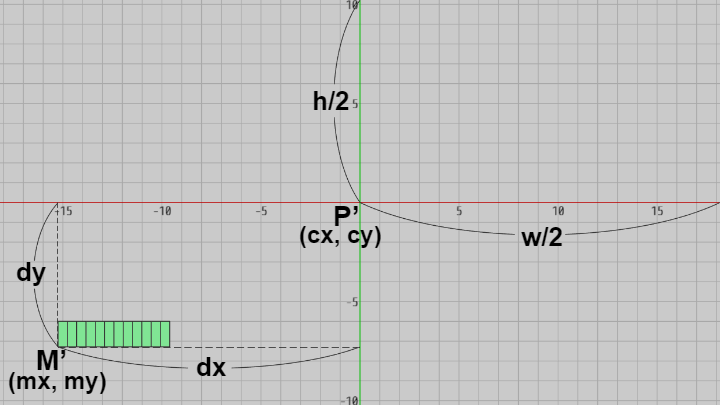
次のプログラムは画面上の $(100,\ 100)$ の位置にテキストを表示するものである (文字列領域の左下隅が $(100,\ 100)$ )。今回の文字数は12で、文字1つの画面上での大きさは $16 \times 44$ pix である (ここでは上記の ConvertScreenToWorld(..) は使っていない)。
[Code3] (実行結果 図16)
if (!i_INITIALIZED)
{
Vector3 E = MainCamera.transform.position;
float d = -E.z;
float FOV = 60.0f;
float theta = FOV * 0.5f * Mathf.Deg2Rad;
float w2 = Screen.width * 0.5f;
float h2 = Screen.height * 0.5f;
float cx = w2;
float cy = h2;
float H2 = d * Mathf.Tan(theta);
float WldPerPix = H2 / h2;
float mx = 100;
float my = 100;
float rw = 16;
float rh = 44;
float RW = rw * WldPerPix;
float RH = rh * WldPerPix;
Vector2 P = E;
string str = "Hello World!";
for (int i = 0; i < str.Length; i++)
{
float dx = mx - cx;
float dy = my - cy;
float s = dx * WldPerPix;
float t = dy * WldPerPix;
Vector2 M = P + new Vector2(s, t);
CharRect[i].transform.localPosition = M;
CharRect[i].transform.localScale = new Vector3(RW, RH, 1);
CharRect[i].SetTexture("images/sample_letters_2");
CharRect[i].SetUVs(GetUVs(str[i]));
mx += rw;
}
i_INITIALIZED = true;
}
18~19行目の rw、rh はスクリーン座標系における1文字分の大きさ($16 \times 44$ pix)、RW、RH はワールド座標系における1文字分の大きさである。すなわちスクリーン座標系における長さ rw、rh をワールド座標系での長さに変換したものが RW、RH であり、これは各CharRectに設定する大きさでもある (34行目)。
16~17行目の mx、my はその初期値として $100$、$100$ がセットされているが、これは文字列領域の左下隅のスクリーン座標を表している。しかしこの後のfor文内で mx の値は rw ずつ($16$ pix ずつ)加算されるので、このプログラムにおける mx、my は実際には各文字の左下隅のスクリーン座標として使われる。
25行目のfor文は12個のCharRectを指定の位置に指定の大きさで配置し、それぞれに指定の文字を貼り付ける(テクスチャの指定の部分を貼り付ける)処理である。ここで使われている cx、cy は画面中心のスクリーン座標、M (31行目)は各文字の左下隅のワールド座標、P は画面中心のワールド座標である (今回は画面中心に原点が来るので P の値は $(0,\ 0)$ )。
各文字はスクリーン座標系で測ると rw ずつ横にずらして置かれているので、先程述べたようにこのfor文ではループ1回ごとに mx の値が rw ずつ加算される (38行目)。

実行結果の画面右下に表示される1組の数字は、マウスカーソルの指すスクリーン座標である。カーソルを文字列領域の適当な位置に置けば、実際に文字列領域の左下隅のスクリーン座標が $(100,\ 100)$ であるか、あるいは各文字の大きさが $16 \times 44$ pix であるかなどを調べることができる (もちろんラスターグラフィックスではないので、1 pix 前後の誤差はある)。
B) マウス操作との連携
では続いて、マウスによるインタラクティブな処理を実装する。具体的にはマウスクリックした位置にオブジェクトを置いたり、あるいはマウスクリックによるオブジェクトの選択、またはマウスドラッグによるオブジェクトの移動といったものである。
なお以降のプログラムではマウス操作の際に、カスタムライブラリーで用意されている以下のメソッドを使用する (以下のメソッドの戻り値はいずれもbool型である)。
IsMousePressed()
: マウスの左ボタンが押された際にtrueが返される (trueが返されるのは押したときのみであり、その後に押し続けていても返される値はfalseである)。IsMouseDragged()
: (左ボタンによる)マウスドラッグが行われている間trueが返される。IsMouseReleased()
: マウスの左ボタンが離された際にtrueが返される。# Code4
まずはマウスでクリックした位置にオブジェクトを配置する。ここで使用するオブジェクトは下図に示される小さな青い丸 Dot である。
次のプログラムはマウスクリックした位置にDotを置くものである。
[Code4] (実行結果 図17)
if (IsMousePressed())
{
float mx = Input.mousePosition.x;
float my = Input.mousePosition.y;
Vector2 pos = ConvertScreenToWorld(mx, my);
Dot.transform.position = pos;
}
プログラムは簡単である。このプログラムではマウスの左ボタンが押されるとifブロックに入るが、そこでは単にマウスのスクリーン座標(mx、my)を取得し、そのスクリーン座標をワールド座標に変換して、Dotをその位置に移動させるだけである。
5行目の ConvertScreenToWorld(..) は上で解説したものであり、引数にセットされたスクリーン座標をワールド座標(XY座標)に変換するメソッドである。
# Code5
次にマウスによるオブジェクトの選択を実装する。オブジェクトの選択とはこの場合、マウスクリックした位置にオブジェクトがあればそのオブジェクトを選択されたオブジェクトとみなすものであるが、その処理自体は簡単である。マウスクリックした位置のスクリーン座標をワールド座標に変換し、そのワールド座標がオブジェクトに含まれているかを調べるだけである。ワールド座標とはここではXY平面上の点であるから、具体的にいえばマウスの位置に対応するXY平面上の点が円盤や長方形、あるいは三角形に含まれているかを調べ、含まれていればそのオブジェクトを選択されたものとして処理を進めればよい。
ここでは選択対象として長方形、実際には下図に示されるトランプのカードを使用する。
そしてマウスクリックによってあるカードが選択されたと判定された場合には、選択されたことを示すためにそのカードを裏返す処理を入れている。

プログラムは以下のとおり。
[Code5] (実行結果 図18)
if (!i_INITIALIZED)
{
Card[0].transform.position = new Vector2(8, 5);
Card[0].transform.rotation = TH2DMath.GetRotation(-50);
Card[1].transform.position = new Vector2(-8, 5);
Card[1].transform.rotation = TH2DMath.GetRotation(30);
Card[2].transform.position = new Vector2(-8, -5);
Card[2].transform.rotation = TH2DMath.GetRotation(-80);
Card[3].transform.position = new Vector2(8, -5);
Card[3].transform.rotation = TH2DMath.GetRotation(-120);
i_turnCardIndex = -1;
i_INITIALIZED = true;
}
if (IsMousePressed() && i_turnCardIndex == -1)
{
Vector2 Md = Input.mousePosition;
Vector2 M = ConvertScreenToWorld(Md);
for (int i = 0; i < Card.Length; i++)
{
THMatrix3x3 mtx = Card[i].GetMatrix();
Vector2 P = mtx.inverse * TH2DMath.ToVector3(M);
bool bColl = CollisionTest_Point_AABB(P, c_CardMinMax);
if (bColl)
{
i_turnCardIndex = i;
break;
}
}
}

プログラム中ではCardは配列として使われており(要素数 4)、初期化ブロックにおいてそれぞれ適当な位置に適当な向きで配置される (3~10行目)。
処理の手順は、まずマウスクリック時のスクリーン座標(Md)を取得し、そのスクリーン座標(Md)をワールド座標(M)に変換する (19~20行目)。そしてそのワールド座標が4枚のCardのいずれかに含まれているかを調べ、もしあるCardに含まれているならば、そのCardをマウスによって選択されたCardとみなして次のフレームから裏返す処理を実行する (23行目のfor文)。
スクリーン座標から変換されたワールド座標が4枚のCardのいずれかに含まれているかを調べる処理(23行目のfor文)は、簡単にいえばXY平面上のある点が4つの長方形のいずれかに含まれているかを調べているだけであり、この処理は2-13~2-14節で扱った長方形と点の衝突判定と同じである (26行目の c_CardMinMax は初期状態におけるCardの左下、右上の頂点(図19における $min$、$max$)がセットされた配列)。
プログラム中で使われている i_turnCardIndex は選択されたCardのインデックスをセットするためのインスタンス変数である (int型)。あるCardが選択されるとこのインスタンス変数にそのCardのインデックスがセットされ(30行目)、次のフレームから一定の時間そのCardを裏返す処理が行われる。その裏返す処理が終わると自動的にこのインスタンス変数には $-1$ がセットされ、次に他のCardが選択されるまでは $-1$ のままである (ほとんどの状況においてはこのインスタンス変数の値は $-1$ であり、Cardが選択されてから裏返す処理が終わるまでの間だけ選択されたCardのインデックスがセットされている)。Cardを裏返す処理の解説については省略する。
# Code6
では続いてマウスクリックによって一般のオブジェクト(三角形の集合)を選択する。しかし内容自体はCode5と同じであり、マウスの位置をスクリーン座標からワールド座標に変換し、その座標がオブジェクトに含まれているかを調べるだけである。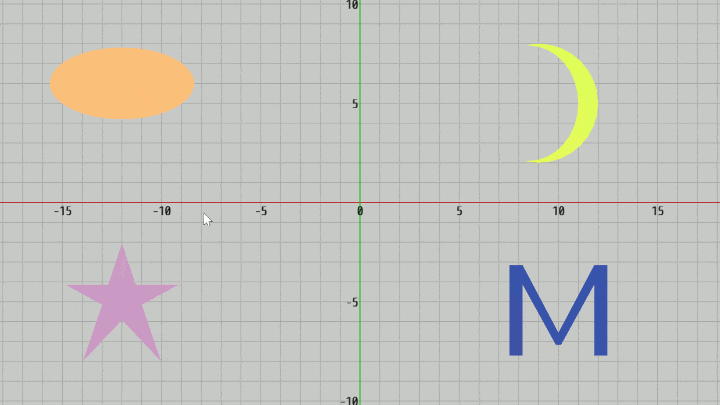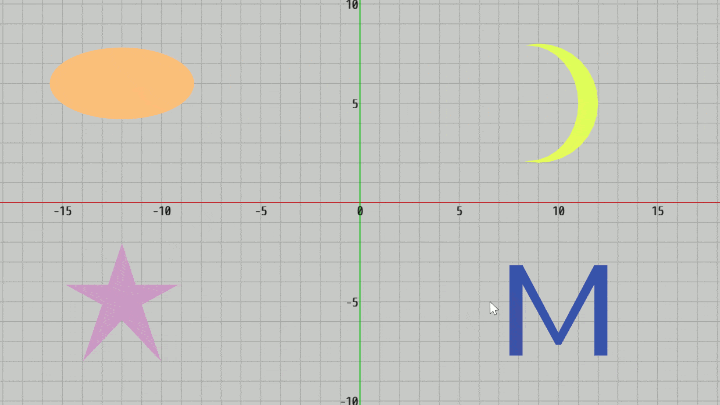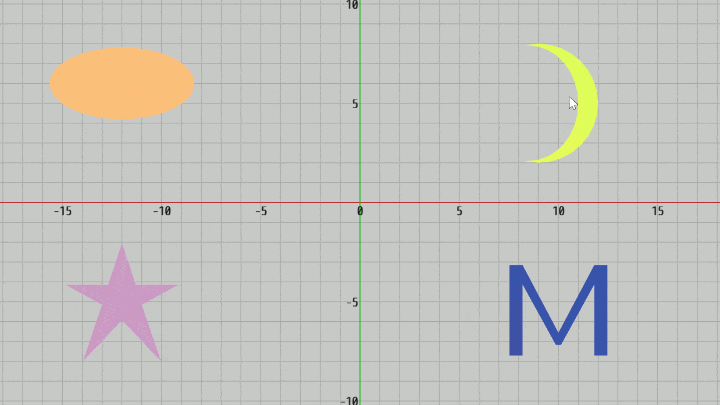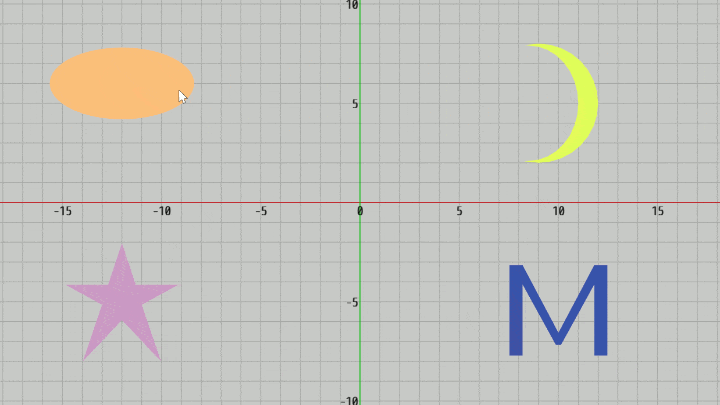
プログラムは以下のとおり。
[Code6] (実行結果 図20)
if (!i_INITIALIZED)
{
i_targets = new THAlphaObject2D[]
{
Moon, Star, Ellipse, Letter
};
i_INITIALIZED = true;
}
if (IsMousePressed())
{
Vector2 Md = Input.mousePosition;
Vector2 M = ConvertScreenToWorld(Md);
foreach (var obj in i_targets)
{
THMatrix3x3 mtx = obj.GetMatrix();
Vector2 P = mtx.inverse * TH2DMath.ToVector3(M);
bool bColl = CollisionTest_Point_TriMesh(P, obj.initTriangleCoords);
if (bColl)
{
SelectObject(obj);
break;
}
}
}
今回は4つのオブジェクト Moon、Ellipse、Star、Letter が適当な位置にそれぞれ置かれている。いずれのオブジェクトも三角形の集合であり、そのオブジェクトを構成するすべての三角形の頂点配列を取得するために initTriangleCoords というVector2[]型のプロパティが用意されている(2-15節参照)。
マウスがクリックされると、まずその位置をスクリーン座標(Md)からワールド座標(M)に変換する (13~14行目)。そしてそのワールド座標が4つのオブジェクトのいずれかに含まれているかを調べ(16行目のforeach文)、あるオブジェクトに含まれていればそのオブジェクトが選択されたことを示すために、今回はオブジェクトの色を一時的に変化させる (23行目の SelectObject(..) は引数にセットされたオブジェクトの色を一時的に変化させるための補助メソッド)。
マウスの位置に対応するワールド座標がオブジェクトに含まれているかを調べる処理は18~20行目で行われるが、この処理はXY平面上のある点が三角形の集合に含まれているかを調べることと同じである (2-15節参照)。
# Code7
マウス関連のプログラムの最後として、マウスドラッグによるオブジェクトの移動を実装する。ここではXY平面上に置かれた以下の4つのオブジェクトをマウスドラッグによって動かす。オブジェクトの形状は円盤、長方形、三角形の集合と分かれているが処理自体は同じであり、マウスでクリックした位置にオブジェクトがあれば、そのオブジェクトを選択されたオブジェクトとし、さらにその後にマウスドラッグが行われればそのオブジェクトをドラッグした分だけ移動させるだけである。

ここで重要なのがマウスドラッグ時のオブジェクトの移動量であるが、これは次のように求められる。
下図22の円盤をマウスでクリックしたときのワールド座標を $M_1$ とし、その位置からマウスを右下にドラッグしたときのマウスの位置(ワールド座標)を $M_2$ とする。すなわち $M_1$ がドラッグ前のワールド座標、$M_2$ がドラッグ後のワールド座標である ($M_1$、$M_2$ はワールド座標である。スクリーン座標ではない)。


図22に示されるようにドラッグ前のマウスカーソルは円盤上の赤い点 $M_1$ を指しているが、マウスドラッグによってオブジェクトを移動させる場合にはドラッグ後においてもマウスカーソルがオブジェクトの同じ位置を指していることが望ましい。つまり、この場合にはドラッグ後においてもマウスカーソルが円盤上の赤い点を指すようにするということである。
マウスドラッグ後のマウスカーソルは点 $M_2$ を指しているので、ドラッグ後においてもマウスカーソルが円盤上の赤い点を指した状態にするためには、マウスドラッグ後に円盤上の赤い点の位置が $M_2$ に来ていればよいわけである。
このとき図23に示されるように円盤上の赤い点は $M_1$ から $M_2$ に移動することになるから、結局このマウスドラッグでは円盤を $M_2 - M_1$ だけ移動させれば目的が達せられることになる。
以下のプログラムは上記の4つのオブジェクトをマウスドラッグによって移動させるものである。
[Code7] (実行結果 図24)
if (!i_INITIALIZED)
{
i_targets = new THAlphaObject2D[]
{
Block, Moon, Disk, Star
};
i_selectObject = null;
i_INITIALIZED = true;
}
if (IsMousePressed())
{
Vector2 Md = Input.mousePosition;
Vector2 M1 = ConvertScreenToWorld(Md);
foreach (var obj in i_targets)
{
bool bColl = CollisionTest_Point_AllTypes(M1, obj);
if (bColl)
{
SelectObject(obj);
i_selectObject = obj;
i_M1 = M1;
break;
}
}
}
if (i_selectObject != null)
{
if (IsMouseDragged())
{
Vector2 Md = Input.mousePosition;
Vector2 M2 = ConvertScreenToWorld(Md);
Vector3 dif = M2 - i_M1;
i_selectObject.transform.position += dif;
i_M1 = M2;
}
else if(IsMouseReleased())
{
i_selectObject = null;
}
}
初期化ブロックにおけるインスタンス変数 i_selectObject はマウスクリックした位置にオブジェクトがあれば、そのオブジェクトがこのインスタンス変数にセットされ、マウスリリース(マウスボタンが離される)までこの変数にはそのオブジェクトがセットされた状態になる。つまりクリック後にマウスドラッグが続いて起これば、マウスドラッグ中もこのインスタンス変数には選択されたオブジェクトがセットされたままである。マウスリリースの時点で null になる。
13行目はマウスクリック時の処理であるが、これは上で見てきたプログラムと同じである。ただしここではマウスクリックした位置にオブジェクトがあれば21行目のifブロック内で、まずオブジェクトの色を変え(SelectObject(..))、次に2つのインスタンス変数 i_selectObject、i_M1 の値を更新する。i_selectObject は上で述べたものであり、i_M1 はマウスクリックした位置のワールド座標を表すインスタンス変数で、これは上記解説中の $M_1$ と同じである (ドラッグ前のマウスのワールド座標)。
インスタンス変数 i_selectObject が null でない場合には(オブジェクトが選択されている場合には)、32行目のifブロックに処理が進むが、このときにマウスドラッグが行われていればオブジェクトの移動処理が行われる。それは34行目のifブロックで、この部分では上で述べた、オブジェクトを $M_2 - M_1$ だけ移動させるという処理を行っている (プログラム中の M2 は上記解説中の $M_2$ と同じで、ドラッグ後のマウスのワールド座標)。
i_selectObject がnullでない状態で、マウスドラッグが続く場合には毎フレームこの34行目のifブロックに入り続ける (ドラッグ中は13行目のifブロックには入らない)。そのため、ドラッグ前の位置を表すインスタンス変数 i_M1 を毎フレーム更新する必要があるが、それは単にそのフレームにおけるドラッグ後の位置 $M_2$ を次のフレームにおけるドラッグ前の位置として使えばよい (41行目)。
(なお、このプログラムではマウスがオブジェクトの上空に入った時点でオブジェクトの色を変える処理を裏側で行っている)

C) スクリーンショット
最後にスクリーンショットに関する基本的な事柄について見ていく。以下のプログラムにおいてはスクリーンショットを撮影するために MakeScreenshot(..) という補助的なメソッドが使われる。このメソッドの引数にはファイル名及び画像のサイズを指定するが、出力される画像ファイル(PNGファイル)の中心には必ず画面の中心が来る。
例えば実行画面が以下の内容であるとしよう。青い長方形のスクリーン座標系での大きさは $400 \times 300$ pix、図中の点 $P$ は長方形の中心であり、画面の中心でもある。

このときスクリーンショットを撮影するために MakeScreenshot(..) を次のように実行したとき、
MakeScreenshot("image.png", 400, 300);
ここからはXY平面上における指定の領域を指定の大きさの画像として出力することについて考えていく。
(引き続き以降の文章中においても、XY座標(XY平面上の座標)の代わりに「ワールド座標」、XY平面の代わりに「ワールド座標系」という語を用いる。同様にスクリーン座標系の単位を「pix」、ワールド座標系の単位を「wld」として進める)。
下図における青い枠の大きさはワールド座標系において $RW \times RH$ wld であり、青い枠の中心 $P$ は画面の中心でもある ($P$ はワールド座標)。先程と同様にワールド座標系で測ったときの画面の横の長さ、縦の長さを $W$、$H$ とし、横半分、縦半分の長さそれぞれ $W/2$、$H/2$ で表す (図26)。

ここで、図の青い枠に囲まれた領域を $rw \times rh$ pix のスクリーンショットとして出力するとしよう。以下の解説においては、撮影対象の領域(ここでは青い枠)のアスペクト比とスクリーンショットのアスペクト比が等しいことを前提として進める。つまり、以下では $RW : RH = rw : rh$ であることが前提である。
この例の場合ではすでに青い枠の中心 $P$ は画面の中心であるので、出力される画像の中心には $P$ が来る。したがってカメラの x座標、y座標を変える必要はないが、もし $P$ が画面の中心でない場合にはまず出力される画像の中心に $P$ が来るようにカメラの位置を合わせる必要がある。しかし、それは単にカメラの x座標、y座標を $P.\!x$、$P.\!y$ とすればよい (2-27節)。カメラの x座標、y座標をこのように定めたときに画面中心には確かに $P$ が来るが、ここで問題となるのがスクリーン座標系で測ったときの青い枠の大きさである。
2-28節で見たように画面に表示されるオブジェクトの大きさは、カメラをXY平面に近づければ大きくなり、カメラがXY平面から離れていくにしたがって小さくなる。すなわち画面上における青い枠の大きさはカメラのXY平面からの距離で決まるので、画面上における青い枠の大きさを $rw \times rh$ pix にするためには、XY平面からの適切な距離を求める必要があるわけである。
しかしこの問題も結局は、スクリーン座標とワールド座標の変換の応用に過ぎない。
スクリーン座標系における青い枠の大きさが $rw \times rh$ であるとき、その縦の長さは $rh$ pix である。そしてこの青い枠はワールド座標系では $RW \times RH$ であるから、その縦の長さは $RH$ wld である。すなわちこの場合には、スクリーン座標系における $rh$ pix がワールド座標系では $RH$ wld に相当するわけである。
したがって、ここでも 1 pix が何 wld に相当するかを表す変数を $WldPerPix$ とすれば、\[ RH/rh = WldPerPix \]である。
スクリーン座標系で測ったときの画面の縦方向の長さを $h$ とし、縦半分の長さを $h/2$ とするとき、この $h/2$ pix に対応するワールド座標系の長さは上図26の $H/2$ wld であるが、$H/2$ は $WldPerPix$ を使って簡単に\[ h/2 \cdot WldPerPix = H/2 \]として求められる。

すなわち、XY平面からカメラまでの距離 $d$ を上のように求めたときに、カメラをXY平面から $d$ だけ離れた位置に置いて撮影すると、実行結果の画面においては $rh$ pix が $RH$ wld に相当するのである。
したがって、カメラの位置を $(P.\!x,\ P.\!y,\ -d)$ とすれば目的のスクリーンショットを撮影できるわけである。
# Code8
では実際に上で述べたことを確認してみよう。下図に示されるようにXY平面上には青い領域があるが、この青い領域の中心は原点に置かれ、青い領域の中心と画面中心は一致する。またこの領域の横の長さと縦の長さの比は $4 : 3$ である。

今回はこの青い領域を $400 \times 300$ pix のスクリーンショットとして撮影する。その際以下のキー操作を用いる。
V : カメラの位置の変更
T : スクリーンショットの撮影
(注意 : T キーを押してスクリーンショットを撮影する際、上記のメソッド MakeScreenshot(..) が実行されるがこのメソッドの第1引数には出力される画像のファイルパスを指定しなければならない。例えば Windows において C ドライブ直下に "image.png" という名前でスクリーンショットを作成する場合はファイルパスを "C:/image.png" とする必要がある。以下のプログラムではデフォルトのファイルパスとして "screenshot1.png" としてあるため、スクリーンショットの出力先はUnityの現在のプロジェクトフォルダである)
プログラムは以下のとおり。
[Code8]
if (Input.GetKeyDown(KeyCode.V))
{
i_SET_VIEW = !i_SET_VIEW;
}
if(i_SET_VIEW)
{
Vector2 P = c_BoardCenter;
float w2 = Screen.width * 0.5f;
float h2 = Screen.height * 0.5f;
float RW = c_BoardW;
float RH = c_BoardH;
float rw = 400;
float rh = 300;
float WldPerPix = RH / rh;
float FOV = 60.0f;
float theta = FOV * 0.5f * Mathf.Deg2Rad;
float H2 = h2 * WldPerPix;
float d = H2 / Mathf.Tan(theta);
MainCamera.transform.position = new Vector3(P.x, P.y, -d);
}
else
{
MainCamera.transform.position = new Vector3(0, 0, -20);
}
if (Input.GetKeyDown(KeyCode.T))
{
string filePath = "screenshot1.png";
MakeScreenshot(filePath, 400, 300);
Debug.Log("= Make Screenshot 1 =");
}
プログラム開始時点ではカメラはXY平面からやや離れた位置に置かれているので、その位置で T キーを押してスクリーンショットを撮影しても出力される画像には青い領域の周りも入ってしまう (下図29はプログラム開始時点における実行画面であり、赤い枠の大きさは $400 \times 300$ pix)。

上図の状態から V キーを押すとインスタンス変数 i_SET_VIEW がtrueになり、6行目のifブロックに処理が進む。このブロックは上で述べたことを実装したものであり、ここで使われている各変数 P、RW、RH、rw、rh などは上記の $P$、$RW$、$RH$、$rw$、$rh$ と同じである。
また c_BoardCenter (8行目)は青い領域の中心を表す定数(ここでは原点)、c_BoardW、c_BoardH はワールド座標系で測った青い領域の横の長さ、縦の長さである (float型定数)。
この6行目のifブロックによってカメラは適切な位置に置かれるが、下図はそのときの実行画面である。この場合には青い領域の大きさは $400 \times 300$ pix になっているので、ここで T キーを押してスクリーンショットを撮影すると目的のスクリーンショットが得られる。



# Code9
次は撮影対象の領域の中心が原点ではない場合である。下図の緑の領域はその横の長さと縦の長さの比が $9 : 16$ であり、この領域の各頂点が $A$~$D$ として与えられている ($A$~$D$ はワールド座標)。
今回はこの緑の領域を $270 \times 480$ pix のスクリーンショットとして撮影する。
使用するキーは前回と同じである。
V : カメラの位置の変更
T : スクリーンショットの撮影
(注意 : このプログラムでもスクリーンショットのファイルパスはデフォルトでは "screenshot2.png" となっているため、ファイルパスを書き換えずに撮影すると、スクリーンショットはUnityのプロジェクトフォルダに作成される)
プログラムを以下に示す。
[Code9]
if (Input.GetKeyDown(KeyCode.V))
{
i_SET_VIEW = !i_SET_VIEW;
}
if (i_SET_VIEW)
{
Vector2 P = (A + C) * 0.5f;
float w2 = Screen.width * 0.5f;
float h2 = Screen.height * 0.5f;
float RW = (D - A).magnitude;
float RH = (A - B).magnitude;
float rw = 270;
float rh = 480;
float WldPerPix = RH / rh;
float FOV = 60.0f;
float theta = FOV * 0.5f * Mathf.Deg2Rad;
float H2 = h2 * WldPerPix;
float d = H2 / Mathf.Tan(theta);
MainCamera.transform.position = new Vector3(P.x, P.y, -d);
}
else
{
MainCamera.transform.position = new Vector3(0, 0, -20);
}
if (Input.GetKeyDown(KeyCode.T))
{
string filePath = "screenshot2.png";
MakeScreenshot(filePath, 270, 480);
Debug.Log("= Make Screenshot 2 =");
}
プログラムの内容はわずかな違いを除いてCode8と同じである。今回は画面の中心 $P$ を緑の領域の2つの頂点 $A$、$C$ から計算し(8行目)、緑の領域の縦横の長さも同様に緑の領域の各頂点から計算している (12~13行目)。違いはその点だけである。
前回と同じくプログラム開始時点ではカメラの位置は調整されていないので、この時点でスクリーンショットを撮影しても画像には緑の領域がほとんど入ることはない (下図34はプログラム開始時点における実行画面であり、赤い枠の大きさは $270 \times 480$ pix)。

上図の状態から V キーを押すとインスタンス変数 i_SET_VIEW がtrueになり、6行目のifブロック内での処理によってカメラは適切な位置に置かれるが、下図はそのときの実行画面である。この場合には緑の領域の大きさは $270 \times 480$ pix になっているので、ここで T キーを押してスクリーンショットを撮影すると目的のスクリーンショットが得られる。

下図36はプログラム開始時点において撮影したときの結果であり、図37は V キーを押してカメラの位置を調整した後の撮影結果である。
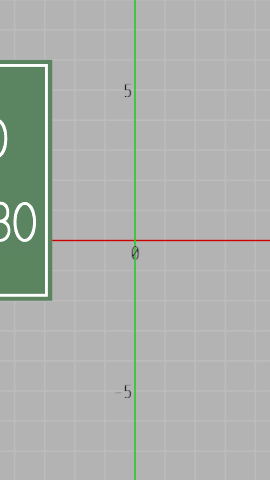

© 2020-2025 Redpoll's 60 (All rights reserved)