Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-20
第2章 2D空間におけるオブジェクトの運動
$§$2-20 衝突判定 7 (円盤 vs 長方形)
本節では円盤と長方形の衝突について見ていく。
長方形は軸平行な場合と傾きのある場合に分かれるが、最終的に使われる判定方法は同じものである。
軸平行な長方形はその中心が原点にあるとき、x軸に関して上下対称、y軸に関して左右対称であるから円盤との位置関係がどのような場合でも、円盤を第1象限に対称移動させて考えても同じである。
これは次のことを意味する。
図2の青い円盤は第2象限において長方形と衝突している。第2象限の円盤を y軸に関して対称移動させると第1象限に移るが、図2には y軸に関して対称移動させたときの円盤が紫色で表示されている。図に示されるように、第1象限に対称移動させた場合でも円盤は長方形と衝突している。
同様に、図3も青い円盤が第2象限にあるときの図であるが、このとき円盤と長方形は衝突していない。この円盤も y軸に関して対称移動させると紫色の円盤の位置に移るが、第1象限においても円盤は長方形と衝突してはいない。
さらに下の場合を見てみよう。
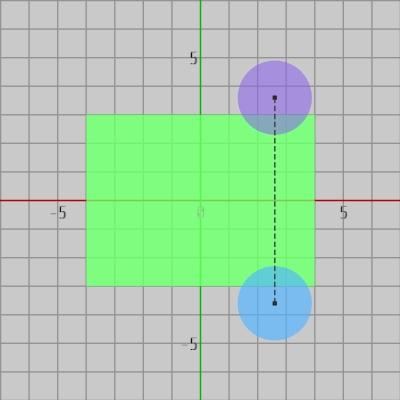
図4 第4象限で衝突しているとき、第1象限に対称移動させた場合でも衝突している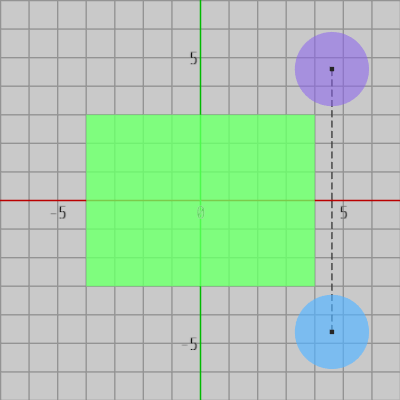 
図5 第4象限で衝突していなければ、第1象限に対称移動させても衝突していない
図4は青い円盤が第4象限にあるときの図であるが、このとき円盤と長方形は衝突している。第4象限の円盤を x軸に関して対称移動させると第1象限の紫色の円盤の位置に移るが、第1象限に対称移動させた場合でも円盤は長方形と衝突している。また、図5は第4象限において青い円盤と長方形が衝突していないときの図であるが、この円盤を第1象限に対称移動させてもやはり円盤と長方形は衝突してはいない。
つまり、円盤が2D空間上(XY平面上)のどの位置に置かれていても、その位置において(軸平行な)長方形と衝突していれば、第1象限に対称移動させた位置でも衝突する、元の位置において衝突していないのであれば、第1象限に対称移動させても衝突することはない。
したがって、円盤がどの位置にあっても、(衝突しているかどうかを調べるだけならば)円盤を第1象限に対称移動させて考えても同じなのである。
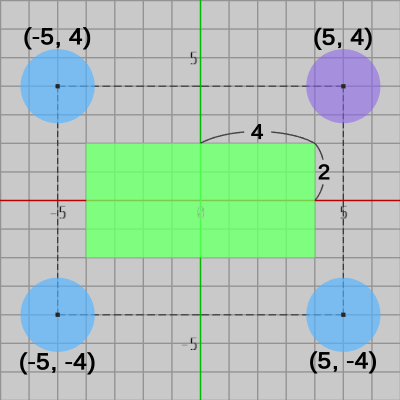
図6 円盤を第1象限に対称移動させると、その中心のx座標、y座標の符号がプラスに変わる。
例えば、右図の第2象限、第3象限、第4象限の円盤の中心位置は $(-5, 4)$、$(-5, -4)$、$(5, -4)$ であるが、それら3つの円盤を第1象限に対称移動させたときの中心位置はすべて $(5, 4)$ である。つまり、円盤を第1象限に対称移動させたときの中心位置を求めるには、その円盤の中心位置の x座標、y座標の符号をプラスにすればよいのである。
また、円盤の中心と円盤に最も近い(長方形の)頂点との距離も第1象限への対称移動で変化しない。
図6を例にとれば、第1象限から第4象限において円盤中心と最も近い頂点を結ぶベクトルは、それぞれ
第1象限 : $(5, 4) - (4, 2) = (1, 2)$
第2象限 : $(-5, 4) - (-4, 2) = (-1, 2)$
第3象限 : $(-5, -4) - (-4, -2) = (-1, -2)$
第4象限 : $(5, -4) - (4, -2) = (1, -2)$
であるが、これらのベクトルの大きさはみな同じである。言い換えれば、円盤中心から最も近い頂点までの距離は各象限においてみな同じである。
では以上をふまえて円盤と軸平行な長方形の衝突について見ていく。
図7の円盤は半径が $r$、図8の長方形は横の長さが $w$、縦の長さが $h$である。
図9の長方形を覆う赤いエリアは、円盤の半径分の長さだけ長方形を上下左右に拡大したものである。
下図 10においてはこの円盤と長方形が衝突しているが、その隣の図11に示されるように このとき 円盤の中心が赤いエリアに含まれている。
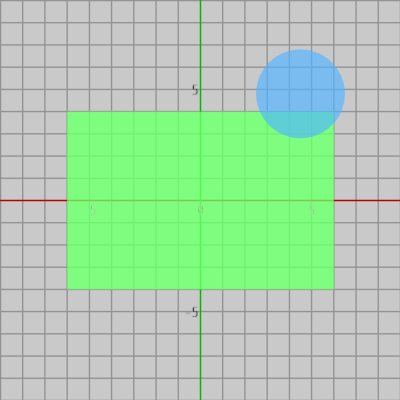
図10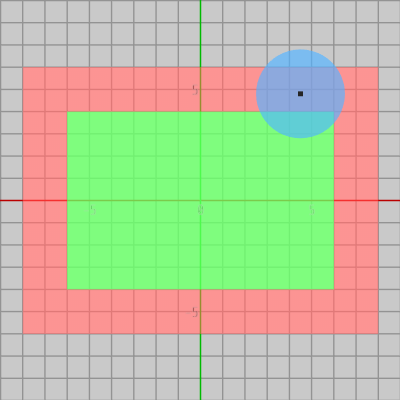 
図11 円盤中心が赤いエリアに含まれている
また、下図12においては円盤と長方形は衝突していないが、図13に示されるようにこのときは 円盤の中心が赤いエリアに含まれていない。
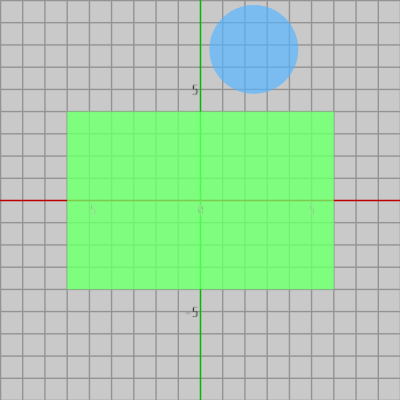
図12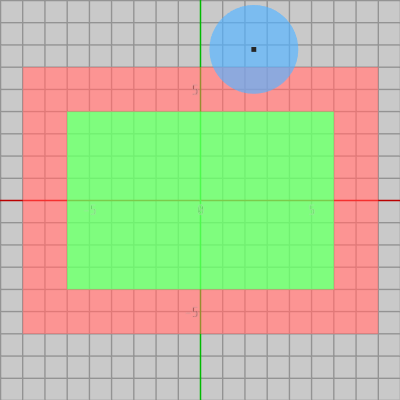 
図13 円盤中心が赤いエリアに含まれていない
したがって、円盤と(軸平行な)長方形が衝突しているかを調べるためには、円盤の中心が赤いエリアに含まれているか(あるいは長方形自体に含まれているか)を 第1のテストとして行えばよい。
このテストだけでは十分ではないが、しかし このエリアに円盤の中心が含まれていなければ、つまり円盤中心が赤いエリアの外側にあるならば、明らかに円盤と長方形は衝突していないことがわかる (赤いエリアの幅は円盤の半径 $r$ である)。
この赤いエリア(及び長方形自体)に円盤の中心が含まれていないことを数式で表すと以下のようになる。ただし、以下の式において $C$、$r$、$w$、$h$ はそれぞれ円盤の中心、円盤の半径、長方形の横の長さ、縦の長さであり、"$||$" は論理和を表している (ここでは赤いエリアの境界部分は赤いエリアの外側としている)。\[ (C.x \geq w/2+r)\ \ ||\ \ (C.y \geq h/2+r) \]以下の図14はこの数式が成り立つ場合であり(円盤中心が赤いエリアの外側にある)、隣図15の場合は成り立たない(赤いエリアに含まれている)。
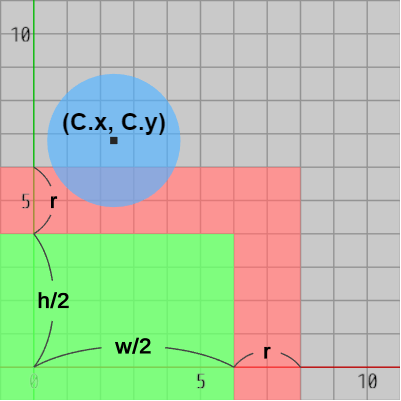
図14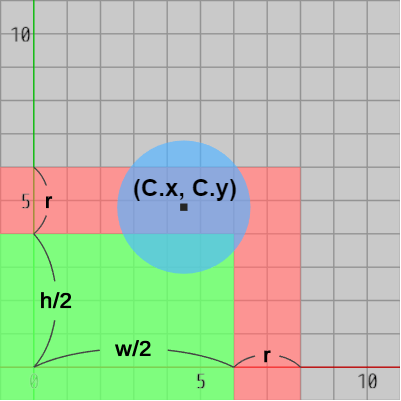 
図15
上の数式や図は第1象限の場合であるが、先程述べたように円盤がどの位置にあっても(衝突しているかどうかについては)第1象限に対称移動させた場合で考えても同じである。以降においても主に第1象限を例にとって進めていく。
第1のテストだけでは円盤と長方形の衝突を正確に検出するには不十分である。それは以下の図に示されるように、円盤中心が赤いエリア内の角の部分にある場合に問題となる (以降赤いエリア内の角の部分を「角区画」と呼ぶ。図16の点線で囲まれた正方形の部分)。
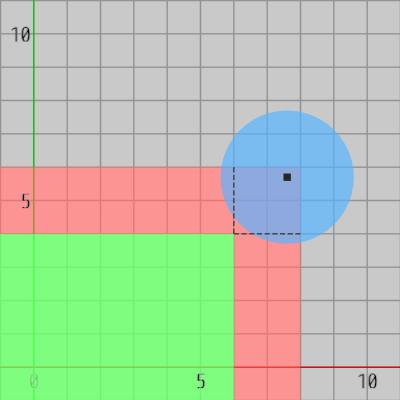
図16 円盤中心が赤いエリアに含まれているが衝突していない (点線で囲まれた正方形が角区画)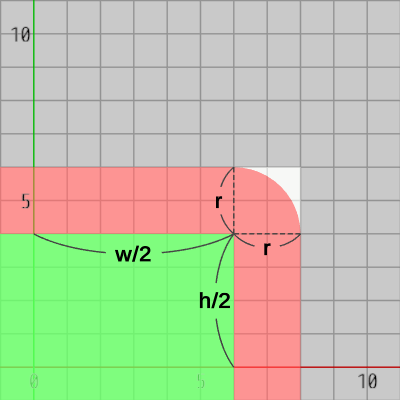 
図17 角区画内の白い部分に円盤中心があるときには、円盤と長方形は衝突していない
図16から分かるように円盤の中心は赤いエリアに含まれているが、この円盤は長方形と衝突しているわけではない。しかし上記のテストだけでは衝突とみなされてしまう。したがって、このような不正な衝突を排除するために第2のテストを追加する必要がある。
この不正な衝突は必ず角区画において発生する。具体的には、図17に示される角区画内の白い部分に円盤中心があるときに「赤いエリアに含まれているが衝突はしていない」という状況が発生するのである。
したがって、第2のテストでは円盤中心が角区画にある場合に、それが白い部分に含まれているかどうかを調べなければならない。
角区画の左下隅、右上隅の座標は $(w/2, h/2)$、$(w/2 + r, h/2 + r)$ である (図17)。そして 角区画の白い部分は、角区画の左下隅を中心とする半径 $r$ の四分円を角区画から取り除いた部分である。つまり、円盤中心が角区画にあるとき、角区画の左下隅から円盤中心までの距離が円盤の半径以上であれば、円盤中心は白い部分に含まれていることがわかる。
数式にすると次のようになる。
円盤中心が角区画にあるとき、円盤中心が白い部分に含まれているならば、\[\sqrt{(C.x - w/2)^2 + (C.y - h/2)^2}\ \geq\ r\]である。
最終的には、円盤と軸平行な長方形の間における衝突判定は次のようにまとめられる。
ただし、以下の衝突判定メソッドは(軸平行な)長方形の中心が原点に置かれていることを前提としている。
[CollisionTest_Disk_AABB(..)] (長方形の中心が原点に置かれている場合)
メソッドの引数 C、r、w、h は上の数式と同じく 円盤中心、円盤の半径、長方形の横の長さ、縦の長さを表している。5~6行目は円盤中心を第1象限へ対称移動させる処理である。上で述べたように x座標、y座標の符号をプラスにすればよい (Mathf.Abs(float v) は引数にセットされたfloat値の絶対値を返すメソッドである)。
10行目のif文は第1のテストであり、円盤中心が赤いエリアの外側にあるかを調べるものである。
ここで外側にあると分かれば、この時点で衝突していないことが分かるので衝突していないことを意味する false を返す。
15行目以降は第2のテストである。この時点での円盤中心は赤いエリアか長方形自体に含まれていることがわかっている。また、第1象限に対称移動しているので、円盤中心は下図18の A1、A2、A3 のいずれかの領域(あるいは長方形自体)に含まれていることなる。
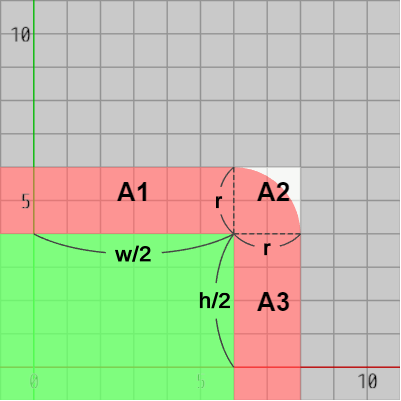
図18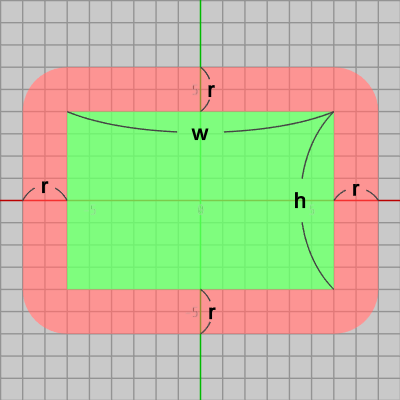 
図19
第2のテストでは円盤中心が角区画にある場合に、角区画内の白い部分に含まれているかどうかを調べるが、円盤中心が角区画である A2 に存在するのは15行目、16行目の C.x - halfW、C.y - halfH がともに $0$ 以上のときである。したがって、その場合に19行目のif文において角区画内の白い部分に含まれているかをテストする (19行目では上の数式と違って平方根にしていないが結果は同じである。わずかではあるが効率的でもある)。
まとめると、半径 $r$ の円盤中心が図19に示される赤いエリアの内側(及び長方形自体)にあるとき、円盤と(原点に置かれた軸平行な)長方形は衝突しているということである。
しかし、上の衝突判定メソッドは軸平行な長方形(の中心)が原点に置かれていることが前提になっている。したがって、軸平行な長方形が2D空間内の任意の位置にある場合は次のようにオーバーロード版を使う必要がある。
[CollisionTest_Disk_AABB(..)] (長方形が2D空間内の任意の位置にある場合)
引数 pos_disk、pos_rect は円盤の(中心)座標、長方形の(中心)座標であり、r、w、h は円盤の半径、長方形の横、縦の長さである。長方形が2D空間内のどこに置かれていても、その位置から原点に戻し、さらに同じだけの移動を円盤に実行すれば、両者の衝突判定は原点に置かれている(軸平行な)長方形と円盤との衝突判定として考えることができる。
(pos_disk - pos_rect) は長方形を原点に戻したときの円盤の相対的な位置であり、この値を使って長方形が原点に置かれている場合の CollisionTest_Disk_AABB(..) を実行しているだけである。
図20 点Pの直線 l 上への射影(その像が点Q) 2-13節での Shellと傾きのある長方形の衝突判定では、傾きのある長方形を初期状態に戻した状態において衝突を考えるという方法をとった。今回の円盤の場合においても同様の方法をとることができるが、ここでは内積による射影を用いて、より効率的な方法で実装する。
前節と同様に ある直線への射影は、その直線に直交する方向への射影を意味するものとする。例えば、以下の右図20においては点$P$を直線 $l$ 上に射影したときの像が点$Q$である。
下図21では、傾きのある長方形と円盤が重なった状態で置かれている。
長方形の各頂点を $P$、$Q$、$R$、$S$ とし、長方形の中心を $T$ とする (長方形の横の長さは $w$、縦の長さは $h$)。また、円盤の中心を $C$ とし、その半径を $r$ とする。
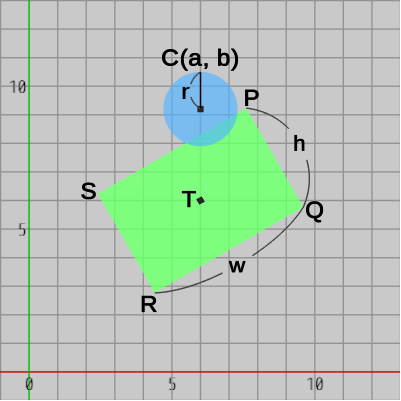
図21 傾きのある長方形と円盤の衝突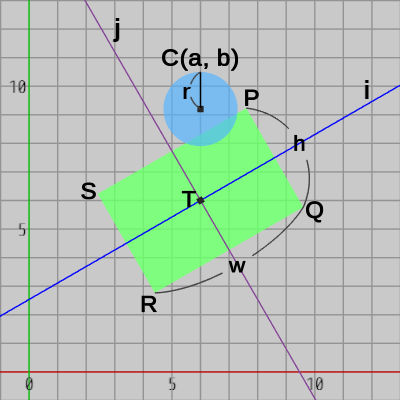 
図22 i軸は辺QRに平行、j軸は辺PQに平行
図22は、長方形の2つの辺$PQ$、$QR$に平行な直線を、中心$T$を通るように引いたときのものである。$QR$に平行な直線(水色の直線)を以降、i 軸と呼ぶことにする。また、$PQ$に平行な直線(紫色の直線)を以降、j 軸と呼ぶことにする。さらに、i 軸と j 軸の交点$T$を原点とし、i 軸、j 軸によって構成される平面を IJ平面 と呼ぶことにする。
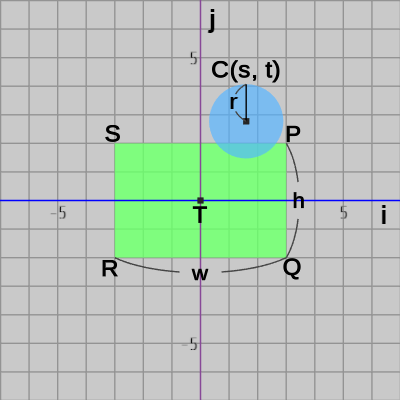
図23 カメラを回転させて i軸、j軸が画面に平行になるようにしたときの様子 図23は、カメラを適当に回転させて i 軸、j 軸が画面の縦横に平行になるようにし、さらに i 軸、j 軸に平行に $1$ ずつの間隔でグリッドを表示したときのものである (ここではXY平面のグリッドは非表示にしてある)。
このように見たときに、長方形は IJ平面において軸平行であり、その中心が原点$T$に置かれている。したがって、この長方形と円盤の衝突は IJ平面においては (原点に置かれている)軸平行な長方形と円盤の衝突と見ることができる。
軸平行な長方形と円盤の衝突において必要であったのは、円盤の中心座標、円盤の半径、そして長方形の縦横の長さであった。
XY平面であっても、IJ平面であっても円盤の半径と長方形の縦横の長さは同じであるが、円盤の中心座標はこの場合は IJ平面における値でなければならない。それは、(IJ平面の)原点$T$からの i 軸方向、j 軸方向の距離のことである。
上図21における円盤の中心$C$の座標は $(a, b)$ であるが、この座標はXY平面における座標である。詳しくは、x軸とy軸の交点$O$を原点とするXY平面上において、$C$ は原点$O$から、x軸方向に $a$、y軸方向に $b$ だけ離れていることを意味している。
ではここで円盤の中心$C$が、i 軸と j 軸の交点$T$を原点とするIJ平面において、$C$ が(IJ平面の)原点$T$から、i 軸方向、j 軸方向にどれだけ離れているかを計算してみよう。
以下では、原点$T$から$C$までの i 軸方向の距離を $s$、j 軸方向の距離を $t$ としている。したがって、IJ平面においては$C$の座標は $(s, t)$ である。
図24に示されるように $T$ と $C$ を結ぶベクトルを $\boldsymbol{\mathsf{v}}$ とし、i 軸方向を表す単位ベクトルを $\boldsymbol{u_i}$、j 軸方向を表す単位ベクトルを $\boldsymbol{u_j}$ とする。
このとき射影を使えば、円盤中心$C$は(IJ平面の)原点$T$から i 軸方向に $ \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_i} $ だけ離れていることが分かる (図25)。同様に、j 軸方向の距離は $ \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_j}$ と計算される。
つまり、円盤の中心$C$の IJ平面における座標は $(s, t) = (\boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_i},\ \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_j})$ である。図26は画面が x軸、y軸に平行になるようにカメラを戻したときのもので、i 軸上の距離 $s$、j 軸上の距離 $t$ は図に示されるとおりである。
今問題としている、円盤と傾きのある長方形の衝突判定は、この座標を使うことによって IJ平面における 円盤と軸平行な長方形の衝突判定として扱うことができるわけである。
以下のメソッド CollisionTest_Disk_OBB(..) は円盤と傾きのある長方形の衝突判定用メソッドであり、今上で述べてきたことを実装したものである。
メソッド名に使われている「OBB」とは傾きのある(軸平行でない)長方形や直方体の略称であり、詳しくは「OBB (Oriented Bounding Box)」である。
[CollisionTest_Disk_OBB(..)]
引数は上記の解説におけるものと同じであり、C (円盤の中心座標)、T (長方形の中心座標)、ui (長方形の横方向の単位ベクトル)、uj (長方形の縦方向の単位ベクトル)、r (円盤の半径)、w (長方形の横の長さ)、h (長方形の縦の長さ) である。
メソッド内で計算される v、s、t も同様に上の解説のものと意味は同じである。
最後に、i 軸方向を表す単位ベクトル $\boldsymbol{u_i}$ 及び j 軸方向を表す単位ベクトル $\boldsymbol{u_j}$ の求め方について見ていこう。
2-13節で解説したように、ある時点におけるオブジェクトの向きを求める際には、オブジェクトに実行された変換行列 と オブジェクトの初期状態における向き の積を計算する。そして、向きの場合はz成分を $0$ にした同次座標を使う必要があった。
2つの単位ベクトル $\boldsymbol{u_i}$、$\boldsymbol{u_j}$ を求める場合も同様である。
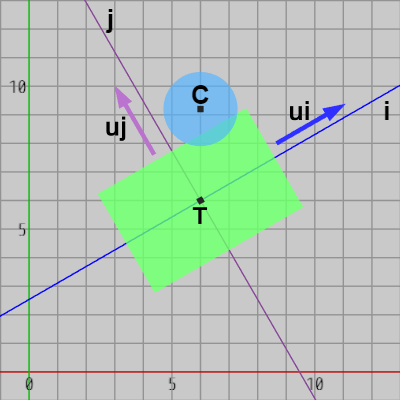
図27 ui、uj は長方形の横方向、縦方向を表す単位ベクトル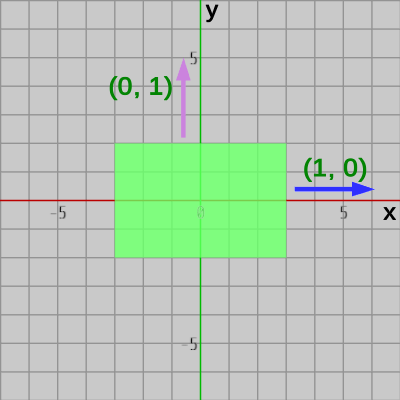 
図28 長方形の初期状態における横方向は (1, 0)、縦方向は (0, 1)
i 軸方向の $\boldsymbol{u_i}$、j 軸方向の $\boldsymbol{u_j}$ は図27に示されるように長方形の横の方向、縦の方向であり、それらは初期状態においてはx軸方向、y軸方向、すなわち $(1, 0)$、$(0, 1)$ を向いている (図28)。
したがって、図27における長方形の横方向、縦方向を求めるには、図27の長方形に実行されている変換行列と初期状態における横方向、縦方向との積を計算すればよい。ただし、初期状態における横方向、縦方向は z成分が $0$ の同次座標 $(1, 0, 0)$、$(0, 1, 0)$ を使う必要がある。
しかし、この場合には行列と同次座標との積を計算する必要はない。
例えば、図27の時点での変換行列を $M$ とし、その内容が次のものであったとしよう。
\begin{align*}M = \begin{pmatrix}a &b &c \\d &e &f \\0 &0 &1\end{pmatrix} \end{align*}($3\times3$の変換行列であれば最後の行は $(0, 0, 1)$ である。このことは 3-12節において $4\times4$の変換行列の場合で解説する)
このとき、$M$ と $(1, 0, 0)$ 及び $(0, 1, 0)$ との積は、\begin{align*}M\begin{pmatrix}1 \\0 \\0\end{pmatrix} = \begin{pmatrix}a &b &c \\d &e &f \\0 &0 &1\end{pmatrix} \begin{pmatrix}1 \\0 \\0\end{pmatrix} =\begin{pmatrix}a \\d \\0\end{pmatrix} \\\\M\begin{pmatrix}0 \\1 \\0\end{pmatrix} = \begin{pmatrix}a &b &c \\d &e &f \\0 &0 &1\end{pmatrix} \begin{pmatrix}0 \\1 \\0\end{pmatrix} =\begin{pmatrix}b \\e \\0\end{pmatrix} \end{align*}
であるが、この結果は $M$ の第1列目、第2列目の内容に過ぎない。したがって、図27における長方形の横方向、縦方向(の単位ベクトル)を求めるには、図27の長方形に実行されている変換行列の第1列目及び第2列目を取得し、それらを正規化すればよいのである。
プログラムにおいて行列の指定の列を取得するためには次のように記述すればよい。
このコードにおける M は THMatrix3x3型であり、ここでは何らかの変換行列を表しているものとする。THMatrix3x3構造体には GetColumn(int col) というメソッドが用意されており、これは名前が示すように行列の列を取得するためのメソッドである ($3\times3$行列の列を取得するので、返される値はVector3型である)。
メソッドの引数には列番号を指定するが、注意すべきは引数の数字が ’$0$ 始め’ である点である。例えば、行列の第1列目を取得する場合は GetColumn(0)、第2列目を取得する場合は GetColumn(1) としなければならない。
以下、簡単に本節で扱った内容を実装する。
円盤の半径は $1$ であり、長方形の大きさは横の長さが $6$、縦の長さが $2$ である。
図29 円盤(半径 1) 
図30 長方形(横の長さ 6、縦の長さ 2)
ここでも以下のキー操作によって円盤及び長方形を動かすことができる。
H : (円盤を)左へ移動
J : 下へ移動
K : 上へ移動
L : 右へ移動
R : 長方形を反時計周りに回転 (Shiftキーと同時押しで逆回転)
なお、プログラムにおいては円盤は Blue、長方形は Green という変数で使われている。
[Code1] (実行結果 図31)
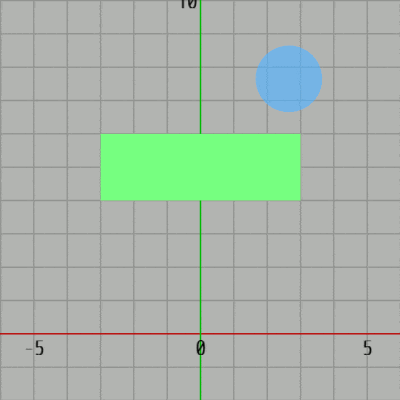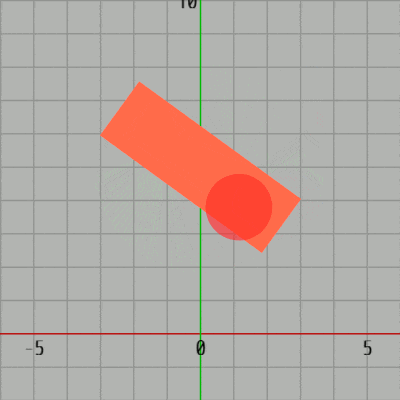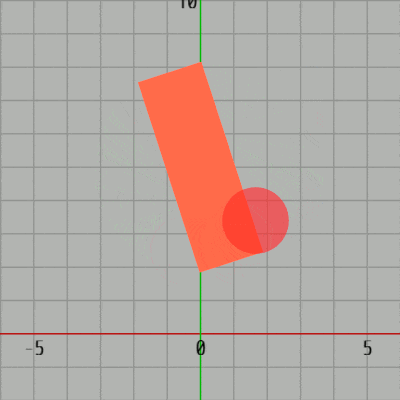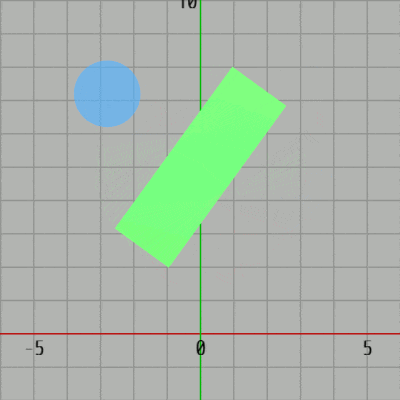
図31 Code1 実行結果 1行目のifブロックは初期化ブロックであり、ここで Green(長方形)の横の長さ、縦の長さを表すインスタンス変数 i_rectW、i_rectH、Blue(円盤)の半径を表すインスタンス変数 i_diskRad に値を設定している。また、i_degGreen はGreenの回転角度を表すインスタンス変数である。
Rキーを押すとGreenが回転するが、12行目のifブロックはその処理が記述されている (毎フレーム$1$°ずつの回転)。
19行目から40行目はキー操作によるBlueの移動処理である。Blueの現在位置を取得し(19行目)、キーを押した方向に $0.05$ だけ移動させる。
44行目以降は衝突判定の処理である。ここでは、Greenが軸平行な場合とそうでない場合とで処理を分けている。
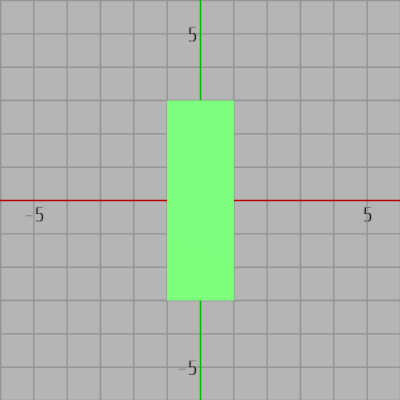
図32 90°回転した状態では縦横が逆転する Greenが軸平行な場合は回転角度i_degGreenが$90$°の倍数であるから、その際には44行目のifブロックに入ることになる。Greenの回転角度が$180$°の倍数であれば上図30のように横の長さが $6$、縦の長さが $2$ であるが、回転角度が$90$°の倍数であり$180$°の倍数でない場合は図32のように縦横の長さが逆転する。47行目と51行目の if/else はこの場合分け処理である (メソッドにおける第4引数と第5引数が入れ替わるだけ)。
円盤と軸平行な長方形の衝突判定用メソッド CollisionTest_Disk_AABB(..) の5つの引数は上でも述べた通り、順番に 円盤の中心座標(posB)、長方形の中心座標(posG)、円盤の半径(i_diskRad)、長方形の横の長さ、縦の長さである。
Greenが軸平行でない場合は回転角度i_degGreenは$90$°の倍数ではないので、その際には58行目のelseブロックに入ることになる。つまり、この elseブロックでは傾きのある長方形と円盤との衝突判定の処理を行う。
60行目から62行目において、その時点での長方形の横方向の単位ベクトル、縦方向の単位ベクトルを求めているが、これは上で解説したようにその時点での長方形に実行されている変換行列の第1列目、第2列目から取得できる。
63行目では傾きのある長方形と円盤との衝突判定用のメソッド CollisionTest_Disk_OBB(..) が実行されるが、このメソッドの内容及びここで使われる引数については上で解説した通りである。
また、このメソッドで使われている Hit(..) は前節と同じく、2つのオブジェクトが衝突してる場合(引数にtrueがセットされる場合)に両者を赤く表示するだけの補助的なメソッドである。
キー操作もCode1とほとんど同じである。
H : (円盤を)左へ移動
J : 下へ移動
K : 上へ移動
L : 右へ移動
S : 長方形の運動の停止/再開
このプログラムにおいても円盤は Blue、長方形は Green として使われている (両者の大きさなども前回と同じである)。
[Code2] (実行結果 図33)
図33 Code2 実行結果 1行目のifブロックは初期化用ブロックであり、i_rectW、i_rectH、i_diskRad についてはCode1と全く同じである。i_MOVE はGreen(長方形)の運動停止/再開ためのスイッチである (bool型インスタンス変数)。
Sキーを押すたびに12行目のifブロックで i_MOVE の値が切り替わるが、これによって19行目の GreenMotion(..) が実行されるか、されないかが決まる (つまり、Greenの運動が停止したり再開したりする)。GreenMotion(..)はGreenの運動が記述されているメソッドであり、引数が $0$ のときは単振動、$1$ のときは原点周りの公転運動である (GreenMotion(..)の内容については特に重要ではないので解説は省略する)。
22行目から43行目はキー操作によってBlueを動かす部分の記述であり、この部分はCode1と同じである。
それ以降は、円盤と傾きのある長方形との衝突判定用の処理である。しかし、この部分についてもCode1の終わりで見たものとほとんど同じであるから解説は省略する。
長方形は軸平行な場合と傾きのある場合に分かれるが、最終的に使われる判定方法は同じものである。
A) 円盤 対 軸平行な長方形 (Disk vs AABB)
まずは、軸平行な長方形の中心が原点に置かれている場合で考える。軸平行な長方形はその中心が原点にあるとき、x軸に関して上下対称、y軸に関して左右対称であるから円盤との位置関係がどのような場合でも、円盤を第1象限に対称移動させて考えても同じである。
これは次のことを意味する。
-
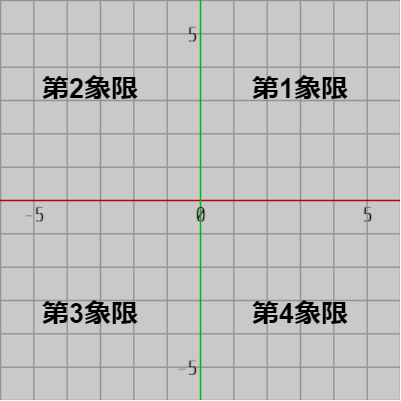図1 第1象限から第4象限 -
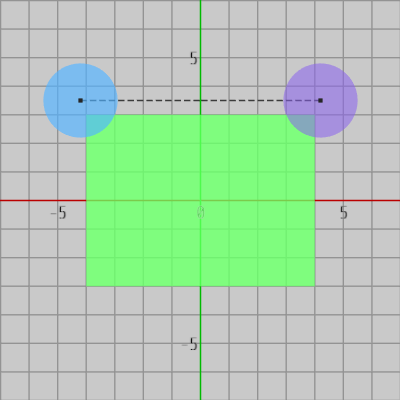図2 第2象限の青い円盤を第1象限に対称移動させると紫色の円盤の位置に移る(ここでも衝突している) -
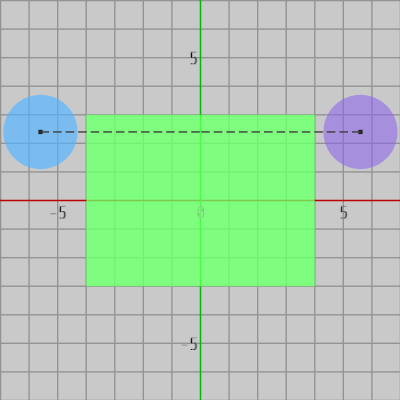図3 第2象限で衝突していなければ、第1象限に対称移動させても衝突していない
図2の青い円盤は第2象限において長方形と衝突している。第2象限の円盤を y軸に関して対称移動させると第1象限に移るが、図2には y軸に関して対称移動させたときの円盤が紫色で表示されている。図に示されるように、第1象限に対称移動させた場合でも円盤は長方形と衝突している。
同様に、図3も青い円盤が第2象限にあるときの図であるが、このとき円盤と長方形は衝突していない。この円盤も y軸に関して対称移動させると紫色の円盤の位置に移るが、第1象限においても円盤は長方形と衝突してはいない。
さらに下の場合を見てみよう。
図4は青い円盤が第4象限にあるときの図であるが、このとき円盤と長方形は衝突している。第4象限の円盤を x軸に関して対称移動させると第1象限の紫色の円盤の位置に移るが、第1象限に対称移動させた場合でも円盤は長方形と衝突している。また、図5は第4象限において青い円盤と長方形が衝突していないときの図であるが、この円盤を第1象限に対称移動させてもやはり円盤と長方形は衝突してはいない。
つまり、円盤が2D空間上(XY平面上)のどの位置に置かれていても、その位置において(軸平行な)長方形と衝突していれば、第1象限に対称移動させた位置でも衝突する、元の位置において衝突していないのであれば、第1象限に対称移動させても衝突することはない。
したがって、円盤がどの位置にあっても、(衝突しているかどうかを調べるだけならば)円盤を第1象限に対称移動させて考えても同じなのである。
例えば、右図の第2象限、第3象限、第4象限の円盤の中心位置は $(-5, 4)$、$(-5, -4)$、$(5, -4)$ であるが、それら3つの円盤を第1象限に対称移動させたときの中心位置はすべて $(5, 4)$ である。つまり、円盤を第1象限に対称移動させたときの中心位置を求めるには、その円盤の中心位置の x座標、y座標の符号をプラスにすればよいのである。
また、円盤の中心と円盤に最も近い(長方形の)頂点との距離も第1象限への対称移動で変化しない。
図6を例にとれば、第1象限から第4象限において円盤中心と最も近い頂点を結ぶベクトルは、それぞれ
第1象限 : $(5, 4) - (4, 2) = (1, 2)$
第2象限 : $(-5, 4) - (-4, 2) = (-1, 2)$
第3象限 : $(-5, -4) - (-4, -2) = (-1, -2)$
第4象限 : $(5, -4) - (4, -2) = (1, -2)$
であるが、これらのベクトルの大きさはみな同じである。言い換えれば、円盤中心から最も近い頂点までの距離は各象限においてみな同じである。
では以上をふまえて円盤と軸平行な長方形の衝突について見ていく。
図7の円盤は半径が $r$、図8の長方形は横の長さが $w$、縦の長さが $h$である。
図9の長方形を覆う赤いエリアは、円盤の半径分の長さだけ長方形を上下左右に拡大したものである。
-
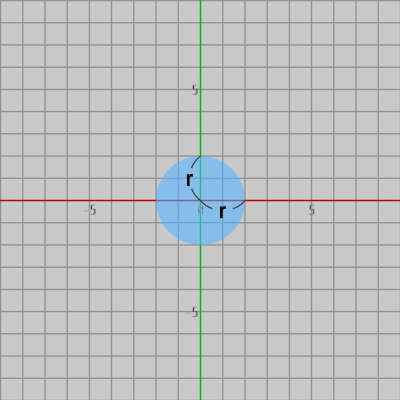図7 円盤 (半径 r) -
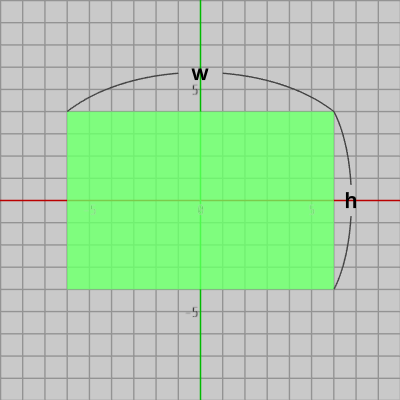図8 長方形 (横の長さ w、縦の長さ h) -
図9 長方形を覆う赤いエリア(円盤の半径分だけ長方形を拡大した大きさ)
下図 10においてはこの円盤と長方形が衝突しているが、その隣の図11に示されるように このとき 円盤の中心が赤いエリアに含まれている。
また、下図12においては円盤と長方形は衝突していないが、図13に示されるようにこのときは 円盤の中心が赤いエリアに含まれていない。
したがって、円盤と(軸平行な)長方形が衝突しているかを調べるためには、円盤の中心が赤いエリアに含まれているか(あるいは長方形自体に含まれているか)を 第1のテストとして行えばよい。
このテストだけでは十分ではないが、しかし このエリアに円盤の中心が含まれていなければ、つまり円盤中心が赤いエリアの外側にあるならば、明らかに円盤と長方形は衝突していないことがわかる (赤いエリアの幅は円盤の半径 $r$ である)。
この赤いエリア(及び長方形自体)に円盤の中心が含まれていないことを数式で表すと以下のようになる。ただし、以下の式において $C$、$r$、$w$、$h$ はそれぞれ円盤の中心、円盤の半径、長方形の横の長さ、縦の長さであり、"$||$" は論理和を表している (ここでは赤いエリアの境界部分は赤いエリアの外側としている)。\[ (C.x \geq w/2+r)\ \ ||\ \ (C.y \geq h/2+r) \]以下の図14はこの数式が成り立つ場合であり(円盤中心が赤いエリアの外側にある)、隣図15の場合は成り立たない(赤いエリアに含まれている)。
上の数式や図は第1象限の場合であるが、先程述べたように円盤がどの位置にあっても(衝突しているかどうかについては)第1象限に対称移動させた場合で考えても同じである。以降においても主に第1象限を例にとって進めていく。
第1のテストだけでは円盤と長方形の衝突を正確に検出するには不十分である。それは以下の図に示されるように、円盤中心が赤いエリア内の角の部分にある場合に問題となる (以降赤いエリア内の角の部分を「角区画」と呼ぶ。図16の点線で囲まれた正方形の部分)。
図16から分かるように円盤の中心は赤いエリアに含まれているが、この円盤は長方形と衝突しているわけではない。しかし上記のテストだけでは衝突とみなされてしまう。したがって、このような不正な衝突を排除するために第2のテストを追加する必要がある。
この不正な衝突は必ず角区画において発生する。具体的には、図17に示される角区画内の白い部分に円盤中心があるときに「赤いエリアに含まれているが衝突はしていない」という状況が発生するのである。
したがって、第2のテストでは円盤中心が角区画にある場合に、それが白い部分に含まれているかどうかを調べなければならない。
角区画の左下隅、右上隅の座標は $(w/2, h/2)$、$(w/2 + r, h/2 + r)$ である (図17)。そして 角区画の白い部分は、角区画の左下隅を中心とする半径 $r$ の四分円を角区画から取り除いた部分である。つまり、円盤中心が角区画にあるとき、角区画の左下隅から円盤中心までの距離が円盤の半径以上であれば、円盤中心は白い部分に含まれていることがわかる。
数式にすると次のようになる。
円盤中心が角区画にあるとき、円盤中心が白い部分に含まれているならば、\[\sqrt{(C.x - w/2)^2 + (C.y - h/2)^2}\ \geq\ r\]である。
最終的には、円盤と軸平行な長方形の間における衝突判定は次のようにまとめられる。
ただし、以下の衝突判定メソッドは(軸平行な)長方形の中心が原点に置かれていることを前提としている。
[CollisionTest_Disk_AABB(..)] (長方形の中心が原点に置かれている場合)
// Disk vs AABB (長方形の中心が原点に置かれている場合)
bool CollisionTest_Disk_AABB(Vector2 C, float r, float w, float h)
{
// 第1象限へ対称移動
C.x = Mathf.Abs(C.x);
C.y = Mathf.Abs(C.y);
float halfW = w * 0.5f;
float halfH = h * 0.5f;
if( (C.x >= halfW + r) || (C.y >= halfH + r))
{
return false;
}
float ax = C.x - halfW;
float ay = C.y - halfH;
if (ax >= 0.0f && ay >= 0.0f)
{
if (ax * ax + ay * ay >= r * r)
{
return false;
}
}
return true;
}
メソッドの引数 C、r、w、h は上の数式と同じく 円盤中心、円盤の半径、長方形の横の長さ、縦の長さを表している。5~6行目は円盤中心を第1象限へ対称移動させる処理である。上で述べたように x座標、y座標の符号をプラスにすればよい (Mathf.Abs(float v) は引数にセットされたfloat値の絶対値を返すメソッドである)。
10行目のif文は第1のテストであり、円盤中心が赤いエリアの外側にあるかを調べるものである。
ここで外側にあると分かれば、この時点で衝突していないことが分かるので衝突していないことを意味する false を返す。
15行目以降は第2のテストである。この時点での円盤中心は赤いエリアか長方形自体に含まれていることがわかっている。また、第1象限に対称移動しているので、円盤中心は下図18の A1、A2、A3 のいずれかの領域(あるいは長方形自体)に含まれていることなる。
第2のテストでは円盤中心が角区画にある場合に、角区画内の白い部分に含まれているかどうかを調べるが、円盤中心が角区画である A2 に存在するのは15行目、16行目の C.x - halfW、C.y - halfH がともに $0$ 以上のときである。したがって、その場合に19行目のif文において角区画内の白い部分に含まれているかをテストする (19行目では上の数式と違って平方根にしていないが結果は同じである。わずかではあるが効率的でもある)。
まとめると、半径 $r$ の円盤中心が図19に示される赤いエリアの内側(及び長方形自体)にあるとき、円盤と(原点に置かれた軸平行な)長方形は衝突しているということである。
しかし、上の衝突判定メソッドは軸平行な長方形(の中心)が原点に置かれていることが前提になっている。したがって、軸平行な長方形が2D空間内の任意の位置にある場合は次のようにオーバーロード版を使う必要がある。
[CollisionTest_Disk_AABB(..)] (長方形が2D空間内の任意の位置にある場合)
// Disk vs AABB (長方形が任意の位置にある場合)
bool CollisionTest_Disk_AABB(Vector2 pos_disk, Vector2 pos_rect,
float r, float w, float h)
{
return CollisionTest_Disk_AABB(pos_disk - pos_rect, r, w, h);
}
引数 pos_disk、pos_rect は円盤の(中心)座標、長方形の(中心)座標であり、r、w、h は円盤の半径、長方形の横、縦の長さである。長方形が2D空間内のどこに置かれていても、その位置から原点に戻し、さらに同じだけの移動を円盤に実行すれば、両者の衝突判定は原点に置かれている(軸平行な)長方形と円盤との衝突判定として考えることができる。
(pos_disk - pos_rect) は長方形を原点に戻したときの円盤の相対的な位置であり、この値を使って長方形が原点に置かれている場合の CollisionTest_Disk_AABB(..) を実行しているだけである。
B) 円盤 対 傾きのある長方形 (Disk vs OBB)
前節と同様に ある直線への射影は、その直線に直交する方向への射影を意味するものとする。例えば、以下の右図20においては点$P$を直線 $l$ 上に射影したときの像が点$Q$である。
下図21では、傾きのある長方形と円盤が重なった状態で置かれている。
長方形の各頂点を $P$、$Q$、$R$、$S$ とし、長方形の中心を $T$ とする (長方形の横の長さは $w$、縦の長さは $h$)。また、円盤の中心を $C$ とし、その半径を $r$ とする。
図22は、長方形の2つの辺$PQ$、$QR$に平行な直線を、中心$T$を通るように引いたときのものである。$QR$に平行な直線(水色の直線)を以降、i 軸と呼ぶことにする。また、$PQ$に平行な直線(紫色の直線)を以降、j 軸と呼ぶことにする。さらに、i 軸と j 軸の交点$T$を原点とし、i 軸、j 軸によって構成される平面を IJ平面 と呼ぶことにする。
このように見たときに、長方形は IJ平面において軸平行であり、その中心が原点$T$に置かれている。したがって、この長方形と円盤の衝突は IJ平面においては (原点に置かれている)軸平行な長方形と円盤の衝突と見ることができる。
軸平行な長方形と円盤の衝突において必要であったのは、円盤の中心座標、円盤の半径、そして長方形の縦横の長さであった。
XY平面であっても、IJ平面であっても円盤の半径と長方形の縦横の長さは同じであるが、円盤の中心座標はこの場合は IJ平面における値でなければならない。それは、(IJ平面の)原点$T$からの i 軸方向、j 軸方向の距離のことである。
上図21における円盤の中心$C$の座標は $(a, b)$ であるが、この座標はXY平面における座標である。詳しくは、x軸とy軸の交点$O$を原点とするXY平面上において、$C$ は原点$O$から、x軸方向に $a$、y軸方向に $b$ だけ離れていることを意味している。
ではここで円盤の中心$C$が、i 軸と j 軸の交点$T$を原点とするIJ平面において、$C$ が(IJ平面の)原点$T$から、i 軸方向、j 軸方向にどれだけ離れているかを計算してみよう。
以下では、原点$T$から$C$までの i 軸方向の距離を $s$、j 軸方向の距離を $t$ としている。したがって、IJ平面においては$C$の座標は $(s, t)$ である。
図24に示されるように $T$ と $C$ を結ぶベクトルを $\boldsymbol{\mathsf{v}}$ とし、i 軸方向を表す単位ベクトルを $\boldsymbol{u_i}$、j 軸方向を表す単位ベクトルを $\boldsymbol{u_j}$ とする。
-
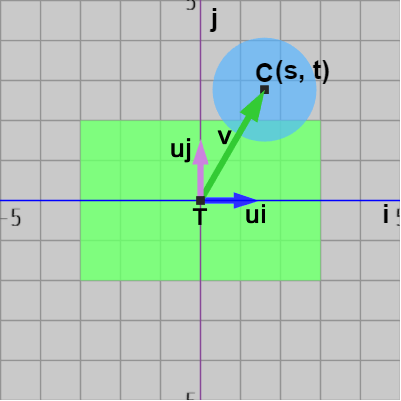図24 -
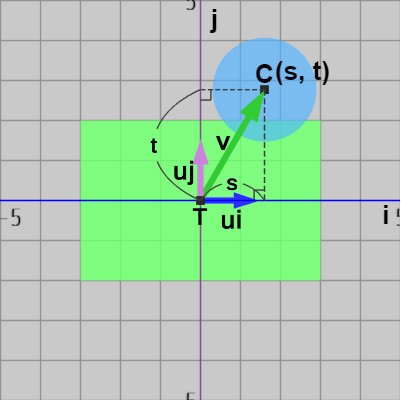図25 -
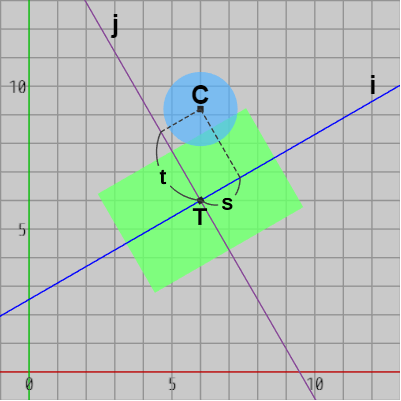図26
このとき射影を使えば、円盤中心$C$は(IJ平面の)原点$T$から i 軸方向に $ \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_i} $ だけ離れていることが分かる (図25)。同様に、j 軸方向の距離は $ \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_j}$ と計算される。
つまり、円盤の中心$C$の IJ平面における座標は $(s, t) = (\boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_i},\ \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_j})$ である。図26は画面が x軸、y軸に平行になるようにカメラを戻したときのもので、i 軸上の距離 $s$、j 軸上の距離 $t$ は図に示されるとおりである。
今問題としている、円盤と傾きのある長方形の衝突判定は、この座標を使うことによって IJ平面における 円盤と軸平行な長方形の衝突判定として扱うことができるわけである。
以下のメソッド CollisionTest_Disk_OBB(..) は円盤と傾きのある長方形の衝突判定用メソッドであり、今上で述べてきたことを実装したものである。
メソッド名に使われている「OBB」とは傾きのある(軸平行でない)長方形や直方体の略称であり、詳しくは「OBB (Oriented Bounding Box)」である。
[CollisionTest_Disk_OBB(..)]
// Disk vs OBB
bool CollisionTest_Disk_OBB(Vector2 C, Vector2 T, Vector2 ui, Vector2 uj,
float r, float w, float h)
{
Vector2 v = C - T;
float s = Vector2.Dot(v, ui);
float t = Vector2.Dot(v, uj);
return CollisionTest_Disk_AABB(new Vector2(s, t), r, w, h);
}
引数は上記の解説におけるものと同じであり、C (円盤の中心座標)、T (長方形の中心座標)、ui (長方形の横方向の単位ベクトル)、uj (長方形の縦方向の単位ベクトル)、r (円盤の半径)、w (長方形の横の長さ)、h (長方形の縦の長さ) である。
メソッド内で計算される v、s、t も同様に上の解説のものと意味は同じである。
最後に、i 軸方向を表す単位ベクトル $\boldsymbol{u_i}$ 及び j 軸方向を表す単位ベクトル $\boldsymbol{u_j}$ の求め方について見ていこう。
2-13節で解説したように、ある時点におけるオブジェクトの向きを求める際には、オブジェクトに実行された変換行列 と オブジェクトの初期状態における向き の積を計算する。そして、向きの場合はz成分を $0$ にした同次座標を使う必要があった。
2つの単位ベクトル $\boldsymbol{u_i}$、$\boldsymbol{u_j}$ を求める場合も同様である。
i 軸方向の $\boldsymbol{u_i}$、j 軸方向の $\boldsymbol{u_j}$ は図27に示されるように長方形の横の方向、縦の方向であり、それらは初期状態においてはx軸方向、y軸方向、すなわち $(1, 0)$、$(0, 1)$ を向いている (図28)。
したがって、図27における長方形の横方向、縦方向を求めるには、図27の長方形に実行されている変換行列と初期状態における横方向、縦方向との積を計算すればよい。ただし、初期状態における横方向、縦方向は z成分が $0$ の同次座標 $(1, 0, 0)$、$(0, 1, 0)$ を使う必要がある。
しかし、この場合には行列と同次座標との積を計算する必要はない。
例えば、図27の時点での変換行列を $M$ とし、その内容が次のものであったとしよう。
\begin{align*}M = \begin{pmatrix}a &b &c \\d &e &f \\0 &0 &1\end{pmatrix} \end{align*}($3\times3$の変換行列であれば最後の行は $(0, 0, 1)$ である。このことは 3-12節において $4\times4$の変換行列の場合で解説する)
このとき、$M$ と $(1, 0, 0)$ 及び $(0, 1, 0)$ との積は、\begin{align*}M\begin{pmatrix}1 \\0 \\0\end{pmatrix} = \begin{pmatrix}a &b &c \\d &e &f \\0 &0 &1\end{pmatrix} \begin{pmatrix}1 \\0 \\0\end{pmatrix} =\begin{pmatrix}a \\d \\0\end{pmatrix} \\\\M\begin{pmatrix}0 \\1 \\0\end{pmatrix} = \begin{pmatrix}a &b &c \\d &e &f \\0 &0 &1\end{pmatrix} \begin{pmatrix}0 \\1 \\0\end{pmatrix} =\begin{pmatrix}b \\e \\0\end{pmatrix} \end{align*}
であるが、この結果は $M$ の第1列目、第2列目の内容に過ぎない。したがって、図27における長方形の横方向、縦方向(の単位ベクトル)を求めるには、図27の長方形に実行されている変換行列の第1列目及び第2列目を取得し、それらを正規化すればよいのである。
プログラムにおいて行列の指定の列を取得するためには次のように記述すればよい。
Vector3 col1 = M.GetColumn(0); // 第1列目 Vector3 col2 = M.GetColumn(1); // 第2列目 Vector3 col3 = M.GetColumn(2); // 第3列目
このコードにおける M は THMatrix3x3型であり、ここでは何らかの変換行列を表しているものとする。THMatrix3x3構造体には GetColumn(int col) というメソッドが用意されており、これは名前が示すように行列の列を取得するためのメソッドである ($3\times3$行列の列を取得するので、返される値はVector3型である)。
メソッドの引数には列番号を指定するが、注意すべきは引数の数字が ’$0$ 始め’ である点である。例えば、行列の第1列目を取得する場合は GetColumn(0)、第2列目を取得する場合は GetColumn(1) としなければならない。
以下、簡単に本節で扱った内容を実装する。
# Code1
以下のプログラムを実行すると下図に示される青い円盤と緑の長方形が表示される。円盤の半径は $1$ であり、長方形の大きさは横の長さが $6$、縦の長さが $2$ である。
ここでも以下のキー操作によって円盤及び長方形を動かすことができる。
H : (円盤を)左へ移動
J : 下へ移動
K : 上へ移動
L : 右へ移動
R : 長方形を反時計周りに回転 (Shiftキーと同時押しで逆回転)
なお、プログラムにおいては円盤は Blue、長方形は Green という変数で使われている。
[Code1] (実行結果 図31)
if (!i_INITIALIZED)
{
i_degGreen = 0;
i_rectW = 6.0f;
i_rectH = 2.0f;
i_diskRad = 1.0f;
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.R)) // 長方形の回転
{
i_degGreen = (THUtil.IsShiftDown()) ? i_degGreen - 1 : i_degGreen + 1;
THMatrix3x3 M = TH2DMath.GetTranslation3x3(0, 5) * TH2DMath.GetRotation3x3(i_degGreen);
Green.SetMatrix(M);
}
Vector2 posB = Blue.GetPosition();
float speed = 0.05f;
if (Input.GetKey(KeyCode.H))
{
posB.x -= speed;
}
else if (Input.GetKey(KeyCode.L))
{
posB.x += speed;
}
if (Input.GetKey(KeyCode.J))
{
posB.y -= speed;
}
else if (Input.GetKey(KeyCode.K))
{
posB.y += speed;
}
Blue.SetPosition(posB);
Vector2 posG = Green.GetPosition();
if(i_degGreen % 90 == 0) // Disk vs AABB
{
bool bColl;
if(i_degGreen % 180 == 0)
{
bColl = CollisionTest_Disk_AABB(posB, posG, i_diskRad, i_rectW, i_rectH);
}
else
{
bColl = CollisionTest_Disk_AABB(posB, posG, i_diskRad, i_rectH, i_rectW);
}
Hit(bColl);
}
else // Disk vs OBB
{
THMatrix3x3 M = Green.GetMatrix();
Vector2 ui = M.GetColumn(0).normalized; // 横方向の単位ベクトル
Vector2 uj = M.GetColumn(1).normalized; // 縦方向の単位ベクトル
bool bColl = CollisionTest_Disk_OBB(posB, posG, ui, uj, i_diskRad, i_rectW, i_rectH);
Hit(bColl);
}
Rキーを押すとGreenが回転するが、12行目のifブロックはその処理が記述されている (毎フレーム$1$°ずつの回転)。
19行目から40行目はキー操作によるBlueの移動処理である。Blueの現在位置を取得し(19行目)、キーを押した方向に $0.05$ だけ移動させる。
44行目以降は衝突判定の処理である。ここでは、Greenが軸平行な場合とそうでない場合とで処理を分けている。
円盤と軸平行な長方形の衝突判定用メソッド CollisionTest_Disk_AABB(..) の5つの引数は上でも述べた通り、順番に 円盤の中心座標(posB)、長方形の中心座標(posG)、円盤の半径(i_diskRad)、長方形の横の長さ、縦の長さである。
Greenが軸平行でない場合は回転角度i_degGreenは$90$°の倍数ではないので、その際には58行目のelseブロックに入ることになる。つまり、この elseブロックでは傾きのある長方形と円盤との衝突判定の処理を行う。
60行目から62行目において、その時点での長方形の横方向の単位ベクトル、縦方向の単位ベクトルを求めているが、これは上で解説したようにその時点での長方形に実行されている変換行列の第1列目、第2列目から取得できる。
63行目では傾きのある長方形と円盤との衝突判定用のメソッド CollisionTest_Disk_OBB(..) が実行されるが、このメソッドの内容及びここで使われる引数については上で解説した通りである。
また、このメソッドで使われている Hit(..) は前節と同じく、2つのオブジェクトが衝突してる場合(引数にtrueがセットされる場合)に両者を赤く表示するだけの補助的なメソッドである。
# Code2
今回のプログラムはキー操作によって円盤を動かすことはCode1と同じであるが、長方形はプログラム実行中に適当な運動を繰り返すようになっている。キー操作もCode1とほとんど同じである。
H : (円盤を)左へ移動
J : 下へ移動
K : 上へ移動
L : 右へ移動
S : 長方形の運動の停止/再開
このプログラムにおいても円盤は Blue、長方形は Green として使われている (両者の大きさなども前回と同じである)。
[Code2] (実行結果 図33)
if (!i_INITIALIZED)
{
i_rectW = 6.0f;
i_rectH = 2.0f;
i_diskRad = 1.0f;
i_MOVE = true;
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S))
{
i_MOVE = !i_MOVE;
}
if (i_MOVE)
{
GreenMotion(1); // Greenの運動 (0 単振動 ; 1 公転)
}
Vector2 posB = Blue.GetPosition();
float speed = 0.10f;
if (Input.GetKey(KeyCode.H))
{
posB.x -= speed;
}
else if (Input.GetKey(KeyCode.L))
{
posB.x += speed;
}
if (Input.GetKey(KeyCode.J))
{
posB.y -= speed;
}
else if (Input.GetKey(KeyCode.K))
{
posB.y += speed;
}
Blue.SetPosition(posB);
Vector2 posG = Green.GetPosition();
THMatrix3x3 M = Green.GetMatrix();
Vector2 ui = M.GetColumn(0).normalized;
Vector2 uj = M.GetColumn(1).normalized;
bool bColl = CollisionTest_Disk_OBB(posB, posG, ui, uj, i_diskRad, i_rectW, i_rectH);
Hit(bColl);
Sキーを押すたびに12行目のifブロックで i_MOVE の値が切り替わるが、これによって19行目の GreenMotion(..) が実行されるか、されないかが決まる (つまり、Greenの運動が停止したり再開したりする)。GreenMotion(..)はGreenの運動が記述されているメソッドであり、引数が $0$ のときは単振動、$1$ のときは原点周りの公転運動である (GreenMotion(..)の内容については特に重要ではないので解説は省略する)。
22行目から43行目はキー操作によってBlueを動かす部分の記述であり、この部分はCode1と同じである。
それ以降は、円盤と傾きのある長方形との衝突判定用の処理である。しかし、この部分についてもCode1の終わりで見たものとほとんど同じであるから解説は省略する。
© 2020-2024 Redpoll's 60 (All rights reserved)