Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-25
第2章 2D空間におけるオブジェクトの運動
$§$2-25 円と直線による補間曲線 1
一般に、補間曲線とはいくつかの指定された点を通る曲線のことである。例えば 5つの点 $P_1$~$P_5$ が与えられたとき(図1)、この5つの点を通過する補間曲線は図2のようになる。
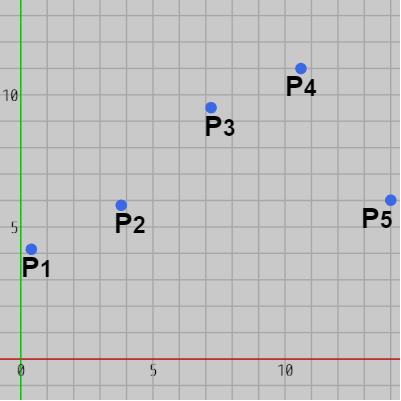
図1 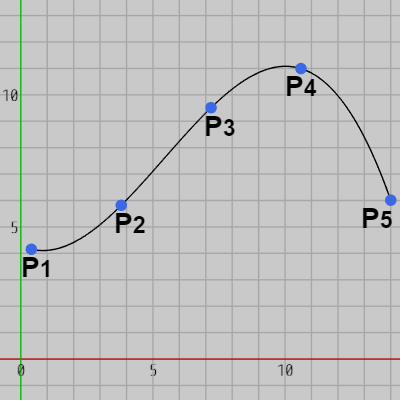
図2
補間曲線は指定された複数個の点から作られるが、必ずしもそれは一意的ではない。上図2の補間曲線は $P_1$~$P_5$ を通る補間曲線であるが、これは $P_1$~$P_5$ を通る数多くの補間曲線のうちの1つに過ぎない (実際にはそのような補間曲線は無数に存在する)。
また 補間曲線には通過する点だけでなく、通過する点における接線を指定する場合もある。例えば以下の図3では4つの点 $P_1$~$P_4$ の他にその点における接線の向き $\boldsymbol{\mathsf{v_1}}$~$\boldsymbol{\mathsf{v_4}}$ が与えられている。図4はこれらの点 及び接線を補間する補間曲線の1つである。
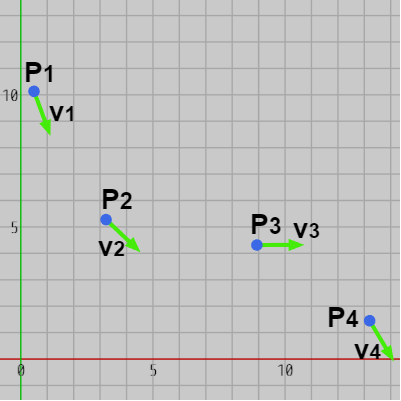
図3 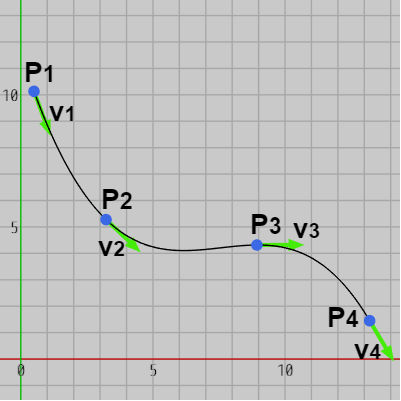
図4
本節で扱う補間曲線は指定された点とそれらの点における接線を補間するタイプのものであり、点と接線を補間する補間曲線としてはおそらく最も簡単に実装できるものである (簡単に実装できる反面、一般的な3次以上の補間曲線に比べると品質はもちろん落ちる)。
まずはその具体的な構成から見ていくことにしよう。
例えば下図の2点 $P$、$Q$ の補間を例に取ろう。図中の $\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ は $P$、$Q$ における接線の方向を表す単位ベクトルである。
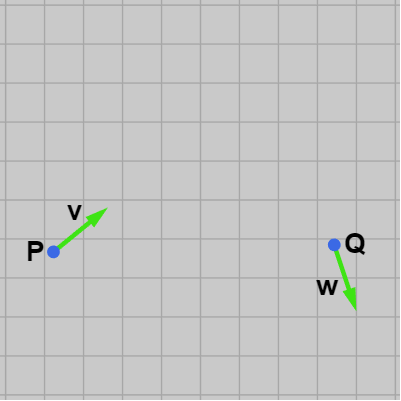
図5 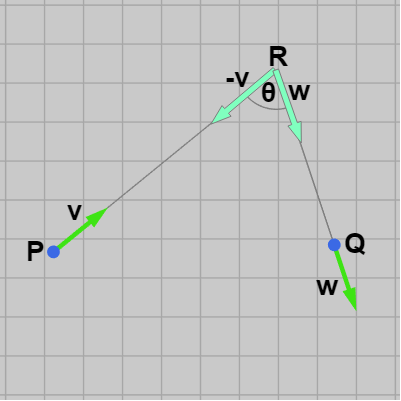
図6 交点 R の角度は θ
$P$ から $\boldsymbol{\mathsf{v}}$ の方向へ引いた半直線と $Q$ から $-\boldsymbol{\mathsf{w}}$ の方向へ引いた半直線との交点を $R$ とし、$\angle{PRQ} = \theta$ とする (図6)。これはベクトル $-\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{w}}$ のなす角が $\theta$ であることを意味するから $-\boldsymbol{\mathsf{v}}\cdot \boldsymbol{\mathsf{w}} = cos\theta$ である。
2つの辺 $PR$、$QR$ は長さに関して $PR > QR$ であるが、このとき $QR$ の長さを $a$ とし、辺 $PR$ 上に点 $S$ を $SR = a$ となるように置く ($S = R - a\boldsymbol{\mathsf{v}}$)。すなわち、$SR = QR = a$ である (図7)。
具体的には、$P$ から $Q$ への補間曲線は図7に示されるように線分 $PS$ と弧 $\overset{\Large\frown}{SQ}$ によって構成される。したがって、補間曲線の作成は弧 $\overset{\Large\frown}{SQ}$ を円周の一部として含む円を見つけることに帰着するわけである。
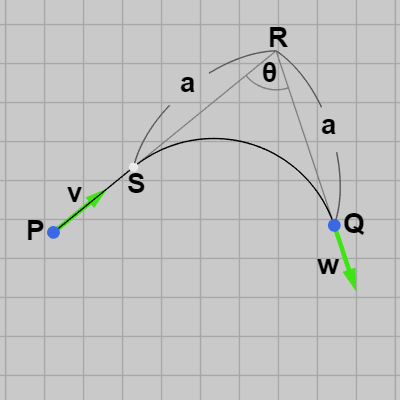
図7 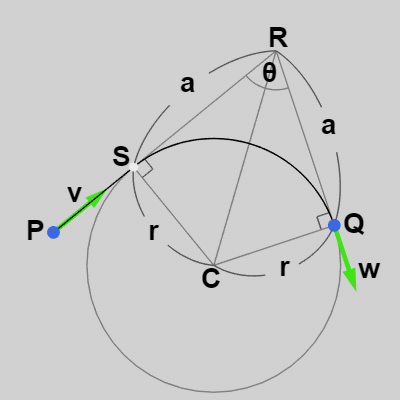
図8
そのために $S$、$Q$ を接点、$SR$、$QR$ を接線とする円を考える。この円の中心を $C$ とし、半径を $r$ とする (図8)。
ここで問題となるのが円の中心 $C$ と半径 $r$ の算出であるが、それは次のように求められる。
$S$、$Q$ はこの円の接点であり、$SR$、$QR$ は接線であるから図8に示されるように $\angle{CSR} = \angle{CQR} = 90^\circ$ である。さらに 2辺 $CS$、$CQ$ はこの円の半径でもあるので $CS = CQ = r$ である。
すなわち、$\triangle{SRC}$ と $\triangle{QRC}$ は三辺の長さが等しいので合同であり、したがって $\angle{SRC} = \angle{QRC} = \theta/2$ であることがわかる。
また $\triangle{SRC}$、$\triangle{QRC}$ は直角三角形であるから\[ \frac{r}{a} = \tan{\frac{\theta}{2}} \]三角関数の公式により\[ \frac{r}{a} = \tan{\frac{\theta}{2}} = \sqrt{\frac{1-\cos\theta}{1+\cos\theta}} \]であるが、この式の右辺は
(1) $P$ から $\boldsymbol{\mathsf{v}}$ の方向に引いた半直線と $Q$ から $-\boldsymbol{\mathsf{w}}$ の方向に引いた半直線との交点を $R$ とするとき、上の解説においては $PR > QR$ として進めていた。
これがもし $PR < QR$ である場合には $PR$ の長さを $a$ とし、辺 $QR$ 上に点 $S$ を $SR = a$ となるように置く ($S = R + a\boldsymbol{\mathsf{w}}$)。すなわち、$SR = PR = a$ である (図9)。あとは上記と同様の手続きで進めればよいが、この場合には弧 $\overset{\Large\frown}{PS}$ と線分 $SQ$ による補間になる。
例えば下図9において $C$ を求めるのであれば\[ C = S + r\boldsymbol{\mathsf{w}^\perp}\]である ($\boldsymbol{\mathsf{w}^\perp}$ は先程と同じく $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ 回転させた(単位)ベクトル)。
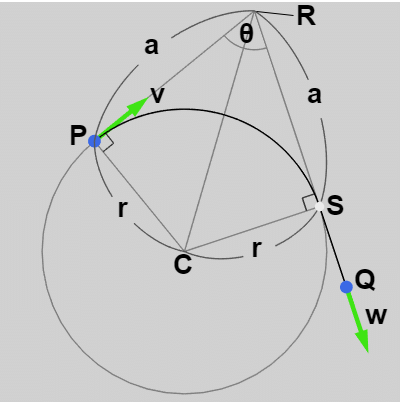
図9 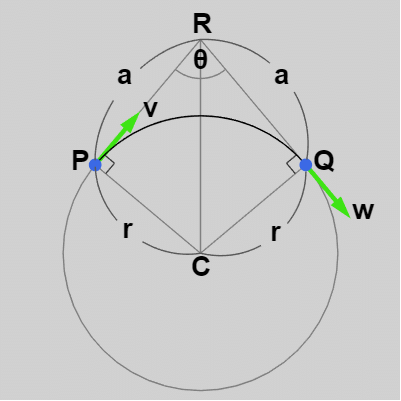
図10
(2) あるいは2辺 $PR$ と $QR$ が同じ長さ、すなわち $PR = QR$ である場合には $P$、$Q$ を補間する際、弧 $\overset{\Large\frown}{PQ}$ だけを作ればよい (図10)。$PR$、$QR$ の間に大小関係がある場合には上の解説のように $PR$ あるいは $QR$ 上に点 $S$ を置いて線分 $PS$ (あるいは $QS$) が必要になったが、$PR = QR$ の場合にはそのような線分は必要ない。
(3) また上の例では円の中心 $C$ を計算するにあたって、点 $Q$ の接線ベクトル $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ 回転させたベクトル $\boldsymbol{\mathsf{w}^\perp}$ を使ったが、状況によっては $\boldsymbol{\mathsf{w}^\perp}$ を求める際は $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ でなく $90^\circ$ 回転させる必要がある。
例えば 下左図は $\boldsymbol{\mathsf{w}^\perp}$ を求める際に $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ 回転させるが、右図の場合は $90^\circ$ である。
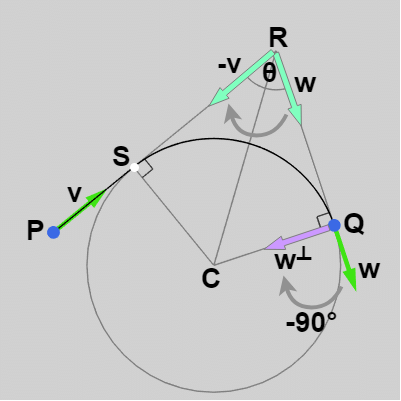
図11 w を -v に重ねる回転が時計周り 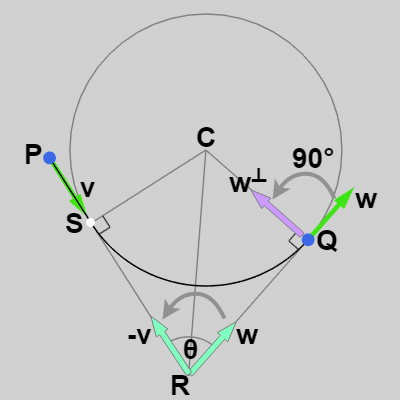
図12 w を -v に重ねる回転が反時計周り
どのような状況で回転角度が $90^\circ$ になり、どのような状況で $-90^\circ$ になるかについては、ベクトル $\boldsymbol{\mathsf{w}}$ を回転させてベクトル $-\boldsymbol{\mathsf{v}}$ に重ねる際の回転の方向(時計周りか反時計周りか)で決まる。
今までと同様に、$P$ から $\boldsymbol{\mathsf{v}}$ の方向に引いた半直線と $Q$ から $-\boldsymbol{\mathsf{w}}$ の方向に引いた半直線との交点を $R$ とし、$\angle{PRQ} = \theta$ とするとき、上図に示されるように角度 $\theta$ は $-\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{w}}$ のなす角でもある。
そして ベクトル $\boldsymbol{\mathsf{w}}$ を角度 $\theta$ だけ回転させてベクトル $-\boldsymbol{\mathsf{v}}$ に重ねるには左図の場合は時計周り、右図の場合は反時計周りに回転させる必要がある (回転角度は必ず $\theta$ でなければならない。$360^\circ - \theta$ だけ回転させても $\boldsymbol{\mathsf{w}}$ を $-\boldsymbol{\mathsf{v}}$ に重ねることはできるがそのようなケースは考えない)。
このとき、$\boldsymbol{\mathsf{w}}$ を $-\boldsymbol{\mathsf{v}}$ に重ねる回転が時計周りであれば、$\boldsymbol{\mathsf{w}^\perp}$ を求める際の回転角度は $-90^\circ$ である (図11)。反時計周りであれば、$\boldsymbol{\mathsf{w}^\perp}$ を求める際の回転角度は $90^\circ$ である (図12)。
問題なのは時計周りか反時計周りかをどうやって調べるかという点であるが、それは次の計算を行ってその正負の符号を調べればよい (以下では $\boldsymbol{\mathsf{v}} = (v_x, v_y)$、$\boldsymbol{\mathsf{w}} = (w_x, w_y)$ とする)。
\[-w_x v_y + w_y v_x\]この計算結果がプラスの値であれば反時計周り、マイナスであれば時計回りである。
つまり、$\boldsymbol{\mathsf{w}^\perp}$ を求める際には
$-w_x v_y + w_y v_x > 0$ であれば $\boldsymbol{\mathsf{w}}$ を $90^\circ$ 回転させる
$-w_x v_y + w_y v_x < 0$ であれば $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ 回転させる
ということである ($-w_x v_y + w_y v_x = 0$ のときは $\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{w}}$ が平行であることを意味し、その際にはまた別の処理を行う)。
以下の InterpolatePQ(..) は上で述べてきたことを実装したものであり、引数に指定された2つの点 及びそれらの点における接線ベクトルを補間する曲線を描画するものである。
[InterpolatePQ(..)]
引数 P、Q が補間される2つの点であり、v、w はそれらの点における接線ベクトルである。ただし、このメソッドでは接線ベクトル v、w は単位ベクトルであることを前提としている。
最後の引数 R3 は P から v の方向へ引いた半直線と Q から w の方向へ引いた半直線との交点を表すが、R3 はVector2型ではなくVector3型である。R3 の xy座標はその交点の座標がセットされているが、z座標の値は $+1$ か $-1$ である。この R3 の z座標の役割については後述する。
実際の補間は9行目以降に記述されている。
上で述べたように交点 $R$ における角度 $\theta\ (= \angle{PRQ})$ は接線ベクトル $-\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{w}}$ のなす角であるから $-\boldsymbol{\mathsf{v}}\cdot \boldsymbol{\mathsf{w}} = cos\theta$ である (11行目)。
また $\boldsymbol{\mathsf{w}}$ を角度 $\theta$ だけ回転させて $-\boldsymbol{\mathsf{v}}$ に重ねるには時計周りの回転か反時計周りの回転かを調べる必要があったが、それは $-w_x v_y + w_y v_x$ の符号からわかるのであった。15行目がその計算であり反時計周りであればローカル変数 ccw には true が、時計周りであれば false がセットされる。
そして、$\boldsymbol{\mathsf{w}^\perp}$ を求める際には時計周りであれば $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ 回転させ、反時計周りであれば $\boldsymbol{\mathsf{w}}$ を $90^\circ$ 回転させるのであった。16行目はその計算でありローカル変数 wr は $\boldsymbol{\mathsf{w}^\perp}$ のことである (ベクトル $(a, b)$ を $90^\circ$ 回転させると $(-b, a)$ になり、$-90^\circ$ 回転させると $(b, -a)$ になる)。
18行目以降は $PR > QR$ であるか $PR < QR$ であるかの場合分けである。ここで使われている各変数は上の解説と同じものであり、各変数の求め方も上で述べたものと同じである。例えば $PR > QR$ であれば19行目のifブロックに入るが、a は $QR$ (あるいは $SR$)の長さであり、r は円の半径、C は円の中心、S は $PR$ 上で $SR = QR$ となるように置かれた点である。
$PR > QR$ の場合に作られる補間曲線は線分 $PS$ と弧 $\overset{\Large\frown}{SQ}$ であるが、27行目の DrawLine(..) は引数に指定された2点を結ぶ線分を描画する補助メソッドであり、28行目の DrawArc(..) は最初の2つの引数に指定された2点を結ぶ弧を描画する補助メソッドである。ただし 弧を描画する場合はこのメソッドの第3引数に(その弧を含む)円の中心 $C$ をセットする。
この19行目のifブロックでは $PR=QR$ の場合にも対応しその場合にも DrawLine(..)、DrawArc(..) が実行されるが、実際に描画されるのは$P$ と $Q$ を結ぶ弧$\overset{\Large\frown}{PQ}$ のみである (このときの線分 $PS$ はただの点)。
30行目のelseブロックは $PR<QR$ の場合である。また42行目の DrawAuxLine(..) は補助線(線分 $PR$、$QR$)を描画するためのものである。
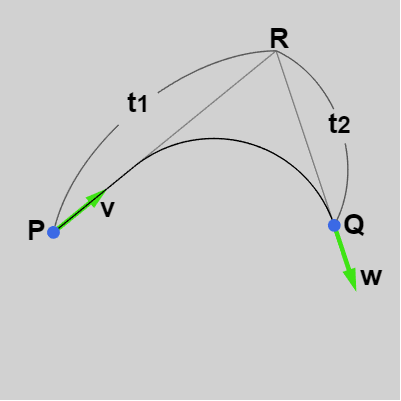
図13 t1 < 0、t2 > 0 (ここでは t1、t2 の値がマイナス値を取り得るものとしている) 最後にこのメソッドで補間曲線が作られる場合とそうでない場合について述べておく。
今までと同じように2点 $P$、$Q$ を与えられた点とし、それらの点における(単位)接線ベクトルを $\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ とする。さらに $P$ から $\boldsymbol{\mathsf{v}}$ の方向へ引いた半直線と $Q$ から $-\boldsymbol{\mathsf{w}}$ の方向へ引いた半直線との交点を $R$ とする。
ここで $PR$ の長さを $t_1$、$QR$ の長さを $t_2$ とし、$t_1$、$t_2$ は長さではあるがマイナスの値もとり得るものとする。具体的には交点 $R$ が $P$ から $\boldsymbol{\mathsf{v}}$ の方向にあるとき $t_1$ をプラスの値、$-\boldsymbol{\mathsf{v}}$ の方向にあるとき $t_1$ をマイナスの値とする。同様に交点 $R$ が $Q$ から $\boldsymbol{\mathsf{w}}$ の方向にあるとき $t_2$ をプラスの値、$-\boldsymbol{\mathsf{w}}$ の方向にあるとき $t_2$ をマイナスの値とする。
右図の場合であれば交点 $R$ は $P$ から $\boldsymbol{\mathsf{v}}$ の方向にあり、$Q$ から $-\boldsymbol{\mathsf{w}}$ の方向にあるので、$t_1 > 0$、$t_2 < 0$ である。
したがって\[R = P + t_1 \boldsymbol{\mathsf{v}} = Q + t_2 \boldsymbol{\mathsf{w}}\]となる。
このように $t_1$、$t_2$ を $P$ 及び $Q$ から交点 $R$ までの長さ(マイナス値にもなる長さ)とするとき、上記の補間メソッドにおいては\[ t_1 > 0\quad\&\&\quad t_2 < 0\]であるときのみ補間曲線が描画される。この条件が成り立たない場合は単に2点 $P$、$Q$ が線分で結ばれるだけである。メソッド冒頭のifブロックはそのためのものである。R3.z は $+1$ か $-1$ のいずれかであるが、上の条件が成り立つときは $+1$、成り立たないときは $-1$ がセットされている。
例えば下左図の場合は $t_1 > 0$、$t_2 > 0$、右図の場合は $t_1 < 0$、$t_2 > 0$ であるが、このような場合はいずれも図に示されるように $P$、$Q$ が線分で結ばれるだけである。

図14 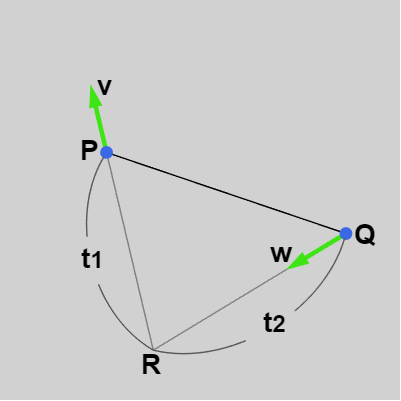
図15
ただし、上の条件が成り立たないからといって $P$、$Q$、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ を補間する線分と弧が存在しないわけではない。実際には $t_1$、$t_2$ の符号がどのような組み合わせであっても線分と弧によって $PQ$ 間を補間することができる。この点については本節の最後に触れる。
では上で述べてきたことをプログラムで実装する。
なお本節のプログラムは 画角(FOV) が $60^\circ$ 、アスペクト比(Aspect Ratio) が 16:9 に設定されていることを前提としている (この設定でない場合はマウス操作が適切に処理されなくなる)。
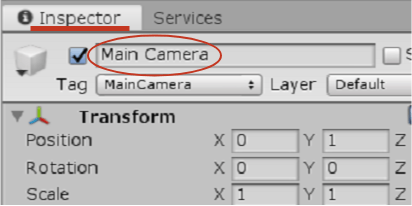
図16 InspectorにMain Cameraの情報を表示する FOVの値が $60^\circ$ であるかを調べるためには Hierarchy Window 内の「Main Camera」をクリックし、Inspector に Main Camera の情報が表示されるようにする (図16)。Inspectorに表示されるいくつかの設定項目の中に「Field of View」という項目があるが、これがFOVのことでありこの値を $60$ に設定する (図17)。
アスペクト比が 16:9 であるかを調べるにはUnityの実行画面上部にある「Gameタブ」をクリックし現在の画面を Game View にする。そのときGameタブの下側に表示される数字の比がアスペクト比であり、この値を 16:9 に設定する (図18)。
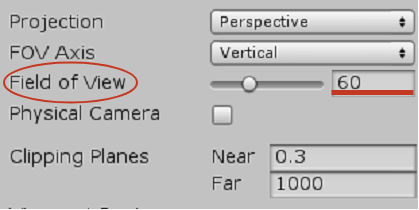
図17 FOV(Field of View)の値を60に設定 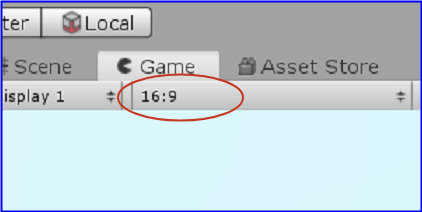
図18 アスペクト比を 16:9 に設定
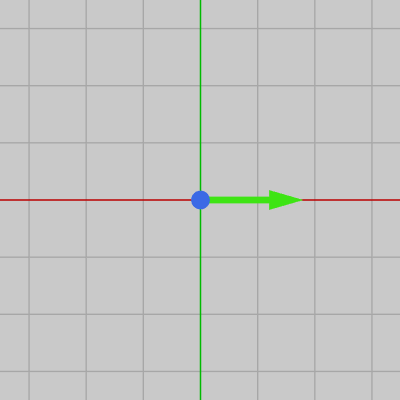
図19 制御点 
図20 制御点の接線を30°にしたとき
最初のプログラムは制御点が2つの場合である。
[Code1] (実行結果 図21)
初期化ブロック内の AddControl(x, y, deg) は制御点を配置するための補助メソッドであり、第1引数、第2引数には制御点の x座標、y座標、第3引数には接線の向きを指定する。接線の向きは初期状態の向きである x軸プラス方向からの角度を指定する。例えば この第3引数を 30 とすれば接線は x軸プラス方向から $30^\circ$ 回転した方向を向く (図20)。
制御点及び接線はプログラム実行中にマウスドラッグによって位置や向きを変更することができる。制御点や接線に何らかの変化があれば9行目の AnyControlChanged() がtrueを返し、このifブロックに処理が進むが、このifブロックにおいて補間曲線の描画処理が行われる。
GetControlPosition(..)、GetControlTangent(..) は制御点の位置及び接線の方向を取得するための補助メソッドであり、その引数には制御点のインデックスを指定する。今回は制御点を2つ使っているのでそれらのインデックスは $0$ あるいは $1$ であり、メソッドの引数として 0、1 をセットすれば各制御点の位置及び接線の方向を取得することができる (接線の方向は単位ベクトルとして返される)。
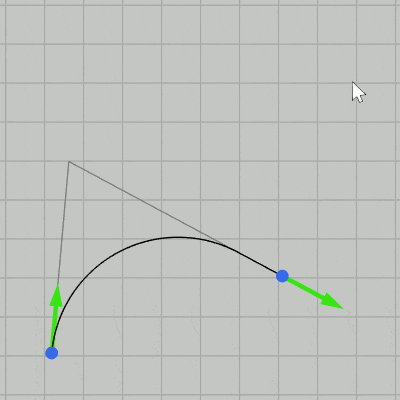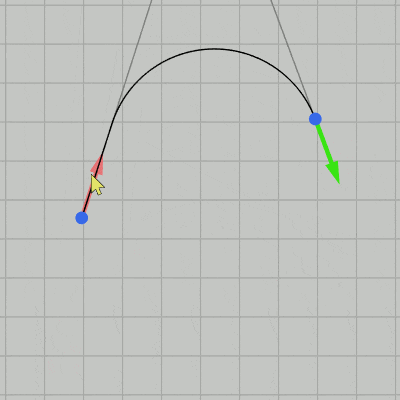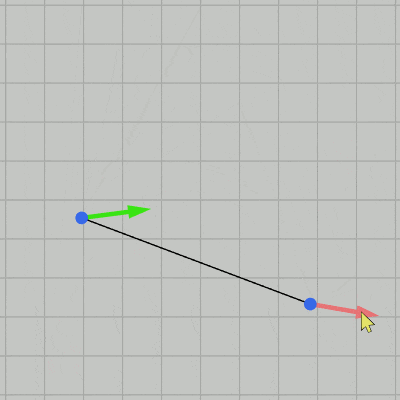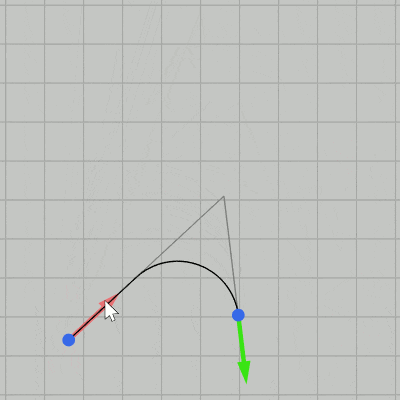
図21 Code1 実行結果 CalcIntersectionOf2Lines(P, v, Q, w) (16行目)は前節で実装したメソッドで、 P を通り向きが v の直線と Q を通り向きが w の直線の交点を計算する (戻り値はVector3型)。戻り値の x座標、y座標には交点の位置がセットされるが、z座標には $1$ か $-1$ がセットされる (z座標にセットされる $1$ あるいは $-1$ は、上で述べた補間の基準を満たすかどうかのフラグである)。
17行目の InterpolatePQ(..) は上で解説したものであり、実際の補間曲線の描画に使われる。
実行結果(図21)に示されるように補助線が表示されているときは2点間が曲線によって補間され、そうでなければ2点間が線分によって結ばれるだけである。
しかしプログラムの内容はほとんど変わらない。
[Code2] (実行結果 図22)
今回は制御点が6個になっているので初期化ブロックにおいては AddControl(..) が6回実行されている。
補間曲線を描画する場合にもfor文(16行目)によって、制御点 0 から制御点 1 までの補間曲線、制御点 1 から制御点 2 までの補間曲線というように複数の区間を1つ1つ描画することで1つの補間曲線が構成される。

図22 Code2 実行結果
しかし実際には $t_1$、$t_2$ の値がどのようなものであっても線分と弧による補間曲線を描くことは可能である。以下のプログラムでその点について見てみよう。
[Code3] (実行結果 図23)
16、17行目以外はCode1と同じである。今回は交点 $R$ の計算に CalcIntersectionOf2Lines_ver2(..) というメソッドが使われており、補間曲線の描画には InterpolatePQ_ver2(..) というメソッドが使われている。これらのメソッドは $t_1$、$t_2$ がどのような値の場合にも、補間曲線が描画されるようにするためのものである。
CalcIntersectionOf2Lines_ver2(..) の戻り値はVector4型であり、x座標、y座標には交点 $R$ の位置がセットされている。この点はCode1と同じであるが、今回は z座標、w座標に $t_1$、$t_2$ の値がセットされる。
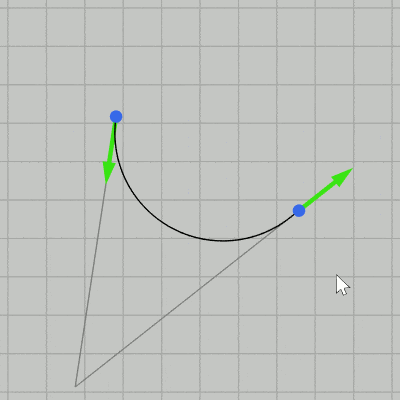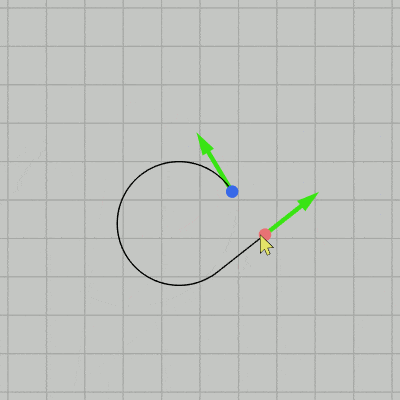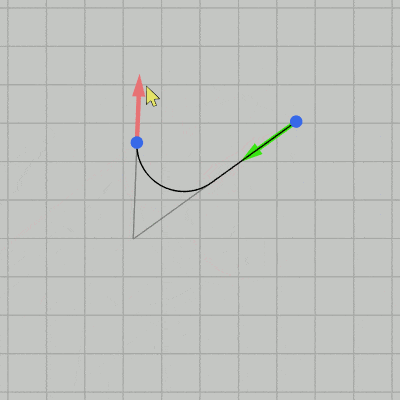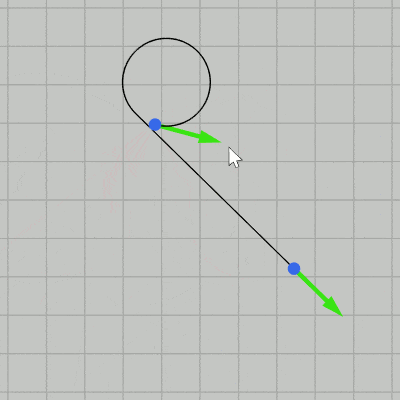
図23 Code3 実行結果 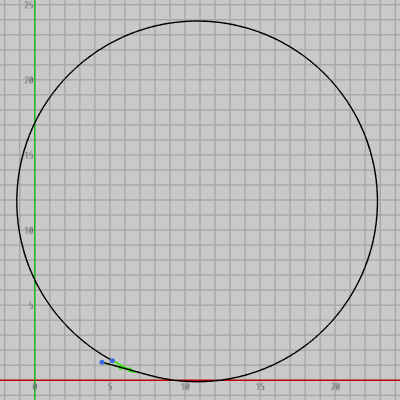
図24
実行結果(図23)に示されるように、制御点の位置や接線をどのように動かしても今回は2つの制御点の間に線分と弧による補間曲線が描画される (薄い灰色の補助線が表示されているときが $t_1 > 0$、$t_2 < 0$ である)。
しかし今回の補間では補間曲線としてはいささか乱暴な補間が行われてしまうこと多く、特に制御点の位置や接線を動かしていく過程で曲線が発散するようなことが起こるが、これは実際には補間曲線を構成する弧の半径が大きくなり過ぎてしまうためにそのように見えているのである。図24はそのような状況を離れて見た場合であり、こういった場合には半径の大きい円に近い補間曲線が描かれる。
以下は今回の補間で使われるメソッド InterpolatePQ_ver2(..) である。
[InterpolatePQ_ver2(..)]
12行目のifブロックは $t_1 > 0$、$t_2 < 0$ の場合であり、この部分は上記の InterpolatePQ(..) と内容は同じである。43行目のifブロックは $t_1 < 0$、$t_2 > 0$ の場合、72行目のifブロックは $t_1 > 0$、$t_2 > 0$ の場合、最後のelseブロック(84行目)が $t_1 < 0$、$t_2 < 0$ の場合である。
詳しい解説については省略するが基本的に行っている処理は同じである (ただし上の解説では円の中心 $C$ を求める際に $\boldsymbol{\mathsf{w}}$ を回転させていたが、このメソッドでは $t_1$、$t_2$ の値によって $\boldsymbol{\mathsf{v}}$ を回転させる場合がある。またその際の回転角度が $90^\circ$ あるいは $-90^\circ$ かを調べる計算についても $t_1$、$t_2$ の値によって若干の違いがある)。


補間曲線は指定された複数個の点から作られるが、必ずしもそれは一意的ではない。上図2の補間曲線は $P_1$~$P_5$ を通る補間曲線であるが、これは $P_1$~$P_5$ を通る数多くの補間曲線のうちの1つに過ぎない (実際にはそのような補間曲線は無数に存在する)。
また 補間曲線には通過する点だけでなく、通過する点における接線を指定する場合もある。例えば以下の図3では4つの点 $P_1$~$P_4$ の他にその点における接線の向き $\boldsymbol{\mathsf{v_1}}$~$\boldsymbol{\mathsf{v_4}}$ が与えられている。図4はこれらの点 及び接線を補間する補間曲線の1つである。


本節で扱う補間曲線は指定された点とそれらの点における接線を補間するタイプのものであり、点と接線を補間する補間曲線としてはおそらく最も簡単に実装できるものである (簡単に実装できる反面、一般的な3次以上の補間曲線に比べると品質はもちろん落ちる)。
まずはその具体的な構成から見ていくことにしよう。
A) 円と直線による補間曲線
今回実装する補間曲線は円と直線による補間曲線である。しかし 実際には「円と直線」ではなく正確にいえば「弧と線分」であり、ここで作成する補間曲線は弧と線分をつなぎ合わせる形で構成される。例えば下図の2点 $P$、$Q$ の補間を例に取ろう。図中の $\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ は $P$、$Q$ における接線の方向を表す単位ベクトルである。


$P$ から $\boldsymbol{\mathsf{v}}$ の方向へ引いた半直線と $Q$ から $-\boldsymbol{\mathsf{w}}$ の方向へ引いた半直線との交点を $R$ とし、$\angle{PRQ} = \theta$ とする (図6)。これはベクトル $-\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{w}}$ のなす角が $\theta$ であることを意味するから $-\boldsymbol{\mathsf{v}}\cdot \boldsymbol{\mathsf{w}} = cos\theta$ である。
2つの辺 $PR$、$QR$ は長さに関して $PR > QR$ であるが、このとき $QR$ の長さを $a$ とし、辺 $PR$ 上に点 $S$ を $SR = a$ となるように置く ($S = R - a\boldsymbol{\mathsf{v}}$)。すなわち、$SR = QR = a$ である (図7)。
具体的には、$P$ から $Q$ への補間曲線は図7に示されるように線分 $PS$ と弧 $\overset{\Large\frown}{SQ}$ によって構成される。したがって、補間曲線の作成は弧 $\overset{\Large\frown}{SQ}$ を円周の一部として含む円を見つけることに帰着するわけである。


そのために $S$、$Q$ を接点、$SR$、$QR$ を接線とする円を考える。この円の中心を $C$ とし、半径を $r$ とする (図8)。
ここで問題となるのが円の中心 $C$ と半径 $r$ の算出であるが、それは次のように求められる。
$S$、$Q$ はこの円の接点であり、$SR$、$QR$ は接線であるから図8に示されるように $\angle{CSR} = \angle{CQR} = 90^\circ$ である。さらに 2辺 $CS$、$CQ$ はこの円の半径でもあるので $CS = CQ = r$ である。
すなわち、$\triangle{SRC}$ と $\triangle{QRC}$ は三辺の長さが等しいので合同であり、したがって $\angle{SRC} = \angle{QRC} = \theta/2$ であることがわかる。
また $\triangle{SRC}$、$\triangle{QRC}$ は直角三角形であるから\[ \frac{r}{a} = \tan{\frac{\theta}{2}} \]三角関数の公式により\[ \frac{r}{a} = \tan{\frac{\theta}{2}} = \sqrt{\frac{1-\cos\theta}{1+\cos\theta}} \]であるが、この式の右辺は
\[\sqrt{\frac{1-\cos\theta}{1+\cos\theta}} = \frac{\sqrt{1-\cos\theta}}{\sqrt{1+\cos\theta}} \frac{\sqrt{1-\cos\theta}}{\sqrt{1-\cos\theta}} = \frac{1-\cos\theta}{\sqrt{1-\cos^2\theta}} = \frac{1-\cos\theta}{\sin\theta}\]
であるから、結局 円の半径 $r$ は次のように算出される。\[ r = \frac{a(1-\cos\theta)}{\sin\theta} \]半径 $r$ がわかれば円の中心 $C$ の算出は容易である。$Q$ における接線ベクトル $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ 回転させた(単位)ベクトルを $\boldsymbol{\mathsf{w}^\perp}$ とすれば、円の中心 $C$ は\[ C = Q + r\boldsymbol{\mathsf{w}^\perp}\]として求められる。B) 実装
上記の補間曲線をプログラムで実装する際にはいくつかの場合について考える必要があるが、ここではその点について見ていく。(1) $P$ から $\boldsymbol{\mathsf{v}}$ の方向に引いた半直線と $Q$ から $-\boldsymbol{\mathsf{w}}$ の方向に引いた半直線との交点を $R$ とするとき、上の解説においては $PR > QR$ として進めていた。
これがもし $PR < QR$ である場合には $PR$ の長さを $a$ とし、辺 $QR$ 上に点 $S$ を $SR = a$ となるように置く ($S = R + a\boldsymbol{\mathsf{w}}$)。すなわち、$SR = PR = a$ である (図9)。あとは上記と同様の手続きで進めればよいが、この場合には弧 $\overset{\Large\frown}{PS}$ と線分 $SQ$ による補間になる。
例えば下図9において $C$ を求めるのであれば\[ C = S + r\boldsymbol{\mathsf{w}^\perp}\]である ($\boldsymbol{\mathsf{w}^\perp}$ は先程と同じく $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ 回転させた(単位)ベクトル)。


(2) あるいは2辺 $PR$ と $QR$ が同じ長さ、すなわち $PR = QR$ である場合には $P$、$Q$ を補間する際、弧 $\overset{\Large\frown}{PQ}$ だけを作ればよい (図10)。$PR$、$QR$ の間に大小関係がある場合には上の解説のように $PR$ あるいは $QR$ 上に点 $S$ を置いて線分 $PS$ (あるいは $QS$) が必要になったが、$PR = QR$ の場合にはそのような線分は必要ない。
(3) また上の例では円の中心 $C$ を計算するにあたって、点 $Q$ の接線ベクトル $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ 回転させたベクトル $\boldsymbol{\mathsf{w}^\perp}$ を使ったが、状況によっては $\boldsymbol{\mathsf{w}^\perp}$ を求める際は $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ でなく $90^\circ$ 回転させる必要がある。
例えば 下左図は $\boldsymbol{\mathsf{w}^\perp}$ を求める際に $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ 回転させるが、右図の場合は $90^\circ$ である。


どのような状況で回転角度が $90^\circ$ になり、どのような状況で $-90^\circ$ になるかについては、ベクトル $\boldsymbol{\mathsf{w}}$ を回転させてベクトル $-\boldsymbol{\mathsf{v}}$ に重ねる際の回転の方向(時計周りか反時計周りか)で決まる。
今までと同様に、$P$ から $\boldsymbol{\mathsf{v}}$ の方向に引いた半直線と $Q$ から $-\boldsymbol{\mathsf{w}}$ の方向に引いた半直線との交点を $R$ とし、$\angle{PRQ} = \theta$ とするとき、上図に示されるように角度 $\theta$ は $-\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{w}}$ のなす角でもある。
そして ベクトル $\boldsymbol{\mathsf{w}}$ を角度 $\theta$ だけ回転させてベクトル $-\boldsymbol{\mathsf{v}}$ に重ねるには左図の場合は時計周り、右図の場合は反時計周りに回転させる必要がある (回転角度は必ず $\theta$ でなければならない。$360^\circ - \theta$ だけ回転させても $\boldsymbol{\mathsf{w}}$ を $-\boldsymbol{\mathsf{v}}$ に重ねることはできるがそのようなケースは考えない)。
このとき、$\boldsymbol{\mathsf{w}}$ を $-\boldsymbol{\mathsf{v}}$ に重ねる回転が時計周りであれば、$\boldsymbol{\mathsf{w}^\perp}$ を求める際の回転角度は $-90^\circ$ である (図11)。反時計周りであれば、$\boldsymbol{\mathsf{w}^\perp}$ を求める際の回転角度は $90^\circ$ である (図12)。
問題なのは時計周りか反時計周りかをどうやって調べるかという点であるが、それは次の計算を行ってその正負の符号を調べればよい (以下では $\boldsymbol{\mathsf{v}} = (v_x, v_y)$、$\boldsymbol{\mathsf{w}} = (w_x, w_y)$ とする)。
\[-w_x v_y + w_y v_x\]この計算結果がプラスの値であれば反時計周り、マイナスであれば時計回りである。
つまり、$\boldsymbol{\mathsf{w}^\perp}$ を求める際には
$-w_x v_y + w_y v_x > 0$ であれば $\boldsymbol{\mathsf{w}}$ を $90^\circ$ 回転させる
$-w_x v_y + w_y v_x < 0$ であれば $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ 回転させる
ということである ($-w_x v_y + w_y v_x = 0$ のときは $\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{w}}$ が平行であることを意味し、その際にはまた別の処理を行う)。
以下の InterpolatePQ(..) は上で述べてきたことを実装したものであり、引数に指定された2つの点 及びそれらの点における接線ベクトルを補間する曲線を描画するものである。
[InterpolatePQ(..)]
void InterpolatePQ(Vector2 P, Vector2 v, Vector2 Q, Vector2 w, Vector3 R3)
{
if (R3.z < 0.0f)
{
DrawLine(P, Q);
return;
}
Vector2 R = R3;
float cosT = Vector2.Dot(-v, w);
float sinT = Mathf.Sqrt(1.0f - cosT * cosT);
float lenPR = (R - P).magnitude;
float lenQR = (R - Q).magnitude;
bool ccw = (-w.x * v.y + w.y * v.x > 0.0f) ? true : false;
Vector2 wr = ccw ? new Vector2(-w.y, w.x) : new Vector2(w.y, -w.x); // counter-clockwise ? rot90 : rot(-90)
Vector2 S, C;
if (lenPR >= lenQR) // PR = QR = a (P=S) の場合を含む(この場合の線分は'点')
{
float a = lenQR;
float r = a * (1 - cosT) / sinT;
S = R - a * v;
C = Q + r * wr;
DrawLine(P, S);
DrawArc(S, Q, C);
}
else
{
float a = lenPR;
float r = a * (1 - cosT) / sinT;
S = R + a * w;
C = S + r * wr;
DrawLine(S, Q);
DrawArc(P, S, C);
}
DrawAuxLine(P, Q, R);
}
引数 P、Q が補間される2つの点であり、v、w はそれらの点における接線ベクトルである。ただし、このメソッドでは接線ベクトル v、w は単位ベクトルであることを前提としている。
最後の引数 R3 は P から v の方向へ引いた半直線と Q から w の方向へ引いた半直線との交点を表すが、R3 はVector2型ではなくVector3型である。R3 の xy座標はその交点の座標がセットされているが、z座標の値は $+1$ か $-1$ である。この R3 の z座標の役割については後述する。
実際の補間は9行目以降に記述されている。
上で述べたように交点 $R$ における角度 $\theta\ (= \angle{PRQ})$ は接線ベクトル $-\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{w}}$ のなす角であるから $-\boldsymbol{\mathsf{v}}\cdot \boldsymbol{\mathsf{w}} = cos\theta$ である (11行目)。
また $\boldsymbol{\mathsf{w}}$ を角度 $\theta$ だけ回転させて $-\boldsymbol{\mathsf{v}}$ に重ねるには時計周りの回転か反時計周りの回転かを調べる必要があったが、それは $-w_x v_y + w_y v_x$ の符号からわかるのであった。15行目がその計算であり反時計周りであればローカル変数 ccw には true が、時計周りであれば false がセットされる。
そして、$\boldsymbol{\mathsf{w}^\perp}$ を求める際には時計周りであれば $\boldsymbol{\mathsf{w}}$ を $-90^\circ$ 回転させ、反時計周りであれば $\boldsymbol{\mathsf{w}}$ を $90^\circ$ 回転させるのであった。16行目はその計算でありローカル変数 wr は $\boldsymbol{\mathsf{w}^\perp}$ のことである (ベクトル $(a, b)$ を $90^\circ$ 回転させると $(-b, a)$ になり、$-90^\circ$ 回転させると $(b, -a)$ になる)。
18行目以降は $PR > QR$ であるか $PR < QR$ であるかの場合分けである。ここで使われている各変数は上の解説と同じものであり、各変数の求め方も上で述べたものと同じである。例えば $PR > QR$ であれば19行目のifブロックに入るが、a は $QR$ (あるいは $SR$)の長さであり、r は円の半径、C は円の中心、S は $PR$ 上で $SR = QR$ となるように置かれた点である。
$PR > QR$ の場合に作られる補間曲線は線分 $PS$ と弧 $\overset{\Large\frown}{SQ}$ であるが、27行目の DrawLine(..) は引数に指定された2点を結ぶ線分を描画する補助メソッドであり、28行目の DrawArc(..) は最初の2つの引数に指定された2点を結ぶ弧を描画する補助メソッドである。ただし 弧を描画する場合はこのメソッドの第3引数に(その弧を含む)円の中心 $C$ をセットする。
この19行目のifブロックでは $PR=QR$ の場合にも対応しその場合にも DrawLine(..)、DrawArc(..) が実行されるが、実際に描画されるのは$P$ と $Q$ を結ぶ弧$\overset{\Large\frown}{PQ}$ のみである (このときの線分 $PS$ はただの点)。
30行目のelseブロックは $PR<QR$ の場合である。また42行目の DrawAuxLine(..) は補助線(線分 $PR$、$QR$)を描画するためのものである。

今までと同じように2点 $P$、$Q$ を与えられた点とし、それらの点における(単位)接線ベクトルを $\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ とする。さらに $P$ から $\boldsymbol{\mathsf{v}}$ の方向へ引いた半直線と $Q$ から $-\boldsymbol{\mathsf{w}}$ の方向へ引いた半直線との交点を $R$ とする。
ここで $PR$ の長さを $t_1$、$QR$ の長さを $t_2$ とし、$t_1$、$t_2$ は長さではあるがマイナスの値もとり得るものとする。具体的には交点 $R$ が $P$ から $\boldsymbol{\mathsf{v}}$ の方向にあるとき $t_1$ をプラスの値、$-\boldsymbol{\mathsf{v}}$ の方向にあるとき $t_1$ をマイナスの値とする。同様に交点 $R$ が $Q$ から $\boldsymbol{\mathsf{w}}$ の方向にあるとき $t_2$ をプラスの値、$-\boldsymbol{\mathsf{w}}$ の方向にあるとき $t_2$ をマイナスの値とする。
右図の場合であれば交点 $R$ は $P$ から $\boldsymbol{\mathsf{v}}$ の方向にあり、$Q$ から $-\boldsymbol{\mathsf{w}}$ の方向にあるので、$t_1 > 0$、$t_2 < 0$ である。
したがって\[R = P + t_1 \boldsymbol{\mathsf{v}} = Q + t_2 \boldsymbol{\mathsf{w}}\]となる。
このように $t_1$、$t_2$ を $P$ 及び $Q$ から交点 $R$ までの長さ(マイナス値にもなる長さ)とするとき、上記の補間メソッドにおいては\[ t_1 > 0\quad\&\&\quad t_2 < 0\]であるときのみ補間曲線が描画される。この条件が成り立たない場合は単に2点 $P$、$Q$ が線分で結ばれるだけである。メソッド冒頭のifブロックはそのためのものである。R3.z は $+1$ か $-1$ のいずれかであるが、上の条件が成り立つときは $+1$、成り立たないときは $-1$ がセットされている。
例えば下左図の場合は $t_1 > 0$、$t_2 > 0$、右図の場合は $t_1 < 0$、$t_2 > 0$ であるが、このような場合はいずれも図に示されるように $P$、$Q$ が線分で結ばれるだけである。


ただし、上の条件が成り立たないからといって $P$、$Q$、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ を補間する線分と弧が存在しないわけではない。実際には $t_1$、$t_2$ の符号がどのような組み合わせであっても線分と弧によって $PQ$ 間を補間することができる。この点については本節の最後に触れる。
では上で述べてきたことをプログラムで実装する。
なお本節のプログラムは 画角(FOV) が $60^\circ$ 、アスペクト比(Aspect Ratio) が 16:9 に設定されていることを前提としている (この設定でない場合はマウス操作が適切に処理されなくなる)。

アスペクト比が 16:9 であるかを調べるにはUnityの実行画面上部にある「Gameタブ」をクリックし現在の画面を Game View にする。そのときGameタブの下側に表示される数字の比がアスペクト比であり、この値を 16:9 に設定する (図18)。


# Code1
補間曲線の作成にあたっては下図19に示される制御点と呼ばれるものを用いる。制御点は補間曲線が通過する点であり、図中の矢印はその点における接線を表している (初期状態では制御点の接線は x軸プラス方向を向いている)。つまりここで作成する補間曲線は下記の制御点の位置及び接線の方向によってその形状が決まる。

最初のプログラムは制御点が2つの場合である。
[Code1] (実行結果 図21)
if (!i_INITIALIZED)
{
AddControl(2, 3, 50);
AddControl(26, 8, -28);
i_INITIALIZED = true;
}
if (AnyControlChanged())
{
Vector2 P = GetControlPosition(0);
Vector2 v = GetControlTangent(0);
Vector2 Q = GetControlPosition(1);
Vector2 w = GetControlTangent(1);
Vector3 R = CalcIntersectionOf2Lines(P, v, Q, w);
InterpolatePQ(P, v, Q, w, R);
}
初期化ブロック内の AddControl(x, y, deg) は制御点を配置するための補助メソッドであり、第1引数、第2引数には制御点の x座標、y座標、第3引数には接線の向きを指定する。接線の向きは初期状態の向きである x軸プラス方向からの角度を指定する。例えば この第3引数を 30 とすれば接線は x軸プラス方向から $30^\circ$ 回転した方向を向く (図20)。
制御点及び接線はプログラム実行中にマウスドラッグによって位置や向きを変更することができる。制御点や接線に何らかの変化があれば9行目の AnyControlChanged() がtrueを返し、このifブロックに処理が進むが、このifブロックにおいて補間曲線の描画処理が行われる。
GetControlPosition(..)、GetControlTangent(..) は制御点の位置及び接線の方向を取得するための補助メソッドであり、その引数には制御点のインデックスを指定する。今回は制御点を2つ使っているのでそれらのインデックスは $0$ あるいは $1$ であり、メソッドの引数として 0、1 をセットすれば各制御点の位置及び接線の方向を取得することができる (接線の方向は単位ベクトルとして返される)。

17行目の InterpolatePQ(..) は上で解説したものであり、実際の補間曲線の描画に使われる。
実行結果(図21)に示されるように補助線が表示されているときは2点間が曲線によって補間され、そうでなければ2点間が線分によって結ばれるだけである。
# Code2
続いては制御点を6個に増やした場合である。しかしプログラムの内容はほとんど変わらない。
[Code2] (実行結果 図22)
if (!i_INITIALIZED)
{
AddControl(0, 4, 60);
AddControl(7, 7, -65);
AddControl(14, 4, 76);
AddControl(19, 12, -70);
AddControl(23, 6, 52);
AddControl(27, 9, -40);
i_INITIALIZED = true;
}
if (AnyControlChanged())
{
int numControl = 6;
for (int i = 0; i < numControl - 1; i++)
{
Vector2 P = GetControlPosition(i);
Vector2 v = GetControlTangent(i);
Vector2 Q = GetControlPosition(i + 1);
Vector2 w = GetControlTangent(i + 1);
Vector3 R = CalcIntersectionOf2Lines(P, v, Q, w);
InterpolatePQ(P, v, Q, w, R);
}
}
今回は制御点が6個になっているので初期化ブロックにおいては AddControl(..) が6回実行されている。
補間曲線を描画する場合にもfor文(16行目)によって、制御点 0 から制御点 1 までの補間曲線、制御点 1 から制御点 2 までの補間曲線というように複数の区間を1つ1つ描画することで1つの補間曲線が構成される。

# Code3
上でも述べたように、$t_1$、$t_2$ を $P$ 及び $Q$ から交点 $R$ までの長さ(マイナス値にもなる長さ)とするとき、今回の実装では\[ t_1 > 0\quad\&\&\quad t_2 < 0\]であるときのみ補間曲線が描画される。しかし実際には $t_1$、$t_2$ の値がどのようなものであっても線分と弧による補間曲線を描くことは可能である。以下のプログラムでその点について見てみよう。
[Code3] (実行結果 図23)
if (!i_INITIALIZED)
{
AddControl(2, 3, 50);
AddControl(26, 8, -28);
i_INITIALIZED = true;
}
if (AnyControlChanged())
{
Vector2 P = GetControlPosition(0);
Vector2 v = GetControlTangent(0);
Vector2 Q = GetControlPosition(1);
Vector2 w = GetControlTangent(1);
Vector4 R = CalcIntersectionOf2Lines_ver2(P, v, Q, w);
InterpolatePQ_ver2(P, v, Q, w, R);
}
16、17行目以外はCode1と同じである。今回は交点 $R$ の計算に CalcIntersectionOf2Lines_ver2(..) というメソッドが使われており、補間曲線の描画には InterpolatePQ_ver2(..) というメソッドが使われている。これらのメソッドは $t_1$、$t_2$ がどのような値の場合にも、補間曲線が描画されるようにするためのものである。
CalcIntersectionOf2Lines_ver2(..) の戻り値はVector4型であり、x座標、y座標には交点 $R$ の位置がセットされている。この点はCode1と同じであるが、今回は z座標、w座標に $t_1$、$t_2$ の値がセットされる。


実行結果(図23)に示されるように、制御点の位置や接線をどのように動かしても今回は2つの制御点の間に線分と弧による補間曲線が描画される (薄い灰色の補助線が表示されているときが $t_1 > 0$、$t_2 < 0$ である)。
しかし今回の補間では補間曲線としてはいささか乱暴な補間が行われてしまうこと多く、特に制御点の位置や接線を動かしていく過程で曲線が発散するようなことが起こるが、これは実際には補間曲線を構成する弧の半径が大きくなり過ぎてしまうためにそのように見えているのである。図24はそのような状況を離れて見た場合であり、こういった場合には半径の大きい円に近い補間曲線が描かれる。
以下は今回の補間で使われるメソッド InterpolatePQ_ver2(..) である。
[InterpolatePQ_ver2(..)]
void InterpolatePQ_ver2(Vector2 P, Vector2 v, Vector2 Q, Vector2 w, Vector4 R4)
{
Vector2 R = R4;
float t1 = R4.z;
float t2 = R4.w;
float cosT = Vector2.Dot(-v, w);
float sinT = Mathf.Sqrt(1.0f - cosT * cosT);
float lenPR = (R - P).magnitude;
float lenQR = (R - Q).magnitude;
if (t1 > 0.0f && t2 < 0.0f)
{
bool ccw = (-w.x * v.y + w.y * v.x > 0.0f) ? true : false;
Vector2 wr = ccw ? new Vector2(-w.y, w.x) : new Vector2(w.y, -w.x); // counter-clockwise ? rot90 : rot(-90)
Vector2 S, C;
if (lenPR >= lenQR)
{
float a = lenQR;
float r = a * (1 - cosT) / sinT;
S = R - a * v;
C = Q + r * wr;
DrawLine(P, S);
DrawArc(S, Q, C);
}
else
{
float a = lenPR;
float r = a * (1 - cosT) / sinT;
S = R + a * w;
C = S + r * wr;
DrawLine(S, Q);
DrawArc(P, S, C);
}
DrawAuxLine(P, Q, R);
}
else if (t1 < 0.0f && t2 > 0.0f)
{
int sign = (v.x * (-w.y) - v.y * (-w.x) > 0.0f) ? 1 : -1;
Vector2 vr = (sign > 0) ? new Vector2(-v.y, v.x) : new Vector2(v.y, -v.x);
Vector2 S, C;
if (lenPR >= lenQR)
{
float a = lenPR;
float r = a * (1 - cosT) / sinT;
S = R - a * w;
C = P + r * vr;
DrawLine(Q, S);
DrawArc(P, S, C, true);
}
else
{
float a = lenQR;
float r = a * (1 - cosT) / sinT;
S = R + a * v;
C = S + r * vr;
DrawLine(P, S);
DrawArc(S, Q, C, true);
}
}
else if (t1 > 0.0f && t2 > 0.0f)
{
float a = lenQR;
float r = a * (1 - cosT) / sinT;
Vector2 S = R + a * v;
int sign = (v.x * (-w.y) - v.y * (-w.x) > 0.0f) ? 1 : -1;
Vector2 vr = (sign > 0) ? new Vector2(-v.y, v.x) : new Vector2(v.y, -v.x);
Vector2 C = S + r * vr;
DrawLine(P, S);
DrawArc(S, Q, C, true);
}
else // (t1 < 0.0f && t2 < 0.0f)
{
float a = lenPR;
float r = a * (1 - cosT) / sinT;
Vector2 S = R - a * w;
int sign = (w.x * v.y - w.y * v.x > 0.0f) ? 1 : -1;
Vector2 wr = (sign > 0) ? new Vector2(-w.y, w.x) : new Vector2(w.y, -w.x);
Vector2 C = S + r * wr;
DrawLine(S, Q);
DrawArc(P, S, C, true);
}
}
12行目のifブロックは $t_1 > 0$、$t_2 < 0$ の場合であり、この部分は上記の InterpolatePQ(..) と内容は同じである。43行目のifブロックは $t_1 < 0$、$t_2 > 0$ の場合、72行目のifブロックは $t_1 > 0$、$t_2 > 0$ の場合、最後のelseブロック(84行目)が $t_1 < 0$、$t_2 < 0$ の場合である。
詳しい解説については省略するが基本的に行っている処理は同じである (ただし上の解説では円の中心 $C$ を求める際に $\boldsymbol{\mathsf{w}}$ を回転させていたが、このメソッドでは $t_1$、$t_2$ の値によって $\boldsymbol{\mathsf{v}}$ を回転させる場合がある。またその際の回転角度が $90^\circ$ あるいは $-90^\circ$ かを調べる計算についても $t_1$、$t_2$ の値によって若干の違いがある)。
© 2020-2025 Redpoll's 60 (All rights reserved)