Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-7
第2章 2D空間におけるオブジェクトの運動
$§$2-7 一体化したオブジェクトの運動 3
本節では2-5節、2-6節の運動を統合する。
使用するオブジェクトとそれらの初期状態は前2節と同じである。
実装する運動は以下のものである。
Foundationが垂直方向に単振動をしている。その Foundation上で Towerが水平方向に単振動をしている。さらに、その Tower上部の指定位置において、Bladesが回転している (具体的にはCode2の実行結果 図8参照)。
考え方は前2節と変わらないが、使われているオブジェクトが2つから3つになったことで、階層構造も2階層から3階層になっている。
この運動を2つの段階に分けて実装する。
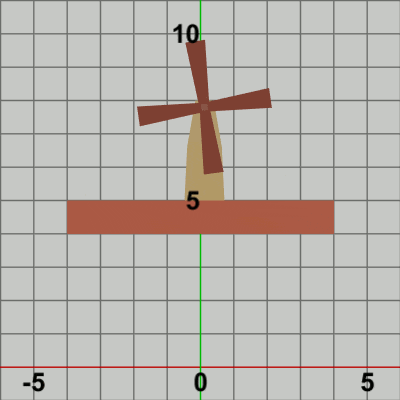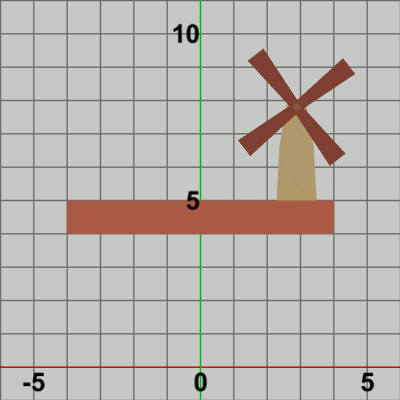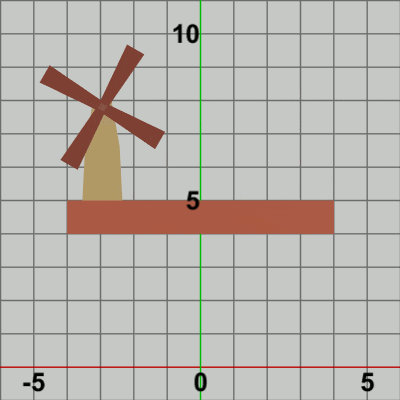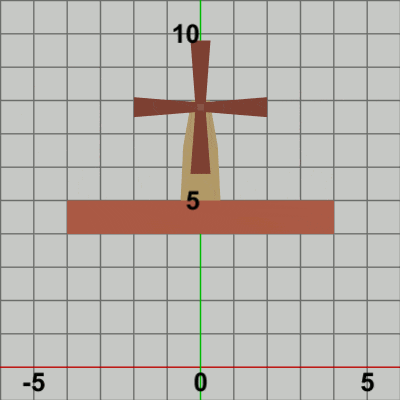
図4 Code1 実行結果 まず第1段階として。
Foundationを何も動かさずに固定した状態で、
「その Foundation上で Towerが水平方向に単振動をしている。さらに、その Tower上部の指定位置において、Bladesが回転している。」という部分を実装する(プログラムの実行結果は図4参照)。
Foundationは初期状態で静止したままにしておく (そのために以下のプログラムでは Foundationには identity行列のみを実行している)。この運動は 2-6節の Code3の運動と全く変わらない。Code3の方では、Towerの単振動は $y = 0$ (x軸上)での単振動であったが、それをここでは $y = 5$ での単振動にすればよいだけである。
[Code1] (実行結果 図4)
1行目から8行目までは 2-6節 Code3と同じである。ただし、上で述べたように この単振動が $y = 5$ の位置で行われるようにするために、8行目の GetRotation3x3(..) の第2引数には 5.0f が指定されている。実行結果(図4)を見ればわかるように、2-6節 Code3ではx軸上の単振動であったものが、ここでは $y = 5$ の位置で行われるようになっただけである。
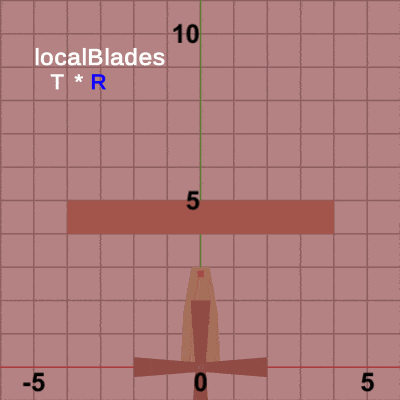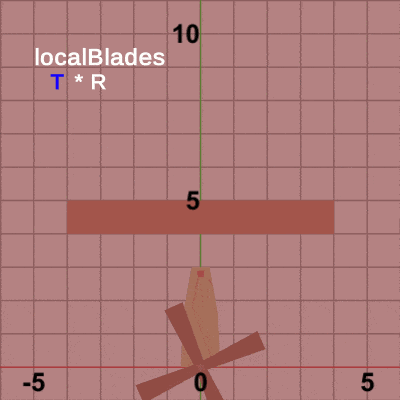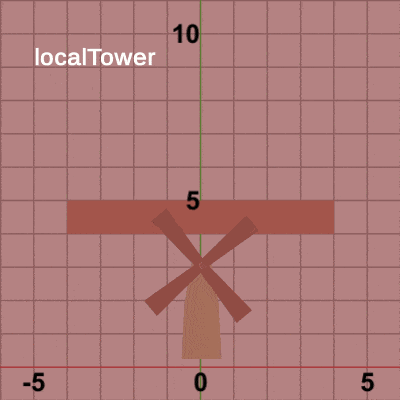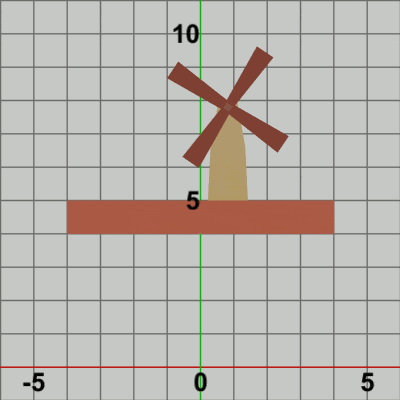
図5 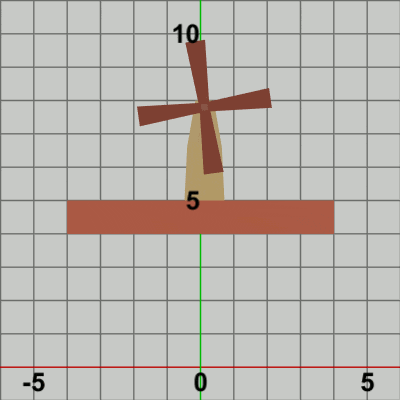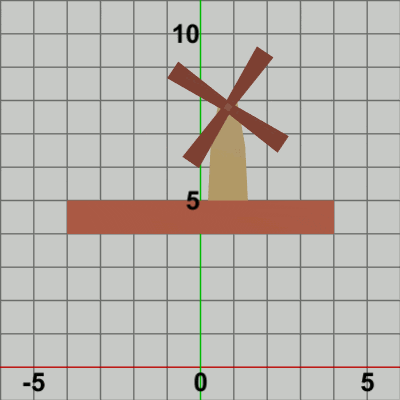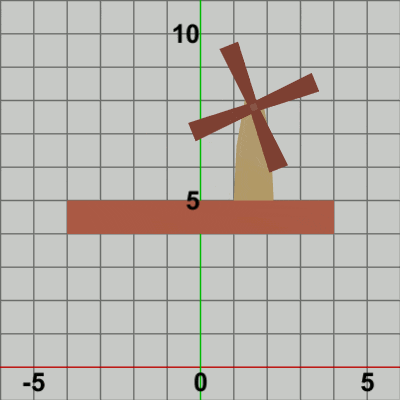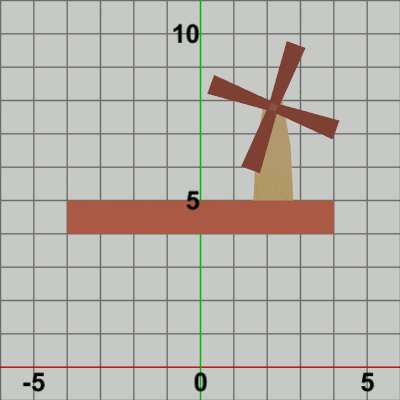
図6
図5は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターのかかっている状態は、オブジェクトに実行される変換行列の実行過程であり、通常色の状態は変換行列の実行結果であることを意味している。赤いフィルターの状態から通常色に切り替わった時点でフレーム描画が発生する。
本節では Blades、Tower、さらに Foundationを含めた3つのオブジェクトの一体化した運動が主題である。12行目から14行目の以下のコードは、
それぞれのオブジェクトに実行する変換行列の計算であるが、今回は Foundationは何も運動は行わないため localFoundの内容は identity行列である。毎フレーム オブジェクトの変換はオブジェクトの初期状態から始まる。例えば Bladesの場合は、毎フレーム初期状態の Bladesに対して localBlades、localTower、localFound の順で変換が実行され、Towerの場合は、毎フレーム初期状態の Towerに対して localTower、localFound の順で変換が実行される。Foundationも同様で、毎フレーム初期状態の Foundationに対して localFound が実行される。
赤いフィルターの状態においては、まず始めに白い文字で localBlades と表示されるが、この状態においては Bladesのみが運動している。つまり、白い文字で localBladesと表示されている間は初期状態の Bladesに対して変換行列localBladesが実行されていることを意味している。Bladesのみの運動となるのは、上の12行目から14行目を見れば分かるように、変換行列localBladesは Bladesにしか実行されないためである。localBladesの実行が終わると、白い文字で localTower と表示されるが、localTower が表示されている間は Blades 及び Towerに対して変換行列localTowerが実行されていることを意味している。このときには Blades、Towerの2つのオブジェクトの運動となるが、それは変換行列localTowerは Bladesと Towerに実行されるためである(12行目、13行目)。毎フレーム localTowerの実行が開始される時点では、Towerは初期状態であり、Bladesは localBladesを実行し終わった状態である。このときに、Tower 及び Bladesに localTowerが実行されると、localBladesを実行し終わった状態の Bladesと 初期状態の Towerが一体となって Foundation上に移動するが、この移動先は水平方向の単振動軌道上の各位置である (毎フレーム移動先は異なる)。一体化した Bladesと Towerが Foundation上に移動した時点で localTowerの実行は終わるが、その次には白い文字で localFound と表示される。localFound が表示されている間は変換行列localFoundが実行されていることを意味しているが、12行目から14行目に示されるように、localFoundは Blades、Tower、Foundationの3つに実行される変換行列であるので、白い文字で localFound と表示されている間は、Blades、Tower、Foundationの3つが一体となって運動するはずであるが、実際には白い文字で localFound が表示されている間は3つとも静止したままである。それは、このプログラムで使われている localFound は identity行列であるためである。identity行列はオブジェクトに対して何の変換も実行しない行列であるので、図5において localFound が表示されている間は3つのオブジェクトは何も変化が起こらないのである。
もし、3つのオブジェクトが一体となって運動する場合には、Bladesは localBlades、localTowerを実行し終わった状態からの運動となり、Towerは localTowerを実行し終わった状態からの運動となる。Foundationの場合は、初期状態からの運動となる。
図6は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図4のアニメーションである)。
親オブジェクトと子オブジェクトを一体化して運動させるには、親オブジェクトと子オブジェクトの両方に同じ行列を実行するが、今回使用する3つオブジェクトの階層構造を図示すると図7のようになる。
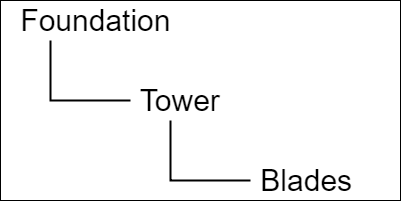
図7 オブジェクトの階層構造 
図8 Code2 実行結果
TowerはFoundationにアタッチされている Foundationの子オブジェクトである。BladesはTowerにアタッチされている Towerの子オブジェクトである。Bladesは Foundationに直接アタッチされているわけではないが、こういった場合でもBladesは Foundationの2階層下の子として、Foundationの子オブジェクトとして扱う。
したがって、Foundationの垂直方向の単振動を Foundation、Tower、Bladesの3つのオブジェクトが一体となって行うようにするためには、垂直方向の単振動行列をこの3つのオブジェクトに実行すればよい。Code1では3つのオブジェクトに localFoundが実行されたが、Code1における localFoundの内容は identity行列であったので何も変化が起こらなかった。ここでは、3つのオブジェクトに実行される localFoundの内容は identity行列ではなく垂直方向の単振動行列となっている。
[Code2]
Code1からの変更点は1箇所のみである。それは、先程も述べたように12行目の localFoundの内容である。ここでは、その内容は振幅$3$の垂直方向の単振動行列になっており、この部分の計算は 2-5節 Code3(5行目から7行目)と同じである。この変更によって Blades、Tower、Foundationが一体となって垂直方向の単振動を行うようになるのである (図8)。Blades、Towerの運動に関しては Code1と変わらない。
図9 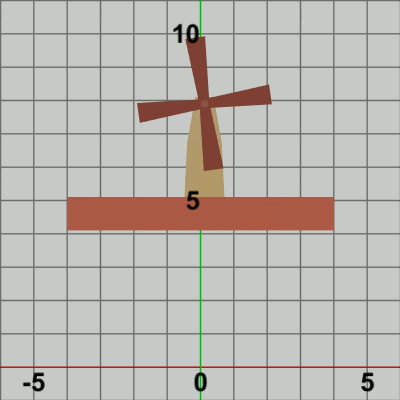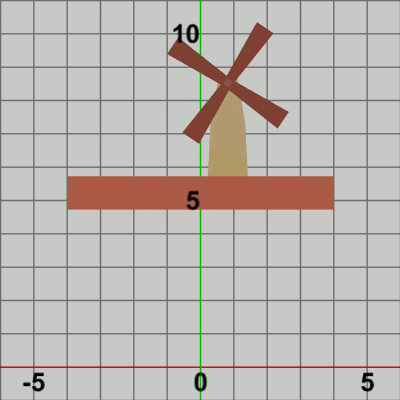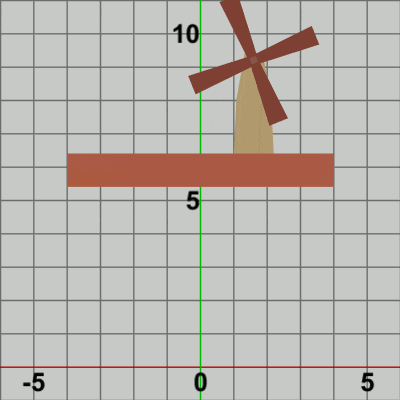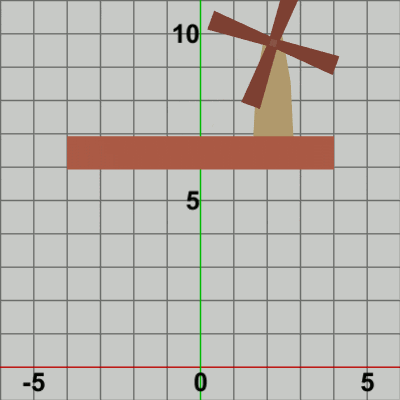
図10 コマ送り表示
図9は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターの状態において、白い文字で localBlades、localTower と表示されている間の運動は図5と同じである。しかし、白い文字で localFound と表示されている間に関しては、図5のアニメーションでは何の変換も起こらなかったのに対し、図9のアニメーションでは、3つのオブジェクトが一体となって垂直方向の平行移動を行っている。これは12行目の localFoundの内容が垂直方向の単振動行列であるので、毎フレーム その単振動軌道上の各位置への移動となるのである。Code1との違いは、この垂直方向の単振動軌道上への移動があるかないかだけである。
先程も述べたが localFoundの実行に関しては、Bladesの場合は localBlades、localTowerを実行し終わった状態のBladesに対して実行され、Towerの場合は localTowerを実行し終わった状態のTowerに対して実行され、Foundationの場合は初期状態のFoundationに対して実行される (図9)。これによって、垂直方向に単振動をするFoundation上において、Towerが水平方向に単振動をし、そのTower上部の指定位置でBladesが回転をする といった3つのオブジェクトの一体化が実現されるのである。
図10は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図8のアニメーションである)。
親子関係にある複数のオブジェクトを一体化して運動させるにあたって基本となるのは、まず 初期状態の子オブジェクトが独自の運動を行い、子オブジェクトの運動が終わった時点で、親オブジェクトと子オブジェクトが一体となって運動を行うが、その際の運動は親オブジェクトの独自の運動である。そして、その親オブジェクトの運動の開始は、親オブジェクトは初期状態から、子オブジェクトは自身の運動が終わった時点の状態から 一体となって運動を行うという点である。
図5や図9を例にとると、まず 3つのオブジェクトのうちで一番下の子オブジェクトである Bladesの独自の運動 localBladesが行われる。
localBladesが終わると、Bladesと親オブジェクトである Towerが一体となって運動を行うが、このときの運動は Towerの独自の運動である localTowerであるが、Towerの場合は初期状態から、Bladesの場合は localBladesが終わった時点での状態から localTowerの実行が開始される。localTowerは Blades、Towerの両者に実行されるので、localTowerが実行されている間は BladesとTowerは一体となって運動(同じ量の平行移動)を行うのである。
localTowerが終わると、Blades、Tower 及び 一番上の親オブジェクトである Foundationが一体となって運動を行うが、このときの運動は Foundationの独自の運動である localFoundである。Foundationの場合は初期状態から、Towerの場合は localTowerが終わった時点の状態から、Bladesの場合は localBlades、localTowerが終わった時点の状態から localFoundの実行が開始される。localFoundは Blades、Tower、Foundationに実行されるので、localFoundが実行されている間は Blades、Tower、Foundationは一体となって運動(同じ量の平行移動)を行うのである。
本節のプログラムにおける以下の部分は、今述べたことを実装しているのである。
このコードは階層構造にあるオブジェクトに最終的に実行される行列の計算である (それらの行列には接頭辞にworldが付けられている)。本節以降のプログラムにおいてもオブジェクトの運動を行列によって実装する場合には、オブジェクトに最終的に実行される行列は上のような形で計算される。
しかし、この形の記述には明らかな'無駄'が含まれる。上の例では localFound * localTower が2回書かれているが、これは同じ計算を2回しているということである。こういった'無駄'を残した形で記述しているのは、階層構造にあるオブジェクトに最終的に実行される行列(接頭辞にworldと付いている行列)の計算過程を印象付けるためであり、そのための形式的な記述として捉えていただきたい。
使用するオブジェクトとそれらの初期状態は前2節と同じである。
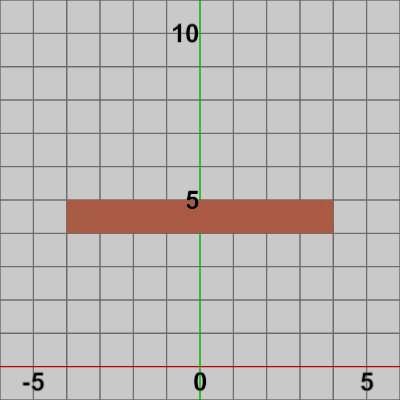 図1 Foundation 初期状態
図1 Foundation 初期状態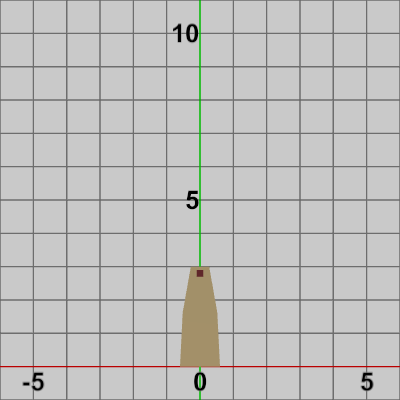 図2 Tower 初期状態
図2 Tower 初期状態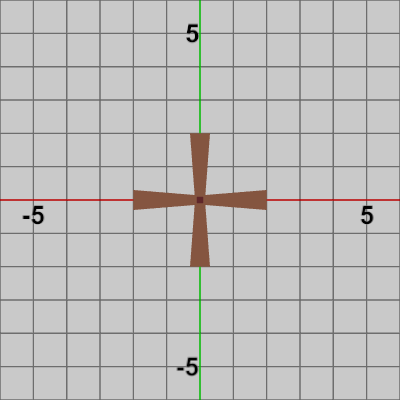 図3 Blades 初期状態
図3 Blades 初期状態
実装する運動は以下のものである。
Foundationが垂直方向に単振動をしている。その Foundation上で Towerが水平方向に単振動をしている。さらに、その Tower上部の指定位置において、Bladesが回転している (具体的にはCode2の実行結果 図8参照)。
考え方は前2節と変わらないが、使われているオブジェクトが2つから3つになったことで、階層構造も2階層から3階層になっている。
この運動を2つの段階に分けて実装する。
# Code1

Foundationを何も動かさずに固定した状態で、
「その Foundation上で Towerが水平方向に単振動をしている。さらに、その Tower上部の指定位置において、Bladesが回転している。」という部分を実装する(プログラムの実行結果は図4参照)。
Foundationは初期状態で静止したままにしておく (そのために以下のプログラムでは Foundationには identity行列のみを実行している)。この運動は 2-6節の Code3の運動と全く変わらない。Code3の方では、Towerの単振動は $y = 0$ (x軸上)での単振動であったが、それをここでは $y = 5$ での単振動にすればよいだけである。
[Code1] (実行結果 図4)
i_degBlades += 8; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degBlades); THMatrix3x3 T = TH2DMath.GetTranslation3x3(c_attachPos_Blades); THMatrix3x3 localBlades = T * R; i_shmTower += 2; float mx = 3.4f * Mathf.Sin(i_shmTower * Mathf.Deg2Rad); THMatrix3x3 localTower = TH2DMath.GetTranslation3x3(mx, 5.0f); THMatrix3x3 localFound = THMatrix3x3.identity; THMatrix3x3 worldBlades = localFound * localTower * localBlades; THMatrix3x3 worldTower = localFound * localTower; THMatrix3x3 worldFound = localFound; Blades.SetMatrix(worldBlades); Tower.SetMatrix(worldTower); Foundation.SetMatrix(worldFound);
1行目から8行目までは 2-6節 Code3と同じである。ただし、上で述べたように この単振動が $y = 5$ の位置で行われるようにするために、8行目の GetRotation3x3(..) の第2引数には 5.0f が指定されている。実行結果(図4)を見ればわかるように、2-6節 Code3ではx軸上の単振動であったものが、ここでは $y = 5$ の位置で行われるようになっただけである。


図5は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターのかかっている状態は、オブジェクトに実行される変換行列の実行過程であり、通常色の状態は変換行列の実行結果であることを意味している。赤いフィルターの状態から通常色に切り替わった時点でフレーム描画が発生する。
本節では Blades、Tower、さらに Foundationを含めた3つのオブジェクトの一体化した運動が主題である。12行目から14行目の以下のコードは、
THMatrix3x3 worldBlades = localFound * localTower * localBlades; THMatrix3x3 worldTower = localFound * localTower; THMatrix3x3 worldFound = localFound;
赤いフィルターの状態においては、まず始めに白い文字で localBlades と表示されるが、この状態においては Bladesのみが運動している。つまり、白い文字で localBladesと表示されている間は初期状態の Bladesに対して変換行列localBladesが実行されていることを意味している。Bladesのみの運動となるのは、上の12行目から14行目を見れば分かるように、変換行列localBladesは Bladesにしか実行されないためである。localBladesの実行が終わると、白い文字で localTower と表示されるが、localTower が表示されている間は Blades 及び Towerに対して変換行列localTowerが実行されていることを意味している。このときには Blades、Towerの2つのオブジェクトの運動となるが、それは変換行列localTowerは Bladesと Towerに実行されるためである(12行目、13行目)。毎フレーム localTowerの実行が開始される時点では、Towerは初期状態であり、Bladesは localBladesを実行し終わった状態である。このときに、Tower 及び Bladesに localTowerが実行されると、localBladesを実行し終わった状態の Bladesと 初期状態の Towerが一体となって Foundation上に移動するが、この移動先は水平方向の単振動軌道上の各位置である (毎フレーム移動先は異なる)。一体化した Bladesと Towerが Foundation上に移動した時点で localTowerの実行は終わるが、その次には白い文字で localFound と表示される。localFound が表示されている間は変換行列localFoundが実行されていることを意味しているが、12行目から14行目に示されるように、localFoundは Blades、Tower、Foundationの3つに実行される変換行列であるので、白い文字で localFound と表示されている間は、Blades、Tower、Foundationの3つが一体となって運動するはずであるが、実際には白い文字で localFound が表示されている間は3つとも静止したままである。それは、このプログラムで使われている localFound は identity行列であるためである。identity行列はオブジェクトに対して何の変換も実行しない行列であるので、図5において localFound が表示されている間は3つのオブジェクトは何も変化が起こらないのである。
もし、3つのオブジェクトが一体となって運動する場合には、Bladesは localBlades、localTowerを実行し終わった状態からの運動となり、Towerは localTowerを実行し終わった状態からの運動となる。Foundationの場合は、初期状態からの運動となる。
図6は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図4のアニメーションである)。
# Code2
第2段階として、Foundationの垂直方向の単振動を追加して3つのオブジェクトの一体化した運動を実装する。親オブジェクトと子オブジェクトを一体化して運動させるには、親オブジェクトと子オブジェクトの両方に同じ行列を実行するが、今回使用する3つオブジェクトの階層構造を図示すると図7のようになる。


TowerはFoundationにアタッチされている Foundationの子オブジェクトである。BladesはTowerにアタッチされている Towerの子オブジェクトである。Bladesは Foundationに直接アタッチされているわけではないが、こういった場合でもBladesは Foundationの2階層下の子として、Foundationの子オブジェクトとして扱う。
したがって、Foundationの垂直方向の単振動を Foundation、Tower、Bladesの3つのオブジェクトが一体となって行うようにするためには、垂直方向の単振動行列をこの3つのオブジェクトに実行すればよい。Code1では3つのオブジェクトに localFoundが実行されたが、Code1における localFoundの内容は identity行列であったので何も変化が起こらなかった。ここでは、3つのオブジェクトに実行される localFoundの内容は identity行列ではなく垂直方向の単振動行列となっている。
[Code2]
i_degBlades += 8; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degBlades); THMatrix3x3 T = TH2DMath.GetTranslation3x3(c_attachPos_Blades); THMatrix3x3 localBlades = T * R; i_shmTower += 2; float mx = 3.4f * Mathf.Sin(i_shmTower * Mathf.Deg2Rad); THMatrix3x3 localTower = TH2DMath.GetTranslation3x3(mx, 5.0f); i_shmFound += 2; float my = 3.0f * Mathf.Sin(i_shmFound * Mathf.Deg2Rad); THMatrix3x3 localFound = TH2DMath.GetTranslation3x3(0.0f, my); THMatrix3x3 worldBlades = localFound * localTower * localBlades; THMatrix3x3 worldTower = localFound * localTower; THMatrix3x3 worldFound = localFound; Blades.SetMatrix(worldBlades); Tower.SetMatrix(worldTower); Foundation.SetMatrix(worldFound);
Code1からの変更点は1箇所のみである。それは、先程も述べたように12行目の localFoundの内容である。ここでは、その内容は振幅$3$の垂直方向の単振動行列になっており、この部分の計算は 2-5節 Code3(5行目から7行目)と同じである。この変更によって Blades、Tower、Foundationが一体となって垂直方向の単振動を行うようになるのである (図8)。Blades、Towerの運動に関しては Code1と変わらない。


図9は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターの状態において、白い文字で localBlades、localTower と表示されている間の運動は図5と同じである。しかし、白い文字で localFound と表示されている間に関しては、図5のアニメーションでは何の変換も起こらなかったのに対し、図9のアニメーションでは、3つのオブジェクトが一体となって垂直方向の平行移動を行っている。これは12行目の localFoundの内容が垂直方向の単振動行列であるので、毎フレーム その単振動軌道上の各位置への移動となるのである。Code1との違いは、この垂直方向の単振動軌道上への移動があるかないかだけである。
先程も述べたが localFoundの実行に関しては、Bladesの場合は localBlades、localTowerを実行し終わった状態のBladesに対して実行され、Towerの場合は localTowerを実行し終わった状態のTowerに対して実行され、Foundationの場合は初期状態のFoundationに対して実行される (図9)。これによって、垂直方向に単振動をするFoundation上において、Towerが水平方向に単振動をし、そのTower上部の指定位置でBladesが回転をする といった3つのオブジェクトの一体化が実現されるのである。
図10は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図8のアニメーションである)。
親子関係にある複数のオブジェクトを一体化して運動させるにあたって基本となるのは、まず 初期状態の子オブジェクトが独自の運動を行い、子オブジェクトの運動が終わった時点で、親オブジェクトと子オブジェクトが一体となって運動を行うが、その際の運動は親オブジェクトの独自の運動である。そして、その親オブジェクトの運動の開始は、親オブジェクトは初期状態から、子オブジェクトは自身の運動が終わった時点の状態から 一体となって運動を行うという点である。
図5や図9を例にとると、まず 3つのオブジェクトのうちで一番下の子オブジェクトである Bladesの独自の運動 localBladesが行われる。
localBladesが終わると、Bladesと親オブジェクトである Towerが一体となって運動を行うが、このときの運動は Towerの独自の運動である localTowerであるが、Towerの場合は初期状態から、Bladesの場合は localBladesが終わった時点での状態から localTowerの実行が開始される。localTowerは Blades、Towerの両者に実行されるので、localTowerが実行されている間は BladesとTowerは一体となって運動(同じ量の平行移動)を行うのである。
localTowerが終わると、Blades、Tower 及び 一番上の親オブジェクトである Foundationが一体となって運動を行うが、このときの運動は Foundationの独自の運動である localFoundである。Foundationの場合は初期状態から、Towerの場合は localTowerが終わった時点の状態から、Bladesの場合は localBlades、localTowerが終わった時点の状態から localFoundの実行が開始される。localFoundは Blades、Tower、Foundationに実行されるので、localFoundが実行されている間は Blades、Tower、Foundationは一体となって運動(同じ量の平行移動)を行うのである。
本節のプログラムにおける以下の部分は、今述べたことを実装しているのである。
THMatrix3x3 worldBlades = localFound * localTower * localBlades; THMatrix3x3 worldTower = localFound * localTower; THMatrix3x3 worldFound = localFound;
このコードは階層構造にあるオブジェクトに最終的に実行される行列の計算である (それらの行列には接頭辞にworldが付けられている)。本節以降のプログラムにおいてもオブジェクトの運動を行列によって実装する場合には、オブジェクトに最終的に実行される行列は上のような形で計算される。
しかし、この形の記述には明らかな'無駄'が含まれる。上の例では localFound * localTower が2回書かれているが、これは同じ計算を2回しているということである。こういった'無駄'を残した形で記述しているのは、階層構造にあるオブジェクトに最終的に実行される行列(接頭辞にworldと付いている行列)の計算過程を印象付けるためであり、そのための形式的な記述として捉えていただきたい。
© 2020-2025 Redpoll's 60 (All rights reserved)