Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-6
第2章 2D空間におけるオブジェクトの運動
$§$2-6 一体化したオブジェクトの運動 2
本節では以下の2つのオブジェクトを一体化させた運動を扱う。それぞれ初期状態で図の位置に置かれている。図1のオブジェクトは前節でも使われたTowerであり、図2のオブジェクトはBladesというオブジェクトでその中心が原点に置かれている。
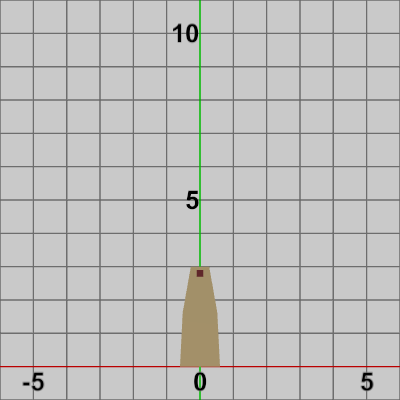
図1 Tower 初期状態 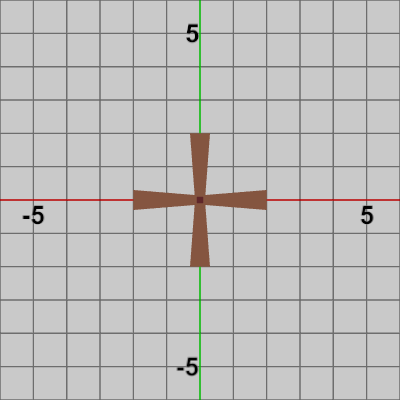
図2 Blades 初期状態
Bladesは初期状態で、その中心が原点に置かれているので毎フレーム回転角度を増加(あるいは減少)させて、Bladesにその角度だけ回転する回転行列を実行すれば図3のように回転する。
[Code1] (実行結果 図3)
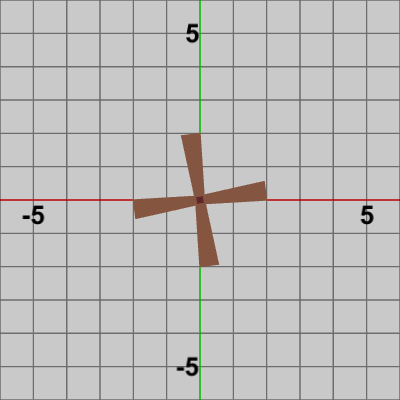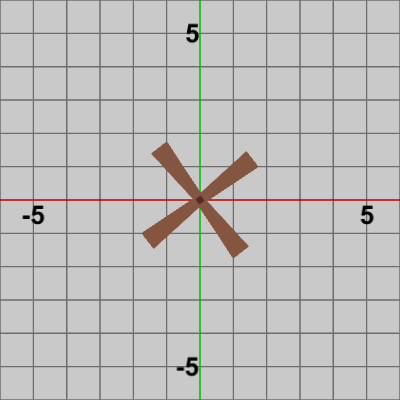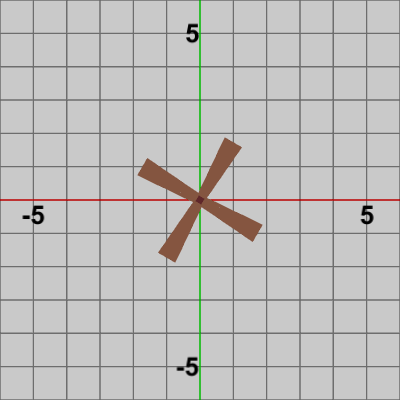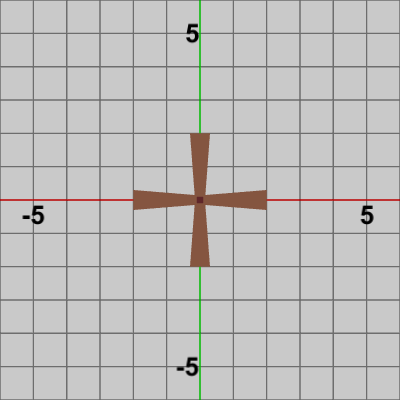
図3 Code1 実行結果 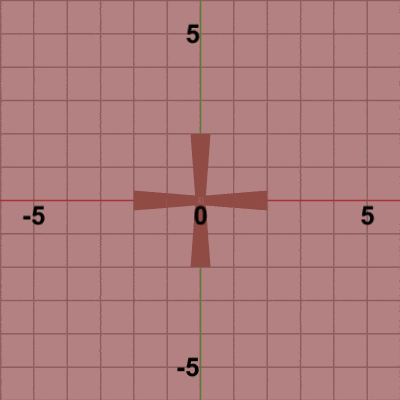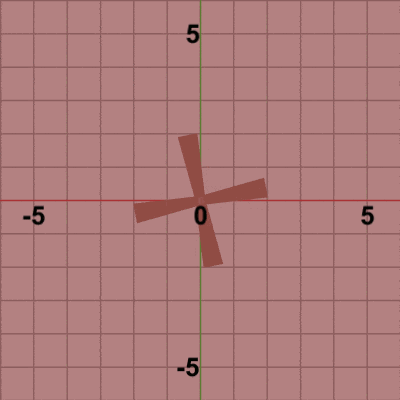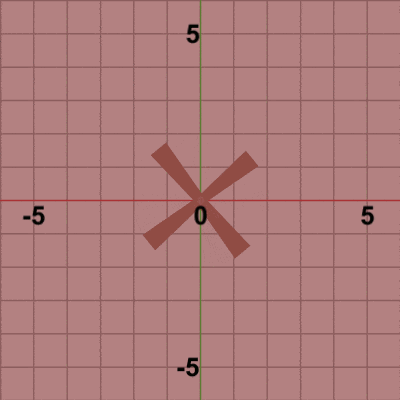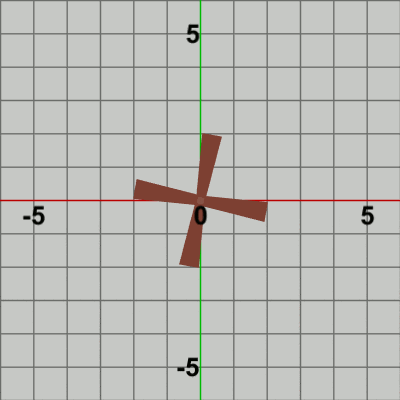
図4
1行目の i_degBladesは現在のBladesの回転角度を表すインスタンス変数であり、そのフレームにおいて初期状態から何度回転するかを表している。毎フレーム $8$ずつ増加するので、Bladesは1フレームあたり$8$°ずつ回転する。
図4は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターのかかっている状態は、Bladesに対して実行される変換行列Rの実行過程であり、通常色の状態は変換行列Rの実行結果の状態である。通常色に切り替わった時点でフレーム描画が発生する。図4に示されるように、Bladesの回転は毎フレーム 初期状態から始まり、最初のフレームでは初期状態から$8$°回転した時点でフレーム描画が発生し、次のフレームでは初期状態から$16$°回転した時点でフレーム描画が発生する。以降のフレームでも同様である。描画されたフレームを連続的に表示したものが図3のアニメーションである。

図5 Code2 実行結果 次に Bladesを Towerの指定位置まで移動させて、そこで Bladesの回転が行われるようにする (Towerの指定位置は Tower上部の色の異なる小さい部分である)。
各フレームでの処理手順は次の通り。
(1) Bladesに回転を実行 (これは Bladesの初期状態の位置である原点において行われる)。
(2) BladesをTowerの指定位置まで移動。
プログラム中で使われる c_attachPos_Blades は、Bladesを初期状態の位置から Towerの指定位置に移動させるための移動量を表すVector2型の定数である。
[Code2] (実行結果 図5)
1行目、2行目は前のコードと同じであり、Rは Bladesを回転させる行列である。3行目の $3\times3$行列Tは Bladesを Tower上部の指定位置に移動させる平行移動行列である。4行目 M = T * R は Bladesに実行される変換行列で、これら2つの変換を1つにまとめたものである。順序としては、まず Bladesを初期位置である原点で回転させ(R)、次に Towerの指定位置に移動させる(T)。
Towerは今回 初期状態のまま動かすことはないので、Towerに実行される変換行列は identity行列である(7行目)。
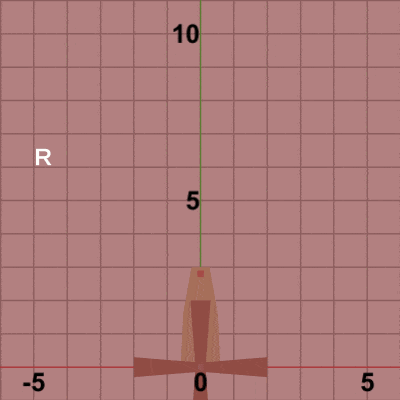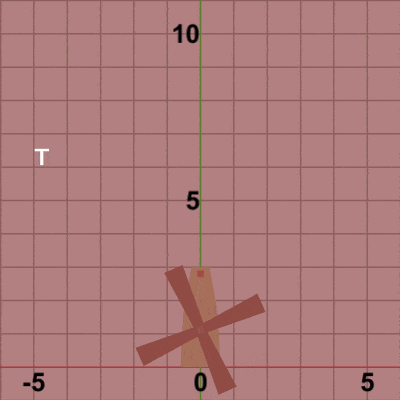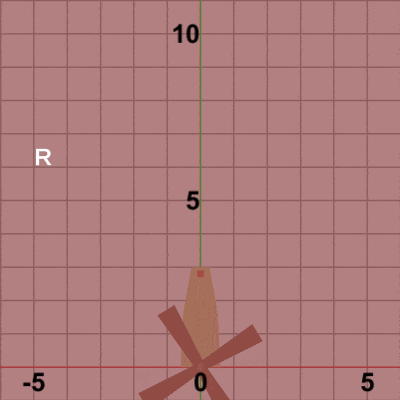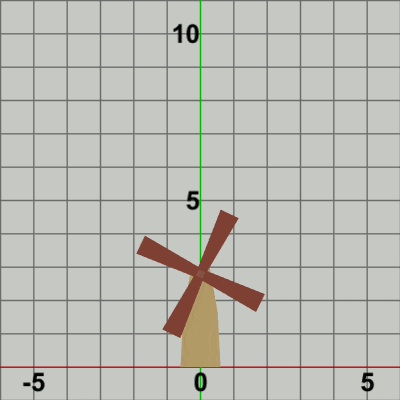
図6 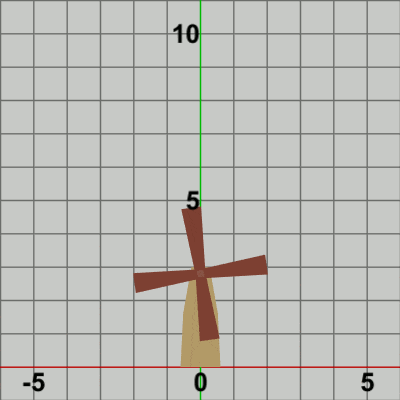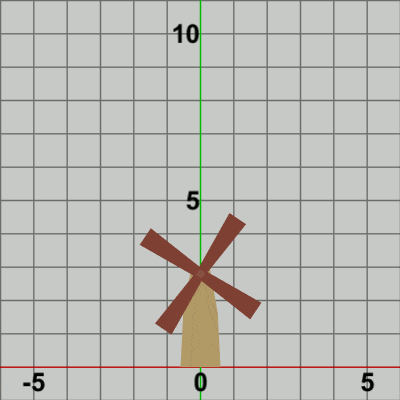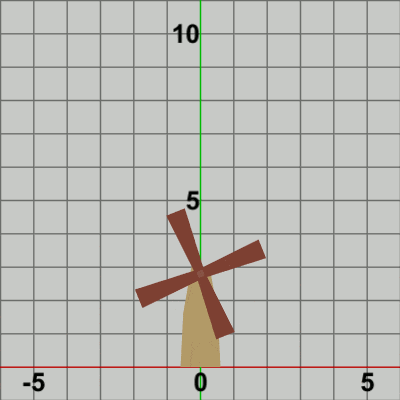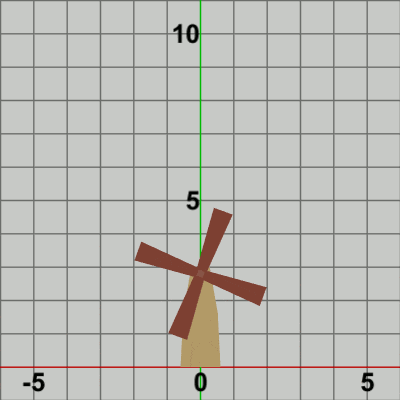
図7 コマ送り表示
図6は Code2の最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。2-2節 Code4でも述べたが、オブジェクトの回転を原点以外の位置で行わせる場合には、毎フレーム まず オブジェクトを原点において回転させ、その状態(回転させた状態)で指定の位置まで移動させるという手順が基本である (ただし 回転の中心が原点に置かれていることが前提)。
Bladesに実行される変換行列Mは、上でも述べたように回転行列Rと平行移動行列Tの2つの変換を1つにまとめたもので、Mを実行した結果は R、Tをこの順序で実行した場合と同じ結果になる。図6のアニメーションでは、白い文字で R、T と表示されるが、Rが表示されている状態は Bladesに回転行列Rを実行している過程を意味し、Tが表示されている状態は Bladesに平行移動行列Tを実行している過程を意味している。最初のフレームでは Bladesは初期状態から$8$°回転し、回転した状態で Towerの指定位置まで移動するが、この移動が終わった時点でフレーム描画が発生する。次のフレームでは Bladesは初期状態から$16$°回転し、回転した状態でTowerの指定位置まで移動する。この移動が終わった時点でフレーム描画となる。それ以降のフレームにおいても同様の処理が繰り返される。
図7は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図5のアニメーションである)。
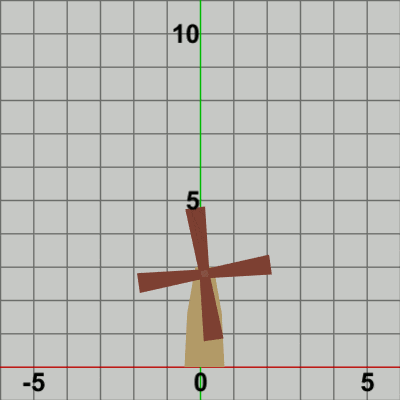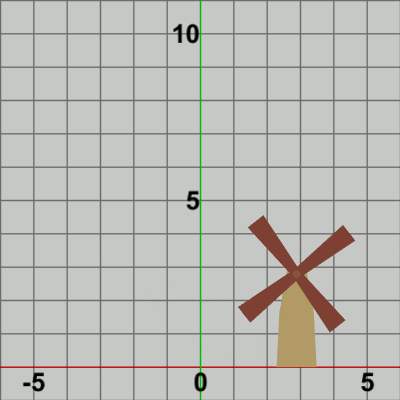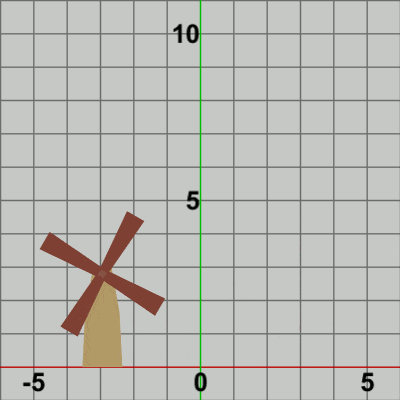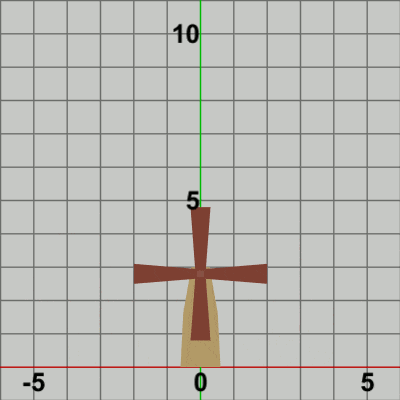
図8 Code3 実行結果 では、最後に Towerと Bladesを一体化して運動させてみよう。Code2においては、Towerには identity行列が実行されるのみで Towerは動くことなく常に静止していた。ここでは、前節と同じように Towerに水平方向の単振動を行わせ、単振動をする Towerの指定位置において Bladesが回転しているプログラムを作成する (Towerの単振動は前節のものと同じものを使う)。
各フレームでの処理手順は以下のようになる。
(1) Bladesに回転を実行 (これは Bladesの初期状態の位置である原点において行われる)。
(2) Bladesを Towerの指定位置まで移動。
(3) Towerと Bladesの両方に(水平方向の)単振動を実行する。
前節の用語を使えば、手順(2)において Bladesを Towerにアタッチしているのである。Towerが親オブジェクトであり、Bladesが子オブジェクトである。
[Code3] (実行結果 図8)
1行目から4行目までは Code2と同じである (TとRの積が ここでは localBladesとなっている)。6行目から8行目は、2-5節の Code3の1行目から3行目と同じである (ただし、ここでは水平方向の単振動は $y = 0$ の位置で行われる)。10行目の worldBlades = localTower * localBlades は Bladesに実行する変換行列であるが、この変換は、まず Bladesを初期位置である原点で回転させ、さらに Towerの指定位置に移動させる (localBlades)。次に、移動した位置から Bladesが、Towerと同じ(水平方向の)単振動を行うようにする (localTower)。Blades、Towerの両者に実行される localTowerは(水平方向の)単振動を行う平行移動行列であり、これによって Blades、Towerには同じだけの平行移動が実行される。ここで重要なのは Bladesの場合は移動した位置から単振動を行うということである。これによって Bladesは Tower上部の指定位置から単振動を行うようになり、Bladesと Towerが一体化して運動をすることになるのである。
最初の方のいくつかのフレームにおけるオブジェクトの変換過程、及びそれらのフレームをコマ送りしたものを図9、図10に示す。

図9 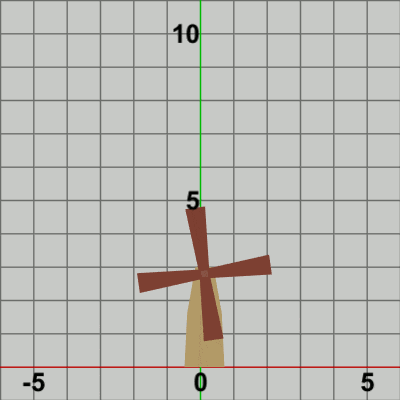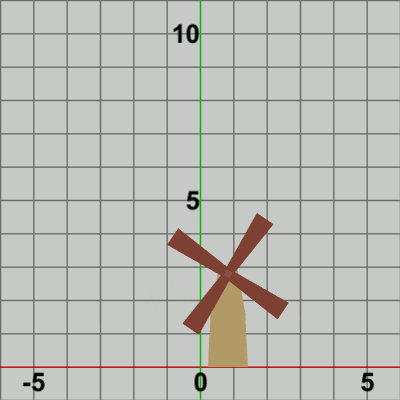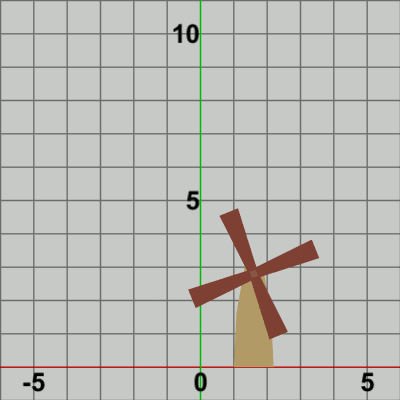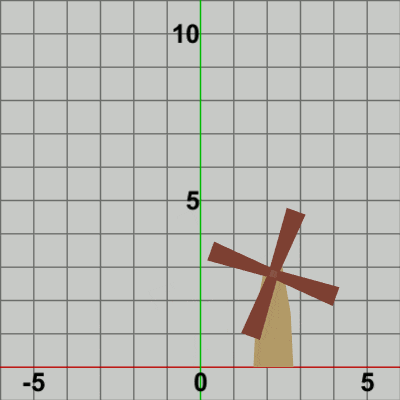
図10 コマ送り表示
図9では赤いフィルターのかかっている状態が変換行列の実行されている過程であり、通常色に切り替わった時点でフレーム描画が発生する。
白い文字で「localBlades」、「localTower」と表示されるが、「localBlades」と表示されている間が、プログラム4行目の変換行列localBladesが実行されている過程であり、「localTower」と表示されている間が、8行目の変換行列localTowerが実行されている過程である。「localBlades」が表示されている状態では、同時に「R * T」という文字も表示されており、それらは「R」「T」の順番で文字の色が青くなる。変換行列localBladesは回転行列Rと平行移動行列Tの積であり、localBladesを実行することは2つの変換行列R、Tをこの順序で実行することと同じである。文字「R」が青く表示されている状態は回転行列Rが実行されている過程であることを意味し、文字「T」が青く表示されている状態は平行移動行列Tが実行されている過程であることを意味している。
このプログラムでは i_degBlades は$8$ずつ増加し(1行目)、i_shmTower は$2$ずつ増加する(6行目)。すなわち、Bladesは毎フレーム$8$°ずつ回転し、Towerは毎フレーム単振動軌道上を$2$°分ずつ移動するということである。最初のフレームでは Bladesが$8$°回転し、アタッチポジションへ移動(BladesをTowerにアタッチ)、そして そのアタッチ後に Bladesと Towerが一体となって単振動軌道上を$2$°分移動し、フレーム描画が発生する。次のフレームでは Bladesが$16$°回転し、アタッチポジションへ移動(アタッチ)、そして そのアタッチ後に Bladesと Towerが一体となって単振動軌道上を$4$°分移動し、フレーム描画が発生する。それ以降のフレームでも同様の処理が繰り返される。
図10は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図8のアニメーションである)。


# Code1
まず始めに、Bladesを回転させる。Bladesは初期状態で、その中心が原点に置かれているので毎フレーム回転角度を増加(あるいは減少)させて、Bladesにその角度だけ回転する回転行列を実行すれば図3のように回転する。
[Code1] (実行結果 図3)
i_degBlades += 8; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degBlades); Blades.SetMatrix(R);


1行目の i_degBladesは現在のBladesの回転角度を表すインスタンス変数であり、そのフレームにおいて初期状態から何度回転するかを表している。毎フレーム $8$ずつ増加するので、Bladesは1フレームあたり$8$°ずつ回転する。
図4は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターのかかっている状態は、Bladesに対して実行される変換行列Rの実行過程であり、通常色の状態は変換行列Rの実行結果の状態である。通常色に切り替わった時点でフレーム描画が発生する。図4に示されるように、Bladesの回転は毎フレーム 初期状態から始まり、最初のフレームでは初期状態から$8$°回転した時点でフレーム描画が発生し、次のフレームでは初期状態から$16$°回転した時点でフレーム描画が発生する。以降のフレームでも同様である。描画されたフレームを連続的に表示したものが図3のアニメーションである。
# Code2

各フレームでの処理手順は次の通り。
(1) Bladesに回転を実行 (これは Bladesの初期状態の位置である原点において行われる)。
(2) BladesをTowerの指定位置まで移動。
プログラム中で使われる c_attachPos_Blades は、Bladesを初期状態の位置から Towerの指定位置に移動させるための移動量を表すVector2型の定数である。
[Code2] (実行結果 図5)
i_degBlades += 8; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degBlades); THMatrix3x3 T = TH2DMath.GetTranslation3x3(c_attachPos_Blades); THMatrix3x3 M = T * R; Blades.SetMatrix(M); Tower.SetMatrix(THMatrix3x3.identity);
1行目、2行目は前のコードと同じであり、Rは Bladesを回転させる行列である。3行目の $3\times3$行列Tは Bladesを Tower上部の指定位置に移動させる平行移動行列である。4行目 M = T * R は Bladesに実行される変換行列で、これら2つの変換を1つにまとめたものである。順序としては、まず Bladesを初期位置である原点で回転させ(R)、次に Towerの指定位置に移動させる(T)。
Towerは今回 初期状態のまま動かすことはないので、Towerに実行される変換行列は identity行列である(7行目)。


図6は Code2の最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。2-2節 Code4でも述べたが、オブジェクトの回転を原点以外の位置で行わせる場合には、毎フレーム まず オブジェクトを原点において回転させ、その状態(回転させた状態)で指定の位置まで移動させるという手順が基本である (ただし 回転の中心が原点に置かれていることが前提)。
Bladesに実行される変換行列Mは、上でも述べたように回転行列Rと平行移動行列Tの2つの変換を1つにまとめたもので、Mを実行した結果は R、Tをこの順序で実行した場合と同じ結果になる。図6のアニメーションでは、白い文字で R、T と表示されるが、Rが表示されている状態は Bladesに回転行列Rを実行している過程を意味し、Tが表示されている状態は Bladesに平行移動行列Tを実行している過程を意味している。最初のフレームでは Bladesは初期状態から$8$°回転し、回転した状態で Towerの指定位置まで移動するが、この移動が終わった時点でフレーム描画が発生する。次のフレームでは Bladesは初期状態から$16$°回転し、回転した状態でTowerの指定位置まで移動する。この移動が終わった時点でフレーム描画となる。それ以降のフレームにおいても同様の処理が繰り返される。
図7は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図5のアニメーションである)。
# Code3

各フレームでの処理手順は以下のようになる。
(1) Bladesに回転を実行 (これは Bladesの初期状態の位置である原点において行われる)。
(2) Bladesを Towerの指定位置まで移動。
(3) Towerと Bladesの両方に(水平方向の)単振動を実行する。
前節の用語を使えば、手順(2)において Bladesを Towerにアタッチしているのである。Towerが親オブジェクトであり、Bladesが子オブジェクトである。
[Code3] (実行結果 図8)
i_degBlades += 8; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degBlades); THMatrix3x3 T = TH2DMath.GetTranslation3x3(c_attachPos_Blades); THMatrix3x3 localBlades = T * R; i_shmTower += 2; float mx = 3.4f * Mathf.Sin(i_shmTower * Mathf.Deg2Rad); THMatrix3x3 localTower = TH2DMath.GetTranslation3x3(mx, 0.0f); THMatrix3x3 worldBlades = localTower * localBlades; THMatrix3x3 worldTower = localTower; Blades.SetMatrix(worldBlades); Tower.SetMatrix(worldTower);
1行目から4行目までは Code2と同じである (TとRの積が ここでは localBladesとなっている)。6行目から8行目は、2-5節の Code3の1行目から3行目と同じである (ただし、ここでは水平方向の単振動は $y = 0$ の位置で行われる)。10行目の worldBlades = localTower * localBlades は Bladesに実行する変換行列であるが、この変換は、まず Bladesを初期位置である原点で回転させ、さらに Towerの指定位置に移動させる (localBlades)。次に、移動した位置から Bladesが、Towerと同じ(水平方向の)単振動を行うようにする (localTower)。Blades、Towerの両者に実行される localTowerは(水平方向の)単振動を行う平行移動行列であり、これによって Blades、Towerには同じだけの平行移動が実行される。ここで重要なのは Bladesの場合は移動した位置から単振動を行うということである。これによって Bladesは Tower上部の指定位置から単振動を行うようになり、Bladesと Towerが一体化して運動をすることになるのである。
最初の方のいくつかのフレームにおけるオブジェクトの変換過程、及びそれらのフレームをコマ送りしたものを図9、図10に示す。


図9では赤いフィルターのかかっている状態が変換行列の実行されている過程であり、通常色に切り替わった時点でフレーム描画が発生する。
白い文字で「localBlades」、「localTower」と表示されるが、「localBlades」と表示されている間が、プログラム4行目の変換行列localBladesが実行されている過程であり、「localTower」と表示されている間が、8行目の変換行列localTowerが実行されている過程である。「localBlades」が表示されている状態では、同時に「R * T」という文字も表示されており、それらは「R」「T」の順番で文字の色が青くなる。変換行列localBladesは回転行列Rと平行移動行列Tの積であり、localBladesを実行することは2つの変換行列R、Tをこの順序で実行することと同じである。文字「R」が青く表示されている状態は回転行列Rが実行されている過程であることを意味し、文字「T」が青く表示されている状態は平行移動行列Tが実行されている過程であることを意味している。
このプログラムでは i_degBlades は$8$ずつ増加し(1行目)、i_shmTower は$2$ずつ増加する(6行目)。すなわち、Bladesは毎フレーム$8$°ずつ回転し、Towerは毎フレーム単振動軌道上を$2$°分ずつ移動するということである。最初のフレームでは Bladesが$8$°回転し、アタッチポジションへ移動(BladesをTowerにアタッチ)、そして そのアタッチ後に Bladesと Towerが一体となって単振動軌道上を$2$°分移動し、フレーム描画が発生する。次のフレームでは Bladesが$16$°回転し、アタッチポジションへ移動(アタッチ)、そして そのアタッチ後に Bladesと Towerが一体となって単振動軌道上を$4$°分移動し、フレーム描画が発生する。それ以降のフレームでも同様の処理が繰り返される。
図10は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図8のアニメーションである)。
© 2020-2025 Redpoll's 60 (All rights reserved)