Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-5
第2章 2D空間におけるオブジェクトの運動
$§$2-5 一体化したオブジェクトの運動 1
コンピューターグラフィックスにおいては2Dであれ3Dであれ、オブジェクトは階層的に構成されている場合が多い。そういったオブジェクトが運動する場合は階層関係にある全てのオブジェクトが一体化して運動するのである。このことについて、まず一番簡単な例から始めよう。
図1 Foundation 初期状態 
図2 Code1 実行結果
[Code1] (実行結果 図2)
1行目の i_shmFound は Foundationの単振動における角度を表すインスタンス変数であり、毎フレーム $2$ずつ増加する (すなわち単振動軌道上を$2$°分ずつ進む)。2行目は単振動の計算であり、3.0fは単振動の振幅を表し、この単振動計算は $-3$ から $3$ の間を往復することを意味する (単振動については 1-10節参照)。3行目の$3\times3$行列Tは、y軸方向に $-3$ から $3$ だけ移動させる平行移動行列であり、Foundationは初期状態で その下側の辺が $y = 4$ の位置にあるので、Tを実行することによって Foundationは $y = 4$ を中心に振幅$3$の単振動(ここでは上下運動)を行うことになる。
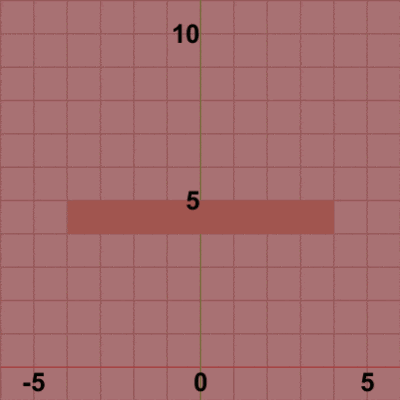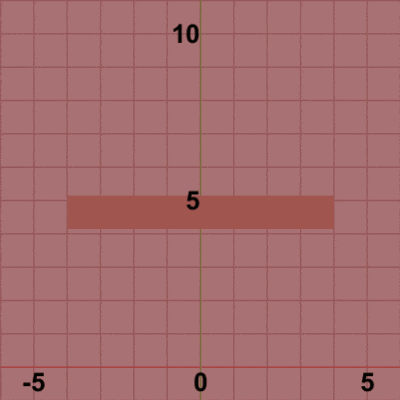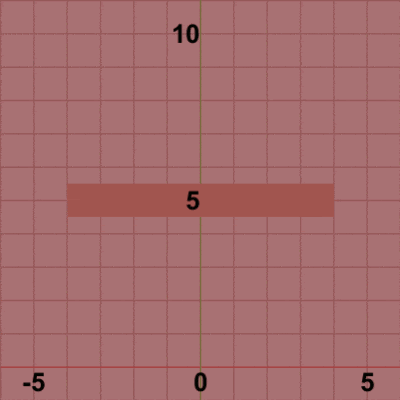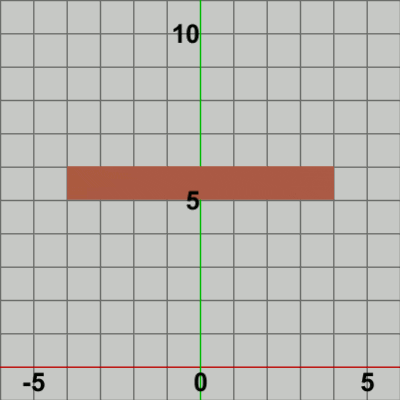
図3 図3は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターの状態のかかっている状態は、Foundationに実行される変換行列の実行過程であり、通常色の状態は変換行列が実行された実行結果の状態である。赤いフィルターの状態から通常色に切り替わった時点でフレーム描画が発生する。毎フレーム 初期状態の位置から単振動軌道上の指定位置に移動する (最初のフレームでは単振動軌道上を$2$°分進んだ位置、次のフレームでは$4$°分進んだ位置。それ以降も $6$°, $8$°, $10$° ... と進んでいく)。その移動した位置においてフレーム描画が発生する。描画された各フレームを連続的に表示すれば図2のアニメーションになる。
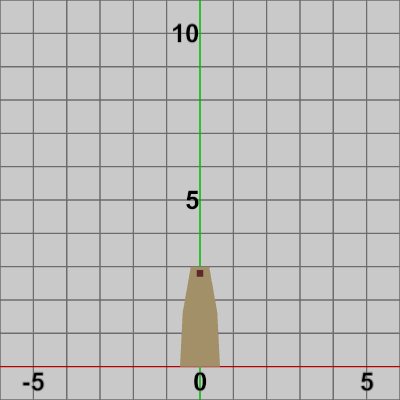
図4 Tower 初期状態 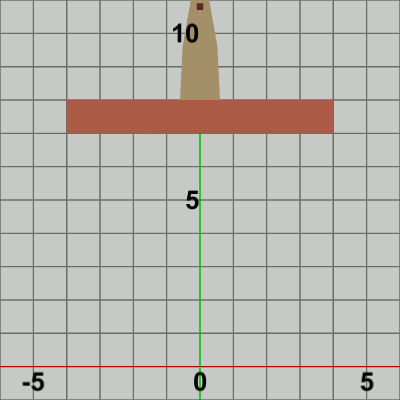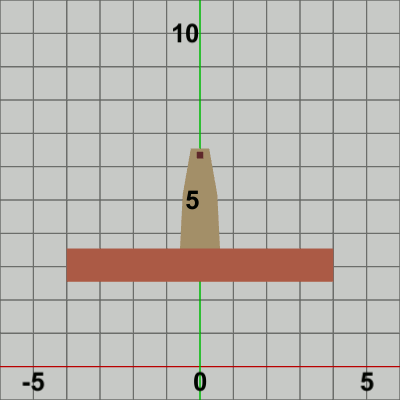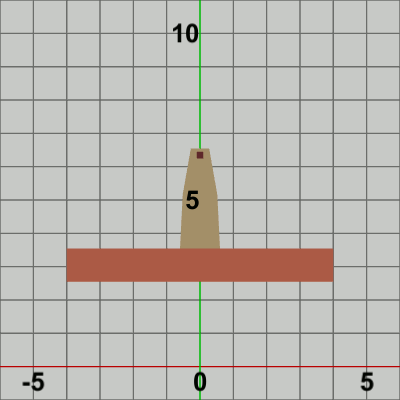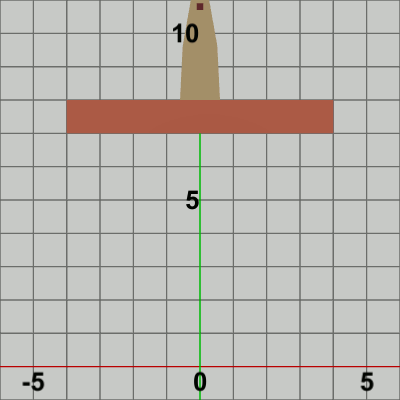
図5 Code2 実行結果
さて、このTowerをFoundationの中央に乗せた状態で、Foundationとともに単振動をするプログラムを以下に作成しよう。
手順は次の通り。
(1) TowerをFoundation上の指定位置(Foundationの上側の辺の中央)に移動させる(この時点ではFoundationは動かしていない)。
(2) TowerとFoundationの両方に単振動を実行する(具体的にはCode1で使った単振動行列を両者に実行する)。
[Code2] (実行結果 図5)
(2-3節と同様にここでも変換行列を表す変数に local や world という接頭辞が付けられている。これらは複数のオブジェクトを一体化させる際の形式的な記述であり、これ以降も頻繁に使用されるが、詳しい解説は第4章において行う)
c_attachPos_Towerは Towerを Foundation上の指定位置に移動させるための移動量を表すVector2型の定数である (値は$(0, 5)$である。この移動によりTowerの下側の辺がFoundationの上側の辺の中央に移動する)。この平行移動を実行する行列が localTower である。3行目から5行目はCode1の1行目から3行目と処理は同じであり、5行目で計算される localFound はCode1と同じく振幅$3$の単振動行列である。7行目の worldTower = localFound * localTower は Towerに実行する変換行列であるが、その内容は2つの変換行列 localTower、localFoundを1つにまとめたものである。この変換は、まず Towerを Foundationの指定位置に移動させ(localTower)、次にその位置から Towerが、Foundationと同じ平行移動を行うようにする(localFound)。ここで重要なのはTowerの場合は移動した位置から平行移動を行うということである。これによって Towerと Foundationに乗った状態で単振動(ここでは上下運動)をしているように見えるのである。
図6 
図7 コマ送り表示
図6は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。フレーム描画前の赤いフィルターのかかっている状態において白い文字で localTower、localFound と表示されるが、それらの文字が表示されている状態はプログラム中の変換行列 localTower、localFound が実行されている過程であることを意味する。
毎フレーム 変換は localTowerから始まるが、この変換は Towerを初期状態の位置から Foundationの指定位置(上側の辺の中央)まで平行移動させる処理で、その内容は毎フレーム変わらない。そして、Towerが Foundationの指定位置まで移動した時点で次の変換である localFoundが実行されるが、localFoundは Tower、Foundationの両者に実行されるので、Tower、Foundationは全く同じ運動を行う。具体的には、Foundationの場合は初期状態の位置である $y = 4$ の位置から、Towerの場合は Foundationの上側の辺の中央から 方向も移動量も同じ平行移動が行われるので、毎フレーム Towerが Foundationに乗っている状態でフレーム描画が発生する。
図7は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図5のアニメーションである)。
上に示した2つの手順を以下に別の形で述べよう。
(1) では、TowerをFoundation上の指定位置(Foundationの上側の辺)まで移動させて、この2つのオブジェクトをいわば一体化させたわけである。このように、あるオブジェクトを別のオブジェクトと一体化させるために、指定の位置あるいは指定の領域まで移動させることを、以降この講義ではアタッチと呼ぶことにする。

図8 今回の例ではTowerをFoundationにアタッチしたのである。また、アタッチされる側のオブジェクトを親オブジェクト、アタッチする側(移動する側)のオブジェクトを子オブジェクトと呼ぶことにする。今回の例では、Foundationが親でありTowerが子である。
(2) では、TowerとFoundationに同じ単振動行列localFoundを実行することによって、この2つのオブジェクトが一体となって単振動を行うようになったが、重要なのは(1)でTowerをアタッチしただけでは2つのオブジェクトが一体となって運動をするわけではないことである。今回の例では毎フレーム Towerに localTowerを実行して、Towerを Foundationにアタッチするが、その後、一体化して運動させるために Tower、Foundationの両者に localFoundを実行している。
プログラムでは次のコードである。
この部分を次のように記述してしまうと一体化した運動にはならないのである。
Code2の7行目をこのように記述した場合、実行結果は図8のようになる。
この場合には、Towerは毎フレーム Foundationの指定位置まで移動するが、その後 Towerに特に変換が起こるわけではないので、Towerは その位置のままフレーム描画が発生することになる (結果的には Foundationの位置だけが毎フレーム変化する)。
親オブジェクトと子オブジェクトを一体化して運動させるためには、親オブジェクトに実行する行列と同じものを、アタッチ後の子オブジェクトにも実行しなければならない。
手順は次の通り。
(1) Towerに対して単振動を実行する。単振動の内容は Foundationの上側の辺における水平方向の単振動とする(今回は Foundation上の固定位置ではないので毎フレーム移動させる位置は異なる)。
(2) Towerと Foundationの両方に垂直方向の単振動を実行する。
手順(2)についてはCode2と同じである。Code2の手順(1)では、Towerを毎フレームFoundation上の同じ位置にアタッチしていたが、今回は、Foundationの上側の辺において水平方向の単振動を行うので、毎フレーム Towerをアタッチする位置が異なる。
次のプログラムは手順(1)だけを実装したものである。
[Beta3] (実行結果 図9、図10)
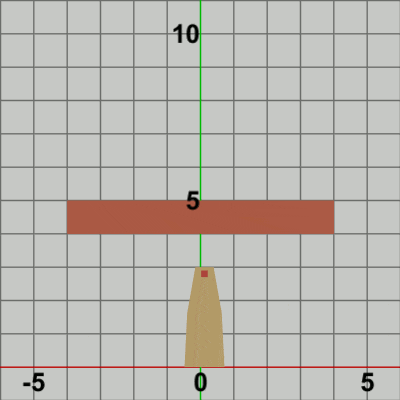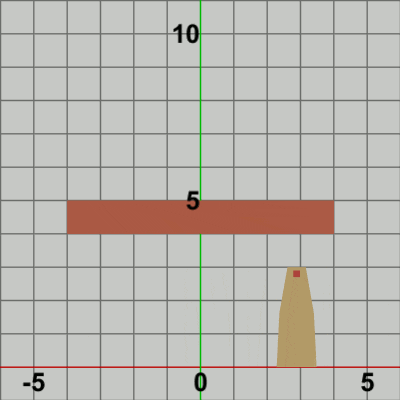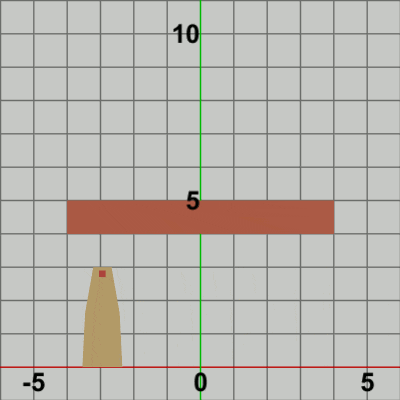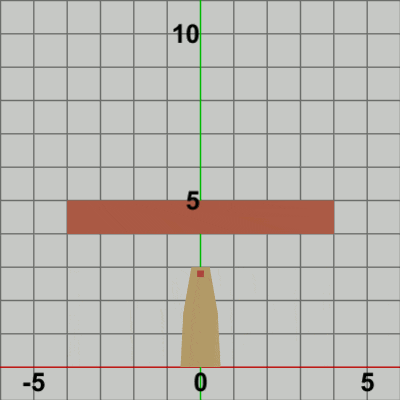
図9 Beta3 実行結果 (3行目の第2引数が 0.0f の場合) 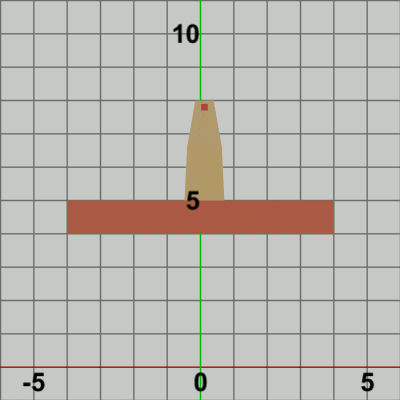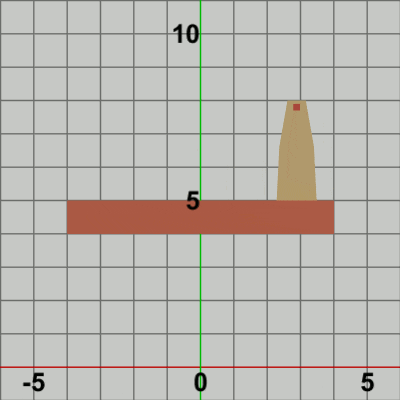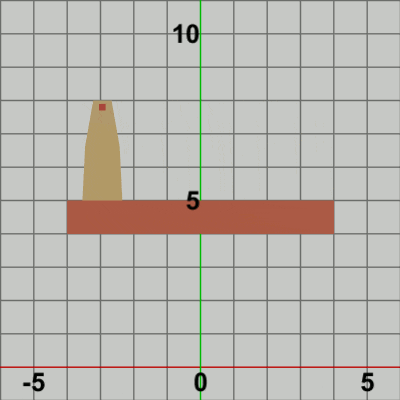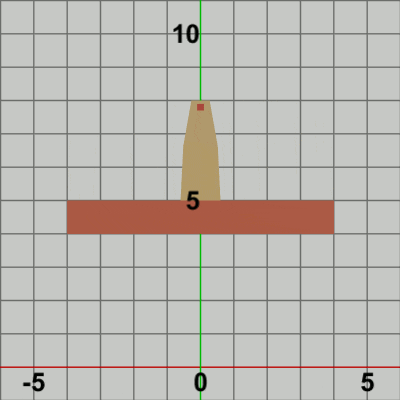
図10 Beta3 実行結果 (3行目の第2引数が 5.0f の場合)
1行目の i_shmTower は Towerの単振動おける角度を表すインスタンス変数であり、毎フレーム $2$ずつ増加する (すなわち単振動軌道上を$2$°分ずつ進む)。2行目は単振動の計算であり、3.4fは単振動の振幅を表し、この単振動計算は $-3.4$ から $3.4$ の間を往復することを意味する。3.4という数値になっているのは、この値であれば Towerの水平方向の単振動の範囲がちょうど Foundation上の端から端までの往復になる (Foundation上側の辺の半分の長さは$4$、Tower下側の辺の半分の長さは$0.6$である)。
3行目の$3\times3$行列localTowerは、上記の範囲の単振動を実行する平行移動行列であるが、この平行移動行列を取得するためのメソッドの第2引数には 5.0f という値が指定されている。この第2引数には平行移動行列のy軸方向の移動量を指定するが、このプログラムの場合では水平方向の単振動がy軸上のどの位置で行われるかにつながってくる。例えば、第2引数に 0.0f を指定したときは、Towerは y = 0 上(すなわち x軸上)において単振動を行うことになる (図9)。したがって、Foundation上側の辺で単振動を行わせるためには第2引数の値を 5.0f とすればよい。
実行結果(図10)を見ればわかるとおり、TowerがFoundation上で水平方向に単振動をするだけの結果になる (5行目の localFound はここでは identity行列であり、その内容は何も変換を実行しないという意味である)。
では、Foundationが垂直方向に単振動を行っており、その Foundation上において Towerが水平方向に単振動を行っているプログラムを作成する。
[Code3] (実行結果 図11)
このプログラムの5行目以降は Code2の3行目以降と同じである。Code2との違いは、Code2では localTowerの内容が毎フレーム Foundation上の指定位置までの平行移動であったのに対し、今回の Code3では Foundation上における単振動軌道上の各位置に毎フレーム移動することになる。すなわち、1行目から3行目は Beta3の1行目から3行目と同じである。
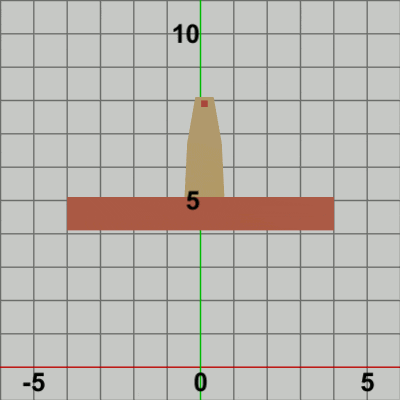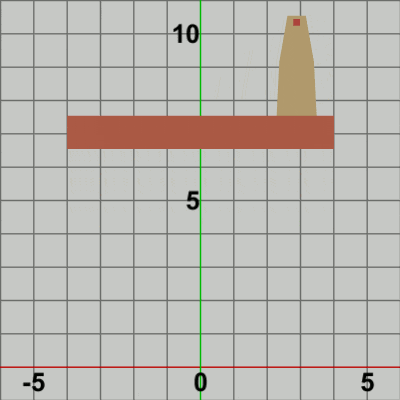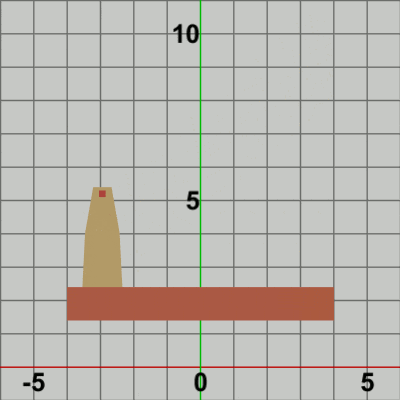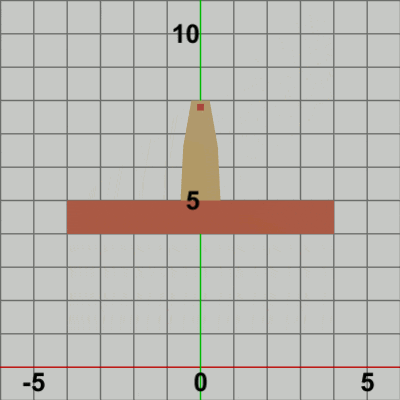
図11 Code3 実行結果 Beta3では localFoundは identity行列であったので、毎フレーム Towerが localTowerによって Foundation上に移動してもそこから先の動きはなかった (一体化して動くようなことがなかった)。そのために Beta3の実行結果(図10)では、Towerの単振動は、静止しているFoundation上での単振動となったのである。しかし、今回の localFound は、毎フレーム垂直方向の単振動のための平行移動を行う。すなわち、毎フレーム垂直方向の単振動軌道上の各位置に移動する。そして、Code2でそうであったように localFoundは Tower、Foundationの両者に実行される。つまり、Tower、Foundationの移動量は同じであり、Towerの場合は Foundation上に移動してから localFoundが実行されるので、実行結果においても Towerは Foundation上に乗った状態になっている。毎フレームこの処理が繰り返されるので、これらのフレームを連続的に表示すれば、垂直方向に単振動を行っているFoundationの上でTowerが水平方向に単振動を行っているという結果になるのである (図11)。
図12 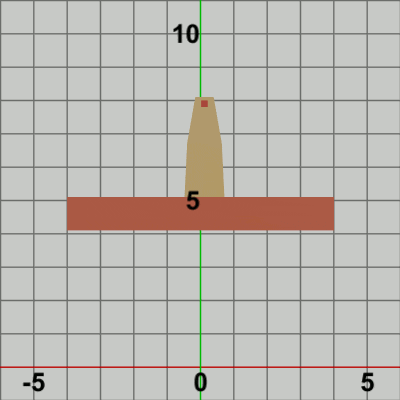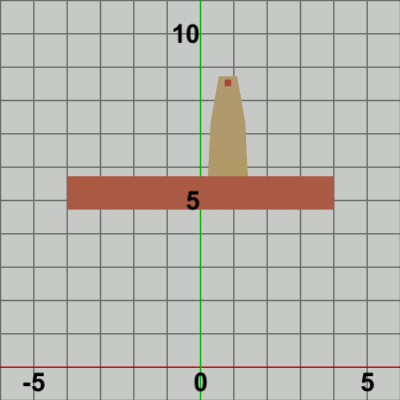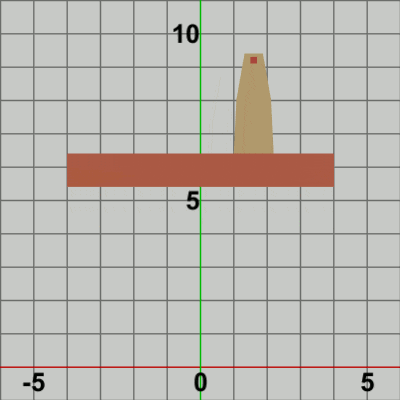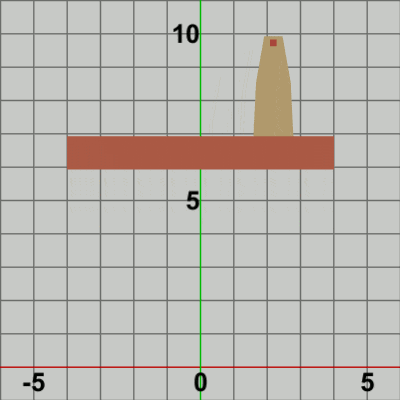
図13
図12は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。上で述べたように、Code2との違いは1点である。Code2では、毎フレーム Towerが Foundation上側の辺の中央へ移動し、そこから Tower、Foundationが一体となって垂直方向に移動したが(図6)、今回は Towerの移動先が Foundation上において毎フレーム異なる。localTowerによって Towerは毎フレーム 初期状態の位置から Foundation上における水平方向の単振動軌道上の各位置へ移動する。その後に localFoundによって Tower、Foundationが一体となって垂直方向への移動が行われ、 垂直方向の移動が終了した時点でフレーム描画となる。
図13は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図11のアニメーションである)。
最後にアタッチについて補足しておこう。
Code2では、Towerは毎フレーム Foundationの上側の辺の中央に移動していた。つまり、Code2ではTowerを親オブジェクトFoundationにアタッチする際の移動先は毎フレーム同じ位置であった。しかし、Code3では、TowerはFoundation上で水平方向の単振動を行うので、毎フレームの移動先は異なっていた。つまり、Code3の場合はTowerを親オブジェクトFoundationにアタッチする際の移動先は毎フレーム同じ位置ではなかった。
このように、子オブジェクトを親オブジェクトと一体化して運動させる場合には、子オブジェクトの移動先(アタッチポジション)は親オブジェクト上の常に同じ位置とは限らない。例えばCode3では、TowerをFoundationにアタッチする際の移動先は Foundationの上側の辺全体 となる。
親オブジェクトへのアタッチは、親オブジェクト上の常に同じ位置となる場合もあり、親オブジェクト上のある領域となる場合もあるのである。
# Code1
図1はオブジェクトFoundationの初期状態である。このオブジェクトの一番下の辺が$y = 4$に一致するように置かれている。Foundationが振幅$3$の範囲で単振動をするプログラムを以下に示す。

[Code1] (実行結果 図2)
i_shmFound += 2; float my = 3.0f * Mathf.Sin(i_shmFound * Mathf.Deg2Rad); THMatrix3x3 T = TH2DMath.GetTranslation3x3(0.0f, my); Foundation.SetMatrix(T);
1行目の i_shmFound は Foundationの単振動における角度を表すインスタンス変数であり、毎フレーム $2$ずつ増加する (すなわち単振動軌道上を$2$°分ずつ進む)。2行目は単振動の計算であり、3.0fは単振動の振幅を表し、この単振動計算は $-3$ から $3$ の間を往復することを意味する (単振動については 1-10節参照)。3行目の$3\times3$行列Tは、y軸方向に $-3$ から $3$ だけ移動させる平行移動行列であり、Foundationは初期状態で その下側の辺が $y = 4$ の位置にあるので、Tを実行することによって Foundationは $y = 4$ を中心に振幅$3$の単振動(ここでは上下運動)を行うことになる。

# Code2
さらにもう1つのオブジェクトTowerを用意する(図4)。初期状態で下側の辺がx軸に一致するように置かれている。

さて、このTowerをFoundationの中央に乗せた状態で、Foundationとともに単振動をするプログラムを以下に作成しよう。
手順は次の通り。
(1) TowerをFoundation上の指定位置(Foundationの上側の辺の中央)に移動させる(この時点ではFoundationは動かしていない)。
(2) TowerとFoundationの両方に単振動を実行する(具体的にはCode1で使った単振動行列を両者に実行する)。
[Code2] (実行結果 図5)
THMatrix3x3 localTower = TH2DMath.GetTranslation3x3(c_attachPos_Tower); i_shmFound += 2; float my = 3.0f * Mathf.Sin(i_shmFound * Mathf.Deg2Rad); THMatrix3x3 localFound = TH2DMath.GetTranslation3x3(0.0f, my); THMatrix3x3 worldTower = localFound * localTower; THMatrix3x3 worldFound = localFound; Tower.SetMatrix(worldTower); Foundation.SetMatrix(worldFound);
(2-3節と同様にここでも変換行列を表す変数に local や world という接頭辞が付けられている。これらは複数のオブジェクトを一体化させる際の形式的な記述であり、これ以降も頻繁に使用されるが、詳しい解説は第4章において行う)
c_attachPos_Towerは Towerを Foundation上の指定位置に移動させるための移動量を表すVector2型の定数である (値は$(0, 5)$である。この移動によりTowerの下側の辺がFoundationの上側の辺の中央に移動する)。この平行移動を実行する行列が localTower である。3行目から5行目はCode1の1行目から3行目と処理は同じであり、5行目で計算される localFound はCode1と同じく振幅$3$の単振動行列である。7行目の worldTower = localFound * localTower は Towerに実行する変換行列であるが、その内容は2つの変換行列 localTower、localFoundを1つにまとめたものである。この変換は、まず Towerを Foundationの指定位置に移動させ(localTower)、次にその位置から Towerが、Foundationと同じ平行移動を行うようにする(localFound)。ここで重要なのはTowerの場合は移動した位置から平行移動を行うということである。これによって Towerと Foundationに乗った状態で単振動(ここでは上下運動)をしているように見えるのである。


図6は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。フレーム描画前の赤いフィルターのかかっている状態において白い文字で localTower、localFound と表示されるが、それらの文字が表示されている状態はプログラム中の変換行列 localTower、localFound が実行されている過程であることを意味する。
毎フレーム 変換は localTowerから始まるが、この変換は Towerを初期状態の位置から Foundationの指定位置(上側の辺の中央)まで平行移動させる処理で、その内容は毎フレーム変わらない。そして、Towerが Foundationの指定位置まで移動した時点で次の変換である localFoundが実行されるが、localFoundは Tower、Foundationの両者に実行されるので、Tower、Foundationは全く同じ運動を行う。具体的には、Foundationの場合は初期状態の位置である $y = 4$ の位置から、Towerの場合は Foundationの上側の辺の中央から 方向も移動量も同じ平行移動が行われるので、毎フレーム Towerが Foundationに乗っている状態でフレーム描画が発生する。
図7は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図5のアニメーションである)。
上に示した2つの手順を以下に別の形で述べよう。
(1) では、TowerをFoundation上の指定位置(Foundationの上側の辺)まで移動させて、この2つのオブジェクトをいわば一体化させたわけである。このように、あるオブジェクトを別のオブジェクトと一体化させるために、指定の位置あるいは指定の領域まで移動させることを、以降この講義ではアタッチと呼ぶことにする。

(2) では、TowerとFoundationに同じ単振動行列localFoundを実行することによって、この2つのオブジェクトが一体となって単振動を行うようになったが、重要なのは(1)でTowerをアタッチしただけでは2つのオブジェクトが一体となって運動をするわけではないことである。今回の例では毎フレーム Towerに localTowerを実行して、Towerを Foundationにアタッチするが、その後、一体化して運動させるために Tower、Foundationの両者に localFoundを実行している。
プログラムでは次のコードである。
THMatrix3x3 worldTower = localFound * localTower; THMatrix3x3 worldFound = localFound;
この部分を次のように記述してしまうと一体化した運動にはならないのである。
THMatrix3x3 worldTower = localTower; THMatrix3x3 worldFound = localFound;
この場合には、Towerは毎フレーム Foundationの指定位置まで移動するが、その後 Towerに特に変換が起こるわけではないので、Towerは その位置のままフレーム描画が発生することになる (結果的には Foundationの位置だけが毎フレーム変化する)。
親オブジェクトと子オブジェクトを一体化して運動させるためには、親オブジェクトに実行する行列と同じものを、アタッチ後の子オブジェクトにも実行しなければならない。
# Code3
Code2ではTowerはFoundation上で固定されていたが、今回はTowerをFoundation上で水平方向に単振動させるプログラムを作成する。手順は次の通り。
(1) Towerに対して単振動を実行する。単振動の内容は Foundationの上側の辺における水平方向の単振動とする(今回は Foundation上の固定位置ではないので毎フレーム移動させる位置は異なる)。
(2) Towerと Foundationの両方に垂直方向の単振動を実行する。
手順(2)についてはCode2と同じである。Code2の手順(1)では、Towerを毎フレームFoundation上の同じ位置にアタッチしていたが、今回は、Foundationの上側の辺において水平方向の単振動を行うので、毎フレーム Towerをアタッチする位置が異なる。
次のプログラムは手順(1)だけを実装したものである。
[Beta3] (実行結果 図9、図10)
i_shmTower += 2; float mx = 3.4f * Mathf.Sin(i_shmTower * Mathf.Deg2Rad); THMatrix3x3 localTower = TH2DMath.GetTranslation3x3(mx, 5.0f); THMatrix3x3 localFound = THMatrix3x3.identity; THMatrix3x3 worldTower = localFound * localTower; THMatrix3x3 worldFound = localFound; Tower.SetMatrix(worldTower); Foundation.SetMatrix(worldFound);


1行目の i_shmTower は Towerの単振動おける角度を表すインスタンス変数であり、毎フレーム $2$ずつ増加する (すなわち単振動軌道上を$2$°分ずつ進む)。2行目は単振動の計算であり、3.4fは単振動の振幅を表し、この単振動計算は $-3.4$ から $3.4$ の間を往復することを意味する。3.4という数値になっているのは、この値であれば Towerの水平方向の単振動の範囲がちょうど Foundation上の端から端までの往復になる (Foundation上側の辺の半分の長さは$4$、Tower下側の辺の半分の長さは$0.6$である)。
3行目の$3\times3$行列localTowerは、上記の範囲の単振動を実行する平行移動行列であるが、この平行移動行列を取得するためのメソッドの第2引数には 5.0f という値が指定されている。この第2引数には平行移動行列のy軸方向の移動量を指定するが、このプログラムの場合では水平方向の単振動がy軸上のどの位置で行われるかにつながってくる。例えば、第2引数に 0.0f を指定したときは、Towerは y = 0 上(すなわち x軸上)において単振動を行うことになる (図9)。したがって、Foundation上側の辺で単振動を行わせるためには第2引数の値を 5.0f とすればよい。
実行結果(図10)を見ればわかるとおり、TowerがFoundation上で水平方向に単振動をするだけの結果になる (5行目の localFound はここでは identity行列であり、その内容は何も変換を実行しないという意味である)。
では、Foundationが垂直方向に単振動を行っており、その Foundation上において Towerが水平方向に単振動を行っているプログラムを作成する。
[Code3] (実行結果 図11)
i_shmTower += 2; float mx = 3.4f * Mathf.Sin(i_shmTower * Mathf.Deg2Rad); THMatrix3x3 localTower = TH2DMath.GetTranslation3x3(mx, 5.0f); i_shmFound += 2; float my = 3.0f * Mathf.Sin(i_shmFound * Mathf.Deg2Rad); THMatrix3x3 localFound = TH2DMath.GetTranslation3x3(0.0f, my); THMatrix3x3 worldTower = localFound * localTower; THMatrix3x3 worldFound = localFound; Tower.SetMatrix(worldTower); Foundation.SetMatrix(worldFound);
このプログラムの5行目以降は Code2の3行目以降と同じである。Code2との違いは、Code2では localTowerの内容が毎フレーム Foundation上の指定位置までの平行移動であったのに対し、今回の Code3では Foundation上における単振動軌道上の各位置に毎フレーム移動することになる。すなわち、1行目から3行目は Beta3の1行目から3行目と同じである。



図12は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。上で述べたように、Code2との違いは1点である。Code2では、毎フレーム Towerが Foundation上側の辺の中央へ移動し、そこから Tower、Foundationが一体となって垂直方向に移動したが(図6)、今回は Towerの移動先が Foundation上において毎フレーム異なる。localTowerによって Towerは毎フレーム 初期状態の位置から Foundation上における水平方向の単振動軌道上の各位置へ移動する。その後に localFoundによって Tower、Foundationが一体となって垂直方向への移動が行われ、 垂直方向の移動が終了した時点でフレーム描画となる。
図13は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図11のアニメーションである)。
最後にアタッチについて補足しておこう。
Code2では、Towerは毎フレーム Foundationの上側の辺の中央に移動していた。つまり、Code2ではTowerを親オブジェクトFoundationにアタッチする際の移動先は毎フレーム同じ位置であった。しかし、Code3では、TowerはFoundation上で水平方向の単振動を行うので、毎フレームの移動先は異なっていた。つまり、Code3の場合はTowerを親オブジェクトFoundationにアタッチする際の移動先は毎フレーム同じ位置ではなかった。
このように、子オブジェクトを親オブジェクトと一体化して運動させる場合には、子オブジェクトの移動先(アタッチポジション)は親オブジェクト上の常に同じ位置とは限らない。例えばCode3では、TowerをFoundationにアタッチする際の移動先は Foundationの上側の辺全体 となる。
親オブジェクトへのアタッチは、親オブジェクト上の常に同じ位置となる場合もあり、親オブジェクト上のある領域となる場合もあるのである。
© 2020-2025 Redpoll's 60 (All rights reserved)