Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-14
第2章 2D空間におけるオブジェクトの運動
$§$2-14 衝突判定 2
前節では円盤及び長方形の場合についての衝突判定について学習した。
本節では2D空間に配置されている円盤や長方形に対して、実際に Shellを当てるプログラムを作成し、前節で扱った衝突判定メソッドが意図した通りに動作するかを確認する。
以下の図1はオブジェクトPlaneの初期状態であり、本節以降2-17節まではキー操作による Shellの発射はこのPlaneから行う。
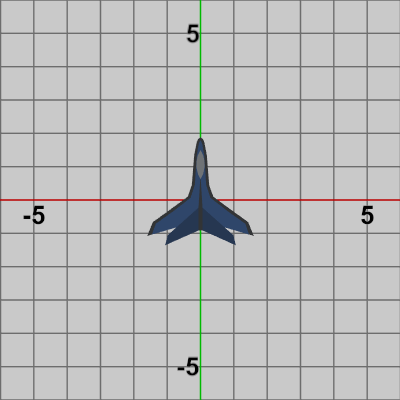
図1 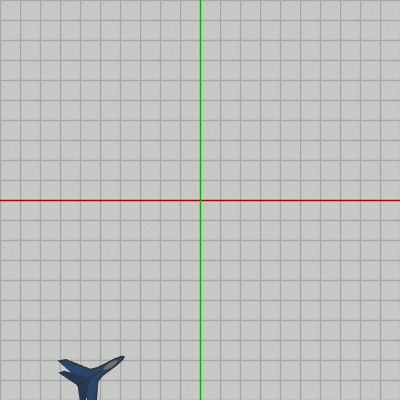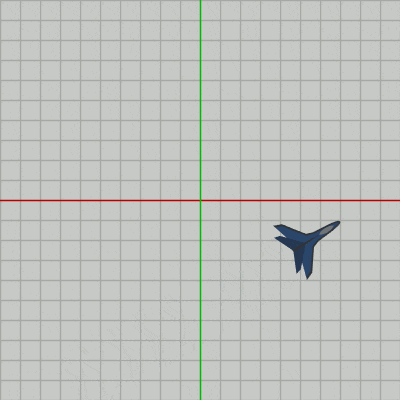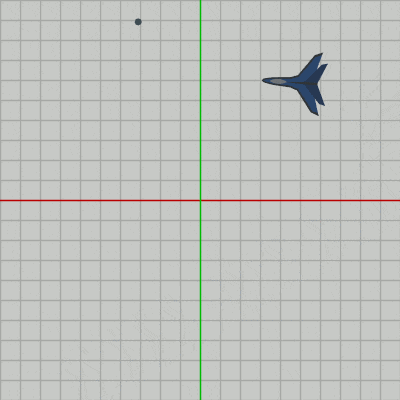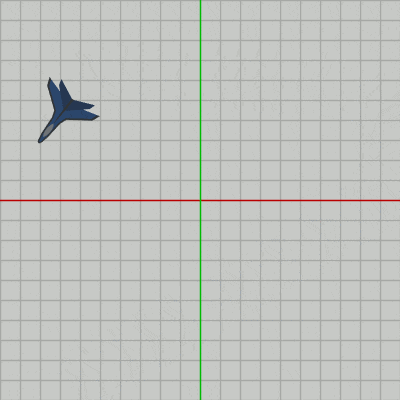
図2
以下のプログラムはキー操作によってPlaneを移動させ、Shellを発射するものであるが、その内容は2-11節 Code3と同様のものである。2-11節 Code3はヘリコプターの移動中あるいは移動した位置においてShellを(単発)発射するプログラムであった。今回は操作するオブジェクトがヘリコプターからPlaneに変わっただけである。2-11節のヘリコプターはBodyとRotorの2階層からなるオブジェクトであったが、今回のPlaneは親オブジェクトを持たない単一のオブジェクトであるため、2-11節 Code3よりもやや単純になっている。
また、Planeは単一のオブジェクトであるので、複数のオブジェクトを一体化させるプログラムで使用していた変換行列の接頭辞 local や world はここでは使用していない。
また、プログラム中ではShellは「OneShell」という名前で使われている。
[Code1] (実行結果 図2)
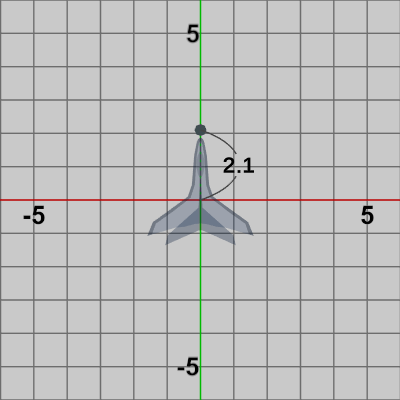
図3 27行目の 2.1f はPlaneからShellが発射される際の、Plane中心から発射開始位置までの距離である。具体的には、初期状態では図3に示されるようにPlaneは原点に置かれているが、このときShellを発射する場合、その発射開始位置は図に示されるように原点からPlaneの先端方向に$2.1$だけ離れた位置になる (プログラムの詳細に関しては2-11節で解説してきたことと同様あるのでここでは省略する)。
キー操作についても2-11節と同様である。
H : Planeの向きを反時計周りに回転 (回転は$1$°ずつ)。
L : Planeの向きを時計周りに回転。
S : オブジェクトの移動/停止用スイッチ。静止中に押すと、Planeの向いている方向へ(16行目のforwardDirの方向へ)一定速度で移動を開始する。再度キーを押すまでこの移動は続く。
A : Shellの発射 (長押しには対応していない)。
なお、本節及び次節では発射されたShellがオブジェクトと衝突した場合に、そのShellがオブジェクトと衝突したことがはっきりとわかるようにShellの発射は単発の発射にしている (キーの長押しによる連射にはなっていない)。Shellは1つのオブジェクトを使い回しているので、Shellの移動中にAキーを押すとそのShellは再度 発射開始位置に戻り、発射開始位置からの移動となる (Aキーを連打するとShellは発射開始位置に戻ることを繰り返す)。
これは、Code1のShell発射処理の部分であるが、プログラム内 27行目の startPos 及び 30行目の OneShell.direction の算出を次のように変更する。
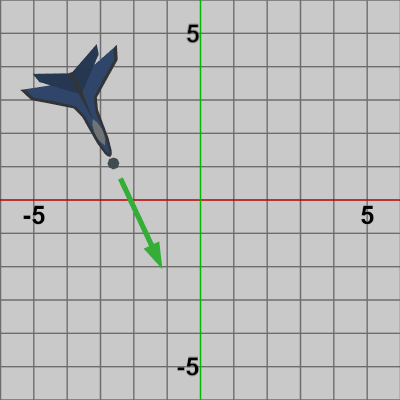
図4 前節の終わりに、ある時点での オブジェクト上の各位置の計算、あるいは ある時点におけるオブジェクトの方向の計算について見てきた。そこでは、ある時点でオブジェクトに実行されている変換行列を$M$とすれば、その時点でのオブジェクト上のある位置$A$は、初期状態におけるオブジェクト上の位置$A$(の同次座標)に変換行列$M$を掛けることによって求めることができ、その時点でのオブジェクトの方向は、初期状態におけるオブジェクトの方向に変換行列$M$を掛けることによって求めることができたのであった (ただし、方向の場合は同次座標のz成分を$0$にする)。
今回求めたいのは、ある時点における Shellの発射開始位置及び Shellの発射方向であるが、それらは図4でいえば Planeの先端から少し離れた位置及び その時点での Planeの方向(緑色の矢印)に等しい。
以下の図5は 初期状態のPlaneにおけるShellの発射開始位置及び 発射方向を示したものである (Shellの発射方向はPlaneの向きと同じである)。
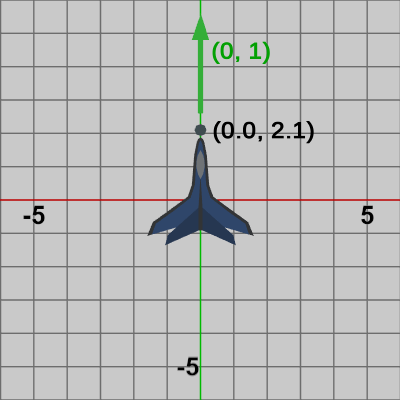
図5 前節で学習したことをここで適用すれば、ある時点において Planeから発射される Shellの発射開始位置は、その時点で Planeに実行されている変換行列と初期状態のPlaneにおけるShellの発射開始位置の積を計算することで求められる (Shellの発射開始位置はPlaneの外側にあるが、その位置もPlaneの一部とみなして考える)。また、ある時点において Planeから発射される Shellの発射方向は、その時点で Planeに実行されている変換行列と初期状態のPlaneにおけるShellの発射方向の積を計算することで求められる。
衝突判定のプログラムで使用されるオブジェクトはすべて、カスタムライブラリの THObject2D クラスを継承した THAlphaObject2D クラスのインスタンスであり、このクラスにはShell発射のために以下のプロパティが用意されている。
たとえば、Planeの場合であれば初期状態における Shellの発射開始位置は Plane.initShootPosition、発射方向は Plane.initShootDirection で取得できる。したがって この2つのプロパティを用いることにより、ある時点において Planeから発射される Shellの発射開始位置、発射方向は次のように計算される。
この計算方法を使うことで、Code1は次のように書き換えられる。
[Code2] (実行結果 図2)
Code1から変更された部分は2箇所あり、1つは上で述べた Code1 25行目のifブロック内の startPos、OneShell.direction の計算方法である。その部分は今回のCode2では33行目の ifブロックにおいて記述されている。35、38行目で使われているローカル変数 M は Planeに実行された変換行列である(30行目)。もう1つは、1行目に初期化ブロックが追加されており、このifブロックはプログラム開始時に1度だけ実行される (i_INITIALIZEDはbool型インスタンス変数で初期値はfalseである)。その内容は PlaneのShell発射に関する2つのプロパティ initShootPosition、initShootDirection の値を設定することである。ここでは、2つのプロパティには Vector2 の値がセットされているが、この2つのプロパティを取得する際には自動的に同次座標化されて Vector3 の値で返される。
このような形に書き換えたのは、後のプログラムでさまざまなオブジェクトが Shellを発射する場合に、Shellの発射開始位置、Shellの発射方向の計算をより統一的なものにしておくためである。
実行結果は、もちろん Code1と同じである (図2)。
2D空間内に図6に示されるように、3つの円盤オブジェクトが置かれている。これらのオブジェクトは半径の小さい順に Disk0、Disk1、Disk2という名前で初期状態では図7に示されるように、その中心が原点に置かれている。
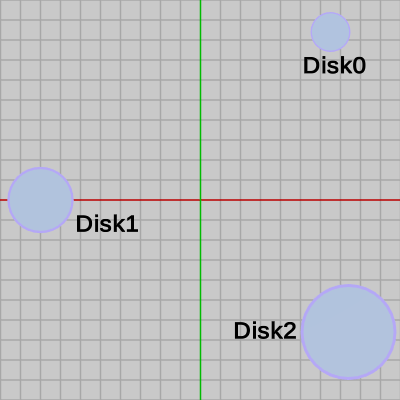
図6 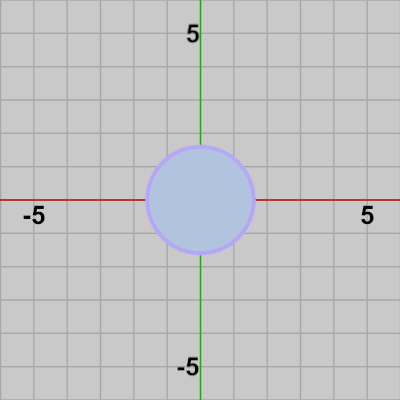
図7 3つのDiskは初期状態ではその中心が原点に置かれている (上図はDisk1の初期状態)
以下が実際のプログラムであるが、これ以降のプログラムについては前半部分(Planeを動かしてShellを発射させる部分 ; 44行目まで)はCode2と同じなので、衝突判定に関係のある後半部分のみを表示する。
[Code3] (実行結果 図9)
53行目のforeach文で使われている i_collisionObjects は、衝突判定対象となるオブジェクトがセットされた配列(インスタンス変数)であり、このプログラムでは以下のように3つのDiskがセットされている。
先程少し触れたが本節から2-17節の衝突判定のプログラムで使われるオブジェクトは THObject2Dクラスを継承した衝突判定用のクラスである THAlphaObject2Dクラスのインスタンスになっている。THAlphaObject2Dクラスには衝突判定に必要となるデータを取得するためのプロパティがいくつか用意されているが、例えば次のようなものである。
また、プログラム中でも使われている GetPosition()、SetPosition(a, b) は今までにも何度か使われてきたが、この2つのメソッドは THObject2Dクラスのメソッドであり、GetPosition()はオブジェクトの現在位置がVector2型で返される (正確には初期状態からどれだけ平行移動したかがVector2型で返される)。
SetPosition(a, b)は、オブジェクトを初期状態の位置から $(a, b)$ だけの平行移動を実行するためのメソッドであり、行列で記述すれば以下の処理に等しい。
たとえば、46行目では Disk0.SetPosition(6.0f, 8.0f) によって Disk0を初期状態の位置から $(6, 8)$ だけ平行移動させている。その後の foreachループ内の55行目では obj.GetPosition() という処理が実行されるが、ここでの obj は Disk0、Disk1、Disk2のいずれかである。Disk0の場合であれば、GetPosition() は上記46行目で設定した (6.0f, 8.0f) が返されることになる。
各Diskはその中心が初期状態において原点に置かれているので、Diskの場合 GetPosition() で返される値は現時点でのDiskの中心の位置を表すことになる。
プログラム自体は単純な構成である。46行目から48行目で各Diskを適当な位置に配置し、51行目においてShellの現在位置を取得する。53行目のforeachループはシーン内の全てのオブジェクト1つ1つに対して衝突判定を行うものである。このプログラムでは3つのオブジェクト Disk0、Disk1、Disk2に対して衝突判定を行うが、使用されるメソッドは前節で作成した円盤用の衝突判定メソッド CollisionTest_Point_Disk(..) である。
[CollisionTest_Point_Disk(..)]
メソッドに送られてくる引数 P、C、r はそれぞれShellの現在位置、Diskの現在の中心位置、Diskの半径であり、Code3では51行目、55行目、56行目で取得される。また、以下の図8は前節でも用いたものだが、図中の $P$、$C$、$r$ が表すものはメソッドの引数と同じである (図中の $d$ は CollisionTest_Point_Disk(..) 3行目の d のことで、ShellからDiskの中心位置までの距離を表している)。

図8 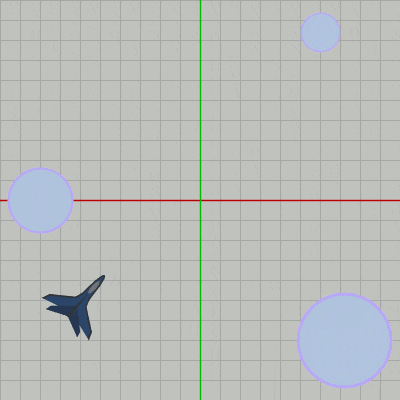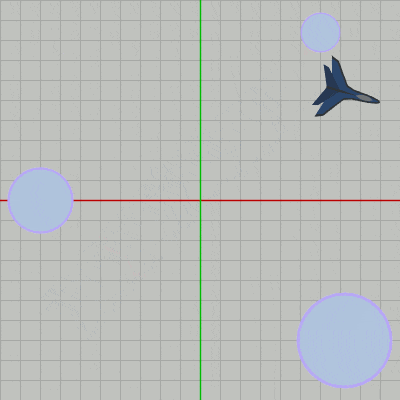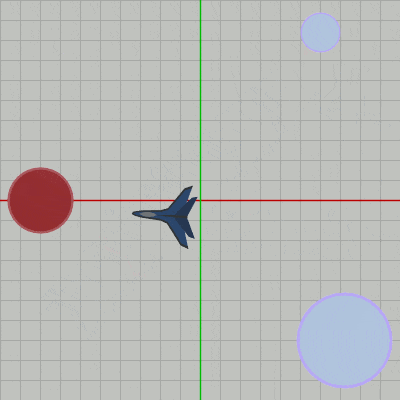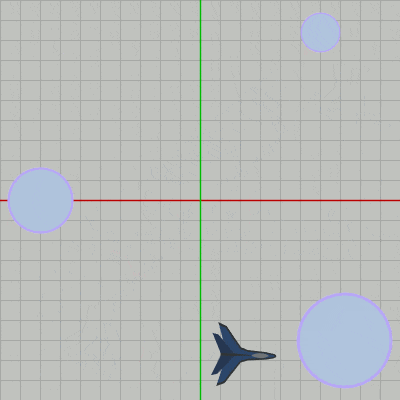
図9 Code3 実行結果
図9はプログラムの実行結果である。ShellとDiskが衝突した際にDiskが赤い色に変わるが、この処理はプログラム60行目の Hit(..) という一時的に用意されたメソッドによるものである (このメソッドは本節から2-17節のプログラムで使われるだけのカスタムメソッドである)。
ShellとDiskとの間で衝突が発生すると57行目の CollisionTest_Point_Disk(..) がtrueを返し58行目のifブロックに入るが、そこで この Hit(..) が実行される。Hit(..) は THAlphaObject2D型のオブジェクトを引数に設定し、引数として送られてきたオブジェクトをわずかの間赤く表示するだけの処理を行うもので、衝突が起こったことを視覚的に確認できるようにするためのものであり、それ以外に特に重要な役割を持っているわけではない (そのため、Hit(..) の解説はここでは省略するが、オブジェクトの色を実行中に変更するなどについては後の章において解説する)。
また、このプログラムでは実行中の画面内には1つのShellしか存在しないので、あるオブジェクトとの衝突が検出され Hit(..) が実行された後は、他のオブジェクトとの衝突を調べずに61行目でforeachループをbreakする。
今回は図10のように2つの軸平行な長方形 Rect0、Rect1と、2つの傾きのある長方形 Rect2、Rect3が適当な位置に配置されている。それぞれの長方形は図11に示されるように初期状態では軸平行であり、その中心が原点に置かれている。
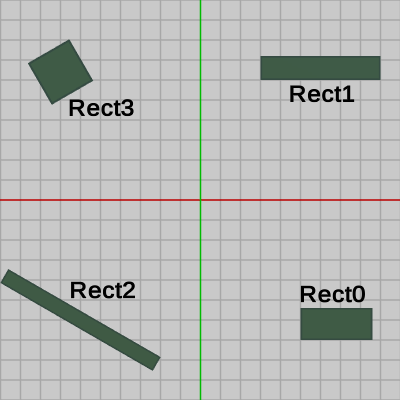
図10 
図11
[Code4] (実行結果 図12)

図12 Code4 実行結果 46行目から60行目で4つのRectを適当な位置に配置し、63行目においてShellの現在位置を取得し shell_pos へセットする。65行目のforeachループにおいて4つのRectとの衝突判定を1つ1つ順番に行っていく。もし ShellがRectの1つと衝突していれば73行目の Hit(..) が実行され、Shellと衝突したRectが一時的に赤い色に変化する。
67行目の initRectBounds は上で述べたように長方形の初期状態における左下隅、右上隅の座標を Vector2[]型で取得するものであり、ここではローカル変数 bounds にセットされる。68行目の mtx は長方形オブジェクトに実行された変換行列を表しており、69行目の mtx.inverse は mtx の逆行列である。
65行目のforeachループで使用されている i_collisionObjects は先程のプログラムと同様に、衝突判定対象となるオブジェクトがセットされている配列(インスタンス変数)である。今回は4つのRectであり、次のように初期化されている。

図13 図13はCode4実行中のあるフレームにおいて Planeから発射された Shellが、シーン内の長方形オブジェクト Rect2に衝突したときの様子である (Shellの位置をわかりやすくするために、ここではShellを水色にしてある)。このときのShellの位置はプログラム63行目の shell_pos によって表される。Rect2には $-30$°の回転、$(-6, -6)$ の平行移動がこの順序で実行されており、図13に示されるように Rect2の中心位置は $(-6, -6)$ に移動している。
$-30$°の回転を表す行列を$R$、$(-6, -6)$ の平行移動を表す行列を$T$とし、その積を $M = TR$ とする。Rect2にはこの回転と平行移動を1つにまとめた変換行列$M$が実行されているわけであるが、ここでは Rect2 に、この変換行列$M$の逆行列を実行して、Rect2を初期状態に戻すことを考える。$M = TR$ の逆行列は \[ M^{-1} = (TR)^{-1} = R^{-1}T^{-1} \]であるが、$T^{-1}$ の内容は $(6, 6)$ の平行移動であり、$R^{-1}$ の内容は $30$°の回転であるから、$R^{-1}T^{-1}$ が意味する変換は、$(6, 6)$ の平行移動、$30$°の回転をこの順序で実行するものである。
以下の図14は図13から他のオブジェクトを非表示にしたものであり、Rect2には変換行列$M$が実行されている。ここで、$(6, 6)$ の平行移動を実行したときの結果が図15であり、さらにその状態から $30$°の回転を実行したときの結果が図16である。つまり、図14のRect2に逆行列$M^{-1}$を実行した結果が図16のRect2であり、図16では Rect2は初期状態に戻っている。Shellに対しても同じ逆行列が実行されているので、図16では初期状態のRect2に対してShellが衝突した状態になっている。図16におけるShellの位置 $P$ がプログラムにおける69行目の P のことである。
そして、上で述べた bounds、P を用いて70行目では衝突判定を行うが、ここで使用されるメソッドは前節で作成した長方形用の衝突判定メソッド CollisionTest_Point_AABB(..) である。
[CollisionTest_Point_AABB(..)]
CollisionTest_Point_AABB(..)は軸平行な長方形の左下隅の頂点 min と右上隅の頂点 max の間に引数 P が含まれるかを判定するものである。したがって、第2引数の minmax は軸平行な長方形の左下隅、右上隅の頂点座標がセットされた配列でなければならない。
オブジェクトに運動をさせるため、その部分のコードが追加されてはいるが、衝突判定の部分についてはオブジェクトが運動をしている場合でも、内容の点では今までのものとほとんど変わりはない。
[Code5] (実行結果 図18)
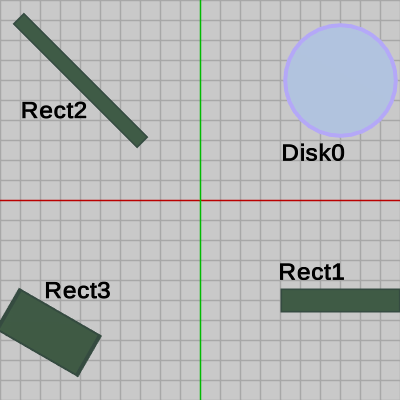
図17 
図18 Code5 実行結果
今回、使われるオブジェクトは1つの円盤オブジェクトのと3つの長方形オブジェクトで図17のように配置されている。
図18の実行結果に見られるように、このプログラムではこれら4つのオブジェクトがそれぞれ運動を行っている。Disk0は指定の位置において拡大縮小を繰り返し、Rect1は上下方向の単振動を行っている (図右下)。また、Rect2は指定の位置において回転しており (図左上)、Rect3は指定の位置において拡大縮小を行っている (図左下)。これらの運動はプログラム中の46行目から67行目において記述されている。たとえば、Disk0の拡大縮小は$1$倍から$3$倍の範囲を往復するが、この倍率は47行目で単振動を使って計算される。Rect1の往復運動における位置や Rect3の拡大縮小の倍率も同様に単振動から算出される。プログラム中で使われているインスタンス変数 i_shm、i_deg は、それぞれ単振動のための角度、回転のための角度である。
また、今回も衝突判定の対象となるオブジェクトは i_collisionObjects に次のようにセットされている。
69行目以降が衝突判定の処理であるが、衝突判定の対象オブジェクトが今回は2種類であるため、72行目の foreachループ内では CollisionTest_AllTypes(..) というメソッドを呼んでいる。このメソッドは衝突判定対象のオブジェクトの種類が複数ある場合のためのもので、各衝突判定メソッドの入り口の役目を果たしている。
[CollisionTest_AllTypes(..)]
衝突判定のプログラムで使われる THAlphaObject2Dクラスには GetType() というメソッドが用意されており、メソッド名から明らかなようにそのオブジェクトの種類が返される。4行目の switch文の冒頭で衝突判定対象のオブジェクトの種類を取得し、オブジェクトが円盤であれば6行目の case に処理が移り、長方形であれば12行目の case に処理が移る。
8行目は円盤オブジェクトの半径を求める計算であるが、計算で使われている GetDiskScale() は円盤オブジェクトに実行されているスケール倍率を返すメソッドである (THAlphaObject2Dクラスのメソッド ; 円盤オブジェクトでない場合は $1$ が返される)。今回のプログラムにおいては Disk0 は拡大縮小をしているので、常に半径が変化する。そのような場合においても、初期状態の半径に現在実行されているスケール倍率を掛けることで、その時点での半径を求めることができる。
また、図18左下の長方形 Rect3 も拡大縮小を行っているが、拡大縮小をしている長方形オブジェクトとの衝突判定も上で述べた方法が使える。すなわち、長方形オブジェクトに逆行列を実行して初期状態に戻した状態で考える方法である。
あるオブジェクトにShellが衝突しているかどうかを調べるにあたって、そのオブジェクトを初期状態に戻した状態で考えるという方法は長方形のような単純な形のオブジェクトばかりではなく、より複雑な一般形状のオブジェクトに対しても適用できるが、その点については次節で解説する。
本節では2D空間に配置されている円盤や長方形に対して、実際に Shellを当てるプログラムを作成し、前節で扱った衝突判定メソッドが意図した通りに動作するかを確認する。
# Code1
しかし、衝突判定を始める前に本節と次節のプログラムにおいて、Shellを発射するオブジェクトの操作の仕方から解説する。以下の図1はオブジェクトPlaneの初期状態であり、本節以降2-17節まではキー操作による Shellの発射はこのPlaneから行う。


以下のプログラムはキー操作によってPlaneを移動させ、Shellを発射するものであるが、その内容は2-11節 Code3と同様のものである。2-11節 Code3はヘリコプターの移動中あるいは移動した位置においてShellを(単発)発射するプログラムであった。今回は操作するオブジェクトがヘリコプターからPlaneに変わっただけである。2-11節のヘリコプターはBodyとRotorの2階層からなるオブジェクトであったが、今回のPlaneは親オブジェクトを持たない単一のオブジェクトであるため、2-11節 Code3よりもやや単純になっている。
また、Planeは単一のオブジェクトであるので、複数のオブジェクトを一体化させるプログラムで使用していた変換行列の接頭辞 local や world はここでは使用していない。
また、プログラム中ではShellは「OneShell」という名前で使われている。
[Code1] (実行結果 図2)
if (Input.GetKey(KeyCode.H))
{
i_forwardDegree += 2;
}
else if (Input.GetKey(KeyCode.L))
{
i_forwardDegree -= 2;
}
if (Input.GetKeyDown(KeyCode.S)) // 移動/停止
{
i_MOVE = !i_MOVE;
}
THMatrix3x3 R = TH2DMath.GetRotation3x3(i_forwardDegree);
Vector2 forwardDir = R * new Vector3(0, 1, 1);
Vector2 curP = Plane.GetPosition();
Vector2 newP = (i_MOVE) ? curP + 0.12f * forwardDir : curP;
THMatrix3x3 T = TH2DMath.GetTranslation3x3(newP);
THMatrix3x3 M = T * R;
Plane.SetMatrix(M);
// Shell
if (Input.GetKeyDown(KeyCode.A))
{
Vector2 startPos = newP + 2.1f * forwardDir;
OneShell.SetPosition(startPos);
OneShell.direction = forwardDir;
}
else
{
Vector2 newShellPos = OneShell.GetPosition() + 0.50f * OneShell.direction;
OneShell.SetPosition(newShellPos);
}

キー操作についても2-11節と同様である。
H : Planeの向きを反時計周りに回転 (回転は$1$°ずつ)。
L : Planeの向きを時計周りに回転。
S : オブジェクトの移動/停止用スイッチ。静止中に押すと、Planeの向いている方向へ(16行目のforwardDirの方向へ)一定速度で移動を開始する。再度キーを押すまでこの移動は続く。
A : Shellの発射 (長押しには対応していない)。
なお、本節及び次節では発射されたShellがオブジェクトと衝突した場合に、そのShellがオブジェクトと衝突したことがはっきりとわかるようにShellの発射は単発の発射にしている (キーの長押しによる連射にはなっていない)。Shellは1つのオブジェクトを使い回しているので、Shellの移動中にAキーを押すとそのShellは再度 発射開始位置に戻り、発射開始位置からの移動となる (Aキーを連打するとShellは発射開始位置に戻ることを繰り返す)。
# Code2
Code1ではPlaneがShellを発射する処理を実装したが、プログラム自体は2-11節や2-12節で扱った、ヘリコプターや戦車からのShellの単発発射プログラムをPlane版に書き換えたといった程度のものである。ここでは、Code1のShellの発射処理について多少の変更を行う。それは次の部分である。
// Shell
if (Input.GetKeyDown(KeyCode.A))
{
Vector2 startPos = newP + 2.1f * forwardDir;
OneShell.SetPosition(startPos);
OneShell.direction = forwardDir;
}
else
{
Vector2 newShellPos = OneShell.GetPosition() + 0.50f * OneShell.direction;
OneShell.SetPosition(newShellPos);
}
これは、Code1のShell発射処理の部分であるが、プログラム内 27行目の startPos 及び 30行目の OneShell.direction の算出を次のように変更する。

今回求めたいのは、ある時点における Shellの発射開始位置及び Shellの発射方向であるが、それらは図4でいえば Planeの先端から少し離れた位置及び その時点での Planeの方向(緑色の矢印)に等しい。
以下の図5は 初期状態のPlaneにおけるShellの発射開始位置及び 発射方向を示したものである (Shellの発射方向はPlaneの向きと同じである)。

衝突判定のプログラムで使用されるオブジェクトはすべて、カスタムライブラリの THObject2D クラスを継承した THAlphaObject2D クラスのインスタンスであり、このクラスにはShell発射のために以下のプロパティが用意されている。
Vector3 initShootPosition
: オブジェクトの初期状態における Shellの発射開始位置を同次座標の形で取得するためのプロパティ。そのz成分は $1$。Vector3 initShootDirection
: オブジェクトの初期状態における Shellの発射方向を同次座標の形で取得するためのプロパティ。そのz成分は $0$。たとえば、Planeの場合であれば初期状態における Shellの発射開始位置は Plane.initShootPosition、発射方向は Plane.initShootDirection で取得できる。したがって この2つのプロパティを用いることにより、ある時点において Planeから発射される Shellの発射開始位置、発射方向は次のように計算される。
THMatrix3x3 M = Plane.GetMatrix(); Vector2 startPos = M * Plane.initShootPosition; // 発射開始位置 Vector2 shellDir = (M * Plane.initShootDirection).normalized; // 発射方向
この計算方法を使うことで、Code1は次のように書き換えられる。
[Code2] (実行結果 図2)
if (!i_INITIALIZED)
{
Plane.initShootPosition = new Vector2(0.0f, 2.1f);
Plane.initShootDirection = new Vector2(0.0f, 1.0f);
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.H))
{
i_forwardDegree += 2;
}
else if (Input.GetKey(KeyCode.L))
{
i_forwardDegree -= 2;
}
if (Input.GetKeyDown(KeyCode.S)) // 移動/停止
{
i_MOVE = !i_MOVE;
}
THMatrix3x3 R = TH2DMath.GetRotation3x3(i_forwardDegree);
Vector2 forwardDir = R * new Vector3(0, 1, 1);
Vector2 curP = Plane.GetPosition();
Vector2 newP = (i_MOVE) ? curP + 0.12f * forwardDir : curP;
THMatrix3x3 T = TH2DMath.GetTranslation3x3(newP);
THMatrix3x3 M = T * R;
Plane.SetMatrix(M);
// Shell
if (Input.GetKeyDown(KeyCode.A))
{
Vector2 startPos = M * Plane.initShootPosition;
OneShell.SetPosition(startPos);
OneShell.direction = (M * Plane.initShootDirection).normalized;
}
else
{
Vector2 newShellPos = OneShell.GetPosition() + 0.50f * OneShell.direction;
OneShell.SetPosition(newShellPos);
}
Code1から変更された部分は2箇所あり、1つは上で述べた Code1 25行目のifブロック内の startPos、OneShell.direction の計算方法である。その部分は今回のCode2では33行目の ifブロックにおいて記述されている。35、38行目で使われているローカル変数 M は Planeに実行された変換行列である(30行目)。もう1つは、1行目に初期化ブロックが追加されており、このifブロックはプログラム開始時に1度だけ実行される (i_INITIALIZEDはbool型インスタンス変数で初期値はfalseである)。その内容は PlaneのShell発射に関する2つのプロパティ initShootPosition、initShootDirection の値を設定することである。ここでは、2つのプロパティには Vector2 の値がセットされているが、この2つのプロパティを取得する際には自動的に同次座標化されて Vector3 の値で返される。
このような形に書き換えたのは、後のプログラムでさまざまなオブジェクトが Shellを発射する場合に、Shellの発射開始位置、Shellの発射方向の計算をより統一的なものにしておくためである。
実行結果は、もちろん Code1と同じである (図2)。
# Code3
まずは、Shellと円盤との衝突から始める。2D空間内に図6に示されるように、3つの円盤オブジェクトが置かれている。これらのオブジェクトは半径の小さい順に Disk0、Disk1、Disk2という名前で初期状態では図7に示されるように、その中心が原点に置かれている。


以下が実際のプログラムであるが、これ以降のプログラムについては前半部分(Planeを動かしてShellを発射させる部分 ; 44行目まで)はCode2と同じなので、衝突判定に関係のある後半部分のみを表示する。
[Code3] (実行結果 図9)
// ..
// 44行目まではCode2と同じ
// ..
Disk0.SetPosition(6.0f, 8.0f);
Disk1.SetPosition(-12.0f, 0.0f);
Disk2.SetPosition(12.0f, -6.0f);
// Collision Test
Vector2 shell_pos = OneShell.GetPosition();
foreach(var obj in i_collisionObjects)
{
Vector2 C = obj.GetPosition();
float r = obj.initRadius;
bool bColl = CollisionTest_Point_Disk(shell_pos, C, r);
if (bColl)
{
Hit(obj);
break;
}
}
53行目のforeach文で使われている i_collisionObjects は、衝突判定対象となるオブジェクトがセットされた配列(インスタンス変数)であり、このプログラムでは以下のように3つのDiskがセットされている。
// 衝突判定対象となるオブジェクト
i_collisionObjects = new THAlphaObject2D[] { Disk0, Disk1, Disk2 };
先程少し触れたが本節から2-17節の衝突判定のプログラムで使われるオブジェクトは THObject2Dクラスを継承した衝突判定用のクラスである THAlphaObject2Dクラスのインスタンスになっている。THAlphaObject2Dクラスには衝突判定に必要となるデータを取得するためのプロパティがいくつか用意されているが、例えば次のようなものである。
float initRadius
: 円盤オブジェクトの場合に、初期状態の円盤の半径を取得する (円盤オブジェクトでない場合は$0$が返される)。Vector2[] initRectBounds
: 長方形オブジェクトの場合に、初期状態の長方形の左下隅、右上隅の頂点座標を配列の形で取得する (長方形オブジェクトでない場合は空の配列が返される)。また、プログラム中でも使われている GetPosition()、SetPosition(a, b) は今までにも何度か使われてきたが、この2つのメソッドは THObject2Dクラスのメソッドであり、GetPosition()はオブジェクトの現在位置がVector2型で返される (正確には初期状態からどれだけ平行移動したかがVector2型で返される)。
SetPosition(a, b)は、オブジェクトを初期状態の位置から $(a, b)$ だけの平行移動を実行するためのメソッドであり、行列で記述すれば以下の処理に等しい。
THMatrix3x3 T = TH2DMath.GetTranslation3x3(a, b); Obj.SetMatrix(T); // 初期状態の位置から(a, b)だけの平行移動を実行する
たとえば、46行目では Disk0.SetPosition(6.0f, 8.0f) によって Disk0を初期状態の位置から $(6, 8)$ だけ平行移動させている。その後の foreachループ内の55行目では obj.GetPosition() という処理が実行されるが、ここでの obj は Disk0、Disk1、Disk2のいずれかである。Disk0の場合であれば、GetPosition() は上記46行目で設定した (6.0f, 8.0f) が返されることになる。
各Diskはその中心が初期状態において原点に置かれているので、Diskの場合 GetPosition() で返される値は現時点でのDiskの中心の位置を表すことになる。
プログラム自体は単純な構成である。46行目から48行目で各Diskを適当な位置に配置し、51行目においてShellの現在位置を取得する。53行目のforeachループはシーン内の全てのオブジェクト1つ1つに対して衝突判定を行うものである。このプログラムでは3つのオブジェクト Disk0、Disk1、Disk2に対して衝突判定を行うが、使用されるメソッドは前節で作成した円盤用の衝突判定メソッド CollisionTest_Point_Disk(..) である。
[CollisionTest_Point_Disk(..)]
bool CollisionTest_Point_Disk(Vector2 P, Vector2 C, float r)
{
float d = (P - C).magnitude;
if (r >= d)
{
return true;
}
return false;
}
メソッドに送られてくる引数 P、C、r はそれぞれShellの現在位置、Diskの現在の中心位置、Diskの半径であり、Code3では51行目、55行目、56行目で取得される。また、以下の図8は前節でも用いたものだが、図中の $P$、$C$、$r$ が表すものはメソッドの引数と同じである (図中の $d$ は CollisionTest_Point_Disk(..) 3行目の d のことで、ShellからDiskの中心位置までの距離を表している)。


図9はプログラムの実行結果である。ShellとDiskが衝突した際にDiskが赤い色に変わるが、この処理はプログラム60行目の Hit(..) という一時的に用意されたメソッドによるものである (このメソッドは本節から2-17節のプログラムで使われるだけのカスタムメソッドである)。
ShellとDiskとの間で衝突が発生すると57行目の CollisionTest_Point_Disk(..) がtrueを返し58行目のifブロックに入るが、そこで この Hit(..) が実行される。Hit(..) は THAlphaObject2D型のオブジェクトを引数に設定し、引数として送られてきたオブジェクトをわずかの間赤く表示するだけの処理を行うもので、衝突が起こったことを視覚的に確認できるようにするためのものであり、それ以外に特に重要な役割を持っているわけではない (そのため、Hit(..) の解説はここでは省略するが、オブジェクトの色を実行中に変更するなどについては後の章において解説する)。
また、このプログラムでは実行中の画面内には1つのShellしか存在しないので、あるオブジェクトとの衝突が検出され Hit(..) が実行された後は、他のオブジェクトとの衝突を調べずに61行目でforeachループをbreakする。
# Code4
次のプログラムは Shellと長方形との衝突を扱うものである。今回は図10のように2つの軸平行な長方形 Rect0、Rect1と、2つの傾きのある長方形 Rect2、Rect3が適当な位置に配置されている。それぞれの長方形は図11に示されるように初期状態では軸平行であり、その中心が原点に置かれている。


[Code4] (実行結果 図12)
// ..
// 44行目まではCode2と同じ
// ..
T = TH2DMath.GetTranslation3x3(6.8f, -6.2f);
Rect0.SetMatrix(T);
T = TH2DMath.GetTranslation3x3(6f, 6.6f);
Rect1.SetMatrix(T);
R = TH2DMath.GetRotation3x3(-30f);
T = TH2DMath.GetTranslation3x3(-6f, -6f);
M = T * R;
Rect2.SetMatrix(M);
R = TH2DMath.GetRotation3x3(120f);
T = TH2DMath.GetTranslation3x3(-7f, 6.4f);
M = T * R;
Rect3.SetMatrix(M);
// Collision Test
Vector2 shell_pos = OneShell.GetPosition();
foreach (var obj in i_collisionObjects)
{
Vector2[] bounds = obj.initRectBounds;
THMatrix3x3 mtx = obj.GetMatrix();
Vector2 P = mtx.inverse * TH2DMath.ToVector3(shell_pos);
bool bColl = CollisionTest_Point_AABB(P, bounds);
if (bColl)
{
Hit(obj);
break;
}
}

67行目の initRectBounds は上で述べたように長方形の初期状態における左下隅、右上隅の座標を Vector2[]型で取得するものであり、ここではローカル変数 bounds にセットされる。68行目の mtx は長方形オブジェクトに実行された変換行列を表しており、69行目の mtx.inverse は mtx の逆行列である。
65行目のforeachループで使用されている i_collisionObjects は先程のプログラムと同様に、衝突判定対象となるオブジェクトがセットされている配列(インスタンス変数)である。今回は4つのRectであり、次のように初期化されている。
// 衝突判定対象となるオブジェクト
i_collisionObjects = new THAlphaObject2D[] { Rect0, Rect1, Rect2, Rect3 };

$-30$°の回転を表す行列を$R$、$(-6, -6)$ の平行移動を表す行列を$T$とし、その積を $M = TR$ とする。Rect2にはこの回転と平行移動を1つにまとめた変換行列$M$が実行されているわけであるが、ここでは Rect2 に、この変換行列$M$の逆行列を実行して、Rect2を初期状態に戻すことを考える。$M = TR$ の逆行列は \[ M^{-1} = (TR)^{-1} = R^{-1}T^{-1} \]であるが、$T^{-1}$ の内容は $(6, 6)$ の平行移動であり、$R^{-1}$ の内容は $30$°の回転であるから、$R^{-1}T^{-1}$ が意味する変換は、$(6, 6)$ の平行移動、$30$°の回転をこの順序で実行するものである。
以下の図14は図13から他のオブジェクトを非表示にしたものであり、Rect2には変換行列$M$が実行されている。ここで、$(6, 6)$ の平行移動を実行したときの結果が図15であり、さらにその状態から $30$°の回転を実行したときの結果が図16である。つまり、図14のRect2に逆行列$M^{-1}$を実行した結果が図16のRect2であり、図16では Rect2は初期状態に戻っている。Shellに対しても同じ逆行列が実行されているので、図16では初期状態のRect2に対してShellが衝突した状態になっている。図16におけるShellの位置 $P$ がプログラムにおける69行目の P のことである。
-
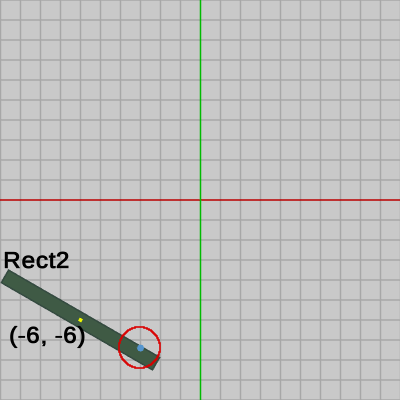 図14
図14 -
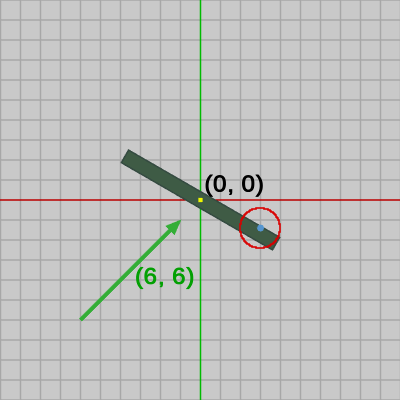 図15
図15 -
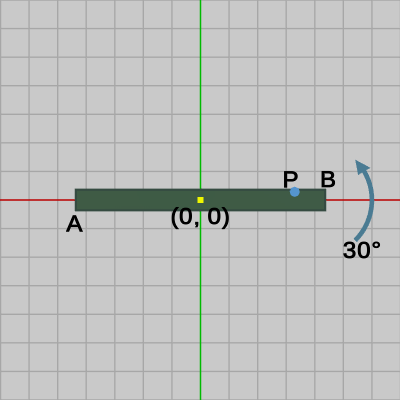 図16
図16
そして、上で述べた bounds、P を用いて70行目では衝突判定を行うが、ここで使用されるメソッドは前節で作成した長方形用の衝突判定メソッド CollisionTest_Point_AABB(..) である。
[CollisionTest_Point_AABB(..)]
bool CollisionTest_Point_AABB(Vector2 P, Vector2[] minmax)
{
Vector2 min = minmax[0];
Vector2 max = minmax[1];
if (min.x <= P.x && P.x <= max.x &&
min.y <= P.y && P.y <= max.y)
{
return true;
}
return false;
}
CollisionTest_Point_AABB(..)は軸平行な長方形の左下隅の頂点 min と右上隅の頂点 max の間に引数 P が含まれるかを判定するものである。したがって、第2引数の minmax は軸平行な長方形の左下隅、右上隅の頂点座標がセットされた配列でなければならない。
# Code5
今までのプログラムでは衝突判定の対象となるオブジェクトはいずれも静止していたが、ここではオブジェクト(円盤あるいは長方形)に適当な運動を行わせ、動いているオブジェクトを対象とする衝突判定を行う。オブジェクトに運動をさせるため、その部分のコードが追加されてはいるが、衝突判定の部分についてはオブジェクトが運動をしている場合でも、内容の点では今までのものとほとんど変わりはない。
[Code5] (実行結果 図18)
// ..
// 44行目まではCode2と同じ
// ..
i_shm += 2;
float scale = 1.0f * Mathf.Sin(i_shm * Mathf.Deg2Rad) + 2.0f;
THMatrix3x3 S = TH2DMath.GetScale3x3(scale);
T = TH2DMath.GetTranslation3x3(11f, 6f);
M = T * S;
Disk0.SetMatrix(M);
float my = 2.0f * Mathf.Sin(i_shm * Mathf.Deg2Rad);
T = TH2DMath.GetTranslation3x3(11.0f, -5.0f + my);
Rect1.SetMatrix(T);
i_deg += 2;
R = TH2DMath.GetRotation3x3(i_deg);
T = TH2DMath.GetTranslation3x3(-11f, 5.4f);
M = T * R;
Rect2.SetMatrix(M);
S = TH2DMath.GetScale3x3(1.0f, scale);
R = TH2DMath.GetRotation3x3(60f);
T = TH2DMath.GetTranslation3x3(-11f, -5.6f);
M = T * R * S;
Rect3.SetMatrix(M);
// Collision Test
Vector2 shell_pos = OneShell.GetPosition();
foreach(var obj in i_collisionObjects)
{
bool bColl = CollisionTest_AllTypes(obj, shell_pos);
if (bColl)
{
Hit(obj);
break;
}
}


今回、使われるオブジェクトは1つの円盤オブジェクトのと3つの長方形オブジェクトで図17のように配置されている。
図18の実行結果に見られるように、このプログラムではこれら4つのオブジェクトがそれぞれ運動を行っている。Disk0は指定の位置において拡大縮小を繰り返し、Rect1は上下方向の単振動を行っている (図右下)。また、Rect2は指定の位置において回転しており (図左上)、Rect3は指定の位置において拡大縮小を行っている (図左下)。これらの運動はプログラム中の46行目から67行目において記述されている。たとえば、Disk0の拡大縮小は$1$倍から$3$倍の範囲を往復するが、この倍率は47行目で単振動を使って計算される。Rect1の往復運動における位置や Rect3の拡大縮小の倍率も同様に単振動から算出される。プログラム中で使われているインスタンス変数 i_shm、i_deg は、それぞれ単振動のための角度、回転のための角度である。
また、今回も衝突判定の対象となるオブジェクトは i_collisionObjects に次のようにセットされている。
// 衝突判定対象となるオブジェクト
i_collisionObjects = new THAlphaObject2D[] { Disk0, Rect1, Rect2, Rect3 };
69行目以降が衝突判定の処理であるが、衝突判定の対象オブジェクトが今回は2種類であるため、72行目の foreachループ内では CollisionTest_AllTypes(..) というメソッドを呼んでいる。このメソッドは衝突判定対象のオブジェクトの種類が複数ある場合のためのもので、各衝突判定メソッドの入り口の役目を果たしている。
[CollisionTest_AllTypes(..)]
bool CollisionTest_AllTypes(THAlphaObject2D obj, Vector2 shell_pos)
{
bool bColl = false;
switch (obj.GetType())
{
case THAlphaObject2D.DISK :
Vector2 C = obj.GetPosition();
float r = obj.GetDiskScale() * obj.initRadius;
bColl = CollisionTest_Point_Disk(shell_pos, C, r);
break;
case THAlphaObject2D.RECT :
Vector2[] bounds = obj.initRectBounds;
THMatrix3x3 mtx = obj.GetMatrix();
Vector2 P = mtx.inverse * TH2DMath.ToVector3(shell_pos);
bColl = CollisionTest_Point_AABB(P, bounds);
break;
default : break;
}
return bColl;
}
衝突判定のプログラムで使われる THAlphaObject2Dクラスには GetType() というメソッドが用意されており、メソッド名から明らかなようにそのオブジェクトの種類が返される。4行目の switch文の冒頭で衝突判定対象のオブジェクトの種類を取得し、オブジェクトが円盤であれば6行目の case に処理が移り、長方形であれば12行目の case に処理が移る。
8行目は円盤オブジェクトの半径を求める計算であるが、
float r = obj.GetDiskScale() * obj.initRadius;
また、図18左下の長方形 Rect3 も拡大縮小を行っているが、拡大縮小をしている長方形オブジェクトとの衝突判定も上で述べた方法が使える。すなわち、長方形オブジェクトに逆行列を実行して初期状態に戻した状態で考える方法である。
あるオブジェクトにShellが衝突しているかどうかを調べるにあたって、そのオブジェクトを初期状態に戻した状態で考えるという方法は長方形のような単純な形のオブジェクトばかりではなく、より複雑な一般形状のオブジェクトに対しても適用できるが、その点については次節で解説する。
© 2020-2025 Redpoll's 60 (All rights reserved)