Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-27
第2章 2D空間におけるオブジェクトの運動
$§$2-27 その他の重要事項 1 (UnityのTransformクラスによる記述 ; カメラ移動の基本)
もともとこの講義における2D空間の内容は、3D空間において扱ういくつかの項目のうちで2D空間において解説できるもの、あるいは2D空間で解説した方がわかりやすいものを中心として配列されている。例えばオブジェクトの一体化運動などは2D空間においても原理は同じであるため、2Dオブジェクトの場合で解説する方がより簡単かつ明確に表現ができる。あるいは衝突判定なども原理が同じであれば、3Dオブジェクトを使って例示するよりは2Dオブジェクトを使う方が理解しやすい上に解説も行いやすい。そういった経緯によって、3D空間で解説する予定であった内容を2D空間に移動させていくうちに、2D空間で扱う内容が当初の予定を大幅に越えてしまうことになった。
もちろんまだ扱わなければならない内容は多く、そういったものは後の3D空間の各章で解説される。しかし、一般的な需要という点では3Dグラフィックスよりも2Dグラフィックスの方が明らかに必要とされるケースが多く、それに比べれば3Dグラフィックスはまだ一部の需要に過ぎない。(開発者を含め)一般の人々にとって必要となるコンピューターグラフィックスとは3Dグラフィックスではなく、2Dグラフィックスというのが現状である。3D空間における議論は次の第3章から始まるが、3D空間までは必要としない読者もいるであろう (おそらくはそういった読者の方が多いであろう)。
そこで以下3節では、本来3D空間のしかるべき箇所で展開すべき内容のうち重要ないくつかを、2D限定版として編集し直した形で解説していく。
まずここでは今まで行列によって実装されていたオブジェクトの運動を、Unityに用意されているTransformクラスのプロパティを用いた実装に書き換える。さらに本節後半においては2D空間のカメラ移動の基礎について扱う (今までと同じく解説中における「2D空間」とはXY平面のことである)
今までのプログラムにおけるオブジェクトの運動は一部の例を除いて、すべて行列で実装してきた。しかし、行列による実装はこの講義で独自に用意したものであり、Unityで標準的に用意されているものではない。本節の前半ではこの行列の実装をUnityで提供している標準的なAPIによって書き換える。
UnityのAPIを使用する場合、一般的にはオブジェクトの運動は Transform クラスを経由して行われる。Transform クラスにはオブジェクトを動かすためのプロパティやメソッドが多く含まれるが、そのうちで重要なのが以下の3つのプロパティ localPosition、localRotation、localScale である。
localPosition はVector3型、localRotation はQuaternion型、localScale はVector3型である。Vector3 はいわゆる $(x, y, z)$ の形の3次元ベクトルのことであり、今までにもプログラム中で何度か使われてきた。Quaternion は行列と同じく回転を表すために使われるが、UnityのAPIでは Vector3、Matrix4x4 などと同じく構造体として用意されている。
例えば今までのプログラムでは、角度 deg の回転を表す回転行列を次のように取得した。
Quaternion も同じく回転を表すことができるが、これを Quaternion で書き換えると以下のようになる。
AngleAxis(..) は Quaternion に用意されているstaticメソッドで第1引数には回転角度、第2引数には回転軸をセットする。ここで回転軸として指定されている Vector3.forward は z軸プラス方向 $(0, 0, 1)$ を表す定数であり、第2引数を new Vector3(0, 0, 1) としても同じである。上記の AngleAxis(..) によって「z軸(プラス方向)を回転軸として角度 deg の回転を表す Quaternion」が返されることになる。
そして重要なのが2D空間(XY平面)においては回転軸は常に z軸プラス方向であり、そのため上記の AngleAxis(..) の第2引数は常に Vector3.forward にしておくという点である。つまり、2D空間でQuaternionによる回転を取得する際には毎回 AngleAxis(deg, Vector3.forward) の形でこのメソッドを使えばよいのである (2D空間における回転については後述する)。
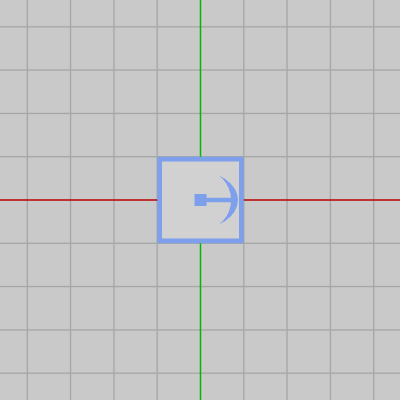
図1 Box 初期状態 (正方形であり、中心が原点に位置している) localPosition や localScale はVector3型であるが、2D空間における位置やスケールでは x座標、y座標のみを使うのでこれらのプロパティに対しても x座標、y座標のみを指定すればよい。z座標については常に同じ値でよい、具体的には localPosition の場合は常に $0$、localScale の場合は常に $1$ とするのである (ただし例外的なケースもあるが、その点については次節を参照)。
これは、2D空間におけるオブジェクトはXY平面上で運動を行うので、その z座標は常に $0$、z軸方向のスケール倍率は常に $1$ ということを意味している。
右図はオブジェクト Box の初期状態である。Boxは各辺の長さが等しい正方形であり、初期状態では中心が原点に位置している。行列を使う場合、オブジェクトを初期状態にするためには以下のように記述した。
上記の3つのプロパティ localPosition、localRotation、localScale を使う場合、オブジェクトを初期状態にするためには以下のように記述する。
先程述べたように2D空間における位置及びスケールの指定では x座標、y座標のみを変更すればよく、z座標については常に同じ値を使用する (位置の場合は $0$、スケールの場合は $1$)。z座標は常に同じ値なので、上記の設定でも x座標、y座標だけを読めばよい。
その場合 localPosition は $(0,\ 0)$ であるが、これは x軸方向、y軸方向の移動量がともに $0$ を意味する (平行移動を行わない)。 localScale は $(1,\ 1)$ であるが、これは x軸方向、y軸方向のスケール倍率がともに $1$ であることを意味する (スケールを行わない)。
localRotation には Quaternion.identity というプロパティがセットされているが、このプロパティは Quaternion に用意されている定数で、何も回転を行わない Quaternion を表す。したがって localRotation に identity をセットすることはオブジェクトに対して何も回転を行わないことを意味する。
したがってBoxに対する上記の設定は、平行移動を行わず、回転も行わず、スケールも行わない、すなわち Boxに対しては何の変換も行わないこと、それはBoxを初期状態のままにしておくことを意味する。
では続いてこれらのプロパティを使って上記のBoxに対し変換を実行する。
以下の記述はBoxを初期状態の位置から $(3,\ 1)$ だけ平行移動させるものである (図2 ; localPosition に Vector2 をセットしているが、この場合には自動的に z座標が $0$ になる)。
Boxを初期状態の向きから $45^\circ$ だけ回転させるには次のように記述する (図3)。
以下の記述はBoxを初期状態の大きさから各軸方向に $2$ 倍の拡大を実行するものである (図4 ; localPosition の場合とは異なり、Vector2 をセットしてはならない。その場合 z座標が自動的に $0$ になり、z軸方向の倍率が $0$ として扱われるためオブジェクトの表示が不自然なものになりやすい)。
上記の変換はすべて初期状態のBoxに対しての個別の変換である。例えば図2は初期状態のBoxに対して平行移動だけを行ったものである。同様に図3は初期状態のBoxに対して回転だけを、図4はスケールだけを行ったものである。
行列によってオブジェクトに変換を実行する際、ほとんどの場合において複数の変換をまとめたものをオブジェクトに実行した。例えば平行移動行列を $T$、回転行列を $R$、スケール行列を $S$ とするとき、それらの積 $M = SRT$ をオブジェクトに実行することは、オブジェクトに対し平行移動、回転、スケールの順で変換を実行することを意味し、$M = TSR$ ならばオブジェクトに対し回転、スケール、平行移動の順で変換を実行することを意味した (行列の積は右から読む)。
そしてその際、行列の積の順序がそのまま変換順序になるので、積の順序には注意する必要があった。例えば行列の積が $RT$ ならば、変換順序は平行移動、回転の順になるが、積が $TR$ ならば回転、平行移動の順になる。
上記の3つのプロパティ localPosition、localRotation、localScale を使って複数の変換(具体的には平行移動、回転、スケールの3つの変換)をまとめたものをオブジェクトに実行することもできる。そして、その場合の変換順序は常にスケール、回転、平行移動の順になる。
以下具体的な例で見ていこう。
初期状態のBoxに対して(先程と同じ)以下の変換を順番に実行する (スケール、回転、平行移動の順 ; 実行結果 図6)。
(1) 各軸方向に $2$ 倍のスケール
(2) $45^\circ$ の回転
(3) $(3,\ 1)$ の平行移動
この変換を行列で記述すると以下のようになる。
localPosition、localRotation、localScale を使った場合は以下のようになる。
行列で記述した場合も3つのプロパティによって記述した場合も実行結果は同じである (下図6)。まず初期状態においてBoxを $2$ 倍拡大し、その後 $45^\circ$ の回転を実行、最後に $(3,\ 1)$ だけの平行移動を行う。3つの変換をこの順序で実行すると図6の状態になる。
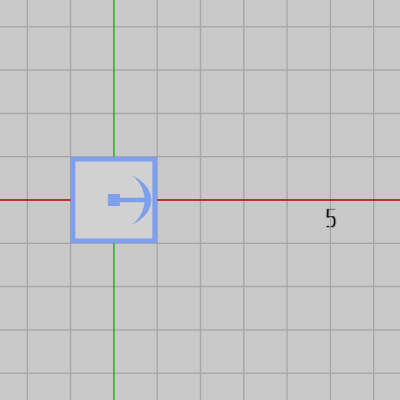
図5 Box 初期状態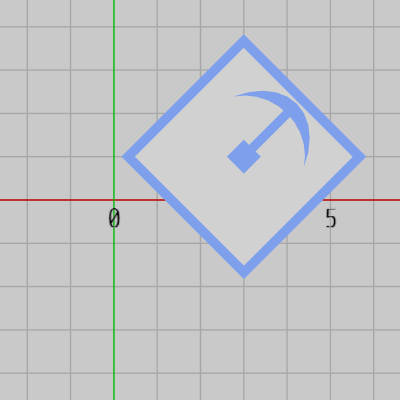 
図6 上記の変換(1)、(2)、(3)を順番に行った結果
なお、プロパティの記述順序は変換順序には影響しない。つまり3つのプロパティをどのような順序でセットしても必ずスケール、回転、平行移動の順で変換が実行される。例えば下のコードでも実行結果は変わらない (図6)。
今までは単独のオブジェクトを前提としていたが、ここからは複数のオブジェクトの一体化運動を行列ではなく、上記の3つのプロパティによって書き換えることについて見ていく。
例えば2つのオブジェクト Obj1、Obj2 が親子関係にある場合、今までのプログラムではこの2つのオブジェクトの一体化した運動は次のように記述されていた (ここでは Obj1 が親オブジェクト、Obj2 を子オブジェクトとする)。
一体化運動を行列によって実装する場合には local や world という接頭辞の付けられた行列が使われており、このプログラムでも localObj2 や worldObj1 としてそれらは使われているが、ここでは接頭辞として local の付いている行列を「ローカル行列」、world の付いている行列を「ワールド行列」と呼ぶことにする。
最終的にオブジェクトに対して実行されるのはワールド行列であり(16~17行目)、ワールド行列はローカル行列の積として構成される (13~14行目 ; 一番上の親オブジェクトの場合はローカル行列とワールド行列は同じである)。
各オブジェクトのローカル行列は上記の場合、スケール、回転、平行移動の3つの変換行列の積から構成されている。例えば Obj2 のローカル行列 localObj2 は、sclObj2 (スケール)、rotObj2 (回転)、traObj2 (平行移動)の積である (5行目)。同様に Obj1 のローカル行列 localObj1 は、sclObj1 (スケール)、rotObj1 (回転)、traObj1 (平行移動)の積として構成されている (11行目)。
そして、いずれのローカル行列もそれを構成する行列の実行順序はスケール、回転、平行移動の順になっているが、この点は重要である。それは行列による実装を以下に示す3つのプロパティによる実装に書き換えるには、ローカル行列の内容がスケール、回転、平行移動の順で行われていることが前提となるためである。
上記の行列による一体化運動の実装を3つのプロパティ(localPosition、localRotation、localScale)による実装に書き換えるには、以下の手続きを形式的に行えばよい。
すなわち、localPosition、localRotation、localScale の内容を、各オブジェクトのローカル行列を構成する平行移動行列、回転行列、スケール行列の内容と同じになるようにするのである。
具体的な例で見ていこう。ローカル行列 localObj2 は traObj2、rotObj2、sclObj2 の3つの積であるが、そのうちの平行移動行列 traObj2 の内容は (x2, y2) だけの平行移動である (2行目)。したがって平行移動を指定するプロパティ localPosition の内容も同じく (x2, y2) だけの平行移動にすればよい。
同様に回転行列 rotObj2 の内容は角度 deg2 だけの回転であるので(3行目)、回転を指定するプロパティ localRotation の内容も角度 deg2 だけの回転とする。
スケール行列 sclObj2 の内容は x軸方向、y軸方向ともに s2 倍の拡大であるため、スケールを指定するプロパティ localScale の内容も s2 倍の拡大とする。
今述べた書き換えを Obj1、Obj2 のローカル行列に行うと以下のようなコードになる (初期化ブロックの処理は親子関係の設定である)。
Obj2の3つのプロパティ localPosition、localRotation、localScale (10~12行目)の内容が、行列版のプログラムにおいて localObj2 を構成していた3つの変換行列の内容と同じになっていることがわかるであろう。同様にObj1の3つのプロパティ(15~17行目)の内容も、行列版のプログラムにおいて localObj1 を構成していた3つの変換行列の内容と同じになっているのである (Unityの標準的な変換方法ではこのように localPosition、localRotation、localScale の3つのプロパティに値をセットすればよいだけであり、行列版の実装のように最後にワールド行列を計算して、オブジェクトにワールド行列を実行するといった処理は必要ない)。
また初期化ブロックに見られるようにプログラムでオブジェクトの親子関係を設定する場合には SetParent(..) というメソッドを使用する。そして注意すべきはこのメソッドは Transform クラスのメソッドであり、オブジェクトの transform プロパティを経由しなければならないという点である。すなわち Obj2 の親オブジェクトとして Obj1 を設定する場合にはと記述するのが正しい ( Obj2.SetParent(Obj1) ではない)。
最後に1点だけ補足する。
上記のプログラムではUnity標準の変換方法として3つのプロパティ localPosition、localRotation、localScale を使用した。確かに複数のオブジェクトが親子関係を構成し、一体化した運動をしているのであればこの3つのプロパティを使う必要があるが、親子関係のない単独のオブジェクトの場合には localPosition、localRotation の代わりに表記の軽い position、rotation というプロパティを使うことができる。
簡単にいえば親子関係のない単独のオブジェクトの場合には localPosition、localRotation を使っても、position、rotation を使っても実行結果は変わらないのである。そのため以下では簡単のため単独のオブジェクトの場合には localPosition、localRotation ではなく、position、rotation を使い、親子関係を構成する複数のオブジェクトの場合に localPosition、localRotation を使うことにする (詳しくは position、rotation はワールド座標系における位置及び回転状態のことであり、localPosition、localRotation は親座標系における位置及び回転状態のことである。これらのことについては第4章、第5章で解説する)。
では実際に、今までに扱ったプログラム及びそれと類似のものをUnity標準の方法で書き換えていこう。
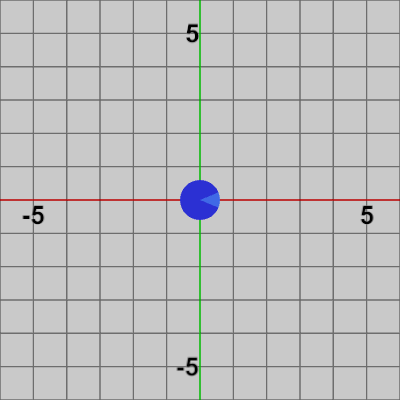
図7 Disk 初期状態 
図8 Code1 実行結果
[2-4節 Code3] (実行結果 図8)
local や world という接頭辞が省略されているが、Diskは親子関係のない単独のオブジェクトであるため10行目の M がローカル行列でありワールド行列でもある。したがって この M を構成する2つの変換行列(平行移動行列 T、回転行列 R)の内容と同じになるようにプロパティを定めればよい。
この行列による実装を position、rotation による実装に書き換えたものを以下に示す。
[Code1] (実行結果 図8)
6行目では半径 $3$ の円周上の位置を毎フレーム計算しているが、ここでは Quaternion と Vector2 の積を行っている。その際には行列の場合と異なりベクトルを同次座標にする必要はない (すなわち6行目のベクトルを new Vector3(3, 0, 1) のようにする必要はない)。
例えば、XY平面上の点 $(a,\ b)$ を原点周りに $120^\circ$ 回転させる処理であれば以下のように記述すればよい。
UserMotion() には下図9に示されるオブジェクト Plane をキー操作によって動かす処理が記述されている。
図9 Plane 初期状態 
図10 Code2 実行結果
キー操作は以下のとおり。
H : 左に旋回 (回転は $2^\circ$ ずつ)
L : 右に旋回
S : オブジェクトの移動/停止用スイッチ
[2-15節 UserMotion()]
このプログラムにおけるPlaneも単独のオブジェクトであるため、Planeに実行される変換行列 M (23行目)はローカル行列であり、ワールド行列でもある。したがって今回も M を構成する2つの変換行列(平行移動行列 T、回転行列 R)の内容と同じになるようにプロパティの値を定めればよい。
以下のプログラムは上記の UserMotion() を position、rotation の2つのプロパティを使って書き換えたものである。
[Code2] (実行結果 図10)
図11 Beta3 実行結果 Code1ではDiskが自転しながら公転軌道上を移動するものであった。そのため、Diskの位置は常に変化し続けた。
例えばDiskの位置を変えずに自転だけ行わせるとしよう。その場合、行列による実装であれば毎フレームにおける平行移動行列の内容を常に同じ位置への移動とすればよい。具体的には以下のように記述することになる。
下記のプログラムはXY平面上の $(3,\ 2)$ において毎フレーム $6^\circ$ ずつDiskに自転を行わせるものである。Diskに実行される平行移動行列は毎フレーム 同じものであるため、右図の実行結果に示されるようにDiskの位置は常に $(3,\ 2)$ から動くことはない。
[Beta3A] (実行結果 図11)
これをUnity標準の方法で書き換えると以下のように記述される。
[Beta3B] (実行結果 図11)
このコードにおいて4行目の position へセットされる値は毎フレーム同じである。このように position や rotation (あるいは localPosition や localRotation でも)プログラム実行中にその内容が変わらないのであれば、それらのプロパティには初期化ブロックなどで1度だけ値をセットすればよい。上記のように毎フレーム同じ値をセットし続ける必要はないのである。
具体的には次のように書き換えられる。
[Beta3C] (実行結果 図11)
Diskの位置は $(3,\ 2)$ から変化することはないので、初期化ブロックにおいて position にその位置をセットし、プログラム実行中は rotation だけが更新されるようにしている。
では今述べた例と類似の問題を考える。
下図12はオブジェクト Arrow の初期状態であり、初期状態においてArrowは y軸プラス方向を指している。ここでは、このオブジェクトを下図13に示されるように $-60^\circ$ 回転した状態で、その方向に移動させる。
図12 Arrow 初期状態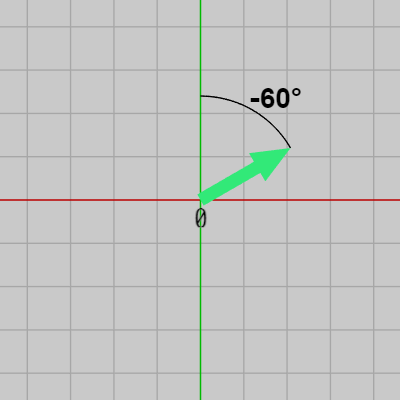 
図13 y軸周りに -60°回転
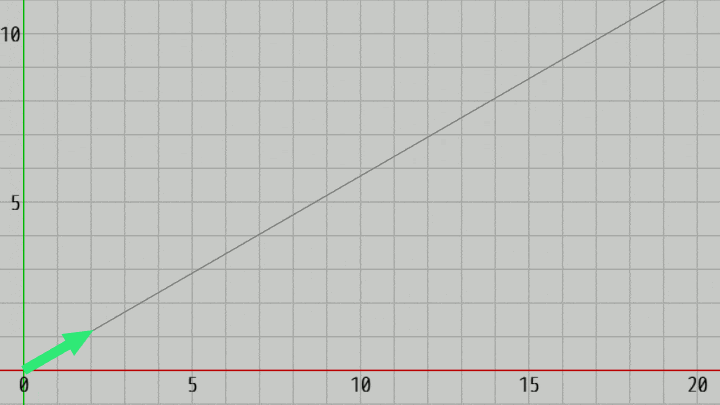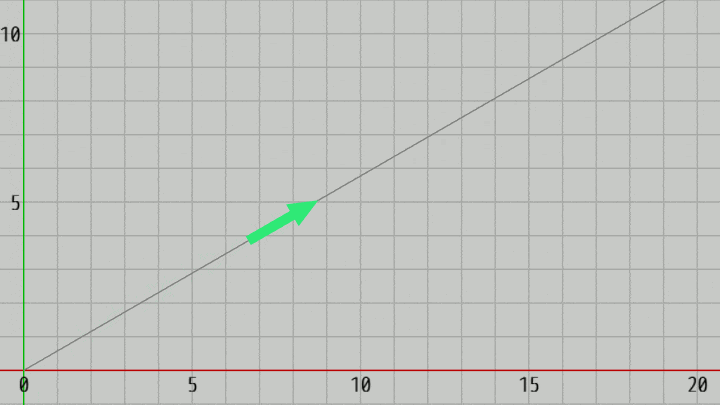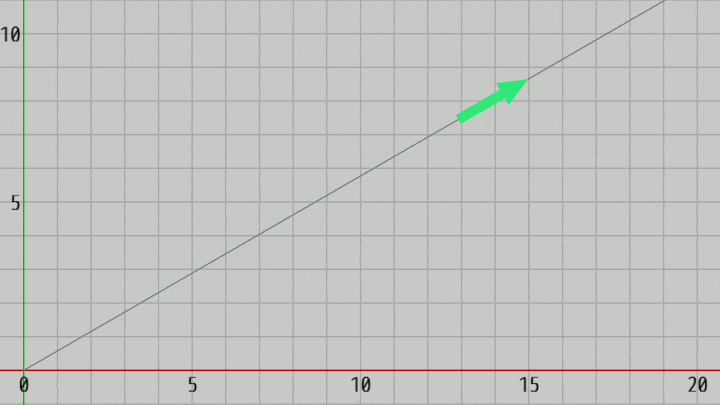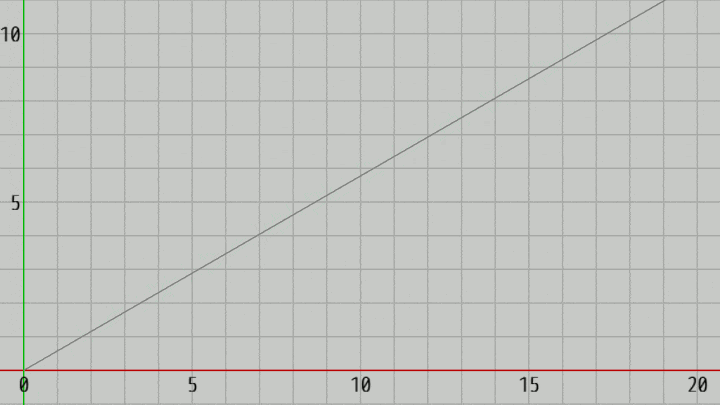
図14 Code3 実行結果
まずは行列による実装である。
[Beta3D] (実行結果 図14)
初期化ブロックではArrowを(y軸プラス方向から) $-60^\circ$ の方向に回転させている (図13の状態になる。回転だけであり、位置は動かさない)。S キーを押すことで $-60^\circ$ の方向に毎フレーム $0.1$ ずつ進んでいくが、その際 Arrowは常に $-60^\circ$ の方向を向いている (図14)。
ではこのプログラムをUnity標準の方法に書き換える。上の実行結果あるいはプログラムから明らかなように、Arrowの向きはプログラム実行中 常に同じであり、位置だけを更新すればよい。したがって、プログラムは次のようになる。
[Code3] (実行結果 図14)
このプログラムでも開始時点ではArrowは $-60^\circ$ の方向を向いており、S キーを押すことで移動が始まるが、今回は C キーを押すことで開始地点に戻る処理を追加している (10~14行目 ; 開始地点に戻るが向きは $-60^\circ$ のまま)。
以下は行列による実装である。
[Beta4] (実行結果 図17)
2~12行目までがBallのローカル行列の計算であり、15~18行目までがNeedleのローカル行列の計算である。
Ballのローカル行列 localBall (12行目)の内容は、$1$~$1.5$ 倍の間での拡大縮小の繰り返し(sclBall)、Needle先端を中心とする半径 $1$ の円周上の公転(traBall)である。
3行目の CalcShmValue(..) は $1$~$1.5$ の間の数値を単振動によって計算する補助メソッドであり、ローカル変数 s は$1$~$1.5$ の間を往復し続ける (第1引数に単振動計算のための角度、第2引数、第3引数は最小値、最大値である)。
Needleのローカル行列 localNeedle (18行目)の内容は、毎フレーム $3^\circ$ ずつの回転(rotNeedle)、$(-4,\ 1)$ への平行移動(traNeedle)である (traNeedle の値は常に同じなのでNeedleは同じ位置で回転をし続ける)。
では上のプログラムをUnity標準の方法で書き換える。今回は親子関係にある2つのオブジェクトの一体化した運動なので使用するプロパティは localPosition、localRotation、localScale である。
[Code4] (実行結果 図17)
初期化ブロック 3行目は親子関係の設定である。Ballのローカル行列 localBall の内容はスケールと平行移動であったが、それらの内容と同じものを19~20行目で localScale、localPosition にセットしている。
Needleのローカル行列 localNeedle の内容は回転と平行移動であったが、それらの内容と同じものをNeedleの localRotation、localPosition にセットしている。Needleは毎フレーム回転するので localRotation の内容は24行目で毎フレーム更新されるが、その位置は変化しないので localPosition は初期化ブロックで1度セットされるだけである (5行目)。
キー操作は以下のとおり。
H : 左に旋回 (回転は $1^\circ$ ずつ)
L : 右に旋回
S : オブジェクトの移動/停止用スイッチ
[2-10節 Code4] (実行結果 図20)
では上のプログラムをUnity標準の方法で書き換える。Rotorのローカル行列 localRotor (19行目)の内容は回転(rotRotor)と平行移動(traRotor)から構成されるが、これらの行列と同じ内容になるように localRotation 及び localPosition に対して値をセットする。
また、Bodyのローカル行列 localBody (28行目)の内容は回転(rotBody)と平行移動(traBall)から構成されるが、やはりこれらの行列と同じ内容になるように localRotation 及び localPosition に対して値をセットすればよい。
プログラムは次のとおり。
[Code5] (実行結果 図20)
使用するオブジェクトは以下の Red、Green、Blue である。
上図はそれぞれの初期状態であり、各オブジェクトの階層構造はRedが一番上の親オブジェクト、その子オブジェクトとしてGreen、一番下の子オブジェクトがBlueである (図24)。
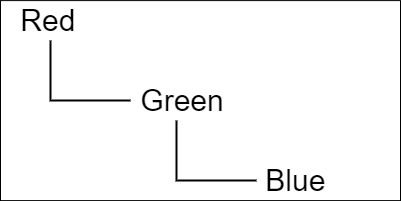
図24 オブジェクトの階層構造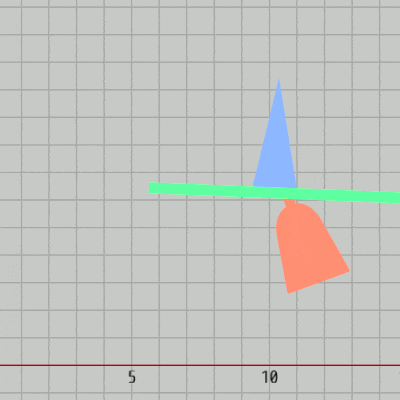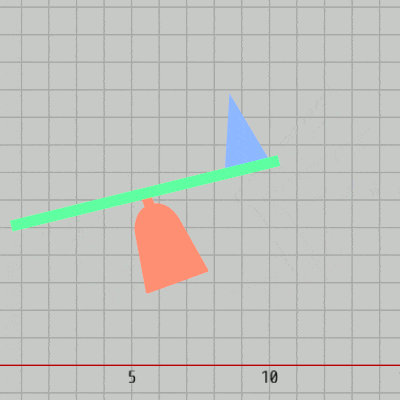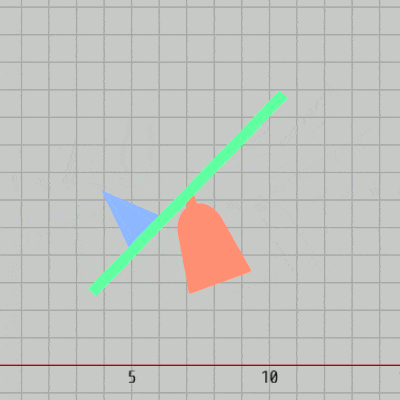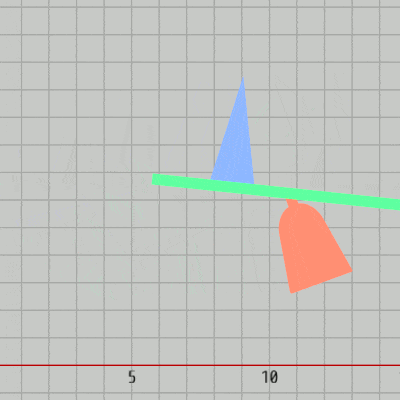 
図25 Code6 実行結果
それぞれのオブジェクトは次の運動を行う。
BlueはGreenの上で x軸方向に $-4.2$ から $4.2$ の範囲の往復運動、及びその運動中に y軸方向の大きさが $1$ 倍から $2$ 倍の間で変化し続ける (図26)。
GreenはRedの先端において、$-30^\circ$ から $30^\circ$ の範囲の往復回転を行う (図27)。
Redは $20^\circ$ 傾いた状態で、$(6,\ 3)$ から $(12,\ 3)$ までの区間を往復し続ける (図28)。
プログラムは以下のとおり。
[Code6] (実行結果 図25)
初期化ブロックは親子関係の設定とプログラム実行中に変化しないプロパティへの値をセットしている。例えば、Greenであればアタッチポジション(Redの先端)は変化しないので初期化ブロックはにおいてその位置 c_attachPos_Green がセットされる。また Redの場合は実行中は $20^\circ$ 傾いたままなので、これも初期化ブロックにおいてセットされる。
初期化ブロック以降の内容は上で述べた各オブジェクトの運動の記述であり、いずれも単振動による往復運動である。CalcShmValue(..) はCode4でも使われたが、単振動の計算を行うための補助メソッドであり、第1引数に単振動計算のための角度、第2引数、第3引数には最小値、最大値をセットする。
2D空間におけるカメラ移動は上下左右の2次元的な平行移動であり、一般のオブジェクトの平行移動と同じく基本的にはカメラの x座標、y座標を変更するだけである。しかし一般のオブジェクトとは異なり、2D空間限定で使用する場合でもカメラの場合は3次元的に考える状況がいくつか生じる。
x軸、y軸の2つの軸で構成される2D空間とは異なり、3D空間の場合はさらに第3の軸である z軸が加わる (図29 ; グリッド線はXZ平面に引かれている)。
他のオブジェクトと同様にカメラにも初期状態があり、Unityではカメラは初期状態において原点に置かれ、z軸プラス方向を向いている (図30)。
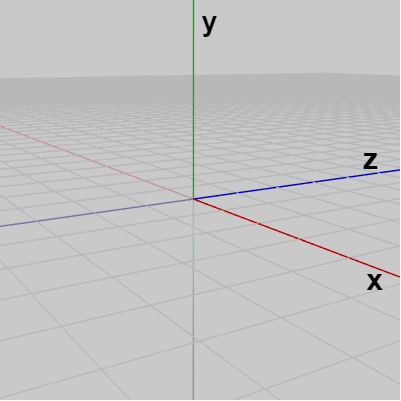
図29 3D空間における x軸、y軸、z軸 (グリッド線はXZ平面に引かれている) 
図30 カメラ 初期状態
2D空間、すなわちXY平面をカメラによって撮影する場合には、カメラの位置は z軸マイナス側に置き、カメラの向きを z軸プラス方向に向ける (図31 ; ただしこれは左手系の場合である (3-3節参照))。
もちろんこれは今までのプログラムでも同様であり、今までのプログラムではカメラは下図32に示されるように、z軸マイナス側の適当な位置で z軸プラス方向を向いて置かれており、そこからXY平面を撮影していたのである。
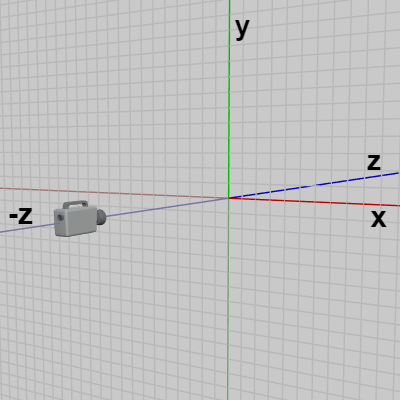
図31 XY平面を撮影する場合はカメラを z軸マイナス側に置く (グリッド線はXY平面)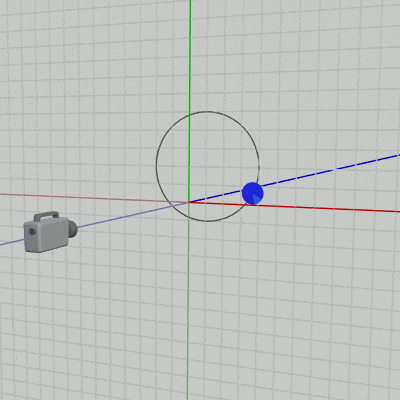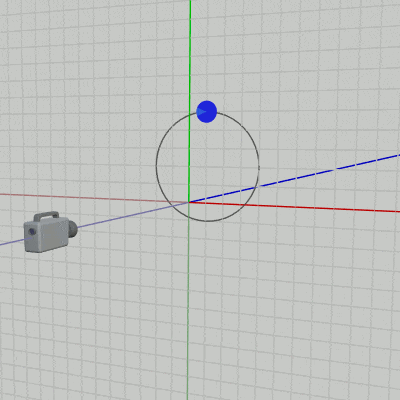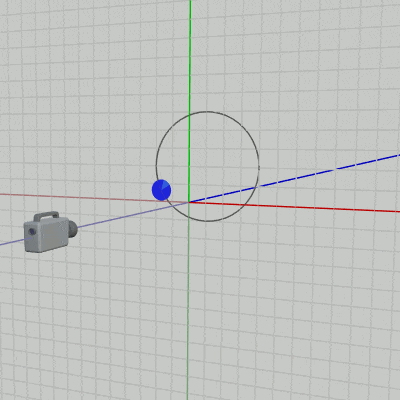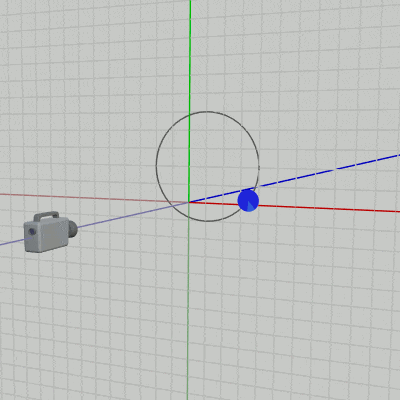 
図32 z軸マイナス側からXY平面を撮影する
下図は図32のカメラからの撮影結果である。
図33
また他のオブジェクトと同様にカメラに対しても回転や平行移動などの変換を行うことができる (カメラに対してスケールを行うことはない)。しかし、ここで扱うカメラに関しては回転は行わない。以下3節においてカメラに対して行う変換は平行移動のみである。
(Unity画面上において Hierarchy Window 内にある「Main Camera」を選択すると(図34)、Inspector 内にカメラに関する情報が表示されるが(図35)、カメラに回転を行わない場合はこのInspector内の Transform という項目にある「Rotation」の各値が常に「x 0 y 0 z 0」となる。
図34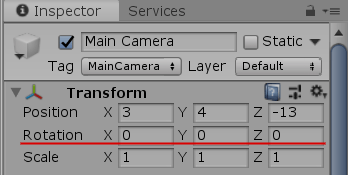 
図35
カメラの場合 2D空間、3D空間のいずれにおいても「Scale」の各値は常に $1$ である)
カメラに対して回転を行わず平行移動のみを行う場合、実行結果の画面においては画面の横方向、縦方向は常に x軸、y軸に平行になる (図36)。
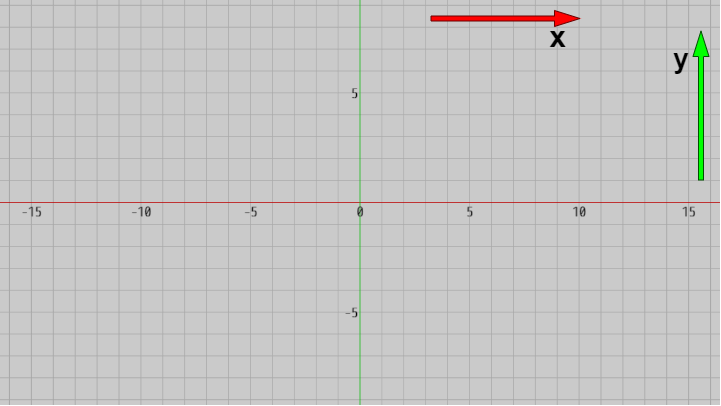
図36 画面の横方向は x軸に平行、画面の縦方向は y軸に平行
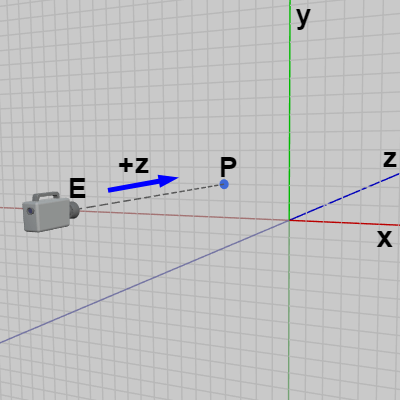
図37 またカメラに対して回転を行わなければ、カメラの向きは初期状態の向きである z軸プラス方向のままである。その場合カメラの位置を $E = (E.\!x,\ E.\!y,\ E.\!z)$ とすると、$E$ から z軸プラス方向に伸ばした直線とXY平面との交点 $P$ の座標は $P = (E.\!x,\ E.\!y,\ 0)$ であるが(図37)、この交点 $P$ は実行結果の画面において画面の中心に来る点である (下図38はこのときの撮影結果)。
簡単にいえば、(2D空間を撮影する場合)カメラの位置を $(E.\!x,\ E.\!y,\ E.\!z)$ とするとき、画面の中心に来る座標は $(E.\!x,\ E.\!y)$ である。
例えばカメラの位置が $(0, 0, z)$ であるとき($z < 0$)、画面の中心には原点が来る。
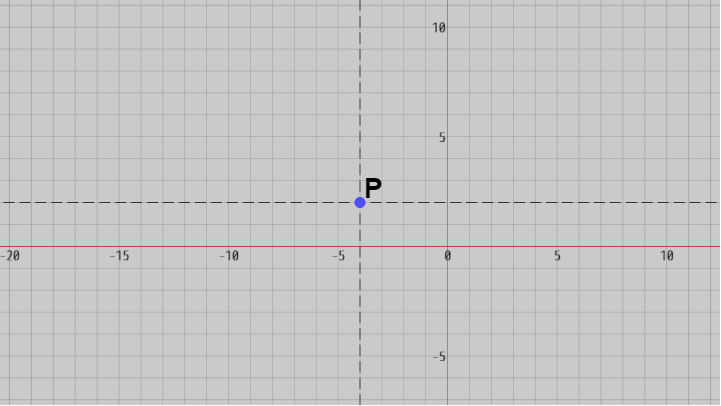
図38 カメラの位置が (E.x, E.y, E.z) であるとき、画面の中心は (E.x, E.y)
最後に回転に関して1つ補足する。
2D空間において回転のプラス方向(角度を増加させる回転)は反時計周りであった。2D空間における回転とは具体的には z軸周りの回転であり、下図39に見られるようにオブジェクトを z軸周りに回転させているのである。そして詳しくは第3章で扱うが、z軸周りの回転とは(左手系の場合)左手の親指を z軸プラス方向に向けた際に、残りの指の曲がっている方向がプラス方向の回転(角度を増加させる回転)である。
実際、下図39の場合 左手の親指を z軸プラス方向に向けると、残りの指の曲がっている方向が図中のオブジェクトの回転方向(反時計周り)と一致しているのが確かめられるであろう (詳しくは 3-3節、3-10節参照)。右図はこのときの実行結果の画面である。
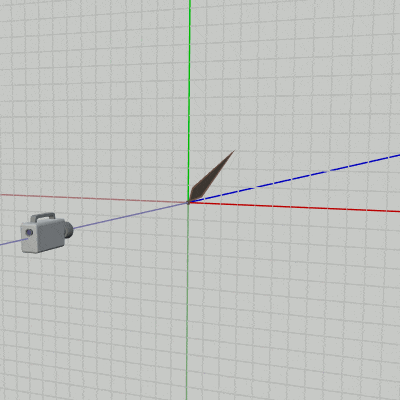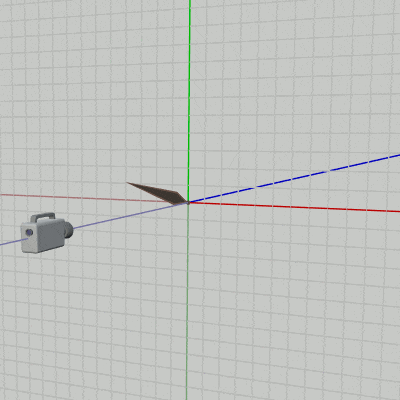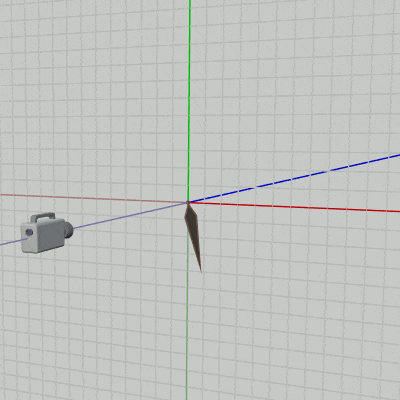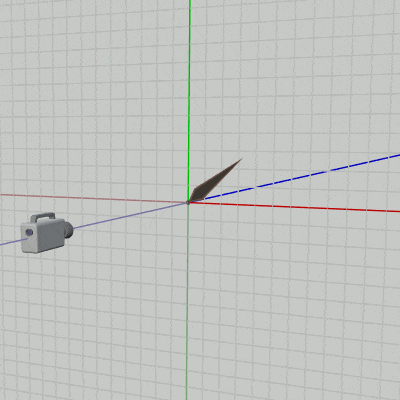
図39 2D空間のオブジェクトは z軸周りに回転する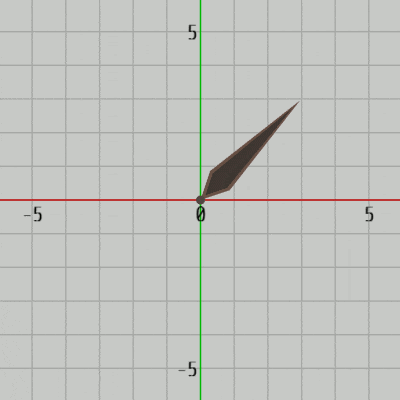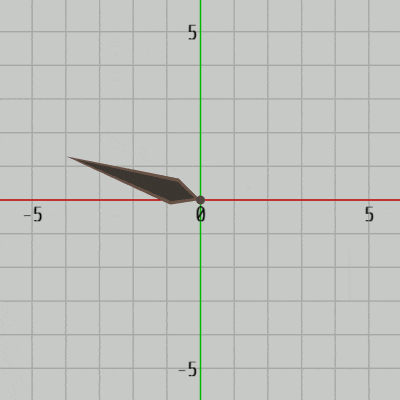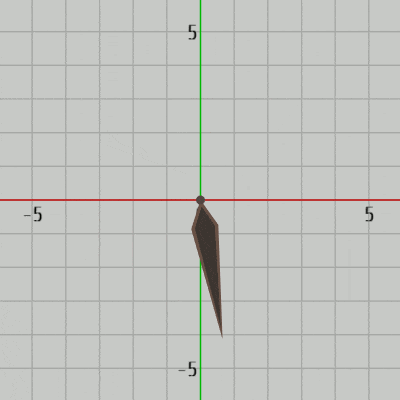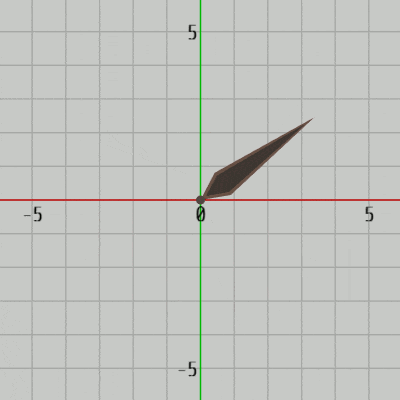 
図40 実行結果の画面
では以上をふまえてプログラム実行中におけるカメラ移動を実装する。
本節から 2-29節のプログラムにおいてはカメラは「MainCamera」という名前で使われているが、Unityではプログラムからカメラを操作する場合、次のような記述によってカメラを表すオブジェクトを取得する必要がある。
ここで使われている Find(..) はHierarchy内のオブジェクトを取得するためのメソッドで、メソッドの引数にはHierarchy内に表示されているオブジェクトの名前をセットする。例えばカメラの場合デフォルトでは "Main Camera" という名前であるため(上図34)、この名前をセットすればよい。
なお、プログラム中ではこのような処理は初期化ブロックで1度だけ行えばよいが、以降のプログラムではこのカメラの取得処理は開始時点において裏側であらかじめ行われているので、プログラムでは特に何も記述しなくてもMainCameraを使用することができる。
またプログラム実行中は画面の中心を示すために図42のオブジェクト Dot が常に画面中心に置かれるようにする。そのためにはカメラの移動中において、上で述べたようにカメラの位置の z座標を $0$ にした位置にDotを置き続ければよい (図43 ; Dotの動く範囲はXY平面上)。
H : カメラを左に動かす
L : カメラを右に動かす
J : カメラを下に動かす
K : カメラを上に動かす
[Code7] (実行結果 図44)
H、J、K、L のいずれかが押されている間はカメラを上下左右に $0.1$ ずつ移動させる。その際、Dotはカメラの位置の z座標を $0$ にした位置(XY平面上)に置かれ続けるが、これによってDotは常に画面中心に表示されるようになる。
なお26行目は次のように記述しても同じである (自動的に E の z座標が取り除かれる)。
そのため今回はVehicleの移動をカメラによって追跡する形に変更する。具体的にはカメラの位置を(XY平面上の)Vehicleの位置から、常に z軸マイナス方向に $7.2$ だけ離れた位置に置き続けるのである (図46)。これは単に上のCode7と逆のことをするだけである。
図45 Vehicle 初期状態 
図46 プログラム実行中はカメラをVehicleから z軸マイナス方向に 7.2 だけ離れた位置に置き続ける
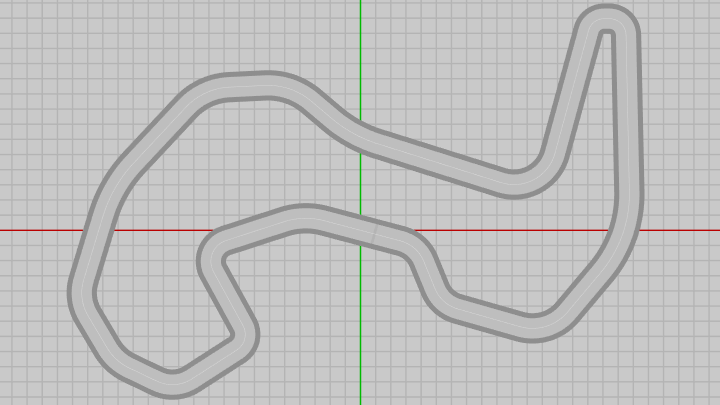
図47 XY平面上に置かれたサーキット
使用するキー操作は以下のとおり。
J, K : Vehicleの移動
[Code8] (実行結果 図48)
このプログラムは基本的にはVehicleを補間曲線上で移動させるものであり、27行目までの内容は前節のCode2と同じである。今回のVehicleの移動経路もサーキットのセンターラインであり、初期化ブロックの ConstructCurve() はそのセンターラインと形、大きさが同じ補間曲線を作成するための補助メソッドである。
また前節のプログラムと異なり、Vehicleに対する変換は行列ではなく上で解説したUnityのプロパティを使って行われている (26~27行目)。25行目の CalcRotation_V1toV2(..) はカスタムライブラリーのメソッドで、第1引数に指定されたベクトルの向きを第2引数に指定されたベクトルの向きと同じにするための回転を返すものである (第1引数のベクトル、第2引数のベクトルを $\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ とすれば、このメソッドから取得される回転を $\boldsymbol{\mathsf{v_1}}$ に実行すると、 $\boldsymbol{\mathsf{v_1}}$ の向きは $\boldsymbol{\mathsf{v_2}}$ の向きと同じになる)。このメソッドは行列版のものが前節でも使われ、前節ではメソッドから返される回転は回転行列であったが、本節の場合は返される回転がQuaternionになっている (もちろんメソッドの内容は同じであり、回転が行列で表されるのかQuaternionで表されるのかの違いに過ぎない)。
走行中は常に、その時点でのサーキット上の進行方向にVehicleの向きを向ける必要があるが、「その時点でのサーキット上の進行方向」とはプログラム23行目で取得される dir であり、毎フレーム Vehicle をこの dir の方向に向けるようにすればよい。初期状態ではVehicleは y軸プラス方向を向いているので、y軸プラス方向から dir に向ける回転(rot)を毎フレーム計算し(25行目)、その回転を毎フレーム VehicleにセットすればVehicleは常にサーキット上の進行方向を向いて走行するようになるわけである。
なお29行目以降はカメラの移動処理であるが、これは上で述べたように毎フレーム Vehicleの現在位置から z軸マイナス方向に $7.2$ 離れた位置に置くだけである。
(以下 2-22節で用いた用語をそのまま使用する)
下図49は迷路を移動するオブジェクト Square の初期状態であり、初期状態ではSquareは1辺の長さが $2$ の正方形である。図50、図51は迷路を構成するオブジェクト Floor、Block であり、どちらも正方形でその大きさはSquareと同じである。
2-22節と同じく、Floorはその上を移動できる通路の部分であり、Blockはその上を移動することのできない壁に相当する部分である。
図52 右図は今回のプログラムで使用する迷路であり、FloorとBlockのみで構成されている。緑色の場所がスタート地点、青い場所がゴール地点である (上記のFloorとは色が異なるがスタート地点、ゴール地点もFloorである)。
この迷路も先程のサーキットと同じく全体を画面内に収めるにはやや大きいため、カメラ移動に関してはSquareを追跡する形をとる (すなわち、Squareの移動中はカメラをSquareから一定の距離だけ離れた位置に置き続ける)。
キー操作は以下のとおり。
H : Squareを左に動かす
L : Squareを右に動かす
J : Squareを下に動かす
K : Squareを上に動かす
C : 画面上のカバー(黒い覆い)の表示 / 非表示のためのスイッチ
今回のプログラムではSquareの周辺以外はカバー(黒い覆い)で覆われており、Squareの移動に合わせてこのカバーも表示され続けるので、迷路移動中は常にSquareの周辺以外は表示されない。しかし、C キーを押すことでこのカバーの表示、非表示を切り替えることができる。
プログラムを以下に示す。
[Code9] (実行結果 図53)
今回カメラはXY平面上のSquareから毎フレーム z軸マイナス方向に $20$ だけ離れた位置に置かれるようにしている (12~13行目)。
8行目の MoveSquare() はSquareの移動処理を行うメソッドであるが、その内容はわずかな違いを除いて 2-22節 Code2 と同じである (Squareに行われる変換が行列ではなく position、rotation による方法で実装されている)。
もちろんまだ扱わなければならない内容は多く、そういったものは後の3D空間の各章で解説される。しかし、一般的な需要という点では3Dグラフィックスよりも2Dグラフィックスの方が明らかに必要とされるケースが多く、それに比べれば3Dグラフィックスはまだ一部の需要に過ぎない。(開発者を含め)一般の人々にとって必要となるコンピューターグラフィックスとは3Dグラフィックスではなく、2Dグラフィックスというのが現状である。3D空間における議論は次の第3章から始まるが、3D空間までは必要としない読者もいるであろう (おそらくはそういった読者の方が多いであろう)。
そこで以下3節では、本来3D空間のしかるべき箇所で展開すべき内容のうち重要ないくつかを、2D限定版として編集し直した形で解説していく。
まずここでは今まで行列によって実装されていたオブジェクトの運動を、Unityに用意されているTransformクラスのプロパティを用いた実装に書き換える。さらに本節後半においては2D空間のカメラ移動の基礎について扱う (今までと同じく解説中における「2D空間」とはXY平面のことである)
A) Unityにおける標準的な変換方法
以降しばらくは、使用するオブジェクトについては親子関係のない単独のオブジェクトであることを前提として進める。今までのプログラムにおけるオブジェクトの運動は一部の例を除いて、すべて行列で実装してきた。しかし、行列による実装はこの講義で独自に用意したものであり、Unityで標準的に用意されているものではない。本節の前半ではこの行列の実装をUnityで提供している標準的なAPIによって書き換える。
UnityのAPIを使用する場合、一般的にはオブジェクトの運動は Transform クラスを経由して行われる。Transform クラスにはオブジェクトを動かすためのプロパティやメソッドが多く含まれるが、そのうちで重要なのが以下の3つのプロパティ localPosition、localRotation、localScale である。
localPosition はVector3型、localRotation はQuaternion型、localScale はVector3型である。Vector3 はいわゆる $(x, y, z)$ の形の3次元ベクトルのことであり、今までにもプログラム中で何度か使われてきた。Quaternion は行列と同じく回転を表すために使われるが、UnityのAPIでは Vector3、Matrix4x4 などと同じく構造体として用意されている。
例えば今までのプログラムでは、角度 deg の回転を表す回転行列を次のように取得した。
// 角度degの回転を表す回転行列 THMatrix3x3 R = TH2DMath.GetRotation3x3(deg);
Quaternion も同じく回転を表すことができるが、これを Quaternion で書き換えると以下のようになる。
// 角度degの回転を表すQuaternion Quaternion q = Quaternion.AngleAxis(deg, Vector3.forward);
そして重要なのが2D空間(XY平面)においては回転軸は常に z軸プラス方向であり、そのため上記の AngleAxis(..) の第2引数は常に Vector3.forward にしておくという点である。つまり、2D空間でQuaternionによる回転を取得する際には毎回 AngleAxis(deg, Vector3.forward) の形でこのメソッドを使えばよいのである (2D空間における回転については後述する)。
これは、2D空間におけるオブジェクトはXY平面上で運動を行うので、その z座標は常に $0$、z軸方向のスケール倍率は常に $1$ ということを意味している。
右図はオブジェクト Box の初期状態である。Boxは各辺の長さが等しい正方形であり、初期状態では中心が原点に位置している。行列を使う場合、オブジェクトを初期状態にするためには以下のように記述した。
Box.SetMatrix(THMatrix3x3.identity);
上記の3つのプロパティ localPosition、localRotation、localScale を使う場合、オブジェクトを初期状態にするためには以下のように記述する。
Box.transform.localPosition = new Vector3(0, 0, 0); Box.transform.localRotation = Quaternion.identity; Box.transform.localScale = new Vector3(1, 1, 1);
先程述べたように2D空間における位置及びスケールの指定では x座標、y座標のみを変更すればよく、z座標については常に同じ値を使用する (位置の場合は $0$、スケールの場合は $1$)。z座標は常に同じ値なので、上記の設定でも x座標、y座標だけを読めばよい。
その場合 localPosition は $(0,\ 0)$ であるが、これは x軸方向、y軸方向の移動量がともに $0$ を意味する (平行移動を行わない)。 localScale は $(1,\ 1)$ であるが、これは x軸方向、y軸方向のスケール倍率がともに $1$ であることを意味する (スケールを行わない)。
localRotation には Quaternion.identity というプロパティがセットされているが、このプロパティは Quaternion に用意されている定数で、何も回転を行わない Quaternion を表す。したがって localRotation に identity をセットすることはオブジェクトに対して何も回転を行わないことを意味する。
したがってBoxに対する上記の設定は、平行移動を行わず、回転も行わず、スケールも行わない、すなわち Boxに対しては何の変換も行わないこと、それはBoxを初期状態のままにしておくことを意味する。
では続いてこれらのプロパティを使って上記のBoxに対し変換を実行する。
以下の記述はBoxを初期状態の位置から $(3,\ 1)$ だけ平行移動させるものである (図2 ; localPosition に Vector2 をセットしているが、この場合には自動的に z座標が $0$ になる)。
// 初期状態の位置から (3, 1) だけ平行移動 Box.transform.localPosition = new Vector2(3, 1);
Boxを初期状態の向きから $45^\circ$ だけ回転させるには次のように記述する (図3)。
// 初期状態の向きから45°回転 Box.transform.localRotation = Quaternion.AngleAxis(45, Vector3.forward);
以下の記述はBoxを初期状態の大きさから各軸方向に $2$ 倍の拡大を実行するものである (図4 ; localPosition の場合とは異なり、Vector2 をセットしてはならない。その場合 z座標が自動的に $0$ になり、z軸方向の倍率が $0$ として扱われるためオブジェクトの表示が不自然なものになりやすい)。
// 初期状態の大きさから2倍拡大 Box.transform.localScale = new Vector3(2, 2, 1);
-
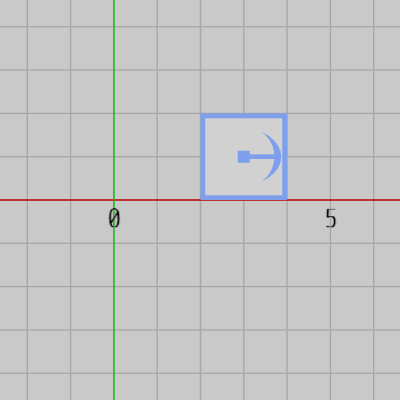図2 (3, 1) だけ平行移動 -
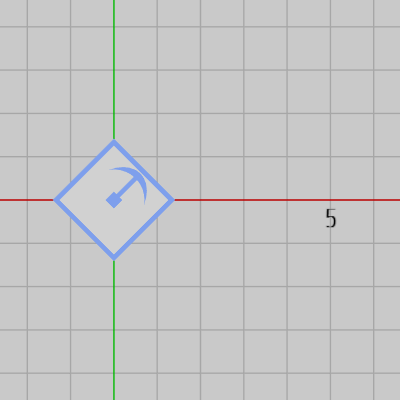図3 45°回転 -
図3 x軸方向、y軸方向に2倍拡大
上記の変換はすべて初期状態のBoxに対しての個別の変換である。例えば図2は初期状態のBoxに対して平行移動だけを行ったものである。同様に図3は初期状態のBoxに対して回転だけを、図4はスケールだけを行ったものである。
行列によってオブジェクトに変換を実行する際、ほとんどの場合において複数の変換をまとめたものをオブジェクトに実行した。例えば平行移動行列を $T$、回転行列を $R$、スケール行列を $S$ とするとき、それらの積 $M = SRT$ をオブジェクトに実行することは、オブジェクトに対し平行移動、回転、スケールの順で変換を実行することを意味し、$M = TSR$ ならばオブジェクトに対し回転、スケール、平行移動の順で変換を実行することを意味した (行列の積は右から読む)。
そしてその際、行列の積の順序がそのまま変換順序になるので、積の順序には注意する必要があった。例えば行列の積が $RT$ ならば、変換順序は平行移動、回転の順になるが、積が $TR$ ならば回転、平行移動の順になる。
上記の3つのプロパティ localPosition、localRotation、localScale を使って複数の変換(具体的には平行移動、回転、スケールの3つの変換)をまとめたものをオブジェクトに実行することもできる。そして、その場合の変換順序は常にスケール、回転、平行移動の順になる。
以下具体的な例で見ていこう。
初期状態のBoxに対して(先程と同じ)以下の変換を順番に実行する (スケール、回転、平行移動の順 ; 実行結果 図6)。
(1) 各軸方向に $2$ 倍のスケール
(2) $45^\circ$ の回転
(3) $(3,\ 1)$ の平行移動
この変換を行列で記述すると以下のようになる。
THMatrix3x3 S = TH2DMath.GetScale3x3(2, 2); THMatrix3x3 R = TH2DMath.GetRotation3x3(45); THMatrix3x3 T = TH2DMath.GetTranslation3x3(3, 1); THMatrix3x3 M = T * R * S; Box.SetMatrix(M);
localPosition、localRotation、localScale を使った場合は以下のようになる。
Box.transform.localScale = new Vector3(2, 2, 1); Box.transform.localRotation = Quaternion.AngleAxis(45, Vector3.forward); Box.transform.localPosition = new Vector2(3, 1);
行列で記述した場合も3つのプロパティによって記述した場合も実行結果は同じである (下図6)。まず初期状態においてBoxを $2$ 倍拡大し、その後 $45^\circ$ の回転を実行、最後に $(3,\ 1)$ だけの平行移動を行う。3つの変換をこの順序で実行すると図6の状態になる。
なお、プロパティの記述順序は変換順序には影響しない。つまり3つのプロパティをどのような順序でセットしても必ずスケール、回転、平行移動の順で変換が実行される。例えば下のコードでも実行結果は変わらない (図6)。
// 3つのプロパティをどのような順序で記述しても結果は同じ (スケール、回転、平行移動の順で変換が行われる) Box.transform.localRotation = Quaternion.AngleAxis(45, Vector3.forward); Box.transform.localPosition = new Vector2(3, 1); Box.transform.localScale = new Vector3(2, 2, 1);
今までは単独のオブジェクトを前提としていたが、ここからは複数のオブジェクトの一体化運動を行列ではなく、上記の3つのプロパティによって書き換えることについて見ていく。
例えば2つのオブジェクト Obj1、Obj2 が親子関係にある場合、今までのプログラムではこの2つのオブジェクトの一体化した運動は次のように記述されていた (ここでは Obj1 が親オブジェクト、Obj2 を子オブジェクトとする)。
// Obj2 (子オブジェクト) THMatrix3x3 traObj2 = TH2DMath.GetTranslation3x3(x2, y2); THMatrix3x3 rotObj2 = TH2DMath.GetRotation3x3(deg2); THMatrix3x3 sclObj2 = TH2DMath.GetScale3x3(s2, s2); THMatrix3x3 localObj2 = traObj2 * rotObj2 * sclObj2; // Obj1 (親オブジェクト) THMatrix3x3 traObj1 = TH2DMath.GetTranslation3x3(x1, y1); THMatrix3x3 rotObj1 = TH2DMath.GetRotation3x3(deg1); THMatrix3x3 sclObj1 = TH2DMath.GetScale3x3(s1, s1); THMatrix3x3 localObj1 = traObj1 * rotObj1 * sclObj1; THMatrix3x3 worldObj2 = localObj1 * localObj2; THMatrix3x3 worldObj1 = localObj1; Obj2.SetMatrix(worldObj2); Obj1.SetMatrix(worldObj1);
一体化運動を行列によって実装する場合には local や world という接頭辞の付けられた行列が使われており、このプログラムでも localObj2 や worldObj1 としてそれらは使われているが、ここでは接頭辞として local の付いている行列を「ローカル行列」、world の付いている行列を「ワールド行列」と呼ぶことにする。
最終的にオブジェクトに対して実行されるのはワールド行列であり(16~17行目)、ワールド行列はローカル行列の積として構成される (13~14行目 ; 一番上の親オブジェクトの場合はローカル行列とワールド行列は同じである)。
各オブジェクトのローカル行列は上記の場合、スケール、回転、平行移動の3つの変換行列の積から構成されている。例えば Obj2 のローカル行列 localObj2 は、sclObj2 (スケール)、rotObj2 (回転)、traObj2 (平行移動)の積である (5行目)。同様に Obj1 のローカル行列 localObj1 は、sclObj1 (スケール)、rotObj1 (回転)、traObj1 (平行移動)の積として構成されている (11行目)。
そして、いずれのローカル行列もそれを構成する行列の実行順序はスケール、回転、平行移動の順になっているが、この点は重要である。それは行列による実装を以下に示す3つのプロパティによる実装に書き換えるには、ローカル行列の内容がスケール、回転、平行移動の順で行われていることが前提となるためである。
上記の行列による一体化運動の実装を3つのプロパティ(localPosition、localRotation、localScale)による実装に書き換えるには、以下の手続きを形式的に行えばよい。
すなわち、localPosition、localRotation、localScale の内容を、各オブジェクトのローカル行列を構成する平行移動行列、回転行列、スケール行列の内容と同じになるようにするのである。
具体的な例で見ていこう。ローカル行列 localObj2 は traObj2、rotObj2、sclObj2 の3つの積であるが、そのうちの平行移動行列 traObj2 の内容は (x2, y2) だけの平行移動である (2行目)。したがって平行移動を指定するプロパティ localPosition の内容も同じく (x2, y2) だけの平行移動にすればよい。
Obj2.transform.localPosition = new Vector2(x2, y2);
同様に回転行列 rotObj2 の内容は角度 deg2 だけの回転であるので(3行目)、回転を指定するプロパティ localRotation の内容も角度 deg2 だけの回転とする。
Obj2.transform.localRotation = Quaternion.AngleAxis(deg2, Vector3.forward);
スケール行列 sclObj2 の内容は x軸方向、y軸方向ともに s2 倍の拡大であるため、スケールを指定するプロパティ localScale の内容も s2 倍の拡大とする。
Obj2.transform.localScale = new Vector3(s2, s2, 1);
今述べた書き換えを Obj1、Obj2 のローカル行列に行うと以下のようなコードになる (初期化ブロックの処理は親子関係の設定である)。
if(!i_INITIALIZED)
{
// 親子関係の設定
Obj2.transform.SetParent(Obj1.transform);
i_INITIALIZED = true;
}
// Obj2
Obj2.transform.localPosition = new Vector2(x2, y2);
Obj2.transform.localRotation = Quaternion.AngleAxis(deg2, Vector3.forward);
Obj2.transform.localScale = new Vector3(s2, s2, 1);
// Obj1
Obj1.transform.localPosition = new Vector2(x1, y1);
Obj1.transform.localRotation = Quaternion.AngleAxis(deg1, Vector3.forward);
Obj1.transform.localScale = new Vector3(s1, s1, 1);
Obj2の3つのプロパティ localPosition、localRotation、localScale (10~12行目)の内容が、行列版のプログラムにおいて localObj2 を構成していた3つの変換行列の内容と同じになっていることがわかるであろう。同様にObj1の3つのプロパティ(15~17行目)の内容も、行列版のプログラムにおいて localObj1 を構成していた3つの変換行列の内容と同じになっているのである (Unityの標準的な変換方法ではこのように localPosition、localRotation、localScale の3つのプロパティに値をセットすればよいだけであり、行列版の実装のように最後にワールド行列を計算して、オブジェクトにワールド行列を実行するといった処理は必要ない)。
また初期化ブロックに見られるようにプログラムでオブジェクトの親子関係を設定する場合には SetParent(..) というメソッドを使用する。そして注意すべきはこのメソッドは Transform クラスのメソッドであり、オブジェクトの transform プロパティを経由しなければならないという点である。すなわち Obj2 の親オブジェクトとして Obj1 を設定する場合には
Obj2.transform.SetParent(Obj1.transform);
最後に1点だけ補足する。
上記のプログラムではUnity標準の変換方法として3つのプロパティ localPosition、localRotation、localScale を使用した。確かに複数のオブジェクトが親子関係を構成し、一体化した運動をしているのであればこの3つのプロパティを使う必要があるが、親子関係のない単独のオブジェクトの場合には localPosition、localRotation の代わりに表記の軽い position、rotation というプロパティを使うことができる。
簡単にいえば親子関係のない単独のオブジェクトの場合には localPosition、localRotation を使っても、position、rotation を使っても実行結果は変わらないのである。そのため以下では簡単のため単独のオブジェクトの場合には localPosition、localRotation ではなく、position、rotation を使い、親子関係を構成する複数のオブジェクトの場合に localPosition、localRotation を使うことにする (詳しくは position、rotation はワールド座標系における位置及び回転状態のことであり、localPosition、localRotation は親座標系における位置及び回転状態のことである。これらのことについては第4章、第5章で解説する)。
では実際に、今までに扱ったプログラム及びそれと類似のものをUnity標準の方法で書き換えていこう。
# Code1
以下は 2-4節のCode3である。このプログラムは下図7の円盤型オブジェクト Disk を $(1,\ 2)$ を中心とする半径 $3$ の円周上で自転及び公転させるというものである。 [2-4節 Code3] (実行結果 図8)
i_degRot += 6; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degRot); i_degRev += 3; THMatrix3x3 Rev = TH2DMath.GetRotation3x3(i_degRev); Vector2 pos = Rev * new Vector3(3, 0, 1); pos += new Vector2(1, 2); THMatrix3x3 T = TH2DMath.GetTranslation3x3(pos); THMatrix3x3 M = T * R; Disk.SetMatrix(M);
local や world という接頭辞が省略されているが、Diskは親子関係のない単独のオブジェクトであるため10行目の M がローカル行列でありワールド行列でもある。したがって この M を構成する2つの変換行列(平行移動行列 T、回転行列 R)の内容と同じになるようにプロパティを定めればよい。
この行列による実装を position、rotation による実装に書き換えたものを以下に示す。
[Code1] (実行結果 図8)
i_degRot += 6; Quaternion rot = Quaternion.AngleAxis(i_degRot, Vector3.forward); i_degRev += 3; Quaternion rev = Quaternion.AngleAxis(i_degRev, Vector3.forward); Vector2 pos = rev * new Vector2(3, 0); pos += new Vector2(1, 2); Disk.transform.position = pos; Disk.transform.rotation = rot;
6行目では半径 $3$ の円周上の位置を毎フレーム計算しているが、ここでは Quaternion と Vector2 の積を行っている。その際には行列の場合と異なりベクトルを同次座標にする必要はない (すなわち6行目のベクトルを new Vector3(3, 0, 1) のようにする必要はない)。
例えば、XY平面上の点 $(a,\ b)$ を原点周りに $120^\circ$ 回転させる処理であれば以下のように記述すればよい。
Quaternion q = Quaternion.AngleAxis(120, Vector3.forward); Vector2 pos = q * new Vector2(a, b);
# Code2
以下のプログラムは2-15節の最後に作成したメソッド UserMotion() である。UserMotion() には下図9に示されるオブジェクト Plane をキー操作によって動かす処理が記述されている。
キー操作は以下のとおり。
H : 左に旋回 (回転は $2^\circ$ ずつ)
L : 右に旋回
S : オブジェクトの移動/停止用スイッチ
[2-15節 UserMotion()]
void UserMotion()
{
if (Input.GetKey(KeyCode.H))
{
i_forwardDegree += 2;
}
else if (Input.GetKey(KeyCode.L))
{
i_forwardDegree -= 2;
}
if (Input.GetKeyDown(KeyCode.S)) // 移動/停止
{
i_MOVE = !i_MOVE;
}
THMatrix3x3 R = TH2DMath.GetRotation3x3(i_forwardDegree);
Vector2 forwardDir = R * new Vector3(0, 1, 1);
Vector2 curP = Plane.GetPosition();
Vector2 newP = (i_MOVE) ? curP + 0.20f * forwardDir : curP;
THMatrix3x3 T = TH2DMath.GetTranslation3x3(newP);
THMatrix3x3 M = T * R;
Plane.SetMatrix(M);
}
このプログラムにおけるPlaneも単独のオブジェクトであるため、Planeに実行される変換行列 M (23行目)はローカル行列であり、ワールド行列でもある。したがって今回も M を構成する2つの変換行列(平行移動行列 T、回転行列 R)の内容と同じになるようにプロパティの値を定めればよい。
以下のプログラムは上記の UserMotion() を position、rotation の2つのプロパティを使って書き換えたものである。
[Code2] (実行結果 図10)
if (Input.GetKey(KeyCode.H))
{
i_forwardDegree += 2;
}
else if (Input.GetKey(KeyCode.L))
{
i_forwardDegree -= 2;
}
if (Input.GetKeyDown(KeyCode.S)) // 移動/停止
{
i_MOVE = !i_MOVE;
}
Quaternion rot = Quaternion.AngleAxis(i_forwardDegree, Vector3.forward);
Vector2 forwardDir = rot * new Vector2(0, 1);
Vector2 curP = Plane.transform.position;
Vector2 newP = (i_MOVE) ? curP + 0.20f * forwardDir : curP;
Plane.transform.position = newP;
Plane.transform.rotation = rot;
# Code3
例えばDiskの位置を変えずに自転だけ行わせるとしよう。その場合、行列による実装であれば毎フレームにおける平行移動行列の内容を常に同じ位置への移動とすればよい。具体的には以下のように記述することになる。
下記のプログラムはXY平面上の $(3,\ 2)$ において毎フレーム $6^\circ$ ずつDiskに自転を行わせるものである。Diskに実行される平行移動行列は毎フレーム 同じものであるため、右図の実行結果に示されるようにDiskの位置は常に $(3,\ 2)$ から動くことはない。
[Beta3A] (実行結果 図11)
i_degRot += 6; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degRot); THMatrix3x3 T = TH2DMath.GetTranslation3x3(3, 2); THMatrix3x3 M = T * R; Disk.SetMatrix(M);
これをUnity標準の方法で書き換えると以下のように記述される。
[Beta3B] (実行結果 図11)
i_degRot += 6; Quaternion rot = Quaternion.AngleAxis(i_degRot, Vector3.forward); Disk.transform.position = new Vector2(3, 2); Disk.transform.rotation = rot;
このコードにおいて4行目の position へセットされる値は毎フレーム同じである。このように position や rotation (あるいは localPosition や localRotation でも)プログラム実行中にその内容が変わらないのであれば、それらのプロパティには初期化ブロックなどで1度だけ値をセットすればよい。上記のように毎フレーム同じ値をセットし続ける必要はないのである。
具体的には次のように書き換えられる。
[Beta3C] (実行結果 図11)
if(!i_INITIALIZED)
{
Disk.transform.position = new Vector2(3, 2);
i_INITIALIZED = true;
}
i_degRot += 6;
Quaternion rot = Quaternion.AngleAxis(i_degRot, Vector3.forward);
Disk.transform.rotation = rot;
Diskの位置は $(3,\ 2)$ から変化することはないので、初期化ブロックにおいて position にその位置をセットし、プログラム実行中は rotation だけが更新されるようにしている。
では今述べた例と類似の問題を考える。
下図12はオブジェクト Arrow の初期状態であり、初期状態においてArrowは y軸プラス方向を指している。ここでは、このオブジェクトを下図13に示されるように $-60^\circ$ 回転した状態で、その方向に移動させる。
まずは行列による実装である。
[Beta3D] (実行結果 図14)
if (!i_INITIALIZED)
{
THMatrix3x3 R0 = TH2DMath.GetRotation3x3(-60);
Arrow.SetMatrix(R0);
i_forwardDir = R0 * new Vector3(0, 1, 1);
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S)) // 移動/停止
{
i_MOVE = !i_MOVE;
}
Vector2 curP = Arrow.GetPosition();
Vector2 newP = (i_MOVE) ? curP + 0.1f * i_forwardDir : curP;
THMatrix3x3 R = TH2DMath.GetRotation3x3(-60);
THMatrix3x3 T = TH2DMath.GetTranslation3x3(newP);
THMatrix3x3 M = T * R;
Arrow.SetMatrix(M);
初期化ブロックではArrowを(y軸プラス方向から) $-60^\circ$ の方向に回転させている (図13の状態になる。回転だけであり、位置は動かさない)。S キーを押すことで $-60^\circ$ の方向に毎フレーム $0.1$ ずつ進んでいくが、その際 Arrowは常に $-60^\circ$ の方向を向いている (図14)。
ではこのプログラムをUnity標準の方法に書き換える。上の実行結果あるいはプログラムから明らかなように、Arrowの向きはプログラム実行中 常に同じであり、位置だけを更新すればよい。したがって、プログラムは次のようになる。
[Code3] (実行結果 図14)
if (!i_INITIALIZED)
{
Quaternion rot = Quaternion.AngleAxis(-60, Vector3.forward);
Arrow.transform.rotation = rot;
i_forwardDir = rot * new Vector2(0, 1);
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.C))
{
Arrow.transform.position = Vector2.zero;
i_MOVE = false;
}
if (Input.GetKeyDown(KeyCode.S)) // 移動/停止
{
i_MOVE = !i_MOVE;
}
Vector2 curP = Arrow.transform.position;
Vector2 newP = (i_MOVE) ? curP + 0.1f * i_forwardDir : curP;
Arrow.transform.position = newP;
このプログラムでも開始時点ではArrowは $-60^\circ$ の方向を向いており、S キーを押すことで移動が始まるが、今回は C キーを押すことで開始地点に戻る処理を追加している (10~14行目 ; 開始地点に戻るが向きは $-60^\circ$ のまま)。
# Code4
2-3節では以下の図15、16のオブジェクト Needle 及び Ball を一体化させる運動を扱ったが、今回のプログラムは 2-3節 Code4 にいくつかの処理を追加したものであり、具体的には図17に示される運動である (Needleが親オブジェクト、Ballが子オブジェクト)。-
図15 Needle 初期状態 -
図16 Ball 初期状態 -
図17 Code4 実行結果
以下は行列による実装である。
[Beta4] (実行結果 図17)
// Ball i_shmBall += 9; float s = CalcShmValue(i_shmBall, 1.0f, 1.5f); i_revBall += 9; THMatrix3x3 Rev = TH2DMath.GetRotation3x3(i_revBall); Vector2 pos = Rev * new Vector3(0, 1, 1); pos += new Vector2(0, 4); THMatrix3x3 sclBall = TH2DMath.GetScale3x3(s, s); THMatrix3x3 traBall = TH2DMath.GetTranslation3x3(pos); THMatrix3x3 localBall = traBall * sclBall; // Needle i_degNeedle -= 3; THMatrix3x3 rotNeedle = TH2DMath.GetRotation3x3(i_degNeedle); THMatrix3x3 traNeedle = TH2DMath.GetTranslation3x3(-4, 1); THMatrix3x3 localNeedle = traNeedle * rotNeedle; // ワールド行列 THMatrix3x3 worldBall = localNeedle * localBall; THMatrix3x3 worldNeedle = localNeedle; Ball.SetMatrix(worldBall); Needle.SetMatrix(worldNeedle);
2~12行目までがBallのローカル行列の計算であり、15~18行目までがNeedleのローカル行列の計算である。
Ballのローカル行列 localBall (12行目)の内容は、$1$~$1.5$ 倍の間での拡大縮小の繰り返し(sclBall)、Needle先端を中心とする半径 $1$ の円周上の公転(traBall)である。
3行目の CalcShmValue(..) は $1$~$1.5$ の間の数値を単振動によって計算する補助メソッドであり、ローカル変数 s は$1$~$1.5$ の間を往復し続ける (第1引数に単振動計算のための角度、第2引数、第3引数は最小値、最大値である)。
Needleのローカル行列 localNeedle (18行目)の内容は、毎フレーム $3^\circ$ ずつの回転(rotNeedle)、$(-4,\ 1)$ への平行移動(traNeedle)である (traNeedle の値は常に同じなのでNeedleは同じ位置で回転をし続ける)。
では上のプログラムをUnity標準の方法で書き換える。今回は親子関係にある2つのオブジェクトの一体化した運動なので使用するプロパティは localPosition、localRotation、localScale である。
[Code4] (実行結果 図17)
if (!i_INITIALIZED)
{
Ball.transform.SetParent(Needle.transform);
Needle.transform.localPosition = new Vector2(-4, 1);
i_INITIALIZED = true;
}
// Ball
i_shmBall += 9;
float s = CalcShmValue(i_shmBall, 1.0f, 1.5f);
i_revBall += 9;
Quaternion rev = Quaternion.AngleAxis(i_revBall, Vector3.forward);
Vector2 pos = rev * new Vector3(0, 1);
pos += new Vector2(0, 4);
Ball.transform.localScale = new Vector3(s, s, 1);
Ball.transform.localPosition = pos;
// Needle
i_degNeedle -= 3;
Needle.transform.localRotation = Quaternion.AngleAxis(i_degNeedle, Vector3.forward);
初期化ブロック 3行目は親子関係の設定である。Ballのローカル行列 localBall の内容はスケールと平行移動であったが、それらの内容と同じものを19~20行目で localScale、localPosition にセットしている。
Needleのローカル行列 localNeedle の内容は回転と平行移動であったが、それらの内容と同じものをNeedleの localRotation、localPosition にセットしている。Needleは毎フレーム回転するので localRotation の内容は24行目で毎フレーム更新されるが、その位置は変化しないので localPosition は初期化ブロックで1度セットされるだけである (5行目)。
# Code5
以下のプログラムは 2-10節 Code4 である。このプログラムは2D空間においてヘリコプターを動かすものであり、図18、図19はヘリコプターを構成するオブジェクト Rotor、Body の初期状態である。-
図18 Body 初期状態 -
図19 Rotor 初期状態 -
図20 Code5 実行結果
キー操作は以下のとおり。
H : 左に旋回 (回転は $1^\circ$ ずつ)
L : 右に旋回
S : オブジェクトの移動/停止用スイッチ
[2-10節 Code4] (実行結果 図20)
if (Input.GetKey(KeyCode.H))
{
i_degBody += 1;
}
else if (Input.GetKey(KeyCode.L))
{
i_degBody -= 1;
}
if (Input.GetKeyDown(KeyCode.S)) // 移動/停止
{
i_MOVE = !i_MOVE;
}
// Rotor
i_degRotor += 12;
THMatrix3x3 rotRotor = TH2DMath.GetRotation3x3(i_degRotor);
THMatrix3x3 traRotor = TH2DMath.GetTranslation3x3(c_attachPos_Rotor);
THMatrix3x3 localRotor = traRotor * rotRotor;
// Body
THMatrix3x3 rotBody = TH2DMath.GetRotation3x3(i_degBody);
Vector2 direBody = rotBody * new Vector3(0, 1, 1);
Vector2 curP = Body.GetPosition();
Vector2 newP = (i_MOVE) ? (curP + 0.075f * direBody) : curP;
THMatrix3x3 traBody = TH2DMath.GetTranslation3x3(newP);
THMatrix3x3 localBody = traBody * rotBody;
// ワールド行列
THMatrix3x3 worldRotor = localBody * localRotor;
THMatrix3x3 worldBody = localBody;
Rotor.SetMatrix(worldRotor);
Body.SetMatrix(worldBody);
では上のプログラムをUnity標準の方法で書き換える。Rotorのローカル行列 localRotor (19行目)の内容は回転(rotRotor)と平行移動(traRotor)から構成されるが、これらの行列と同じ内容になるように localRotation 及び localPosition に対して値をセットする。
また、Bodyのローカル行列 localBody (28行目)の内容は回転(rotBody)と平行移動(traBall)から構成されるが、やはりこれらの行列と同じ内容になるように localRotation 及び localPosition に対して値をセットすればよい。
プログラムは次のとおり。
[Code5] (実行結果 図20)
if (!i_INITIALIZED)
{
Rotor.transform.SetParent(Body.transform);
Rotor.transform.localPosition = c_attachPos_Rotor;
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.H))
{
i_degBody += 1;
}
else if (Input.GetKey(KeyCode.L))
{
i_degBody -= 1;
}
if (Input.GetKeyDown(KeyCode.S)) // 移動/停止
{
i_MOVE = !i_MOVE;
}
// Rotor
i_degRotor += 12;
Quaternion rotRotor = Quaternion.AngleAxis(i_degRotor, Vector3.forward);
Rotor.transform.localRotation = rotRotor;
// Body
Quaternion rotBody = Quaternion.AngleAxis(i_degBody, Vector3.forward);
Vector2 direBody = rotBody * new Vector2(0, 1);
Vector2 curP = Body.transform.localPosition;
Vector2 newP = (i_MOVE) ? (curP + 0.075f * direBody) : curP;
Body.transform.localPosition = newP;
Body.transform.localRotation = rotBody;
# Code6
では一体化運動の最後の例として3つのオブジェクトを一体化させる場合を見てみよう。使用するオブジェクトは以下の Red、Green、Blue である。
-
図21 Red 初期状態 -
図22 Green 初期状態 -
図23 Blue 初期状態
上図はそれぞれの初期状態であり、各オブジェクトの階層構造はRedが一番上の親オブジェクト、その子オブジェクトとしてGreen、一番下の子オブジェクトがBlueである (図24)。
それぞれのオブジェクトは次の運動を行う。
BlueはGreenの上で x軸方向に $-4.2$ から $4.2$ の範囲の往復運動、及びその運動中に y軸方向の大きさが $1$ 倍から $2$ 倍の間で変化し続ける (図26)。
GreenはRedの先端において、$-30^\circ$ から $30^\circ$ の範囲の往復回転を行う (図27)。
Redは $20^\circ$ 傾いた状態で、$(6,\ 3)$ から $(12,\ 3)$ までの区間を往復し続ける (図28)。
-
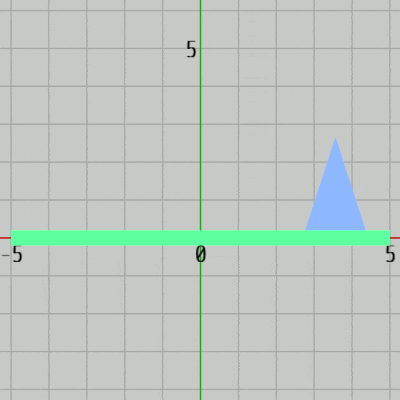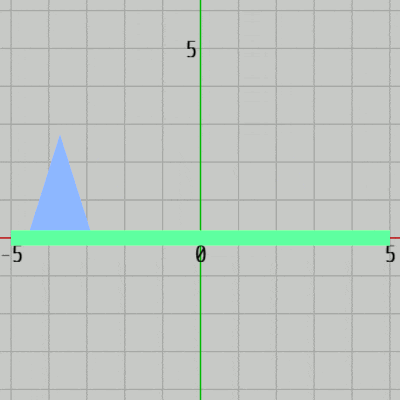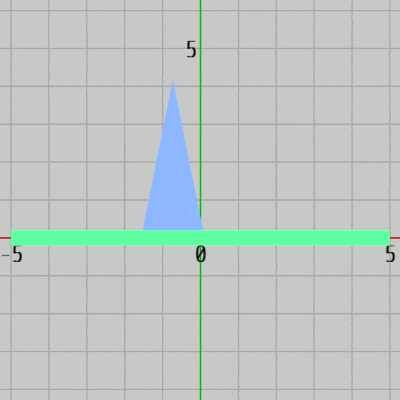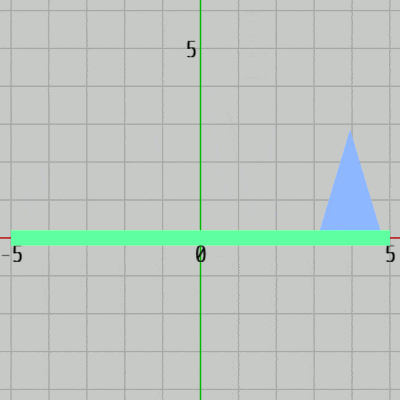図26 Blueの運動 -
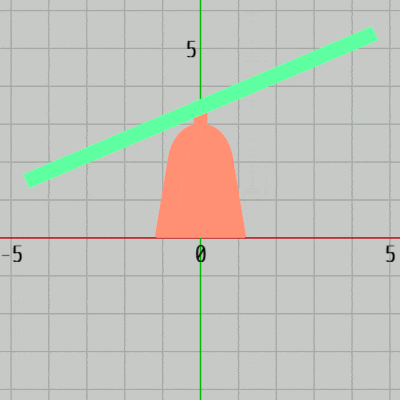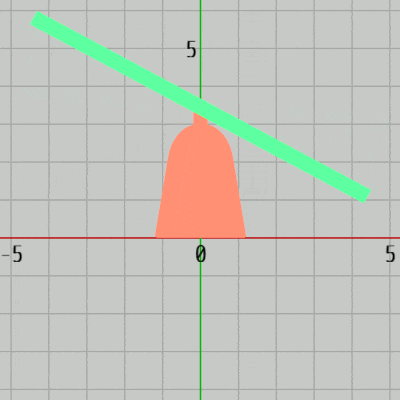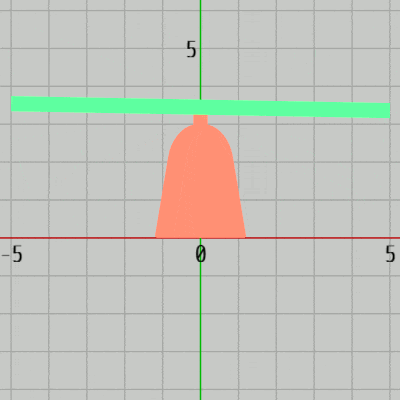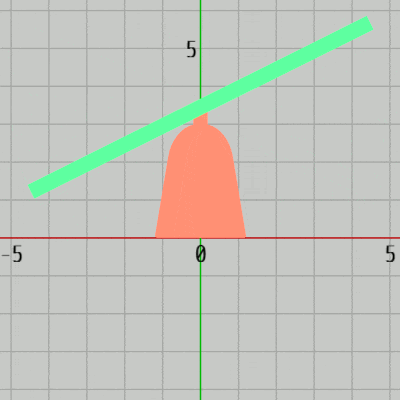図27 Greenの運動 -
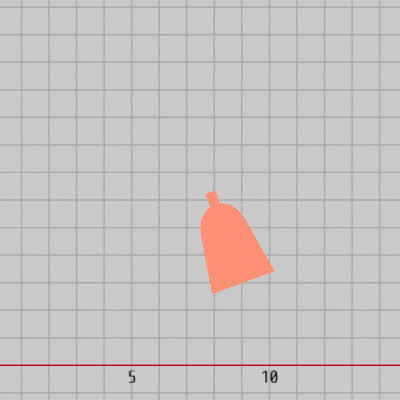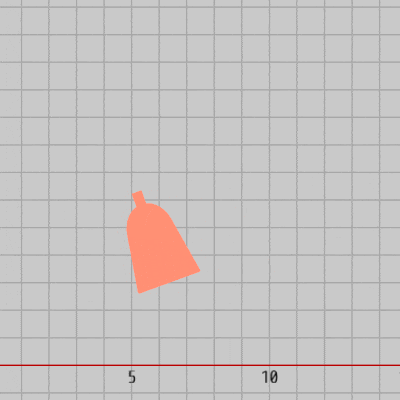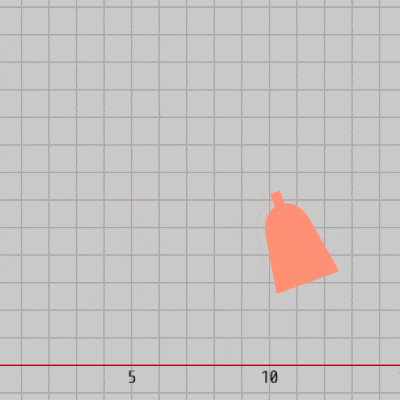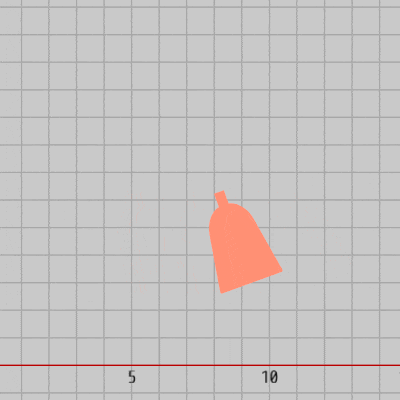図28 Redの運動
プログラムは以下のとおり。
[Code6] (実行結果 図25)
if (!i_INITIALIZED)
{
Blue.transform.SetParent(Green.transform);
Green.transform.SetParent(Red.transform);
Green.transform.localPosition = c_attachPos_Green;
Red.transform.localRotation = TH2DMath.GetRotation(20);
i_INITIALIZED = true;
}
// Blue
i_shmB += 4;
float x = CalcShmValue(i_shmB, -4.2f, 4.2f);
Blue.transform.localPosition = new Vector2(x, 0.2f);
float s = CalcShmValue(i_shmB + 90, 1.0f, 2.0f);
Blue.transform.localScale = new Vector3(1, s, 1);
// Green
i_shmG += 2;
float deg = CalcShmValue(i_shmG, -30.0f, 30.0f);
Green.transform.localRotation = TH2DMath.GetRotation(deg);
// Red
i_shmR += 1;
x = CalcShmValue(i_shmR, 6.0f, 12.0f);
Red.transform.localPosition = new Vector2(x, 3);
初期化ブロックは親子関係の設定とプログラム実行中に変化しないプロパティへの値をセットしている。例えば、Greenであればアタッチポジション(Redの先端)は変化しないので初期化ブロックはにおいてその位置 c_attachPos_Green がセットされる。また Redの場合は実行中は $20^\circ$ 傾いたままなので、これも初期化ブロックにおいてセットされる。
初期化ブロック以降の内容は上で述べた各オブジェクトの運動の記述であり、いずれも単振動による往復運動である。CalcShmValue(..) はCode4でも使われたが、単振動の計算を行うための補助メソッドであり、第1引数に単振動計算のための角度、第2引数、第3引数には最小値、最大値をセットする。
B) 2D空間におけるカメラの移動
本節後半では2D空間におけるカメラの移動について見ていく。2D空間におけるカメラ移動は上下左右の2次元的な平行移動であり、一般のオブジェクトの平行移動と同じく基本的にはカメラの x座標、y座標を変更するだけである。しかし一般のオブジェクトとは異なり、2D空間限定で使用する場合でもカメラの場合は3次元的に考える状況がいくつか生じる。
x軸、y軸の2つの軸で構成される2D空間とは異なり、3D空間の場合はさらに第3の軸である z軸が加わる (図29 ; グリッド線はXZ平面に引かれている)。
他のオブジェクトと同様にカメラにも初期状態があり、Unityではカメラは初期状態において原点に置かれ、z軸プラス方向を向いている (図30)。
2D空間、すなわちXY平面をカメラによって撮影する場合には、カメラの位置は z軸マイナス側に置き、カメラの向きを z軸プラス方向に向ける (図31 ; ただしこれは左手系の場合である (3-3節参照))。
もちろんこれは今までのプログラムでも同様であり、今までのプログラムではカメラは下図32に示されるように、z軸マイナス側の適当な位置で z軸プラス方向を向いて置かれており、そこからXY平面を撮影していたのである。
下図は図32のカメラからの撮影結果である。
また他のオブジェクトと同様にカメラに対しても回転や平行移動などの変換を行うことができる (カメラに対してスケールを行うことはない)。しかし、ここで扱うカメラに関しては回転は行わない。以下3節においてカメラに対して行う変換は平行移動のみである。
(Unity画面上において Hierarchy Window 内にある「Main Camera」を選択すると(図34)、Inspector 内にカメラに関する情報が表示されるが(図35)、カメラに回転を行わない場合はこのInspector内の Transform という項目にある「Rotation」の各値が常に「x 0 y 0 z 0」となる。
カメラの場合 2D空間、3D空間のいずれにおいても「Scale」の各値は常に $1$ である)
カメラに対して回転を行わず平行移動のみを行う場合、実行結果の画面においては画面の横方向、縦方向は常に x軸、y軸に平行になる (図36)。
簡単にいえば、(2D空間を撮影する場合)カメラの位置を $(E.\!x,\ E.\!y,\ E.\!z)$ とするとき、画面の中心に来る座標は $(E.\!x,\ E.\!y)$ である。
例えばカメラの位置が $(0, 0, z)$ であるとき($z < 0$)、画面の中心には原点が来る。
最後に回転に関して1つ補足する。
2D空間において回転のプラス方向(角度を増加させる回転)は反時計周りであった。2D空間における回転とは具体的には z軸周りの回転であり、下図39に見られるようにオブジェクトを z軸周りに回転させているのである。そして詳しくは第3章で扱うが、z軸周りの回転とは(左手系の場合)左手の親指を z軸プラス方向に向けた際に、残りの指の曲がっている方向がプラス方向の回転(角度を増加させる回転)である。
実際、下図39の場合 左手の親指を z軸プラス方向に向けると、残りの指の曲がっている方向が図中のオブジェクトの回転方向(反時計周り)と一致しているのが確かめられるであろう (詳しくは 3-3節、3-10節参照)。右図はこのときの実行結果の画面である。
では以上をふまえてプログラム実行中におけるカメラ移動を実装する。
本節から 2-29節のプログラムにおいてはカメラは「MainCamera」という名前で使われているが、Unityではプログラムからカメラを操作する場合、次のような記述によってカメラを表すオブジェクトを取得する必要がある。
// カメラの取得
MainCamera = GameObject.Find("Main Camera");
ここで使われている Find(..) はHierarchy内のオブジェクトを取得するためのメソッドで、メソッドの引数にはHierarchy内に表示されているオブジェクトの名前をセットする。例えばカメラの場合デフォルトでは "Main Camera" という名前であるため(上図34)、この名前をセットすればよい。
なお、プログラム中ではこのような処理は初期化ブロックで1度だけ行えばよいが、以降のプログラムではこのカメラの取得処理は開始時点において裏側であらかじめ行われているので、プログラムでは特に何も記述しなくてもMainCameraを使用することができる。
# Code7
XY平面から $18$ だけ離れた位置にカメラが置かれている (図41 ; 開始時点におけるカメラの位置は $(0,\ 0, -18)$ )。ここでは、カメラを以下のキー操作によって上下左右に移動させる (z軸方向には移動しないのでカメラの z座標は常に同じ)。またプログラム実行中は画面の中心を示すために図42のオブジェクト Dot が常に画面中心に置かれるようにする。そのためにはカメラの移動中において、上で述べたようにカメラの位置の z座標を $0$ にした位置にDotを置き続ければよい (図43 ; Dotの動く範囲はXY平面上)。
-
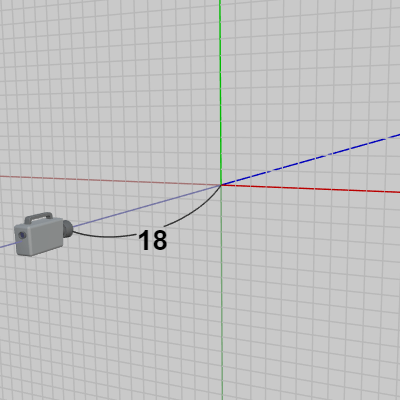図41 -
図42 Dot 初期状態 -
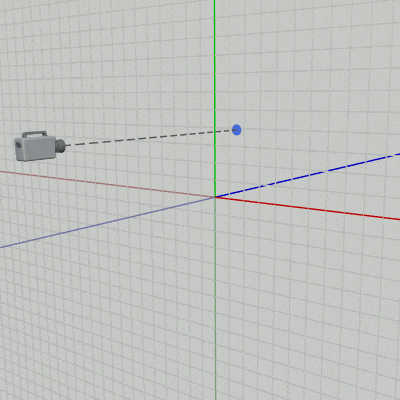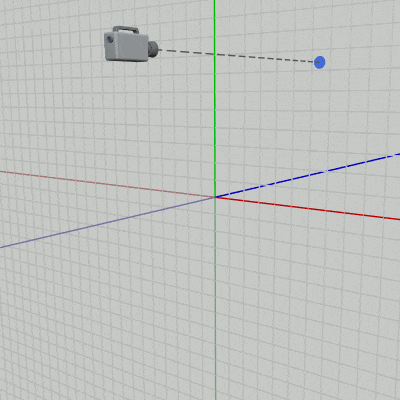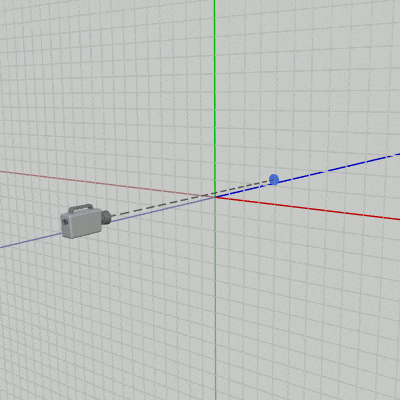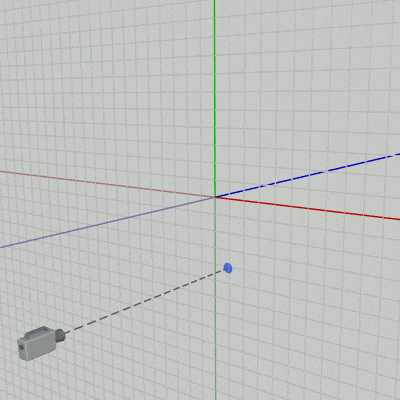図43
H : カメラを左に動かす
L : カメラを右に動かす
J : カメラを下に動かす
K : カメラを上に動かす
[Code7] (実行結果 図44)
Vector3 E = MainCamera.transform.position;
if (Input.GetKey(KeyCode.H))
{
E.x -= 0.1f;
}
else if (Input.GetKey(KeyCode.L))
{
E.x += 0.1f;
}
else if (Input.GetKey(KeyCode.J))
{
E.y -= 0.1f;
}
else if (Input.GetKey(KeyCode.K))
{
E.y += 0.1f;
}
else
{
return;
}
MainCamera.transform.position = E;
Vector3 pos = new Vector3(E.x, E.y, 0);
Dot.transform.position = pos;
H、J、K、L のいずれかが押されている間はカメラを上下左右に $0.1$ ずつ移動させる。その際、Dotはカメラの位置の z座標を $0$ にした位置(XY平面上)に置かれ続けるが、これによってDotは常に画面中心に表示されるようになる。
なお26行目は次のように記述しても同じである (自動的に E の z座標が取り除かれる)。
Vector2 pos = E;
図44 Code3 実行結果 (Dotは画面中心を表している)
# Code8
前節のCode2では下図45のオブジェクト Vehicle をサーキット上で移動させるプログラムを扱った。今回も同様であるが、今回使用するサーキット(下図47)はサイズが大きいため常に全体を表示するようにすると、表示されるVehicleの大きさがやや小さくなり過ぎてしまう。そのため今回はVehicleの移動をカメラによって追跡する形に変更する。具体的にはカメラの位置を(XY平面上の)Vehicleの位置から、常に z軸マイナス方向に $7.2$ だけ離れた位置に置き続けるのである (図46)。これは単に上のCode7と逆のことをするだけである。
使用するキー操作は以下のとおり。
J, K : Vehicleの移動
[Code8] (実行結果 図48)
if (!i_INITIALIZED)
{
Curve = ConstructCurve();
t = 0.0f;
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.K))
{
t += 0.001f;
if(t > 1.0f) { t -= 1.0f; }
}
else if (Input.GetKey(KeyCode.J))
{
t -= 0.001f;
if(t < 0.0f) { t += 1.0f; }
}
Vector2[] vrr = Curve.ComputePositionAndTangent(t);
Vector2 pos = vrr[0];
Vector2 dir = vrr[1];
Quaternion rot = TH2DMath.CalcRotation_V1toV2(Vector2.up, dir);
Vehicle.transform.position = pos;
Vehicle.transform.rotation = rot;
Vector3 E = new Vector3(pos.x, pos.y, -7.2f);
MainCamera.transform.position = E;
このプログラムは基本的にはVehicleを補間曲線上で移動させるものであり、27行目までの内容は前節のCode2と同じである。今回のVehicleの移動経路もサーキットのセンターラインであり、初期化ブロックの ConstructCurve() はそのセンターラインと形、大きさが同じ補間曲線を作成するための補助メソッドである。
また前節のプログラムと異なり、Vehicleに対する変換は行列ではなく上で解説したUnityのプロパティを使って行われている (26~27行目)。25行目の CalcRotation_V1toV2(..) はカスタムライブラリーのメソッドで、第1引数に指定されたベクトルの向きを第2引数に指定されたベクトルの向きと同じにするための回転を返すものである (第1引数のベクトル、第2引数のベクトルを $\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ とすれば、このメソッドから取得される回転を $\boldsymbol{\mathsf{v_1}}$ に実行すると、 $\boldsymbol{\mathsf{v_1}}$ の向きは $\boldsymbol{\mathsf{v_2}}$ の向きと同じになる)。このメソッドは行列版のものが前節でも使われ、前節ではメソッドから返される回転は回転行列であったが、本節の場合は返される回転がQuaternionになっている (もちろんメソッドの内容は同じであり、回転が行列で表されるのかQuaternionで表されるのかの違いに過ぎない)。
走行中は常に、その時点でのサーキット上の進行方向にVehicleの向きを向ける必要があるが、「その時点でのサーキット上の進行方向」とはプログラム23行目で取得される dir であり、毎フレーム Vehicle をこの dir の方向に向けるようにすればよい。初期状態ではVehicleは y軸プラス方向を向いているので、y軸プラス方向から dir に向ける回転(rot)を毎フレーム計算し(25行目)、その回転を毎フレーム VehicleにセットすればVehicleは常にサーキット上の進行方向を向いて走行するようになるわけである。
なお29行目以降はカメラの移動処理であるが、これは上で述べたように毎フレーム Vehicleの現在位置から z軸マイナス方向に $7.2$ 離れた位置に置くだけである。
図48 Code8 実行結果
# Code9
2-22節では正方形同士の衝突判定の簡単な例として「倉庫番」のプログラムを作成した。そして 2-22節でも触れたようにそこで扱ったプログラムは簡単に「迷路ゲーム」に変更することができる。ここでは実際にその例を示そう。(以下 2-22節で用いた用語をそのまま使用する)
下図49は迷路を移動するオブジェクト Square の初期状態であり、初期状態ではSquareは1辺の長さが $2$ の正方形である。図50、図51は迷路を構成するオブジェクト Floor、Block であり、どちらも正方形でその大きさはSquareと同じである。
2-22節と同じく、Floorはその上を移動できる通路の部分であり、Blockはその上を移動することのできない壁に相当する部分である。
-
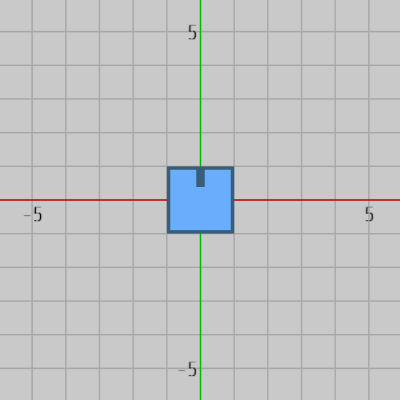図49 Square 初期状態 -
図50 Floor -
図51 Block
この迷路も先程のサーキットと同じく全体を画面内に収めるにはやや大きいため、カメラ移動に関してはSquareを追跡する形をとる (すなわち、Squareの移動中はカメラをSquareから一定の距離だけ離れた位置に置き続ける)。
キー操作は以下のとおり。
H : Squareを左に動かす
L : Squareを右に動かす
J : Squareを下に動かす
K : Squareを上に動かす
C : 画面上のカバー(黒い覆い)の表示 / 非表示のためのスイッチ
今回のプログラムではSquareの周辺以外はカバー(黒い覆い)で覆われており、Squareの移動に合わせてこのカバーも表示され続けるので、迷路移動中は常にSquareの周辺以外は表示されない。しかし、C キーを押すことでこのカバーの表示、非表示を切り替えることができる。
プログラムを以下に示す。
[Code9] (実行結果 図53)
if (!i_INITIALIZED)
{
Square.transform.position = c_StartPosition;
i_INITIALIZED = true;
}
MoveSquare();
Vector2 pos = Square.transform.position;
Vector3 E = new Vector3(pos.x, pos.y, -20.0f);
MainCamera.transform.position = E;
if (Input.GetKeyDown(KeyCode.C))
{
i_flag = !i_flag;
ShowBlackCover(i_flag);
}
今回カメラはXY平面上のSquareから毎フレーム z軸マイナス方向に $20$ だけ離れた位置に置かれるようにしている (12~13行目)。
8行目の MoveSquare() はSquareの移動処理を行うメソッドであるが、その内容はわずかな違いを除いて 2-22節 Code2 と同じである (Squareに行われる変換が行列ではなく position、rotation による方法で実装されている)。
void MoveSquare()
{
if (i_MOVE) // 移動処理
{
i_moveCount++;
Vector2 wp = Square.transform.position;
Vector2 newSqrPos = wp + i_moveVtr;
Quaternion rotSqr = Quaternion.AngleAxis(i_degSquare, Vector3.forward);
Square.transform.position = newSqrPos;
Square.transform.rotation = rotSqr;
if (i_moveCount == c_maxMoveCount)
{
i_MOVE = false;
}
return;
}
if (Input.GetKey(KeyCode.H)) // 左へ進む
{
i_MOVE = true;
i_moveCount = 0;
i_moveVtr = new Vector2(-i_moveSpeed, 0.0f);
i_degSquare = 90;
}
else if (Input.GetKey(KeyCode.L)) // 右へ進む
{
i_MOVE = true;
i_moveCount = 0;
i_moveVtr = new Vector2(i_moveSpeed, 0.0f);
i_degSquare = 270;
}
else if (Input.GetKey(KeyCode.J)) // 下へ進む
{
i_MOVE = true;
i_moveCount = 0;
i_moveVtr = new Vector2(0.0f, -i_moveSpeed);
i_degSquare = 180;
}
else if (Input.GetKey(KeyCode.K)) // 上へ進む
{
i_MOVE = true;
i_moveCount = 0;
i_moveVtr = new Vector2(0.0f, i_moveSpeed);
i_degSquare = 0;
}
else
{
// キーが押されていないときは、以降の処理は行わない
return;
}
// Square vs Block
Vector2 posSqr = Square.transform.position;
bool CANCEL_MOVE = CollisionTest_vs_Block(posSqr, i_moveVtr);
if (CANCEL_MOVE)
{
i_MOVE = false;
Quaternion rotSqr = Quaternion.AngleAxis(i_degSquare, Vector3.forward);
Square.transform.position = posSqr;
Square.transform.rotation = rotSqr;
}
}
図53 Code9 実行結果
© 2020-2024 Redpoll's 60 (All rights reserved)