Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-23
第2章 2D空間におけるオブジェクトの運動
$§$2-23 衝突判定 10 (円盤 vs 三角形)
本節では三角形と円盤との衝突判定について解説する。三角形と円盤の衝突判定はあまり見ることはないが、比較的簡単に実装することができる。
ここでは円盤の中心を $T$、半径を $r$ とし、三角形の各頂点を $A$、$B$、$C$ とする (各頂点の並び方は時計周りであることを前提とする(これを clockwise winding order という) )。
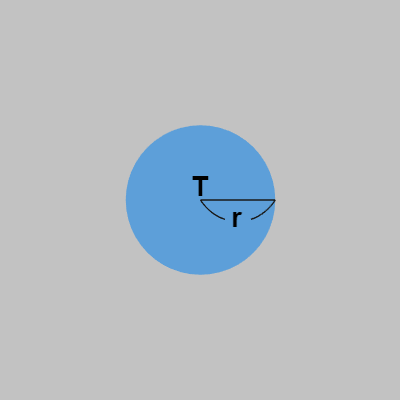
図1 円盤 
図2 三角形
まず辺 $AB$ を含む直線を便宜上「直線 $A$」とし、その進行方向を $\overrightarrow{AB}$ とする。このとき直線 $A$ の進行方向に関して左側を領域 a、右側を領域 ⓐ とする (図3)。
同様に辺 $BC$ を含む直線を「直線 $B$」、その進行方向を $\overrightarrow{BC}$ とし、この進行方向に関して直線 $B$ の左側を領域 b、右側を領域 ⓑ とする (図4)。さらに辺 $CA$ を含む直線を「直線 $C$」、その進行方向を $\overrightarrow{CA}$ とし、この進行方向に関して直線 $C$ の左側を領域 c、右側を領域 ⓒ とする (図5)。
このとき直線 $A$、直線 $B$、直線 $C$ によって三角形の周囲は 6 個の領域に分割され、三角形自体を含めると下図に示されるように 7 個の領域に分割される。各領域は3つの文字で表されているが下図の直線 $A$ の左側の3つの領域は、直線 $A$ の左側なのでいずれの領域においても a が含まれ、直線 $A$ の右側4つの領域は直線 $A$ の右側なのでいずれの領域においても ⓐ が含まれる。
例えば領域 aⓑⓒ であれば、この領域は直線 $A$ の左側、直線 $B$ の右側、直線 $C$ の右側という意味であり、領域 ⓐbⓒ であれば、この領域は直線 $A$ の右側、直線 $B$ の左側、直線 $C$ の右側という意味である。
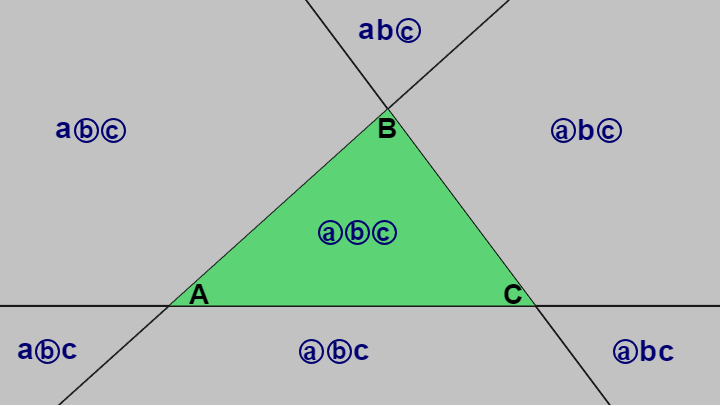
図6
ここで各領域を表す3つの文字を、丸で囲まれていないものを $0$、丸で囲まれているものを $1$ に置き換える (下図7)。このとき3つの文字は「010」「011」のような3桁の数字になるが、この3桁の数字を2進数として考えると各領域は下図に示されるように 1~7 の番号が割り当てられる (以下この番号によって各領域を [1]~[7] で表す。領域 [0] は存在しない)。
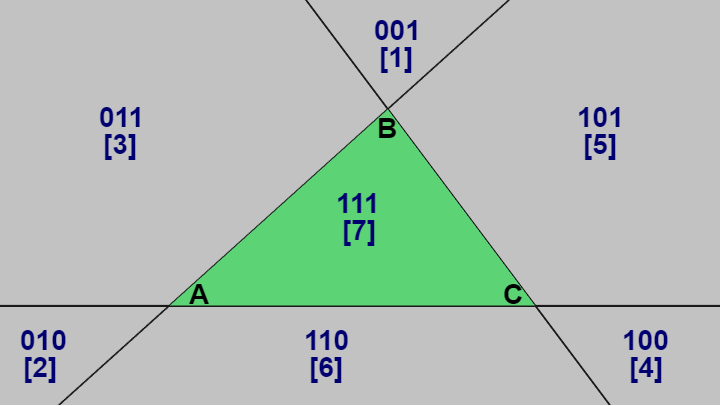
図7
円盤の中心 $T$ が領域 [5] にあったとしよう (下図8)。この場合には中心 $T$ が領域 [5] のどの位置あっても、円盤から最も近い三角形の部分は辺 $BC$ である。そのため円盤が辺 $BC$ に触れることなく三角形に衝突することはできない。したがって中心 $T$ が領域 [5] にある場合には、円盤と三角形の衝突判定は円盤と辺 $BC$ の衝突判定に帰着するわけである。
この場合には中心 $T$ と辺 $BC$ の最短距離が半径 $r$ より大きいかどうかを調べればよい (ある点と線分の最短距離の求め方については後述する)。
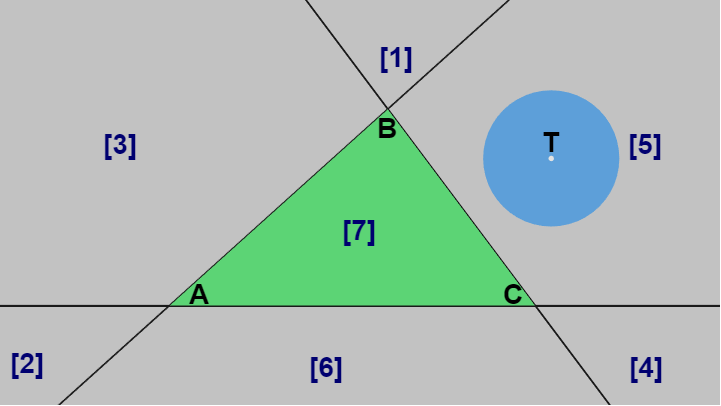
図8
円盤の中心 $T$ が領域 [2] にあったとする (下図9)。中心 $T$ が領域 [2] にある限りその位置がどこであっても、円盤から最も近い三角形の部分は辺 $CA$ または辺 $AB$ である。そのため円盤の中心 $T$ が領域 [2] にある場合には、辺 $CA$ あるいは辺 $AB$ のいずれかに触れることなしに三角形と衝突することはできない。したがってこの場合には円盤と三角形の衝突判定は、円盤と辺 $CA$ あるいは円盤と辺 $AB$ の衝突判定に帰着するわけである。
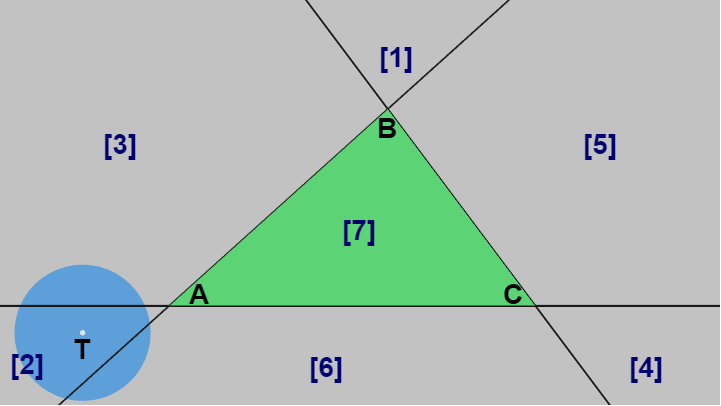
図9
中心 $T$ が他の領域にある場合も同様である。例えば $T$ が領域 [1] にある場合には円盤と三角形の衝突判定は、円盤と辺 $AB$ あるいは円盤と辺 $BC$ の衝突判定に帰着する。$T$ が領域 [3] にある場合には円盤と三角形の衝突判定は円盤と辺 $AB$ が衝突するかどうかを調べればよい。
つまり上記のように三角形及びその周囲を7つの領域に分割するとき円盤と三角形の衝突判定は、円盤とある1つの辺、あるいは(多くても)2つの辺との衝突判定に帰着するのである ($T$ が領域 [7] にある場合にはもちろん衝突している)。
したがって、この方法においては以下のようなテーブルを事前に用意しておくと効率的である。
i_vi はint[,]型のインスタンス変数であり(2次元配列)、各要素は各領域において衝突判定で使われる辺(の頂点)を表している。i_vi[i, j] の1次元目は領域であり、i_vi[1, j] ならば領域 [1]、i_vi[2, j] ならば領域 [2] のデータを意味する (そのため i_vi[1, j]~i_vi[7, j] までが用意されている。領域 [0] は存在しないので i_vi[0, j] は使われない)。
例えば中心 $T$ が領域 [2] にある場合には円盤と辺 $CA$ または辺 $AB$ との衝突判定を行うので i_vi にはとしてセットされている。
同様に $T$ が領域 [4] にある場合には辺 $BC$ または辺 $CA$ との衝突判定を行うので i_vi にはとしてセットされている。
$T$ が領域 [5] にある場合には衝突判定は辺 $BC$ のみが対象となるので i_vi にはとしてセットされている (1つの辺のみと衝突判定を行う場合には2次元目の最後の要素に $-1$ がセットされる)。
上で見たように3つ直線の右側か左側かに分けることで、三角形及びその周囲は自動的に7つの領域に分割されるが、XY平面上のある点が指定の直線の右にあるか左にあるかは次のようにして調べることができる。
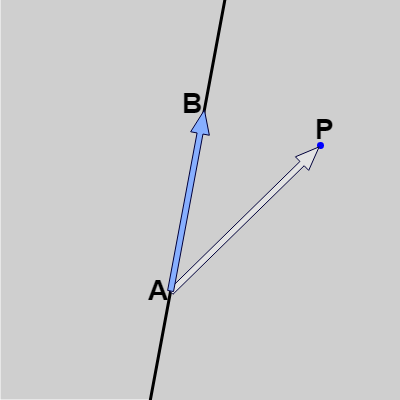
図10 点A、Bは直線上の2点 (P が直線よりも右にある場合) 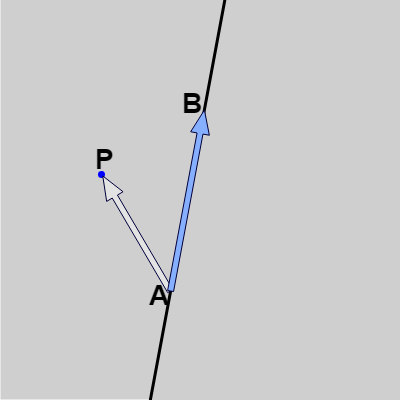
図11 P が直線よりも左にある場合
XY平面上に引かれた直線上の2点を $A$、$B$ とし、直線外に置かれた点を $P$ とする。また、$\overrightarrow{AP} = (a_x,\ a_y)$、$\overrightarrow{AB} = (b_x,\ b_y)$ とする。
このとき、点 $P$ が直線の右側にある場合には $a_x b_y - a_y b_x > 0$ であり、直線の左側にある場合には $a_x b_y - a_y b_x < 0$ である ($=0$ のときは $P$ は直線上にある。詳しくは3-6節参照)。
つまり、点 $P$ が2点 $A$、$B$ を通る直線の右にあるか左にあるかを調べるには $a_x b_y - a_y b_x$ の符号を調べればよいわけである。例えば上図10の場合はこの符号はプラスになり、図11の場合にはマイナスになる。
最終的に円盤と三角形の衝突判定は次の形にまとめられる。
[CollisionTest_Disk_Triangle(..) (24/04/01 修正版)]
引数には円盤の中心 $T$、半径 $r$、三角形の頂点がセットされたVector2型配列 vrts が送られてくる (頂点 $A$ が vrts[0]、$B$ が vrts[1]、$C$ が vrts[2] にセットされており、上でも述べたように $A$、$B$、$C$ の並びは時計周りである)。
このメソッドでは最終的に円盤の半径 $r$ との大小を比較するが、実際に使うのは $r$ ではなく、効率化のためその2乗で比較する。3行目の rr はそのための変数である。それに関連して比較の際にはベクトルの大きさの2乗を表すプロパティ sqrMagnitude が使われる。例えば v.sqrMagnitude であればベクトル $\boldsymbol{\mathsf{v}}$ の大きさの2乗 $|\boldsymbol{\mathsf{v}}|^2$ のことであり、(B - A).sqrMagnitude であればベクトル $\overrightarrow{AB}$ の大きさの2乗 $|\overrightarrow{AB}|^2$ を意味する。
まず19行目までにおいて、円盤の中心 $T$ が7つの領域のうちどの領域に含まれているのかを調べるが、それは $T$ が3つの直線の右にあるか左にあるかを調べることに帰着する。7~9行目が直線 $A$、12~14行目が直線 $B$、17~19行目が直線 $C$ に関する処理である。3つの直線のそれぞれに対し、右側にあるか左側にあるかを調べることで上で述べたように各領域が、ⓐbⓒ や aⓑⓒ のように3つの文字として表される (上図6)。
そしてこの3つの文字を2進数に変換すると(丸で囲まれていなければ $0$、囲まれているならば $1$)、「101」「011」のようになるがこれを10進数に変換した値が領域の番号である。10進数に変換するには「101」であれば $4 + 0 + 1 = 5$、「011」であれば $0 + 2 + 1 = 3$ であるが、9行目の k += 4、14行目の k += 2、19行目の k += 1 はこの2進数から10進数への変換の計算である (ローカル変数 k は $T$ が含まれる領域番号を表す)。
中心 $T$ がどの領域にあるかが分かれば円盤と三角形の衝突判定は、円盤と1つの辺、あるいは多くても2つの辺との衝突判定に帰着するが、23行目以降がその処理である ($T$ が領域 [7] にある場合には衝突しているものとして、その時点で処理を返す(21行目) )。
三角形のある辺と円盤が衝突しているかどうかは、円盤の中心とその辺との最短距離を求め、その最短距離が円盤の半径より大きいかどうかを調べればよい。すなわち、点と線分の最短距離を求めることに帰着するわけである。
26、27行目の ComputeSqrDistance_Point_Segment(..) は点と線分の最短距離を求め、その2乗を返すメソッドである。その内容を以下に示す。
[ComputeSqrDistance_Point_Segment(..)]
このメソッドは具体的には、引数として送られてくる点 $P$ と線分 $AB$ の最短距離の2乗を計算して返すものである。
例えば点 $P$ と線分 $AB$ が次のような位置関係にあったとしよう。
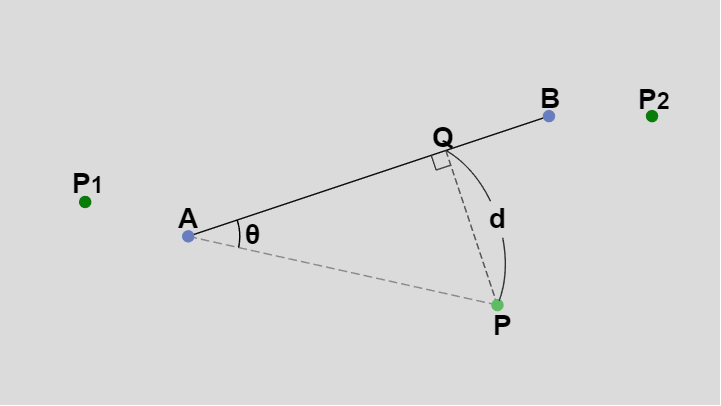
図12 点 P と線分 AB
このとき、$P$ と $AB$ 間が最短になるのは $P$ から $AB$ に下ろした垂線の足 $Q$ においてであり、$|PQ| = d$、$AP$ と $AB$ のなす角を $\theta$ とすれば $d = |AP|\sin\theta$ であるから\[ d^2 = |AP|^2 - (|AP|\cos\theta)^2 \]また $AP\cdot AB = |AP||AB|\cos\theta$ であるから\[ \frac{(AP\cdot AB)^2}{|AB|^2} = |AP|^2 \cos ^2 \theta \]したがって、\[ d^2 = |AP|^2 - \frac{(AP\cdot AB)^2}{|AB|^2} = AP\cdot AP - \frac{(AP\cdot AB)^2}{AB\cdot AB} \]として $d$ (の2乗)が求められる。
ただし上図の $P_1$ や $P_2$ の位置に $P$ がある場合には線分 $AB$ に垂線を下ろすことはできないので、このような状況では $P$ と線分 $AB$ の最短距離は $AP$ あるいは $BP$ となる。具体的には $AP\cdot AB < 0$ であれば最短距離は $AP$、 $AP\cdot AB > AB\cdot AB$ であるときは最短距離は $BP$ となる (上記のメソッドでいえば $AP\cdot AB < 0$ の場合には9行目、$AP\cdot AB > AB\cdot AB$ の場合には15行目で処理が返される)。
三角形の衝突判定に関しては本節の「三角形 vs 円盤」だけでなく、他にも「三角形 vs 三角形」「三角形 vs 長方形」について扱うが、これらの衝突判定ではベクトルの外積に関する知識が必要になってくるため詳しい解説については3-6節を参照。
ここでもDiskの中心を $T$、三角形の各頂点を $A$、$B$、$C$ とする。
実行中のキー操作は以下のとおり。
H, J, K, L : Diskを上下左右に動かす。
R : Triangleを回転させる。
S, T : Triangleを拡大/縮小させる (Shiftと同時押しで縮小) 。
[Code1] (実行結果 図15)
12~34行目がDiskに対する変換処理、36~55行目がTriangleに対する変換処理、それ以降が衝突判定である。
ここでは円盤の中心を $T$、半径を $r$ とし、三角形の各頂点を $A$、$B$、$C$ とする (各頂点の並び方は時計周りであることを前提とする(これを clockwise winding order という) )。


まず辺 $AB$ を含む直線を便宜上「直線 $A$」とし、その進行方向を $\overrightarrow{AB}$ とする。このとき直線 $A$ の進行方向に関して左側を領域 a、右側を領域 ⓐ とする (図3)。
同様に辺 $BC$ を含む直線を「直線 $B$」、その進行方向を $\overrightarrow{BC}$ とし、この進行方向に関して直線 $B$ の左側を領域 b、右側を領域 ⓑ とする (図4)。さらに辺 $CA$ を含む直線を「直線 $C$」、その進行方向を $\overrightarrow{CA}$ とし、この進行方向に関して直線 $C$ の左側を領域 c、右側を領域 ⓒ とする (図5)。
-
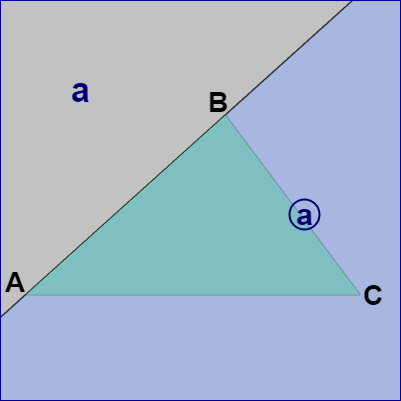 図3 直線 A よりも左側が領域 a、右側が領域 ⓐ
図3 直線 A よりも左側が領域 a、右側が領域 ⓐ -
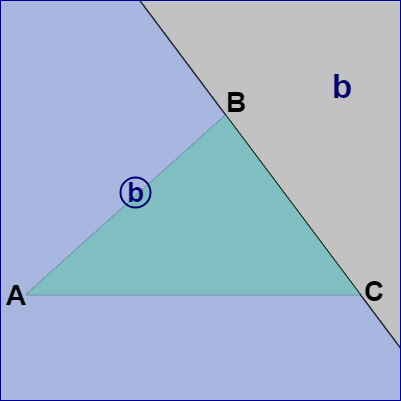 図4 直線 B よりも左側が領域 b、右側が領域 ⓑ (直線の進行方向はBからC)
図4 直線 B よりも左側が領域 b、右側が領域 ⓑ (直線の進行方向はBからC) -
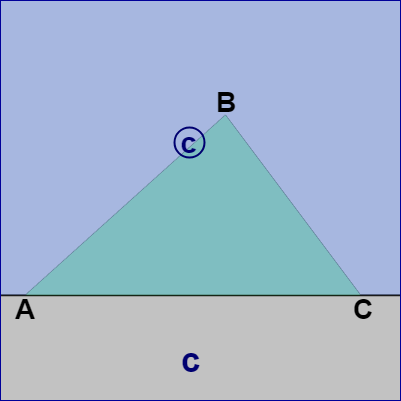 図5 直線 C よりも左側が領域 c、右側が領域 ⓒ (直線の進行方向はCからA)
図5 直線 C よりも左側が領域 c、右側が領域 ⓒ (直線の進行方向はCからA)
このとき直線 $A$、直線 $B$、直線 $C$ によって三角形の周囲は 6 個の領域に分割され、三角形自体を含めると下図に示されるように 7 個の領域に分割される。各領域は3つの文字で表されているが下図の直線 $A$ の左側の3つの領域は、直線 $A$ の左側なのでいずれの領域においても a が含まれ、直線 $A$ の右側4つの領域は直線 $A$ の右側なのでいずれの領域においても ⓐ が含まれる。
例えば領域 aⓑⓒ であれば、この領域は直線 $A$ の左側、直線 $B$ の右側、直線 $C$ の右側という意味であり、領域 ⓐbⓒ であれば、この領域は直線 $A$ の右側、直線 $B$ の左側、直線 $C$ の右側という意味である。

ここで各領域を表す3つの文字を、丸で囲まれていないものを $0$、丸で囲まれているものを $1$ に置き換える (下図7)。このとき3つの文字は「010」「011」のような3桁の数字になるが、この3桁の数字を2進数として考えると各領域は下図に示されるように 1~7 の番号が割り当てられる (以下この番号によって各領域を [1]~[7] で表す。領域 [0] は存在しない)。

円盤の中心 $T$ が領域 [5] にあったとしよう (下図8)。この場合には中心 $T$ が領域 [5] のどの位置あっても、円盤から最も近い三角形の部分は辺 $BC$ である。そのため円盤が辺 $BC$ に触れることなく三角形に衝突することはできない。したがって中心 $T$ が領域 [5] にある場合には、円盤と三角形の衝突判定は円盤と辺 $BC$ の衝突判定に帰着するわけである。
この場合には中心 $T$ と辺 $BC$ の最短距離が半径 $r$ より大きいかどうかを調べればよい (ある点と線分の最短距離の求め方については後述する)。

円盤の中心 $T$ が領域 [2] にあったとする (下図9)。中心 $T$ が領域 [2] にある限りその位置がどこであっても、円盤から最も近い三角形の部分は辺 $CA$ または辺 $AB$ である。そのため円盤の中心 $T$ が領域 [2] にある場合には、辺 $CA$ あるいは辺 $AB$ のいずれかに触れることなしに三角形と衝突することはできない。したがってこの場合には円盤と三角形の衝突判定は、円盤と辺 $CA$ あるいは円盤と辺 $AB$ の衝突判定に帰着するわけである。

中心 $T$ が他の領域にある場合も同様である。例えば $T$ が領域 [1] にある場合には円盤と三角形の衝突判定は、円盤と辺 $AB$ あるいは円盤と辺 $BC$ の衝突判定に帰着する。$T$ が領域 [3] にある場合には円盤と三角形の衝突判定は円盤と辺 $AB$ が衝突するかどうかを調べればよい。
つまり上記のように三角形及びその周囲を7つの領域に分割するとき円盤と三角形の衝突判定は、円盤とある1つの辺、あるいは(多くても)2つの辺との衝突判定に帰着するのである ($T$ が領域 [7] にある場合にはもちろん衝突している)。
したがって、この方法においては以下のようなテーブルを事前に用意しておくと効率的である。
const int A = 0, B = 1, C = 2; // 頂点 A、B、C (clockwise) i_vi[1, 0] = A; i_vi[1, 1] = B; i_vi[1, 2] = C; i_vi[2, 0] = C; i_vi[2, 1] = A; i_vi[2, 2] = B; i_vi[3, 0] = A; i_vi[3, 1] = B; i_vi[3, 2] = -1; i_vi[4, 0] = B; i_vi[4, 1] = C; i_vi[4, 2] = A; i_vi[5, 0] = B; i_vi[5, 1] = C; i_vi[5, 2] = -1; i_vi[6, 0] = C; i_vi[6, 1] = A; i_vi[6, 2] = -1; i_vi[7, 0] = -1; i_vi[7, 1] = -1; i_vi[7, 2] = -1;
i_vi はint[,]型のインスタンス変数であり(2次元配列)、各要素は各領域において衝突判定で使われる辺(の頂点)を表している。i_vi[i, j] の1次元目は領域であり、i_vi[1, j] ならば領域 [1]、i_vi[2, j] ならば領域 [2] のデータを意味する (そのため i_vi[1, j]~i_vi[7, j] までが用意されている。領域 [0] は存在しないので i_vi[0, j] は使われない)。
例えば中心 $T$ が領域 [2] にある場合には円盤と辺 $CA$ または辺 $AB$ との衝突判定を行うので i_vi には
i_vi[2, 0] = C; i_vi[2, 1] = A; i_vi[2, 2] = B;
同様に $T$ が領域 [4] にある場合には辺 $BC$ または辺 $CA$ との衝突判定を行うので i_vi には
i_vi[4, 0] = B; i_vi[4, 1] = C; i_vi[4, 2] = A;
$T$ が領域 [5] にある場合には衝突判定は辺 $BC$ のみが対象となるので i_vi には
i_vi[5, 0] = B; i_vi[5, 1] = C; i_vi[5, 2] = -1;
上で見たように3つ直線の右側か左側かに分けることで、三角形及びその周囲は自動的に7つの領域に分割されるが、XY平面上のある点が指定の直線の右にあるか左にあるかは次のようにして調べることができる。


XY平面上に引かれた直線上の2点を $A$、$B$ とし、直線外に置かれた点を $P$ とする。また、$\overrightarrow{AP} = (a_x,\ a_y)$、$\overrightarrow{AB} = (b_x,\ b_y)$ とする。
このとき、点 $P$ が直線の右側にある場合には $a_x b_y - a_y b_x > 0$ であり、直線の左側にある場合には $a_x b_y - a_y b_x < 0$ である ($=0$ のときは $P$ は直線上にある。詳しくは3-6節参照)。
つまり、点 $P$ が2点 $A$、$B$ を通る直線の右にあるか左にあるかを調べるには $a_x b_y - a_y b_x$ の符号を調べればよいわけである。例えば上図10の場合はこの符号はプラスになり、図11の場合にはマイナスになる。
最終的に円盤と三角形の衝突判定は次の形にまとめられる。
[CollisionTest_Disk_Triangle(..) (24/04/01 修正版)]
bool CollisionTest_Disk_Triangle(Vector2 T, float r, Vector2[] vrts)
{
float rr = r * r;
int k = 0;
// AT x AB
Vector2 a = (T - vrts[0]);
Vector2 b = (vrts[1] - vrts[0]);
if (a.x * b.y - a.y * b.x >= 0.0f) { k += 4; }
// BT x BC
a = (T - vrts[1]);
b = (vrts[2] - vrts[1]);
if (a.x * b.y - a.y * b.x >= 0.0f) { k += 2; }
// CT x CA
a = (T - vrts[2]);
b = (vrts[0] - vrts[2]);
if (a.x * b.y - a.y * b.x >= 0.0f) { k += 1; }
if (k == 7) { return true; }
int i0 = i_vi[k, 0];
int i1 = i_vi[k, 1];
int i2 = i_vi[k, 2];
return (ComputeSqrDistance_Point_Segment(T, vrts[i0], vrts[i1]) <= rr) ||
(i2 != -1 && ComputeSqrDistance_Point_Segment(T, vrts[i1], vrts[i2]) <= rr);
}
引数には円盤の中心 $T$、半径 $r$、三角形の頂点がセットされたVector2型配列 vrts が送られてくる (頂点 $A$ が vrts[0]、$B$ が vrts[1]、$C$ が vrts[2] にセットされており、上でも述べたように $A$、$B$、$C$ の並びは時計周りである)。
このメソッドでは最終的に円盤の半径 $r$ との大小を比較するが、実際に使うのは $r$ ではなく、効率化のためその2乗で比較する。3行目の rr はそのための変数である。それに関連して比較の際にはベクトルの大きさの2乗を表すプロパティ sqrMagnitude が使われる。例えば v.sqrMagnitude であればベクトル $\boldsymbol{\mathsf{v}}$ の大きさの2乗 $|\boldsymbol{\mathsf{v}}|^2$ のことであり、(B - A).sqrMagnitude であればベクトル $\overrightarrow{AB}$ の大きさの2乗 $|\overrightarrow{AB}|^2$ を意味する。
まず19行目までにおいて、円盤の中心 $T$ が7つの領域のうちどの領域に含まれているのかを調べるが、それは $T$ が3つの直線の右にあるか左にあるかを調べることに帰着する。7~9行目が直線 $A$、12~14行目が直線 $B$、17~19行目が直線 $C$ に関する処理である。3つの直線のそれぞれに対し、右側にあるか左側にあるかを調べることで上で述べたように各領域が、ⓐbⓒ や aⓑⓒ のように3つの文字として表される (上図6)。
そしてこの3つの文字を2進数に変換すると(丸で囲まれていなければ $0$、囲まれているならば $1$)、「101」「011」のようになるがこれを10進数に変換した値が領域の番号である。10進数に変換するには「101」であれば $4 + 0 + 1 = 5$、「011」であれば $0 + 2 + 1 = 3$ であるが、9行目の k += 4、14行目の k += 2、19行目の k += 1 はこの2進数から10進数への変換の計算である (ローカル変数 k は $T$ が含まれる領域番号を表す)。
中心 $T$ がどの領域にあるかが分かれば円盤と三角形の衝突判定は、円盤と1つの辺、あるいは多くても2つの辺との衝突判定に帰着するが、23行目以降がその処理である ($T$ が領域 [7] にある場合には衝突しているものとして、その時点で処理を返す(21行目) )。
三角形のある辺と円盤が衝突しているかどうかは、円盤の中心とその辺との最短距離を求め、その最短距離が円盤の半径より大きいかどうかを調べればよい。すなわち、点と線分の最短距離を求めることに帰着するわけである。
26、27行目の ComputeSqrDistance_Point_Segment(..) は点と線分の最短距離を求め、その2乗を返すメソッドである。その内容を以下に示す。
[ComputeSqrDistance_Point_Segment(..)]
float ComputeSqrDistance_Point_Segment(Vector2 P, Vector2 A, Vector2 B)
{
Vector2 AB = B - A;
Vector2 AP = P - A;
float dot1 = Vector2.Dot(AP, AB);
if(dot1 < 0.0f)
{
return AP.sqrMagnitude;
}
float dot2 = AB.sqrMagnitude;
if(dot1 > dot2)
{
return (P - B).sqrMagnitude;
}
return AP.sqrMagnitude - (dot1 * dot1) / dot2;
}
このメソッドは具体的には、引数として送られてくる点 $P$ と線分 $AB$ の最短距離の2乗を計算して返すものである。
例えば点 $P$ と線分 $AB$ が次のような位置関係にあったとしよう。

このとき、$P$ と $AB$ 間が最短になるのは $P$ から $AB$ に下ろした垂線の足 $Q$ においてであり、$|PQ| = d$、$AP$ と $AB$ のなす角を $\theta$ とすれば $d = |AP|\sin\theta$ であるから\[ d^2 = |AP|^2 - (|AP|\cos\theta)^2 \]また $AP\cdot AB = |AP||AB|\cos\theta$ であるから\[ \frac{(AP\cdot AB)^2}{|AB|^2} = |AP|^2 \cos ^2 \theta \]したがって、\[ d^2 = |AP|^2 - \frac{(AP\cdot AB)^2}{|AB|^2} = AP\cdot AP - \frac{(AP\cdot AB)^2}{AB\cdot AB} \]として $d$ (の2乗)が求められる。
ただし上図の $P_1$ や $P_2$ の位置に $P$ がある場合には線分 $AB$ に垂線を下ろすことはできないので、このような状況では $P$ と線分 $AB$ の最短距離は $AP$ あるいは $BP$ となる。具体的には $AP\cdot AB < 0$ であれば最短距離は $AP$、 $AP\cdot AB > AB\cdot AB$ であるときは最短距離は $BP$ となる (上記のメソッドでいえば $AP\cdot AB < 0$ の場合には9行目、$AP\cdot AB > AB\cdot AB$ の場合には15行目で処理が返される)。
三角形の衝突判定に関しては本節の「三角形 vs 円盤」だけでなく、他にも「三角形 vs 三角形」「三角形 vs 長方形」について扱うが、これらの衝突判定ではベクトルの外積に関する知識が必要になってくるため詳しい解説については3-6節を参照。
# Code1
次のプログラムは下図の円盤(Disk)と三角形(Triangle)の衝突判定を行うものである。ここでもDiskの中心を $T$、三角形の各頂点を $A$、$B$、$C$ とする。
-
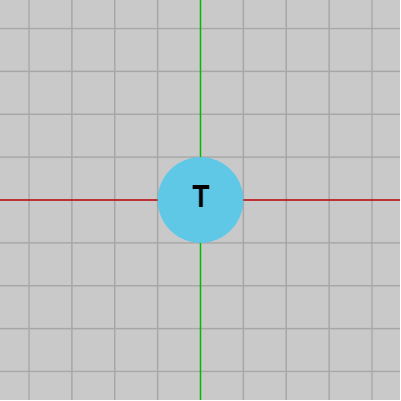 図13 Disk 初期状態 (T はDiskの中心であり、初期状態では原点に置かれている)
図13 Disk 初期状態 (T はDiskの中心であり、初期状態では原点に置かれている) -
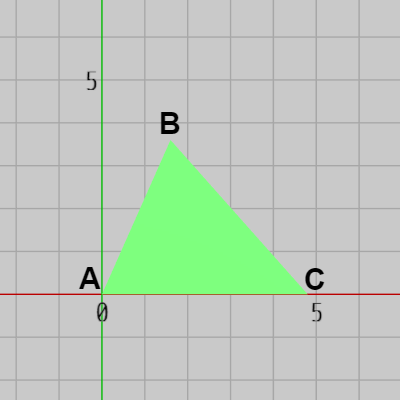 図14 Triangle 初期状態
図14 Triangle 初期状態 -
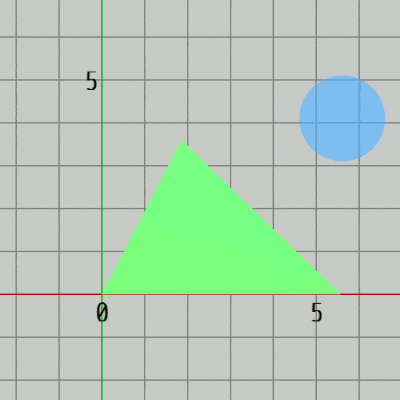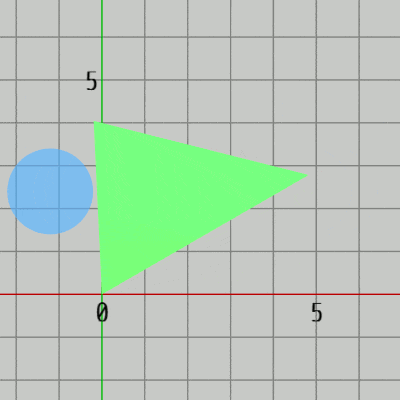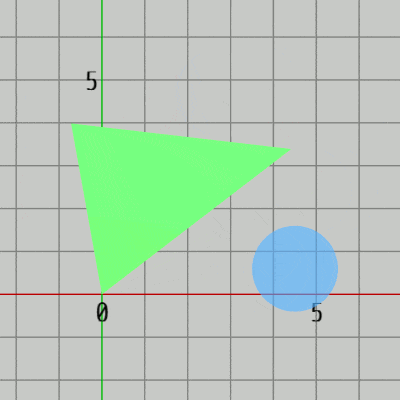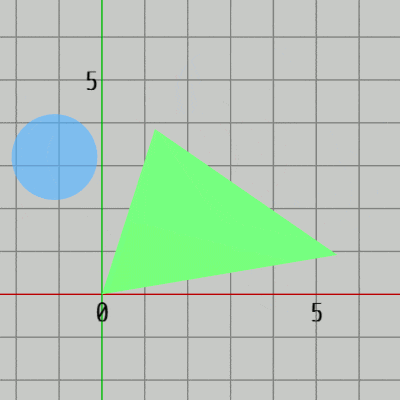 図15 Code1 実行結果
図15 Code1 実行結果
実行中のキー操作は以下のとおり。
H, J, K, L : Diskを上下左右に動かす。
R : Triangleを回転させる。
S, T : Triangleを拡大/縮小させる (Shiftと同時押しで縮小) 。
[Code1] (実行結果 図15)
if (!i_INITIALIZED)
{
Disk.SetPosition(-4, 0);
i_scaleX = 2.0f;
i_scaleY = 2.0f;
Triangle.SetMatrix(TH2DMath.GetScale3x3(i_scaleX, i_scaleY));
i_INITIALIZED = true;
}
// Disk
Vector2 T = Disk.GetPosition();
float speed = 0.10f;
if (Input.GetKey(KeyCode.H))
{
T.x -= speed;
}
else if (Input.GetKey(KeyCode.L))
{
T.x += speed;
}
if (Input.GetKey(KeyCode.J))
{
T.y -= speed;
}
else if (Input.GetKey(KeyCode.K))
{
T.y += speed;
}
Disk.SetPosition(T);
// Triangle
if (Input.GetKey(KeyCode.R) || Input.GetKey(KeyCode.S) || Input.GetKey(KeyCode.T))
{
if (Input.GetKey(KeyCode.R))
{
i_rotDeg += THUtil.IsShiftDown() ? -0.5f : 0.5f;
}
else if (Input.GetKey(KeyCode.S))
{
i_scaleX += THUtil.IsShiftDown() ? -0.02f : 0.02f;
}
else if (Input.GetKey(KeyCode.T))
{
i_scaleY += THUtil.IsShiftDown() ? -0.02f : 0.02f;
}
THMatrix3x3 R = TH2DMath.GetRotation3x3(i_rotDeg);
THMatrix3x3 S = TH2DMath.GetScale3x3(i_scaleX, i_scaleY);
Triangle.SetMatrix(R * S);
}
// Collision Test
THMatrix3x3 M = Triangle.GetMatrix();
Vector2 A = Vector2.zero; // A,B,C は時計周り
Vector2 B = M * new Vector3(0.8f, 1.8f, 1.0f);
Vector2 C = M * new Vector3(2.4f, 0.0f, 1.0f);
float r = 1.0f;
bool bColl = CollisionTest_Disk_Triangle(T, r, new Vector2[]{A, B, C});
Hit(bColl);
12~34行目がDiskに対する変換処理、36~55行目がTriangleに対する変換処理、それ以降が衝突判定である。
© 2020-2025 Redpoll's 60 (All rights reserved)