Redpoll's 60
第3章 3D空間の基礎
§3-6 ベクトルの外積
3D空間内のベクトル \boldsymbol{a} = (a_x, a_y, a_z)、\boldsymbol{b} = (b_x, b_y, b_z) に関して、次の成分で表されるベクトルを \boldsymbol{a} と \boldsymbol{b} の外積(Cross Product)といい、\boldsymbol{a} \times \boldsymbol{b} で表す。
ベクトル \boldsymbol{a} = (a_x, a_y, a_z)、\boldsymbol{b} = (b_x, b_y, b_z) の外積 \boldsymbol{a} \times \boldsymbol{b}
\boldsymbol{a} \times \boldsymbol{b}\ =\ (a_yb_z - a_zb_y,\ a_zb_x - a_xb_z,\ a_xb_y - a_yb_x)
(計算例)
ベクトル \boldsymbol{\mathsf{v_1}} = (1, 2, 3)、\boldsymbol{\mathsf{v_2}} = (4, 5, 6) の外積 \boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}}
\begin{align*}\boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}}\ &=\ (2\cdot6 - 3\cdot5,\ 3\cdot4 - 1\cdot6,\ 1\cdot5 - 2\cdot4) \\&= (12-15,\ 12-6,\ 5-8) = (-3,\ 6, -3)\end{align*}上の計算における \boldsymbol{\mathsf{v_1}}、\boldsymbol{\mathsf{v_2}} の積の順序を入れ替えた場合
\begin{align*}\boldsymbol{\mathsf{v_2}} \times \boldsymbol{\mathsf{v_1}}\ &=\ (5\cdot3 - 6\cdot2,\ 6\cdot1 - 4\cdot3,\ 4\cdot2 - 5\cdot1) \\&= (15-12,\ 6-12,\ 8-5) = (3, -6,\ 3)\end{align*}
上の結果からわかるように、外積の積の順序は交換可能ではない。つまり、積の順序を入れ替えた場合、算出されるベクトルは異なる。より正確には、外積の積の順序については次の関係が成り立つ。(\boldsymbol{a}、\boldsymbol{b} を3次元ベクトルとすると)
\boldsymbol{a} \times \boldsymbol{b} = -\boldsymbol{b} \times \boldsymbol{a}
ベクトルの内積が2つのベクトルから1つの実数値を算出する演算であったのに対し、ベクトルの外積は2つのベクトルから新たにもう1つのベクトルを算出する演算である。
具体的な例として、図1の2つのベクトル \boldsymbol{a} = (0, 0, 2)、\boldsymbol{b} = (3, 0, 1) の外積 \boldsymbol{a} \times \boldsymbol{b} を求めてみよう(以下では \boldsymbol{a} \times \boldsymbol{b} = \boldsymbol{c} とおく ; 図中の緑色の数値はベクトルの成分を表している)。
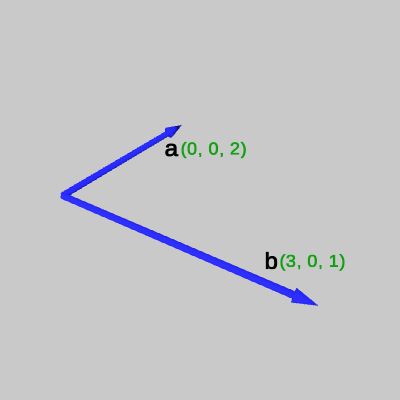
図1 ベクトルa、b 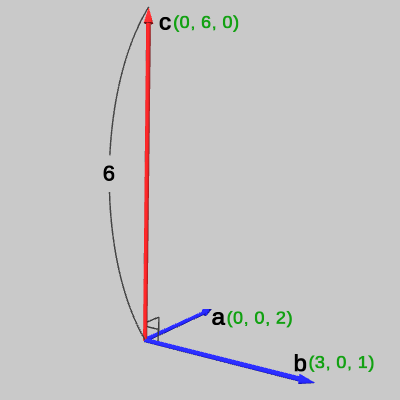
図2 外積 a×b = c
\begin{align*}\boldsymbol{a} \times \boldsymbol{b}\ &=\ (0\cdot1 - 2\cdot0,\ 2\cdot3 - 0\cdot1,\ 0\cdot0 - 0\cdot3) \\&=(0,\ 6,\ 0) = \boldsymbol{c}\end{align*}
図2における赤いベクトルが、外積 \boldsymbol{a} \times \boldsymbol{b}\ ( = \boldsymbol{c}) である。
外積とは一体どのようなものなのであろうか。まず、外積の幾何的な意味から見ていこう。

図3 外積 a×b の大きさは a、b の作る平行四辺形の面積に等しい ベクトル \boldsymbol{a}、\boldsymbol{b} を3次元ベクトルとし、\boldsymbol{a}、\boldsymbol{b} のなす角を T とすると、外積 \boldsymbol{a} \times \boldsymbol{b} の大きさに関して以下の等式が成立する(角度Tは、0^\circ <= T <= 180^\circ の範囲にあるものとする)。
|\boldsymbol{a} \times \boldsymbol{b}| = |\boldsymbol{a}||\boldsymbol{b}|\sin{T} この等式の意味を図3を用いて説明しよう。
ベクトル \boldsymbol{b} の終点からベクトル \boldsymbol{a} に垂線をおろしたとき、その垂線の足(ベクトル \boldsymbol{a} と垂線の交点)とベクトル \boldsymbol{b} の始点、及び終点は直角三角形を作る。\boldsymbol{a} と \boldsymbol{b} のなす角が T であるから、垂線の長さ(図中の点線の長さ)は |\boldsymbol{b}|\sin{T} である。したがって、|\boldsymbol{a}||\boldsymbol{b}|\sin{T} はベクトル \boldsymbol{a}、\boldsymbol{b} によって作られる平行四辺形の面積に等しい。
上の図1、図2の例でいえば、\boldsymbol{a} = (0, 0, 2)、\boldsymbol{b} = (3, 0, 1) の外積は \boldsymbol{a} \times \boldsymbol{b} = (0,\ 6,\ 0)\ (= \boldsymbol{c}) であったが、外積の大きさは |\boldsymbol{a} \times \boldsymbol{b}| = |\boldsymbol{c}| = 6 である。これは、ベクトル \boldsymbol{a} と \boldsymbol{b} が作る平行四辺形の面積が 6 であることを意味している。
下の図4、図5のように2つのベクトル \boldsymbol{\mathsf{v_1}}、\boldsymbol{\mathsf{v_2}} が平行である場合の外積について見てみよう。
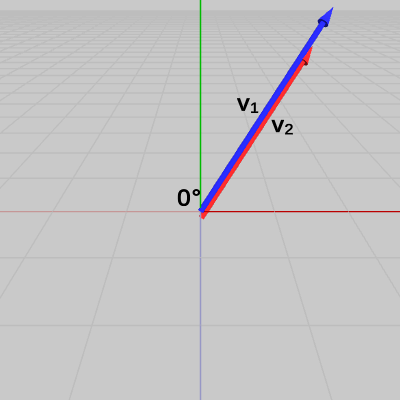
図4 平行なベクトル(なす角0°) 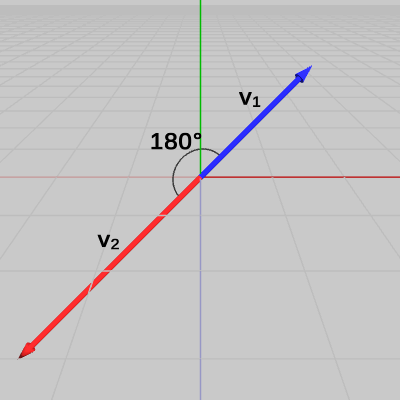
図5 平行なベクトル(なす角180°)
外積の大きさは |\boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}}| = |\boldsymbol{\mathsf{v_1}}||\boldsymbol{\mathsf{v_2}}|\sin{T} で表されるが、この場合は \boldsymbol{\mathsf{v_1}}、\boldsymbol{\mathsf{v_2}} のなす角が 0^\circ、180^\circ となり、\sin{T} の値は 0 になってしまう。つまり |\boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}}| = 0 である。
これは \boldsymbol{\mathsf{v_1}} と \boldsymbol{\mathsf{v_2}} が平行であるときは、外積 \boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}} の大きさは 0、すなわち外積 \boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}} が存在しないことを意味する。したがって外積を考えるときには一般に2つのベクトルのなす角が 0^\circ < T < 180^\circ であることを前提とする。
法線の場合にもそうであったが、ある面に垂直な方向は2つあるが、左手系における外積の向きは以下のように定義される。
例えば、図6のベクトル \boldsymbol{a}、\boldsymbol{b} の外積 \boldsymbol{a} \times \boldsymbol{b} の向きは、図7に示されるように左手の親指を \boldsymbol{a}、人差し指を \boldsymbol{b} としたときに中指が指している方向が、外積 \boldsymbol{a} \times \boldsymbol{b} の向きである (図7の赤いベクトル)。この \boldsymbol{a} \times \boldsymbol{b} は \boldsymbol{a} に対しても \boldsymbol{b} に対しても垂直、すなわち \boldsymbol{a}、\boldsymbol{b} を含む平面に対して垂直なベクトルである。
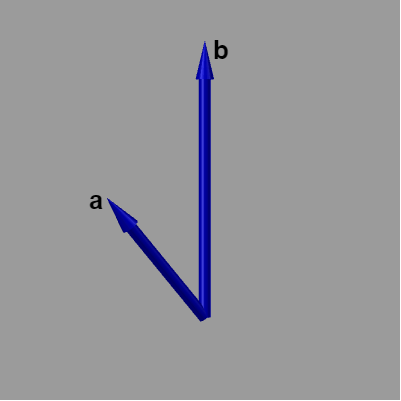
図6 ベクトルa, b 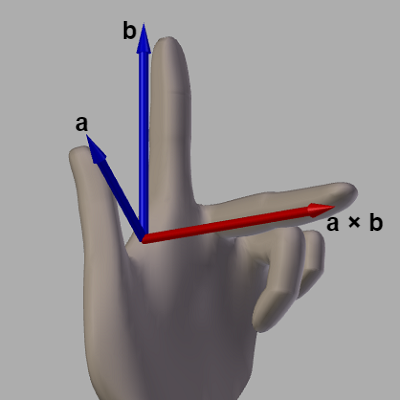
図7 ベクトルa, bの外積a×b(左手系における外積)
先ほども少し触れたが、外積の積の順序を入れ替えると、算出されるベクトルが反転する。すなわち、 \boldsymbol{a} \times \boldsymbol{b} = -\boldsymbol{b} \times \boldsymbol{a} である。これは \boldsymbol{b} \times \boldsymbol{a} の方向は \boldsymbol{a} \times \boldsymbol{b} とは反対の方向になることを意味している。上の例において左手の親指を \boldsymbol{b} にあて、人差し指を \boldsymbol{a} にあてたときの中指の指している方向が外積 \boldsymbol{b} \times \boldsymbol{a} の方向である (右手系では右手の親指を \boldsymbol{a}、人差し指を \boldsymbol{b} としたときに中指が指している方向が右手系の外積 \boldsymbol{a} \times \boldsymbol{b} の向きである。右手系の外積は左手系とは反対の方向を指すことに注意)。
実際に外積 \boldsymbol{a} \times \boldsymbol{b} が \boldsymbol{a}、\boldsymbol{b} のそれぞれと直交していることを調べるには、内積を計算すればよい。つまり、上で示した \boldsymbol{a} \times \boldsymbol{b}\ =\ (a_yb_z - a_zb_y,\ a_zb_x - a_xb_z,\ a_xb_y - a_yb_x) と \boldsymbol{a} 及び \boldsymbol{b} との内積を計算すれば、いずれも 0 になることが簡単に確かめられる。
まとめるとベクトルの外積 \boldsymbol{a} \times \boldsymbol{b} とは、2つの3次元ベクトル \boldsymbol{a}、\boldsymbol{b} に対し以下の定義 (\mathrm{i})~(\mathrm{iii}) を満たすベクトルのことである。
実際にはこの定義からベクトルの外積が上に示した成分を持つベクトルとして一意的決定されるのである (詳しくは14-1節参照)。

図9 面PQRS 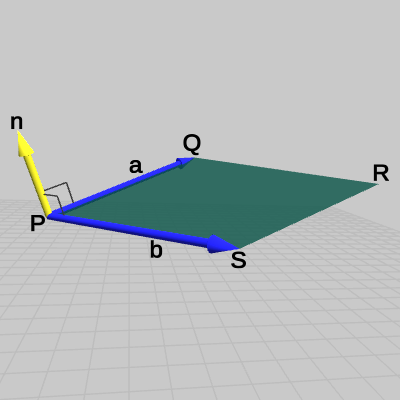
図10 面PQRSの法線n(単位ベクトル)
3D空間内に四角形の面PQRSが置かれている(図9)。この面の法線は次のようにして求めることができる。
まず、Pを始点、Qを終点とするベクトルを \boldsymbol{a} とし、Pを始点、Sを終点とするベクトルを \boldsymbol{b} とする(図10)。
Q - P = \boldsymbol{a} \qquad\qquad\qquad S - P = \boldsymbol{b}このベクトル \boldsymbol{a}、\boldsymbol{b} の外積\boldsymbol{a} \times \boldsymbol{b}は、ベクトル \boldsymbol{a}、\boldsymbol{b} の両方に対して垂直、すなわち \boldsymbol{a}、 \boldsymbol{b} を含む平面に対して垂直なベクトルである(もちろん面PQRSに対しても垂直である)。したがって、外積\boldsymbol{a} \times \boldsymbol{b}は面PQRSの法線ベクトルになるが、方向を表すベクトルは正規化して単位ベクトルの形にしておく方が望ましいので、ここでも\boldsymbol{a} \times \boldsymbol{b}を正規化した単位ベクトル \boldsymbol{n} を面PQRSの法線ベクトルとする。
\frac{\boldsymbol{a} \times \boldsymbol{b}}{|\boldsymbol{a} \times \boldsymbol{b}|} = \boldsymbol{n}(図10におけるベクトル \boldsymbol{a} に左手の親指を合わせ、ベクトル \boldsymbol{b} に左手の人差し指を合わせたとき、法線ベクトル \boldsymbol{n} の方向は左手の中指の方向になる。)
3-5節でも述べたが、Unityでは面の表側のみが描画され、面の裏側は何も描画されない。そして、面の表側とは法線の出ている側である。図9や図10で面PQRSが描画されているのは見えている部分が面の表側、つまり法線\boldsymbol{n}の出ている側だからである。もし、法線\boldsymbol{n}が逆向きであった場合は、面PQRSの(図中において)見えていない側が表側となり、(Unityでは)描画されなくなってしまう。
例えば、3Dオブジェクトを作成する際、ある面の法線を上で述べた外積経由で定める場合などでは、法線の方向が\boldsymbol{a} \times \boldsymbol{b}の方向なのか、\boldsymbol{b} \times \boldsymbol{a}の方向なのかに気を付ける必要がある。
3D空間内の適当な位置に平面が置かれており、下図11に示されるようにこの平面は黒い線分によって分断されている。図中の点 A、B は黒い線分上の点であり、点 P はこの平面上において線分の右側に置かれている。
このとき、ベクトル \overrightarrow{AP} と ベクトル \overrightarrow{AB} の外積 \overrightarrow{AP} \times \overrightarrow{AB} の向きは、左手の親指を \overrightarrow{AP} に、人差し指を \overrightarrow{AB} に合わせたときの左手の中指の指す方向であるから、図12における \boldsymbol{\mathsf{v}} の方向になる。もし点 P が黒い線分の右側ではなく左側に置かれている場合には、外積 \overrightarrow{AP} \times \overrightarrow{AB} の向きは図13における \boldsymbol{\mathsf{w}} の方向になる (左手の親指を \overrightarrow{AP} に、人差し指を \overrightarrow{AB} に合わせれば中指は \boldsymbol{\mathsf{w}} の方向を向く ; 下図における \boldsymbol{\mathsf{v}}、\boldsymbol{\mathsf{w}} はいずれもこの平面に直交する方向)。
より詳しくは、上の状況では平面上の点 P が黒い線分よりも右側にある場合には外積 \overrightarrow{AP} \times \overrightarrow{AB} の方向は \boldsymbol{\mathsf{v}} の方向になり、点 P が線分よりも左側にある場合には \boldsymbol{\mathsf{w}} の方向になるのである。
状況を簡単にするために考える平面をXY平面とし、XY平面の y軸上にベクトル \overrightarrow{AB} が置かれているものとしよう (図14)。この場合には図に示されるように点 P が y軸より右側にあるとき、外積 \overrightarrow{AP} \times \overrightarrow{AB} の方向はここでも同様に左手の親指を \overrightarrow{AP} に、人差し指を \overrightarrow{AB} に合わせたときの中指の指す方向であるから、この場合には z軸プラス方向となる。点 P が y軸よりも左側にある場合には \overrightarrow{AP} \times \overrightarrow{AB} の方向は z軸マイナス方向になる(図15)。
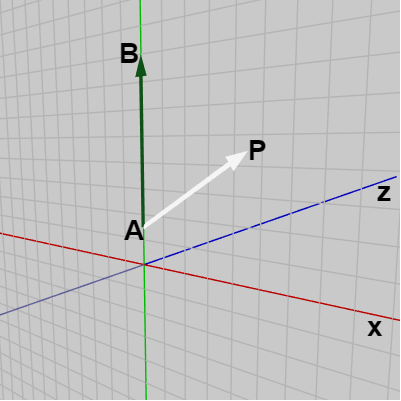
図14 外積 AP x AB は z軸プラス方向 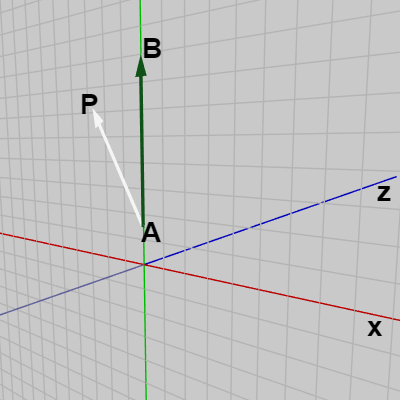
図15 外積 AP x AB は z軸マイナス方向
このことを実際に外積を計算して確認してみよう。この例では \overrightarrow{AB}、\overrightarrow{AP} はいずれもXY平面上のベクトルであり、いずれも z成分は 0 である。したがって、\overrightarrow{AP} = (a_x, a_y, 0)、\overrightarrow{AB} = (b_x, b_y, 0) とすれば、\overrightarrow{AP} \times \overrightarrow{AB} は
つまり、上記のようにXY平面がある直線によって分断されているとき、XY平面上の点 P がその直線のどちら側にあるかを調べるには直線上のベクトル \overrightarrow{AB} と \overrightarrow{AP} との外積を計算し、その z成分を調べればよいのである。そして、(XY平面上の)三角形の内外判定ではこの z成分の計算 a_xb_y - a_yb_x を特別に Edge Function と呼ぶ。
XY平面上において、ある点が三角形に含まれるかどうかは、この Edge Function を用いて以下のように行われる。
点 P が三角形 ABC に含まれていたとしよう (図16)。このとき、図17のようにベクトル \overrightarrow{AP} と \overrightarrow{AB} の外積 \overrightarrow{AP} \times \overrightarrow{AB} を考えれば、左手の親指を \overrightarrow{AP} に、人差し指を \overrightarrow{AB} に合わせると中指は z軸プラス方向を指す。すなわち、\overrightarrow{AP} \times \overrightarrow{AB} は z軸プラス方向を指す。同様に、残りの2つの辺との外積 \overrightarrow{BP} \times \overrightarrow{BC}、\overrightarrow{CP} \times \overrightarrow{CA} の場合も左手の中指は z軸プラス方向を指す。
つまり、点 P が三角形 ABC に含まれる場合には、三角形の各辺との外積 \overrightarrow{AP} \times \overrightarrow{AB}、\overrightarrow{BP} \times \overrightarrow{BC}、\overrightarrow{CP} \times \overrightarrow{CA} はいずれも z軸プラス方向を指すのである。これは言い換えれば、点 P が三角形 ABC に含まれる場合にはこれらの Edge Function がいずれもプラスの値になるということである。
逆に、点 P が三角形の外側にある場合には少なくとも1つの辺との Edge Function がマイナスになる。例えば、図18の場合 \overrightarrow{BP} \times \overrightarrow{BC} がマイナスになる。
したがって、ある点が三角形に含まれるかどうかを調べるには3つの辺との Edge Function の正負を調べればよいのである (Edge Function が 0 である場合には三角形のいずれかの辺を含む直線上に点があることを意味する)。
以下のメソッド CollisionTest_Point_Triangle(..) はXY平面上において、点 P が三角形 ABC に含まれるかを調べるものであり、上で述べてきたことを実装したものである (引数には各点の座標をセットする)。
3つの辺との Edge Function が行われるが、3つともプラスである場合のみ点 P が三角形 ABC に含まれると判定される。1つでもマイナスである場合には三角形に含まれていないと判定され、その場で false が返される。
まずは解説の便宜のためいくつかの用語の定義から始める。
下図では三角形 ABC の他にその各辺を延長した直線が表示されているが、辺 AB を含む直線の進行方向を \overrightarrow{AB} とするとき、この進行方向に関して直線の右側を「辺 AB の内側」と呼ぶことにする。同様にこの進行方向に関して直線の左側を「辺 AB の外側」と呼ぶことにする (内側は三角形を含む側であり、外側は三角形を含まない)。
辺 BC、辺 CA の場合も同様である。「辺 BC の内側」であれば \overrightarrow{BC} を進行方向とするとき、辺 BC を含む直線の右側のことであり、「辺 CA の外側」であれば \overrightarrow{CA} を進行方向とするとき、辺 CA を含む直線の左側のことである。
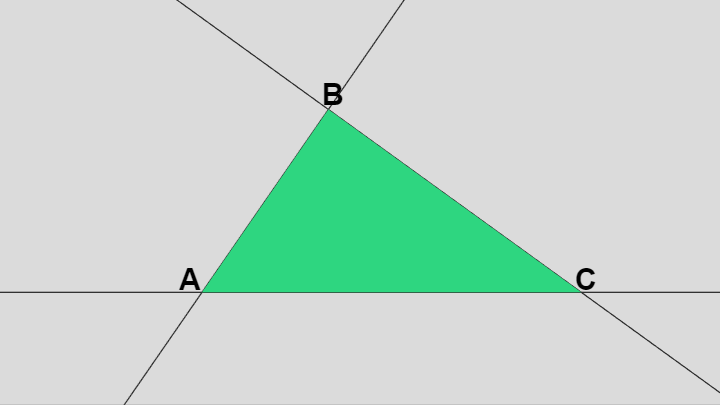
図19
また上で見たようにベクトルの外積の大きさは2つのベクトルによって作られる平行四辺形の面積に等しいのであった。例えば下図20の場合は |\overrightarrow{AB}\times \overrightarrow{AC}| は2つのベクトル \overrightarrow{AB}、\overrightarrow{AC} によって作られる平行四辺形の面積を表す。
もし \overrightarrow{AB}、\overrightarrow{AC} がXY平面上にある場合には上記の内外判定で示したようにその外積は\overrightarrow{AB} \times \overrightarrow{AC} = (0,\ 0,\ z) の形になり、z の符号は2つのベクトルの位置関係によって決まるのであった (\overrightarrow{AB} が \overrightarrow{AC} よりも右にあれば z はプラスであり左であればマイナスになる)。
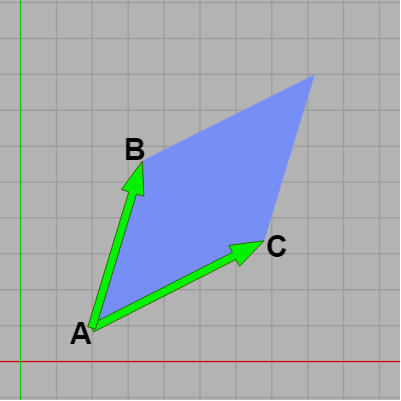
図20 |\overrightarrow{AB}\times \overrightarrow{AC}| は2つのベクトルによって作られる平行四辺形の面積を表し、符号は必ずプラス。 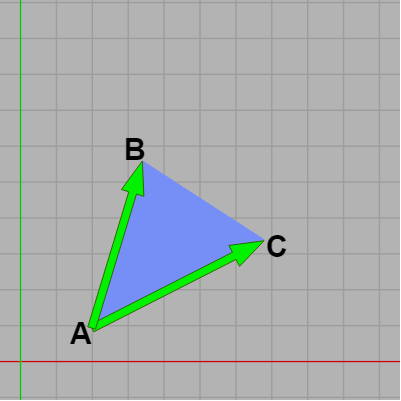
図21 \Delta(\overrightarrow{AB}\times \overrightarrow{AC}) はその絶対値が2つのベクトルによって作られる三角形の面積を表すが、\Delta(\overrightarrow{AB}\times \overrightarrow{AC}) の符号はプラスとは限らない。
ここで \Delta(\overrightarrow{AB}\times \overrightarrow{AC}) = z/2 と定める。このとき、\Delta(\overrightarrow{AB}\times \overrightarrow{AC}) は2つのベクトル \overrightarrow{AB}、\overrightarrow{AC} によって作られる三角形 ABC の面積を表すことになるが、注意すべきは必ずしも符号はプラスになるとは限らないという点である。例えば上図21の場合 \Delta(\overrightarrow{AB}\times \overrightarrow{AC}) は符号はマイナスであり (\overrightarrow{AB} に左手の親指を置き、\overrightarrow{AC} に左手の人差し指を置くと中指は z軸マイナス方向を指す)、正確にいえばその絶対値が三角形 ABC の面積に相当する。
三角形同士の衝突判定では、両者が衝突していない場合における次の性質を利用する。
「2つの三角形が衝突していない場合(重なりがない場合)、一方の三角形の頂点はすべて、もう一方の三角形の少なくとも1つの辺の外側にある」
例えば以下は衝突していない2つのケースであるが下左図では三角形 DEF の頂点はすべて辺 BC の外側にあり、下右図の場合は三角形 ABC の頂点はすべて辺 DE の外側にある。
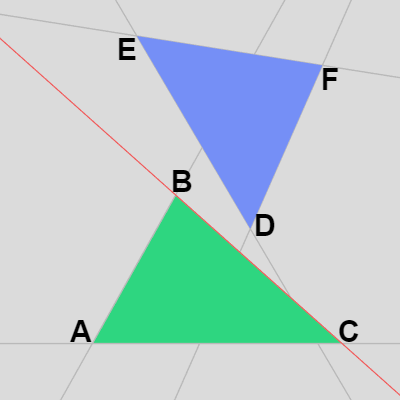
図22 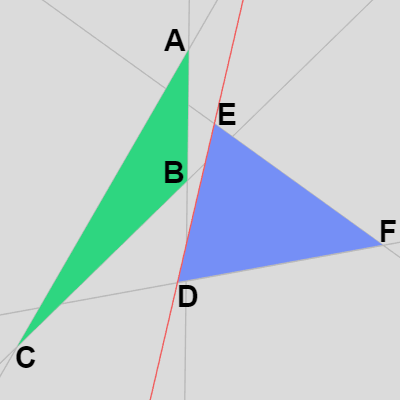
図23
したがって三角形同士の衝突判定では一方の三角形のすべての頂点が、もう一方の三角形のいずれか1つの辺の外側にあるかどうかを調べることに帰着するのである。
三角形 DEF が三角形 ABC のいずれか1つの辺の外側にあるかを調べる場合であれば、まず三角形 DEF の3つの頂点が辺 AB の外側にあるかを調べる。(XY平面上において)ある点がある直線のどちらの側にあるかを調べるには上でも見たように外積(Edge Function)を1回行えばよいから、3つの頂点が辺 AB の外側にあるかを調べるには外積を3回行えばよい。
3つの頂点すべてが辺 AB の外側にない場合には、次に辺 BC の外側にあるかを調べる。辺 BC の外側でもない場合には、最後に辺 CA の外側かどうかを調べればよい。すなわち、一方の三角形のすべての頂点がもう一方の三角形のいずれか1つの辺の外側にあるかどうかを調べるには、多くとも外積を9回行えばよいのである。
しかし以下に示す方法をとることで外積の計算回数を9回から7回に減らすことができる。
三角形 ABC に対して点 D が下図24に示される位置にあったとする。この位置は辺 AB 及び辺 CA の内側であるから、\Delta(\overrightarrow{AD}\times \overrightarrow{AB}) > 0 かつ \Delta(\overrightarrow{AC}\times \overrightarrow{AD}) > 0 である。
点 D が辺 BC の内側か外側を調べるには辺 BC との外積を計算すればよいが、もしすでに \Delta(\overrightarrow{AD}\times \overrightarrow{AB})、\Delta(\overrightarrow{AC}\times \overrightarrow{AD}) がわかっているのであれば、\Delta(\overrightarrow{AC}\times \overrightarrow{AB}) を計算することで D が辺 BC の内側か外側かを判定できる (下図の場合には \Delta(\overrightarrow{AC}\times \overrightarrow{AB}) の符号もプラスである)。
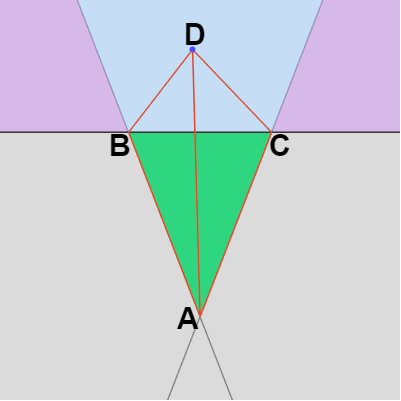
図24 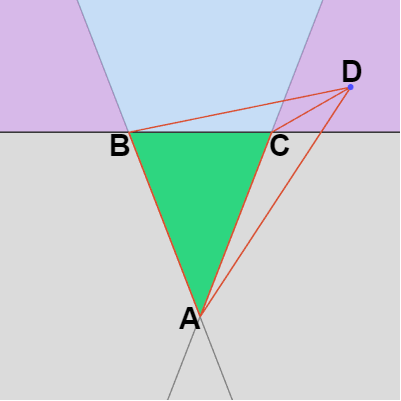
図25
実際、上図24の場合では \Delta(\overrightarrow{AD}\times \overrightarrow{AB}) は三角形 ABD の面積、\Delta(\overrightarrow{AC}\times \overrightarrow{AD}) は三角形 ACD の面積、\Delta(\overrightarrow{AC}\times \overrightarrow{AB}) は三角形 ABC の面積であるが、点 D が図の水色の領域にある場合どの位置にあっても三角形 ABD と三角形 ACD の面積の和は三角形 ABC の面積よりも大きい。
すなわち、上で定めた記号を用いれば\Delta(\overrightarrow{AD}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AD}) > \Delta(\overrightarrow{AC}\times \overrightarrow{AB}) \tag{1} である。
つまり D が図の水色の領域にある場合どの位置であっても (1) が成り立つのである。そしてこれは水色の領域だけでなく、D が辺 BC の外側にあればどの位置であっても成り立つ。例えば D が上図25の右側の紫の領域にあったとしよう。このとき \Delta(\overrightarrow{AC}\times \overrightarrow{AD}) < 0 なので \Delta(\overrightarrow{AD}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AD}) は三角形 ABD の面積から三角形 ACD の面積を引いた値になるが、図から明らかなようにそれでも三角形 ABC の面積よりも大きい (点 D が左側の紫の領域にあっても同様である)。つまり D が辺 BC の外側にある場合、その位置がどこであっても上記の (1) が成り立つのである。
点 D が辺 BC の内側にある場合には上記の不等号は逆転する。すなわち点 D が辺 BC の内側にある場合には\Delta(\overrightarrow{AD}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AD}) < \Delta(\overrightarrow{AC}\times \overrightarrow{AB}) \tag{2} となる。
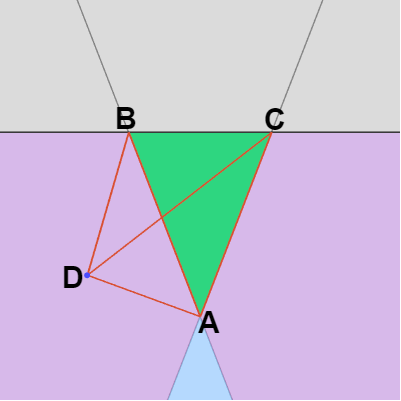
図26 内側にある場合 例えば右図26では D が辺 BC の内側の左側の紫の領域にあるが、このとき \Delta(\overrightarrow{AD}\times \overrightarrow{AB}) < 0 であるから \Delta(\overrightarrow{AD}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AD}) は三角形 ACD の面積から三角形 ABD の面積を引いた値になるが、この場合にも図から明らかなようにその値は三角形 ABC の面積よりも小さい。すなわち点 D が図26の左側の紫の領域にあるときその位置がどこであっても上記 (2) が成り立つ (これは右側の紫の領域の場合も同様である)。また D が図26の水色の領域にある場合は、\Delta(\overrightarrow{AD}\times \overrightarrow{AB})、\Delta(\overrightarrow{AC}\times \overrightarrow{AD}) はいずれもマイナスになるため明らかに (2) が成り立つ。つまり D が辺 BC の内側にある場合、その位置がどこであっても上記の (2) が成り立つのである (D が辺 BC を含む直線上にあるときには上記 (1) (及び(2)) の両辺の値は一致する)。
今の例のようにある1つの頂点がある辺のどちら側にあるかを調べるだけならば、この方法は特に効果的ではないが1つではなく3つの頂点の場合にはこの方法が効果を発揮する。
例えば三角形 ABC に対し三角形 DEF が図の位置に置かれていたとしよう。そして先程と同様に頂点 D、E、F が辺 AB、辺 CA のどちら側にあるかの計算がすでに行われていたとする。すなわち D については \Delta(\overrightarrow{AD}\times \overrightarrow{AB}) 及び \Delta(\overrightarrow{AC}\times \overrightarrow{AD})、E については \Delta(\overrightarrow{AE}\times \overrightarrow{AB}) 及び \Delta(\overrightarrow{AC}\times \overrightarrow{AE})、F については \Delta(\overrightarrow{AF}\times \overrightarrow{AB}) 及び \Delta(\overrightarrow{AC}\times \overrightarrow{AF}) の計算が行われていたとする。
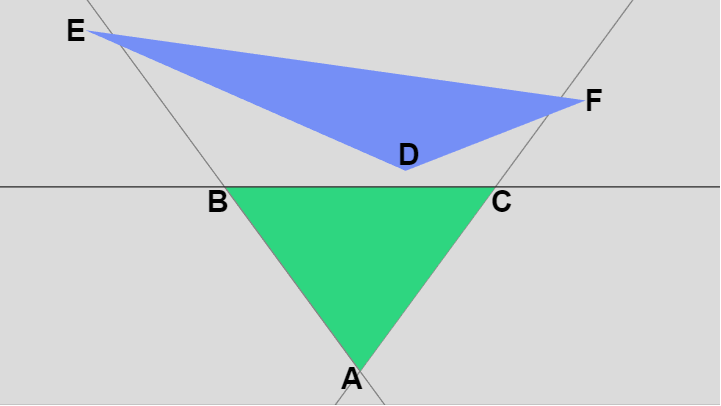
図27
ここで D、E、F がそれぞれ辺 BC のどちら側にあるかを調べるには、上で行ったように \Delta(\overrightarrow{AC}\times \overrightarrow{AB}) だけを計算すればよい (3つの頂点それぞれと辺 BC との外積を計算する必要はない)。そして上記 (1)、(2) と同じく \Delta(\overrightarrow{AD}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AD})、 \Delta(\overrightarrow{AE}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AE})、 \Delta(\overrightarrow{AF}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AF}) のそれぞれと \Delta(\overrightarrow{AC}\times \overrightarrow{AB}) との大小を比較すれば D、E、F が辺 BC のどちら側にあるのかがわかる。つまり外積は多くとも7回で済むわけである。
ただし注意すべきは一方の三角形の3つの頂点がすべて、もう一方の三角形のいずれかの辺の外側にある ということが成り立たない場合でも、その時点で両者が衝突していると判定することはできない。逆のケースを調べなければならないためである。例えば上図23の場合、三角形 DEF の頂点がすべて三角形 ABC のいずれかの辺の外側にあるということは成り立たないが、この場合にはさらに三角形 ABC の頂点がすべて三角形の DEF のいずれかの辺の外側にあるかを調べなければならない。
以上が外積を応用した三角形同士の衝突判定のアルゴリズムである。この手続きをプログラムにすることは容易であるから詳しい実装については読者の課題とする (下記 Code3)。
では本節に関連したプログラムを作成する。
[Code1] (実行結果 図28)
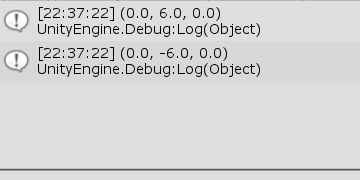
図28 Code1 実行結果 このプログラムは本節の始めに示した外積の計算例である。1行目、2行目の a、b は2つのベクトルを表し、この2つのベクトルの外積を求めている。最初の計算が \boldsymbol{a} \times \boldsymbol{b} であり、次の計算が \boldsymbol{b} \times \boldsymbol{a} である。
実行結果(図28)に示されるように、外積の順序を入れ替えると算出されるベクトルの向きが逆になる。
各点の座標は A = (3.92,\ 4.35, -4.31)、B = (0.52,\ 4.0, -7.95)、C = (0,\ 4, -5) である。
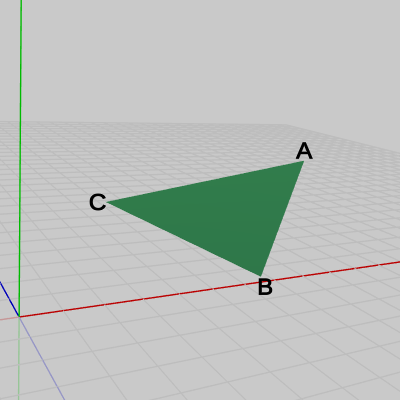
図29 △ABC 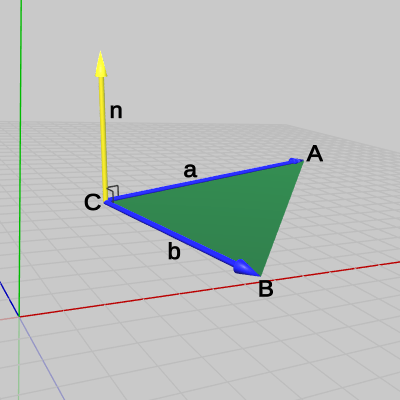
図30 ベクトルa、bと法線ベクトルn
[Code2] (実行結果 31)
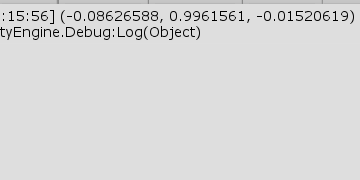
図31 Code2 実行結果 1行目から3行目の A、B、C は\triangle ABCの各点を表している。5行目の a は始点を C、終点を A とするベクトルであり、6行目の b は始点を C、終点を B とするベクトルである (図30)。7行目において、この2つのベクトルの外積を計算している。図30の \boldsymbol{a} を左手の親指とし、\boldsymbol{b} を左手の人差し指としたときの中指の向いている方向が外積 \boldsymbol{a} \times \boldsymbol{b} の向きであり、図中では \boldsymbol{n} で表されているベクトルである。
実行結果(図31)は、外積 n の正規化された値である (ほぼy軸に平行である)。
まずは上で述べた三角形同士の衝突判定の実装である。
今回のプログラムでは開始時点で以下に示されるように2つの三角形 ABC、DEF が適当な位置に置かれている (三角形の各頂点の並び方はいずれも時計回り、いわゆる clockwise order である)。
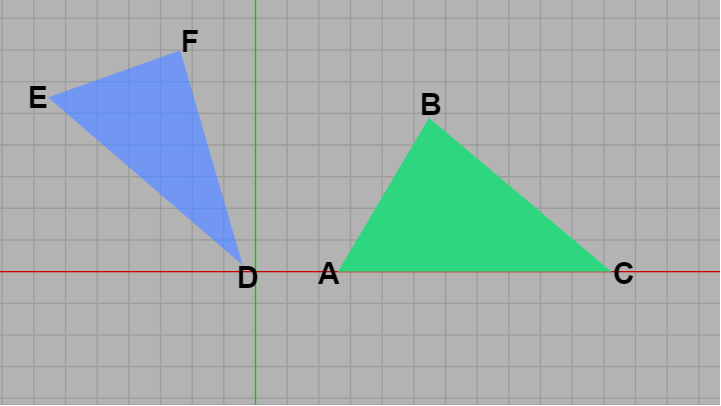
図32
プログラムを以下に示す。
[Code3]
6行目の衝突判定用メソッド CollisionTest_Triangle_Triangle(..) は以下に示されるように具体的な処理が記述されていないので、このメソッド内に三角形同士の衝突判定を実装することがここでの課題である。
[CollisionTest_Triangle_Triangle(..)]
なおプログラム実行中は次のキー操作によって2つの三角形を動かすことができる。
H、J、K、L : 三角形 DEF を縦横に移動させる。
Y、U、I、O : 三角形 DEF の頂点 E を縦横に移動させる (+Shift の場合は頂点 F が移動する)。
R : 三角形 DEF の回転 (+Shift の場合は逆回転)。
Q : 三角形 ABC の回転 (+Shift の場合は逆回転)。
細かい点ではあるが最後に1つ注意しておこう。上の解説から三角形 DEF が三角形 ABC のいずれか1つの辺の外側にあるかどうかのコードは明らかに以下のような形になる。
このコードは以下のように書き換えても同じである。
一見すると上のコードの方が効率的に見えるが、上のコードと下のコードのどちらが速いかは実装に依存する。必ずしも上のコードの方が速いわけではない。むしろ上記の解説をそのまま実装するのであれば下のコードを使った方が速いはずである。
解答例については Sec306_Ans.txt を参照 (このファイルはダウンロードコンテンツ内「txt_ans」フォルダに含まれている。ファイル内には三角形同士の衝突判定として2つの実装 ver1、ver2 が記述されているが、ver1 は上記の解説をそのまま実装したものである。ver2 は ver1 を改良したものであり衝突の頻度が3割以上になる場合には ver2 の方が効率的である (ただし初回実行時のみ ver2 は時間がかかる)。解説が面倒であるため ver2 についてはいつか機会があれば解説する)。
しかし次のように考えればその処理を効率化することができる。
長方形は各辺を引き延ばすことで下図に示されるように、長方形とその周りは9個の領域に分割される。
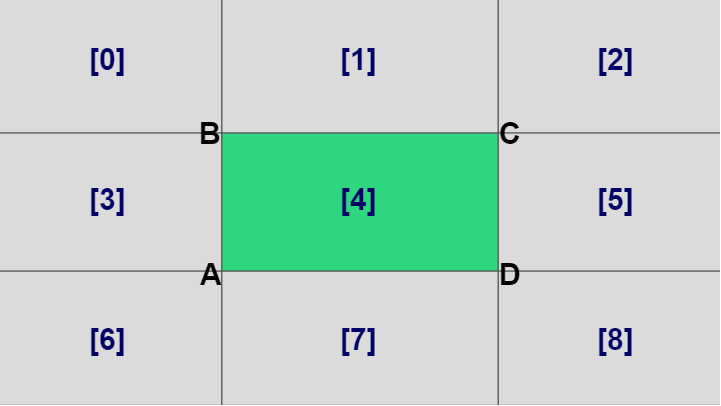
図35 長方形とその周りは9個の領域に分割される
例えば三角形 PQR の頂点 P が領域 [6] に含まれていたとする。このとき三角形と長方形が衝突しているならば、三角形 PQR がどのような形であっても長方形の左下側の三角形 ABD と必ず衝突している (図36)。すなわち三角形の1つの頂点が領域 [6] にあることがわかっている場合には、長方形の左下側の三角形と衝突しているかどうかを調べればよい。
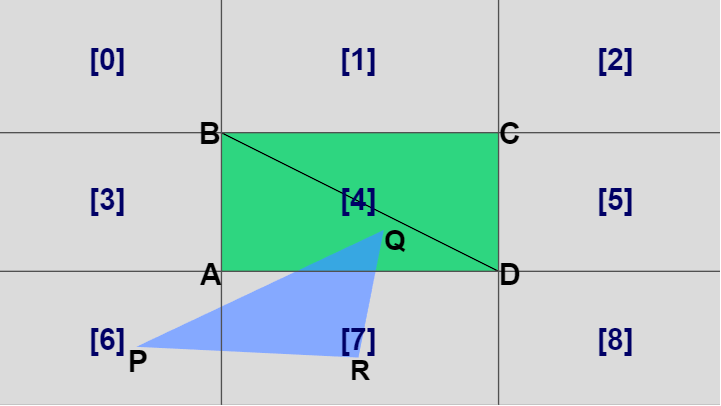
図36 点Pが領域[6]にあるときは三角形ABDと衝突しているかを調べる
また点 P が領域 [1] に含まれている場合、両者が衝突しているならば三角形 PQR がどのような形であっても長方形の辺 BC を含む三角形と必ず衝突している (図37)。したがって三角形の1つの頂点が領域 [1] にあることがわかっている場合には長方形の辺 BC を含む三角形 BCD と衝突しているかどうかを調べればよい (もちろん三角形 ABC と衝突しているかを調べても同じである)。
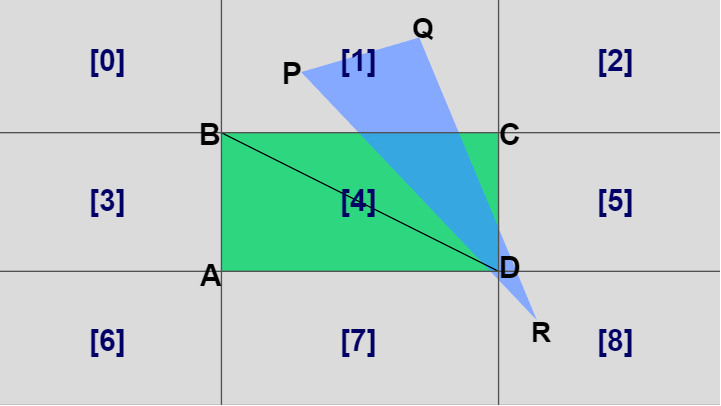
図37 点Pが領域[1]にあるときは三角形BCDと衝突しているかを調べる
つまり三角形の頂点の1つが上記の9つの領域のうちどの領域に含まれているかがわかれば、長方形を構成する2つの三角形のうちのどちらと衝突判定を行えばよいかが決められるのである。したがって三角形と長方形の衝突判定も結局は三角形同士の衝突判定を1回だけ行えばよいわけである (上の例では対角線 BD によって長方形は分割されているが、三角形の置かれている位置によっては対角線 AC で考えなければならない場合がある)。
プログラムを以下に示す (開始時点では三角形と長方形が適当な位置にそれぞれ置かれている。またCode3と同じく図形の頂点の並び方は時計回りである)。
[Code4]
6行目の衝突判定用メソッド CollisionTest_Triangle_Rect(..) は以下に示されるように具体的な処理が記述されていないので、このメソッド内に三角形と長方形の衝突判定を実装することがここでの課題である (引数の vtsTri、vtsRect は三角形及び長方形の頂点がセットされた配列であり、要素数はそれぞれ 3、4 である)。
[CollisionTest_Triangle_Rect(..)]
プログラム実行中は次のキー操作によって三角形及び長方形を動かすことができる。
H、J、K、L : 三角形を縦横に移動させる。
R : 三角形の回転 (+Shift の場合は逆回転)。
Q : 長方形の回転 (+Shift の場合は逆回転)。
(解答例については Sec306_Ans.txt を参照)
(参考資料)
https://www.scratchapixel.com/lessons/3d-basic-rendering/rasterization-practical-implementation/rasterization-stage.html
https://stackoverflow.com/questions/2778240/detection-of-triangle-collision-in-2d-space
ベクトル \boldsymbol{a} = (a_x, a_y, a_z)、\boldsymbol{b} = (b_x, b_y, b_z) の外積 \boldsymbol{a} \times \boldsymbol{b}
\boldsymbol{a} \times \boldsymbol{b}\ =\ (a_yb_z - a_zb_y,\ a_zb_x - a_xb_z,\ a_xb_y - a_yb_x)
(計算例)
ベクトル \boldsymbol{\mathsf{v_1}} = (1, 2, 3)、\boldsymbol{\mathsf{v_2}} = (4, 5, 6) の外積 \boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}}
\begin{align*}\boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}}\ &=\ (2\cdot6 - 3\cdot5,\ 3\cdot4 - 1\cdot6,\ 1\cdot5 - 2\cdot4) \\&= (12-15,\ 12-6,\ 5-8) = (-3,\ 6, -3)\end{align*}上の計算における \boldsymbol{\mathsf{v_1}}、\boldsymbol{\mathsf{v_2}} の積の順序を入れ替えた場合
\begin{align*}\boldsymbol{\mathsf{v_2}} \times \boldsymbol{\mathsf{v_1}}\ &=\ (5\cdot3 - 6\cdot2,\ 6\cdot1 - 4\cdot3,\ 4\cdot2 - 5\cdot1) \\&= (15-12,\ 6-12,\ 8-5) = (3, -6,\ 3)\end{align*}
上の結果からわかるように、外積の積の順序は交換可能ではない。つまり、積の順序を入れ替えた場合、算出されるベクトルは異なる。より正確には、外積の積の順序については次の関係が成り立つ。(\boldsymbol{a}、\boldsymbol{b} を3次元ベクトルとすると)
\boldsymbol{a} \times \boldsymbol{b} = -\boldsymbol{b} \times \boldsymbol{a}
ベクトルの内積が2つのベクトルから1つの実数値を算出する演算であったのに対し、ベクトルの外積は2つのベクトルから新たにもう1つのベクトルを算出する演算である。
具体的な例として、図1の2つのベクトル \boldsymbol{a} = (0, 0, 2)、\boldsymbol{b} = (3, 0, 1) の外積 \boldsymbol{a} \times \boldsymbol{b} を求めてみよう(以下では \boldsymbol{a} \times \boldsymbol{b} = \boldsymbol{c} とおく ; 図中の緑色の数値はベクトルの成分を表している)。


\begin{align*}\boldsymbol{a} \times \boldsymbol{b}\ &=\ (0\cdot1 - 2\cdot0,\ 2\cdot3 - 0\cdot1,\ 0\cdot0 - 0\cdot3) \\&=(0,\ 6,\ 0) = \boldsymbol{c}\end{align*}
図2における赤いベクトルが、外積 \boldsymbol{a} \times \boldsymbol{b}\ ( = \boldsymbol{c}) である。
外積とは一体どのようなものなのであろうか。まず、外積の幾何的な意味から見ていこう。
A) 外積の大きさ

|\boldsymbol{a} \times \boldsymbol{b}| = |\boldsymbol{a}||\boldsymbol{b}|\sin{T} この等式の意味を図3を用いて説明しよう。
ベクトル \boldsymbol{b} の終点からベクトル \boldsymbol{a} に垂線をおろしたとき、その垂線の足(ベクトル \boldsymbol{a} と垂線の交点)とベクトル \boldsymbol{b} の始点、及び終点は直角三角形を作る。\boldsymbol{a} と \boldsymbol{b} のなす角が T であるから、垂線の長さ(図中の点線の長さ)は |\boldsymbol{b}|\sin{T} である。したがって、|\boldsymbol{a}||\boldsymbol{b}|\sin{T} はベクトル \boldsymbol{a}、\boldsymbol{b} によって作られる平行四辺形の面積に等しい。
上の図1、図2の例でいえば、\boldsymbol{a} = (0, 0, 2)、\boldsymbol{b} = (3, 0, 1) の外積は \boldsymbol{a} \times \boldsymbol{b} = (0,\ 6,\ 0)\ (= \boldsymbol{c}) であったが、外積の大きさは |\boldsymbol{a} \times \boldsymbol{b}| = |\boldsymbol{c}| = 6 である。これは、ベクトル \boldsymbol{a} と \boldsymbol{b} が作る平行四辺形の面積が 6 であることを意味している。
下の図4、図5のように2つのベクトル \boldsymbol{\mathsf{v_1}}、\boldsymbol{\mathsf{v_2}} が平行である場合の外積について見てみよう。


外積の大きさは |\boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}}| = |\boldsymbol{\mathsf{v_1}}||\boldsymbol{\mathsf{v_2}}|\sin{T} で表されるが、この場合は \boldsymbol{\mathsf{v_1}}、\boldsymbol{\mathsf{v_2}} のなす角が 0^\circ、180^\circ となり、\sin{T} の値は 0 になってしまう。つまり |\boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}}| = 0 である。
これは \boldsymbol{\mathsf{v_1}} と \boldsymbol{\mathsf{v_2}} が平行であるときは、外積 \boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}} の大きさは 0、すなわち外積 \boldsymbol{\mathsf{v_1}} \times \boldsymbol{\mathsf{v_2}} が存在しないことを意味する。したがって外積を考えるときには一般に2つのベクトルのなす角が 0^\circ < T < 180^\circ であることを前提とする。
B) 外積の向き
外積 \boldsymbol{a} \times \boldsymbol{b} が示す向きは、3次元ベクトル \boldsymbol{a}、\boldsymbol{b} が作る平行四辺形に対して垂直になる(より一般的ないいかたをすれば、外積 \boldsymbol{a} \times \boldsymbol{b} は3次元ベクトル \boldsymbol{a}、\boldsymbol{b} を含む平面に対して垂直になる)。すなわち外積 \boldsymbol{a} \times \boldsymbol{b} は、ベクトル \boldsymbol{a} に対しても垂直であり、\boldsymbol{b} に対しても垂直である。法線の場合にもそうであったが、ある面に垂直な方向は2つあるが、左手系における外積の向きは以下のように定義される。
例えば、図6のベクトル \boldsymbol{a}、\boldsymbol{b} の外積 \boldsymbol{a} \times \boldsymbol{b} の向きは、図7に示されるように左手の親指を \boldsymbol{a}、人差し指を \boldsymbol{b} としたときに中指が指している方向が、外積 \boldsymbol{a} \times \boldsymbol{b} の向きである (図7の赤いベクトル)。この \boldsymbol{a} \times \boldsymbol{b} は \boldsymbol{a} に対しても \boldsymbol{b} に対しても垂直、すなわち \boldsymbol{a}、\boldsymbol{b} を含む平面に対して垂直なベクトルである。


先ほども少し触れたが、外積の積の順序を入れ替えると、算出されるベクトルが反転する。すなわち、 \boldsymbol{a} \times \boldsymbol{b} = -\boldsymbol{b} \times \boldsymbol{a} である。これは \boldsymbol{b} \times \boldsymbol{a} の方向は \boldsymbol{a} \times \boldsymbol{b} とは反対の方向になることを意味している。上の例において左手の親指を \boldsymbol{b} にあて、人差し指を \boldsymbol{a} にあてたときの中指の指している方向が外積 \boldsymbol{b} \times \boldsymbol{a} の方向である (右手系では右手の親指を \boldsymbol{a}、人差し指を \boldsymbol{b} としたときに中指が指している方向が右手系の外積 \boldsymbol{a} \times \boldsymbol{b} の向きである。右手系の外積は左手系とは反対の方向を指すことに注意)。
実際に外積 \boldsymbol{a} \times \boldsymbol{b} が \boldsymbol{a}、\boldsymbol{b} のそれぞれと直交していることを調べるには、内積を計算すればよい。つまり、上で示した \boldsymbol{a} \times \boldsymbol{b}\ =\ (a_yb_z - a_zb_y,\ a_zb_x - a_xb_z,\ a_xb_y - a_yb_x) と \boldsymbol{a} 及び \boldsymbol{b} との内積を計算すれば、いずれも 0 になることが簡単に確かめられる。
まとめるとベクトルの外積 \boldsymbol{a} \times \boldsymbol{b} とは、2つの3次元ベクトル \boldsymbol{a}、\boldsymbol{b} に対し以下の定義 (\mathrm{i})~(\mathrm{iii}) を満たすベクトルのことである。
| (\mathrm{i}) | \boldsymbol{a} \times \boldsymbol{b} は2つのベクトル \boldsymbol{a}、\boldsymbol{b} と直交する。 |
| (\mathrm{ii}) | \boldsymbol{a} を左手の親指に、\boldsymbol{b} を左手の人差し指に合わせたとき、\boldsymbol{a} \times \boldsymbol{b} の向きは中指の方向を指す。 |
| (\mathrm{iii}) | \boldsymbol{a} \times \boldsymbol{b} の大きさは \boldsymbol{a}、\boldsymbol{b} によって張られる平行四辺形の大きさに等しい。 |
実際にはこの定義からベクトルの外積が上に示した成分を持つベクトルとして一意的決定されるのである (詳しくは14-1節参照)。
C) 法線の計算
外積の使用例として、3D空間内にある面の法線ベクトルを外積を使って求めてみよう。

3D空間内に四角形の面PQRSが置かれている(図9)。この面の法線は次のようにして求めることができる。
まず、Pを始点、Qを終点とするベクトルを \boldsymbol{a} とし、Pを始点、Sを終点とするベクトルを \boldsymbol{b} とする(図10)。
Q - P = \boldsymbol{a} \qquad\qquad\qquad S - P = \boldsymbol{b}このベクトル \boldsymbol{a}、\boldsymbol{b} の外積\boldsymbol{a} \times \boldsymbol{b}は、ベクトル \boldsymbol{a}、\boldsymbol{b} の両方に対して垂直、すなわち \boldsymbol{a}、 \boldsymbol{b} を含む平面に対して垂直なベクトルである(もちろん面PQRSに対しても垂直である)。したがって、外積\boldsymbol{a} \times \boldsymbol{b}は面PQRSの法線ベクトルになるが、方向を表すベクトルは正規化して単位ベクトルの形にしておく方が望ましいので、ここでも\boldsymbol{a} \times \boldsymbol{b}を正規化した単位ベクトル \boldsymbol{n} を面PQRSの法線ベクトルとする。
\frac{\boldsymbol{a} \times \boldsymbol{b}}{|\boldsymbol{a} \times \boldsymbol{b}|} = \boldsymbol{n}(図10におけるベクトル \boldsymbol{a} に左手の親指を合わせ、ベクトル \boldsymbol{b} に左手の人差し指を合わせたとき、法線ベクトル \boldsymbol{n} の方向は左手の中指の方向になる。)
3-5節でも述べたが、Unityでは面の表側のみが描画され、面の裏側は何も描画されない。そして、面の表側とは法線の出ている側である。図9や図10で面PQRSが描画されているのは見えている部分が面の表側、つまり法線\boldsymbol{n}の出ている側だからである。もし、法線\boldsymbol{n}が逆向きであった場合は、面PQRSの(図中において)見えていない側が表側となり、(Unityでは)描画されなくなってしまう。
例えば、3Dオブジェクトを作成する際、ある面の法線を上で述べた外積経由で定める場合などでは、法線の方向が\boldsymbol{a} \times \boldsymbol{b}の方向なのか、\boldsymbol{b} \times \boldsymbol{a}の方向なのかに気を付ける必要がある。
D) 三角形の内外判定
ある点が三角形に含まれるかどうかを外積を用いて調べることができるが、以下この点について説明する。3D空間内の適当な位置に平面が置かれており、下図11に示されるようにこの平面は黒い線分によって分断されている。図中の点 A、B は黒い線分上の点であり、点 P はこの平面上において線分の右側に置かれている。
このとき、ベクトル \overrightarrow{AP} と ベクトル \overrightarrow{AB} の外積 \overrightarrow{AP} \times \overrightarrow{AB} の向きは、左手の親指を \overrightarrow{AP} に、人差し指を \overrightarrow{AB} に合わせたときの左手の中指の指す方向であるから、図12における \boldsymbol{\mathsf{v}} の方向になる。もし点 P が黒い線分の右側ではなく左側に置かれている場合には、外積 \overrightarrow{AP} \times \overrightarrow{AB} の向きは図13における \boldsymbol{\mathsf{w}} の方向になる (左手の親指を \overrightarrow{AP} に、人差し指を \overrightarrow{AB} に合わせれば中指は \boldsymbol{\mathsf{w}} の方向を向く ; 下図における \boldsymbol{\mathsf{v}}、\boldsymbol{\mathsf{w}} はいずれもこの平面に直交する方向)。
-
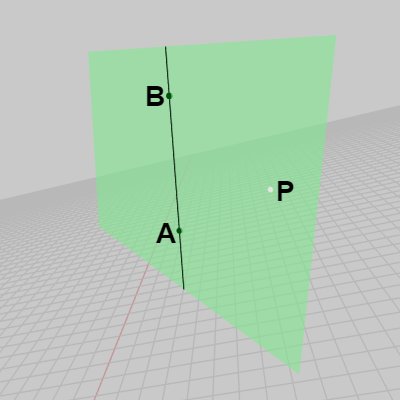 図11 黒い線分によって平面が分断されている。A、Bは線分上にあり、P は平面上において線分より右側にある
図11 黒い線分によって平面が分断されている。A、Bは線分上にあり、P は平面上において線分より右側にある -
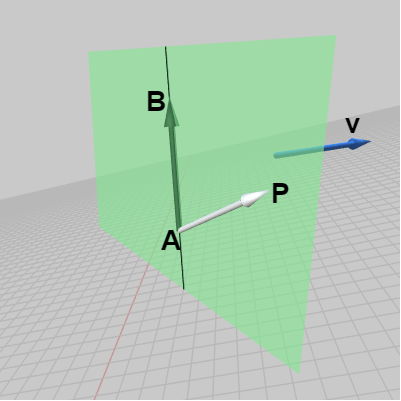 図12 外積 AP x AB は v の方向を向く
図12 外積 AP x AB は v の方向を向く -
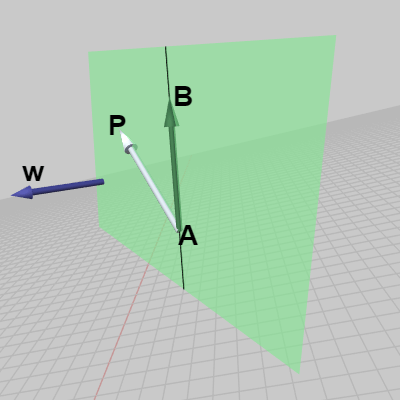 図13 外積 AP x AB は w の方向を向く
図13 外積 AP x AB は w の方向を向く
より詳しくは、上の状況では平面上の点 P が黒い線分よりも右側にある場合には外積 \overrightarrow{AP} \times \overrightarrow{AB} の方向は \boldsymbol{\mathsf{v}} の方向になり、点 P が線分よりも左側にある場合には \boldsymbol{\mathsf{w}} の方向になるのである。
状況を簡単にするために考える平面をXY平面とし、XY平面の y軸上にベクトル \overrightarrow{AB} が置かれているものとしよう (図14)。この場合には図に示されるように点 P が y軸より右側にあるとき、外積 \overrightarrow{AP} \times \overrightarrow{AB} の方向はここでも同様に左手の親指を \overrightarrow{AP} に、人差し指を \overrightarrow{AB} に合わせたときの中指の指す方向であるから、この場合には z軸プラス方向となる。点 P が y軸よりも左側にある場合には \overrightarrow{AP} \times \overrightarrow{AB} の方向は z軸マイナス方向になる(図15)。


このことを実際に外積を計算して確認してみよう。この例では \overrightarrow{AB}、\overrightarrow{AP} はいずれもXY平面上のベクトルであり、いずれも z成分は 0 である。したがって、\overrightarrow{AP} = (a_x, a_y, 0)、\overrightarrow{AB} = (b_x, b_y, 0) とすれば、\overrightarrow{AP} \times \overrightarrow{AB} は
\overrightarrow{AP} \times \overrightarrow{AB}\ =\ (a_y\!\cdot\!0 - 0\!\cdot\!b_y,\ 0\!\cdot\!b_x - a_x\!\cdot\!0,\ a_xb_y - a_yb_x)\ =\ (0,\ 0,\ a_xb_y - a_yb_x)
となり、その方向は z軸プラス方向、マイナス方向のいずれかである (点 P の位置による)。つまり、上記のようにXY平面がある直線によって分断されているとき、XY平面上の点 P がその直線のどちら側にあるかを調べるには直線上のベクトル \overrightarrow{AB} と \overrightarrow{AP} との外積を計算し、その z成分を調べればよいのである。そして、(XY平面上の)三角形の内外判定ではこの z成分の計算 a_xb_y - a_yb_x を特別に Edge Function と呼ぶ。
XY平面上において、ある点が三角形に含まれるかどうかは、この Edge Function を用いて以下のように行われる。
点 P が三角形 ABC に含まれていたとしよう (図16)。このとき、図17のようにベクトル \overrightarrow{AP} と \overrightarrow{AB} の外積 \overrightarrow{AP} \times \overrightarrow{AB} を考えれば、左手の親指を \overrightarrow{AP} に、人差し指を \overrightarrow{AB} に合わせると中指は z軸プラス方向を指す。すなわち、\overrightarrow{AP} \times \overrightarrow{AB} は z軸プラス方向を指す。同様に、残りの2つの辺との外積 \overrightarrow{BP} \times \overrightarrow{BC}、\overrightarrow{CP} \times \overrightarrow{CA} の場合も左手の中指は z軸プラス方向を指す。
つまり、点 P が三角形 ABC に含まれる場合には、三角形の各辺との外積 \overrightarrow{AP} \times \overrightarrow{AB}、\overrightarrow{BP} \times \overrightarrow{BC}、\overrightarrow{CP} \times \overrightarrow{CA} はいずれも z軸プラス方向を指すのである。これは言い換えれば、点 P が三角形 ABC に含まれる場合にはこれらの Edge Function がいずれもプラスの値になるということである。
-
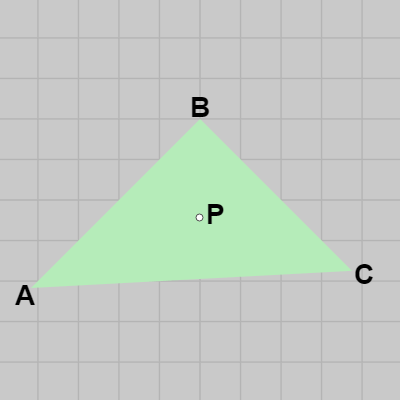 図16 XY平面上の三角形ABCと点P
図16 XY平面上の三角形ABCと点P -
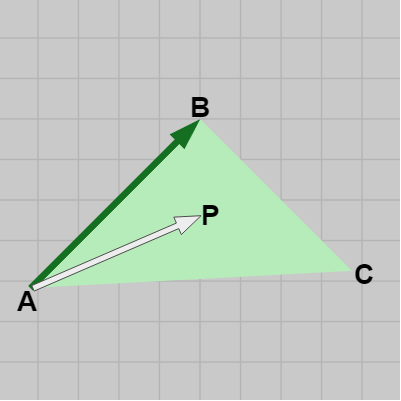 図17 左手の親指をAPに、人差し指をABに合わせたとき、中指は z軸プラス方向を指す
図17 左手の親指をAPに、人差し指をABに合わせたとき、中指は z軸プラス方向を指す -
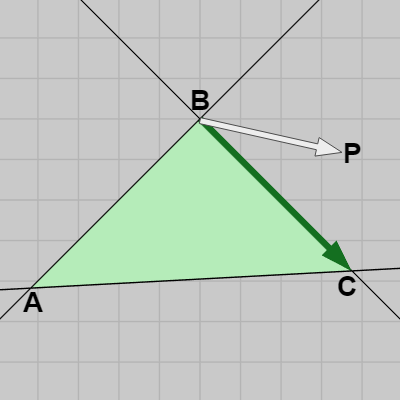 図18 左手の親指をBPに、人差し指をBCに合わせたとき、中指は z軸マイナス方向を指す
図18 左手の親指をBPに、人差し指をBCに合わせたとき、中指は z軸マイナス方向を指す
逆に、点 P が三角形の外側にある場合には少なくとも1つの辺との Edge Function がマイナスになる。例えば、図18の場合 \overrightarrow{BP} \times \overrightarrow{BC} がマイナスになる。
したがって、ある点が三角形に含まれるかどうかを調べるには3つの辺との Edge Function の正負を調べればよいのである (Edge Function が 0 である場合には三角形のいずれかの辺を含む直線上に点があることを意味する)。
以下のメソッド CollisionTest_Point_Triangle(..) はXY平面上において、点 P が三角形 ABC に含まれるかを調べるものであり、上で述べてきたことを実装したものである (引数には各点の座標をセットする)。
- bool CollisionTest_Point_Triangle(Vector2 P, Vector2 A, Vector2 B, Vector2 C)
- {
- // AP x AB
- Vector2 a = (P - A);
- Vector2 b = (B - A);
- if (a.x * b.y - a.y * b.x < 0.0f) { return false; }
- // BP x BC
- a = (P - B);
- b = (C - B);
- if (a.x * b.y - a.y * b.x < 0.0f) { return false; }
- // CP x CA
- a = (P - C);
- b = (A - C);
- if (a.x * b.y - a.y * b.x < 0.0f) { return false; }
- return true;
- }
3つの辺との Edge Function が行われるが、3つともプラスである場合のみ点 P が三角形 ABC に含まれると判定される。1つでもマイナスである場合には三角形に含まれていないと判定され、その場で false が返される。
E) 三角形同士の衝突判定
上で述べた三角形の内外判定と同様に、ベクトルの外積を応用して平面上における三角形同士の衝突判定を行うことができる (以下の解説では2つの三角形がXY平面上にあることを前提としている)。まずは解説の便宜のためいくつかの用語の定義から始める。
下図では三角形 ABC の他にその各辺を延長した直線が表示されているが、辺 AB を含む直線の進行方向を \overrightarrow{AB} とするとき、この進行方向に関して直線の右側を「辺 AB の内側」と呼ぶことにする。同様にこの進行方向に関して直線の左側を「辺 AB の外側」と呼ぶことにする (内側は三角形を含む側であり、外側は三角形を含まない)。
辺 BC、辺 CA の場合も同様である。「辺 BC の内側」であれば \overrightarrow{BC} を進行方向とするとき、辺 BC を含む直線の右側のことであり、「辺 CA の外側」であれば \overrightarrow{CA} を進行方向とするとき、辺 CA を含む直線の左側のことである。

また上で見たようにベクトルの外積の大きさは2つのベクトルによって作られる平行四辺形の面積に等しいのであった。例えば下図20の場合は |\overrightarrow{AB}\times \overrightarrow{AC}| は2つのベクトル \overrightarrow{AB}、\overrightarrow{AC} によって作られる平行四辺形の面積を表す。
もし \overrightarrow{AB}、\overrightarrow{AC} がXY平面上にある場合には上記の内外判定で示したようにその外積は\overrightarrow{AB} \times \overrightarrow{AC} = (0,\ 0,\ z) の形になり、z の符号は2つのベクトルの位置関係によって決まるのであった (\overrightarrow{AB} が \overrightarrow{AC} よりも右にあれば z はプラスであり左であればマイナスになる)。


ここで \Delta(\overrightarrow{AB}\times \overrightarrow{AC}) = z/2 と定める。このとき、\Delta(\overrightarrow{AB}\times \overrightarrow{AC}) は2つのベクトル \overrightarrow{AB}、\overrightarrow{AC} によって作られる三角形 ABC の面積を表すことになるが、注意すべきは必ずしも符号はプラスになるとは限らないという点である。例えば上図21の場合 \Delta(\overrightarrow{AB}\times \overrightarrow{AC}) は符号はマイナスであり (\overrightarrow{AB} に左手の親指を置き、\overrightarrow{AC} に左手の人差し指を置くと中指は z軸マイナス方向を指す)、正確にいえばその絶対値が三角形 ABC の面積に相当する。
三角形同士の衝突判定では、両者が衝突していない場合における次の性質を利用する。
「2つの三角形が衝突していない場合(重なりがない場合)、一方の三角形の頂点はすべて、もう一方の三角形の少なくとも1つの辺の外側にある」
例えば以下は衝突していない2つのケースであるが下左図では三角形 DEF の頂点はすべて辺 BC の外側にあり、下右図の場合は三角形 ABC の頂点はすべて辺 DE の外側にある。


したがって三角形同士の衝突判定では一方の三角形のすべての頂点が、もう一方の三角形のいずれか1つの辺の外側にあるかどうかを調べることに帰着するのである。
三角形 DEF が三角形 ABC のいずれか1つの辺の外側にあるかを調べる場合であれば、まず三角形 DEF の3つの頂点が辺 AB の外側にあるかを調べる。(XY平面上において)ある点がある直線のどちらの側にあるかを調べるには上でも見たように外積(Edge Function)を1回行えばよいから、3つの頂点が辺 AB の外側にあるかを調べるには外積を3回行えばよい。
3つの頂点すべてが辺 AB の外側にない場合には、次に辺 BC の外側にあるかを調べる。辺 BC の外側でもない場合には、最後に辺 CA の外側かどうかを調べればよい。すなわち、一方の三角形のすべての頂点がもう一方の三角形のいずれか1つの辺の外側にあるかどうかを調べるには、多くとも外積を9回行えばよいのである。
しかし以下に示す方法をとることで外積の計算回数を9回から7回に減らすことができる。
三角形 ABC に対して点 D が下図24に示される位置にあったとする。この位置は辺 AB 及び辺 CA の内側であるから、\Delta(\overrightarrow{AD}\times \overrightarrow{AB}) > 0 かつ \Delta(\overrightarrow{AC}\times \overrightarrow{AD}) > 0 である。
点 D が辺 BC の内側か外側を調べるには辺 BC との外積を計算すればよいが、もしすでに \Delta(\overrightarrow{AD}\times \overrightarrow{AB})、\Delta(\overrightarrow{AC}\times \overrightarrow{AD}) がわかっているのであれば、\Delta(\overrightarrow{AC}\times \overrightarrow{AB}) を計算することで D が辺 BC の内側か外側かを判定できる (下図の場合には \Delta(\overrightarrow{AC}\times \overrightarrow{AB}) の符号もプラスである)。


実際、上図24の場合では \Delta(\overrightarrow{AD}\times \overrightarrow{AB}) は三角形 ABD の面積、\Delta(\overrightarrow{AC}\times \overrightarrow{AD}) は三角形 ACD の面積、\Delta(\overrightarrow{AC}\times \overrightarrow{AB}) は三角形 ABC の面積であるが、点 D が図の水色の領域にある場合どの位置にあっても三角形 ABD と三角形 ACD の面積の和は三角形 ABC の面積よりも大きい。
すなわち、上で定めた記号を用いれば\Delta(\overrightarrow{AD}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AD}) > \Delta(\overrightarrow{AC}\times \overrightarrow{AB}) \tag{1} である。
つまり D が図の水色の領域にある場合どの位置であっても (1) が成り立つのである。そしてこれは水色の領域だけでなく、D が辺 BC の外側にあればどの位置であっても成り立つ。例えば D が上図25の右側の紫の領域にあったとしよう。このとき \Delta(\overrightarrow{AC}\times \overrightarrow{AD}) < 0 なので \Delta(\overrightarrow{AD}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AD}) は三角形 ABD の面積から三角形 ACD の面積を引いた値になるが、図から明らかなようにそれでも三角形 ABC の面積よりも大きい (点 D が左側の紫の領域にあっても同様である)。つまり D が辺 BC の外側にある場合、その位置がどこであっても上記の (1) が成り立つのである。
点 D が辺 BC の内側にある場合には上記の不等号は逆転する。すなわち点 D が辺 BC の内側にある場合には\Delta(\overrightarrow{AD}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AD}) < \Delta(\overrightarrow{AC}\times \overrightarrow{AB}) \tag{2} となる。

今の例のようにある1つの頂点がある辺のどちら側にあるかを調べるだけならば、この方法は特に効果的ではないが1つではなく3つの頂点の場合にはこの方法が効果を発揮する。
例えば三角形 ABC に対し三角形 DEF が図の位置に置かれていたとしよう。そして先程と同様に頂点 D、E、F が辺 AB、辺 CA のどちら側にあるかの計算がすでに行われていたとする。すなわち D については \Delta(\overrightarrow{AD}\times \overrightarrow{AB}) 及び \Delta(\overrightarrow{AC}\times \overrightarrow{AD})、E については \Delta(\overrightarrow{AE}\times \overrightarrow{AB}) 及び \Delta(\overrightarrow{AC}\times \overrightarrow{AE})、F については \Delta(\overrightarrow{AF}\times \overrightarrow{AB}) 及び \Delta(\overrightarrow{AC}\times \overrightarrow{AF}) の計算が行われていたとする。

ここで D、E、F がそれぞれ辺 BC のどちら側にあるかを調べるには、上で行ったように \Delta(\overrightarrow{AC}\times \overrightarrow{AB}) だけを計算すればよい (3つの頂点それぞれと辺 BC との外積を計算する必要はない)。そして上記 (1)、(2) と同じく \Delta(\overrightarrow{AD}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AD})、 \Delta(\overrightarrow{AE}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AE})、 \Delta(\overrightarrow{AF}\times \overrightarrow{AB}) + \Delta(\overrightarrow{AC}\times \overrightarrow{AF}) のそれぞれと \Delta(\overrightarrow{AC}\times \overrightarrow{AB}) との大小を比較すれば D、E、F が辺 BC のどちら側にあるのかがわかる。つまり外積は多くとも7回で済むわけである。
ただし注意すべきは一方の三角形の3つの頂点がすべて、もう一方の三角形のいずれかの辺の外側にある ということが成り立たない場合でも、その時点で両者が衝突していると判定することはできない。逆のケースを調べなければならないためである。例えば上図23の場合、三角形 DEF の頂点がすべて三角形 ABC のいずれかの辺の外側にあるということは成り立たないが、この場合にはさらに三角形 ABC の頂点がすべて三角形の DEF のいずれかの辺の外側にあるかを調べなければならない。
以上が外積を応用した三角形同士の衝突判定のアルゴリズムである。この手続きをプログラムにすることは容易であるから詳しい実装については読者の課題とする (下記 Code3)。
では本節に関連したプログラムを作成する。
# Code1
Unityで外積を求める場合には次のメソッドが用意されている。Vecotr3.Cross(Vector3 v1, Vector3 v2)
: 引数に指定される2つのベクトルの外積 \boldsymbol{\mathsf{v_1}}\times\boldsymbol{\mathsf{v_2}} を計算する Vector3構造体のstaticメソッドで、戻り値は Vector3型 (引数の2つのベクトルの双方と直交するベクトルが返される ; 引数の順序に注意)。[Code1] (実行結果 図28)
- Vector3 a = new Vector3(0, 0, 2);
- Vector3 b = new Vector3(3, 0, 1);
- Vector3 c = Vector3.Cross(a, b); // a x b
- Debug.Log(c);
- c = Vector3.Cross(b, a); // b x a
- Debug.Log(c);

実行結果(図28)に示されるように、外積の順序を入れ替えると算出されるベクトルの向きが逆になる。
# Code2
次に、図29に示される\triangle ABCの法線ベクトルを求めてみよう。各点の座標は A = (3.92,\ 4.35, -4.31)、B = (0.52,\ 4.0, -7.95)、C = (0,\ 4, -5) である。


[Code2] (実行結果 31)
- Vector3 A = new Vector3(3.92f, 4.35f, -4.31f);
- Vector3 B = new Vector3(0.52f, 4.0f, -7.95f);
- Vector3 C = new Vector3(0.0f, 4.0f, -5.0f);
- Vector3 a = A - C;
- Vector3 b = B - C;
- Vector3 n = Vector3.Cross(a, b).normalized;
- Debug.Log("(" + n.x + ", " + n.y + ", " + n.z + ")");

実行結果(図31)は、外積 n の正規化された値である (ほぼy軸に平行である)。
# Code3
以下2つのプログラムは読者用の課題である。まずは上で述べた三角形同士の衝突判定の実装である。
今回のプログラムでは開始時点で以下に示されるように2つの三角形 ABC、DEF が適当な位置に置かれている (三角形の各頂点の並び方はいずれも時計回り、いわゆる clockwise order である)。

プログラムを以下に示す。
[Code3]
- ObjectMotion();
- Vector2[] vtsABC = GetGreenVerts();
- Vector2[] vtsDEF = GetBlueVerts();
- bool bColl = CollisionTest_Triangle_Triangle(vtsABC, vtsDEF);
- Hit(bColl);
6行目の衝突判定用メソッド CollisionTest_Triangle_Triangle(..) は以下に示されるように具体的な処理が記述されていないので、このメソッド内に三角形同士の衝突判定を実装することがここでの課題である。
[CollisionTest_Triangle_Triangle(..)]
- bool CollisionTest_Triangle_Triangle(Vector2[] vtsABC, Vector2[] vtsDEF)
- {
- // 三角形の頂点の並び方は時計回り
- // vtsABC[0] : A
- // vtsABC[1] : B
- // vtsABC[2] : C
- // vtsDEF[0] : D
- // vtsDEF[1] : E
- // vtsDEF[2] : F
- return false;
- }
なおプログラム実行中は次のキー操作によって2つの三角形を動かすことができる。
H、J、K、L : 三角形 DEF を縦横に移動させる。
Y、U、I、O : 三角形 DEF の頂点 E を縦横に移動させる (+Shift の場合は頂点 F が移動する)。
R : 三角形 DEF の回転 (+Shift の場合は逆回転)。
Q : 三角形 ABC の回転 (+Shift の場合は逆回転)。
細かい点ではあるが最後に1つ注意しておこう。上の解説から三角形 DEF が三角形 ABC のいずれか1つの辺の外側にあるかどうかのコードは明らかに以下のような形になる。
- ... ... 辺ABに関する計算 ... ...
- if( 3つの頂点が辺ABの外側にあるか ) { return true; }
- ... ... 辺CAに関する計算 ... ...
- if( 3つの頂点が辺CAの外側にあるか ) { return true; }
- ... ... 辺BCに関する計算 ... ...
- if( 3つの頂点が辺BCの外側にあるか ) { return true; }
- return false;
このコードは以下のように書き換えても同じである。
- ... ... 辺ABに関する計算 ... ...
- ... ... 辺CAに関する計算 ... ...
- ... ... 辺BCに関する計算 ... ...
- if( 3つの頂点が辺ABの外側にあるか or
- 3つの頂点が辺CAの外側にあるか or
- 3つの頂点が辺BCの外側にあるか )
- { return true }
- return false;
一見すると上のコードの方が効率的に見えるが、上のコードと下のコードのどちらが速いかは実装に依存する。必ずしも上のコードの方が速いわけではない。むしろ上記の解説をそのまま実装するのであれば下のコードを使った方が速いはずである。
解答例については Sec306_Ans.txt を参照 (このファイルはダウンロードコンテンツ内「txt_ans」フォルダに含まれている。ファイル内には三角形同士の衝突判定として2つの実装 ver1、ver2 が記述されているが、ver1 は上記の解説をそのまま実装したものである。ver2 は ver1 を改良したものであり衝突の頻度が3割以上になる場合には ver2 の方が効率的である (ただし初回実行時のみ ver2 は時間がかかる)。解説が面倒であるため ver2 についてはいつか機会があれば解説する)。
# Code4
三角形同士の衝突判定を用いることで三角形と長方形の衝突判定も簡単に行える。なぜなら長方形は対角線によって2つの三角形に分割されるので、三角形と長方形が衝突しているかどうかは、長方形を構成する2つの三角形のうちのいずれかと衝突しているかを調べればよい。しかし次のように考えればその処理を効率化することができる。
長方形は各辺を引き延ばすことで下図に示されるように、長方形とその周りは9個の領域に分割される。

例えば三角形 PQR の頂点 P が領域 [6] に含まれていたとする。このとき三角形と長方形が衝突しているならば、三角形 PQR がどのような形であっても長方形の左下側の三角形 ABD と必ず衝突している (図36)。すなわち三角形の1つの頂点が領域 [6] にあることがわかっている場合には、長方形の左下側の三角形と衝突しているかどうかを調べればよい。

また点 P が領域 [1] に含まれている場合、両者が衝突しているならば三角形 PQR がどのような形であっても長方形の辺 BC を含む三角形と必ず衝突している (図37)。したがって三角形の1つの頂点が領域 [1] にあることがわかっている場合には長方形の辺 BC を含む三角形 BCD と衝突しているかどうかを調べればよい (もちろん三角形 ABC と衝突しているかを調べても同じである)。

つまり三角形の頂点の1つが上記の9つの領域のうちどの領域に含まれているかがわかれば、長方形を構成する2つの三角形のうちのどちらと衝突判定を行えばよいかが決められるのである。したがって三角形と長方形の衝突判定も結局は三角形同士の衝突判定を1回だけ行えばよいわけである (上の例では対角線 BD によって長方形は分割されているが、三角形の置かれている位置によっては対角線 AC で考えなければならない場合がある)。
プログラムを以下に示す (開始時点では三角形と長方形が適当な位置にそれぞれ置かれている。またCode3と同じく図形の頂点の並び方は時計回りである)。
[Code4]
- ObjectMotion();
- Vector2[] vtsTri = GetTriangleVerts();
- Vector2[] vtsRect = GetRectVerts();
- bool bColl = CollisionTest_Triangle_Rect(vtsTri, vtsRect);
- Hit(bColl);
6行目の衝突判定用メソッド CollisionTest_Triangle_Rect(..) は以下に示されるように具体的な処理が記述されていないので、このメソッド内に三角形と長方形の衝突判定を実装することがここでの課題である (引数の vtsTri、vtsRect は三角形及び長方形の頂点がセットされた配列であり、要素数はそれぞれ 3、4 である)。
[CollisionTest_Triangle_Rect(..)]
- bool CollisionTest_Triangle_Rect(Vector2[] vtsTri, Vector2[] vtsRect)
- {
- // 三角形及び長方形の頂点の並び方は時計回り
- // vtsRect[0] : A
- // vtsRect[1] : B
- // vtsRect[2] : C
- // vtsRect[3] : D
- return false;
- }
プログラム実行中は次のキー操作によって三角形及び長方形を動かすことができる。
H、J、K、L : 三角形を縦横に移動させる。
R : 三角形の回転 (+Shift の場合は逆回転)。
Q : 長方形の回転 (+Shift の場合は逆回転)。
(解答例については Sec306_Ans.txt を参照)
(参考資料)
https://www.scratchapixel.com/lessons/3d-basic-rendering/rasterization-practical-implementation/rasterization-stage.html
https://stackoverflow.com/questions/2778240/detection-of-triangle-collision-in-2d-space
© 2020-2025 Redpoll's 60 (All rights reserved)