Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-1
第3章 3D空間の基礎
$§$3-1 点とベクトル
本章では3D空間においてオブジェクトを運動させる際に必要となる基礎的事項について解説する。ただし始めの部分では2D空間と内容が類似する記述もあるが、そういった部分についても疎かにせず確認のつもりで読み進めてほしい。
なお、以降の図においては赤い軸がx軸、緑色の軸がy軸、青色の軸がz軸であり、それぞれ色の濃いほうがプラス側、色の薄い方がマイナス側を表している。
それぞれの位置は
\[R : \begin{cases} x = 1 \\ y = 2 \\ z = 4 \end{cases}\qquad G : \begin{cases} x = -2 \\ y = 5 \\ z = 2 \end{cases}\qquad B : \begin{cases} x = 3 \\ y = 3 \\ z = -3 \end{cases}\]である。
コンピューターグラフィックスでは点も位置ベクトルというベクトルとして扱われる。例えば、上図の点$R$、$G$、$B$は位置ベクトルとして次のように表される。\[R = \begin{pmatrix}1 \\2 \\4 \end{pmatrix}\qquad G = \begin{pmatrix}-2 \\5 \\2 \end{pmatrix} \qquad B = \begin{pmatrix}3 \\3 \\-3 \end{pmatrix}\] 第1章でも述べたが、講義では基本的に縦並びの列ベクトルを使っていくが、スペース的な問題で文章中や図の中においては横並びの行ベクトルを用いる。
3次元ベクトルの加算、減算は2D空間の場合と同様であり、具体的には次のように定義される。
\begin{align*}\begin{pmatrix}x_{1} \\y_{1} \\z_{1} \end{pmatrix} +\begin{pmatrix}x_{2} \\y_{2} \\z_{2} \end{pmatrix} =\begin{pmatrix}x_{1} + x_{2}\\y_{1} + y_{2}\\z_{1} + z_{2}\end{pmatrix} \\ \\\begin{pmatrix}x_{1} \\y_{1} \\z_{1} \end{pmatrix} -\begin{pmatrix}x_{2} \\y_{2} \\z_{2} \end{pmatrix} =\begin{pmatrix}x_{1} - x_{2}\\y_{1} - y_{2}\\z_{1} - z_{2}\end{pmatrix} \end{align*}
2次元ベクトルと同様に3次元ベクトルも始点と終点を持っており、ベクトル自体は終点から始点を引くことで求められる。以下の図4~6は、3次元ベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{\mathsf{v_3}}$を可視化したものであるが、これらのベクトルを計算をしてみよう。
ベクトル$\boldsymbol{\mathsf{v_1}}$(図4)は始点$(0, 0, 0)$、終点$(4, 3, 2)$であり次のように求められる。\begin{equation} \boldsymbol{\mathsf{v_1}} = \begin{pmatrix}4 \\3 \\2 \end{pmatrix} -\begin{pmatrix}0 \\0 \\0 \end{pmatrix} =\begin{pmatrix}4 \\3 \\2 \end{pmatrix} \end{equation}ベクトル$\boldsymbol{\mathsf{v_2}}$(図5) : 始点$(2, 4, -2)$、終点$(5, 1, -6)$\begin{equation} \boldsymbol{\mathsf{v_2}} = \begin{pmatrix}5 \\1 \\-6 \end{pmatrix} -\begin{pmatrix}2 \\4 \\-2 \end{pmatrix} =\begin{pmatrix}3 \\-3 \\-4 \end{pmatrix} \end{equation}ベクトル$\boldsymbol{\mathsf{v_3}}$(図6) : 始点$(-3, 1, -2)$、終点$(3, 2, 0)$\begin{equation} \boldsymbol{\mathsf{v_3}} = \begin{pmatrix}3 \\2 \\0 \end{pmatrix} -\begin{pmatrix}-3 \\1 \\-2 \end{pmatrix} =\begin{pmatrix}6 \\1 \\2 \end{pmatrix} \end{equation}
なお、第1章でも述べたがこの講義では図の中で点(位置)を表す数値については黒色のフォントを使用し、ベクトルを表す数値については緑色のフォントを使用している。例えば、図5のベクトル$\boldsymbol{\mathsf{v_2}}$は $(3, -3, -4)$ であるが、この数値はベクトルを表すので緑色のフォントを使用し、$\boldsymbol{\mathsf{v_2}}$の始点 $(2, 4, -2)$、終点 $(5, 1, -6)$ は点(位置)を表すので黒色のフォントを使用している。
始点から終点へ向かう方向をベクトルの向き(Direction)といい、始点から終点までの距離をベクトルの大きさ(Magnitude)(あるいは長さ)という。3次元ベクトルの大きさは次のように計算される。
ベクトル $\boldsymbol{\mathsf{v}} = (x, y, z)$ の大きさ $|\boldsymbol{\mathsf{v}}|$ ($|\ |$ はベクトルの大きさを表す時に用いる記号である)
\begin{equation} |\boldsymbol{\mathsf{v}}| = \sqrt{x^2 + y^2 + z^2}\end{equation}
では実際に上図4~6の各ベクトルの大きさを計算してみよう。
向きも大きさも等しいベクトルは、始点がどこにあろうとも、それらは皆ベクトルとしては同じものである。次の3つのベクトルを例に取ろう。
これらのベクトルは始点と終点の位置が違うだけで、以下に示すように全て同じベクトルである。\begin{align*}&\boldsymbol{\mathsf{v_a}} = \begin{pmatrix}-2 \\4 \\2 \end{pmatrix} -\begin{pmatrix}0 \\0 \\0 \end{pmatrix} =\begin{pmatrix}-2 \\4 \\2 \end{pmatrix} \\ \\&\boldsymbol{\mathsf{v_b}} = \begin{pmatrix}-5 \\6 \\-2 \end{pmatrix} -\begin{pmatrix}-3 \\2 \\-4 \end{pmatrix} =\begin{pmatrix}-2 \\4 \\2 \end{pmatrix} \\ \\&\boldsymbol{\mathsf{v_c}} = \begin{pmatrix}0 \\5 \\-1 \end{pmatrix} -\begin{pmatrix}2 \\1 \\-3 \end{pmatrix} =\begin{pmatrix}-2 \\4 \\2 \end{pmatrix} \end{align*}
\begin{align*}&\boldsymbol{\mathsf{v}} = Q - P = \begin{pmatrix}5 \\4 \\1 \end{pmatrix} -\begin{pmatrix}1 \\3 \\-1 \end{pmatrix}=\begin{pmatrix}4 \\1 \\2 \end{pmatrix} \\ \\ &|\boldsymbol{\mathsf{v}}| = \sqrt{4^2 + 1^2 + 2^2} = \sqrt{21} = 4.5825\ldots \quad\risingdotseq 4.58 \end{align*}

図10 点P、Q 
図11 点P、Qを結ぶベクトルv
実際、
このことは、ベクトルを$2$倍、$3$倍したときの大きさは、もとのベクトルの大きさの$2$倍、$3$倍になることを意味する。
例えば、図12に示されるベクトル$\boldsymbol{\mathsf{v}} = (a, b, c)$ は大きさ$2$のベクトルであるが、このベクトルを$4$倍したベクトル $4\boldsymbol{\mathsf{v}} = (4a, 4b, 4c)$ (図13)、及び $-4$倍したベクトル $-4\boldsymbol{\mathsf{v}} = (-4a, -4b, -4c)$ (図14)の大きさは以下の計算で示されるように、ベクトル$\boldsymbol{\mathsf{v}}$の大きさの$4$倍の$8$になる (以下の図においては、すべて始点は $(0, 0, 0)$ である ; 図12、図13はXZ平面を見下ろす位置から見たときの様子であるが、図14はXZ平面の下側から見たときの様子である)。
$\boldsymbol{\mathsf{v}}$の大きさ$|\boldsymbol{\mathsf{v}}|$は、\[|\boldsymbol{\mathsf{v}}| = \sqrt{a^2 + b^2 + c^2} = 2 \]であるから、$4\boldsymbol{\mathsf{v}}$、$-4\boldsymbol{\mathsf{v}}$ の大きさはそれぞれ、
実数倍されたベクトルの加算、減算についても通常のベクトルの場合と同様である。
(計算例)
ここからは、本節で述べた内容に関してのプログラムを作成する。
Vector4構造体は Vector3構造体を同次座標化する場合に必要なもので、主に行列演算のときに使用される。
まずは、本節の始めに求めたベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{\mathsf{v_3}}$をプログラムにおいて求め、それらの大きさを表示する。
[Code1] (実行結果 図15)
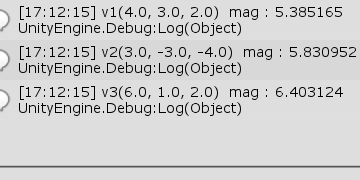
図15 Code1 実行結果 あるベクトルの大きさは Vector3のプロパティである magnitude から取得できる。プログラムで記述されているように v1.magnitude でアクセスすればよい。
3D空間上の2点間の距離を求める場合でも、その2点をベクトルの始点、終点とみなして、そのベクトルの大きさを計算すればよい。例えば、このプログラムでは v3の大きさは約$6.40$であるが、それはベクトル v3の始点$(-3, 1, -2)$と終点$(3, 2, 0)$の間の距離が約$6.40$であることを意味している (なお、1行目の Vector3.zero はVector3構造体のstaticなプロパティで $(0, 0, 0)$ を表すものである)。
[Code2] (実行結果 図16)

図16 Code2 実行結果 最初の2つの計算は上で行ったものであり、後半の2つの計算は小数値による適当な計算である。
後半2つの出力の際に A.x、A.y、A.z のようにして各座標を直接出力しているのは、Debug.Log(A) とした場合は小数第2位が四捨五入されて小数第1位までしか表示されなくなるためである。
A) 点
点は3D空間の位置を示すために使われる。以下の図1~3に3D空間の点$R$、$G$、$B$を示す。なお、以降の図においては赤い軸がx軸、緑色の軸がy軸、青色の軸がz軸であり、それぞれ色の濃いほうがプラス側、色の薄い方がマイナス側を表している。
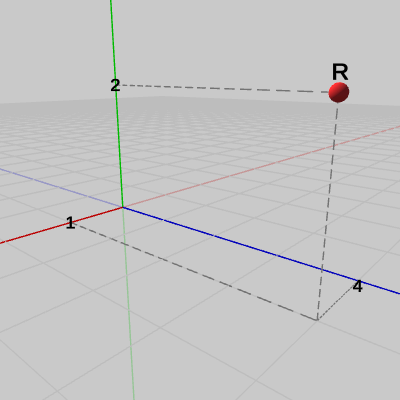 図1 点R
図1 点R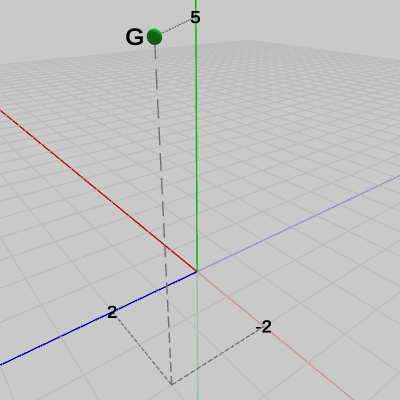 図2 点G
図2 点G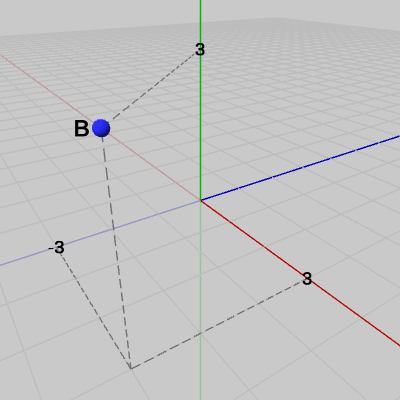 図3 点B
図3 点B
それぞれの位置は
\[R : \begin{cases} x = 1 \\ y = 2 \\ z = 4 \end{cases}\qquad G : \begin{cases} x = -2 \\ y = 5 \\ z = 2 \end{cases}\qquad B : \begin{cases} x = 3 \\ y = 3 \\ z = -3 \end{cases}\]である。
B) ベクトル
3D空間で主に使われる3次元ベクトルとは、3つの実数値の組からなり次のように書き表される。\begin{equation*}\begin{pmatrix}5 \\1 \\2 \end{pmatrix} \qquad\begin{pmatrix}x \\y \\z \end{pmatrix} \qquad\begin{pmatrix}0.98 \quad -0.32 \quad 1.112\end{pmatrix} \qquad\begin{pmatrix}v_x \quad v_y \quad v_z \end{pmatrix} \end{equation*}
要素が縦に並んだベクトル(左側2つ)を列ベクトル、要素が横に並んだベクトル(右側2つ)を行ベクトルという。列ベクトルでは上の要素がx座標、中央の要素がy座標、下の要素がz座標であり、行ベクトルでは左の要素がx座標、中央の要素がy座標、右の要素がz座標である。コンピューターグラフィックスでは点も位置ベクトルというベクトルとして扱われる。例えば、上図の点$R$、$G$、$B$は位置ベクトルとして次のように表される。\[R = \begin{pmatrix}1 \\2 \\4 \end{pmatrix}\qquad G = \begin{pmatrix}-2 \\5 \\2 \end{pmatrix} \qquad B = \begin{pmatrix}3 \\3 \\-3 \end{pmatrix}\] 第1章でも述べたが、講義では基本的に縦並びの列ベクトルを使っていくが、スペース的な問題で文章中や図の中においては横並びの行ベクトルを用いる。
3次元ベクトルの加算、減算は2D空間の場合と同様であり、具体的には次のように定義される。
\begin{align*}\begin{pmatrix}x_{1} \\y_{1} \\z_{1} \end{pmatrix} +\begin{pmatrix}x_{2} \\y_{2} \\z_{2} \end{pmatrix} =\begin{pmatrix}x_{1} + x_{2}\\y_{1} + y_{2}\\z_{1} + z_{2}\end{pmatrix} \\ \\\begin{pmatrix}x_{1} \\y_{1} \\z_{1} \end{pmatrix} -\begin{pmatrix}x_{2} \\y_{2} \\z_{2} \end{pmatrix} =\begin{pmatrix}x_{1} - x_{2}\\y_{1} - y_{2}\\z_{1} - z_{2}\end{pmatrix} \end{align*}
2次元ベクトルと同様に3次元ベクトルも始点と終点を持っており、ベクトル自体は終点から始点を引くことで求められる。以下の図4~6は、3次元ベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{\mathsf{v_3}}$を可視化したものであるが、これらのベクトルを計算をしてみよう。
-
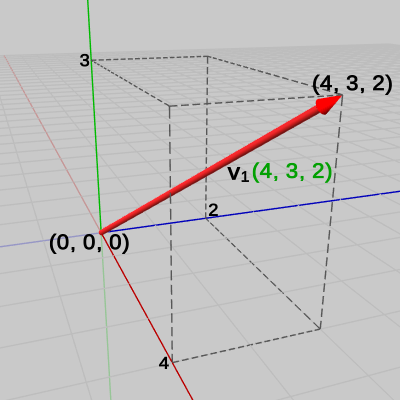 図4 ベクトルv1
図4 ベクトルv1 -
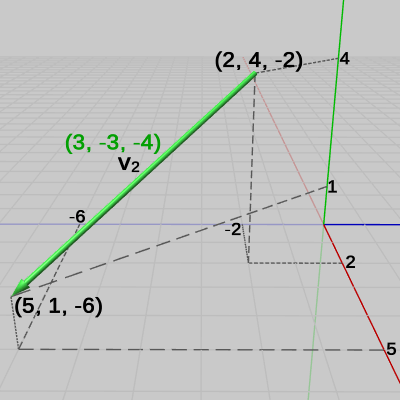 図5 ベクトルv2
図5 ベクトルv2 -
 図6 ベクトルv3
図6 ベクトルv3
ベクトル$\boldsymbol{\mathsf{v_1}}$(図4)は始点$(0, 0, 0)$、終点$(4, 3, 2)$であり次のように求められる。\begin{equation} \boldsymbol{\mathsf{v_1}} = \begin{pmatrix}4 \\3 \\2 \end{pmatrix} -\begin{pmatrix}0 \\0 \\0 \end{pmatrix} =\begin{pmatrix}4 \\3 \\2 \end{pmatrix} \end{equation}ベクトル$\boldsymbol{\mathsf{v_2}}$(図5) : 始点$(2, 4, -2)$、終点$(5, 1, -6)$\begin{equation} \boldsymbol{\mathsf{v_2}} = \begin{pmatrix}5 \\1 \\-6 \end{pmatrix} -\begin{pmatrix}2 \\4 \\-2 \end{pmatrix} =\begin{pmatrix}3 \\-3 \\-4 \end{pmatrix} \end{equation}ベクトル$\boldsymbol{\mathsf{v_3}}$(図6) : 始点$(-3, 1, -2)$、終点$(3, 2, 0)$\begin{equation} \boldsymbol{\mathsf{v_3}} = \begin{pmatrix}3 \\2 \\0 \end{pmatrix} -\begin{pmatrix}-3 \\1 \\-2 \end{pmatrix} =\begin{pmatrix}6 \\1 \\2 \end{pmatrix} \end{equation}
なお、第1章でも述べたがこの講義では図の中で点(位置)を表す数値については黒色のフォントを使用し、ベクトルを表す数値については緑色のフォントを使用している。例えば、図5のベクトル$\boldsymbol{\mathsf{v_2}}$は $(3, -3, -4)$ であるが、この数値はベクトルを表すので緑色のフォントを使用し、$\boldsymbol{\mathsf{v_2}}$の始点 $(2, 4, -2)$、終点 $(5, 1, -6)$ は点(位置)を表すので黒色のフォントを使用している。
始点から終点へ向かう方向をベクトルの向き(Direction)といい、始点から終点までの距離をベクトルの大きさ(Magnitude)(あるいは長さ)という。3次元ベクトルの大きさは次のように計算される。
ベクトル $\boldsymbol{\mathsf{v}} = (x, y, z)$ の大きさ $|\boldsymbol{\mathsf{v}}|$ ($|\ |$ はベクトルの大きさを表す時に用いる記号である)
\begin{equation} |\boldsymbol{\mathsf{v}}| = \sqrt{x^2 + y^2 + z^2}\end{equation}
では実際に上図4~6の各ベクトルの大きさを計算してみよう。
\begin{align*} &|\boldsymbol{\mathsf{v_1}}| = \sqrt{4^2 + 3^2 + 2^2} = \sqrt{29} = 5.3851\ldots \quad\risingdotseq 5.39 \\ &|\boldsymbol{\mathsf{v_2}}| = \sqrt{3^2 + (-3)^2 + (-4)^2} = \sqrt{34} = 5.8309\ldots \quad\risingdotseq 5.83 \\ &|\boldsymbol{\mathsf{v_3}}| = \sqrt{6^2 + 1^2 + 2^2} = \sqrt{41} = 6.4031\ldots \quad\risingdotseq 6.40\end{align*}
向きも大きさも等しいベクトルは、始点がどこにあろうとも、それらは皆ベクトルとしては同じものである。次の3つのベクトルを例に取ろう。
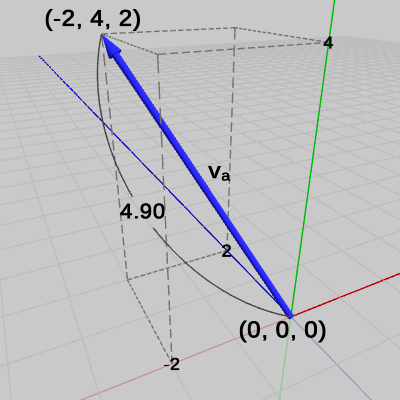 図7 ベクトルva
図7 ベクトルva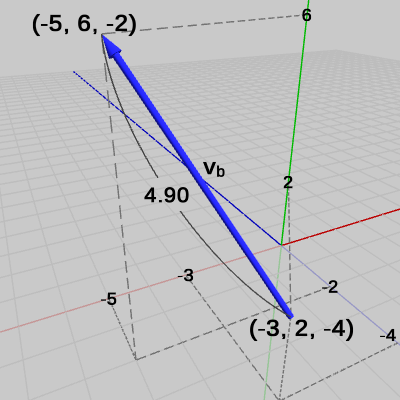 図8 ベクトルvb
図8 ベクトルvb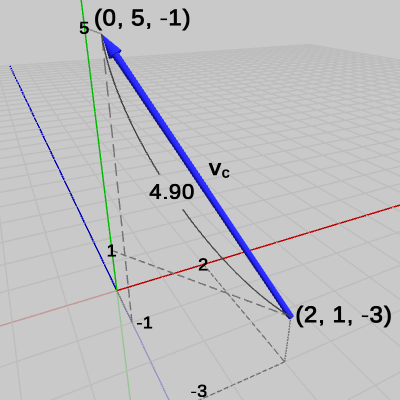 図9 ベクトルvc
図9 ベクトルvc
これらのベクトルは始点と終点の位置が違うだけで、以下に示すように全て同じベクトルである。\begin{align*}&\boldsymbol{\mathsf{v_a}} = \begin{pmatrix}-2 \\4 \\2 \end{pmatrix} -\begin{pmatrix}0 \\0 \\0 \end{pmatrix} =\begin{pmatrix}-2 \\4 \\2 \end{pmatrix} \\ \\&\boldsymbol{\mathsf{v_b}} = \begin{pmatrix}-5 \\6 \\-2 \end{pmatrix} -\begin{pmatrix}-3 \\2 \\-4 \end{pmatrix} =\begin{pmatrix}-2 \\4 \\2 \end{pmatrix} \\ \\&\boldsymbol{\mathsf{v_c}} = \begin{pmatrix}0 \\5 \\-1 \end{pmatrix} -\begin{pmatrix}2 \\1 \\-3 \end{pmatrix} =\begin{pmatrix}-2 \\4 \\2 \end{pmatrix} \end{align*}
C) 2点間の距離
2D空間の場合と同じく、3D空間においても2点間の距離は、それらの点を結ぶベクトルの大きさに等しい。例えば図10の点$P = (1, 3, -1)$、点$Q = (5, 4, 1)$の間の距離は、点$P$を始点、点$Q$を終点とするベクトルを$\boldsymbol{\mathsf{v}}$とすれば次のように計算される(図11)。\begin{align*}&\boldsymbol{\mathsf{v}} = Q - P = \begin{pmatrix}5 \\4 \\1 \end{pmatrix} -\begin{pmatrix}1 \\3 \\-1 \end{pmatrix}=\begin{pmatrix}4 \\1 \\2 \end{pmatrix} \\ \\ &|\boldsymbol{\mathsf{v}}| = \sqrt{4^2 + 1^2 + 2^2} = \sqrt{21} = 4.5825\ldots \quad\risingdotseq 4.58 \end{align*}


D) ベクトルの実数倍
2次元ベクトルの場合と同様に、あるベクトル$\boldsymbol{\mathsf{v}} = (x, y, z)$に実数$s$を掛けたときのベクトル$s\boldsymbol{\mathsf{v}}$は、次のように表される。\[ s\boldsymbol{\mathsf{v}} = s\begin{pmatrix}x \\y \\ z\end{pmatrix} =\begin{pmatrix}sx \\sy \\sz\end{pmatrix} \]そして、このときのベクトル$s\boldsymbol{\mathsf{v}}$の大きさ$|s\boldsymbol{\mathsf{v}}|$は、ベクトル$\boldsymbol{\mathsf{v}}$の大きさ$|\boldsymbol{\mathsf{v}}|$の $|s|$倍である。すなわち、ベクトル$s\boldsymbol{\mathsf{v}}$の大きさは $|s||\boldsymbol{\mathsf{v}}|$である。実際、
\begin{align*}|s\boldsymbol{\mathsf{v}}| = \sqrt{(sx)^2 + (sy)^2 + (sz)^2} = \sqrt{s^2(x^2 + y^2 + z^2)} = |s|\sqrt{x^2 + y^2 + z^2} = |s||\boldsymbol{\mathsf{v}}|\end{align*}
となる。このことは、ベクトルを$2$倍、$3$倍したときの大きさは、もとのベクトルの大きさの$2$倍、$3$倍になることを意味する。
例えば、図12に示されるベクトル$\boldsymbol{\mathsf{v}} = (a, b, c)$ は大きさ$2$のベクトルであるが、このベクトルを$4$倍したベクトル $4\boldsymbol{\mathsf{v}} = (4a, 4b, 4c)$ (図13)、及び $-4$倍したベクトル $-4\boldsymbol{\mathsf{v}} = (-4a, -4b, -4c)$ (図14)の大きさは以下の計算で示されるように、ベクトル$\boldsymbol{\mathsf{v}}$の大きさの$4$倍の$8$になる (以下の図においては、すべて始点は $(0, 0, 0)$ である ; 図12、図13はXZ平面を見下ろす位置から見たときの様子であるが、図14はXZ平面の下側から見たときの様子である)。
-
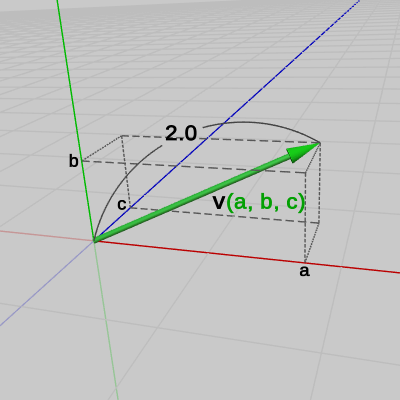 図12 ベクトルv = (a, b, c)
図12 ベクトルv = (a, b, c) -
 図13 vを4倍したベクトル4v = (4a, 4b, 4c)
図13 vを4倍したベクトル4v = (4a, 4b, 4c) -
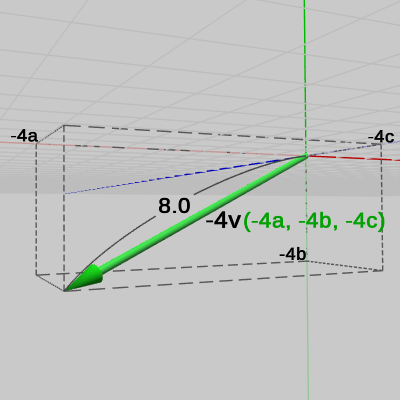 図14 vを-4倍したベクトル-4v = (-4a, -4b, -4c)
図14 vを-4倍したベクトル-4v = (-4a, -4b, -4c)
$\boldsymbol{\mathsf{v}}$の大きさ$|\boldsymbol{\mathsf{v}}|$は、\[|\boldsymbol{\mathsf{v}}| = \sqrt{a^2 + b^2 + c^2} = 2 \]であるから、$4\boldsymbol{\mathsf{v}}$、$-4\boldsymbol{\mathsf{v}}$ の大きさはそれぞれ、
\begin{align*}|4\boldsymbol{\mathsf{v}}| &= \sqrt{(4a)^2 + (4b)^2 + (4c)^2} = \sqrt{16(a^2 + b^2 + c^2)} \\\\&= 4\sqrt{a^2 + b^2 + c^2} = 4\cdot 2 = 8 \\\\|-4\boldsymbol{\mathsf{v}}| &= \sqrt{(-4a)^2 + (-4b)^2 + (-4c)^2} = \sqrt{16(a^2 + b^2 + c^2)} \\\\&= 4\sqrt{a^2 + b^2 + c^2} = 4\cdot 2 = 8\end{align*}
となり、確かに $\boldsymbol{\mathsf{v}}$の大きさの$4$倍の値になっている。実数倍されたベクトルの加算、減算についても通常のベクトルの場合と同様である。
(計算例)
\begin{align*}8&\begin{pmatrix}-2 \\5 \\3\end{pmatrix} +3\begin{pmatrix}4 \\6 \\-5\end{pmatrix} =\begin{pmatrix}-16 \\40 \\24\end{pmatrix} +\begin{pmatrix}12 \\18 \\-15\end{pmatrix} =\begin{pmatrix}-4 \\58 \\9\end{pmatrix} \\ \\5&\begin{pmatrix}2 \\-3 \\11\end{pmatrix} -4\begin{pmatrix}8 \\-12 \\-6\end{pmatrix} =\begin{pmatrix}10 \\-15 \\55\end{pmatrix} -\begin{pmatrix}32 \\-48 \\-24\end{pmatrix} =\begin{pmatrix}-22 \\33 \\79\end{pmatrix} \end{align*}
ここからは、本節で述べた内容に関してのプログラムを作成する。
# Code1
UnityのC#スクリプトでは、3D空間の点やベクトルは以下の構造体によって表される。Vector3
: 3次元ベクトル用の構造体Vector4
: 4次元ベクトル用の構造体Vector4構造体は Vector3構造体を同次座標化する場合に必要なもので、主に行列演算のときに使用される。
まずは、本節の始めに求めたベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$、$\boldsymbol{\mathsf{v_3}}$をプログラムにおいて求め、それらの大きさを表示する。
-
 図4 ベクトルv1
図4 ベクトルv1 -
 図5 ベクトルv2
図5 ベクトルv2 -
 図6 ベクトルv3
図6 ベクトルv3
[Code1] (実行結果 図15)
Vector3 sta = Vector3.zero; // 始点
Vector3 end = new Vector3(4, 3, 2); // 終点
Vector3 v1 = end - sta;
Debug.Log("v1" + v1 + " mag : " + v1.magnitude);
sta = new Vector3(2, 4, -2); // 始点
end = new Vector3(5, 1, -6); // 終点
Vector3 v2 = end - sta;
Debug.Log("v2" + v2 + " mag : " + v2.magnitude);
sta = new Vector3(-3, 1, -2); // 始点
end = new Vector3(3, 2, 0); // 終点
Vector3 v3 = end - sta;
Debug.Log("v3" + v3 + " mag : " + v3.magnitude);

3D空間上の2点間の距離を求める場合でも、その2点をベクトルの始点、終点とみなして、そのベクトルの大きさを計算すればよい。例えば、このプログラムでは v3の大きさは約$6.40$であるが、それはベクトル v3の始点$(-3, 1, -2)$と終点$(3, 2, 0)$の間の距離が約$6.40$であることを意味している (なお、1行目の Vector3.zero はVector3構造体のstaticなプロパティで $(0, 0, 0)$ を表すものである)。
# Code2
次は、実数倍されたベクトルの計算を行うプログラムである。[Code2] (実行結果 図16)
Vector3 v = new Vector3(-2, 5, 3);
Vector3 w = new Vector3(4, 6, -5);
Vector3 A = 8 * v + 3 * w;
Debug.Log(A);
v = new Vector3(2, -3, 11);
w = new Vector3(8, -12, -6);
A = 5 * v - 4 * w;
Debug.Log(A);
v = new Vector3(-4.52f, 0.63f, -8.11f);
w = new Vector3(6.82f, 11.35f, -2.09f);
A = 3.4f * v + 1.8f * w;
Debug.Log("(" + A.x + ", " + A.y + ", " + A.z + ")");
v = new Vector3(2.08f, -3.15f, -9.83f);
w = new Vector3(2.89f, 2.46f, 4.18f);
A = -8.1f * v - 5.4f * w;
Debug.Log("(" + A.x + ", " + A.y + ", " + A.z + ")");

後半2つの出力の際に A.x、A.y、A.z のようにして各座標を直接出力しているのは、Debug.Log(A) とした場合は小数第2位が四捨五入されて小数第1位までしか表示されなくなるためである。
© 2020-2025 Redpoll's 60 (All rights reserved)