Redpoll's 60

$§$ 3-13

第3章 3D空間の基礎

$§$ 3-13 変換行列の積

平行移動や回転、スケールなどの変換の合成は変換行列の積によって表される。
本節では、プログラムを通して3D空間における変換行列の積の具体的な例を見ていく。

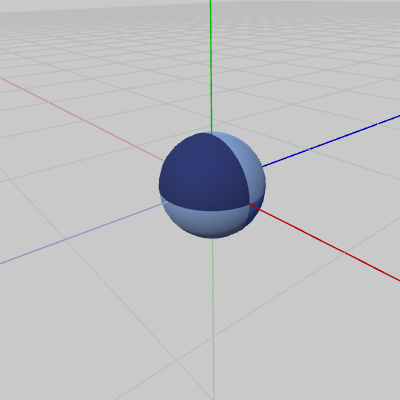
図1は、オブジェクトSphere(中心が原点にある球)の初期状態である。以下では、このオブジェクトに対して変換行列を実行する。

前半の例では、次の3つの行列を使用する。

$T$ :

$(4, 1, -2)$ だけ移動させる平行移動行列

$R$ : y軸周りに

$120$ °回転させる回転行列

$S$ : x軸方向、y軸方向、z軸方向に

$1.5$ 倍拡大させるスケール行列

# Code1

最初にy軸周りに

$120$ °の回転(

$R$ )、次に

$(4, 1, -2)$ の平行移動(

$T$ )。

最終的な変換行列を

$M$ とすれば、

$M = TR$ である。

プログラムは以下のとおり。
[Code1] (実行結果図3)

Matrix4x4 T = TH3DMath.GetTranslation4x4(4.0f, 1.0f, -2.0f);
Matrix4x4 R = TH3DMath.GetRotation4x4(120.0f, Vector3.up);
Matrix4x4 M = T * R;
Sphere.SetMatrix(M);

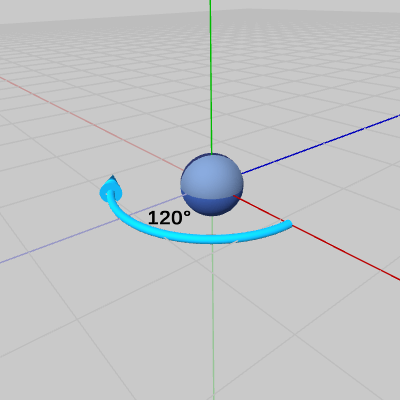
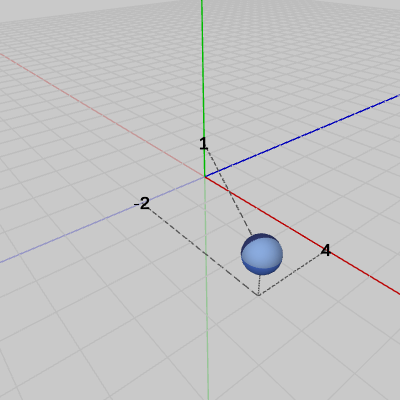
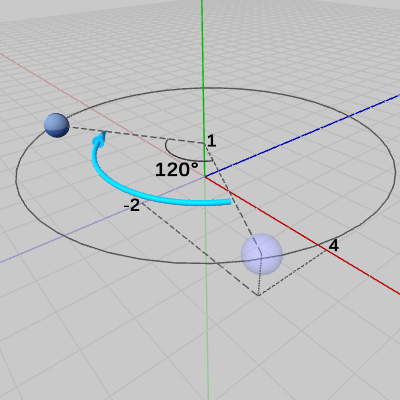
この変換は、回転させてから平行移動という順で行われる。まず初期状態の位置で、y軸周りに120°の回転させて(図2)、回転させた状態のSphereを

$(4, 1, -2)$ だけ平行移動させる(図3)。これが変換行列の積

$M = TR$ の内容である。
(2行目の回転行列を取得するメソッドで回転軸に指定されているVector3.upは、Unityに標準で用意されている定数で

$(0, 1, 0)$ 、すなわちy軸のプラス方向を表す。)

# Code2

最初に

$(4, 1, -2)$ の平行移動(

$T$ )、次にy軸周りに

$120$ °の回転(

$R$ )。

最終的な変換行列を

$M$ とすれば、

$M = RT$ である。

[Code2] (実行結果図5)

Matrix4x4 T = TH3DMath.GetTranslation4x4(4.0f, 1.0f, -2.0f);
Matrix4x4 R = TH3DMath.GetRotation4x4(120.0f, Vector3.up);
Matrix4x4 M = R * T;
Sphere.SetMatrix(M);

Code1との違いは3行目の積が R * T になっていることだけである。
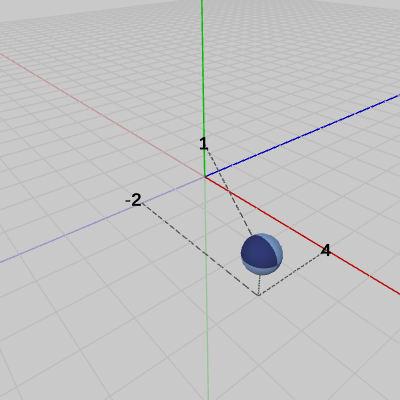
この変換は、平行移動させてから回転という順で行われる。まず初期状態の位置から

$(4, 1, -2)$ だけ平行移動させて(図4)、移動後の位置からSphereをy軸周りに120°の回転させる(図5)。これが変換行列の積

$M = RT$ の内容である。
2D空間の章でも指摘したが、行列の積は交換可能ではない。すなわち、積の順序を入れ替えたときの結果が同じになるとは限らない。この2つの例でも、

$M = TR$ と

$M = RT$ の結果は同じではない。

# Code3

最初にz軸方向に2倍拡大(

$S$ )、次にy軸周りに

$120$ °の回転(

$R$ )、最後に

$(4, 1, -2)$ の平行移動(

$T$ )。

最終的な変換行列を

$M$ とすれば、

$M = TRS$ である。

[Code3] (実行結果図8)

Matrix4x4 T = TH3DMath.GetTranslation4x4(4.0f, 1.0f, -2.0f);
Matrix4x4 R = TH3DMath.GetRotation4x4(120.0f, Vector3.up);
Matrix4x4 S = TH3DMath.GetScale4x4(1.0f, 1.0f, 2.0f);
Matrix4x4 M = T * R * S;
Sphere.SetMatrix(M);

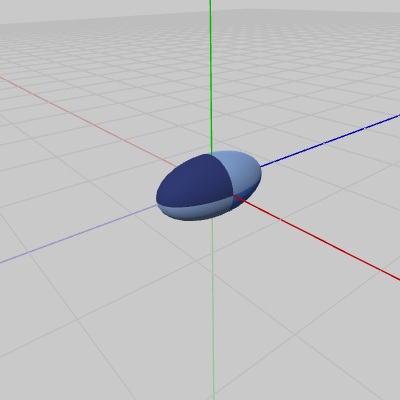図6 z軸方向に2倍拡大
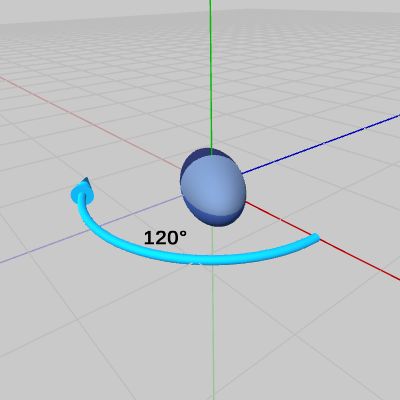図7 y軸周りの120°の回転
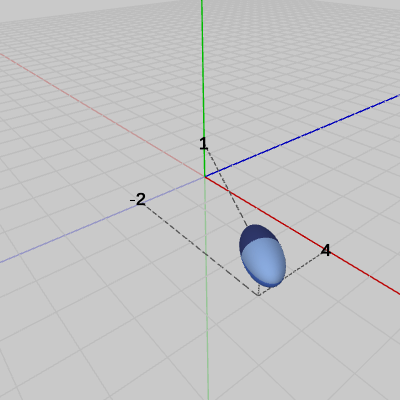図8 (4, 1, -2) の平行移動

この変換は、拡大させてから回転、最後に平行移動という順で行われる。まず初期状態の位置で、z軸方向に

$2$ 倍拡大させて(図6)、拡大させた状態のSphereをy軸周りに120°の回転させる(図7)。そして最後に、回転させた状態のSphereを

$(4, 1, -2)$ だけ平行移動させる(図8)。これが変換行列の積

$M = TRS$ の内容である。

オブジェクトに実行する変換行列では、変換は常に初期状態から始まる。つまり、「オブジェクトを初期状態からどのように変換するか」という内容でなければならい。
上の3つの例では複数の変換の最終的な実行結果は、オブジェクトが静止している状態であるので、初期状態から最終的な状態に変換する変換行列を、あるフレームでオブジェクトに対して1度実行するだけで、それ以降のフレームではオブジェクトに対して新たに変換行列を実行する必要はない。しかし、オブジェクトが運動する場合には、毎フレーム新しい変換行列を計算して、オブジェクトに対して毎フレーム実行する必要がある。この場合でも毎フレーム、オブジェクトに実行する変換行列は、「オブジェクトを初期状態からどのように変換するか」という内容でなければならない。
以下の例でそれを見ていこう。

# Code4

Sphereが原点において、図9に示されるようにy軸周りの自転を(毎フレーム

$3$ °ずつ)行っている。このとき、y軸はSphereの'北極'と'南極'、及び自身の中心を貫通しており、Sphereの位置は初期状態から動いてはいない。この自転を、図10に示されるように

$(2, 0, 2)$ の位置で行わせるようにしたい。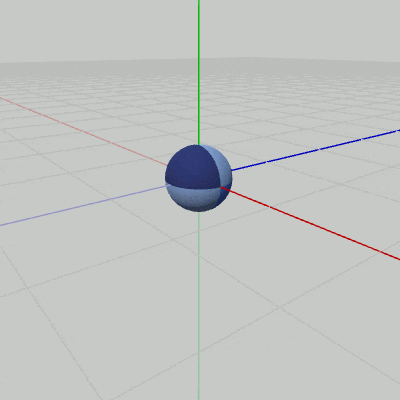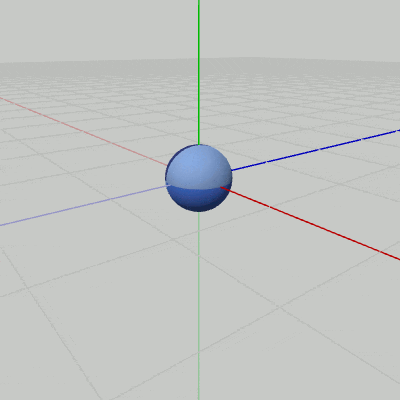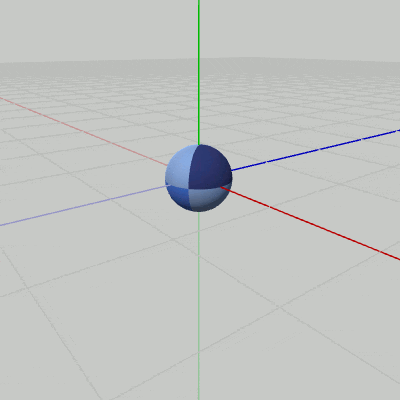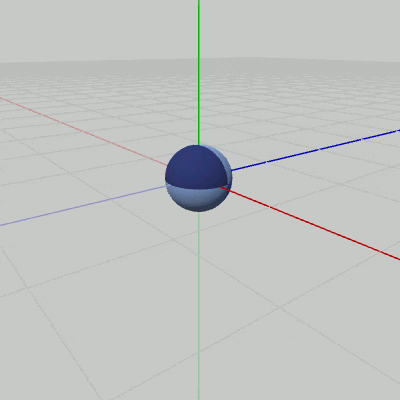

図9の原点における自転のプログラムを以下に示す。
[Beta4] (実行結果図9)

i_degRot += 3;
Matrix4x4 R = TH3DMath.GetRotation4x4(i_degRot, Vector3.up);
Sphere.SetMatrix(R);

i_degRotは回転角度を表すインスタンス変数であり、毎フレーム

$3$ ずつ増加する。このプログラムはSphereを毎フレーム、初期状態からi_degRotだけ回転させるだけの処理である。i_degRotは毎フレーム

$3$ ずつ増加するので、Sphereの初期状態からの回転角度も毎フレーム

$3$ °ずつ増加し、図9のように自転することになる。

図10の

$(2, 0, 2)$ における自転のプログラムを以下に示す。
[Code4] (実行結果図10)

i_degRot += 3;
Matrix4x4 R = TH3DMath.GetRotation4x4(i_degRot, Vector3.up);
Matrix4x4 T = TH3DMath.GetTranslation4x4(2.0f, 0.0f, 2.0f);
Matrix4x4 M = T * R;
Sphere.SetMatrix(M);

このプログラムでは、Sphereに実行される変換行列が

$M = TR$ になっている。この変換の内容は、まず初期状態で i_degRotだけ回転させ(R)、回転させた状態のSphereを

$(2, 0, 2)$ へ移動させる(T)。これを毎フレーム行う。回転は初期状態のSphereに対して実行されるが、これはy軸周りの自転、つまり図9の自転になるが、このプログラムでは毎フレーム i_degRotだけ回転させてからさらに

$(2, 0, 2)$ への移動を実行するので、Sphereは図10のように

$(2, 0, 2)$ において自転をするようになるのである。

# Code5

Sphereが原点において、図13に示されるように伸縮を行っている(原点を中心とする

$1$ 倍から

$2$ 倍の間の拡大縮小。倍率はx軸、y軸、z軸共通)。ここではさらに、この伸縮を図14に示されるように、XZ平面上の原点を中心とする半径

$3$ の円周上を回転しながら行わせることを考える。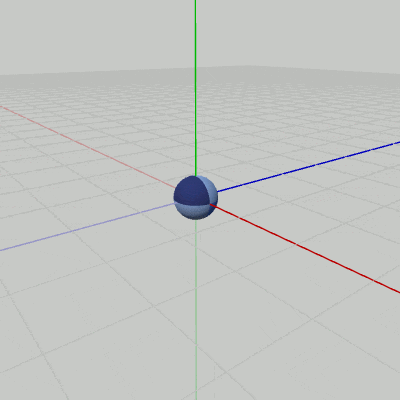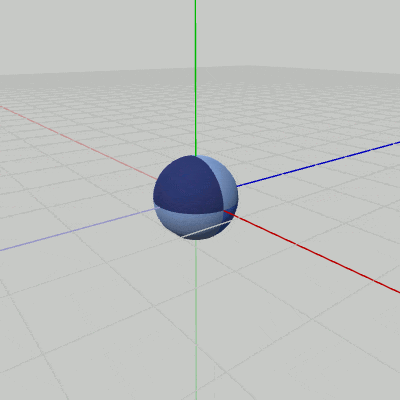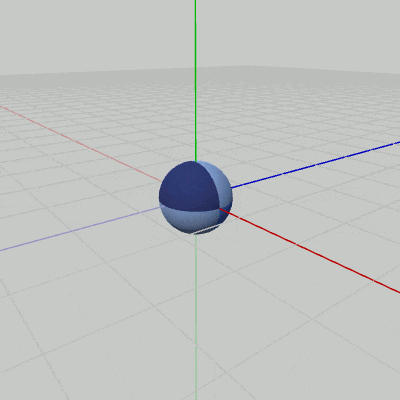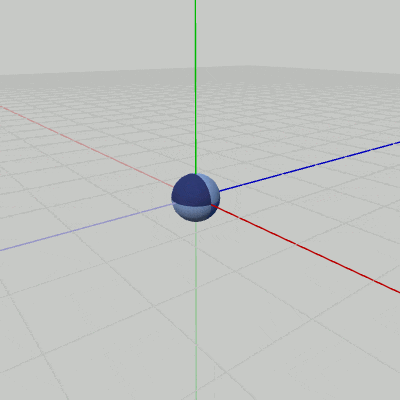

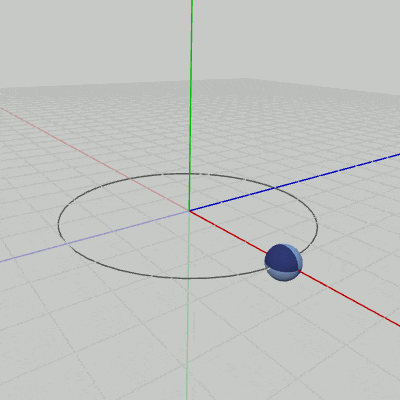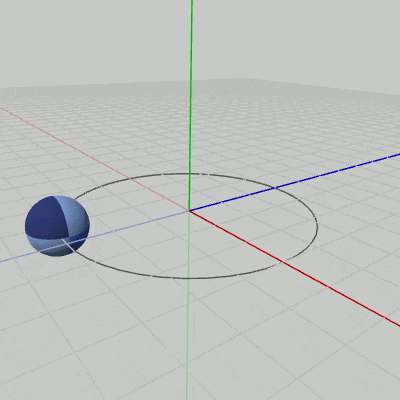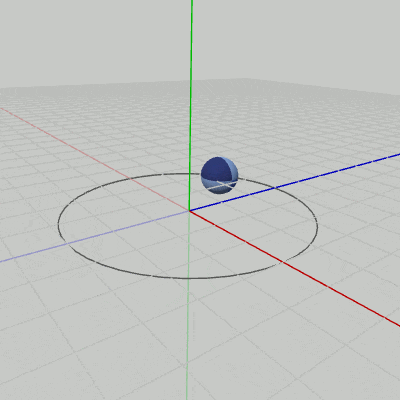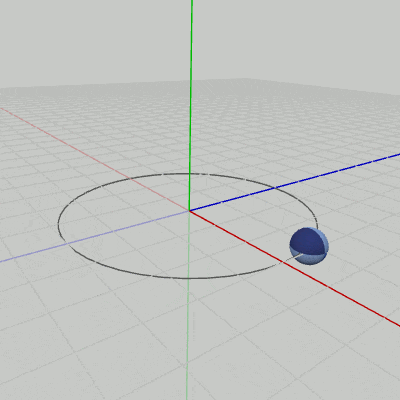
図13の原点における伸縮のプログラムを以下に示す。
[Beta5] (実行結果図13)

i_shm += 2;
float min = 1.0f;
float max = 2.0f;
float A = max - min;
float scale = 0.5f * A * (-Mathf.Cos(i_shm * Mathf.Deg2Rad) + 1.0f) + min;
Matrix4x4 S = TH3DMath.GetScale4x4(scale);
 
Sphere.SetMatrix(M);

伸縮の倍率は

$1$ 倍から

$2$ 倍の間を往復する。そのために1-10節で解説した単振動の式をここでは使用している。i_shmは単振動の角度を表すインスタンス変数であり、毎フレーム

$2$ ずつ増加する。4行目はそのフレームにおける倍率scaleの計算である。
この倍率計算で単振動の式が使われているが、計算結果が

$1$ から

$2$ の間を往復するようにしてある(詳しくは 1-10節参照)。
このプログラムは Sphereを毎フレーム、初期状態からscale倍伸縮させるだけの処理である。scaleはプログラム実行中に

$1$ から

$2$ の間を往復するので、Sphereの初期状態からの倍率もプログラム実行中に

$1$ 倍から

$2$ 倍の間を往復し、図13のように伸縮することになる。

図14の円周上を回転しながら伸縮するプログラムを以下に示す。
[Code5] (実行結果図14)

i_shm += 2;
float min = 1.0f;
float max = 2.0f;
float A = max - min;
float scale = 0.5f * A * (-Mathf.Cos(i_shm * Mathf.Deg2Rad) + 1.0f) + min;
Matrix4x4 S = TH3DMath.GetScale4x4(scale);
 
i_degRev++;
Matrix4x4 rev = TH3DMath.GetRotation4x4(i_degRev, Vector3.up);
Vector3 pos = rev * new Vector4(3, 0, 0, 1);    
Matrix4x4 T = TH3DMath.GetTranslation4x4(pos);
 
Matrix4x4 M = T * S;
Sphere.SetMatrix(M);

6行目までは上のプログラムと同じである。8行目から11行目で、そのフレームにおける、円周上の移動位置を計算している。

$(3, 0, 0)$ をスタート地点として毎フレーム

$1$ °ずつ円周上を回転する。i_degRevは円周上での回転角度を表すインスタンス変数で、具体的には 9行目でy軸周りに角度i_degRevだけ回転させる行列revを取得し、それを10行目でnew Vector4(3, 0, 0, 1)に掛けることによって、そのフレームにおける円周上の移動位置posが計算される (円周上を

$(3, 0, 0)$ から角度i_degRevだけ回転した位置)。11行目で実際にその位置に移動させる行列Tを取得する。
Sphereに実行される変換行列 M = T * S の内容は次の通り。
最初の変換であるスケール(S)は初期状態のSphereに対して実行されるが、これは原点におけるscale倍の伸縮である。さらに、このプログラムでは毎フレーム Sを実行してから円周上への平行移動(T)を実行するので、Sphereは図14のように円周上を回転しながら伸縮するようになるのである。

# Code6

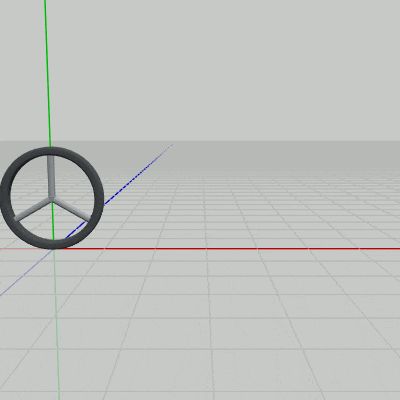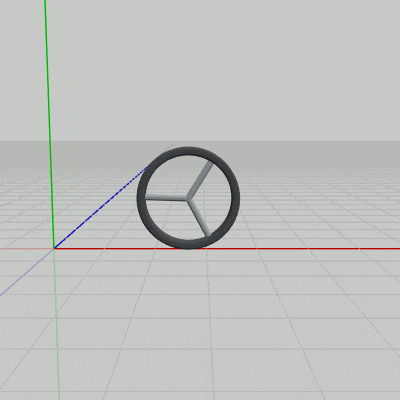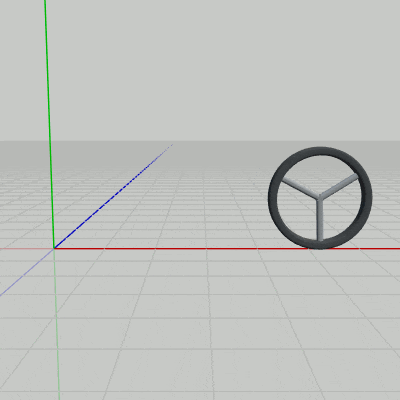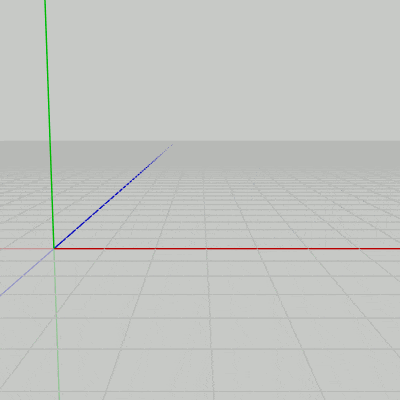
今回のプログラムでは車輪を移動させる問題について扱う。
車輪が移動する場合には、通常図15に見られるように回転しながら移動していくが、この運動も結局は回転行列と平行移動行列の積によって実装される。

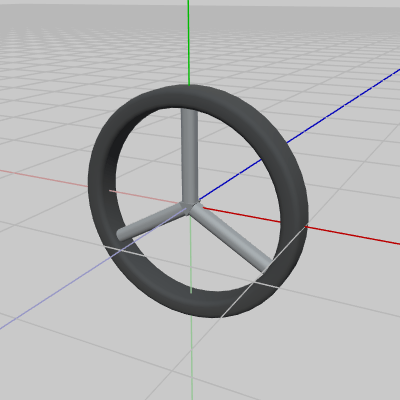
図16はここで使用するオブジェクト Wheel の初期状態であり、半径は

$1$ 、初期状態ではその中心が原点に置かれ、Wheelの中心を z軸が貫いている。

次のプログラムはWheelを x軸上で

$0.05$ ずつ移動させるものである。
[Beta6A] (実行結果図17)

if (!i_INITIALIZED)
{
    Wheel.SetMatrix(TH3DMath.GetTranslation4x4(0.0f, 1.0f, 0.0f));
 
    i_INITIALIZED = true;
}
 
Vector3 pos = Wheel.GetWorldPosition();
pos += 0.05f * Vector3.right;
Matrix4x4 T = TH3DMath.GetTranslation4x4(pos);
 
Wheel.SetMatrix(T);

このプログラムは毎フレーム Wheelの現在位置を取得し、その位置からさらに x軸方向に

$0.05$ だけ移動させるだけである。Wheelに実行される行列は平行移動行列のみなので、実行結果(図17)に見られるようにWheelは回転せずに x軸上を移動していく。
初期化ブロックにおいてWheelを y軸方向に半径分だけ移動させているが、これによってWheelの移動が x軸上で行われることになる。

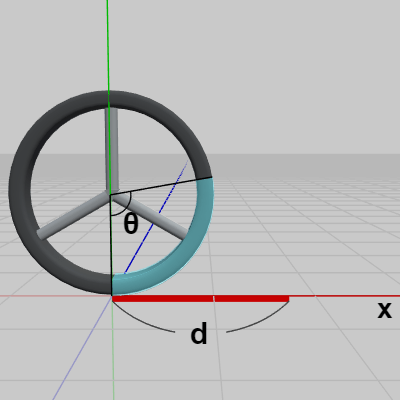
Wheelが回転しながら移動していくようにするためには、Wheelの移動量に見合った分だけ回転させる必要がある。例えば、Wheelが原点から出発して x軸上を距離

$d$ だけ進むとしよう。下図ではWheelの円周の一部が水色になっているが、水色の部分の長さ(弧の長さ)は

$d$ に等しい。また、円周上の水色の部分の角度を

$\theta$ とする (図18)。

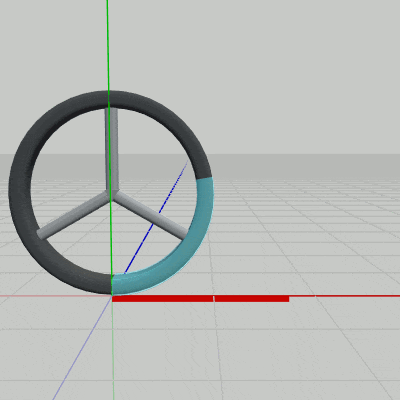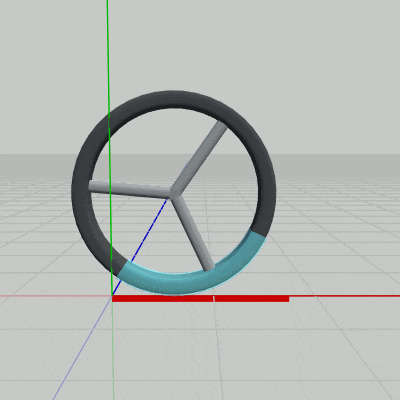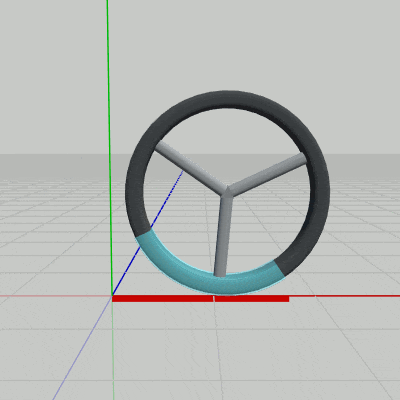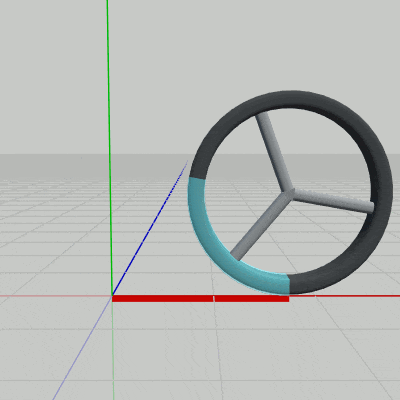
Wheelが x軸上を距離

$d$ だけ進むときには、図19に示されるようにWheelは角度

$\theta$ だけ回転するわけである。進んだ距離

$d$ がWheelの円周長に等しければ角度

$\theta$ は

$360^\circ$ であり、距離

$d$ がWheelの円周長の半分であれば角度

$\theta$ は

$180^\circ$ である。
したがって、Wheelの半径を

$r$ とすれば、Wheelが距離

$d$ だけ進んだときのWheelの回転角度

$\theta$ は

$d \div 2\pi r \times 360 = \theta$ として求められる。

次のプログラムは、先程のプログラムに今述べたWheelの回転を追加したものである。
[Beta6B] (実行結果図20)

if (!i_INITIALIZED)
{
    i_distance = 0.0f;
 
    Wheel.SetMatrix(TH3DMath.GetTranslation4x4(0.0f, 1.0f, 0.0f));
 
    i_INITIALIZED = true;
}
 
Vector3 pos = Wheel.GetWorldPosition();
pos += 0.05f * Vector3.right;
Matrix4x4 T = TH3DMath.GetTranslation4x4(pos);
 
i_distance += 0.05f;
float deg = (i_distance / c_WheelLength) * 360.0f;
Matrix4x4 R = TH3DMath.GetRotation4x4(-deg, Vector3.forward);
 
Wheel.SetMatrix(T * R);

3行目の i_distance はWheelが進んだ距離を表すインスタンス変数である (float型)。
先程のプログラムから追加されたのは14行目以降であり、この部分はWheelの回転行列を計算する部分である。15行目は上記の数式

$d \div 2\pi r \times 360 = \theta$ に相当する部分であるが、ローカル変数 deg は数式中の

$\theta$ に相当し、i_distance が数式中の

$d$ である。c_WheelLength はWheelの円周長を表す定数であり、数式中の

$2\pi r$ に相当する。
このプログラムではWheelは x軸プラス方向に進んでいくが、実行結果(図20)はこの運動を z軸マイナス側から見たときのものである。z軸マイナス側から見るとWheelは時計回りに回転しているが、

$+z$ 軸を回転軸として時計回りに回転させるためには毎フレーム回転角度を減少させていかなければならない。16行目の GetRotation4x4(..) の引数が -deg となっているのはそのためである (マイナスを付けなければWheelの進行方向と逆向きの回転になる)。

次のプログラムはWheelをキー操作によって x軸プラス方向、マイナス方向に移動させるものである。
    H  :  x軸マイナス方向に移動させる。
    L  :  x軸プラス方向に移動させる。

[Code6]  (実行結果図15)

if (!i_INITIALIZED)
{
    i_distance = 0.0f;
 
    Wheel.SetMatrix(TH3DMath.GetTranslation4x4(6.0f, 1.0f, 0.0f));
 
    i_INITIALIZED = true;
}
 
float vel = 0.0f;
if (Input.GetKey(KeyCode.H))
{
    vel = -0.05f;
}
else if (Input.GetKey(KeyCode.L))
{
    vel = 0.05f;
}
 
Vector3 pos = Wheel.GetWorldPosition();
pos += vel * Vector3.right;
Matrix4x4 T = TH3DMath.GetTranslation4x4(pos);
 
i_distance += vel;
float deg = (i_distance / c_WheelLength) * 360.0f;
Matrix4x4 R = TH3DMath.GetRotation4x4(-deg, Vector3.forward);
 
Wheel.SetMatrix(T * R);

キー操作に関する処理(10~18行目)が追加されたことを除けば、このプログラムは先程のBeta6Bと同じ内容である。H を押し続ければWheelは毎フレーム

$0.05$ ずつ x軸マイナス方向に移動し、L を押し続ければ x軸プラス方向に移動する。

# Code7

このプログラムは読者用の課題である。
下図21の立方体を図22のように切断したとする。図中の点

$P$ 、

$Q$ は各辺の中点である。

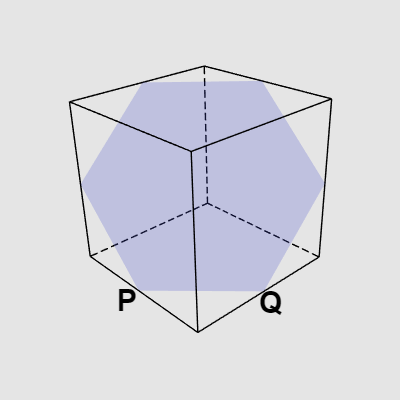
切断後の立方体は2つの部分に分かれるが、以下の図23、図24はその2つの部分であり、ここでは便宜上 Part1、Part2 で呼び分ける。

図24 Part2 初期状態 (点M’は辺P’Q’の中点であり、この図では原点に位置している)

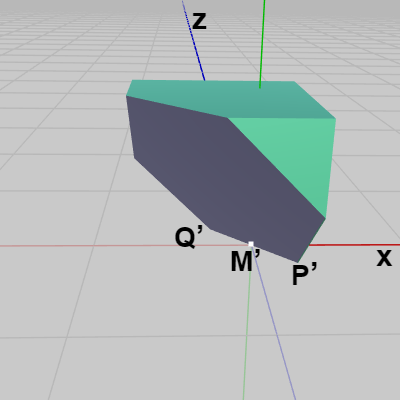
図23、図24はPart1、Part2の初期状態である。Part1の点

$P$ 、

$Q$ は図22のものと同じであり、点

$M$ は辺

$PQ$ の中点である。
Part2の辺

$P'Q'$ はPart1の辺

$PQ$ と平行である。点

$M'$ は辺

$P'Q'$ の中点であるが、Part2の初期状態においては

$M'$ は原点に位置している。また、

$M'$ を

$M$ に一致させるようにPart2を平行移動させると、両者は完全に接着した状態、すなわち図21の立方体になる。

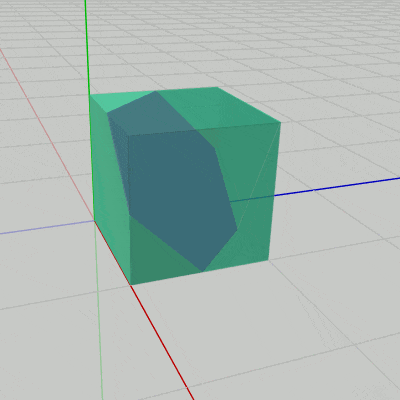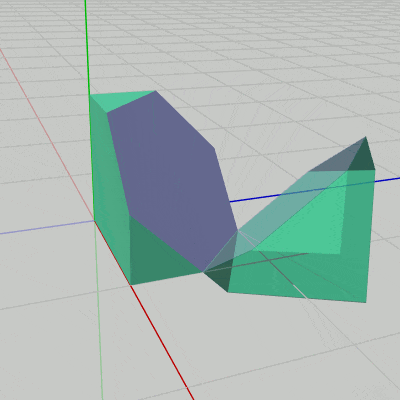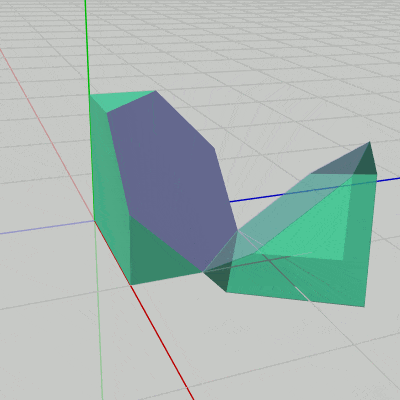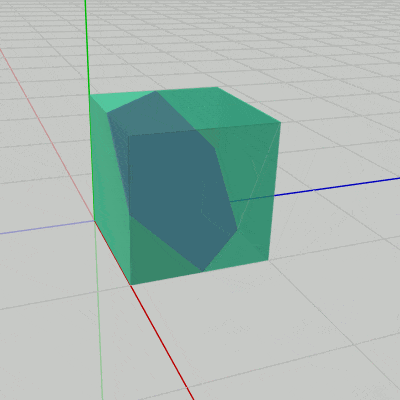
ここでの課題はPart1、Part2を完全に接着させた状態から、上図23に示される辺

$PQ$ を回転軸としてPart2を回転させるプログラムを作成することである (具体的には、実行結果が右図25のようになればよい)。

その際には次のキー操作によってPart2を回転させるものとする。
J : Part1へ近づいていくようにPart2を回転させる。
K : Part1から離れていくようにPart2を回転させる。

プログラムで使用するインスタンス変数及び定数は以下のとおり。

P, Q

: 図22(あるいは図23)の点

$P$ 、

$Q$ の位置を表すVector3型の定数。

i_degPart2

: Part2の回転角度を表すfloat型インスタンス変数で初期値は

$0$ である。

プログラムの作成は Sec313.cs内のCode7に行うものとする (Code7は何も記述されていない空のメソッドである)。なお、このプログラムではPart2は半透明で表示されるが、Tキーを押すことで半透明と不透明の切り替えが行える。
解答例については Sec313_Ans.txt を参照 (Sec313_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。

本節で見てきたように、変換の合成は変換行列の積によって表される。2つの変換の合成ならば2つの変換行列の積によって表され、3つの変換の合成ならば3つの変換行列の積によって表されるのである。

前節でも触れたが、この講義では変換の合成におけるスケールに関しては次の取り決めに従っている。
(1) 非一様スケール(各軸の倍率が異なるスケール)を実行する場合は、変換の合成において一番初めに実行し、それ以降では非一様スケールは実行しないものとする
(2) 倍率が

$0$ 以下のスケール(倍率が

$0$ あるいはマイナスの値をとるスケール)は実行しない

ただし、一様スケール(各軸の倍率が同じスケール ; 倍率はプラスの値)については、変換の合成における順番はどこでもよく、何度使っても構わない。

例えば、複数の変換の合成が以下のような変換行列の積によって表されているとする (以下の積おける

$T_i$ は平行移動行列、

$R_i$ は回転行列、

$S_i$ はスケール行列を表している)。

$M = S_4 T_4 R_4 T_3 R_3 S_3 R_2 T_2 S_2 T_1 R_1 S_1$ この変換の合成において一番初めに実行される変換はスケール

$S_1$ であるが、上の取り決めでいっていることはこの

$S_1$ は非一様スケール(各軸の倍率が異なるスケール)でも構わないが、その後に行われるスケール

$S_2$ 、

$S_3$ 、

$S_4$ については一様スケール(各軸の倍率が同じスケール)でなければいけない。そして、その倍率に関しても

$0$ 以下ではなく

$0$ より上の値でなければならないということである。

<< 3-12
スケール行列

3-14 >>
オイラー角 1

$§$ 3-1 点とベクトル	$§$ 3-13 変換行列の積
$§$ 3-2 ベクトルによる平行移動	$§$ 3-14 オイラー角 1
$§$ 3-3 左手系と右手系	$§$ 3-15 オイラー角 2
$§$ 3-4 ベクトルの内積	$§$ 3-16 一体化運動についての復習
$§$ 3-5 法線ベクトル	$§$ 3-17 応用プログラム 1 (ルービックキューブ)
$§$ 3-6 ベクトルの外積	$§$ 3-18 応用プログラム 2 (スロットマシン)
$§$ 3-7 行列の基礎 1	$§$ 3-19 応用プログラム 3 (サイコロの回転移動)
$§$ 3-8 行列の基礎 2	$§$ 3-20 課題 1
$§$ 3-9 平行移動行列	$§$ 3-21 課題 2
$§$ 3-10 回転行列 1	$§$ 3-22 課題 3
$§$ 3-11 回転行列 2	$§$ 3-23 課題 4
$§$ 3-12 スケール行列

§§3-13 変換行列の積

$§$ 3-13 変換行列の積