Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-5
第3章 3D空間の基礎
$§$3-5 法線ベクトル
コンピューターグラフィックスにおけるオブジェクトは、一般に三角形や四角形の集合として構成される(図1)。オブジェクトを構成する三角形や四角形のことを面(Face)といい、面を構成する複数個(3つ以上)の点のことを頂点(Vertex)という(図2)。

図1 オブジェクトを構成する面 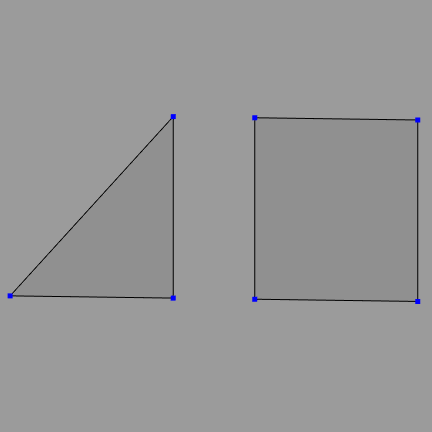
図2 面を構成する頂点
面には表裏の向きがあり、Unityのデフォルトの設定では面の表側は描画されるが、面の裏側は描画されない。まずは、この点についての説明から始める。
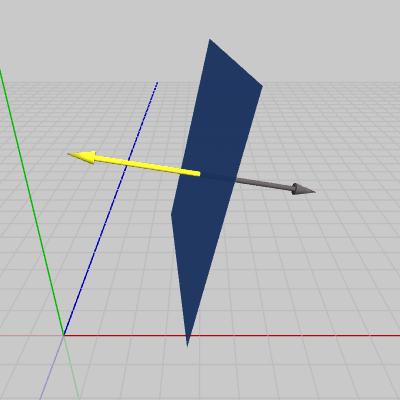
図3 法線ベクトル(それぞれ面に対して垂直) 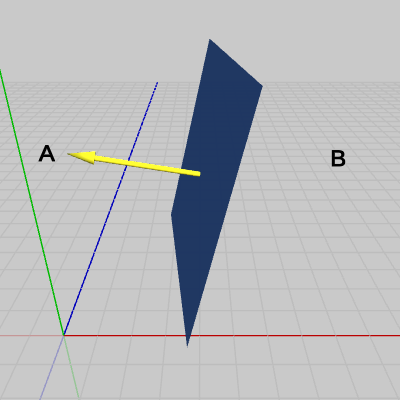
図4 面の表側を示す法線ベクトル
図5はBlenderにおいて、5個の正方形で構成されたオブジェクトの法線ベクトルを表示したものである。全ての面から法線ベクトルを表す水色の線が出ており、これは見えている全ての面が表側であることを意味している。このオブジェクトをUnityで表示した結果を図6に示す。
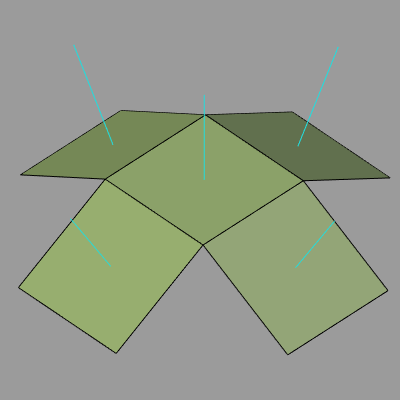
図5 オブジェクトの法線ベクトル(すべての面から法線が出ている) ; Blenderでの表示 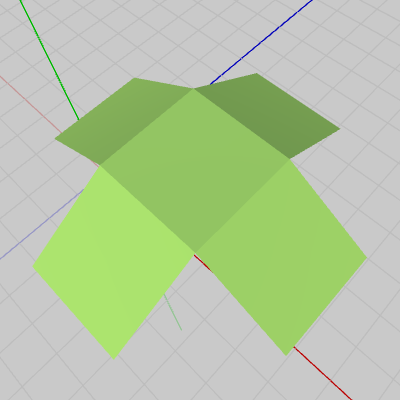
図6 Unityでの表示
図7は、このオブジェクトの中央の面の法線の向きを反転させたときのBlenderでの表示結果である (「法線の向きの反転」は面の表裏を入れ替えることを意味する)。図5と比較すると中央の面だけ水色の線が現れていないことがわかる。これは中央の面で見えているのは面の裏側であることを意味している。図8は、視点位置を下側にずらしてオブジェクトを下から見たときの様子である。この視点からは、図7において見えていなかった側が見えるようになるが、中央の面からだけ法線を表す水色の線が出ているのがわかるだろう(上に向かって伸びている法線も見えるが、これらは反対側の面の法線が見えているだけである)。これは下側の視点で見たときに中央の面で見えているのは、面の表側であることを意味している。
Unityでの表示は図9のようになる。先程も述べたように、Unityのデフォルトの設定では面の表側しか描画されないので、法線を反転させた中央の面は描画されていない (Unityで図8のように下側の視点で見たときは、中央の面だけ描画され他の4つの面は描画されなくなる。モデリングツールなどで作成したオブジェクトをUnityで表示した際に、ある部分が描画されていないといった場合には、法線の反転が第1の原因として考えられる)。
簡単にまとめると、オブジェクトは三角形や四角形の面の集合であり、その面には表裏がある。面の表側とは、法線ベクトルという面に対して垂直なベクトルの出ている側のことである。
以降では、法線ベクトルの使用例について見ていく。
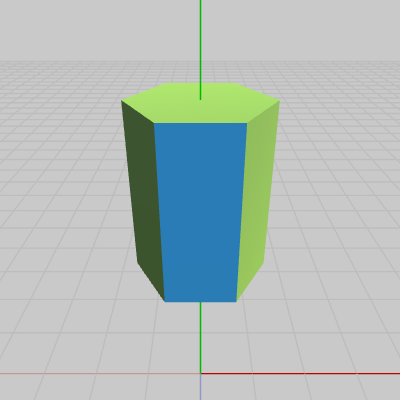
図10 六角柱 
図11 視点E、視線ve、法線n
図10のオブジェクトは六角柱で、側面の1つだけが青色で塗られている。今、図11に示されるように六角柱から少し距離を置いて、青い面を正面に見るような位置に視点$E$を移し、青い面の中心を見るように視線を(ベクトル)$\boldsymbol{\mathsf{v_e}}$の方向に定めた。図中の黄色いベクトル $\boldsymbol{n}$は青い面の法線ベクトルである。
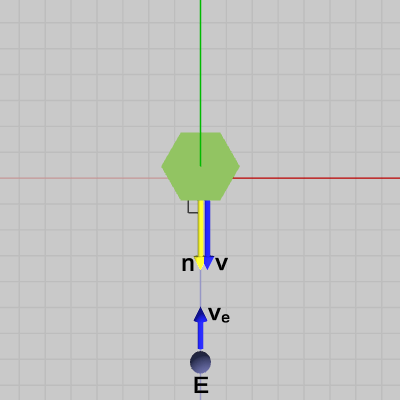
図12 
図13
図12はこの様子を真上から見下ろしたものであり、図13はこのときの視点$E$から見たオブジェクトの表示結果である(青い面を正面に見ている)。
図12において $\boldsymbol{n}$の隣にあるベクトル$\boldsymbol{\mathsf{v}}$は、視線ベクトル$\boldsymbol{\mathsf{v_e}}$の逆方向のベクトルであり、すなわち $\boldsymbol{\mathsf{v}} = -\boldsymbol{\mathsf{v_e}}$ である(便宜上、$\boldsymbol{\mathsf{v}}$を逆視線ベクトルと呼ぶことにする)。図12では逆視線ベクトル$\boldsymbol{\mathsf{v}}$の始点は、法線ベクトル$\boldsymbol{n}$の始点と同じ位置に置かれており、この場合の両者のなす角は$0$°、すなわち法線ベクトル$\boldsymbol{n}$と逆視線ベクトル$\boldsymbol{\mathsf{v}}$は平行である。
$\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$の内積を計算すると次の値になる (以降の計算では $\boldsymbol{\mathsf{v}}$、$\boldsymbol{n}$は単位ベクトルであるものとする)。\[\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n} = \cos{0}^\circ = 1\]
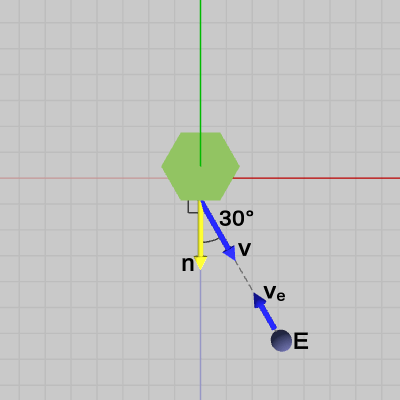
図14 
図15
図14は、視線ベクトル$\boldsymbol{\mathsf{v_e}}$の逆方向のベクトルである逆視線ベクトル$\boldsymbol{\mathsf{v}}$が、法線ベクトル$\boldsymbol{n}$と$30$°の角度をなすように視点$E$を移動させたものである(視点を移動させただけで、見る対象は青い面の中心であることに変わりはない)。
図15は、このときの視点$E$から見たオブジェクトの表示結果である。
$\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$の内積を計算結果は以下の値になる。\[\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n} = \cos{30}^\circ = 0.866\ldots\]
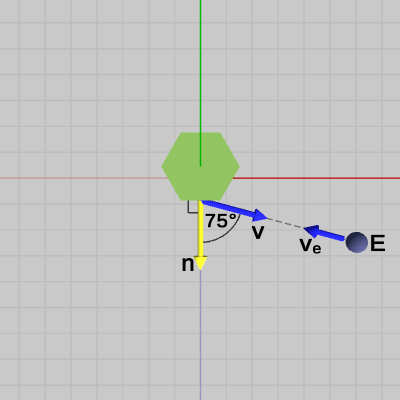
図16 
図17
図16は、逆視線ベクトル$\boldsymbol{\mathsf{v}}$と法線ベクトル$\boldsymbol{n}$のなす角が$75$°になるように視点$E$を移動させたものである(見る対象は青い面の中心である)。
図17は、このときの視点$E$から見たオブジェクトの表示結果である。
$\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$の内積を計算結果は以下の値になる。\[\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n} = \cos{75}^\circ = 0.258\ldots\]
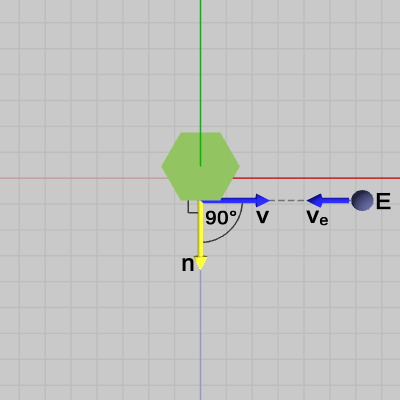
図18 
図19
図18は、逆視線ベクトル$\boldsymbol{\mathsf{v}}$と法線ベクトル$\boldsymbol{n}$のなす角が直交するように視点$E$を移動させたものである(見えてはいないが、見る対象は青い面の中心であることに変わりはない)。
$\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$の内積は次の値になる。\[\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n} = \cos{90}^\circ = 0\]図19は、このときの視点$E$から見たオブジェクトの表示結果である。図からわかるように、視点がちょうど青い面の真横に位置しているため、この位置においては青い面は全く見えていない。
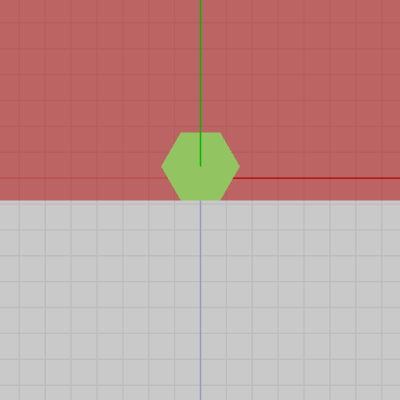
図20 赤いエリアからは青い面は見えない 以上の結果からわかることは、オブジェクトのある面がカメラ(視点)から見えると判断されるためには、その面の法線ベクトルと視線方向の逆方向のベクトルである逆視線ベクトルとのなす角が$90$°未満でなければならない。
今回の例でいえば、カメラ(視点)の視線方向を青い面の中心に向ける場合、図20の無色のエリアにカメラ(視点)があるとき、六角柱の青い面の法線と逆視線ベクトルのなす角が$90$°未満になるので、青い面は見える。しかし、赤いエリアにカメラ(視点)があるときは、青い面の法線と逆視線ベクトルのなす角が$90$°以上になってしまうので、青い面は見えなくなってしまう。
また、法線ベクトル$\boldsymbol{n}$と逆視線ベクトル$\boldsymbol{\mathsf{v}}$の内積$\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n}$に関していえば、($\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$は単位ベクトルであるから)内積の値が最大である$1$(なす角が$0$°)の場合は、図13に示されるように青い面の表示のされ方が最も大きい。$\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$のなす角が$30$°、$75$°と増加するにつれて、内積の値は$0.866\ldots$、$0.258\ldots$と小さくなっていくが、青い面の表示のされ方も同じように減っていく(青い面自体は全て見えているが、斜めから見ることになるので正面から見る場合に比べて圧縮されたような表示になる)。そして、内積の値が$0$(なす角が$90$°)のときには青い面は完全に見えなくなってしまい(図19)、図20の赤いエリアにカメラがある場合はもちろん青い面は見えず、法線と逆視線ベクトルとのなす角は$90$°以上となり、内積は$0$あるいはマイナス値になる。
つまり、法線ベクトル$\boldsymbol{n}$と逆視線ベクトル$\boldsymbol{\mathsf{v}}$の内積$\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n}$がプラス(図20における無色のエリア)であれば青い面は見えるが、$0$以下(赤いエリア)になると見えなくなってしまう。
まとめると、ある面がカメラ(視点)から見えるためには、その面の法線ベクトル$\boldsymbol{n}$とカメラの逆視線ベクトル$\boldsymbol{\mathsf{v}}$の内積が\[\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n} > 0\]であることが必要である。


面には表裏の向きがあり、Unityのデフォルトの設定では面の表側は描画されるが、面の裏側は描画されない。まずは、この点についての説明から始める。
A) 法線ベクトル
2D空間では扱わなかったが、3D空間におけるオブジェクトの場合には法線ベクトル(Normal Vector)というものが非常に重要な役割を担う。(3D空間における)法線ベクトルとは、ある面に垂直なベクトルのことで、図3のように1つの面に対して表向き、裏向きの2つの法線ベクトルが存在する。しかし、一般には法線ベクトルといえば面の表側を示すために、1つの面に対して1つだけ使われる。例えば、図4では面からは法線ベクトルがAの方向に出ているが、Bの方向には出ていない。これが意味することは、Aから見える側が面の表側であり、Bから見える側は面の裏側になるということである。

図5はBlenderにおいて、5個の正方形で構成されたオブジェクトの法線ベクトルを表示したものである。全ての面から法線ベクトルを表す水色の線が出ており、これは見えている全ての面が表側であることを意味している。このオブジェクトをUnityで表示した結果を図6に示す。


図7は、このオブジェクトの中央の面の法線の向きを反転させたときのBlenderでの表示結果である (「法線の向きの反転」は面の表裏を入れ替えることを意味する)。図5と比較すると中央の面だけ水色の線が現れていないことがわかる。これは中央の面で見えているのは面の裏側であることを意味している。図8は、視点位置を下側にずらしてオブジェクトを下から見たときの様子である。この視点からは、図7において見えていなかった側が見えるようになるが、中央の面からだけ法線を表す水色の線が出ているのがわかるだろう(上に向かって伸びている法線も見えるが、これらは反対側の面の法線が見えているだけである)。これは下側の視点で見たときに中央の面で見えているのは、面の表側であることを意味している。
Unityでの表示は図9のようになる。先程も述べたように、Unityのデフォルトの設定では面の表側しか描画されないので、法線を反転させた中央の面は描画されていない (Unityで図8のように下側の視点で見たときは、中央の面だけ描画され他の4つの面は描画されなくなる。モデリングツールなどで作成したオブジェクトをUnityで表示した際に、ある部分が描画されていないといった場合には、法線の反転が第1の原因として考えられる)。
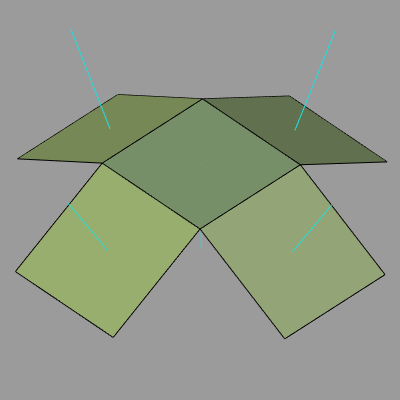 図7 中央の面の法線を反転 ; Blenderでの表示
図7 中央の面の法線を反転 ; Blenderでの表示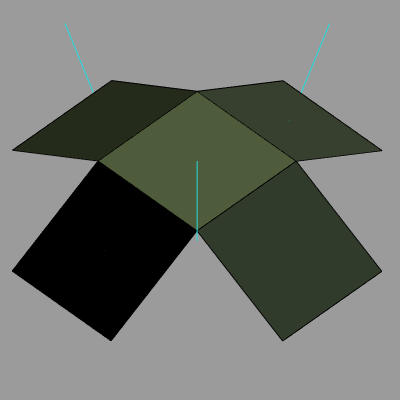 図8 視点を変えて下側から見た様子 ; Blenderでの表示
図8 視点を変えて下側から見た様子 ; Blenderでの表示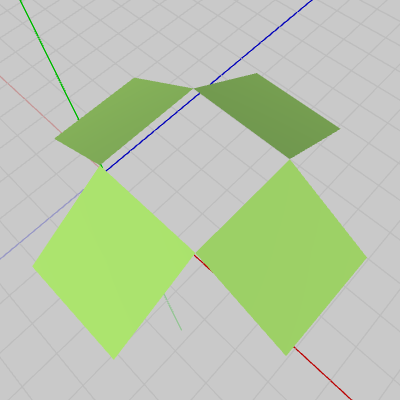 図9 中央の面が表示されない ; Unityでの表示
図9 中央の面が表示されない ; Unityでの表示
簡単にまとめると、オブジェクトは三角形や四角形の面の集合であり、その面には表裏がある。面の表側とは、法線ベクトルという面に対して垂直なベクトルの出ている側のことである。
以降では、法線ベクトルの使用例について見ていく。
B) 面の可視判定


図10のオブジェクトは六角柱で、側面の1つだけが青色で塗られている。今、図11に示されるように六角柱から少し距離を置いて、青い面を正面に見るような位置に視点$E$を移し、青い面の中心を見るように視線を(ベクトル)$\boldsymbol{\mathsf{v_e}}$の方向に定めた。図中の黄色いベクトル $\boldsymbol{n}$は青い面の法線ベクトルである。


図12はこの様子を真上から見下ろしたものであり、図13はこのときの視点$E$から見たオブジェクトの表示結果である(青い面を正面に見ている)。
図12において $\boldsymbol{n}$の隣にあるベクトル$\boldsymbol{\mathsf{v}}$は、視線ベクトル$\boldsymbol{\mathsf{v_e}}$の逆方向のベクトルであり、すなわち $\boldsymbol{\mathsf{v}} = -\boldsymbol{\mathsf{v_e}}$ である(便宜上、$\boldsymbol{\mathsf{v}}$を逆視線ベクトルと呼ぶことにする)。図12では逆視線ベクトル$\boldsymbol{\mathsf{v}}$の始点は、法線ベクトル$\boldsymbol{n}$の始点と同じ位置に置かれており、この場合の両者のなす角は$0$°、すなわち法線ベクトル$\boldsymbol{n}$と逆視線ベクトル$\boldsymbol{\mathsf{v}}$は平行である。
$\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$の内積を計算すると次の値になる (以降の計算では $\boldsymbol{\mathsf{v}}$、$\boldsymbol{n}$は単位ベクトルであるものとする)。\[\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n} = \cos{0}^\circ = 1\]


図14は、視線ベクトル$\boldsymbol{\mathsf{v_e}}$の逆方向のベクトルである逆視線ベクトル$\boldsymbol{\mathsf{v}}$が、法線ベクトル$\boldsymbol{n}$と$30$°の角度をなすように視点$E$を移動させたものである(視点を移動させただけで、見る対象は青い面の中心であることに変わりはない)。
図15は、このときの視点$E$から見たオブジェクトの表示結果である。
$\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$の内積を計算結果は以下の値になる。\[\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n} = \cos{30}^\circ = 0.866\ldots\]


図16は、逆視線ベクトル$\boldsymbol{\mathsf{v}}$と法線ベクトル$\boldsymbol{n}$のなす角が$75$°になるように視点$E$を移動させたものである(見る対象は青い面の中心である)。
図17は、このときの視点$E$から見たオブジェクトの表示結果である。
$\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$の内積を計算結果は以下の値になる。\[\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n} = \cos{75}^\circ = 0.258\ldots\]


図18は、逆視線ベクトル$\boldsymbol{\mathsf{v}}$と法線ベクトル$\boldsymbol{n}$のなす角が直交するように視点$E$を移動させたものである(見えてはいないが、見る対象は青い面の中心であることに変わりはない)。
$\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$の内積は次の値になる。\[\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n} = \cos{90}^\circ = 0\]図19は、このときの視点$E$から見たオブジェクトの表示結果である。図からわかるように、視点がちょうど青い面の真横に位置しているため、この位置においては青い面は全く見えていない。

今回の例でいえば、カメラ(視点)の視線方向を青い面の中心に向ける場合、図20の無色のエリアにカメラ(視点)があるとき、六角柱の青い面の法線と逆視線ベクトルのなす角が$90$°未満になるので、青い面は見える。しかし、赤いエリアにカメラ(視点)があるときは、青い面の法線と逆視線ベクトルのなす角が$90$°以上になってしまうので、青い面は見えなくなってしまう。
また、法線ベクトル$\boldsymbol{n}$と逆視線ベクトル$\boldsymbol{\mathsf{v}}$の内積$\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n}$に関していえば、($\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$は単位ベクトルであるから)内積の値が最大である$1$(なす角が$0$°)の場合は、図13に示されるように青い面の表示のされ方が最も大きい。$\boldsymbol{\mathsf{v}}$と$\boldsymbol{n}$のなす角が$30$°、$75$°と増加するにつれて、内積の値は$0.866\ldots$、$0.258\ldots$と小さくなっていくが、青い面の表示のされ方も同じように減っていく(青い面自体は全て見えているが、斜めから見ることになるので正面から見る場合に比べて圧縮されたような表示になる)。そして、内積の値が$0$(なす角が$90$°)のときには青い面は完全に見えなくなってしまい(図19)、図20の赤いエリアにカメラがある場合はもちろん青い面は見えず、法線と逆視線ベクトルとのなす角は$90$°以上となり、内積は$0$あるいはマイナス値になる。
つまり、法線ベクトル$\boldsymbol{n}$と逆視線ベクトル$\boldsymbol{\mathsf{v}}$の内積$\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n}$がプラス(図20における無色のエリア)であれば青い面は見えるが、$0$以下(赤いエリア)になると見えなくなってしまう。
まとめると、ある面がカメラ(視点)から見えるためには、その面の法線ベクトル$\boldsymbol{n}$とカメラの逆視線ベクトル$\boldsymbol{\mathsf{v}}$の内積が\[\boldsymbol{\mathsf{v}}\cdot\boldsymbol{n} > 0\]であることが必要である。
© 2020-2025 Redpoll's 60 (All rights reserved)