Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-23
第3章 3D空間の基礎
$§$3-23 課題 4
物体を真上に投げ上げる際に、投げ上げの開始地点から最高到達点に達し、再び開始地点に戻ってくるまでの時間を $N$ とする。よく知られているように、投げ上げの開始地点から最高到達点までにかかる時間と最高到達点から開始地点までに戻ってくる時間は同じである。ここでは物体を開始地点から投げ上げて再び開始地点に戻ってくるまでの時間を $N$ としているので、開始地点から最高到達点までにかかる時間及び最高到達点から開始地点までに戻ってくる時間はそれぞれ $N/2$ である。以下では簡単のため $N/2 = M$ とおき、最高到達点までの移動距離を $h$ とする。
物体を真上に投げ上げる際のある時刻 $t$ における速度 $v$ は、初速を $v_0$、重力加速度を $g$ とするとき\[v = v_0 - gt\]であるが、時間 $t$ をフレームとして考えると1フレーム目の速度は $v_0 - g$、2フレーム目の速度は $v_0 - 2g$、3フレーム目の速度は $v_0 - 3g$ となり、例えばプログラムでは以下のように記述することになる。
t はint型のフレームカウント用のインスタンス変数であり、毎フレーム インクリメントされる。
物体の投げ上げをプログラムで実装する際には各フレームにおける物体の位置を求める必要があるが、毎フレームの移動量を v とし、物体の現在位置(高さ)を pos.y とすれば各フレームにおける物体の位置はとして算出される。
まとめると、物体を真上に投げ上げる際の移動処理は以下のように記述すればよい。
以下ではこの鉛直投げ上げにおける初速 $v_0$ 及び重力加速度 $g$ を求めることについて見ていく。
まずは開始地点から最高到達点までにかかる時間(上昇時間)と、最高到達点から開始地点までに戻ってくる時間(落下時間)が同じになるようにすることについて考える。ここではそれぞれ $M(=N/2)$ フレームずつかかるものとする。
ともに $M$ フレームずつかかるので、上昇は $1$~$M$ フレームの間において行われ、落下は $M+1$ ~ $2M(=N)$ フレームの間に行われる。下左図は上昇過程における各フレームでの速度のグラフであり、この合計値が上昇過程における移動量である。下右図は落下過程における各フレームでの速度のグラフであり、この合計値が落下過程における移動量である (上昇時の速度をプラスとし、落下時の速度をマイナスとしている)。
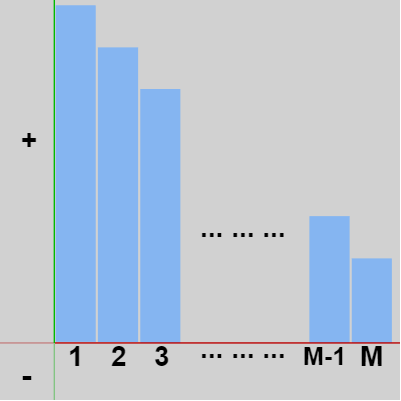
図1 上昇過程のグラフ ; 1~Mフレーム目までの速度の変化(高さ方向が速度。上昇過程ではすべてプラス値)。この棒グラフの合計値が上昇過程における移動量。 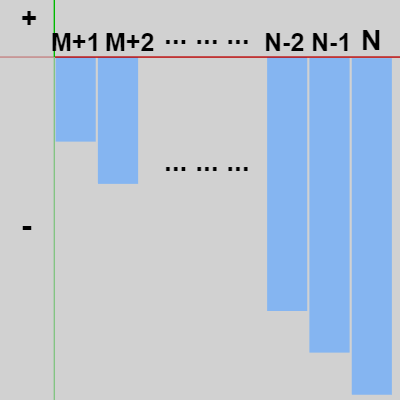
図2 落下過程のグラフ ; M+1~Nフレーム目までの速度の変化(落下過程ではすべてマイナス値)。この棒グラフの合計値が落下過程における移動量。
上昇時間と落下時間が同じというのはここでは同じ時間の間に同じ距離を移動するということであり、具体的には上記の2つのグラフの移動量(の絶対値)が同じであることを意味する (左図の上昇過程の移動量はプラスになるが、右図の落下過程の移動量はマイナスになる)。
上昇過程の最後である $M$ フレーム目における速度は $v_0 - Mg$ であり、落下過程の最初である $M+1$ フレーム目における速度は $v_0 - (M+1)g$ であるが、各フレームにおいて速度は $g$ ずつ減少するのでこの2つの速度の絶対値が等しいならば上の2つのグラフの移動量の絶対値も等しくなる。
つまり上昇時間と落下時間が同じであるようにするためには\begin{align*}&v_0 - Mg = -(v_0 - (M+1)g) \\\\&2v_0 = g(2M + 1) \\\\&v_0 = \frac{g(2M + 1)}{2} \qquad\qquad\qquad\qquad (1)\end{align*}$v_0$ と $g$ の間 $(1)$ の関係式が満たされている必要がある。
上で述べたように最高到達点までの移動距離が $h$ であり、そこまでにかかる時間が $M(=N/2)$ であるが、ここでは時間の単位をフレームとしているので $M$ は最高到達点までにかかるフレーム数であり、具体的には $h$ は次のように算出される。
\begin{align*}&\ (v_0 - g) + (v_0 - 2g) + \cdots + (v_0 - Mg) \\\\=&\ v_0 M - (g + 2g + 3g + \cdots + Mg) \\\\=&\ v_0 M - \frac{g(1 + M)M}{2} = h \qquad\qquad\quad (2)\end{align*}ここで $(2)$ の $v_0$ に上記の $(1)$ を代入すると\begin{align*}&\ \frac{g(2M + 1)M}{2} - \frac{g(1 + M)M}{2} \\\\&= \frac{gM}{2}\{(2M + 1) - (1 + M)\} \\\\&= \frac{gM^2}{2} = h\end{align*}すなわち最高到達点までの移動距離 $h$ 及びそこまでにかかるフレーム数 $M$ が既知であれば重力加速度 $g$ は\[g = \frac{2h}{M^2}\qquad\qquad\qquad (3)\]として求められる。
図3 正方形の初期状態 (1辺の長さは 2) 次のプログラムは右図の正方形を真上に投げ上げる処理、簡単に言えば正方形をジャンプさせる処理を実装したものである。この正方形は各辺の長さが $2$ であり、初期状態ではその中心が原点に置かれている。
なおプログラム中で使われるインスタンス変数は上の解説のものと同じであり、t (int型)はフレームカウント、N (int型)はジャンプしてから着地するまでにかかるフレーム数(ここでの設定は $60$ フレーム)、M は N の半分の値、v0 (float型)は初速、g (float型)は重力加速度でありその値はプラスである。
右図の正方形はプログラム中では Obj という名前で使われている。
[Beta1] (実行結果 図4、図5)
初期化ブロック内 9行目の g、及び10行目の v0 の計算は上記解説における $(3)$ 及び $(1)$ の計算をそのまま実装したものである。
5行目のローカル変数 h はここではジャンプによる(垂直方向の)移動距離を表す。開始時点では正方形の下の辺が x軸上、すなわち $y=0$ に置かれているので、h = 5 であればこのジャンプによる正方形の下の辺の最高到達点は $y=5$ である (図4)。
この h の値を変えるだけでジャンプによる移動距離を変えることができる。例えば h = 8 とすれば下の辺の最高到達点は $y=8$ になる (図5)。
h の値を変えることで最高到達点が変わるが、1回のジャンプにかかる時間は変化しない。下図の実行結果に示されるように h = 5 であっても h = 8 であってもジャンプしてから着地するまでの時間は変わらない (いずれも60フレームである)。
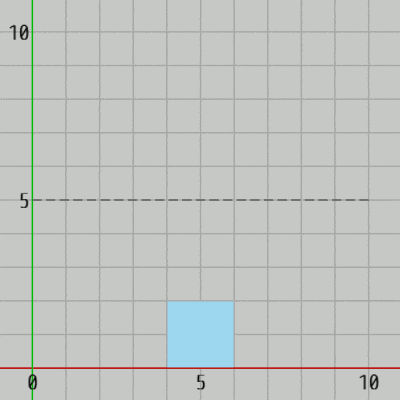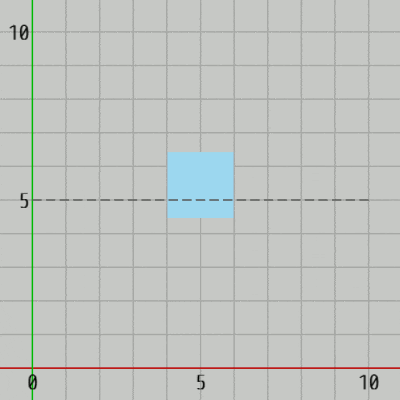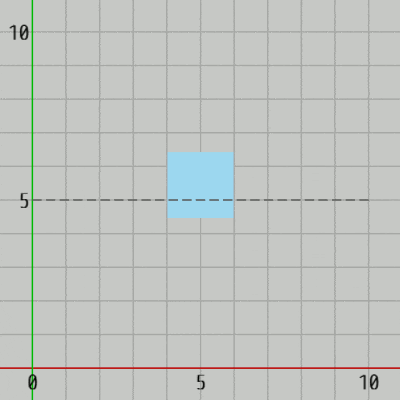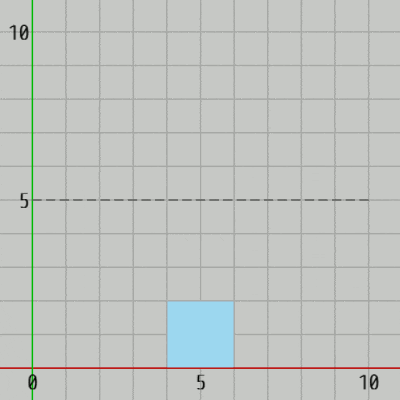
図4 h=5 としたとき 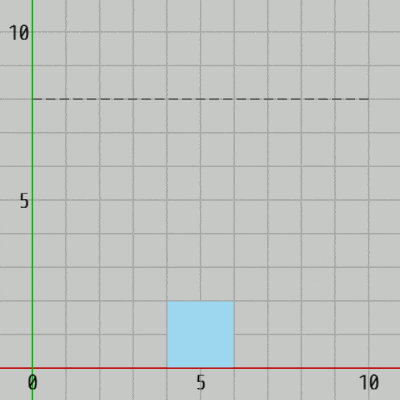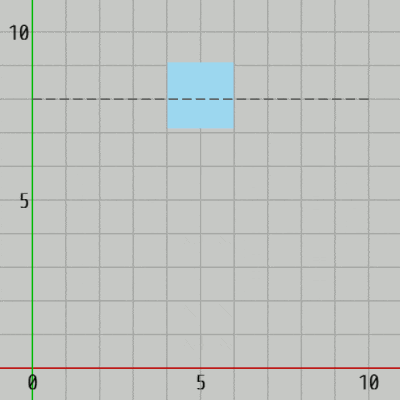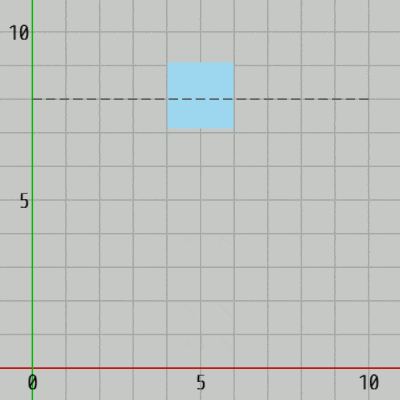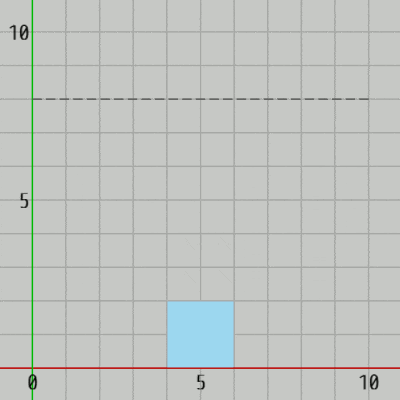
図5 h=8 としたとき
では以上をふまえて本題に入る。
図7はCubeをXZ平面上の適当な位置に置いたときのものであるが、このときのCubeの下の面はXZ平面に接しており、Cubeの中心の y座標は $0.5$ である。

図6 Cube 初期状態 
図7 XZ平面上に置かれたCube (中心の y座標は 0.5)
ここでの課題はこのCubeを用いて下図に示される運動(立方体の回転ジャンプ)を実装することである。
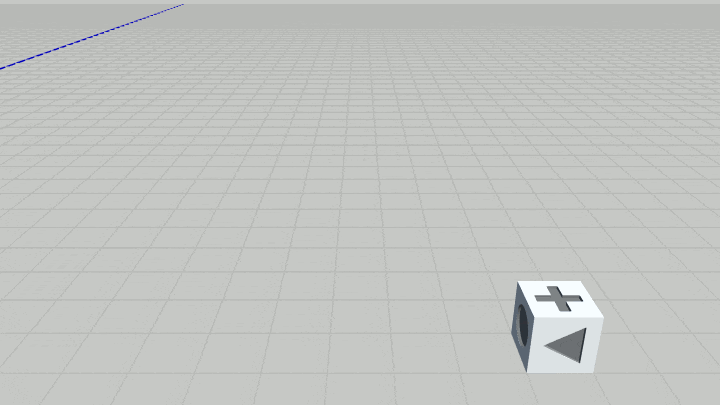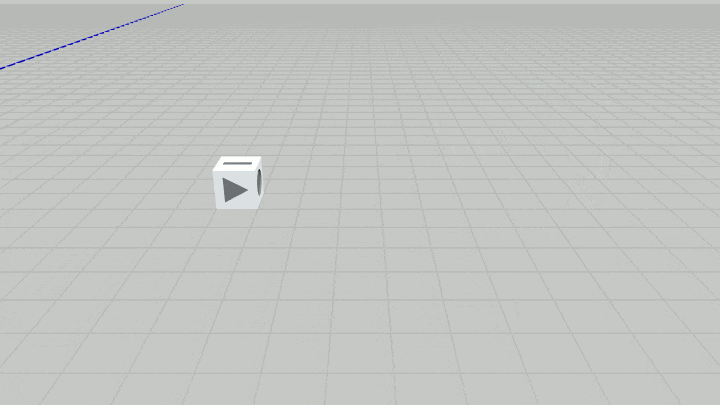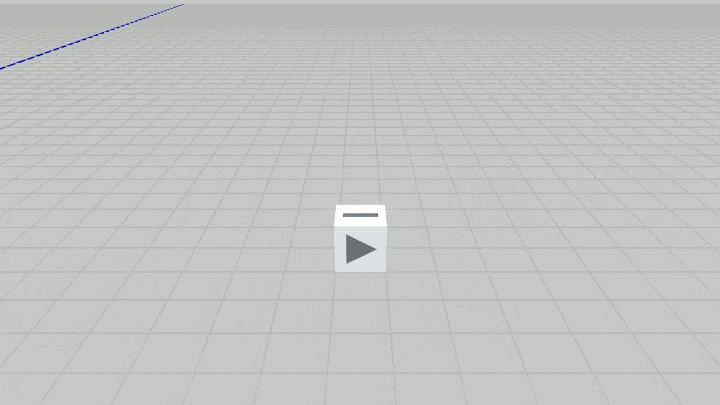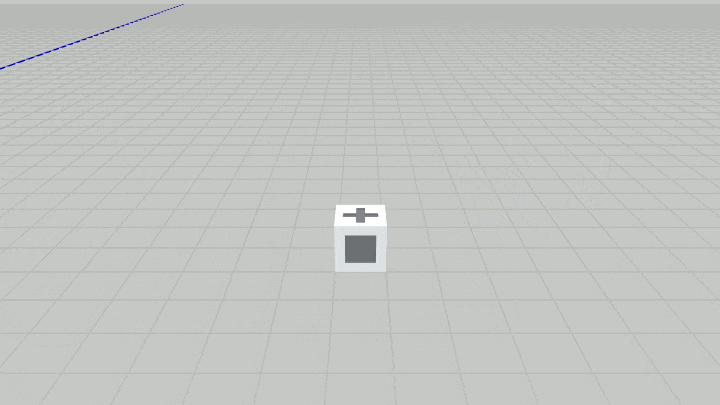
図8 Code1 実行結果
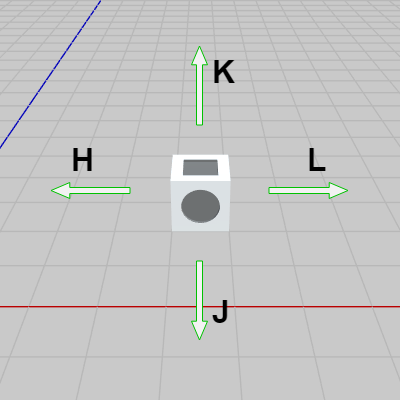
図9 各キーに対応するジャンプの方向 この回転ジャンプはXZ平面上において行われ、x軸プラス方向、x軸マイナス方向、z軸プラス方向、z軸マイナス方向の4方向にジャンプするが、それぞれの方向へのジャンプは次のキー操作によるものとする。
H : x軸マイナス方向へのジャンプ
L : x軸プラス方向へのジャンプ
J : z軸マイナス方向へのジャンプ
K : z軸プラス方向へのジャンプ
なお1回のジャンプにかかる時間や最高到達点の高さ、あるいは1回のジャンプにおける回転角度 及び水平方向(x軸方向、z軸方向)の移動量などは読者に任せる。上図8の場合であれば1回のジャンプは60フレームかけて行われており、1回のジャンプにおける垂直方向の移動量、水平方向の移動量はともに $3$ である。
また上図の場合1回のジャンプにおいてCubeは1回転していない。1回転するためには1回のジャンプにおいてCubeを $360^\circ$ 回転させる必要があるが、そうすると何度ジャンプしてもCubeの同じ面しか表示されなくなる。そのためジャンプするたびに表示される面が変化するように、上の実行結果では1回のジャンプにおける回転角度を $270^\circ$ としている。
そして今回の課題においても必要なインスタンス変数や定数などは読者の側で用意するものとする。
プログラムはCode1に作成するものとする。Code1は始めの段階では以下のコードのみが記述されている。
[Code1]
このまま実行するとXZ平面上の適当な位置に置かれたCubeが表示されるだけである。
(解答例については Sec323_Ans.txt Code1 を参照)
物体を真上に投げ上げる際のある時刻 $t$ における速度 $v$ は、初速を $v_0$、重力加速度を $g$ とするとき\[v = v_0 - gt\]であるが、時間 $t$ をフレームとして考えると1フレーム目の速度は $v_0 - g$、2フレーム目の速度は $v_0 - 2g$、3フレーム目の速度は $v_0 - 3g$ となり、例えばプログラムでは以下のように記述することになる。
t++; v = v0 - g * t;
物体の投げ上げをプログラムで実装する際には各フレームにおける物体の位置を求める必要があるが、毎フレームの移動量を v とし、物体の現在位置(高さ)を pos.y とすれば各フレームにおける物体の位置は
pos.y += v;
まとめると、物体を真上に投げ上げる際の移動処理は以下のように記述すればよい。
t++; Vector2 pos = Obj.GetPosition(); float v = v0 - g * t; pos.y += v; Obj.SetPosition(pos);
以下ではこの鉛直投げ上げにおける初速 $v_0$ 及び重力加速度 $g$ を求めることについて見ていく。
まずは開始地点から最高到達点までにかかる時間(上昇時間)と、最高到達点から開始地点までに戻ってくる時間(落下時間)が同じになるようにすることについて考える。ここではそれぞれ $M(=N/2)$ フレームずつかかるものとする。
ともに $M$ フレームずつかかるので、上昇は $1$~$M$ フレームの間において行われ、落下は $M+1$ ~ $2M(=N)$ フレームの間に行われる。下左図は上昇過程における各フレームでの速度のグラフであり、この合計値が上昇過程における移動量である。下右図は落下過程における各フレームでの速度のグラフであり、この合計値が落下過程における移動量である (上昇時の速度をプラスとし、落下時の速度をマイナスとしている)。


上昇時間と落下時間が同じというのはここでは同じ時間の間に同じ距離を移動するということであり、具体的には上記の2つのグラフの移動量(の絶対値)が同じであることを意味する (左図の上昇過程の移動量はプラスになるが、右図の落下過程の移動量はマイナスになる)。
上昇過程の最後である $M$ フレーム目における速度は $v_0 - Mg$ であり、落下過程の最初である $M+1$ フレーム目における速度は $v_0 - (M+1)g$ であるが、各フレームにおいて速度は $g$ ずつ減少するのでこの2つの速度の絶対値が等しいならば上の2つのグラフの移動量の絶対値も等しくなる。
つまり上昇時間と落下時間が同じであるようにするためには\begin{align*}&v_0 - Mg = -(v_0 - (M+1)g) \\\\&2v_0 = g(2M + 1) \\\\&v_0 = \frac{g(2M + 1)}{2} \qquad\qquad\qquad\qquad (1)\end{align*}$v_0$ と $g$ の間 $(1)$ の関係式が満たされている必要がある。
上で述べたように最高到達点までの移動距離が $h$ であり、そこまでにかかる時間が $M(=N/2)$ であるが、ここでは時間の単位をフレームとしているので $M$ は最高到達点までにかかるフレーム数であり、具体的には $h$ は次のように算出される。
\begin{align*}&\ (v_0 - g) + (v_0 - 2g) + \cdots + (v_0 - Mg) \\\\=&\ v_0 M - (g + 2g + 3g + \cdots + Mg) \\\\=&\ v_0 M - \frac{g(1 + M)M}{2} = h \qquad\qquad\quad (2)\end{align*}ここで $(2)$ の $v_0$ に上記の $(1)$ を代入すると\begin{align*}&\ \frac{g(2M + 1)M}{2} - \frac{g(1 + M)M}{2} \\\\&= \frac{gM}{2}\{(2M + 1) - (1 + M)\} \\\\&= \frac{gM^2}{2} = h\end{align*}すなわち最高到達点までの移動距離 $h$ 及びそこまでにかかるフレーム数 $M$ が既知であれば重力加速度 $g$ は\[g = \frac{2h}{M^2}\qquad\qquad\qquad (3)\]として求められる。

なおプログラム中で使われるインスタンス変数は上の解説のものと同じであり、t (int型)はフレームカウント、N (int型)はジャンプしてから着地するまでにかかるフレーム数(ここでの設定は $60$ フレーム)、M は N の半分の値、v0 (float型)は初速、g (float型)は重力加速度でありその値はプラスである。
右図の正方形はプログラム中では Obj という名前で使われている。
[Beta1] (実行結果 図4、図5)
if (!i_INITIALIZED)
{
Obj.SetPosition(5, 1);
float h = 5.0f;
N = 60;
M = N / 2;
g = 2 * h / (M * M);
v0 = g * (2 * M + 1) / 2.0f;
i_MOVE = false;
i_INITIALIZED = true;
}
if (!i_MOVE && Input.GetKeyDown(KeyCode.S))
{
t = 0;
i_MOVE = true;
}
if(!i_MOVE) { return; }
t++;
Vector2 pos = Obj.GetPosition();
float v = v0 - g * t;
pos.y += v;
Obj.SetPosition(pos);
if(t == N)
{
i_MOVE = false;
}
初期化ブロック内 9行目の g、及び10行目の v0 の計算は上記解説における $(3)$ 及び $(1)$ の計算をそのまま実装したものである。
5行目のローカル変数 h はここではジャンプによる(垂直方向の)移動距離を表す。開始時点では正方形の下の辺が x軸上、すなわち $y=0$ に置かれているので、h = 5 であればこのジャンプによる正方形の下の辺の最高到達点は $y=5$ である (図4)。
この h の値を変えるだけでジャンプによる移動距離を変えることができる。例えば h = 8 とすれば下の辺の最高到達点は $y=8$ になる (図5)。
h の値を変えることで最高到達点が変わるが、1回のジャンプにかかる時間は変化しない。下図の実行結果に示されるように h = 5 であっても h = 8 であってもジャンプしてから着地するまでの時間は変わらない (いずれも60フレームである)。


では以上をふまえて本題に入る。
# Code1
下図6は立方体 Cube の初期状態である。Cubeは各辺の長さが $1$ であり、初期状態においてはその中心が原点に置かれている。図7はCubeをXZ平面上の適当な位置に置いたときのものであるが、このときのCubeの下の面はXZ平面に接しており、Cubeの中心の y座標は $0.5$ である。


ここでの課題はこのCubeを用いて下図に示される運動(立方体の回転ジャンプ)を実装することである。


H : x軸マイナス方向へのジャンプ
L : x軸プラス方向へのジャンプ
J : z軸マイナス方向へのジャンプ
K : z軸プラス方向へのジャンプ
なお1回のジャンプにかかる時間や最高到達点の高さ、あるいは1回のジャンプにおける回転角度 及び水平方向(x軸方向、z軸方向)の移動量などは読者に任せる。上図8の場合であれば1回のジャンプは60フレームかけて行われており、1回のジャンプにおける垂直方向の移動量、水平方向の移動量はともに $3$ である。
また上図の場合1回のジャンプにおいてCubeは1回転していない。1回転するためには1回のジャンプにおいてCubeを $360^\circ$ 回転させる必要があるが、そうすると何度ジャンプしてもCubeの同じ面しか表示されなくなる。そのためジャンプするたびに表示される面が変化するように、上の実行結果では1回のジャンプにおける回転角度を $270^\circ$ としている。
そして今回の課題においても必要なインスタンス変数や定数などは読者の側で用意するものとする。
プログラムはCode1に作成するものとする。Code1は始めの段階では以下のコードのみが記述されている。
[Code1]
if (!i_INITIALIZED)
{
Cube.SetMatrix(TH3DMath.GetTranslation4x4(18.5f, 0.5f, 5.5f));
i_INITIALIZED = true;
}
if ((Input.GetKeyDown(KeyCode.H) || Input.GetKeyDown(KeyCode.J) ||
Input.GetKeyDown(KeyCode.K) || Input.GetKeyDown(KeyCode.L)))
{
}
このまま実行するとXZ平面上の適当な位置に置かれたCubeが表示されるだけである。
(解答例については Sec323_Ans.txt Code1 を参照)
© 2020-2025 Redpoll's 60 (All rights reserved)