Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-9
第3章 3D空間の基礎
$§$3-9 平行移動行列
3D空間における平行移動行列(Translation Matrix)は、以下の$4\times4$行列の形になる。
$(a, b, c)$だけ平行移動させる行列
\[\begin{pmatrix}1 &0 &0 &a \\0 &1 &0 &b \\ 0 &0 &1 &c \\0 &0 &0 &1\end{pmatrix}\]つまり、3D空間上の平行移動行列を作成するためには、x軸方向の移動量$a$、y軸方向の移動量$b$、z軸方向の移動量$c$ の3つのデータを指定する必要がある (プログラムにおいて使用してきたVector3構造体は3つの数値を保持できるので、平行移動行列を作成する際にはVector3インスタンスが1つあればよい)。
3-7節でも述べたように、3D空間における回転やスケールは$3\times3$行列で表すことができるが、平行移動は$4\times4$行列でなければ表せない。
複数の変換の合成は、それらの変換に対応する行列の積で表すが、この積を可能にするために回転行列やスケール行列は、$3\times3$行列を1次元拡張して$4\times4$行列にしたものが使われる(この拡張は平行移動行列との積を可能にするために、平行移動行列に次数を合わせているわけである)。
そして、3D空間で点$(x, y, z)$を行列によって変換する場合も、同次座標として1次元拡張した$(x, y, z, 1)$の形のものを計算で使用する。
まずは、平行移動行列による点の移動から見ていこう。
点$(x, y, z)$をベクトル$(a, b, c)$だけ移動させる計算を以下に示す。
\[\begin{pmatrix}x \\y \\z\end{pmatrix}+\begin{pmatrix}a \\b \\c\end{pmatrix}= \begin{pmatrix}x + a \\y + b \\ z + c \end{pmatrix}\]行列計算による結果は同次座標なので、4次元目の座標(w座標)に1があるが、これを取り除いて考えれば上の2つの計算は同じことをしているのである。
(例)
点$P=(1,\ 5,\ 2)$を平行移動行列によって$(4, -2, -3)$だけ移動させる。
\[\begin{pmatrix}1 &0 &0 &4 \\0 &1 &0 &-2 \\ 0 &0 &1 &-3 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}1 \\5 \\2 \\1\end{pmatrix}=\begin{pmatrix}1 + 4 \\5 - 2 \\ 2 - 3 \\ 1\end{pmatrix}=\begin{pmatrix}5 \\3 \\ -1 \\ 1\end{pmatrix}\]
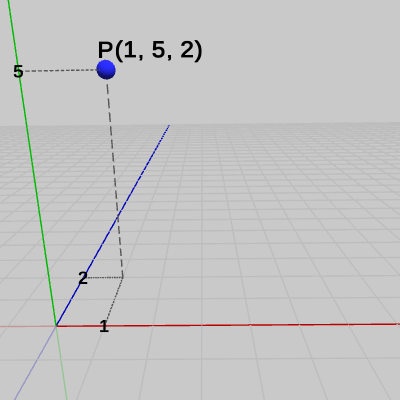
図1 点P=(1, 5, 2) 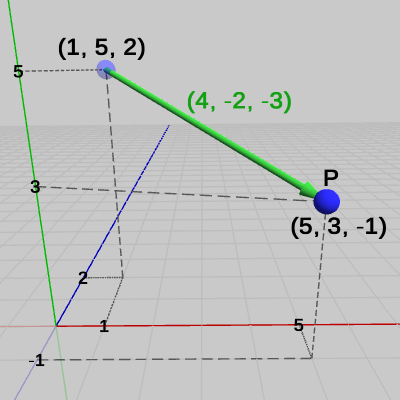
図2 (4, -2, -3)だけ移動した点P=(5, 3, -1)
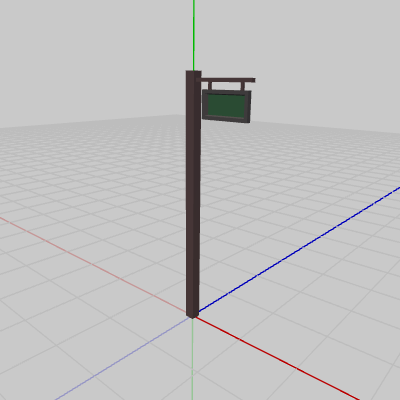
図3 Signboard1 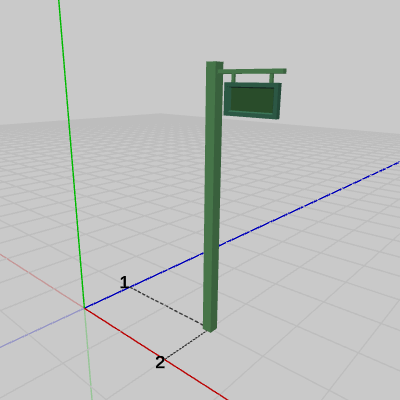
図4 Signboard2
図3のオブジェクトSignboard1は、初期状態でオブジェクトの底面の中心が原点に置かれている。図4のオブジェクトSignboard2は、初期状態でオブジェクトの底面の中心が$(2,\ 0,\ 1)$に置かれている。
復習のために言い換えると、図3、図4はこれらのオブジェクトに次のコードを実行した結果である。
では、実際にこの2つのオブジェクトに平行移動行列を実行しよう。
(3D空間での)平行移動行列を取得するにあたっては、カスタムライブラリーの次のメソッドを使用する。
$(a, b, c)$だけ平行移動させる行列を取得する。
引数の型が違うが、次のメソッドも同じ役割である。
どちらとも、戻り値は$4\times4$の平行移動行列を表す Matrix4x4型のインスタンスである。
次のプログラムは、$(3, 0, 3)$だけ平行移動させる行列を取得して、上記のオブジェクトに実行する処理である。
図5はこのプログラムをSignboard1に対して実行した結果であり、図6はSignboard2に対して実行した結果である。
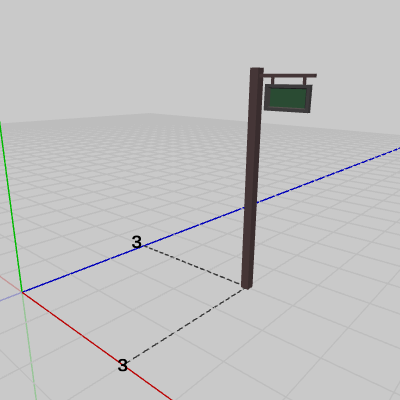
図5 Signboard1の底面の中心は(3, 0, 3)へ移動する 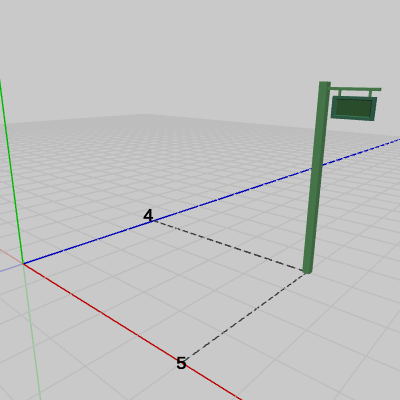
図6 Signboard2の底面の中心は(5, 0, 4)へ移動する
初期状態でのSignboard1の底面の中心は原点に置かれていた。そこから、$(3, 0, 3)$だけ移動させたので、\[\begin{pmatrix}0 \\0 \\ 0 \end{pmatrix}+\begin{pmatrix}3 \\0 \\ 3 \end{pmatrix}=\begin{pmatrix}3 \\0 \\ 3 \end{pmatrix}\]底面の中心は、$(3, 0, 3)$に移動することになる。
初期状態でのSignboard2の底面の中心は$(2, 0, 1)$に置かれていた。そこから、$(3, 0, 3)$だけ移動させたので、\[\begin{pmatrix}2 \\0 \\ 1 \end{pmatrix}+\begin{pmatrix}3 \\0 \\ 3 \end{pmatrix}=\begin{pmatrix}5 \\0 \\ 4 \end{pmatrix}\]底面の中心は、$(5, 0, 4)$に移動することになる。
ここからは、オブジェクトの平行移動に関してやや詳しく見ていく。
オブジェクトを指定されたベクトルだけ平行移動させることは、オブジェクトの初期状態において原点に位置する部分をそのベクトルで表される位置に平行移動させることを意味する。「オブジェクトの初期状態において原点に位置する部分」を、ここではオブジェクト原点と呼ぶことにする。Signboard1、Signboard2におけるオブジェクト原点を図7、図8に示す(黄色い点で示されている)。
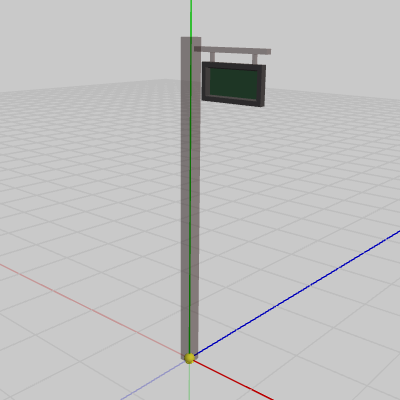
図7 Signboard1のオブジェクト原点 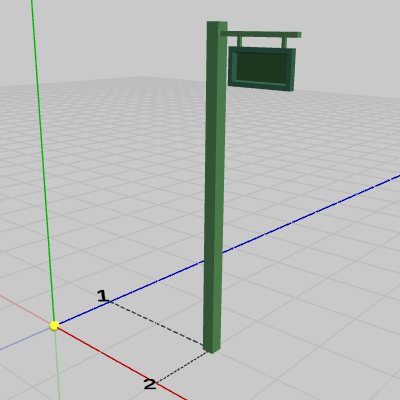
図8 Signboard2のオブジェクト原点
図7のSignboard1の場合では、オブジェクト原点はSignboard1の底面の中央にある。つまり、Signboard1のオブジェクト原点はSignboard1に含まれている。図8のSignboard2の場合では、オブジェクト原点はSignboard2の底面の中央と$(2,\ 0,\ 1)$だけ離れている。つまり、Signboard2のオブジェクト原点はSignboard2に含まれてはいないのである。
上で述べたように、オブジェクトを指定されたベクトルだけ平行移動させることは、オブジェクト原点をそのベクトルで表される位置に平行移動させることを意味する。したがって、上の例のようにオブジェクトを$(3,\ 0,\ 3)$だけ平行移動させることは、オブジェクト原点を$(3,\ 0,\ 3)$に平行移動させることになる。Signboard1、Signboard2を例にとると次の図9、図10のようになる。
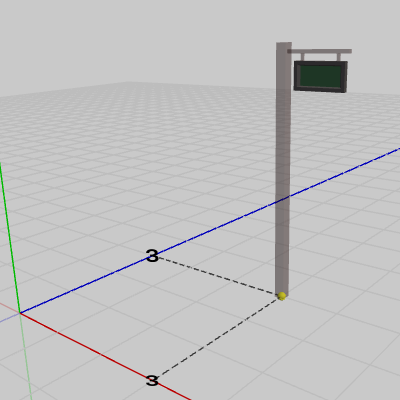
図9 Signboard1のオブジェクト原点は(3, 0, 3)へ移動する 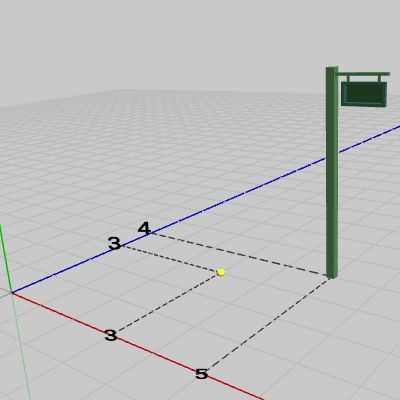
図10 Signboard2のオブジェクト原点は(3, 0, 3)へ移動する
オブジェクトに平行移動を実行した後でも、オブジェクトとオブジェクト原点の位置関係は初期状態と変わらない。
この例のように、$(3,\ 0,\ 3)$移動させた後でも、Signboard1のオブジェクト原点はSignboard1の底面の中央にあり、Signboard2のオブジェクト原点はSignboard2の底面の中央と$(2,\ 0,\ 1)$だけ離れている。オブジェクトの平行移動では、オブジェクトとオブジェクト原点が同じだけ動くのでこのことは明らかであろう。
オブジェクトを平行移動行列によって運動させる場合には、毎フレーム平行移動行列に移動先の位置を指定する。例えば、オブジェクトを円周上で運動させる場合には、毎フレーム円周上の位置を計算して、その位置を平行移動行列に指定する。ただし、実際に平行移動行列に指定される位置に移動するのは、オブジェクト原点である。言い換えれば、各フレームでの平行移動行列に指定される位置をプロットしたものは、(オブジェクトが運動する際の)オブジェクト原点の軌跡に一致する。そのことを簡単な例を用いて以下に示そう。
次のプログラムは、Signboard1、Signboard2を、原点中心の半径3の円周上でy軸周りに運動させるものである(実行結果は図11、図12)。
2行目のrevはy軸周りに角度i_degRevだけ回転させる行列で、1行目からわかるように毎フレーム回転角度は$1$°ずつ増加する。3行目では、半径3の円周上を$(3,\ 0,\ 0)$から角度i_degRevだけ進んだ位置npを計算している。4行目のTはSignboardを移動させる平行移動行列である。この平行移動行列Tを求める際に、移動先の位置としてnpを指定している。このnpは、$(3,\ 0,\ 0)$を開始位置として円周上を毎フレーム$1$°ずつ進んでいくが、上で述べたように実際にこの円周上を運動するのはSignboardのオブジェクト原点である。
図11、図12は上のプログラムをSignboard1、Signboard2に対して実行した結果である。このアニメーションを見ればわかるように、原点中心の半径3の円周上を運動しているのは、どちらの場合においてもSignboardのオブジェクト原点である。そして、運動中であってもオブジェクトとオブジェクト原点の位置関係は初期状態と変わらないので、Signboard1の場合は常にオブジェクト原点はSignboard1の底面の中央にあり、Signboard2の場合は常にオブジェクト原点はSignboard2の底面の中央と$(2,\ 0,\ 1)$だけ離れている。したがって、Signboard2の底面の中央は常にオブジェクト原点と$(2,\ 0,\ 1)$だけ離れて運動することになるので、その運動の軌跡は$(2,\ 0,\ 1)$を中心とする半径3の円周になるのである(図12の薄い円)。
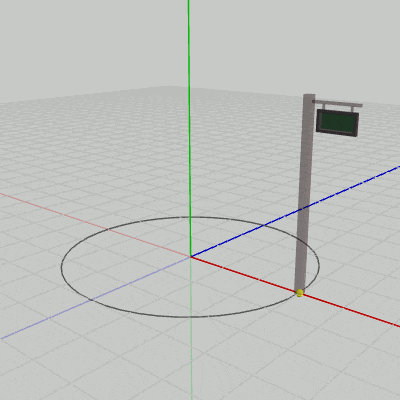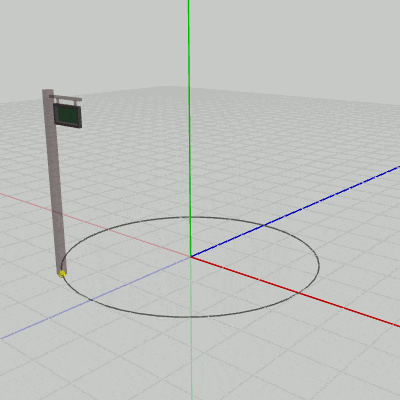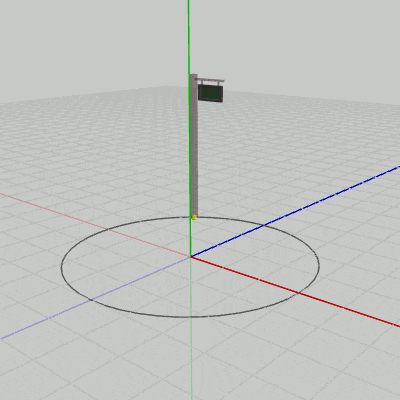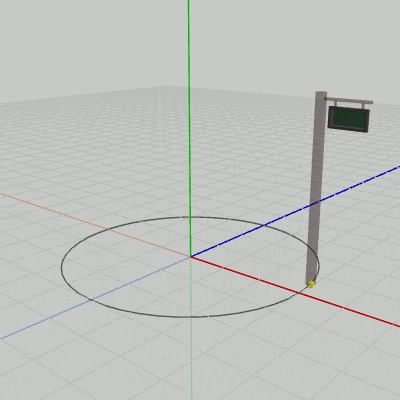
図11 Signboard1に対してプログラムを実行した結果 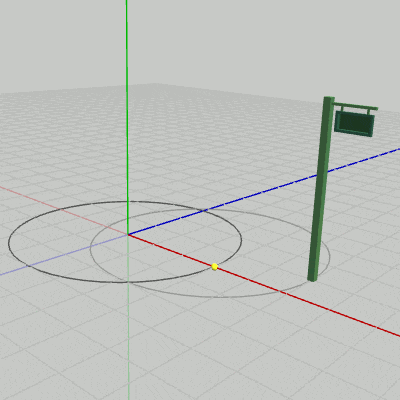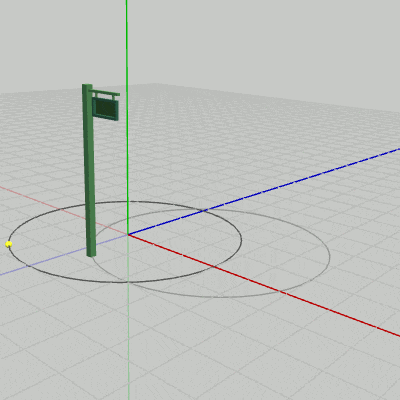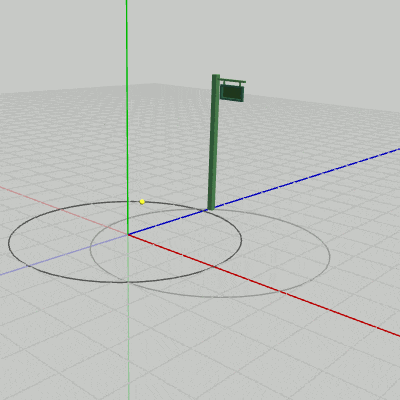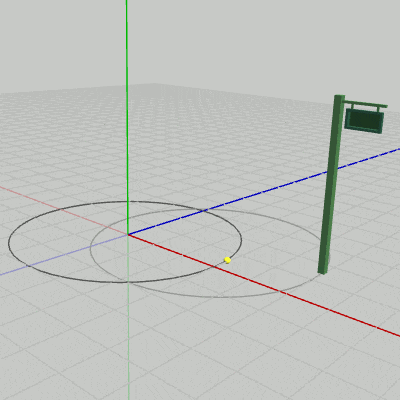
図12 Signboard2に対してプログラムを実行した結果
以下補足。
この処理は、objの位置を$(a, b, c)$だけ移動させるものであるという捉え方が望ましい。つまり、平行移動行列Tはobjを初期状態の位置からx軸方向に$a$、y軸方向に$b$、z軸方向に$c$だけ動かすものである。objの位置を$(a, b, c)$に移動させるという捉え方は正確ではない。$(a, b, c)$に移動するのはobjのオブジェクト原点である。
Unity標準の方法で平行移動を行う際にも同じことがいえる。
後の章でも解説するが、例えば、
この処理は、objを初期状態の位置から$(a, b, c)$だけ移動させる処理であるが、実際に$(a, b, c)$に移動するのはobjのオブジェクト原点である。また、オブジェクト原点が初期状態の位置から動いていないのであれば transform.localPosition の値は $(0, 0, 0)$ である。
(本節において「オブジェクト原点」と呼んできたものは、詳しくは「ローカル座標系」と呼ばれる座標系の原点と同じものである。ローカル座標系については第4章で解説する。)
最後に、本節の内容に関するプログラムを作成する。
点$P=(1,\ 5,\ 2)$を平行移動行列によって$(4, -2, -3)$だけ移動させる。
[Code1] (実行結果 図13)

図13 Code1 実行結果 4行目ではMatrix4x4型のTとVector4型のPの積をVector3型へセットしている。こういった記述は今までにも何度か説明したが、Unityでは このようにVector4型で返される値をVector3型にセットすると自動的に w座標は取り除かれて x座標、y座標、z座標のみがセットされる。$4\times4$の平行移動行列、回転行列、スケール行列と同次座標化された4次元ベクトルとの積の w座標は常に$1$なので、こういった自動的な切り取りは効率的なのである。
[Code2] (実行結果 図5、図6)
1行目のインスタンス変数 i_SB の値を$1$にすると Signboard1の場合で実行され、それ以外の値にすると Signboard2の場合で実行される (それぞれの実行結果は図5、図6)。
このプログラムも上で見たものと処理は同じである。
[Code3] (実行結果 図11、図12)
1行目のインスタンス変数 i_SB の値を$1$にすると Signboard1の場合で実行され、それ以外の値にすると Signboard2の場合で実行される (それぞれの実行結果は図11、図12)。
下図14の立方体を図15のように切断したとする。点$A$、$B$は各辺の中点であり、点$M$は辺$AB$の中点、点$N$は辺$CD$ の中点である。
図14 立方体 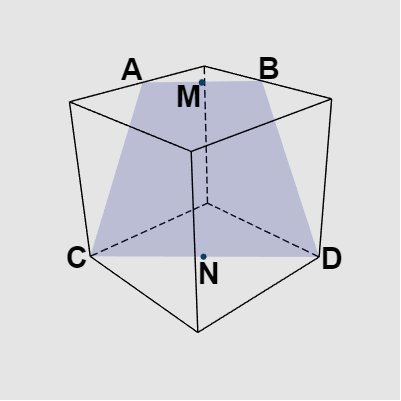
図15 立方体の切断面 (点Mは辺ABの中点。点Nは辺CDの中点)
切断後の立方体は2つの部分に分かれるが、以下の図16、図17はその2つの部分であり、ここでは便宜上 Part1、Part2 で呼び分ける。
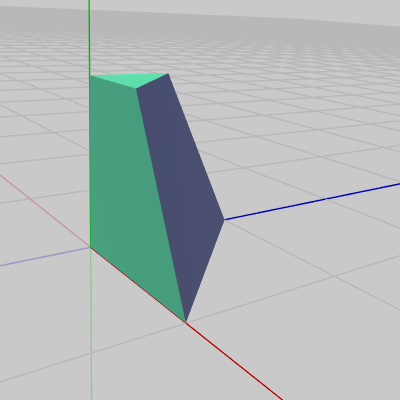
図16 Part1 初期状態 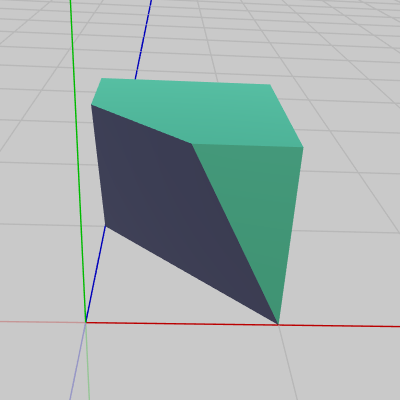
図17 Part2 初期状態
図16、図17はPart1、Part2の初期状態であり、この2つを初期状態のまま表示すると上図14のように通常の立方体になる (Part1、Part2は初期状態において完全に接着した状態になる)。
ここでの課題は、上図15に示される2点$M$、$N$を結んでできる辺$MN$に沿ってPart2を滑らせる(平行移動させる)プログラムの作成である。
その際には次のキー操作によってPart2を滑らせるものとする。
J : Part2を辺$MN$に沿って下に滑らせる。
K : Part2を辺$MN$に沿って上に滑らせる。
プログラムで使用する定数は以下のとおり。
また、このプログラムではPart2を平行移動させていく際に、Part2の現在地(オブジェクト原点の位置)が必要になるが、そのためにはカスタムライブラリーで用意されている次のメソッドを使えばよい。
例えば、Part2の現時点でのオブジェクト原点の位置を取得するためには以下のように記述する。
現時点でのオブジェクト原点の位置は言い換えれば、オブジェクトが初期状態からどれだけ平行移動をしたかを表すものでもある。上図17はPart2の初期状態であるが、Part2は原点から離れた位置に置かれている。しかし、この時点では初期状態であり、平行移動が行われているわけではないので、図17のPart2に GetWorldPosition() を実行しても返される値は $(0, 0, 0)$ である。
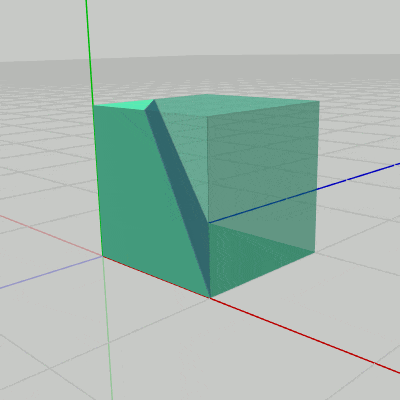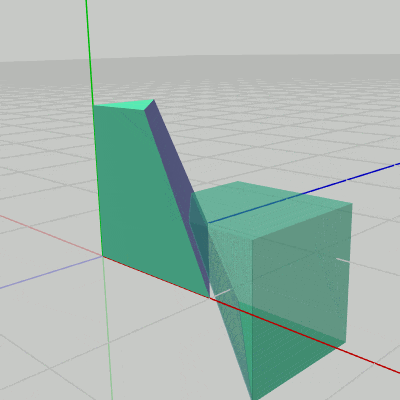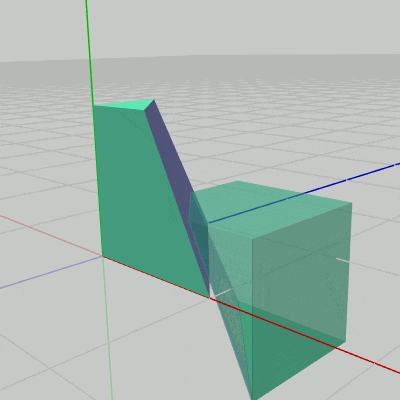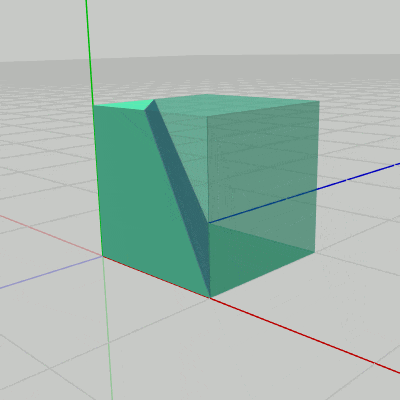
図18 Code4 実行結果 プログラムの作成は Sec309.cs内のCode4に行うものとする (Code4は何も記述されていない空のメソッドである)。なお、このプログラムではPart2は半透明で表示されるが、Tキーを押すことで半透明と不透明の切り替えが行える。
解答例については Sec309_Ans.txt を参照 (Sec309_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
$(a, b, c)$だけ平行移動させる行列
\[\begin{pmatrix}1 &0 &0 &a \\0 &1 &0 &b \\ 0 &0 &1 &c \\0 &0 &0 &1\end{pmatrix}\]つまり、3D空間上の平行移動行列を作成するためには、x軸方向の移動量$a$、y軸方向の移動量$b$、z軸方向の移動量$c$ の3つのデータを指定する必要がある (プログラムにおいて使用してきたVector3構造体は3つの数値を保持できるので、平行移動行列を作成する際にはVector3インスタンスが1つあればよい)。
3-7節でも述べたように、3D空間における回転やスケールは$3\times3$行列で表すことができるが、平行移動は$4\times4$行列でなければ表せない。
複数の変換の合成は、それらの変換に対応する行列の積で表すが、この積を可能にするために回転行列やスケール行列は、$3\times3$行列を1次元拡張して$4\times4$行列にしたものが使われる(この拡張は平行移動行列との積を可能にするために、平行移動行列に次数を合わせているわけである)。
そして、3D空間で点$(x, y, z)$を行列によって変換する場合も、同次座標として1次元拡張した$(x, y, z, 1)$の形のものを計算で使用する。
まずは、平行移動行列による点の移動から見ていこう。
A) 点の平行移動
3D空間内の点$(x, y, z)$を平行移動行列によって$(a, b, c)$だけ移動させる計算を以下に示す。\[\begin{pmatrix}1 &0 &0 &a \\0 &1 &0 &b \\ 0 &0 &1 &c \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}x \\y \\z \\1\end{pmatrix}=\begin{pmatrix}1\cdot x + 0\cdot y + 0\cdot z + a\cdot 1 \\0\cdot x + 1\cdot y + 0\cdot z + b\cdot 1 \\ 0\cdot x + 0\cdot y + 1\cdot z + c\cdot 1 \\0\cdot x + 0\cdot y + 0\cdot z + 1\cdot 1 \end{pmatrix}=\begin{pmatrix}x + a \\y + b \\ z + c \\ 1\end{pmatrix}\]
この計算からわかるように、ある点を平行移動行列によって移動させることは、3-2節で扱った、ある点をベクトル加算によって移動させることと同じである。点$(x, y, z)$をベクトル$(a, b, c)$だけ移動させる計算を以下に示す。
\[\begin{pmatrix}x \\y \\z\end{pmatrix}+\begin{pmatrix}a \\b \\c\end{pmatrix}= \begin{pmatrix}x + a \\y + b \\ z + c \end{pmatrix}\]行列計算による結果は同次座標なので、4次元目の座標(w座標)に1があるが、これを取り除いて考えれば上の2つの計算は同じことをしているのである。
(例)
点$P=(1,\ 5,\ 2)$を平行移動行列によって$(4, -2, -3)$だけ移動させる。
\[\begin{pmatrix}1 &0 &0 &4 \\0 &1 &0 &-2 \\ 0 &0 &1 &-3 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}1 \\5 \\2 \\1\end{pmatrix}=\begin{pmatrix}1 + 4 \\5 - 2 \\ 2 - 3 \\ 1\end{pmatrix}=\begin{pmatrix}5 \\3 \\ -1 \\ 1\end{pmatrix}\]


B) オブジェクトに平行移動行列を実行する
以下の2つのオブジェクトに平行移動行列を実行する。

図3のオブジェクトSignboard1は、初期状態でオブジェクトの底面の中心が原点に置かれている。図4のオブジェクトSignboard2は、初期状態でオブジェクトの底面の中心が$(2,\ 0,\ 1)$に置かれている。
復習のために言い換えると、図3、図4はこれらのオブジェクトに次のコードを実行した結果である。
// # : 1 or 2 Signboard#.SetMatrix(Matrix4x4.identity);
では、実際にこの2つのオブジェクトに平行移動行列を実行しよう。
(3D空間での)平行移動行列を取得するにあたっては、カスタムライブラリーの次のメソッドを使用する。
$(a, b, c)$だけ平行移動させる行列を取得する。
TH3DMath.GetTranslation4x4(float a, float b, float c)
TH3DMath.GetTranslation4x4(Vector3 v)
次のプログラムは、$(3, 0, 3)$だけ平行移動させる行列を取得して、上記のオブジェクトに実行する処理である。
Matrix4x4 T = TH3DMath.GetTranslation4x4(3.0f, 0.0f, 3.0f); Signboard#.SetMatrix(T); // # : 1 or 2
図5はこのプログラムをSignboard1に対して実行した結果であり、図6はSignboard2に対して実行した結果である。


初期状態でのSignboard1の底面の中心は原点に置かれていた。そこから、$(3, 0, 3)$だけ移動させたので、\[\begin{pmatrix}0 \\0 \\ 0 \end{pmatrix}+\begin{pmatrix}3 \\0 \\ 3 \end{pmatrix}=\begin{pmatrix}3 \\0 \\ 3 \end{pmatrix}\]底面の中心は、$(3, 0, 3)$に移動することになる。
初期状態でのSignboard2の底面の中心は$(2, 0, 1)$に置かれていた。そこから、$(3, 0, 3)$だけ移動させたので、\[\begin{pmatrix}2 \\0 \\ 1 \end{pmatrix}+\begin{pmatrix}3 \\0 \\ 3 \end{pmatrix}=\begin{pmatrix}5 \\0 \\ 4 \end{pmatrix}\]底面の中心は、$(5, 0, 4)$に移動することになる。
ここからは、オブジェクトの平行移動に関してやや詳しく見ていく。
オブジェクトを指定されたベクトルだけ平行移動させることは、オブジェクトの初期状態において原点に位置する部分をそのベクトルで表される位置に平行移動させることを意味する。「オブジェクトの初期状態において原点に位置する部分」を、ここではオブジェクト原点と呼ぶことにする。Signboard1、Signboard2におけるオブジェクト原点を図7、図8に示す(黄色い点で示されている)。


図7のSignboard1の場合では、オブジェクト原点はSignboard1の底面の中央にある。つまり、Signboard1のオブジェクト原点はSignboard1に含まれている。図8のSignboard2の場合では、オブジェクト原点はSignboard2の底面の中央と$(2,\ 0,\ 1)$だけ離れている。つまり、Signboard2のオブジェクト原点はSignboard2に含まれてはいないのである。
上で述べたように、オブジェクトを指定されたベクトルだけ平行移動させることは、オブジェクト原点をそのベクトルで表される位置に平行移動させることを意味する。したがって、上の例のようにオブジェクトを$(3,\ 0,\ 3)$だけ平行移動させることは、オブジェクト原点を$(3,\ 0,\ 3)$に平行移動させることになる。Signboard1、Signboard2を例にとると次の図9、図10のようになる。


オブジェクトに平行移動を実行した後でも、オブジェクトとオブジェクト原点の位置関係は初期状態と変わらない。
この例のように、$(3,\ 0,\ 3)$移動させた後でも、Signboard1のオブジェクト原点はSignboard1の底面の中央にあり、Signboard2のオブジェクト原点はSignboard2の底面の中央と$(2,\ 0,\ 1)$だけ離れている。オブジェクトの平行移動では、オブジェクトとオブジェクト原点が同じだけ動くのでこのことは明らかであろう。
オブジェクトを平行移動行列によって運動させる場合には、毎フレーム平行移動行列に移動先の位置を指定する。例えば、オブジェクトを円周上で運動させる場合には、毎フレーム円周上の位置を計算して、その位置を平行移動行列に指定する。ただし、実際に平行移動行列に指定される位置に移動するのは、オブジェクト原点である。言い換えれば、各フレームでの平行移動行列に指定される位置をプロットしたものは、(オブジェクトが運動する際の)オブジェクト原点の軌跡に一致する。そのことを簡単な例を用いて以下に示そう。
次のプログラムは、Signboard1、Signboard2を、原点中心の半径3の円周上でy軸周りに運動させるものである(実行結果は図11、図12)。
i_degRev++; Matrix4x4 rev = TH3DMath.GetRotation4x4(i_degRev, Vector3.up); Vector3 np = rev * new Vector4(3.0f, 0.0f, 0.0f, 1.0f); Matrix4x4 T = TH3DMath.GetTranslation4x4(np); Signboard#.SetMatrix(T); // # : 1 or 2
2行目のrevはy軸周りに角度i_degRevだけ回転させる行列で、1行目からわかるように毎フレーム回転角度は$1$°ずつ増加する。3行目では、半径3の円周上を$(3,\ 0,\ 0)$から角度i_degRevだけ進んだ位置npを計算している。4行目のTはSignboardを移動させる平行移動行列である。この平行移動行列Tを求める際に、移動先の位置としてnpを指定している。このnpは、$(3,\ 0,\ 0)$を開始位置として円周上を毎フレーム$1$°ずつ進んでいくが、上で述べたように実際にこの円周上を運動するのはSignboardのオブジェクト原点である。
図11、図12は上のプログラムをSignboard1、Signboard2に対して実行した結果である。このアニメーションを見ればわかるように、原点中心の半径3の円周上を運動しているのは、どちらの場合においてもSignboardのオブジェクト原点である。そして、運動中であってもオブジェクトとオブジェクト原点の位置関係は初期状態と変わらないので、Signboard1の場合は常にオブジェクト原点はSignboard1の底面の中央にあり、Signboard2の場合は常にオブジェクト原点はSignboard2の底面の中央と$(2,\ 0,\ 1)$だけ離れている。したがって、Signboard2の底面の中央は常にオブジェクト原点と$(2,\ 0,\ 1)$だけ離れて運動することになるので、その運動の軌跡は$(2,\ 0,\ 1)$を中心とする半径3の円周になるのである(図12の薄い円)。


以下補足。
Matrix4x4 T = TH3DMath.GetTranslation4x4(a, b, c); obj.SetMatrix(T);
Unity標準の方法で平行移動を行う際にも同じことがいえる。
後の章でも解説するが、例えば、
obj.transform.localPosition = new Vector3(a, b, c);
(本節において「オブジェクト原点」と呼んできたものは、詳しくは「ローカル座標系」と呼ばれる座標系の原点と同じものである。ローカル座標系については第4章で解説する。)
最後に、本節の内容に関するプログラムを作成する。
# Code1
このプログラムは本節の始めで見た計算例である。点$P=(1,\ 5,\ 2)$を平行移動行列によって$(4, -2, -3)$だけ移動させる。
[Code1] (実行結果 図13)
Vector4 P = new Vector4(1.0f, 5.0f, 2.0f, 1.0f); Matrix4x4 T = TH3DMath.GetTranslation4x4(4.0f, -2.0f, -3.0f); Vector3 P1 = T * P; Debug.Log(P1);

# Code2
これも本節で扱ったもので、初期状態の Signboardを $(3, 0, 3)$ だけ移動させるプログラムである。[Code2] (実行結果 図5、図6)
i_SB = 1;
Matrix4x4 T = TH3DMath.GetTranslation4x4(3.0f, 0.0f, 3.0f);
if (i_SB == 1)
{
Signboard1.SetMatrix(T);
}
else
{
Signboard2.SetMatrix(T);
}
1行目のインスタンス変数 i_SB の値を$1$にすると Signboard1の場合で実行され、それ以外の値にすると Signboard2の場合で実行される (それぞれの実行結果は図5、図6)。
# Code3
続いて、Signboardをある円周上で回転させるプログラムである。このプログラムも上で見たものと処理は同じである。
[Code3] (実行結果 図11、図12)
i_SB = 1;
i_degRev++;
Matrix4x4 rev = TH3DMath.GetRotation4x4(i_degRev, Vector3.up);
Vector3 np = rev * new Vector4(3.0f, 0.0f, 0.0f, 1.0f);
Matrix4x4 T = TH3DMath.GetTranslation4x4(np);
if (i_SB == 1)
{
Signboard1.SetMatrix(T);
}
else
{
Signboard2.SetMatrix(T);
}
1行目のインスタンス変数 i_SB の値を$1$にすると Signboard1の場合で実行され、それ以外の値にすると Signboard2の場合で実行される (それぞれの実行結果は図11、図12)。
# Code4
このプログラムは読者用の課題である。下図14の立方体を図15のように切断したとする。点$A$、$B$は各辺の中点であり、点$M$は辺$AB$の中点、点$N$は辺$CD$ の中点である。


切断後の立方体は2つの部分に分かれるが、以下の図16、図17はその2つの部分であり、ここでは便宜上 Part1、Part2 で呼び分ける。


図16、図17はPart1、Part2の初期状態であり、この2つを初期状態のまま表示すると上図14のように通常の立方体になる (Part1、Part2は初期状態において完全に接着した状態になる)。
ここでの課題は、上図15に示される2点$M$、$N$を結んでできる辺$MN$に沿ってPart2を滑らせる(平行移動させる)プログラムの作成である。
その際には次のキー操作によってPart2を滑らせるものとする。
J : Part2を辺$MN$に沿って下に滑らせる。
K : Part2を辺$MN$に沿って上に滑らせる。
プログラムで使用する定数は以下のとおり。
A, B, C, D
: 上図15の各点$A$、$B$、$C$、$D$の位置を表す定数 (いずれもVector3型)。また、このプログラムではPart2を平行移動させていく際に、Part2の現在地(オブジェクト原点の位置)が必要になるが、そのためにはカスタムライブラリーで用意されている次のメソッドを使えばよい。
GetWorldPosition()
: 現時点でのオブジェクト原点の位置をVector3型で返すメソッド。例えば、Part2の現時点でのオブジェクト原点の位置を取得するためには以下のように記述する。
Vector3 pos = Part2.GetWorldPosition();
現時点でのオブジェクト原点の位置は言い換えれば、オブジェクトが初期状態からどれだけ平行移動をしたかを表すものでもある。上図17はPart2の初期状態であるが、Part2は原点から離れた位置に置かれている。しかし、この時点では初期状態であり、平行移動が行われているわけではないので、図17のPart2に GetWorldPosition() を実行しても返される値は $(0, 0, 0)$ である。

解答例については Sec309_Ans.txt を参照 (Sec309_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
© 2020-2025 Redpoll's 60 (All rights reserved)