Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-16
第3章 3D空間の基礎
$§$3-16 一体化運動についての復習
第2章の前半では2つあるいは3つのオブジェクトの一体化した運動について、やや詳しく見てきた。そこで扱われた運動は、2D空間における2Dオブジェクトの運動であった。
本節では第2章において扱った一体化運動と同様のものを、3D空間において3Dオブジェクトを用いて実装する。すなわち本節は3Dオブジェクトを使った、一体化運動についての復習である。
コンピューターグラフィックスにおけるオブジェクトの運動、特に複数のオブジェクトの一体化した運動を実装する際の原理自体は3Dオブジェクトであれ2Dオブジェクトであれ変わらない。コンピューターグラフィックスにおいてオブジェクトを動かす際にプログラマーに必要とされるのは結局、行列的思考なのである。
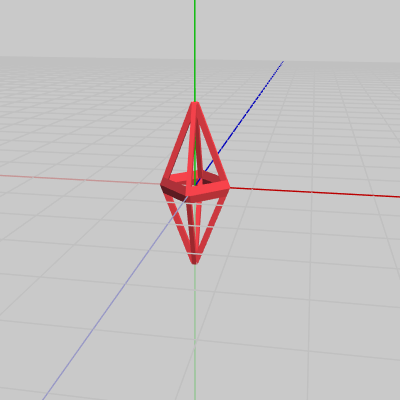
図1 Octah 初期状態 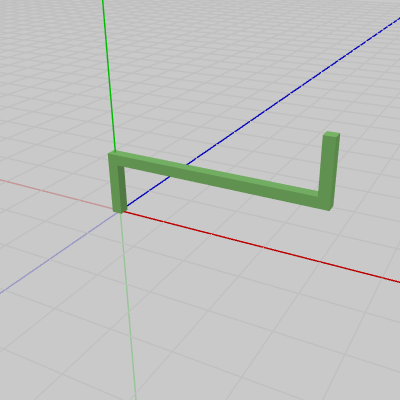
図2 Handle 初期状態

図3 Stand 初期状態 
図4 オブジェクトの階層構造
各図はそれぞれのオブジェクトの初期状態であり、プログラムにおいては Octah(図1)、Handle(図2)、Stand(図3) という名前で使われる。
図4はオブジェクトの階層構造で、一番上の親オブジェクトがStand、Standの子オブジェクトがHandle、Handleの子オブジェクトがOctahである。
以下のプログラムは、OctahとHandleを一体化させるものである。
[Beta1] (実行結果 図5)
1行目の行列 localOctah の内容はOctahを初期状態からHandle先端のアタッチポジションまで移動させるものである (c_attachPos_OctahはHandle先端までの移動量を表すVector3型の定数)。
Octahに実行される行列は4行目の worldOctah であるが、それは localOctah と localHandle の積であり、その内容は まず localOctah が実行され、その次に localHandle が実行される。しかし、localHandle の内容はここではidentity行列であるため(プログラム2行目)、localHandle 自体は何も変換を行わない行列である。したがって、実際にOctahに実行される変換はHandle先端までの移動(localOctah)のみである。Handleに実行される行列 worldHandle (5行目)は、localHandle のコピーでありその内容はidentity行列であるので、Handleに対して worldHandle を実行しても何も変化は起こらない。
実行結果(図5)に見られるように、OctahはHandleの先端まで移動しているが、Handleは初期状態の位置から動いていない。
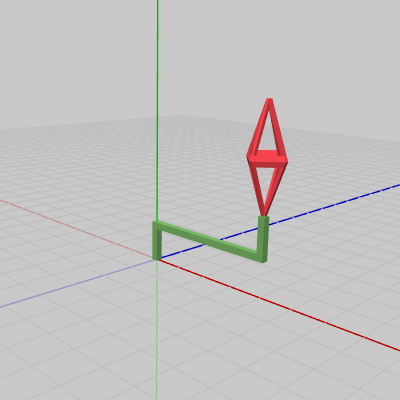
図5 Beta1 実行結果 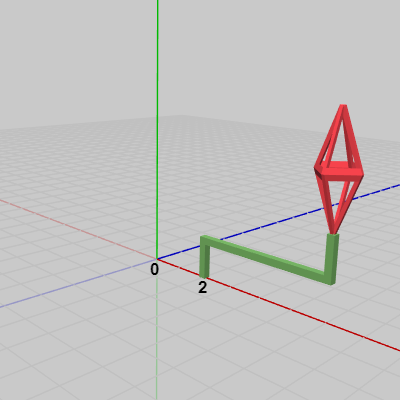
図6 Beta1のlocalHandle(2行目)の内容を平行移動行列に変更した際の実行結果
仮に、2行目の localHandle の内容をidentity行列ではなく、x軸方向に $+2$ だけの平行移動を行うものに変更するとしよう。
つまり、2行目を以下のように変更するのである。
この場合、プログラムの実行結果は図6に示される結果になる。
先程も述べたように、Octahに実行される変換行列 worldOctah (4行目)の内容は、まず localOctah を実行し、次に localHandle を実行する。localOctah によってOctahはHandleの先端まで移動するのは先程と同じであるが、今回の変更により localHandle によってさらにx軸方向に $+2$ だけ移動することになる。
Handleに実行される変換行列 worldHandle (5行目)は localHandle のコピーであり、先程のプログラムではidentity行列であったためHandleには何も変化は起こらなかったが、今回はその内容がx軸方向に $+2$ だけの平行移動行列であるため、worldHandle の実行によりHandleも x軸方向に $+2$ だけ移動する。
結果的にはOctahとHandleは一体化した状態で、図5の状態からx軸方向に $+2$ だけ移動することになる (図6)。両者が一体となって移動するのは両者に同じ変換行列 localHandle が実行されるためである。Octahの場合は localOctah によってHandle先端へ移動した位置から localHandle が実行され、Handleの場合は初期状態の位置から localHandle が実行される。これによってOctah がHandle先端に置かれた状態で両者が一体となって移動するのである。
続いて、HandleをStandにアタッチする。上の過程ですでにHandleはOctahと一体化しているので、HandleをStandにアタッチする際には、Handleと同じ量だけOctahも移動することになる。
[Code1] (実行結果 図7)
1行目の localOctah の内容は先程のプログラムと同じである。 2行目の localHandle は、ここではHandleを初期状態の位置からStand上部のアタッチポジションまで移動させるものである (c_attachPos_HandleはStand上部のアタッチポジションまでの移動量を表すVector3型の定数)。
今回Standに実行される変換行列は7行目の worldStand であるが、これは3行目の localStand のコピーであり、その内容はidentity行列である。したがって、このプログラムではStandには何の変化も起こらない。
Handleに実行される変換行列 worldHandle (6行目)の内容は、まず localHandle を実行し、次に localStand を実行するものであるが、localStand はidentity行列なので実際にHandleに実行される変換は localHandle によるものだけである。したがって、worldHandle によってHandleに起こる変化はStand上部のアタッチポジションまでの移動、具体的には c_attachPos_Handle で表される量の移動だけである。
Octahに実行される変換行列 worldOctah (5行目)はここでは3つの行列の積であり、localOctah、localHandle、localStand の順で実行される。最初の localOctah によって、Octahは初期状態の位置からHandle先端のアタッチポジションまで移動し、次に localHandle が実行されるが、これによってOctahにはHandleと同じく c_attachPos_Handle だけの平行移動が実行される。localStand の内容はidentity行列なのでOctahの変換はここまでである。
図7はこのプログラムの実行結果である。Standは初期状態から動いていないが、HandleはStand上部のアタッチポジションまで移動しており、OctahはHandle先端のアタッチポジションに置かれている。上でも述べたがOctahとHandleには同じ変換行列 localHandle が実行されている。Octahの場合はHandle先端に移動した位置から、Handleの場合は初期状態の位置から実行される。これによって、OctahがHandle先端に置かれた状態で一体となってStand上部へ移動するのである。

図7 Code1 実行結果 
図8 Code1のlocalStand(3行目)の内容を平行移動行列に変更した際の実行結果
3行目の localStand はここではidentity行列であるので、Standには何の変化も起こらなかったが、もしこの行列を以下のようにx軸方向に $-3$ だけの平行移動を行うように変更すると、実行結果は図8に示されるように全体がx軸方向に $-3$ だけ移動する結果になる。
これは、localStand が3つのオブジェクトに実行されるためである。Standの場合は初期状態の位置から、Handleの場合はStand上部にアタッチされた位置から、Octahの場合は(Stand上部にアタッチされた)Handleの先端の位置から localStand が実行される。これによって3つのオブジェクトが一体となって同じだけの移動(x軸方向に$-3$の移動)をするのである。
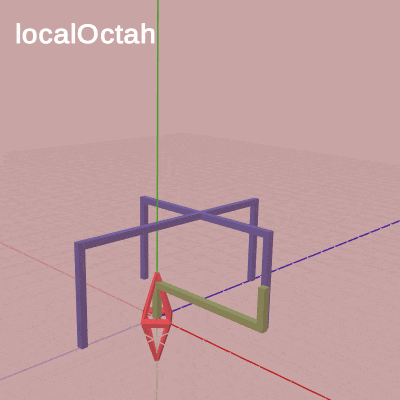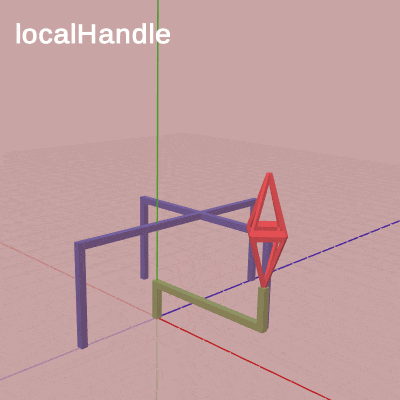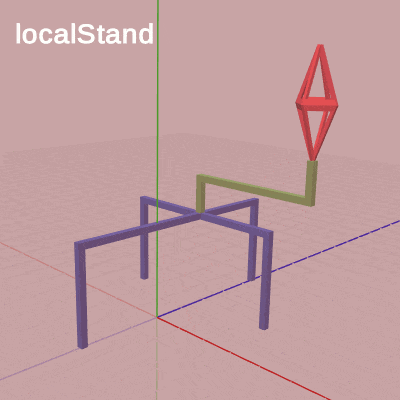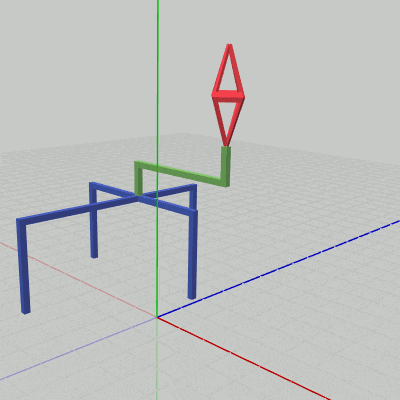
図9 この localStand を平行移動行列にした変更版のCode1における、各変換行列の実行過程をアニメーションで示したものが図9である。
赤いフィルターのかかっている状態がオブジェクトに対して変換行列が実行されている過程である。そして、赤いフィルターのかかっている状態から通常色の状態に切り替わるが、この瞬間にフレーム描画が発生する (描画されたフレームは図8と同じである)。
「localOctah」と表示されている間は変換行列 localOctah が実行されていることを意味しており、「localHandle」と表示されている間は変換行列 localHandle が、「localStand」と表示されている間は変換行列 localStand が実行されていることを意味している。それぞれの変換行列の内容は上で述べた通りである。
以下の2つのプログラムは Octah、Handleのそれぞれに定義された運動である。
[Beta2A] (実行結果 図10)
[Beta2B] (実行結果 図11)
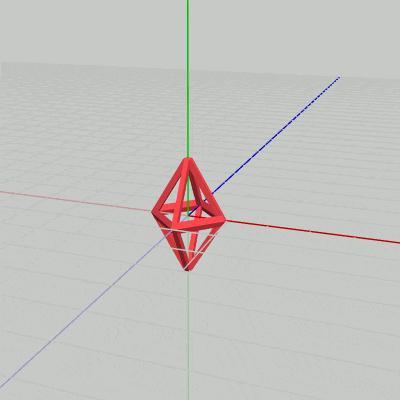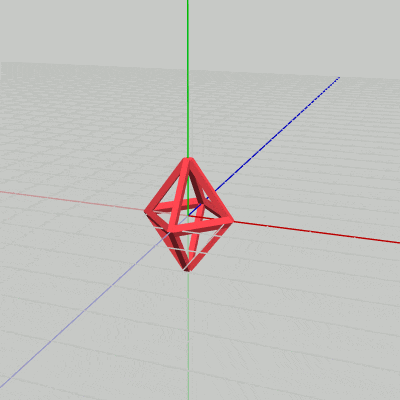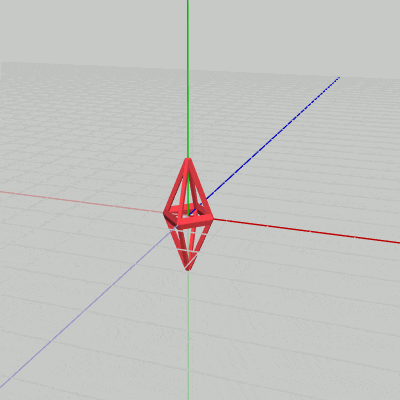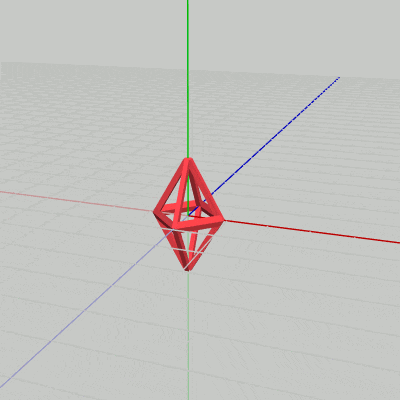
図10 Beta2A 実行結果 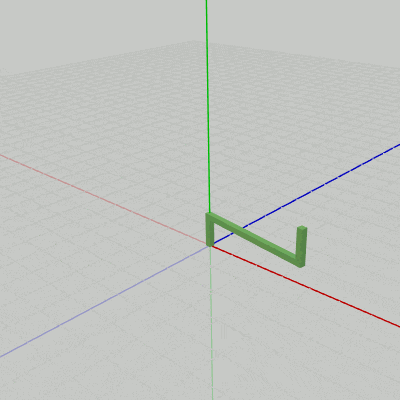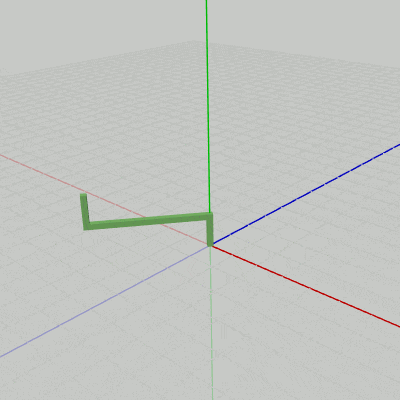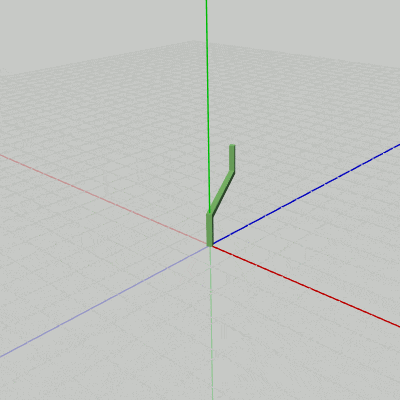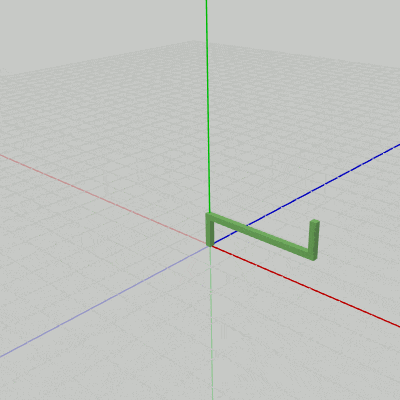
図11 Beta2B 実行結果
Octahの運動はx軸方向、z軸方向への $1$倍から $2$倍の間の拡大縮小の繰り返しであり(図10)、Handleの運動は毎フレーム $1$°ずつの y軸周りの回転である(図11)。
Octahに実行されるスケール行列の倍率はBeta2Aの2行目で計算される。この計算は単振動によるものであり、倍率を表すローカル変数 scale には $1.0$ から $2.0$ の値が算出される。1行目の i_shmOctah は単振動計算に使われる角度を表すインスタンス変数であり、毎フレーム $4$ずつ増加するので scale の値は90フレームごとに $1.0$ から $2.0$ の間を往復することになる。
Beta2Bの i_degHandle はHandleの回転角度を表すインスタンス変数で、毎フレーム $1$ずつ増加するのでHandleは360フレームごとに1回転することになる。
次に、Octahの拡大縮小をHandle先端のアタッチポジションにおいて行わせる。
[Beta2C] (実行結果 図12)
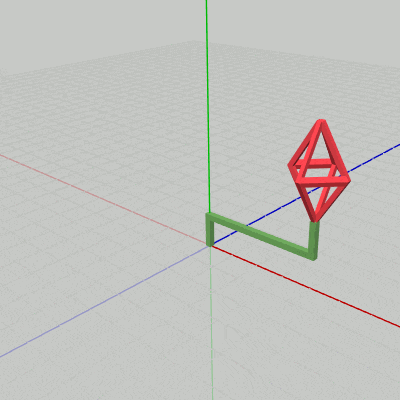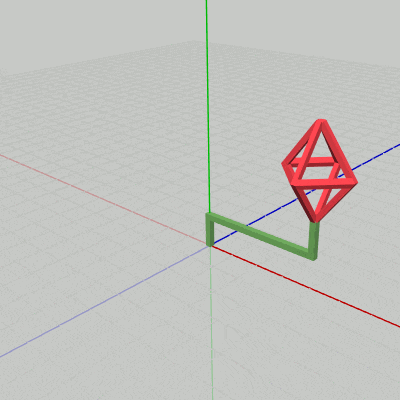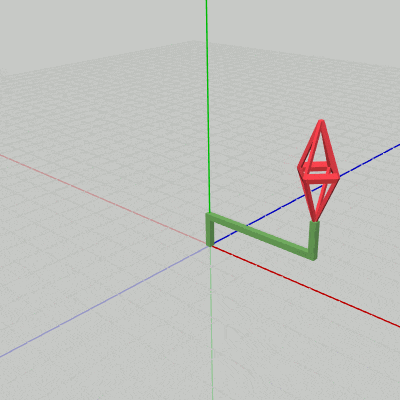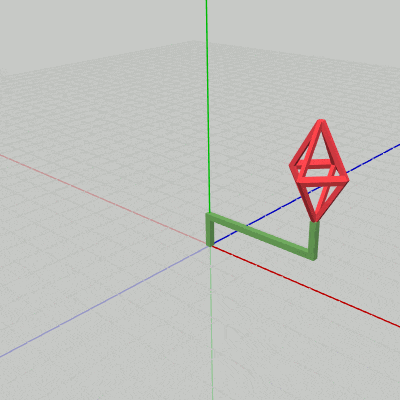
図12 Beta2C 実行結果 実行結果(図12)に見られるように、OctahはHandle先端において拡大縮小を繰り返している。Handleに実行される変換行列 worldHandle (12行目)の内容はidentity行列なので、ここではHandleには何も変化は起こらない。
Octahに実行される4行目のスケール行列 sclOctah の倍率は3行目で算出されローカル変数 scale にセットされるが、その値は最初のフレームでは $1.53$、2フレーム目では $1.57$、3フレーム目では $1.60$、以降も同様に算出され、$1.0$ から $2.0$ の間を往復する。5行目の traOctah はHandle先端のアタッチポジションまで移動する平行移動行列である。
図13は今回のプログラムBeta2Cの最初のいくつかのフレームについて、各フレームにおける変換行列の実行過程をアニメーションで表したものである。
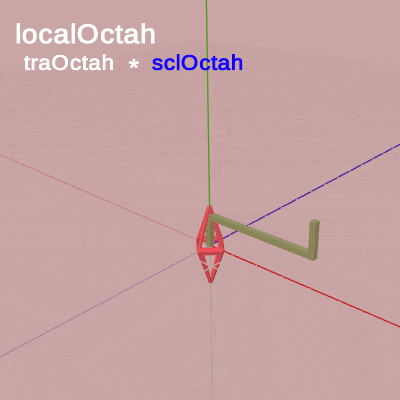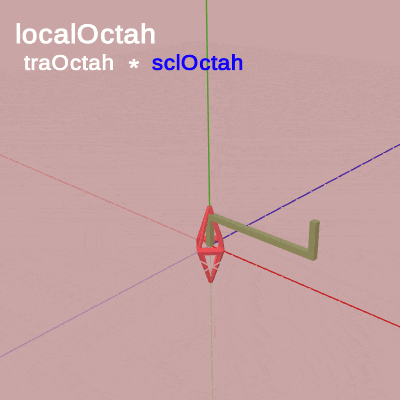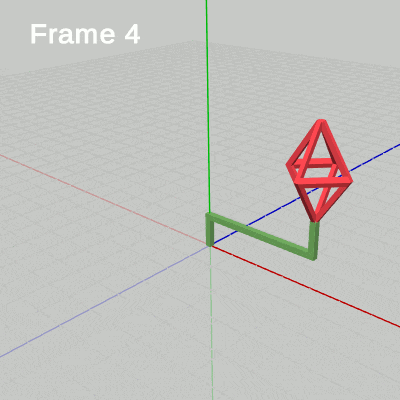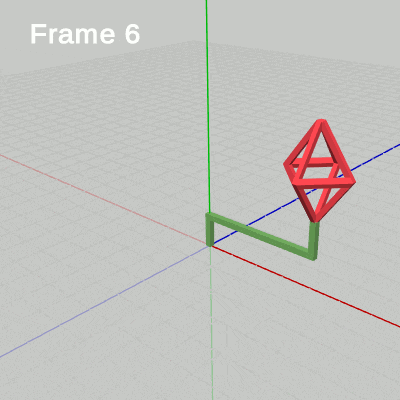
図13 先ほど見た図9と同じように、赤いフィルターのかかっている状態はオブジェクトに対して変換行列が実行されている過程であり、その後赤いフィルターの状態から通常色に切り替わるが、通常色の状態がオブジェクトに対して変換行列を実行し終わった状態、つまり変換行列の実行結果である。フレーム描画は通常色に切り替わった瞬間に発生する。アニメーション中に表示される「Frame 1」、「Frame 2」... はフレーム番号を表しており、この例では6フレーム目までの描画を扱っている。
先程のアニメーション(図9)と同様に、「localOctah」と表示されている間は変換行列 localOctah が実行されていることを意味しており、「localHandle」と表示されている間は変換行列 localHandle が実行されていることを意味している。また、今回は「localOctah」が表示されているときに「traOctah * sclOctah」という式も表示されている。プログラム6行目に示されるように、localOctah はスケール行列sclOctahと平行移動行列traOctahの積であり、Octahに対する変換はスケール、平行移動の順で実行される。アニメーション中では sclOctah が青く表示されているときは sclOctah が実行されていることを意味しており、traOctah が青く表示されているときは traOctah が表示されていることを意味している。
最初のフレームにおいてOctahは初期状態から $1.53$倍拡大し(sclOctah)、拡大した状態でアタッチポジションまで移動する(traOctah)。Handle先端のアタッチポジションまで移動し終わると、次に変換行列localHandleが実行されるが、localHandleの内容はここでは identity行列であるため(9行目)、localHandleの実行によって何も変化は起こらない (「localHandle」と表示されている間は2つのオブジェクトに変化は発生しない)。そして、その状態でフレーム描画が発生する。2フレーム目ではOctahは初期状態から $1.57$倍拡大し、拡大した状態でアタッチポジションまで移動する。移動し終わった後は何も変化することなくフレーム描画が発生する。3フレーム目以降も同様である。
描画されたフレームを連続的に表示すれば図12のアニメーションになる。
では、さらにHandleの回転を加えて、2つのオブジェクトの一体化した運動を作成しよう。
[Code2] (実行結果 図14)
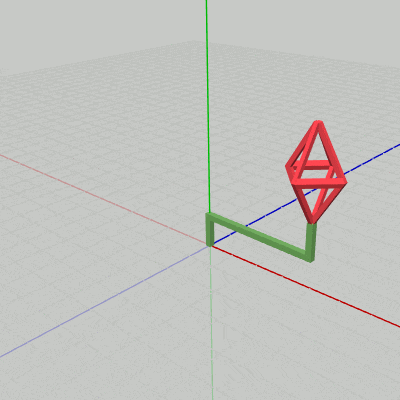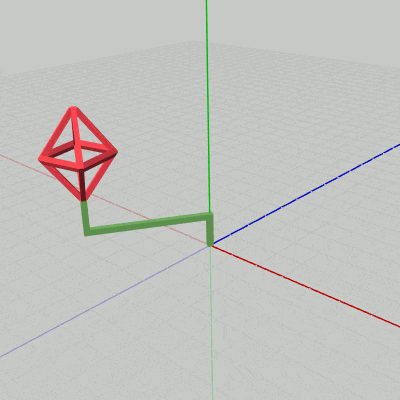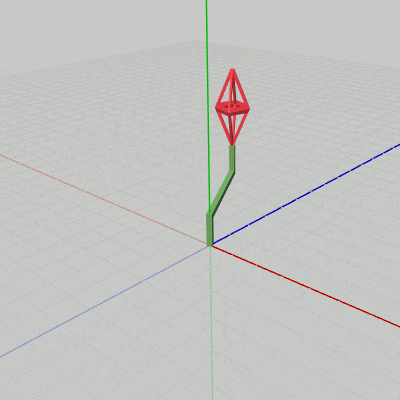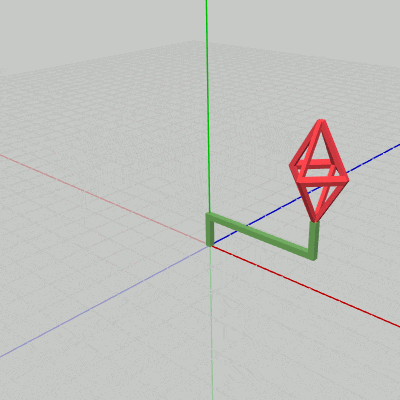
図14 Code2 実行結果 先程のプログラムからの変更点は1箇所である。それは、変換行列localHandleの内容がここではidentity行列ではなく、回転行列になっていることである (9行目~11行目)。9行目の i_degHandle はHandleの回転角度を表すインスタンス変数で、毎フレーム $1$ ずつ増加するのでHandleは毎フレーム $1$°ずつ回転を行う (回転軸はy軸)。
実行結果(図14)に見られるように、今回はHandleが回転しており、その先端においてOctahが拡大縮小を行っている。
下図15はCode2の最初のいくつかのフレームについて、各フレームにおける変換行列の実行過程をアニメーションで表したものである。1フレーム目ではOctahが $1.53$倍拡大し、拡大した状態でアタッチポジションまで移動する。ここまでが変換行列localOctahの内容であり、次に変換行列localHandleが実行される。今回のlocalHandleは毎フレーム$1$°ずつ回転を行う回転行列である。したがって、1フレーム目ではlocalHandleによって2つのオブジェクトがy軸周りに $1$°回転する。この回転は2つのオブジェクトに実行されるが、Handleの場合は初期状態からの回転となり、Octahの場合はHandle先端のアタッチポジションからの回転となる。これによって、2つのオブジェクトが一体となって回転することになるのである。この回転が終わった時点でフレーム描画が発生する。
2フレーム目ではOctahが $1.57$倍拡大し、拡大した状態でアタッチポジションまで移動する。その後、2つのオブジェクトがy軸周りに $2$°回転し、回転が終わった時点でフレーム描画が発生する。3フレーム目ではOctahが $1.60$倍拡大し、拡大した状態でアタッチポジションまで移動する。その後、2つのオブジェクトがy軸周りに $3$°回転し、回転が終わった時点でフレーム描画が発生する。
それ以降のフレームでも同様である。
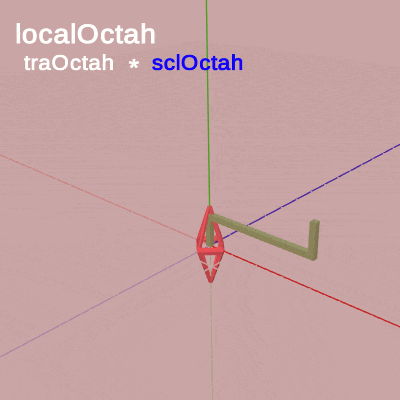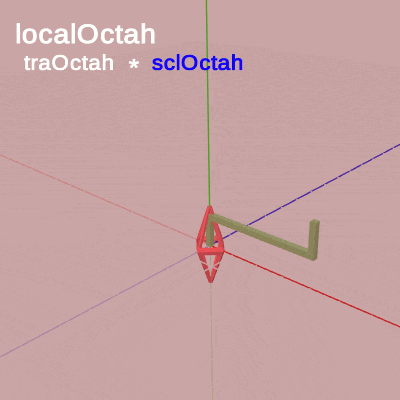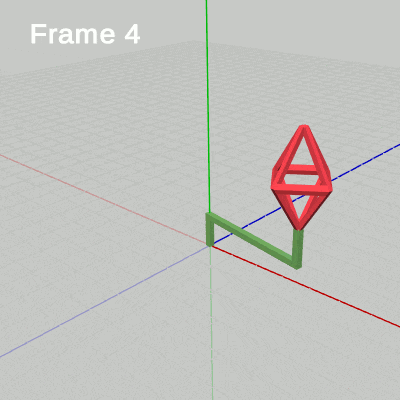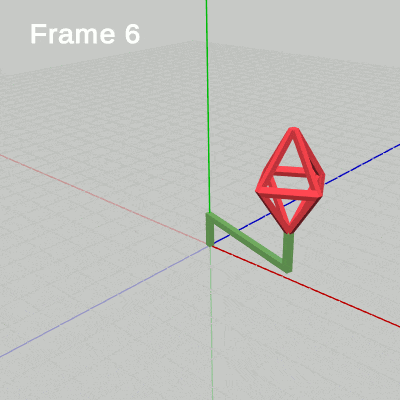
図15 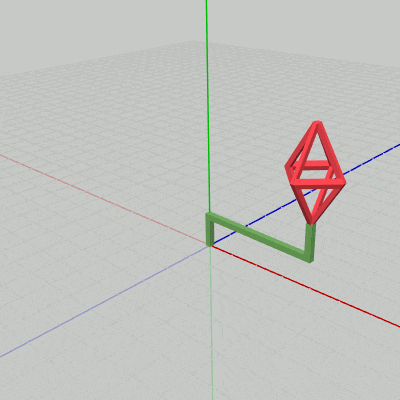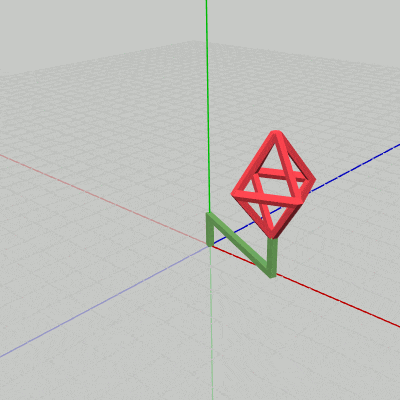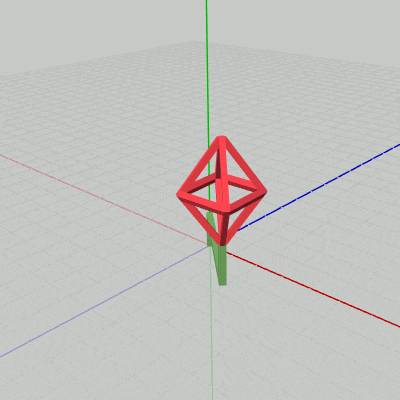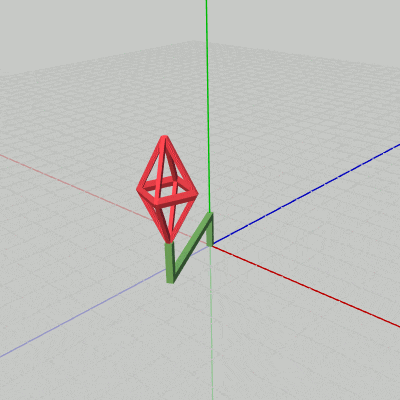
図16
図16は描画された各フレームをコマ送りで表示したものである。これを連続的に表示すれば図14のアニメーションになる。
上記のCode2では、Handleがy軸周りに回転をしており、その先端においてOctahが拡大縮小を行っていた。Handleに実行される変換は回転のみで平行移動は実行されないため、この運動はHandleの初期状態の位置において行われていた。
次のプログラムは、この同じ運動をStand上部(Handleのアタッチポジション)において行うようにしたものである。
[Beta3] (実行結果 図17)

図17 Beta3 実行結果 実行結果(図17)に示されるように、Handleの回転及び(Handleの先端における)Octahの拡大縮小が、ここではStand上部で行われている。
Standに実行される変換行列 worldStand (19行目)は15行目の localStand のコピーであり、その内容はidentity行列であるため、Standには何も変化は起こらない。
Handleに実行される変換行列 worldHandle (18行目)の内容は localHandle、localStand がこの順序で実行されるものであるが、localStand はidentity行列なので実際には localHandle のみによる変換と同じである。今回の localHandle は12行目の計算に示されるように rotHandle と traHandle という2つの変換行列の積である。 rotHandle はCode2と同じく毎フレーム $1$°ずつy軸周りに回転を行う回転行列であり、traHandle はHandleをStand上部のアタッチポジションまで移動させる平行移動行列である (c_attachPos_HandleはStand上部のアタッチポジションまでの移動量を表すVector3型の定数)。したがって、localHandle によってHandleは毎フレーム $1$°ずつ回転し、回転した状態でStand上部のアタッチポジションまで移動することになる。
Octahに実行される変換行列 worldOctah (17行目)の内容は3つの変換行列の積であるが、localStand はidentity行列であるため実際には2つの変換行列 localOctah、localHandle がこの順序で実行されたものと同じである。localOctah の内容はCode2と同じであり、毎フレーム$1$倍から$2$倍の間の拡大を行い、拡大が行われた状態でHandle先端のアタッチポジションまで移動するというものである。その後 localHandle が実行されるが、Octahの場合はHandle先端から(Handleとともに)回転し、回転した状態で(Handleとともに)Stand上部のアタッチポジションまで移動することになる。
最後にStandの運動を追加する。
Standの運動は z軸方向の単振動であり、その移動量は $0$ から $4$ の範囲を往復する。
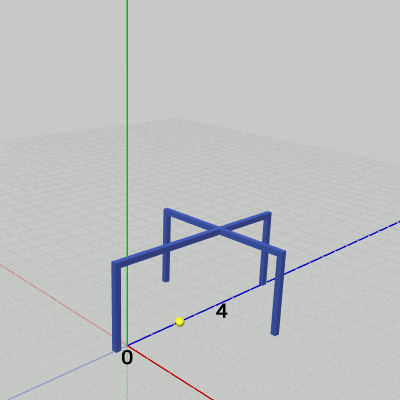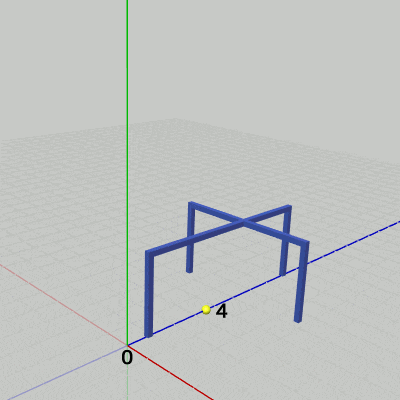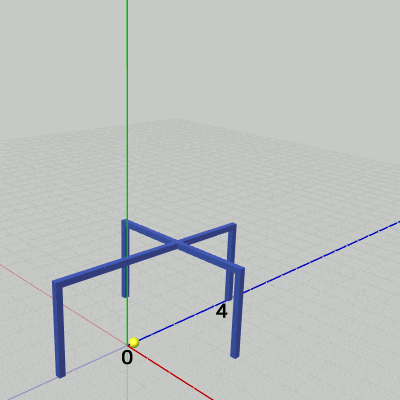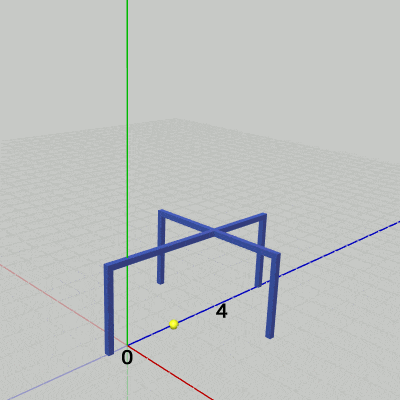
図18 Standの運動(z軸方向の単振動) 2行目の mv はz軸方向のStandの移動量であり、単振動によって計算される。その値は $0$ から $4$ の間を往復する。i_shmStand は単振動計算で使われる角度を表すインスタンス変数で、毎フレーム $1$ずつ増加するので mv の値は360フレームごとに $0$ から $4$ の間を往復する。
図18はこのプログラムの実行結果であるが、Standはz軸上の $0$ から $4$ の間の往復運動を行っている (実際にz軸上の$0$から$4$の間を往復するのは図に示される黄色い小球であるが、これはStandのオブジェクト原点である。Standのオブジェクト原点はStandには含まれずStandの外側に存在している。「オブジェクト原点」については3-9節参照)。
最後のプログラムは、上で見てきた3つのオブジェクトの運動をすべて統合したものである。
[Code3] (実行結果 図19)
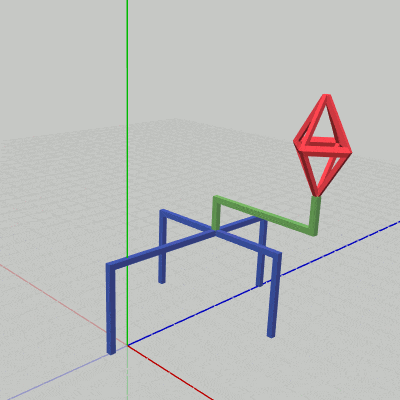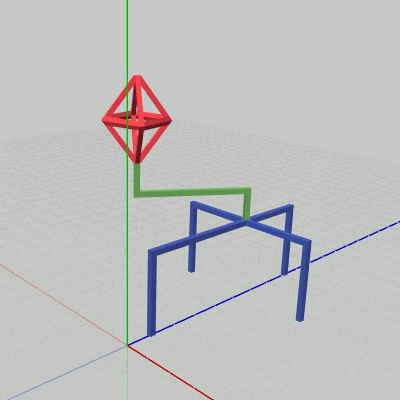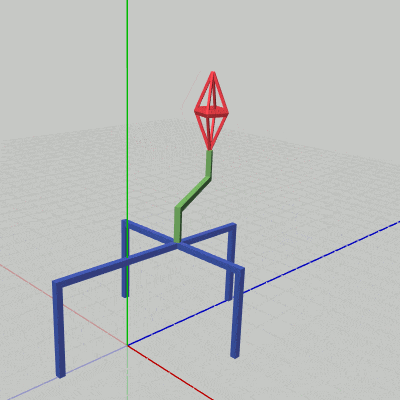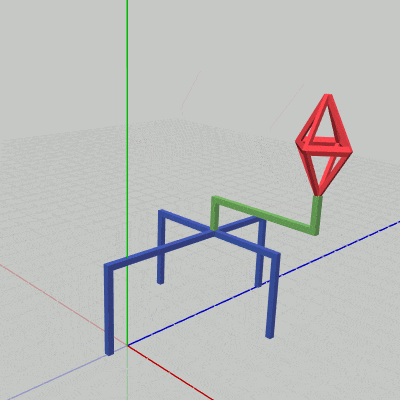
図19 Code3 実行結果 このプログラムは先程のBeta3とほとんど同じである。変更箇所は1箇所で、それは17行目の変換行列 localStand の内容が今回は上で示した z軸方向に単振動を行う平行移動行列に変更されている点のみである。実際、実行結果(図19)に示されるように、Beta3との違いはStandが動いているか静止しているかだけでしかない。
下図20はCode3の最初のいくつかのフレームについて、各フレームにおける変換行列の実行過程をアニメーションで表したものである。
各フレームにおいて変換行列は localOctah、localHandle、localStand の順で実行される。Octahに実行される変換行列 worldOctah (19行目)はそれら3つの変換行列の積であるから、3つの変換行列による変換をすべて受ける。Handleに実行される変換行列 worldHandle (20行目)は localHandle、localStand の積であるため、その2つの変換行列による変換だけを受ける(localOctahが実行されている間は何も変化は発生しない)。Standに実行される変換行列 worldStand (21行目)は localStand のコピーであるので、Standは localStand による変換だけを受ける (localOctah、localHandleが実行されている間は何も変化は発生しない)。
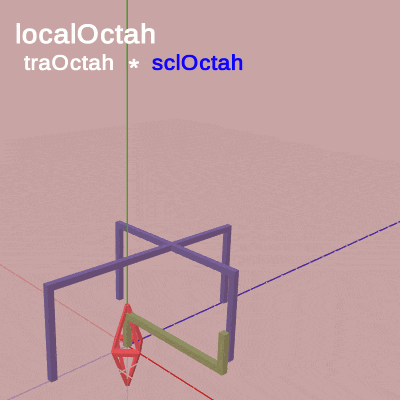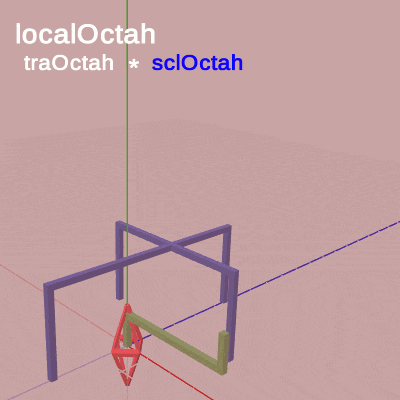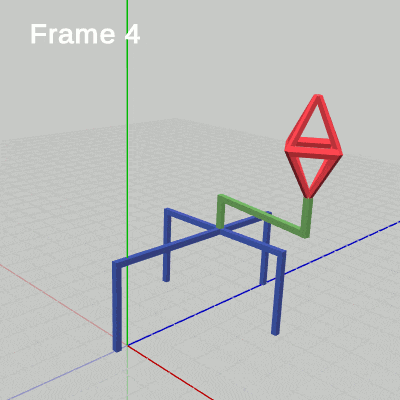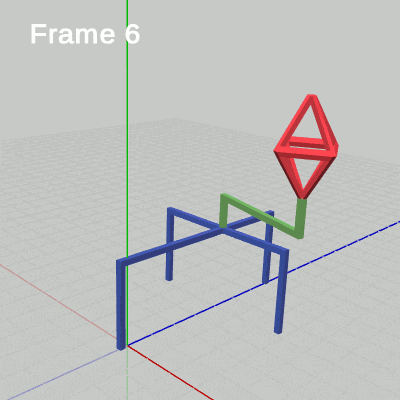
図20 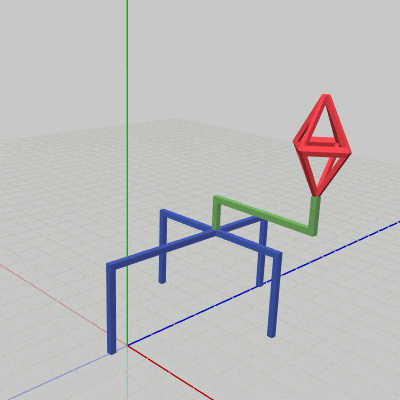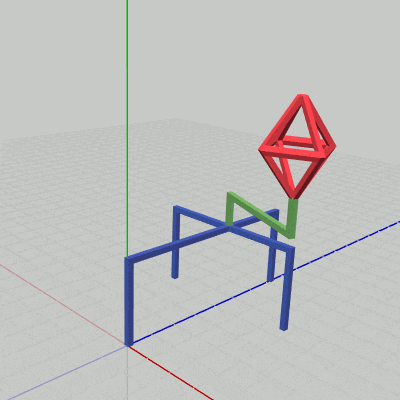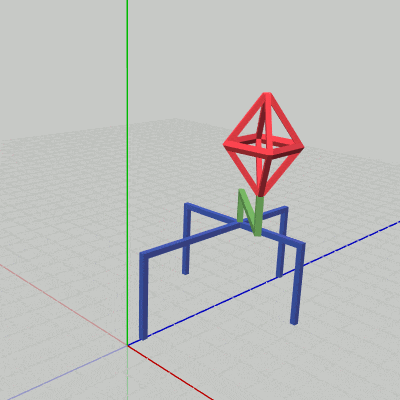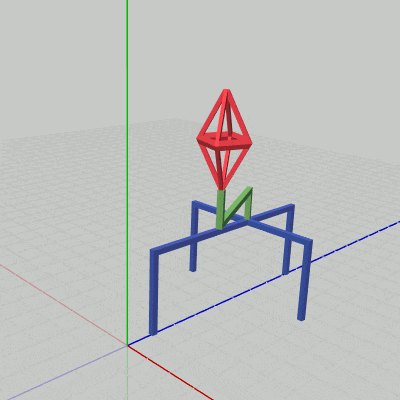
図21
1フレーム目の localOctah によって、Octahは初期状態から $1.53$倍拡大し、拡大した状態でHandle先端のアタッチポジションまで移動する。次に localHandle が実行されるが、これはOctah及びHandleに対して実行される。Handleの場合は初期状態から $1$°回転し、回転した状態でStand上部のアタッチポジションまで移動する。Octahの場合は(初期状態の)Handle先端から $1$°回転し、回転した状態でHandleと同じだけの平行移動を行うので、結果としてはHandleと一体となってStand上部まで移動することになる。
最後に localStand が実行されるが、これは3つのオブジェクト全てに対して実行される。Standの場合は初期状態の位置からz軸方向に $2.03$だけ移動する。Handle、Octahにも同じ平行移動が実行されるが、Handleの場合はStand上部のアタッチポジションからの移動であり、Octahの場合は(Stand上部にアタッチされている)Handle先端からの移動となる。これによって、3つのオブジェクトが一体となって移動することになるのである。このz軸方向への移動が終わった時点でフレーム描画が発生する。
2フレーム目では localOctah によって、Octahが初期状態から $1.57$倍拡大し、拡大した状態でHandle先端のアタッチポジションまで移動する。次に localHandle がOctahとHandleに実行される。Handleの場合は初期状態から $2$°回転し、回転した状態でStand上部のアタッチポジションまで移動する。Octahの場合は(初期状態の)Handle先端から $2$°回転し、回転した状態でHandleと同じだけの平行移動を行う。最後に3つのオブジェクトに対して localStand が実行されるが、2フレーム目ではz軸方向に $2.07$だけの移動となる。Standの場合は初期状態からの移動であり、Handleの場合はStand上部のアタッチポジションからの移動となり、Octahの場合は(Stand上部にアタッチされている)Handle先端からの移動となる。3つのオブジェクトのz軸方向の移動が終わった時点でフレーム描画となる。
3フレーム目以降も同様である。
図21は描画された各フレームをコマ送りで表示したものである。これを連続的に表示すれば図19のアニメーションになる。
複数のオブジェクトが一体化して運動をするのは、子オブジェクトが親オブジェクトにアタッチされた状態で、子オブジェクトと親オブジェクトの両者に同じ変換行列が実行されるためである。このことはオブジェクトの階層構造(すなわち親子階層)が2階層であれ3階層であれ、あるいはそれ以上であっても変わらない。
この講義で扱うオブジェクトの運動は単純なものであるが、一見複雑に見えるオブジェクトの運動であっても、その運動(具体的には、各フレームにおけるオブジェクトの位置、向き、大きさ)はやはり行列の積として考えることができるのである。しかし、ゲームエンジンやDCCツールにおいてオブジェクトの運動を実装する場合に、つまり、あるフレームにおけるオブジェクトの位置や向き、大きさなどを計算する場合には行列ではなく「Position」「Rotation」「Scale」というデータ(あるいはこれに似た名前を持つデータ)に値を設定していくことが普通である。そこでは、行列という概念は目立たないように裏へ追いやられている。
Unityでも事情は同じである。Unityにおいてオブジェクトを動かす際には Transform という変換処理専門のクラスを経由するが、Transformクラスにはこの講義で使用してきた SetMatrix(..) のようなメソッドは標準的には備わってはいない。やはり「Position」「Rotation」「Scale」なのである。
この講義においても第5章、あるいは第6章以降ではオブジェクトを動かす際に、Unityに標準で用意されているTransformクラスの localPosition や position などのプロパティ用いるが、オブジェクトの運動をプログラムで実装するにあたっては「Position」「Rotation」「Scale」による方法よりも、行列による方法の方が初学者向きなのである。
行列は「Position」「Rotation」「Scale」に比べて難しい印象があるが、それはオブジェクトの運動に関して言えば明らかに誤解である。オブジェクトの運動は行列によって考える方が単純であり、直接的なのである。行列はベクトルと並んでコンピューターグラフィックスにおいてはその中心に位置する概念である。特にオブジェクトの運動にこそ、その真価を発揮する。
例えば、次のような6つの変換があったとしよう (括弧内の$Tx$や$Ry$は各変換を表す変換行列である)。
--> x軸方向に$3$の平行移動 ($Tx$)
--> z軸方向に$10$の平行移動 ($Tz$)
--> y軸周りの$60$°の回転 ($Ry$)
--> z軸周りの$120$°の回転 ($Rz$)
--> 各軸方向に$2$倍の拡大 ($S_{2}$)
--> 各軸方向に$0.5$倍の縮小 ($S_{0.5}$)
そして、オブジェクトに対して次のような順序で変換を実行するとする。
(1) 各軸方向に$2$倍の拡大 ($S_{2}$)
(2) y軸周りの$60$°の回転 ($Ry$)
(3) x軸方向に$3$の平行移動 ($Tx$)
(4) z軸周りの$120$°の回転 ($Rz$)
(5) 各軸方向に$0.5$倍の縮小 ($S_{0.5}$)
(6) z軸方向に$10$の平行移動 ($Tz$)
最終的にオブジェクトに対して実行される変換行列を $M$ とすれば、$M$ は以下のように求められる。
\[ M = TzS_{0.5}RzTxRyS_{2}\]つまり、(1)から(6)の変換行列を順番に右から掛けていくだけである。
プログラムで書けば、次のようになる (各変換行列の算出部分は省略している)。
変換の実行順序をかえて、次のような順序で変換を実行するとしよう。
(1) z軸周りの$120$°の回転 ($Rz$)
(2) z軸方向に$10$の平行移動 ($Tz$)
(3) 各軸方向に$0.5$倍の縮小 ($S_{0.5}$)
(4) x軸方向に$3$の平行移動 ($Tx$)
(5) y軸周りの$60$°の回転 ($Ry$)
(6) 各軸方向に$2$倍の拡大 ($S_{2}$)
最終的にオブジェクトに対して実行される変換行列 $M$ は\[ M = S_{2}RyTxS_{0.5}TzRz \]となる。
ここでも先程と同様に、(1)から(6)の変換行列を順番に右から掛けていくだけである。
プログラムで書けば、次のようになる (各変換行列の算出部分は省略している)。
(列優先)行列の場合、その積は右から左へ向かって計算されていくので(3-8節)、変換行列の積の場合においても、その変換順序は右から左へ順に実行されていく。このことは既に何度か述べてきた。したがって、上記で示した例は自明なことであったかもしれない。
しかし上例のような、オブジェクトに対して複数の変換を順番に実行する、というのは行列を使って行ったために簡単にできたのである。先程述べたようにゲームエンジンやDCCツールでは行列による方法ではなく「Position」「Rotation」「Scale」の3つのデータに値をセットしてオブジェクトの運動を実装していく。例えば、今上で示した6つの変換と同じ実行結果になるように「Position」「Rotation」「Scale」のそれぞれにセットする値を求めるのは決して容易なことではない。
オブジェクトに対して複数の変換を実行する場合、行列であればそれらの変換を表す変換行列を順に掛けていくだけである。5個の変換であれば5個の変換行列を右から左へ掛け、10個の変換であれば10個の変換行列を右から左へ掛け、その積をオブジェクト実行すればよい。しかし「Position」「Rotation」「Scale」に値をセットするやり方では、このように簡単にはいかない。上で用いたプログラムは、6個の変換行列をオブジェクトに対して実行するものであった。
「Position」「Rotation」「Scale」に値をセットして、この実行結果と同じ状態になるように、つまりオブジェクトの位置、向き、大きさが同じになるように以下のプログラムにおけるそれぞれの右辺の値を求めることは容易ではないのである。
以上のことからオブジェクトの運動を実装する際には「Position」「Rotation」「Scale」によるやり方よりも、行列による方法の方が単純であり、直接的であることがわかるであろう。しかし、実際にはオブジェクトの運動は行列ではなく「Position」「Rotation」「Scale」の3つのデータによって表現される。その主な理由は計算負荷、変換の最適化、メモリーコスト、及びオブジェクトの状態の可視化である (他にも、行列の積を積み重ねていくとコンピューターの計算誤差が累積していくという問題もある)。
3Dオブジェクトの場合、その運動(正確には各フレームにおける状態)は$4\times4$行列で表されるが、$4\times4$行列の積は計算負荷として低いものではなく、$4\times4$行列を保持しておく場合に必要なメモリ容量も「Position」「Rotation」「Scale」の場合に比べて大きくなる。
また、今までのプログラムではオブジェクトを動かす際には毎フレーム 平行移動行列や回転行列、スケール行列の積を計算していたが、オブジェクトに実行する変換行列は必要なときにだけ計算して求めるのが望ましい。例えば、同じ位置で回転し続けるような場合には今までのプログラムでは平行移動行列と回転行列の積を毎フレーム計算していたが、実際にはこのような計算は無駄なのである。これは後の章で解説するが、位置が変わらずに回転状態だけが変化するといった場合や逆にオブジェクトの姿勢は変化しないが位置だけが変化するといった場合には、オブジェクトに実行する変換行列の一部だけを更新すればよいのである。
さらに、インタラクティブにオブジェクトの状態を画面上で設定していく場合には、行列は全く向いていない。$4\times4$行列は16個の実数値から成るが、それらのデータが画面上に表示されていても、そこからオブジェクトの状態を読み解くのは困難である。
しかし「Position」「Rotation」「Scale」によるやり方も、その根底は行列の積なのである。「Position」「Rotation」「Scale」にセットされたデータは最終的には、その時点におけるオブジェクトの状態を表す行列を求めるために使われるのである。これらのことは第4章や第5章において解説する。
再述するが、コンピューターグラフィックスにおいてオブジェクトを動かす際に最も重要な基礎となるのは行列的思考なのである。
本節では第2章において扱った一体化運動と同様のものを、3D空間において3Dオブジェクトを用いて実装する。すなわち本節は3Dオブジェクトを使った、一体化運動についての復習である。
コンピューターグラフィックスにおけるオブジェクトの運動、特に複数のオブジェクトの一体化した運動を実装する際の原理自体は3Dオブジェクトであれ2Dオブジェクトであれ変わらない。コンピューターグラフィックスにおいてオブジェクトを動かす際にプログラマーに必要とされるのは結局、行列的思考なのである。
# Code1
本節で使用するオブジェクトは以下の3つである。



各図はそれぞれのオブジェクトの初期状態であり、プログラムにおいては Octah(図1)、Handle(図2)、Stand(図3) という名前で使われる。
図4はオブジェクトの階層構造で、一番上の親オブジェクトがStand、Standの子オブジェクトがHandle、Handleの子オブジェクトがOctahである。
以下のプログラムは、OctahとHandleを一体化させるものである。
[Beta1] (実行結果 図5)
Matrix4x4 localOctah = TH3DMath.GetTranslation4x4(c_attachPos_Octah); Matrix4x4 localHandle = Matrix4x4.identity; Matrix4x4 worldOctah = localHandle * localOctah; Matrix4x4 worldHandle = localHandle; Octah.SetMatrix(worldOctah); Handle.SetMatrix(worldHandle);
1行目の行列 localOctah の内容はOctahを初期状態からHandle先端のアタッチポジションまで移動させるものである (c_attachPos_OctahはHandle先端までの移動量を表すVector3型の定数)。
Octahに実行される行列は4行目の worldOctah であるが、それは localOctah と localHandle の積であり、その内容は まず localOctah が実行され、その次に localHandle が実行される。しかし、localHandle の内容はここではidentity行列であるため(プログラム2行目)、localHandle 自体は何も変換を行わない行列である。したがって、実際にOctahに実行される変換はHandle先端までの移動(localOctah)のみである。Handleに実行される行列 worldHandle (5行目)は、localHandle のコピーでありその内容はidentity行列であるので、Handleに対して worldHandle を実行しても何も変化は起こらない。
実行結果(図5)に見られるように、OctahはHandleの先端まで移動しているが、Handleは初期状態の位置から動いていない。


仮に、2行目の localHandle の内容をidentity行列ではなく、x軸方向に $+2$ だけの平行移動を行うものに変更するとしよう。
つまり、2行目を以下のように変更するのである。
Matrix4x4 localHandle = TH3DMath.GetTranslation4x4(2, 0, 0);
この場合、プログラムの実行結果は図6に示される結果になる。
先程も述べたように、Octahに実行される変換行列 worldOctah (4行目)の内容は、まず localOctah を実行し、次に localHandle を実行する。localOctah によってOctahはHandleの先端まで移動するのは先程と同じであるが、今回の変更により localHandle によってさらにx軸方向に $+2$ だけ移動することになる。
Handleに実行される変換行列 worldHandle (5行目)は localHandle のコピーであり、先程のプログラムではidentity行列であったためHandleには何も変化は起こらなかったが、今回はその内容がx軸方向に $+2$ だけの平行移動行列であるため、worldHandle の実行によりHandleも x軸方向に $+2$ だけ移動する。
結果的にはOctahとHandleは一体化した状態で、図5の状態からx軸方向に $+2$ だけ移動することになる (図6)。両者が一体となって移動するのは両者に同じ変換行列 localHandle が実行されるためである。Octahの場合は localOctah によってHandle先端へ移動した位置から localHandle が実行され、Handleの場合は初期状態の位置から localHandle が実行される。これによってOctah がHandle先端に置かれた状態で両者が一体となって移動するのである。
続いて、HandleをStandにアタッチする。上の過程ですでにHandleはOctahと一体化しているので、HandleをStandにアタッチする際には、Handleと同じ量だけOctahも移動することになる。
[Code1] (実行結果 図7)
Matrix4x4 localOctah = TH3DMath.GetTranslation4x4(c_attachPos_Octah); Matrix4x4 localHandle = TH3DMath.GetTranslation4x4(c_attachPos_Handle); Matrix4x4 localStand = Matrix4x4.identity; Matrix4x4 worldOctah = localStand * localHandle * localOctah; Matrix4x4 worldHandle = localStand * localHandle; Matrix4x4 worldStand = localStand; Octah.SetMatrix(worldOctah); Handle.SetMatrix(worldHandle); Stand.SetMatrix(worldStand);
1行目の localOctah の内容は先程のプログラムと同じである。 2行目の localHandle は、ここではHandleを初期状態の位置からStand上部のアタッチポジションまで移動させるものである (c_attachPos_HandleはStand上部のアタッチポジションまでの移動量を表すVector3型の定数)。
今回Standに実行される変換行列は7行目の worldStand であるが、これは3行目の localStand のコピーであり、その内容はidentity行列である。したがって、このプログラムではStandには何の変化も起こらない。
Handleに実行される変換行列 worldHandle (6行目)の内容は、まず localHandle を実行し、次に localStand を実行するものであるが、localStand はidentity行列なので実際にHandleに実行される変換は localHandle によるものだけである。したがって、worldHandle によってHandleに起こる変化はStand上部のアタッチポジションまでの移動、具体的には c_attachPos_Handle で表される量の移動だけである。
Octahに実行される変換行列 worldOctah (5行目)はここでは3つの行列の積であり、localOctah、localHandle、localStand の順で実行される。最初の localOctah によって、Octahは初期状態の位置からHandle先端のアタッチポジションまで移動し、次に localHandle が実行されるが、これによってOctahにはHandleと同じく c_attachPos_Handle だけの平行移動が実行される。localStand の内容はidentity行列なのでOctahの変換はここまでである。
図7はこのプログラムの実行結果である。Standは初期状態から動いていないが、HandleはStand上部のアタッチポジションまで移動しており、OctahはHandle先端のアタッチポジションに置かれている。上でも述べたがOctahとHandleには同じ変換行列 localHandle が実行されている。Octahの場合はHandle先端に移動した位置から、Handleの場合は初期状態の位置から実行される。これによって、OctahがHandle先端に置かれた状態で一体となってStand上部へ移動するのである。


3行目の localStand はここではidentity行列であるので、Standには何の変化も起こらなかったが、もしこの行列を以下のようにx軸方向に $-3$ だけの平行移動を行うように変更すると、実行結果は図8に示されるように全体がx軸方向に $-3$ だけ移動する結果になる。
Matrix4x4 localStand = TH3DMath.GetTranslation4x4(-3, 0, 0);
これは、localStand が3つのオブジェクトに実行されるためである。Standの場合は初期状態の位置から、Handleの場合はStand上部にアタッチされた位置から、Octahの場合は(Stand上部にアタッチされた)Handleの先端の位置から localStand が実行される。これによって3つのオブジェクトが一体となって同じだけの移動(x軸方向に$-3$の移動)をするのである。

赤いフィルターのかかっている状態がオブジェクトに対して変換行列が実行されている過程である。そして、赤いフィルターのかかっている状態から通常色の状態に切り替わるが、この瞬間にフレーム描画が発生する (描画されたフレームは図8と同じである)。
「localOctah」と表示されている間は変換行列 localOctah が実行されていることを意味しており、「localHandle」と表示されている間は変換行列 localHandle が、「localStand」と表示されている間は変換行列 localStand が実行されていることを意味している。それぞれの変換行列の内容は上で述べた通りである。
# Code2
続いて、OctahとHandleの2つのオブジェクトによる一体化した運動を見ていこう。以下の2つのプログラムは Octah、Handleのそれぞれに定義された運動である。
[Beta2A] (実行結果 図10)
i_shmOctah += 4.0f; float scale = 0.5f * Mathf.Sin(i_shmOctah * Mathf.Deg2Rad) + 1.5f; // 1.0 -- 2.0 Matrix4x4 S = TH3DMath.GetScale4x4(scale, 1.0f, scale); Octah.SetMatrix(S);
[Beta2B] (実行結果 図11)
i_degHandle++; Matrix4x4 R = TH3DMath.GetRotation4x4(i_degHandle, Vector3.up); Handle.SetMatrix(R);


Octahの運動はx軸方向、z軸方向への $1$倍から $2$倍の間の拡大縮小の繰り返しであり(図10)、Handleの運動は毎フレーム $1$°ずつの y軸周りの回転である(図11)。
Octahに実行されるスケール行列の倍率はBeta2Aの2行目で計算される。この計算は単振動によるものであり、倍率を表すローカル変数 scale には $1.0$ から $2.0$ の値が算出される。1行目の i_shmOctah は単振動計算に使われる角度を表すインスタンス変数であり、毎フレーム $4$ずつ増加するので scale の値は90フレームごとに $1.0$ から $2.0$ の間を往復することになる。
Beta2Bの i_degHandle はHandleの回転角度を表すインスタンス変数で、毎フレーム $1$ずつ増加するのでHandleは360フレームごとに1回転することになる。
次に、Octahの拡大縮小をHandle先端のアタッチポジションにおいて行わせる。
[Beta2C] (実行結果 図12)
// Octah i_shmOctah += 4.0f; float scale = 0.5f * Mathf.Sin(i_shmOctah * Mathf.Deg2Rad) + 1.5f; // 1.0 -- 2.0 Matrix4x4 sclOctah = TH3DMath.GetScale4x4(scale, 1.0f, scale); Matrix4x4 traOctah = TH3DMath.GetTranslation4x4(c_attachPos_Octah); Matrix4x4 localOctah = traOctah * sclOctah; // Handle Matrix4x4 localHandle = Matrix4x4.identity; Matrix4x4 worldOctah = localHandle * localOctah; Matrix4x4 worldHandle = localHandle; Octah.SetMatrix(worldOctah); Handle.SetMatrix(worldHandle);

Octahに実行される4行目のスケール行列 sclOctah の倍率は3行目で算出されローカル変数 scale にセットされるが、その値は最初のフレームでは $1.53$、2フレーム目では $1.57$、3フレーム目では $1.60$、以降も同様に算出され、$1.0$ から $2.0$ の間を往復する。5行目の traOctah はHandle先端のアタッチポジションまで移動する平行移動行列である。
図13は今回のプログラムBeta2Cの最初のいくつかのフレームについて、各フレームにおける変換行列の実行過程をアニメーションで表したものである。

先程のアニメーション(図9)と同様に、「localOctah」と表示されている間は変換行列 localOctah が実行されていることを意味しており、「localHandle」と表示されている間は変換行列 localHandle が実行されていることを意味している。また、今回は「localOctah」が表示されているときに「traOctah * sclOctah」という式も表示されている。プログラム6行目に示されるように、localOctah はスケール行列sclOctahと平行移動行列traOctahの積であり、Octahに対する変換はスケール、平行移動の順で実行される。アニメーション中では sclOctah が青く表示されているときは sclOctah が実行されていることを意味しており、traOctah が青く表示されているときは traOctah が表示されていることを意味している。
最初のフレームにおいてOctahは初期状態から $1.53$倍拡大し(sclOctah)、拡大した状態でアタッチポジションまで移動する(traOctah)。Handle先端のアタッチポジションまで移動し終わると、次に変換行列localHandleが実行されるが、localHandleの内容はここでは identity行列であるため(9行目)、localHandleの実行によって何も変化は起こらない (「localHandle」と表示されている間は2つのオブジェクトに変化は発生しない)。そして、その状態でフレーム描画が発生する。2フレーム目ではOctahは初期状態から $1.57$倍拡大し、拡大した状態でアタッチポジションまで移動する。移動し終わった後は何も変化することなくフレーム描画が発生する。3フレーム目以降も同様である。
描画されたフレームを連続的に表示すれば図12のアニメーションになる。
では、さらにHandleの回転を加えて、2つのオブジェクトの一体化した運動を作成しよう。
[Code2] (実行結果 図14)
// Octah i_shmOctah += 4.0f; float scale = 0.5f * Mathf.Sin(i_shmOctah * Mathf.Deg2Rad) + 1.5f; // 1.0 -- 2.0 Matrix4x4 sclOctah = TH3DMath.GetScale4x4(scale, 1.0f, scale); Matrix4x4 traOctah = TH3DMath.GetTranslation4x4(c_attachPos_Octah); Matrix4x4 localOctah = traOctah * sclOctah; // Handle i_degHandle++; Matrix4x4 rotHandle = TH3DMath.GetRotation4x4(i_degHandle, Vector3.up); Matrix4x4 localHandle = rotHandle; Matrix4x4 worldOctah = localHandle * localOctah; Matrix4x4 worldHandle = localHandle; Octah.SetMatrix(worldOctah); Handle.SetMatrix(worldHandle);

実行結果(図14)に見られるように、今回はHandleが回転しており、その先端においてOctahが拡大縮小を行っている。
下図15はCode2の最初のいくつかのフレームについて、各フレームにおける変換行列の実行過程をアニメーションで表したものである。1フレーム目ではOctahが $1.53$倍拡大し、拡大した状態でアタッチポジションまで移動する。ここまでが変換行列localOctahの内容であり、次に変換行列localHandleが実行される。今回のlocalHandleは毎フレーム$1$°ずつ回転を行う回転行列である。したがって、1フレーム目ではlocalHandleによって2つのオブジェクトがy軸周りに $1$°回転する。この回転は2つのオブジェクトに実行されるが、Handleの場合は初期状態からの回転となり、Octahの場合はHandle先端のアタッチポジションからの回転となる。これによって、2つのオブジェクトが一体となって回転することになるのである。この回転が終わった時点でフレーム描画が発生する。
2フレーム目ではOctahが $1.57$倍拡大し、拡大した状態でアタッチポジションまで移動する。その後、2つのオブジェクトがy軸周りに $2$°回転し、回転が終わった時点でフレーム描画が発生する。3フレーム目ではOctahが $1.60$倍拡大し、拡大した状態でアタッチポジションまで移動する。その後、2つのオブジェクトがy軸周りに $3$°回転し、回転が終わった時点でフレーム描画が発生する。
それ以降のフレームでも同様である。


図16は描画された各フレームをコマ送りで表示したものである。これを連続的に表示すれば図14のアニメーションになる。
# Code3
さらに、一番上の親オブジェクトStandを追加して、3つのオブジェクトを一体化させた場合の運動について見ていく。上記のCode2では、Handleがy軸周りに回転をしており、その先端においてOctahが拡大縮小を行っていた。Handleに実行される変換は回転のみで平行移動は実行されないため、この運動はHandleの初期状態の位置において行われていた。
次のプログラムは、この同じ運動をStand上部(Handleのアタッチポジション)において行うようにしたものである。
[Beta3] (実行結果 図17)
// Octah i_shmOctah += 4.0f; float scale = 0.5f * Mathf.Sin(i_shmOctah * Mathf.Deg2Rad) + 1.5f; // 1.0 -- 2.0 Matrix4x4 sclOctah = TH3DMath.GetScale4x4(scale, 1.0f, scale); Matrix4x4 traOctah = TH3DMath.GetTranslation4x4(c_attachPos_Octah); Matrix4x4 localOctah = traOctah * sclOctah; // Handle i_degHandle++; Matrix4x4 rotHandle = TH3DMath.GetRotation4x4(i_degHandle, Vector3.up); Matrix4x4 traHandle = TH3DMath.GetTranslation4x4(c_attachPos_Handle); Matrix4x4 localHandle = traHandle * rotHandle; // Stand Matrix4x4 localStand = Matrix4x4.identity; Matrix4x4 worldOctah = localStand * localHandle * localOctah; Matrix4x4 worldHandle = localStand * localHandle; Matrix4x4 worldStand = localStand; Octah.SetMatrix(worldOctah); Handle.SetMatrix(worldHandle); Stand.SetMatrix(worldStand);

Standに実行される変換行列 worldStand (19行目)は15行目の localStand のコピーであり、その内容はidentity行列であるため、Standには何も変化は起こらない。
Handleに実行される変換行列 worldHandle (18行目)の内容は localHandle、localStand がこの順序で実行されるものであるが、localStand はidentity行列なので実際には localHandle のみによる変換と同じである。今回の localHandle は12行目の計算に示されるように rotHandle と traHandle という2つの変換行列の積である。 rotHandle はCode2と同じく毎フレーム $1$°ずつy軸周りに回転を行う回転行列であり、traHandle はHandleをStand上部のアタッチポジションまで移動させる平行移動行列である (c_attachPos_HandleはStand上部のアタッチポジションまでの移動量を表すVector3型の定数)。したがって、localHandle によってHandleは毎フレーム $1$°ずつ回転し、回転した状態でStand上部のアタッチポジションまで移動することになる。
Octahに実行される変換行列 worldOctah (17行目)の内容は3つの変換行列の積であるが、localStand はidentity行列であるため実際には2つの変換行列 localOctah、localHandle がこの順序で実行されたものと同じである。localOctah の内容はCode2と同じであり、毎フレーム$1$倍から$2$倍の間の拡大を行い、拡大が行われた状態でHandle先端のアタッチポジションまで移動するというものである。その後 localHandle が実行されるが、Octahの場合はHandle先端から(Handleとともに)回転し、回転した状態で(Handleとともに)Stand上部のアタッチポジションまで移動することになる。
最後にStandの運動を追加する。
Standの運動は z軸方向の単振動であり、その移動量は $0$ から $4$ の範囲を往復する。
i_shmStand += 1.0f; float mv = 2.0f * Mathf.Sin(i_shmStand * Mathf.Deg2Rad) + 2.0f; // 0.0 -- 4.0 Matrix4x4 T = TH3DMath.GetTranslation4x4(0.0f, 0.0f, mv); Stand.SetMatrix(T);

図18はこのプログラムの実行結果であるが、Standはz軸上の $0$ から $4$ の間の往復運動を行っている (実際にz軸上の$0$から$4$の間を往復するのは図に示される黄色い小球であるが、これはStandのオブジェクト原点である。Standのオブジェクト原点はStandには含まれずStandの外側に存在している。「オブジェクト原点」については3-9節参照)。
最後のプログラムは、上で見てきた3つのオブジェクトの運動をすべて統合したものである。
[Code3] (実行結果 図19)
// Octah i_shmOctah += 4.0f; float scale = 0.5f * Mathf.Sin(i_shmOctah * Mathf.Deg2Rad) + 1.5f; // 1.0 -- 2.0 Matrix4x4 sclOctah = TH3DMath.GetScale4x4(scale, 1.0f, scale); Matrix4x4 traOctah = TH3DMath.GetTranslation4x4(c_attachPos_Octah); Matrix4x4 localOctah = traOctah * sclOctah; // Handle i_degHandle++; Matrix4x4 rotHandle = TH3DMath.GetRotation4x4(i_degHandle, Vector3.up); Matrix4x4 traHandle = TH3DMath.GetTranslation4x4(c_attachPos_Handle); Matrix4x4 localHandle = traHandle * rotHandle; // Stand i_shmStand += 1.0f; float mv = 2.0f * Mathf.Sin(i_shmStand * Mathf.Deg2Rad) + 2.0f; // 0.0 -- 4.0 Matrix4x4 localStand = TH3DMath.GetTranslation4x4(0.0f, 0.0f, mv); Matrix4x4 worldOctah = localStand * localHandle * localOctah; Matrix4x4 worldHandle = localStand * localHandle; Matrix4x4 worldStand = localStand; Octah.SetMatrix(worldOctah); Handle.SetMatrix(worldHandle); Stand.SetMatrix(worldStand);

下図20はCode3の最初のいくつかのフレームについて、各フレームにおける変換行列の実行過程をアニメーションで表したものである。
各フレームにおいて変換行列は localOctah、localHandle、localStand の順で実行される。Octahに実行される変換行列 worldOctah (19行目)はそれら3つの変換行列の積であるから、3つの変換行列による変換をすべて受ける。Handleに実行される変換行列 worldHandle (20行目)は localHandle、localStand の積であるため、その2つの変換行列による変換だけを受ける(localOctahが実行されている間は何も変化は発生しない)。Standに実行される変換行列 worldStand (21行目)は localStand のコピーであるので、Standは localStand による変換だけを受ける (localOctah、localHandleが実行されている間は何も変化は発生しない)。


1フレーム目の localOctah によって、Octahは初期状態から $1.53$倍拡大し、拡大した状態でHandle先端のアタッチポジションまで移動する。次に localHandle が実行されるが、これはOctah及びHandleに対して実行される。Handleの場合は初期状態から $1$°回転し、回転した状態でStand上部のアタッチポジションまで移動する。Octahの場合は(初期状態の)Handle先端から $1$°回転し、回転した状態でHandleと同じだけの平行移動を行うので、結果としてはHandleと一体となってStand上部まで移動することになる。
最後に localStand が実行されるが、これは3つのオブジェクト全てに対して実行される。Standの場合は初期状態の位置からz軸方向に $2.03$だけ移動する。Handle、Octahにも同じ平行移動が実行されるが、Handleの場合はStand上部のアタッチポジションからの移動であり、Octahの場合は(Stand上部にアタッチされている)Handle先端からの移動となる。これによって、3つのオブジェクトが一体となって移動することになるのである。このz軸方向への移動が終わった時点でフレーム描画が発生する。
2フレーム目では localOctah によって、Octahが初期状態から $1.57$倍拡大し、拡大した状態でHandle先端のアタッチポジションまで移動する。次に localHandle がOctahとHandleに実行される。Handleの場合は初期状態から $2$°回転し、回転した状態でStand上部のアタッチポジションまで移動する。Octahの場合は(初期状態の)Handle先端から $2$°回転し、回転した状態でHandleと同じだけの平行移動を行う。最後に3つのオブジェクトに対して localStand が実行されるが、2フレーム目ではz軸方向に $2.07$だけの移動となる。Standの場合は初期状態からの移動であり、Handleの場合はStand上部のアタッチポジションからの移動となり、Octahの場合は(Stand上部にアタッチされている)Handle先端からの移動となる。3つのオブジェクトのz軸方向の移動が終わった時点でフレーム描画となる。
3フレーム目以降も同様である。
図21は描画された各フレームをコマ送りで表示したものである。これを連続的に表示すれば図19のアニメーションになる。
複数のオブジェクトが一体化して運動をするのは、子オブジェクトが親オブジェクトにアタッチされた状態で、子オブジェクトと親オブジェクトの両者に同じ変換行列が実行されるためである。このことはオブジェクトの階層構造(すなわち親子階層)が2階層であれ3階層であれ、あるいはそれ以上であっても変わらない。
この講義で扱うオブジェクトの運動は単純なものであるが、一見複雑に見えるオブジェクトの運動であっても、その運動(具体的には、各フレームにおけるオブジェクトの位置、向き、大きさ)はやはり行列の積として考えることができるのである。しかし、ゲームエンジンやDCCツールにおいてオブジェクトの運動を実装する場合に、つまり、あるフレームにおけるオブジェクトの位置や向き、大きさなどを計算する場合には行列ではなく「Position」「Rotation」「Scale」というデータ(あるいはこれに似た名前を持つデータ)に値を設定していくことが普通である。そこでは、行列という概念は目立たないように裏へ追いやられている。
Unityでも事情は同じである。Unityにおいてオブジェクトを動かす際には Transform という変換処理専門のクラスを経由するが、Transformクラスにはこの講義で使用してきた SetMatrix(..) のようなメソッドは標準的には備わってはいない。やはり「Position」「Rotation」「Scale」なのである。
この講義においても第5章、あるいは第6章以降ではオブジェクトを動かす際に、Unityに標準で用意されているTransformクラスの localPosition や position などのプロパティ用いるが、オブジェクトの運動をプログラムで実装するにあたっては「Position」「Rotation」「Scale」による方法よりも、行列による方法の方が初学者向きなのである。
行列は「Position」「Rotation」「Scale」に比べて難しい印象があるが、それはオブジェクトの運動に関して言えば明らかに誤解である。オブジェクトの運動は行列によって考える方が単純であり、直接的なのである。行列はベクトルと並んでコンピューターグラフィックスにおいてはその中心に位置する概念である。特にオブジェクトの運動にこそ、その真価を発揮する。
例えば、次のような6つの変換があったとしよう (括弧内の$Tx$や$Ry$は各変換を表す変換行列である)。
--> x軸方向に$3$の平行移動 ($Tx$)
--> z軸方向に$10$の平行移動 ($Tz$)
--> y軸周りの$60$°の回転 ($Ry$)
--> z軸周りの$120$°の回転 ($Rz$)
--> 各軸方向に$2$倍の拡大 ($S_{2}$)
--> 各軸方向に$0.5$倍の縮小 ($S_{0.5}$)
そして、オブジェクトに対して次のような順序で変換を実行するとする。
(1) 各軸方向に$2$倍の拡大 ($S_{2}$)
(2) y軸周りの$60$°の回転 ($Ry$)
(3) x軸方向に$3$の平行移動 ($Tx$)
(4) z軸周りの$120$°の回転 ($Rz$)
(5) 各軸方向に$0.5$倍の縮小 ($S_{0.5}$)
(6) z軸方向に$10$の平行移動 ($Tz$)
最終的にオブジェクトに対して実行される変換行列を $M$ とすれば、$M$ は以下のように求められる。
\[ M = TzS_{0.5}RzTxRyS_{2}\]つまり、(1)から(6)の変換行列を順番に右から掛けていくだけである。
プログラムで書けば、次のようになる (各変換行列の算出部分は省略している)。
M = Tz * S05 * Rz * Tx * Ry * S2; Obj.SetMatrix(M);
変換の実行順序をかえて、次のような順序で変換を実行するとしよう。
(1) z軸周りの$120$°の回転 ($Rz$)
(2) z軸方向に$10$の平行移動 ($Tz$)
(3) 各軸方向に$0.5$倍の縮小 ($S_{0.5}$)
(4) x軸方向に$3$の平行移動 ($Tx$)
(5) y軸周りの$60$°の回転 ($Ry$)
(6) 各軸方向に$2$倍の拡大 ($S_{2}$)
最終的にオブジェクトに対して実行される変換行列 $M$ は\[ M = S_{2}RyTxS_{0.5}TzRz \]となる。
ここでも先程と同様に、(1)から(6)の変換行列を順番に右から掛けていくだけである。
プログラムで書けば、次のようになる (各変換行列の算出部分は省略している)。
M = S2 * Ry * Tx * S05 * Tz * Rz; Obj.SetMatrix(M);
(列優先)行列の場合、その積は右から左へ向かって計算されていくので(3-8節)、変換行列の積の場合においても、その変換順序は右から左へ順に実行されていく。このことは既に何度か述べてきた。したがって、上記で示した例は自明なことであったかもしれない。
しかし上例のような、オブジェクトに対して複数の変換を順番に実行する、というのは行列を使って行ったために簡単にできたのである。先程述べたようにゲームエンジンやDCCツールでは行列による方法ではなく「Position」「Rotation」「Scale」の3つのデータに値をセットしてオブジェクトの運動を実装していく。例えば、今上で示した6つの変換と同じ実行結果になるように「Position」「Rotation」「Scale」のそれぞれにセットする値を求めるのは決して容易なことではない。
オブジェクトに対して複数の変換を実行する場合、行列であればそれらの変換を表す変換行列を順に掛けていくだけである。5個の変換であれば5個の変換行列を右から左へ掛け、10個の変換であれば10個の変換行列を右から左へ掛け、その積をオブジェクト実行すればよい。しかし「Position」「Rotation」「Scale」に値をセットするやり方では、このように簡単にはいかない。上で用いたプログラムは、6個の変換行列をオブジェクトに対して実行するものであった。
M = S2 * Ry * Tx * S05 * Tz * Rz; Obj.SetMatrix(M);
「Position」「Rotation」「Scale」に値をセットして、この実行結果と同じ状態になるように、つまりオブジェクトの位置、向き、大きさが同じになるように以下のプログラムにおけるそれぞれの右辺の値を求めることは容易ではないのである。
Obj.Position = ..; Obj.Rotation = ..; Obj.Scale = ..;
以上のことからオブジェクトの運動を実装する際には「Position」「Rotation」「Scale」によるやり方よりも、行列による方法の方が単純であり、直接的であることがわかるであろう。しかし、実際にはオブジェクトの運動は行列ではなく「Position」「Rotation」「Scale」の3つのデータによって表現される。その主な理由は計算負荷、変換の最適化、メモリーコスト、及びオブジェクトの状態の可視化である (他にも、行列の積を積み重ねていくとコンピューターの計算誤差が累積していくという問題もある)。
3Dオブジェクトの場合、その運動(正確には各フレームにおける状態)は$4\times4$行列で表されるが、$4\times4$行列の積は計算負荷として低いものではなく、$4\times4$行列を保持しておく場合に必要なメモリ容量も「Position」「Rotation」「Scale」の場合に比べて大きくなる。
また、今までのプログラムではオブジェクトを動かす際には毎フレーム 平行移動行列や回転行列、スケール行列の積を計算していたが、オブジェクトに実行する変換行列は必要なときにだけ計算して求めるのが望ましい。例えば、同じ位置で回転し続けるような場合には今までのプログラムでは平行移動行列と回転行列の積を毎フレーム計算していたが、実際にはこのような計算は無駄なのである。これは後の章で解説するが、位置が変わらずに回転状態だけが変化するといった場合や逆にオブジェクトの姿勢は変化しないが位置だけが変化するといった場合には、オブジェクトに実行する変換行列の一部だけを更新すればよいのである。
さらに、インタラクティブにオブジェクトの状態を画面上で設定していく場合には、行列は全く向いていない。$4\times4$行列は16個の実数値から成るが、それらのデータが画面上に表示されていても、そこからオブジェクトの状態を読み解くのは困難である。
しかし「Position」「Rotation」「Scale」によるやり方も、その根底は行列の積なのである。「Position」「Rotation」「Scale」にセットされたデータは最終的には、その時点におけるオブジェクトの状態を表す行列を求めるために使われるのである。これらのことは第4章や第5章において解説する。
再述するが、コンピューターグラフィックスにおいてオブジェクトを動かす際に最も重要な基礎となるのは行列的思考なのである。
© 2020-2025 Redpoll's 60 (All rights reserved)