Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-7
第3章 3D空間の基礎
$§$3-7 行列 1
1-4節から1-7節では2D空間における行列についての簡単な紹介を行った。そして、第1章、第2章では2D空間でのオブジェクトの運動を、主に行列を用いて実装したのであった。そこでも述べたことであるが、もう一度繰り返そう。
3D空間や2D空間においてオブジェクトに対して行う平行移動や回転、スケールなどの操作を変換(Transformation)という(注1)。コンピューターグラフィックスでは、これらの変換を行列の形で表して使用する。変換を表す行列を変換行列(Transformation Matrix)といい、平行移動行列や回転行列、スケール行列などがそれにあたる。また、変換を連続して行うことを変換の合成といい、平行移動、回転、スケールなどの変換の合成は、それらの変換を表す変換行列の積によって表される。
(注1) 他にも「せん断」という変換があるが、この講義では扱わない。
ここでは、まず2D空間における行列計算について再度復習しよう。
\[\begin{pmatrix}s &0 \\0 &t\end{pmatrix} \qquad\begin{pmatrix}\cos\theta &-\sin\theta \\\sin\theta & \cos\theta \end{pmatrix} \qquad\begin{pmatrix}1 &0 &a \\0 &1 &b \\ 0 &0 &1\end{pmatrix}\]上の行列は左から2D空間におけるスケール行列、回転行列、平行移動行列である。2D空間ではスケール行列や回転行列は$2\times2$行列で表せるが、平行移動行列は$3\times3$行列でしか表せない。そこで、平行移動行列との積を可能にするためにスケール行列や回転行列も1次元拡張して以下のように$3\times3$行列にしたものを計算に使う。
\[\begin{pmatrix}s &0 &0 \\0 &t &0 \\0 &0 &1\end{pmatrix} \qquad\begin{pmatrix}\cos\theta &-\sin\theta &0 \\\sin\theta & \cos\theta &0 \\0 &0 &1\end{pmatrix}\]2D空間内のある点$(x, y)$を行列によって変換する場合も、やはり1次元拡張して$(x, y, 1)$とし、以下のように計算で用いる。
$(x, y, 1)$をスケール、回転、平行移動の順で変換 (変換後の座標を$(x', y', 1)$とする ; 以下の行列の積は右から左に進む)
そして、このように1次元拡張した座標を同次座標というのであった。
つまり、2D空間においてある点を行列を用いて変換する場合は、その点は同次座標として3次元ベクトルで表されたものを使い、スケール行列、回転行列、平行移動行列などの変換行列は$3\times3$行列で表されたものを使うのである。
3D空間における行列計算もまた事情は同じである。
詳しくは3-9以降で解説するが3D空間におけるスケール行列、回転行列、平行移動行列は以下の形で表される。
\[\begin{pmatrix}s_x &0 &0 &0\\0 &s_y &0 &0\\0 &0 &s_z &0\\0 &0 &0 &1\end{pmatrix} \qquad\begin{pmatrix}r_{11} &r_{12} &r_{13} &0 \\r_{21} &r_{22} &r_{23} &0 \\r_{31} &r_{32} &r_{33} &0 \\0 &0 &0 &1 \end{pmatrix}\]3D空間のある点$(x, y, z)$を行列によって変換する場合も、その点を1次元拡張した4次元ベクトルの同次座標$(x, y, z, 1)$にする。2次元ベクトルを拡張する場合もそうであったが、同次座標に拡張する場合は常に1を追加する。同次座標$(x, y, z, 1)$を用いた計算は次のようになる。
$(x, y, z, 1)$をスケール、回転、平行移動の順で変換 (変換後の座標を$(x', y', z', 1)$とする ; 以下の計算においても行列の積は右から左へ進む)
つまり、2D空間であれ3D空間であれ、ある点を行列を用いて変換する場合は、その点は同次座標として1次元拡張したベクトルで表され、変換行列は同次座標に対応した次数の正方行列で表されるのである (3次元ベクトルなら$3\times3$行列、4次元ベクトルなら$4\times4$行列 ; 正方行列とは行数と列数が等しい行列)。
したがって、3D空間での行列計算は$(x, y, z, 1)$の形の4次元ベクトルと$4\times4$行列が主として用いられるのである。
以降のプログラムでは $4\times4$行列を表す構造体として次のものを使用する。
3D空間における行列計算は基本的に$4\times4$行列を使用するので、Matrix4x4構造体はこの先非常に多く使われる。
では、3D空間で最も頻繁に使われる行列である$4\times4$行列の積の定義から始めよう。
$4\times4$行列の積は次のように定義される(積も$4\times4$行列である)。
つまり、上の行列の積の$i$行$j$列目の成分を$c_{ij}$とすれば、
$4\times4$の単位行列$I$を以下に示す。
\[I = \begin{pmatrix} 1 &0 &0 &0 \\0 &1 &0 &0 \\0 &0 &1 &0 \\0 &0 &0 &1 \end{pmatrix} \]
単位行列の性質として、単位行列$I$に任意の行列$A$(ここでは$4\times4$行列)を、右から掛けても左から掛けても、積は$A$に等しいことがあげられる。つまり、
\[ AI = A \qquad\qquad IA = A \]である。
単位行列$I$にベクトル$\boldsymbol{\mathsf{v}}$を掛ける場合でも積は変わらない(ただし行列を掛ける場合とは違い、ベクトルは右からしか掛けられない ; 詳しくは次節の「積が可能になる条件」を参照)。
\[ I\boldsymbol{\mathsf{v}} = \boldsymbol{\mathsf{v}} \]
また、第2章において何度か見てきたが、オブジェクトに単位行列(identity行列)をセットすると、オブジェクトは何の変換も受けていない状態、すなわちオブジェクトの初期状態(2-1節)になる。
Matrix4x4構造体には単位行列を表す identity というstaticプロパティがある。その内容は上記の$I$と同じである。
$A$の逆行列は $A^{-1}$ として表される。すなわち、\[ AA^{-1} = A^{-1}A = I \]である。
1-4節で見たように、2つ以上の行列の積の場合には逆行列は次のようになる (以下の $A$、$B$、$C$、$D$ は n次正方行列で、逆行列が存在するものとする)。
\begin{align*}&(AB)^{-1} = B^{-1}A^{-1} \\\\&(ABC)^{-1} = C^{-1}B^{-1}A^{-1} \\\\&(ABCD)^{-1} = D^{-1}C^{-1}B^{-1}A^{-1} \end{align*}
Matrix4x4構造体には逆行列を表す inverse というプロパティがある。
例えば、Aが Matrix4x4のインスタンスであるとき、A.inverse は Aの逆行列を表している (つまり $A^{-1}$)。
$A$、$B$、$C$、$D$ を n次正方行列とする。
そのとき、これらの行列は積に関して以下の結合法則が成り立つ。
\begin{align*}&(AB)C = A(BC) \\\\&(AB)(CD) = (ABC)D = A(BCD) = ABCD\end{align*}すなわち、積の一部分を先に計算しても、積を右から順に1つ1つ順に計算しても同じ結果が得られる。
例えば、ある位置を表すベクトル $\boldsymbol{\mathsf{v}}$ に10個の変換を実行するとする。10個の変換を表す変換行列を $M_1, \ldots, M_{10}$ とし、それらの積を $M_{10} \cdots M_1 = M$ とする。
変換後の $\boldsymbol{\mathsf{v}}$ の位置を $\boldsymbol{\mathsf{w}}$ とすれば、$\boldsymbol{\mathsf{w}}$ は次のように求められる。
行列 $A$、$A'$、$B$ について、$A$ と $B$、$A'$ と $B$ の間で積$AB$、$A'B$が定義されており、さらに $A$、$A'$ の間で和が定義されているものとする。そのとき、この3つの行列の和と積に関して以下の分配法則が成り立つ。
\[ (A + A')B = AB + A'B \]また、行列 $A$、$B$、$B'$ について、$A$ と $B$、$A$ と $B'$ の間で積$AB$、$AB'$が定義されており、さらに $B$、$B'$ の間で和が定義されているものとする。そのとき、この3つの行列の和と積に関して以下の分配法則が成り立つ。
\[ A(B + B') = AB + AB' \]$4\times4$行列$M$と4次元ベクトル$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$を例にとると、分配法則によって以下の等式が成り立つ。
\[ M(\boldsymbol{\mathsf{v}} + \boldsymbol{\mathsf{w}}) = M\boldsymbol{\mathsf{v}} + M\boldsymbol{\mathsf{w}} \]
最後に、本節で述べた内容に関してのプログラムを作成する。
さらに $M_1$に対して新たに$R^{-1}$を掛け、その積を$M_2$とすると\[ M_2 = R^{-1}M_1 = R^{-1}(RS) = (R^{-1}R)S = IS = S \]となる。すなわち、$M_2 = S$ である。
最後に $M_2$に対して$S^{-1}$を掛け、その積を$M_3$とすると\[ M_3 = S^{-1}M_2 = S^{-1}S = I\]となる。
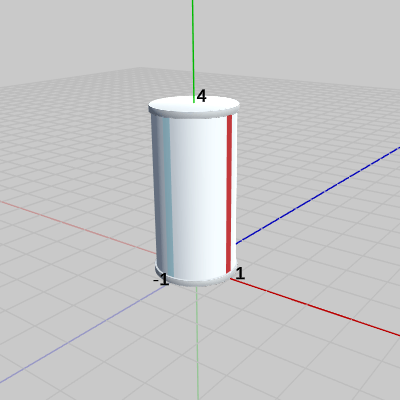
図1 Clinder 初期状態 今ここで示した計算結果をプログラムを用いて確認してみよう。
図1は円柱オブジェクトCylinderの初期状態である。Cylinderは初期状態において半径が$1$、高さが$4$で 底面の中心が原点に置かれている。
この Cylinderに対して次の3つの変換を順に実行していく。
1 : x軸、y軸、z軸方向へ$2$倍の拡大
2 : x軸周りに$30$°の回転
3 : z軸プラス方向へ$4$だけ平行移動
それぞれの変換は スケール行列$S$、回転行列$R$、平行移動行列$T$によって表されるものとする。
2D空間と同様に3D空間においてもオブジェクトに変換行列を実行する場合には、以下のメソッドを実行する (3D空間で使用するオブジェクトはすべて、カスタムライブラリで用意されている THObject3Dクラスのインスタンスである)。
実行するプログラムを以下に示す。
[Code1] (実行結果 図1)
1行目の I は単位行列を表し、13行目の Cylinder.SetMatrix(..) の引数に Iを渡して実行した結果が図1である。
2行目～4行目の S、R、T は上で述べた、各軸方向へ$2$倍の拡大を実行するスケール行列、x軸周りに$30$°の回転を実行する回転行列、$(0, 0, 4)$だけの平行移動を実行する平行移動行列を表している (それぞれの行列を取得するカスタムライブラリのメソッドについては次節以降で解説する)。5行目、6行目の RS、TRS も変数名が表すとおりそれらの積である。
以下の図2～図4は、13行目の Cylinder.SetMatrix(..) の引数に渡す行列を変えて実行した結果である。
図2は Cylinderに2行目のスケール行列Sを実行した結果である。実行前と比べて半径、高さが$2$倍になっている。図3は5行目の変換行列RSを実行した結果である (図2の状態からx軸周りに$30$°回転した状態である)。RSはスケール、回転を1つの行列にまとめたものであり、RSの実行結果はスケール、回転をこの順で実行した結果に等しい。図4は6行目の変換行列TRSを実行した結果である (図3の状態からz軸方向に$4$だけ平行移動している)。TRSはスケール、回転、平行移動を1つの行列にまとめたものであり、TRSの実行結果はスケール、回転、平行移動をこの順で実行した結果に等しい。
8行目以降は逆行列を使った計算である。
8行目のMはスケール、回転、平行移動を1つの行列にまとめたものである (6行目のTRSと内容は同じ)。9行目における T.inverse は平行移動行列Tの逆行列であるから、T.inverse * M は MにTの逆行列を掛ける処理であり、$T^{-1}M$ を意味している。
以下の図5～図7は 9行目～11行目の変換行列M1、M2、M3を実行した結果である。
9行目～11行目の M1、M2、M3 は先程の計算における $M_1$、$M_2$、$M_3$ を表している。そこで示されたように、$M_1 = RS$、$M_2 = S$、$M_3 = I$ であるから、M1を実行した結果である図5は RSを実行した結果である図3と同じ状態になっている。同様に、M2を実行した結果である図6は Sを実行した結果である図2と同じ状態であり、M3を実行した結果である図7は初期状態の図1と同じ状態になっている。
3D空間や2D空間においてオブジェクトに対して行う平行移動や回転、スケールなどの操作を変換(Transformation)という(注1)。コンピューターグラフィックスでは、これらの変換を行列の形で表して使用する。変換を表す行列を変換行列(Transformation Matrix)といい、平行移動行列や回転行列、スケール行列などがそれにあたる。また、変換を連続して行うことを変換の合成といい、平行移動、回転、スケールなどの変換の合成は、それらの変換を表す変換行列の積によって表される。
(注1) 他にも「せん断」という変換があるが、この講義では扱わない。
ここでは、まず2D空間における行列計算について再度復習しよう。
\[\begin{pmatrix}s &0 \\0 &t\end{pmatrix} \qquad\begin{pmatrix}\cos\theta &-\sin\theta \\\sin\theta & \cos\theta \end{pmatrix} \qquad\begin{pmatrix}1 &0 &a \\0 &1 &b \\ 0 &0 &1\end{pmatrix}\]上の行列は左から2D空間におけるスケール行列、回転行列、平行移動行列である。2D空間ではスケール行列や回転行列は$2\times2$行列で表せるが、平行移動行列は$3\times3$行列でしか表せない。そこで、平行移動行列との積を可能にするためにスケール行列や回転行列も1次元拡張して以下のように$3\times3$行列にしたものを計算に使う。
\[\begin{pmatrix}s &0 &0 \\0 &t &0 \\0 &0 &1\end{pmatrix} \qquad\begin{pmatrix}\cos\theta &-\sin\theta &0 \\\sin\theta & \cos\theta &0 \\0 &0 &1\end{pmatrix}\]2D空間内のある点$(x, y)$を行列によって変換する場合も、やはり1次元拡張して$(x, y, 1)$とし、以下のように計算で用いる。
$(x, y, 1)$をスケール、回転、平行移動の順で変換 (変換後の座標を$(x', y', 1)$とする ; 以下の行列の積は右から左に進む)
\[\begin{pmatrix}1 &0 &a \\0 &1 &b \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}\cos\theta &-\sin\theta &0 \\\sin\theta & \cos\theta &0 \\0 &0 &1\end{pmatrix}\begin{pmatrix}s &0 &0 \\0 &t &0 \\0 &0 &1\end{pmatrix}\begin{pmatrix}x \\y \\1\end{pmatrix}=\begin{pmatrix}x' \\y' \\1\end{pmatrix}\]
そして、このように1次元拡張した座標を同次座標というのであった。
つまり、2D空間においてある点を行列を用いて変換する場合は、その点は同次座標として3次元ベクトルで表されたものを使い、スケール行列、回転行列、平行移動行列などの変換行列は$3\times3$行列で表されたものを使うのである。
3D空間における行列計算もまた事情は同じである。
詳しくは3-9以降で解説するが3D空間におけるスケール行列、回転行列、平行移動行列は以下の形で表される。
\[\begin{pmatrix}s_x &0 &0 \\0 &s_y &0 \\0 &0 &s_z\end{pmatrix} \qquad\begin{pmatrix}r_{11} &r_{12} &r_{13} \\r_{21} &r_{22} &r_{23} \\r_{31} &r_{32} &r_{33} \end{pmatrix} \qquad \begin{pmatrix}1 &0 &0 &a \\0 &1 &0 &b \\ 0 &0 &1 &c \\0 &0 &0 &1\end{pmatrix}\]
3D空間ではスケール行列や回転行列は$3\times3$行列で表せるが、平行移動行列は$4\times4$行列でしか表せない。そこで、ここでもまた平行移動行列との積を可能にするためにスケール行列や回転行列も1次元拡張して以下のように$4\times4$行列にしたものを計算に使う。\[\begin{pmatrix}s_x &0 &0 &0\\0 &s_y &0 &0\\0 &0 &s_z &0\\0 &0 &0 &1\end{pmatrix} \qquad\begin{pmatrix}r_{11} &r_{12} &r_{13} &0 \\r_{21} &r_{22} &r_{23} &0 \\r_{31} &r_{32} &r_{33} &0 \\0 &0 &0 &1 \end{pmatrix}\]3D空間のある点$(x, y, z)$を行列によって変換する場合も、その点を1次元拡張した4次元ベクトルの同次座標$(x, y, z, 1)$にする。2次元ベクトルを拡張する場合もそうであったが、同次座標に拡張する場合は常に1を追加する。同次座標$(x, y, z, 1)$を用いた計算は次のようになる。
$(x, y, z, 1)$をスケール、回転、平行移動の順で変換 (変換後の座標を$(x', y', z', 1)$とする ; 以下の計算においても行列の積は右から左へ進む)
\[\begin{pmatrix}1 &0 &0 &a \\0 &1 &0 &b \\ 0 &0 &1 &c \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}r_{11} &r_{12} &r_{13} &0 \\r_{21} &r_{22} &r_{23} &0 \\r_{31} &r_{32} &r_{33} &0 \\0 &0 &0 &1 \end{pmatrix}\begin{pmatrix}s_x &0 &0 &0\\0 &s_y &0 &0\\0 &0 &s_z &0\\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}x \\y \\z \\1\end{pmatrix}=\begin{pmatrix}x' \\y' \\z' \\1\end{pmatrix}\]
つまり、2D空間であれ3D空間であれ、ある点を行列を用いて変換する場合は、その点は同次座標として1次元拡張したベクトルで表され、変換行列は同次座標に対応した次数の正方行列で表されるのである (3次元ベクトルなら$3\times3$行列、4次元ベクトルなら$4\times4$行列 ; 正方行列とは行数と列数が等しい行列)。
したがって、3D空間での行列計算は$(x, y, z, 1)$の形の4次元ベクトルと$4\times4$行列が主として用いられるのである。
以降のプログラムでは $4\times4$行列を表す構造体として次のものを使用する。
Matrix4x4
: Unityに用意されている$4\times4$行列を表す構造体3D空間における行列計算は基本的に$4\times4$行列を使用するので、Matrix4x4構造体はこの先非常に多く使われる。
では、3D空間で最も頻繁に使われる行列である$4\times4$行列の積の定義から始めよう。
A) 行列の積
1-4節でも述べたが、行列演算を実際に実行するのはCPUやGPUであり、プログラマーはプログラムに数式を記述するだけでよい。実際に、内部で行われる計算をプログラマーが常に確認する必要もない。したがって、$4\times4$行列の積のような煩雑な計算はその手順だけを確実に把握しておく程度で十分である。重要なのは行列演算を正しく行えるかではなく、ある目的を達成するためにどういう行列をどのように使うかといことである。具体的には、オブジェクトに目的の運動をさせる場合などでは、どういった変換行列をどのような順番で実行するかということを考えることが重要なのである。それがわかれば、あとはプログラムに数式を記述するだけであり、その先の計算処理についてはコンピューター側の仕事になる。$4\times4$行列の積は次のように定義される(積も$4\times4$行列である)。
\[\begin{pmatrix}a_{11} &a_{12} &a_{13} &a_{14}\\a_{21} &a_{22} &a_{23} &a_{24}\\a_{31} &a_{32} &a_{33} &a_{34}\\a_{41} &a_{42} &a_{43} &a_{44}\end{pmatrix}\begin{pmatrix}\color{blue}{b_{11}} &\color{blue}{b_{12}} &\color{blue}{b_{13}} &\color{blue}{b_{14}}\\\color{blue}{b_{21}} &\color{blue}{b_{22}} &\color{blue}{b_{23}} &\color{blue}{b_{24}}\\\color{blue}{b_{31}} &\color{blue}{b_{32}} &\color{blue}{b_{33}} &\color{blue}{b_{34}}\\ \color{blue}{b_{41}} &\color{blue}{b_{42}} &\color{blue}{b_{43}} &\color{blue}{b_{44}}\end{pmatrix}= \]
\[\begin{pmatrix}a_{11}\color{blue}{b_{11}}+a_{12}\color{blue}{b_{21}}+a_{13}\color{blue}{b_{31}}+a_{14}\color{blue}{b_{41}}&a_{11}\color{blue}{b_{12}}+a_{12}\color{blue}{b_{22}}+a_{13}\color{blue}{b_{32}}+a_{14}\color{blue}{b_{42}}&a_{11}\color{blue}{b_{13}}+a_{12}\color{blue}{b_{23}}+a_{13}\color{blue}{b_{33}}+a_{14}\color{blue}{b_{43}}&a_{11}\color{blue}{b_{14}}+a_{12}\color{blue}{b_{24}}+a_{13}\color{blue}{b_{34}}+a_{14}\color{blue}{b_{44}}\\a_{21}\color{blue}{b_{11}}+a_{22}\color{blue}{b_{21}}+a_{23}\color{blue}{b_{31}}+a_{24}\color{blue}{b_{41}}&a_{21}\color{blue}{b_{12}}+a_{22}\color{blue}{b_{22}}+a_{23}\color{blue}{b_{32}}+a_{24}\color{blue}{b_{42}}&a_{21}\color{blue}{b_{13}}+a_{22}\color{blue}{b_{23}}+a_{23}\color{blue}{b_{33}}+a_{24}\color{blue}{b_{43}}&a_{21}\color{blue}{b_{14}}+a_{22}\color{blue}{b_{24}}+a_{23}\color{blue}{b_{34}}+a_{24}\color{blue}{b_{44}}\\a_{31}\color{blue}{b_{11}}+a_{32}\color{blue}{b_{21}}+a_{33}\color{blue}{b_{31}}+a_{34}\color{blue}{b_{41}}&a_{31}\color{blue}{b_{12}}+a_{32}\color{blue}{b_{22}}+a_{33}\color{blue}{b_{32}}+a_{34}\color{blue}{b_{42}} &a_{31}\color{blue}{b_{13}}+a_{32}\color{blue}{b_{23}}+a_{33}\color{blue}{b_{33}}+a_{34}\color{blue}{b_{43}}&a_{31}\color{blue}{b_{14}}+a_{32}\color{blue}{b_{24}}+a_{33}\color{blue}{b_{34}}+a_{34}\color{blue}{b_{44}}\\a_{41}\color{blue}{b_{11}}+a_{42}\color{blue}{b_{21}}+a_{43}\color{blue}{b_{31}}+a_{44}\color{blue}{b_{41}}&a_{41}\color{blue}{b_{12}}+a_{42}\color{blue}{b_{22}}+a_{43}\color{blue}{b_{32}}+a_{44}\color{blue}{b_{42}} &a_{41}\color{blue}{b_{13}}+a_{42}\color{blue}{b_{23}}+a_{43}\color{blue}{b_{33}}+a_{44}\color{blue}{b_{43}}&a_{41}\color{blue}{b_{14}}+a_{42}\color{blue}{b_{24}}+a_{43}\color{blue}{b_{34}}+a_{44}\color{blue}{b_{44}}\\\end{pmatrix}\]
つまり、上の行列の積の$i$行$j$列目の成分を$c_{ij}$とすれば、
\[ c_{ij} = a_{i1}\color{blue}{b_{1j}} + a_{i2}\color{blue}{b_{2j}} + a_{i3}\color{blue}{b_{3j}} + a_{i4}\color{blue}{b_{4j}}\qquad( 1\leq i \leq4\ ,\ 1\leq j \leq4) \]
である。B) 行列とベクトルの積
4次元ベクトルは見方を変えれば$4\times1$行列でもあるので、$4\times4$行列と4次元ベクトルの積は行列同士の積の特殊な場合として、次のように計算される。\[\begin{pmatrix}a_{11} &a_{12} &a_{13} &a_{14}\\a_{21} &a_{22} &a_{23} &a_{24}\\a_{31} &a_{32} &a_{33} &a_{34}\\a_{41} &a_{42} &a_{43} &a_{44}\end{pmatrix}\begin{pmatrix}\color{blue}{v_x} \\\color{blue}{v_y} \\\color{blue}{v_z} \\\color{blue}{v_w} \end{pmatrix}=\begin{pmatrix}a_{11}\color{blue}{v_x}+a_{12}\color{blue}{v_y}+a_{13}\color{blue}{v_z}+a_{14}\color{blue}{v_w}\\a_{21}\color{blue}{v_x}+a_{22}\color{blue}{v_y}+a_{23}\color{blue}{v_z}+a_{24}\color{blue}{v_w}\\a_{31}\color{blue}{v_x}+a_{32}\color{blue}{v_y}+a_{33}\color{blue}{v_z}+a_{34}\color{blue}{v_w}\\a_{41}\color{blue}{v_x}+a_{42}\color{blue}{v_y}+a_{43}\color{blue}{v_z}+a_{44}\color{blue}{v_w}\end{pmatrix} \]
C) 単位行列
2D空間でも頻繁に使われたが、3D空間においても単位行列(Identity Matrix)を使用する (3D空間では$4\times4$の単位行列を主に用いる)。$4\times4$の単位行列$I$を以下に示す。
\[I = \begin{pmatrix} 1 &0 &0 &0 \\0 &1 &0 &0 \\0 &0 &1 &0 \\0 &0 &0 &1 \end{pmatrix} \]
単位行列の性質として、単位行列$I$に任意の行列$A$(ここでは$4\times4$行列)を、右から掛けても左から掛けても、積は$A$に等しいことがあげられる。つまり、
\[ AI = A \qquad\qquad IA = A \]である。
単位行列$I$にベクトル$\boldsymbol{\mathsf{v}}$を掛ける場合でも積は変わらない(ただし行列を掛ける場合とは違い、ベクトルは右からしか掛けられない ; 詳しくは次節の「積が可能になる条件」を参照)。
\[ I\boldsymbol{\mathsf{v}} = \boldsymbol{\mathsf{v}} \]
また、第2章において何度か見てきたが、オブジェクトに単位行列(identity行列)をセットすると、オブジェクトは何の変換も受けていない状態、すなわちオブジェクトの初期状態(2-1節)になる。
Matrix4x4構造体には単位行列を表す identity というstaticプロパティがある。その内容は上記の$I$と同じである。
Matrix4x4.identity
: Matrix4x4構造体のstaticプロパティで、$4\times4$の単位行列を表すD) 逆行列
n次正方行列$A$に対して、\[ AB = BA = I \]となる n次正方行列$B$が存在するとき、$B$を$A$の逆行列 (Inverse Matrix)という ($I$はn次単位行列である)。$A$の逆行列は $A^{-1}$ として表される。すなわち、\[ AA^{-1} = A^{-1}A = I \]である。
1-4節で見たように、2つ以上の行列の積の場合には逆行列は次のようになる (以下の $A$、$B$、$C$、$D$ は n次正方行列で、逆行列が存在するものとする)。
\begin{align*}&(AB)^{-1} = B^{-1}A^{-1} \\\\&(ABC)^{-1} = C^{-1}B^{-1}A^{-1} \\\\&(ABCD)^{-1} = D^{-1}C^{-1}B^{-1}A^{-1} \end{align*}
Matrix4x4構造体には逆行列を表す inverse というプロパティがある。
inverse
: Matrix4x4構造体のプロパティで、Matrix4x4インスタンスの逆行列を表す。例えば、Aが Matrix4x4のインスタンスであるとき、A.inverse は Aの逆行列を表している (つまり $A^{-1}$)。
E) 結合法則、分配法則
1-4節でも解説したが、ここでも行列の結合法則、及び分配法則について簡単に触れておく。$A$、$B$、$C$、$D$ を n次正方行列とする。
そのとき、これらの行列は積に関して以下の結合法則が成り立つ。
\begin{align*}&(AB)C = A(BC) \\\\&(AB)(CD) = (ABC)D = A(BCD) = ABCD\end{align*}すなわち、積の一部分を先に計算しても、積を右から順に1つ1つ順に計算しても同じ結果が得られる。
例えば、ある位置を表すベクトル $\boldsymbol{\mathsf{v}}$ に10個の変換を実行するとする。10個の変換を表す変換行列を $M_1, \ldots, M_{10}$ とし、それらの積を $M_{10} \cdots M_1 = M$ とする。
変換後の $\boldsymbol{\mathsf{v}}$ の位置を $\boldsymbol{\mathsf{w}}$ とすれば、$\boldsymbol{\mathsf{w}}$ は次のように求められる。
\[M_{10} \cdots M_1\boldsymbol{\mathsf{v}} = (M_{10} \cdots M_1)\boldsymbol{\mathsf{v}}= M\boldsymbol{\mathsf{v}} = \boldsymbol{\mathsf{w}}\]
つまり、10個の変換行列の積を先に計算し その積を $M$ とし、$M$ とベクトル $\boldsymbol{\mathsf{v}}$ の積を計算すれば変換後の位置 $\boldsymbol{\mathsf{w}}$ が求められるわけである。行列 $A$、$A'$、$B$ について、$A$ と $B$、$A'$ と $B$ の間で積$AB$、$A'B$が定義されており、さらに $A$、$A'$ の間で和が定義されているものとする。そのとき、この3つの行列の和と積に関して以下の分配法則が成り立つ。
\[ (A + A')B = AB + A'B \]また、行列 $A$、$B$、$B'$ について、$A$ と $B$、$A$ と $B'$ の間で積$AB$、$AB'$が定義されており、さらに $B$、$B'$ の間で和が定義されているものとする。そのとき、この3つの行列の和と積に関して以下の分配法則が成り立つ。
\[ A(B + B') = AB + AB' \]$4\times4$行列$M$と4次元ベクトル$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$を例にとると、分配法則によって以下の等式が成り立つ。
\[ M(\boldsymbol{\mathsf{v}} + \boldsymbol{\mathsf{w}}) = M\boldsymbol{\mathsf{v}} + M\boldsymbol{\mathsf{w}} \]
最後に、本節で述べた内容に関してのプログラムを作成する。
# Code1
例えば、3つの$4\times4$行列$T$、$R$、$S$を次の順序で掛けていき、その積を$M$とする。\[ M = TRS \] ここで、$M$に$T$の逆行列$T^{-1}$を掛ける。次節で詳しく述べるが、この講義における行列の積は右から左へ進むので、$M$に対して新たに$T^{-1}$を掛ける場合は、$T^{-1}$が左側に来る。したがって、その積を$M_1$とすれば\begin{align*}M_1 &= T^{-1}M = T^{-1}(TRS) = (T^{-1}T)(RS) \\\\&= I(RS) = RS\end{align*}となる。すなわち、$M_1 = RS$ である (式中の$I$は単位行列)。さらに $M_1$に対して新たに$R^{-1}$を掛け、その積を$M_2$とすると\[ M_2 = R^{-1}M_1 = R^{-1}(RS) = (R^{-1}R)S = IS = S \]となる。すなわち、$M_2 = S$ である。
最後に $M_2$に対して$S^{-1}$を掛け、その積を$M_3$とすると\[ M_3 = S^{-1}M_2 = S^{-1}S = I\]となる。
図1は円柱オブジェクトCylinderの初期状態である。Cylinderは初期状態において半径が$1$、高さが$4$で 底面の中心が原点に置かれている。
この Cylinderに対して次の3つの変換を順に実行していく。
1 : x軸、y軸、z軸方向へ$2$倍の拡大
2 : x軸周りに$30$°の回転
3 : z軸プラス方向へ$4$だけ平行移動
それぞれの変換は スケール行列$S$、回転行列$R$、平行移動行列$T$によって表されるものとする。
2D空間と同様に3D空間においてもオブジェクトに変換行列を実行する場合には、以下のメソッドを実行する (3D空間で使用するオブジェクトはすべて、カスタムライブラリで用意されている THObject3Dクラスのインスタンスである)。
SetMatrix(Matrix4x4 m)
: 3D空間のオブジェクトに対して、引数で指定された変換行列を実行する (THObject3Dクラスのメソッド)。実行するプログラムを以下に示す。
[Code1] (実行結果 図1)
Matrix4x4 I = Matrix4x4.identity; Matrix4x4 S = TH3DMath.GetScale4x4(2.0f); Matrix4x4 R = TH3DMath.GetRotation4x4(30.0f, Vector3.right); Matrix4x4 T = TH3DMath.GetTranslation4x4(0.0f, 0.0f, 4.0f); Matrix4x4 RS = R * S; Matrix4x4 TRS = T * R * S; Matrix4x4 M = T * R * S; Matrix4x4 M1 = T.inverse * M; Matrix4x4 M2 = R.inverse * M1; Matrix4x4 M3 = S.inverse * M2; Cylinder.SetMatrix(TRS);
1行目の I は単位行列を表し、13行目の Cylinder.SetMatrix(..) の引数に Iを渡して実行した結果が図1である。
2行目～4行目の S、R、T は上で述べた、各軸方向へ$2$倍の拡大を実行するスケール行列、x軸周りに$30$°の回転を実行する回転行列、$(0, 0, 4)$だけの平行移動を実行する平行移動行列を表している (それぞれの行列を取得するカスタムライブラリのメソッドについては次節以降で解説する)。5行目、6行目の RS、TRS も変数名が表すとおりそれらの積である。
以下の図2～図4は、13行目の Cylinder.SetMatrix(..) の引数に渡す行列を変えて実行した結果である。
-
図2 スケールのみを実行した結果 (2行目のSを実行した結果) -
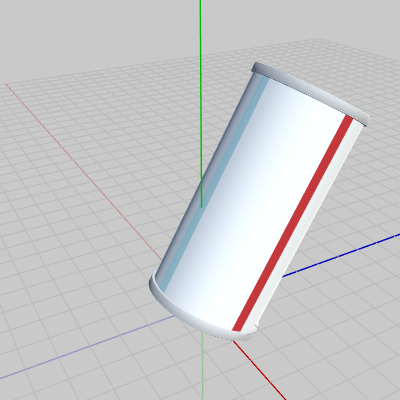図3 スケール後に回転を実行した結果 (5行目のRSを実行した結果) -
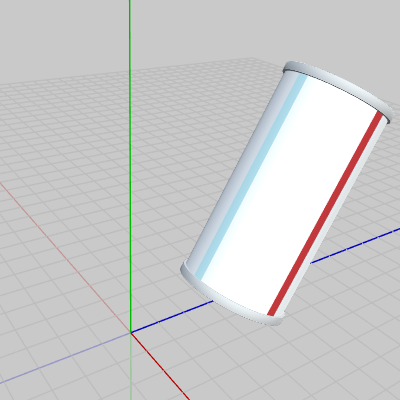図4 回転後に平行移動を実行した結果 (6行目のTRSを実行した結果)
図2は Cylinderに2行目のスケール行列Sを実行した結果である。実行前と比べて半径、高さが$2$倍になっている。図3は5行目の変換行列RSを実行した結果である (図2の状態からx軸周りに$30$°回転した状態である)。RSはスケール、回転を1つの行列にまとめたものであり、RSの実行結果はスケール、回転をこの順で実行した結果に等しい。図4は6行目の変換行列TRSを実行した結果である (図3の状態からz軸方向に$4$だけ平行移動している)。TRSはスケール、回転、平行移動を1つの行列にまとめたものであり、TRSの実行結果はスケール、回転、平行移動をこの順で実行した結果に等しい。
8行目以降は逆行列を使った計算である。
8行目のMはスケール、回転、平行移動を1つの行列にまとめたものである (6行目のTRSと内容は同じ)。9行目における T.inverse は平行移動行列Tの逆行列であるから、T.inverse * M は MにTの逆行列を掛ける処理であり、$T^{-1}M$ を意味している。
以下の図5～図7は 9行目～11行目の変換行列M1、M2、M3を実行した結果である。
- 図5 9行目のM1を実行した結果
- 図6 10行目のM2を実行した結果
- 図7 11行目のM3を実行した結果
9行目～11行目の M1、M2、M3 は先程の計算における $M_1$、$M_2$、$M_3$ を表している。そこで示されたように、$M_1 = RS$、$M_2 = S$、$M_3 = I$ であるから、M1を実行した結果である図5は RSを実行した結果である図3と同じ状態になっている。同様に、M2を実行した結果である図6は Sを実行した結果である図2と同じ状態であり、M3を実行した結果である図7は初期状態の図1と同じ状態になっている。
© 2020-2024 Redpoll's 60 (All rights reserved)