Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-20
第3章 3D空間の基礎
$§$3-20 課題 1
コンピューターグラフィックス 特に3DCGにおいては座標変換が頻繁に行われる。本節及び次節では3DCGの世界において日常的に使われる座標変換を課題として取り上げる。
本節の課題は左手系と右手系の座標変換である。
まずは準備的な説明から始める。
下図1~3はいずれも異なる座標系であり、図1が左手系、図2、図3が右手系である (図1はUnityの座標系である。図2、図3は右手の親指、人差し指を座標系の x軸、y軸に重ねたときに右手の中指と z軸の方向が一致する)。
いずれの座標系にも点 $P$ が置かれているが、$P$ のワールド座標は各座標系ですべて異なる値になっている (点 $P$ の $(x, y, z)$ の形の座標のことを本節では「ワールド座標」と呼ぶことにする)。
ここで、上記のような異なる座標系における座標の違いを解消し、統一的に表すための'絶対座標'を導入する。
そのためにまずカメラを用意する。カメラはこの絶対座標を測る際の基準となるものである。
図4はカメラの初期状態であり、コンピューターグラフィックスにおいてはカメラは初期状態で原点に置かれている (より正確にはカメラのレンズが原点に来るように置かれている)。そして、カメラを基準にして右の方向を right、上の方向を up、カメラの向いている方向を forward という (図5)。
図4 カメラは初期状態において原点に置かれている 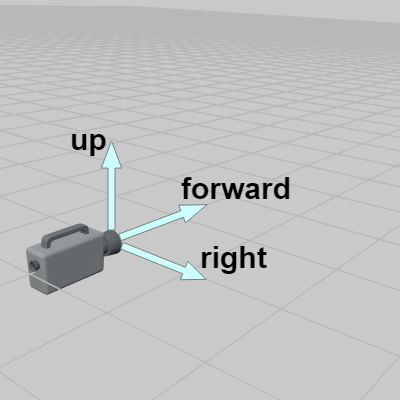
図5 カメラを基準にして右の方向が right、上の方向が up、カメラの向いている方向が forward
上で述べたようにカメラは初期状態では座標系の原点に置かれているので、上記の right、up、forward は座標系の軸の方向に一致する。しかし、注意しなければならないのは right、up、forward がどの軸に一致するかは座標系によって異なるという点である。
例えば下図は先程の3つの座標系に(初期状態の)カメラを置いたときのものであるが、図6では「x軸 : right、y軸 : up、z軸 : forward」であり、図7では「x軸 : right、y軸 : up、-z軸(マイナス z軸) : forward」、図8では「y軸 : right 、x軸 : up、z軸 : forward」である。
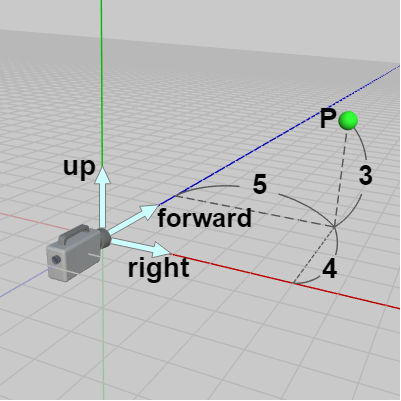
図9 そして点 $P$ の位置をカメラからright方向、up方向、forward方向に測ると、上記の3つの座標系のいずれにおいても「right方向に $5$、up方向に $3$、forward方向に $4$」となっている (右図は図1の座標系の場合)。すなわち カメラを基準にしたright、up、forward方向による計測では点 $P$ の位置はどの座標系でも $(5, 3, 4)$ ということになる。
以下では便宜上、この(初期状態の)カメラを基準にしてright、up、forward方向に測ったときの座標を「$RUF$座標」と呼ぶことにし、$RUF(a, b, c)$ のように表すことにする。例えば上記の点 $P$ はどの座標系でも $RUF(5, 3, 4)$ である。
つまり異なる座標系であっても原点からの相対位置が同じであれば$RUF$座標は同じになるわけである。
では本題に入ろう。
図10は右手座標系であり「x:right、y:up、-z:forward」である。図に示されるようにこの座標系の中に点 $P$ が置かれておりそのワールド座標は $(6,\ 4, -5)$ であり、$RUF(6, 4, 5)$ である。図11は左手座標系であり「x:right、y:up、z:forward」である (以下でも左手座標系は常にこのタイプの座標系、すなわち Unity座標系のみを用いる)。
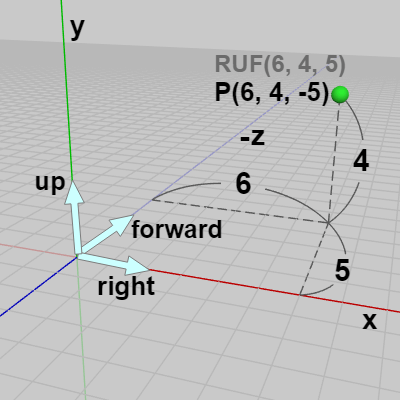
図10 右手系
(x:right, y:up, -z:forward) 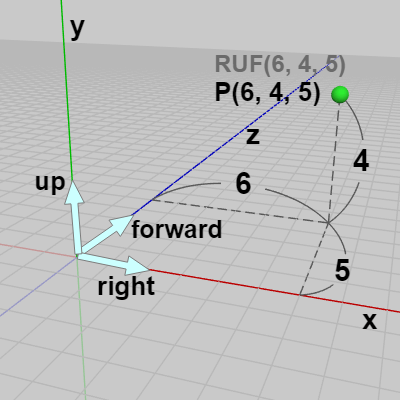
図11 左手系
(x:right, y:up, z:forward)
図10の点 $P$ のワールド座標 $(6,\ 4, -5)$ は右手系の座標であるが、これを左手系の座標に座標変換したときのものが図11のワールド座標 $(6, 4, 5)$ であり、図に示されるように2つの座標系で$RUF$座標は同じである (ともに $RUF(6, 4, 5)$)。
詳しくいえば左手系と右手系の間における座標変換とは、2つの座標系においてRUF座標が等しくなるように座標を変換することを意味する。
ここで肝心なことは具体的にどのようにして座標変換を行うかということである。考え方はいくつかあるが、おそらく次の考え方がイメージしやすいであろう。
それは一方の座標系をもう一方の座標系に一致させる変換を考えるのである。例えば下図12、13は状況を簡単にするため上記の右手系(図10)、左手系(図11)の座標軸とカメラのみを表示したものである。この場合に2つの座標系を一致させるには図14に示されるように右手系の z軸の向きを入れ替えればよい。
座標系の z軸の向きを入れ替えることは、座標に関してはその z座標の符号が逆になることを意味する。すなわち 上図10の点 $P$ の場合ではとすればよい (右手系のワールド座標 $(6,\ 4,-5)$ から左手系のワールド座標 $(6,\ 4,\ 5)$ に変換される)。
そしてこれが「x:right、y:up、-z:forward」タイプの右手座標系から「x:right、y:up、z:forward」タイプの左手座標系への座標変換の'公式'である。
続いて別の右手座標系を用意する。図15は右手座標系であるが、そのタイプは「y:right、x:up、z:forward」である。今回も適当な位置に点 $P$ が置かれており、そのワールド座標は $(2, 5, 7)$、$RUF$座標は $(5, 2, 7)$ である。
右図16は図15の $P$ を左手系の座標に変換したときのものであり、変換後の $P$ のワールド座標は $(5, 2, 7)$ である (前の例でもそうであったが、「x:right、y:up、z:forward」タイプの左手系のワールド座標は常に$RUF$座標に等しい)。
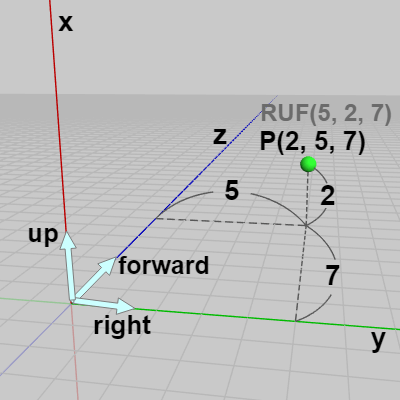
図15 右手系 (y:right, x:up, z:forward) 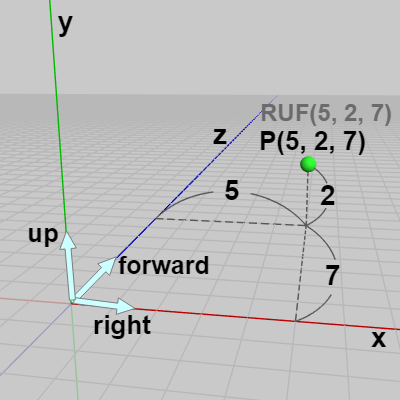
図16 左手系 (x:right, y:up, z:forward)
前の例と同様に状況を簡単にするために座標系の座標軸とカメラのみを表示したものが下図17~19である。図17が今回の右手座標系、図18が左手座標系で、図19は右手座標系を左手座標系に一致させるための変換の様子である。この図に示されるように、今回の変換はまず x軸の向きを入れ替え、その後に z軸周りに $90^\circ$ の回転を行う。
座標系の3つの軸のうちの1つの軸の向きを入れ替えると右手系と左手系が入れ替わる、つまり右手座標系のある1つの軸の向きを入れ替えるとその座標系は左手座標系になり、逆に左手座標系のある1つの軸の向きを入れ替えるとその座標系は右手座標系になる。
上図19の場合は x軸の向きを入れ替えた時点で、座標系は右手系から左手系になっているので、その後の z軸周りの $90^\circ$ の回転は具体的には左手系の $+90^\circ$ の回転である。
そして注意すべきは、点 $P$ を固定して座標系を z軸周りに $90^\circ$ 回転させることは、座標系を固定して点 $P$ を z軸周りに $-90^\circ$ 回転させることと同じである。
したがって、今回の点 $P$ の座標変換は以下のようになる。
上記の R90 は z軸周りの $-90^\circ$ の回転を表す回転行列であり、この変換によって点 $P$ は右手系のワールド座標 $(2, 5, 7)$ から左手系のワールド座標 $(5, 2, 7)$ へ変換される。
すなわち これが「y:right、x:up、z:forward」タイプの右手座標系から「x:right、y:up、z:forward」タイプの左手座標系への座標変換の'公式'である。
次の座標変換は読者用の課題である。
図20は右手座標系であり x軸が right、z軸が up、y軸が forward、つまり「x:right、z:up、y:forward」タイプの右手座標系である。この座標系はBlenderで使われている座標系であり、以下簡単のため「Blender座標系」と呼ぶことにする。
Blender座標系において図21に示されるように青いボールがある円周上を公転している。この円周の中心は $RUF(4, 3, 6)$ で、半径は $3$ である。
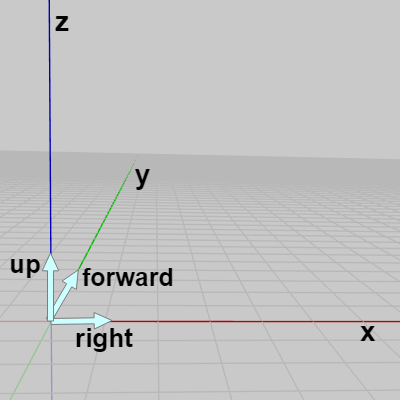
図20 右手系 : Blender座標系
(x:right, z:up, y:forward) 
図21 青いボールによる円周上の公転 (この円周の中心は RUF(4, 3, 6) で半径は 3)
図22は左手座標系であり今までと同じくUnity座標系(x:right、y:up、z:forward)である。今回はこの座標系の原点に緑のボールが置かれているが、この緑のボールは上記の青いボールと大きさは同じであり、初期状態では両方ともその中心が原点に置かれている (図23)。
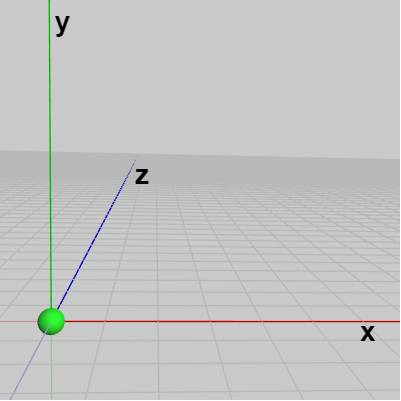
図22 左手系 : Unity座標系
(x:right, y:up, z:forward) 
図23 2つのボールの初期状態 (緑のボールも青いボールも大きさは同じ)
ある時点において青いボールの運動を止めてその時点における座標を取得したとする。その座標はBlender座標系における座標であるが、この座標をUnity座標系の座標に変換して緑のボールをその位置に移動させると2つのボールの位置はそれぞれの座標系において同じになる ($RUF$座標が同じになる)。そしてこれを毎フレーム行えば青いボールと緑のボールは全く同じ運動、すなわち $RUF(4, 3, 6)$ を中心とする半径 $3$ の円周上で公転をすることになる。
ここでの課題は今述べたように青いボールの座標を毎フレーム Blender座標系からUnity座標系に座標変換し、2つのボールの運動が全く同じ運動になるようにプログラムを作成することである。具体的には下図のような実行結果になればよい (今回のプログラムでは実行結果が2つの画面に分かれており、左側がUnity座標系、右側がBlender座標系となっている)。

図24 左がUnity座標系、右がBlender座標系
プログラムはCode1に作成するものとする。 Code1は始めの段階では以下の1行のコードのみが記述されており、そのまま実行するとBlender座標系では青いボールが公転しているが、Unity座標系では緑のボールが原点に置かれたままの状態である。
[Code1]
GetBluePosition() はその時点における青いボールの位置が返されるが、この座標はBlender座標系における座標である。
また プログラム中においては緑のボールは Green という名前で用意されている。したがって、緑のボールを移動させる際には行列を使ってとするか、あるいは簡単にとすればよい。
(解答例については Sec320_Ans.txt を参照)
本節の課題は左手系と右手系の座標変換である。
まずは準備的な説明から始める。
下図1~3はいずれも異なる座標系であり、図1が左手系、図2、図3が右手系である (図1はUnityの座標系である。図2、図3は右手の親指、人差し指を座標系の x軸、y軸に重ねたときに右手の中指と z軸の方向が一致する)。
いずれの座標系にも点 $P$ が置かれているが、$P$ のワールド座標は各座標系ですべて異なる値になっている (点 $P$ の $(x, y, z)$ の形の座標のことを本節では「ワールド座標」と呼ぶことにする)。
-
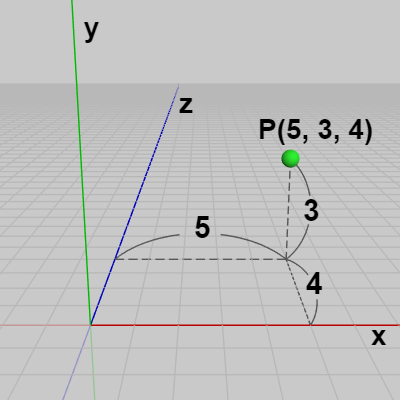 図1 左手系 (Unity座標系)
図1 左手系 (Unity座標系) -
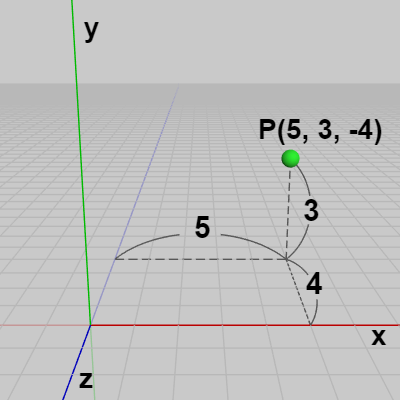 図2 右手系
図2 右手系 -
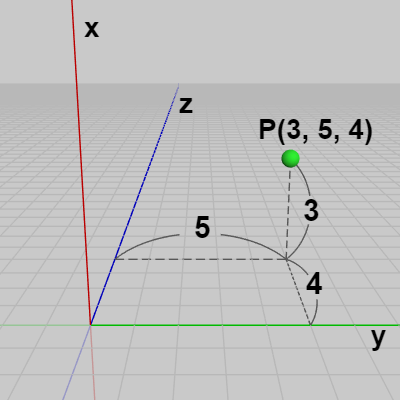 図3 右手系
図3 右手系
ここで、上記のような異なる座標系における座標の違いを解消し、統一的に表すための'絶対座標'を導入する。
そのためにまずカメラを用意する。カメラはこの絶対座標を測る際の基準となるものである。
図4はカメラの初期状態であり、コンピューターグラフィックスにおいてはカメラは初期状態で原点に置かれている (より正確にはカメラのレンズが原点に来るように置かれている)。そして、カメラを基準にして右の方向を right、上の方向を up、カメラの向いている方向を forward という (図5)。


上で述べたようにカメラは初期状態では座標系の原点に置かれているので、上記の right、up、forward は座標系の軸の方向に一致する。しかし、注意しなければならないのは right、up、forward がどの軸に一致するかは座標系によって異なるという点である。
例えば下図は先程の3つの座標系に(初期状態の)カメラを置いたときのものであるが、図6では「x軸 : right、y軸 : up、z軸 : forward」であり、図7では「x軸 : right、y軸 : up、-z軸(マイナス z軸) : forward」、図8では「y軸 : right 、x軸 : up、z軸 : forward」である。
-
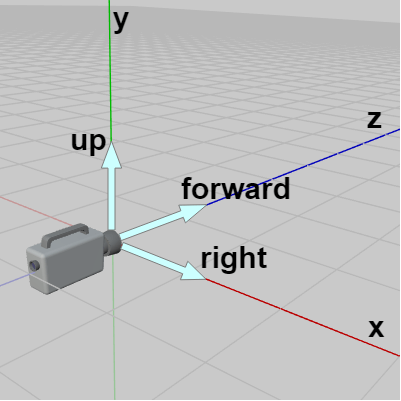 図6 左手系
図6 左手系
(x:right、y:up、z:forward) -
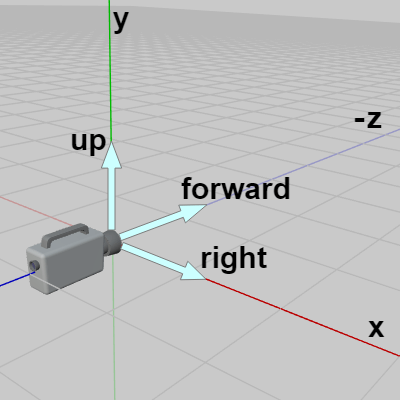 図7 右手系
図7 右手系
(x:right、y:up、-z:forward) -
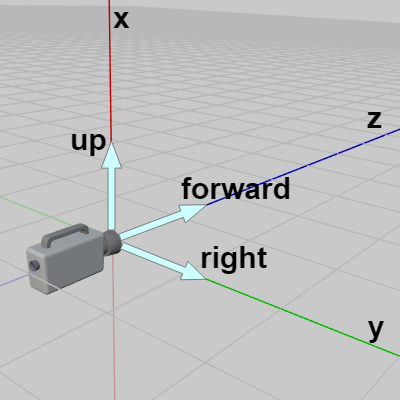 図8 右手系
図8 右手系
(y:right、x:up、z:forward)

以下では便宜上、この(初期状態の)カメラを基準にしてright、up、forward方向に測ったときの座標を「$RUF$座標」と呼ぶことにし、$RUF(a, b, c)$ のように表すことにする。例えば上記の点 $P$ はどの座標系でも $RUF(5, 3, 4)$ である。
つまり異なる座標系であっても原点からの相対位置が同じであれば$RUF$座標は同じになるわけである。
では本題に入ろう。
図10は右手座標系であり「x:right、y:up、-z:forward」である。図に示されるようにこの座標系の中に点 $P$ が置かれておりそのワールド座標は $(6,\ 4, -5)$ であり、$RUF(6, 4, 5)$ である。図11は左手座標系であり「x:right、y:up、z:forward」である (以下でも左手座標系は常にこのタイプの座標系、すなわち Unity座標系のみを用いる)。

(x:right, y:up, -z:forward)

(x:right, y:up, z:forward)
図10の点 $P$ のワールド座標 $(6,\ 4, -5)$ は右手系の座標であるが、これを左手系の座標に座標変換したときのものが図11のワールド座標 $(6, 4, 5)$ であり、図に示されるように2つの座標系で$RUF$座標は同じである (ともに $RUF(6, 4, 5)$)。
詳しくいえば左手系と右手系の間における座標変換とは、2つの座標系においてRUF座標が等しくなるように座標を変換することを意味する。
ここで肝心なことは具体的にどのようにして座標変換を行うかということである。考え方はいくつかあるが、おそらく次の考え方がイメージしやすいであろう。
それは一方の座標系をもう一方の座標系に一致させる変換を考えるのである。例えば下図12、13は状況を簡単にするため上記の右手系(図10)、左手系(図11)の座標軸とカメラのみを表示したものである。この場合に2つの座標系を一致させるには図14に示されるように右手系の z軸の向きを入れ替えればよい。
-
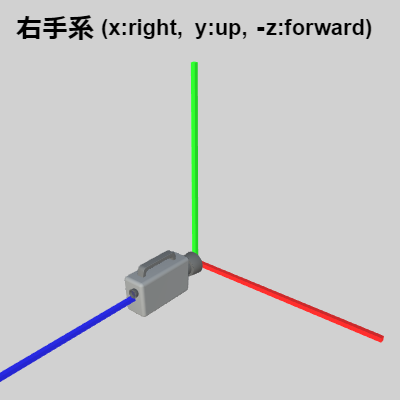 図12 右手系
図12 右手系
(x:right, y:up, -z:forward) -
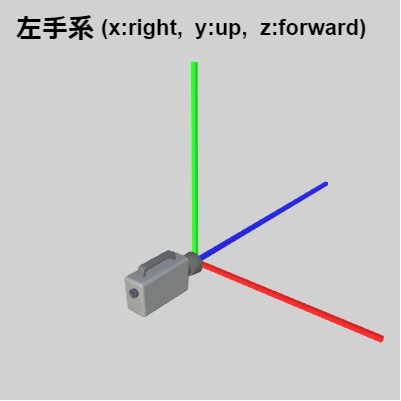 図13 左手系
図13 左手系
(x:right, y:up, z:forward) -
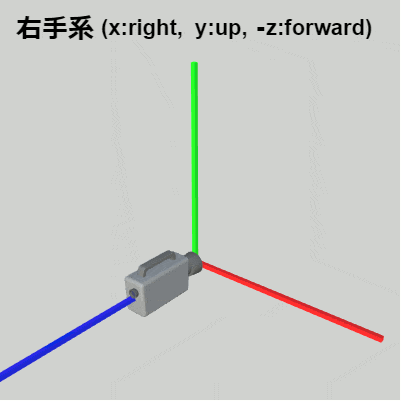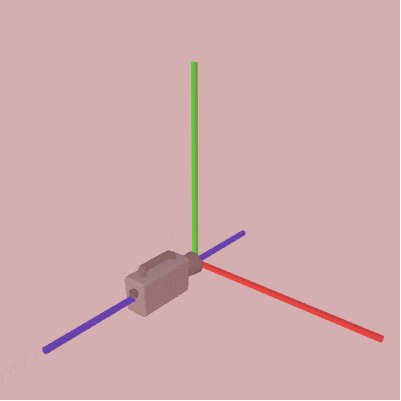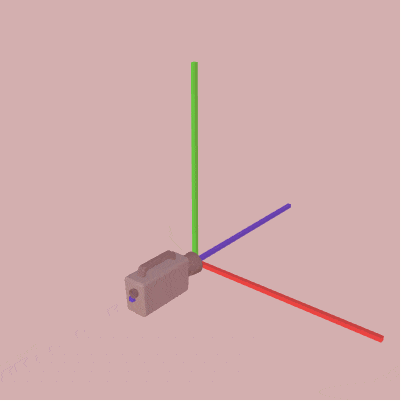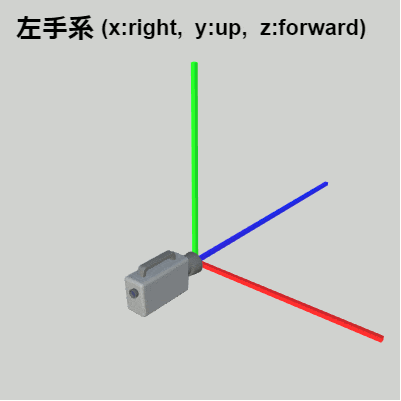 図14 右手系から左手系への変換
図14 右手系から左手系への変換
座標系の z軸の向きを入れ替えることは、座標に関してはその z座標の符号が逆になることを意味する。すなわち 上図10の点 $P$ の場合では
P.z = -P.z;
そしてこれが「x:right、y:up、-z:forward」タイプの右手座標系から「x:right、y:up、z:forward」タイプの左手座標系への座標変換の'公式'である。
続いて別の右手座標系を用意する。図15は右手座標系であるが、そのタイプは「y:right、x:up、z:forward」である。今回も適当な位置に点 $P$ が置かれており、そのワールド座標は $(2, 5, 7)$、$RUF$座標は $(5, 2, 7)$ である。
右図16は図15の $P$ を左手系の座標に変換したときのものであり、変換後の $P$ のワールド座標は $(5, 2, 7)$ である (前の例でもそうであったが、「x:right、y:up、z:forward」タイプの左手系のワールド座標は常に$RUF$座標に等しい)。


前の例と同様に状況を簡単にするために座標系の座標軸とカメラのみを表示したものが下図17~19である。図17が今回の右手座標系、図18が左手座標系で、図19は右手座標系を左手座標系に一致させるための変換の様子である。この図に示されるように、今回の変換はまず x軸の向きを入れ替え、その後に z軸周りに $90^\circ$ の回転を行う。
-
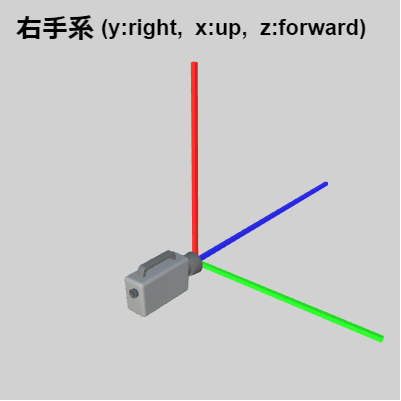 図17 右手系
図17 右手系
(y:right, x:up, z:forward) -
 図18 左手系
図18 左手系
(x:right, y:up, z:forward) -
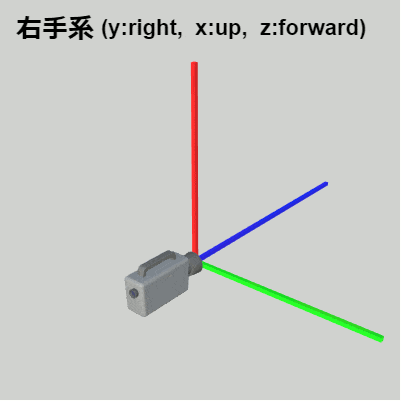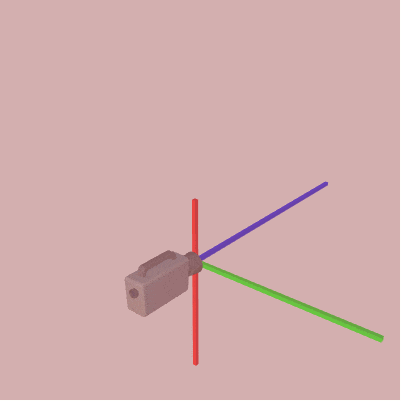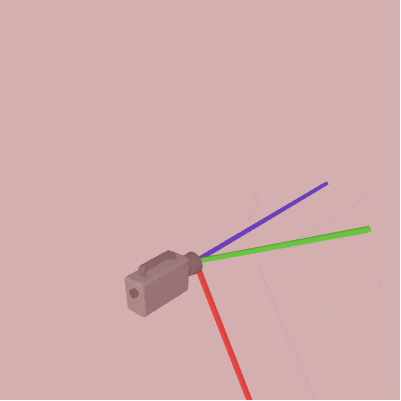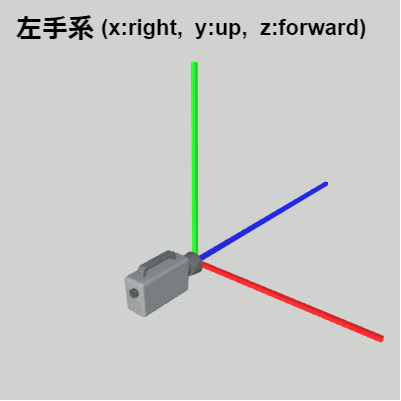 図19 右手系から左手系への変換
図19 右手系から左手系への変換
座標系の3つの軸のうちの1つの軸の向きを入れ替えると右手系と左手系が入れ替わる、つまり右手座標系のある1つの軸の向きを入れ替えるとその座標系は左手座標系になり、逆に左手座標系のある1つの軸の向きを入れ替えるとその座標系は右手座標系になる。
上図19の場合は x軸の向きを入れ替えた時点で、座標系は右手系から左手系になっているので、その後の z軸周りの $90^\circ$ の回転は具体的には左手系の $+90^\circ$ の回転である。
そして注意すべきは、点 $P$ を固定して座標系を z軸周りに $90^\circ$ 回転させることは、座標系を固定して点 $P$ を z軸周りに $-90^\circ$ 回転させることと同じである。
したがって、今回の点 $P$ の座標変換は以下のようになる。
P.x = -P.x; P = R90 * P;
すなわち これが「y:right、x:up、z:forward」タイプの右手座標系から「x:right、y:up、z:forward」タイプの左手座標系への座標変換の'公式'である。
次の座標変換は読者用の課題である。
図20は右手座標系であり x軸が right、z軸が up、y軸が forward、つまり「x:right、z:up、y:forward」タイプの右手座標系である。この座標系はBlenderで使われている座標系であり、以下簡単のため「Blender座標系」と呼ぶことにする。
Blender座標系において図21に示されるように青いボールがある円周上を公転している。この円周の中心は $RUF(4, 3, 6)$ で、半径は $3$ である。

(x:right, z:up, y:forward)

図22は左手座標系であり今までと同じくUnity座標系(x:right、y:up、z:forward)である。今回はこの座標系の原点に緑のボールが置かれているが、この緑のボールは上記の青いボールと大きさは同じであり、初期状態では両方ともその中心が原点に置かれている (図23)。

(x:right, y:up, z:forward)

ある時点において青いボールの運動を止めてその時点における座標を取得したとする。その座標はBlender座標系における座標であるが、この座標をUnity座標系の座標に変換して緑のボールをその位置に移動させると2つのボールの位置はそれぞれの座標系において同じになる ($RUF$座標が同じになる)。そしてこれを毎フレーム行えば青いボールと緑のボールは全く同じ運動、すなわち $RUF(4, 3, 6)$ を中心とする半径 $3$ の円周上で公転をすることになる。
ここでの課題は今述べたように青いボールの座標を毎フレーム Blender座標系からUnity座標系に座標変換し、2つのボールの運動が全く同じ運動になるようにプログラムを作成することである。具体的には下図のような実行結果になればよい (今回のプログラムでは実行結果が2つの画面に分かれており、左側がUnity座標系、右側がBlender座標系となっている)。

プログラムはCode1に作成するものとする。 Code1は始めの段階では以下の1行のコードのみが記述されており、そのまま実行するとBlender座標系では青いボールが公転しているが、Unity座標系では緑のボールが原点に置かれたままの状態である。
[Code1]
Vector3 posB = GetBluePosition();
GetBluePosition() はその時点における青いボールの位置が返されるが、この座標はBlender座標系における座標である。
また プログラム中においては緑のボールは Green という名前で用意されている。したがって、緑のボールを移動させる際には行列を使って
Matrix4x4 T = TH3DMath.GetTranslation4x4(pos); Green.SetMatrix(T);
Green.SetWorldPosition(pos);
(解答例については Sec320_Ans.txt を参照)
© 2020-2025 Redpoll's 60 (All rights reserved)