Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-17
第3章 3D空間の基礎
$§$3-17 応用プログラム 1 (ルービックキューブ)
本章では3D空間の基礎的な事柄について学習したが、扱ってきたプログラムはいずれも教材的なものであった。本節以下3節では簡単な応用として、より実際的なプログラムを作成する。
本節において作成するプログラムはルービックキューブである (正確にはルービックキューブを回転させるプログラムである)。
ルービックキューブ(Rubik's Cube)は図1に示されるような複数の小さな立方体によって構成される立体パズルである。ルービックキューブを構成する小さな立方体は Cubeと呼ばれ、Cubeは全部で26個ある。図2に見られるように、ルービックキューブは各段各列のCubeを回転させることができ、最終的に各面が1つの色で構成されるようにすることが このパズルの目的である。
図1 ルービックキューブ (各Cubeは初期状態)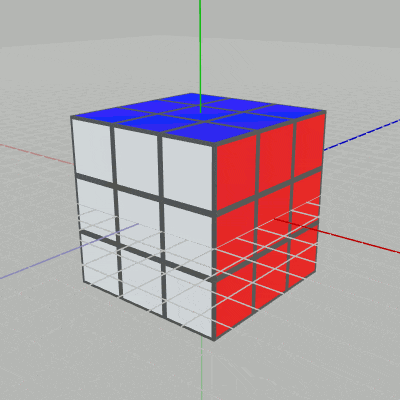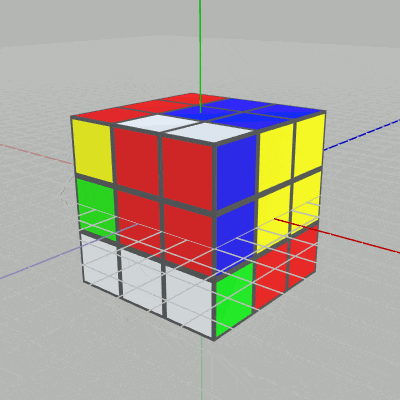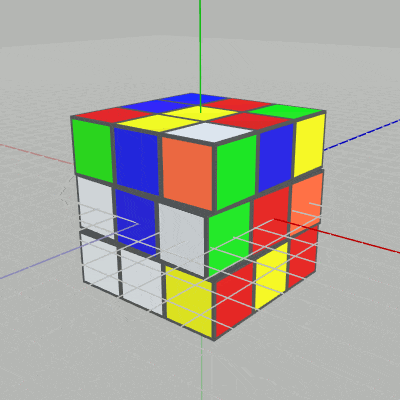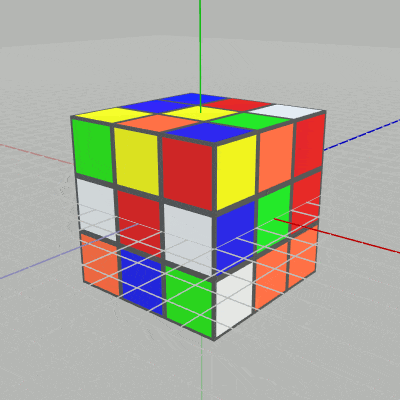 
図2 各段各列のCubeを回転させることができる
図3 Cubeは (2, 2, -2) に置かれている まず注意すべきことは各Cubeは初期状態において原点に置かれていないことである。今までのオブジェクトのほとんどは、初期状態においてオブジェクトの中心が原点に置かれていた (あるいはオブジェクトの一部が原点に位置していた)。しかし、今回のルービックキューブではルービックキューブを構成する26個のCubeはすべて初期状態で(その中心が)原点に置かれていない。実際の各Cubeの初期状態の位置は上図1に示される位置である。
例えば、図1における上の段の右の列のCubeのうち一番手前のCubeだけを表示したものが図3である。
図中の $(2, 2, -2)$ はCubeの位置(中心座標)である。そして、この状態がこのCubeの初期状態である。この状態のCubeは平行移動が行われていないので3-9節でも述べたように、transform.localPosition(あるいは transform.position) の値は $(0, 0, 0)$ である、$(2, 2, -2)$ ではない。
なお 以降の文章中において、ルービックキューブを構成する各Cubeの位置について述べている箇所では、特にことわりがなくても「Cubeの位置(あるいは座標)」といえば、Cubeの中心座標を表すものとする。
また、以降の解説においては図4に示されるように、ルービックキューブの6つの面のうちで z軸マイナス側を向いている面をルービックキューブの正面とする。さらに、x軸プラス側をルービックキューブの右側、x軸マイナス側をルービックキューブの左側とする。
中央の図5は初期状態のルービックキューブの正面である。図中に赤い数字が並んでいるが、この赤い数字はルービックキューブの各列の x座標を表している。すなわち、左の列のCubeの x座標はすべて $-2$ であり、中央の列のCubeの x座標はすべて $0$、右の列のCubeの x座標はすべて $2$ という意味である。
緑の数字についても同様である。図5の緑の数字はルービックキューブの各段の y座標を表している。(図5における)上の段のCubeの y座標はすべて $2$、中央の段はすべて $0$、下の段はすべて $-2$ という意味である。
図6は初期状態のルービックキューブを真上から見たときのものである (詳しくは z軸プラス側が上、x軸プラス側が右に来るように見たときのものである)。この図における赤い数字は図5と同じくルービックキューブの各列の x座標である。青い数字はルービックキューブの各段の z座標を表している。すなわち、(図6における)上の段のCubeの z座標はすべて $2$、中央の段のCubeの z座標はすべて $0$、下の段のCubeの z座標はすべて $-2$ という意味である。
繰り返しになるが、各Cubeは初期状態において(その中心が)原点に置かれていない。図1に示される位置が初期状態の位置であり、初期状態における各Cubeの(中心の)座標は $(2, 0, 2)$ や $(-2, 2, 0)$ のような値である。
そして、ルービックキューブをどのように回転させても各Cubeの位置は、x座標、y座標、z座標 いずれも $2$ か $0$ か $-2$ であり、これ以外の値はとらない。
次のプログラムは、右の列を一定の速度で回転させるだけのものである。
なお、ルービックキューブを構成するCubeは26個あるが、本節のプログラムにおいてはそれらは Cube[i] のように配列の形で使われている。
[Code1] (実行結果 図7)
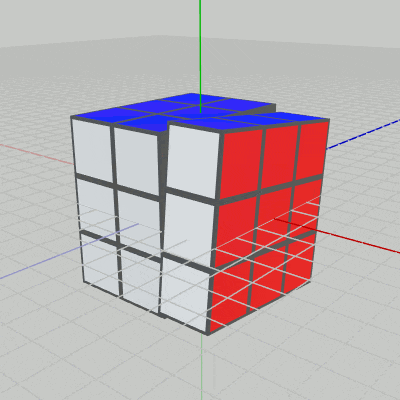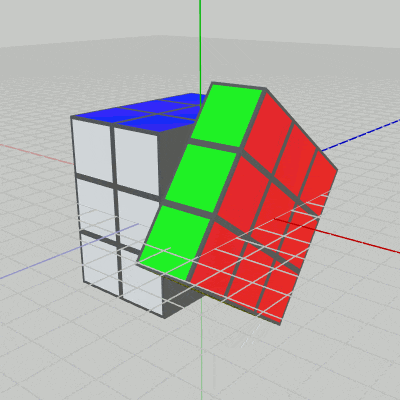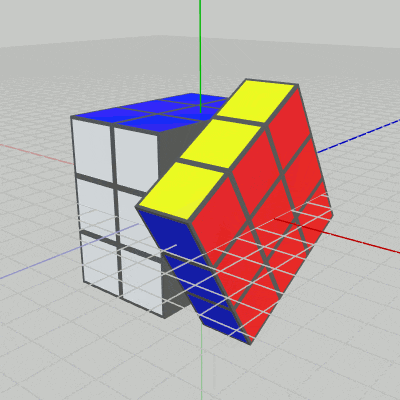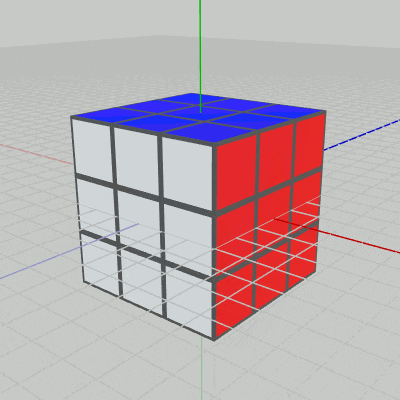
図7 Code1 実行結果 1行目の i_degX は現在の回転角度であり、毎フレーム $1$ずつ増加する。右列の9個のCubeの回転軸は x軸であるので、2行目では x軸周りに i_degX だけ回転させる行列 R を取得している。
5行目の idcs には、右列の9個のCubeのインデックスがセットされる。その下の foreach文において その9個のCubeに回転行列Rを実行することで、実行結果(図7)に見られるように右の列の9個のCube(いずれも赤い面を持っている)が毎フレーム $1$°ずつ回転することになる。
しかし、ルービックキューブの回転を実装するためにはこのプログラムの方法では不十分である。
このCode1の方法は確かに右の列を回転させることができるが、この右の列は詳しくは初期状態における右の列である。5行目の idcs で指定している9個のCubeはいずれも赤い面を持っているが、このプログラムで回転させることができるのは idcs で指定した赤い面を持った9個のCubeである。
図8 右列は赤い面を持たないCubeも含まれる ルービックキューブは任意の時点で任意の列、任意の段を回転させることができなければならない。確かに初期状態においては、赤い面を持ったCubeはすべて右の列にあるが、いくつもの回転を続けていって例えば図8のような状態になったときには右列の9個のCubeは赤い面を持っていないものも含まれる。このような状態では、Code1の方法によって右列のCubeすべてを回転させることはできないわけである。
また 各Cubeの回転は、ときに x軸周りであったり、ときに y軸周り、z軸周りとなり、さらにその順番もさまざまである。x軸周りに回転後、z軸周りに回転し、その後再び x軸周りの回転 といった形で常に回転軸が変化する。そのため、あるCubeがどの軸周りにどれだけ回転したかを管理しておくことは簡単ではない。
上のCode1におけるインスタンス変数 i_degX は 9個のCubeの x軸周りの回転角度を表すものであるが、つまり このように1つの軸の周りに何度回転したかを保持する変数を用意しても意味がないわけである。
先程の図5からわかるように、初期状態においては右列のCubeは x座標がすべて $2$ である。これはルービックキューブをどのように回転させても変わらない。つまり、どの時点においても右列のCubeの x座標は $2$ である。このことを利用すればある時点における右列のCubeのインデックスは次のように取得できる。
ここで使われている i_curCubePos は現在の各Cubeの位置(Cubeの中心座標)を保持する Vector3[]型のインスタンス変数である。Cubeは26個なのでこの配列の要素数も 26 であり、Cube[i]の現在位置は i_curCubePos[i] にセットされている (各Cubeの現在位置の計算については後述する)。
3行目のfor文において各Cubeの現在位置を調べ、その x座標が $2$ であるもののインデックスをList<int>型のローカル変数 wL に追加していく。ただし、小数値の比較は a == b のような形で行うのはよくないので、x座標が $2$ であるかを調べるために5行目のように x >= 2.0f-0.01f となっている。この比較では xの値が $2$以上であればすべて true となってしまうが、上でも述べたように各Cubeの位置は、x座標、y座標、z座標 いずれも $0$ か $2$ か $-2$ なのでこの比較でも問題はない (xが$2$以上であるかを調べるために x >= 2.0 とすることもまた控えるべきである。小数値の比較の場合は演算誤差を考慮に入れてわずかな’余裕’を持たせて 2.0-0.01 のようにしておくことが望ましい)。
同様にして一番上の段を回転させる場合、その時点での上段にある9個のCubeのインデックスを取得する必要があるが、その場合は以下のようにすればよい。
上段のCubeの y座標はすべて $2$ であるから、ここでは5行目の if文で y >= 2.0f-0.01f となっている。
また ルービックキューブの回転では回転軸が常に変化するが、以下ではこの点について考えていこう。
例えば、オブジェクトを x軸周りに毎フレーム $3$°ずつ回転させる場合、今までは次のようにプログラムを記述していた。
i_degX は x軸周りの回転角度を表すインスタンス変数であり、毎フレーム $3$ずつ増加する。このプログラムの記述はCode1とほとんど同じである。そして、Code1で指摘したようにこの方法は x軸周りに $90$°回転させた後に y軸周りにさらに $90$°回転させるといった処理には向いていない。
以下のプログラムはオブジェクトを回転させる別の方法である。その内容は上のプログラムと同様にオブジェクトを x軸周りに毎フレーム $3$°ずつ回転させるものである。
1行目の R は x軸周りに $3$°回転を行う回転行列である。R の内容は毎フレーム同じであり、x軸周りの $3$°の回転である。2行目の curM は現時点でオブジェクトに実行されている変換行列である。したがって、3行目の M = R * curM の内容は「オブジェクトを現在の状態から x軸周りに $3$°回転させる」というものになる。そして4行目で実際にオブジェクトにはその M が実行される。
具体的には 1フレーム目においてはオブジェクトは初期状態であるので curM の内容は identity行列である。そして、このときの M の内容は「x軸周りに $3$°回転」である。2フレーム目ではオブジェクトは x軸周りに $3$°回転した状態であるため、curM の内容は同じく「x軸周りに $3$°回転」となっている。したがって、2フレーム目における M は curM をさらに $3$°回転させることになるから、その内容は「x軸周りに $6$°回転」である。3フレーム目も同様である。3フレーム目における curM の内容は、オブジェクトはこの時点で x軸周りに $6$°回転しているから「x軸周りに $6$°回転」となる。したがって、3フレーム目における M も curM をさらに $3$°回転させることになるから、その内容は「x軸周りに $9$°回転」である。
このようにして、オブジェクトは毎フレーム x軸周りに $3$°ずつ回転していくことになる。
この方法では x軸周りに $3$°ずつ回転させていくために、毎フレーム オブジェクトの現在の変換行列を取得して、それに x軸周りに $3$°の回転行列を掛けている。先程のインスタンス変数 i_degX を使ったやり方に比べて、やや計算負荷が増加するが、この方法はオブジェクトを回転させる上で非常に柔軟な性質を持っている。
例えば、ある時点でオブジェクトが x軸周りに $90$°回転しているとしよう。便宜上ここでは、それを30フレーム目とする。そして、その次のフレームから(31フレーム目から) オブジェクトを y軸周りに $5$°ずつ回転させるとしよう。その場合には次のように記述すればよい。
先程のプログラムとの違いは1箇所で、それは1行目の GetRotation4x4(..) の引数であり、y軸周りに $5$°の回転を表している。
31フレーム目では、オブジェクトは x軸周りに $90$°回転した状態なので curM の内容は同じく「x軸周りに $90$°回転」である。したがって、M はその状態から y軸周りに $5$°の回転を行うので、31フレーム目の M の内容は「x軸周りに $90$°回転、さらに続けて y軸周りに $5$°の回転」となる。
32フレーム目では、オブジェクトは x軸周りに $90$°回転、さらに y軸周りに $5$°回転しているから、32フレーム目の curM の内容も「x軸周りに $90$°、y軸周りに $5$°」である。そして、32フレーム目における M の内容は curM をさらに y軸周りに $5$°回転させるものになるから「x軸周りに $90$°回転、さらに続けて y軸周りに $10$°の回転」となる。
このようにして x軸周りに $90$°回転したオブジェクトを、その後 続けて y軸周りに $5$°ずつ回転させるということができるわけである。
次のプログラムはルービックキューブの右の列 及び上の段を、以下のキー操作によって回転させるものである。
R : 右の列のCubeをx軸周りに $90$°回転させる (Shift同時押しで逆回転)。
U : 上の段のCubeをy軸周りに $90$°回転させる (Shift同時押しで逆回転)。
ルービックキューブがどのような状態であっても、R が押されればその時点で右の列にある9個のCubeが回転し、U が押されればその時点で上の段にある9個のCubeが回転する。
[Code2] (実行結果 図9)
図9 Code2 実行結果 冒頭の初期化ブロックではいくつかのインスタンス変数を初期化する。i_ROTATE は U または R キーが押された際に true になる bool型の変数で、この変数が true の間は17行目のifブロックに入り回転処理を行う。
指定のキーが1回押されるとCubeの回転が始まるが、その回転角度は $90$°である。4行目の i_rotMaxCount は、その $90$°の回転を何フレームかけて行うかを表す変数であり、ここでは $30$ が設定されているが、これはCubeの $90$°の回転が30フレームかけて行われることを意味する。i_rotCounter は30フレームかけて行われる回転において、今は何フレーム目かを表す変数である。この変数は回転のためのキーが押されるたびに $0$ にセットされる。
i_rotCubeIndices は回転を行うCubeのインデックス配列である。ここでは適当な要素数で初期化されている。
また、本節の上部で述べたように、ルービックキューブを構成する各Cubeは初期状態においてそれぞれの指定の位置に配置されている。したがって、transform.localPosition(あるいは transform.position)などを用いても、3D空間上でのCubeの位置(中心座標)を取得することはできない。そのために各Cubeの位置を常に保持しておくインスタンス変数が必要になるわけであるが、このプログラムでは i_curCubePos というVector3[]型の配列がそれにあたる。ある時点でのCube[i]の位置は i_curCubePos[i] にセットされている。
8行目の for文において i_curCubePos の各要素に初期値を設定するが、その値は各Cubeの初期状態での位置である。c_initCubePos は初期状態における各Cubeの位置がセットされているので、ここではそれらの値を i_curCubePos にコピーしているだけである。
まず、43行目以降から解説する。43行目から68行目は上で解説した その時点での上の段のCube、右の列のCubeのインデックスを取得する部分である。例えば、U が押されると45行目のifブロックに入るが、ここでは その時点で上の段にある9個のCubeのインデックスを List<int>型変数の wL に追加している。
55行目では i_rotAxis という変数に Vector3.up がセットされているが、i_rotAxis はCubeが回転する際の回転軸を表す Vector3型のインスタンス変数である。U が押された場合は上段のCubeが y軸周りに回転することになるので、ここでは i_rotAxis に Vector3.up がセットされているわけである。
R が押された場合は右列のCubeが x軸周りに回転することになるが、67行目では確かに i_rotAxis に x軸プラス方向を表す Vector3.right がセットされている。
U または R が押されると45行目または57行目のifブロックに入るが、何も押されていない場合は69行目の else ブロックに入り そこで return されるので、それ以降に処理が進まない。
しかし、U または R が押された場合には 75行目以降の処理が行われる。ここでは次のフレームからCubeの回転処理が行われるように、回転に必要なインスタンス変数に値をセットしている。
i_rotCubeIndices には、回転するCubeのインデックス配列がセットされる。U または R が押されれば上の部分でList型変数 wL にインデックスがセットされるので、ここではそれを配列の形でコピーしているだけである。i_ROTATE や i_rotCounter については上で述べたとおりである。i_addDeg は1フレームあたりの回転角度であり、i_rotMaxCount の値が$30$なので i_addDeg は $3$ である (Shiftが押されているときは $-3$)。
17行目のifブロックはCubeの回転処理が記述されており、このプログラムの場合は回転対象となるCubeは上の段、あるいは右の列の9個のCubeである。19行目の R は $3$°(あるいは $-3$°)の回転行列であり、回転軸はそのときに押されたキーによって異なるが、ここでは x軸か y軸である。
21行目の foreach文では i_rotCubeIndices にセットされているインデックスのCubeのみを回転させる。このプログラムの場合は i_rotCubeIndices には上段あるいは右列の9個のCubeのインデックスがセットされている。23~25行目のCubeを回転させるコードについては上で述べた方法と同様である。curM は現時点でのCubeの状態を表す変換行列である。curM と R の積 M は、現時点でのCubeをさらに $3$°(あるいは$-3$°)回転させた状態にする行列であり、それをCubeに実行する。毎フレームこのようにCubeを回転させることで各Cubeは30フレームかけて $90$°の回転を行うことになる。そして 上でも述べたように、この方法であればCubeを回転させる際の回転軸はどのような順序にしても構わない。x軸周り、y軸周り、x軸周り であっても y軸周り、x軸周り、x軸周り であっても、そのときにキーで指定した回転軸の周りを回転することになる。
回転処理中は毎フレーム 28行目において i_rotCounter をインクリメントし、その値が $30$ になった時点で回転処理を停止させるために 29行目のifブロックに入る。実際には、ただ i_ROTATE を false にするだけであるが、ここでもう1つ重要な処理がある。それは各Cubeの現在位置の更新である。i_curCubePos には現時点での各Cubeの位置がセットされているが、回転が終わるたびに 回転したCubeの位置を更新しなければならない。33行目の foreach文で行っているのは その更新処理である (位置の更新は回転したCubeのみが対象となるので i_rotCubeIndices が表すCubeだけでよい)。
現時点でのCubeの位置を求める方法は、2-13節において解説した現時点でのオブジェクト上のある位置の求め方と同様である (2-13節における解説は2Dオブジェクトが対象であったが、3Dオブジェクトの場合も同様である。4-12節参照)。
現時点でCubeに実行されている変換行列と 初期状態におけるCubeの位置の同次座標との積を計算すればよい (ただし、位置の場合は同次座標における $w$成分を $1$ にする。ToVector4(..) は引数のVector3型の値をVector4型に変換するカスタムライブラリーのメソッドであるが、その際 $w$成分は $1$ になる。実際には、ここではCubeには回転だけで平行移動が行われることはないので同次座標の $w$成分が $1$ でも $0$ でも算出される値は同じである)。
ルービックキューブの回転については、一般には以下のように記号が定められている。
Code2で実装したのはこのうちで U (上の段の回転)、R (右の列の回転) の2つである。
ここでの課題は上図に示される回転を実装し、ルービックキューブの回転プログラムを完成させることである。ただし、上の12種類の回転をすべて実装する必要はない。作成したプログラムが実際のルービックキューブと同じパズルゲームとして成り立つように必要な回転だけを選べばよい。
プログラムはCode3に作成するものとする (Code3は空の初期化ブロックだけ用意されている)。
このプログラムの作成に使用するインスタンス変数を以下に示す (いずれも Code2で使われたものであり、新しいものはない)。
解答例は Sec317_Ans.txt 内を参照 (ただし、この課題は容易である。Code2のキー操作の部分を適当に変えてコピーすれば解決する。Sec317_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
本節において作成するプログラムはルービックキューブである (正確にはルービックキューブを回転させるプログラムである)。
ルービックキューブ(Rubik's Cube)は図1に示されるような複数の小さな立方体によって構成される立体パズルである。ルービックキューブを構成する小さな立方体は Cubeと呼ばれ、Cubeは全部で26個ある。図2に見られるように、ルービックキューブは各段各列のCubeを回転させることができ、最終的に各面が1つの色で構成されるようにすることが このパズルの目的である。
例えば、図1における上の段の右の列のCubeのうち一番手前のCubeだけを表示したものが図3である。
図中の $(2, 2, -2)$ はCubeの位置(中心座標)である。そして、この状態がこのCubeの初期状態である。この状態のCubeは平行移動が行われていないので3-9節でも述べたように、transform.localPosition(あるいは transform.position) の値は $(0, 0, 0)$ である、$(2, 2, -2)$ ではない。
なお 以降の文章中において、ルービックキューブを構成する各Cubeの位置について述べている箇所では、特にことわりがなくても「Cubeの位置(あるいは座標)」といえば、Cubeの中心座標を表すものとする。
-
図4 ルービックキューブの正面 及び 右、左 -
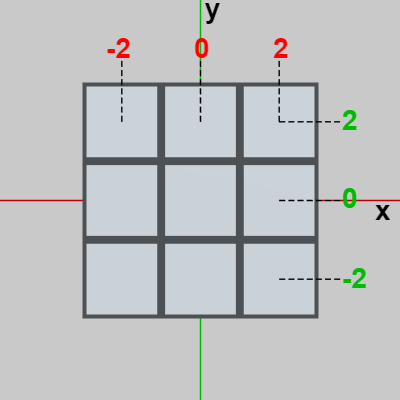図5 ルービックキューブを正面から見たとき -
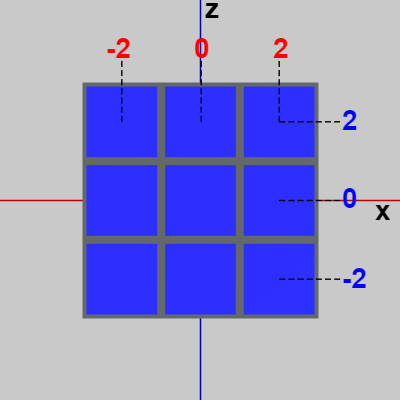図6 ルービックキューブを真上から見たとき
また、以降の解説においては図4に示されるように、ルービックキューブの6つの面のうちで z軸マイナス側を向いている面をルービックキューブの正面とする。さらに、x軸プラス側をルービックキューブの右側、x軸マイナス側をルービックキューブの左側とする。
中央の図5は初期状態のルービックキューブの正面である。図中に赤い数字が並んでいるが、この赤い数字はルービックキューブの各列の x座標を表している。すなわち、左の列のCubeの x座標はすべて $-2$ であり、中央の列のCubeの x座標はすべて $0$、右の列のCubeの x座標はすべて $2$ という意味である。
緑の数字についても同様である。図5の緑の数字はルービックキューブの各段の y座標を表している。(図5における)上の段のCubeの y座標はすべて $2$、中央の段はすべて $0$、下の段はすべて $-2$ という意味である。
図6は初期状態のルービックキューブを真上から見たときのものである (詳しくは z軸プラス側が上、x軸プラス側が右に来るように見たときのものである)。この図における赤い数字は図5と同じくルービックキューブの各列の x座標である。青い数字はルービックキューブの各段の z座標を表している。すなわち、(図6における)上の段のCubeの z座標はすべて $2$、中央の段のCubeの z座標はすべて $0$、下の段のCubeの z座標はすべて $-2$ という意味である。
繰り返しになるが、各Cubeは初期状態において(その中心が)原点に置かれていない。図1に示される位置が初期状態の位置であり、初期状態における各Cubeの(中心の)座標は $(2, 0, 2)$ や $(-2, 2, 0)$ のような値である。
そして、ルービックキューブをどのように回転させても各Cubeの位置は、x座標、y座標、z座標 いずれも $2$ か $0$ か $-2$ であり、これ以外の値はとらない。
# Code1
ルービックキューブは $90$°ずつ回転させていくことが基本であるが、ルービックキューブの回転において重要なことは任意の時点で任意の列、任意の段を回転させることができなければいけない点である。次のプログラムは、右の列を一定の速度で回転させるだけのものである。
なお、ルービックキューブを構成するCubeは26個あるが、本節のプログラムにおいてはそれらは Cube[i] のように配列の形で使われている。
[Code1] (実行結果 図7)
i_degX += 1;
Matrix4x4 R = TH3DMath.GetRotation4x4(i_degX, Vector3.right);
// 初期状態における右列のCubeのインデックス (9個のCube)
int[] idcs = { 2, 5, 8, 11, 13, 16, 19, 22, 25 };
foreach (int i in idcs)
{
Cube[i].SetMatrix(R);
}
5行目の idcs には、右列の9個のCubeのインデックスがセットされる。その下の foreach文において その9個のCubeに回転行列Rを実行することで、実行結果(図7)に見られるように右の列の9個のCube(いずれも赤い面を持っている)が毎フレーム $1$°ずつ回転することになる。
しかし、ルービックキューブの回転を実装するためにはこのプログラムの方法では不十分である。
このCode1の方法は確かに右の列を回転させることができるが、この右の列は詳しくは初期状態における右の列である。5行目の idcs で指定している9個のCubeはいずれも赤い面を持っているが、このプログラムで回転させることができるのは idcs で指定した赤い面を持った9個のCubeである。
また 各Cubeの回転は、ときに x軸周りであったり、ときに y軸周り、z軸周りとなり、さらにその順番もさまざまである。x軸周りに回転後、z軸周りに回転し、その後再び x軸周りの回転 といった形で常に回転軸が変化する。そのため、あるCubeがどの軸周りにどれだけ回転したかを管理しておくことは簡単ではない。
上のCode1におけるインスタンス変数 i_degX は 9個のCubeの x軸周りの回転角度を表すものであるが、つまり このように1つの軸の周りに何度回転したかを保持する変数を用意しても意味がないわけである。
# Code2
ここではCode1で示した問題点について考えていく。先程の図5からわかるように、初期状態においては右列のCubeは x座標がすべて $2$ である。これはルービックキューブをどのように回転させても変わらない。つまり、どの時点においても右列のCubeの x座標は $2$ である。このことを利用すればある時点における右列のCubeのインデックスは次のように取得できる。
List<int> wL = new List<int>();
for (int i = 0; i < i_curCubePos.Length; i++)
{
if (i_curCubePos[i].x >= 2.0f - 0.01f)
{
wL.Add(i);
}
}
ここで使われている i_curCubePos は現在の各Cubeの位置(Cubeの中心座標)を保持する Vector3[]型のインスタンス変数である。Cubeは26個なのでこの配列の要素数も 26 であり、Cube[i]の現在位置は i_curCubePos[i] にセットされている (各Cubeの現在位置の計算については後述する)。
3行目のfor文において各Cubeの現在位置を調べ、その x座標が $2$ であるもののインデックスをList<int>型のローカル変数 wL に追加していく。ただし、小数値の比較は a == b のような形で行うのはよくないので、x座標が $2$ であるかを調べるために5行目のように x >= 2.0f-0.01f となっている。この比較では xの値が $2$以上であればすべて true となってしまうが、上でも述べたように各Cubeの位置は、x座標、y座標、z座標 いずれも $0$ か $2$ か $-2$ なのでこの比較でも問題はない (xが$2$以上であるかを調べるために x >= 2.0 とすることもまた控えるべきである。小数値の比較の場合は演算誤差を考慮に入れてわずかな’余裕’を持たせて 2.0-0.01 のようにしておくことが望ましい)。
同様にして一番上の段を回転させる場合、その時点での上段にある9個のCubeのインデックスを取得する必要があるが、その場合は以下のようにすればよい。
List<int> wL = new List<int>();
for (int i = 0; i < i_curCubePos.Length; i++)
{
if (i_curCubePos[i].y >= 2.0f - 0.01f)
{
wL.Add(i);
}
}
上段のCubeの y座標はすべて $2$ であるから、ここでは5行目の if文で y >= 2.0f-0.01f となっている。
また ルービックキューブの回転では回転軸が常に変化するが、以下ではこの点について考えていこう。
例えば、オブジェクトを x軸周りに毎フレーム $3$°ずつ回転させる場合、今までは次のようにプログラムを記述していた。
i_degX += 3; Matrix4x4 R = TH3DMath.GetRotation4x4(i_degX, Vector3.right); Obj.SetMatrix(R);
i_degX は x軸周りの回転角度を表すインスタンス変数であり、毎フレーム $3$ずつ増加する。このプログラムの記述はCode1とほとんど同じである。そして、Code1で指摘したようにこの方法は x軸周りに $90$°回転させた後に y軸周りにさらに $90$°回転させるといった処理には向いていない。
以下のプログラムはオブジェクトを回転させる別の方法である。その内容は上のプログラムと同様にオブジェクトを x軸周りに毎フレーム $3$°ずつ回転させるものである。
Matrix4x4 R = TH3DMath.GetRotation4x4(3, Vector3.right); Matrix4x4 curM = Obj.GetMatrix(); Matrix4x4 M = R * curM; Obj.SetMatrix(M);
1行目の R は x軸周りに $3$°回転を行う回転行列である。R の内容は毎フレーム同じであり、x軸周りの $3$°の回転である。2行目の curM は現時点でオブジェクトに実行されている変換行列である。したがって、3行目の M = R * curM の内容は「オブジェクトを現在の状態から x軸周りに $3$°回転させる」というものになる。そして4行目で実際にオブジェクトにはその M が実行される。
具体的には 1フレーム目においてはオブジェクトは初期状態であるので curM の内容は identity行列である。そして、このときの M の内容は「x軸周りに $3$°回転」である。2フレーム目ではオブジェクトは x軸周りに $3$°回転した状態であるため、curM の内容は同じく「x軸周りに $3$°回転」となっている。したがって、2フレーム目における M は curM をさらに $3$°回転させることになるから、その内容は「x軸周りに $6$°回転」である。3フレーム目も同様である。3フレーム目における curM の内容は、オブジェクトはこの時点で x軸周りに $6$°回転しているから「x軸周りに $6$°回転」となる。したがって、3フレーム目における M も curM をさらに $3$°回転させることになるから、その内容は「x軸周りに $9$°回転」である。
このようにして、オブジェクトは毎フレーム x軸周りに $3$°ずつ回転していくことになる。
この方法では x軸周りに $3$°ずつ回転させていくために、毎フレーム オブジェクトの現在の変換行列を取得して、それに x軸周りに $3$°の回転行列を掛けている。先程のインスタンス変数 i_degX を使ったやり方に比べて、やや計算負荷が増加するが、この方法はオブジェクトを回転させる上で非常に柔軟な性質を持っている。
例えば、ある時点でオブジェクトが x軸周りに $90$°回転しているとしよう。便宜上ここでは、それを30フレーム目とする。そして、その次のフレームから(31フレーム目から) オブジェクトを y軸周りに $5$°ずつ回転させるとしよう。その場合には次のように記述すればよい。
Matrix4x4 R = TH3DMath.GetRotation4x4(5, Vector3.up); Matrix4x4 curM = Obj.GetMatrix(); Matrix4x4 M = R * curM; Obj.SetMatrix(M);
先程のプログラムとの違いは1箇所で、それは1行目の GetRotation4x4(..) の引数であり、y軸周りに $5$°の回転を表している。
31フレーム目では、オブジェクトは x軸周りに $90$°回転した状態なので curM の内容は同じく「x軸周りに $90$°回転」である。したがって、M はその状態から y軸周りに $5$°の回転を行うので、31フレーム目の M の内容は「x軸周りに $90$°回転、さらに続けて y軸周りに $5$°の回転」となる。
32フレーム目では、オブジェクトは x軸周りに $90$°回転、さらに y軸周りに $5$°回転しているから、32フレーム目の curM の内容も「x軸周りに $90$°、y軸周りに $5$°」である。そして、32フレーム目における M の内容は curM をさらに y軸周りに $5$°回転させるものになるから「x軸周りに $90$°回転、さらに続けて y軸周りに $10$°の回転」となる。
このようにして x軸周りに $90$°回転したオブジェクトを、その後 続けて y軸周りに $5$°ずつ回転させるということができるわけである。
次のプログラムはルービックキューブの右の列 及び上の段を、以下のキー操作によって回転させるものである。
R : 右の列のCubeをx軸周りに $90$°回転させる (Shift同時押しで逆回転)。
U : 上の段のCubeをy軸周りに $90$°回転させる (Shift同時押しで逆回転)。
ルービックキューブがどのような状態であっても、R が押されればその時点で右の列にある9個のCubeが回転し、U が押されればその時点で上の段にある9個のCubeが回転する。
[Code2] (実行結果 図9)
if (!i_INITIALIZED)
{
i_ROTATE = false;
i_rotMaxCount = 30;
i_rotCounter = 0;
i_rotCubeIndices = new int[0];
for (int i = 0; i < c_initCubePos.Length; i++)
{
i_curCubePos[i] = c_initCubePos[i];
}
i_INITIALIZED = true;
}
if (i_ROTATE)
{
Matrix4x4 R = TH3DMath.GetRotation4x4(i_addDeg, i_rotAxis);
foreach (int idx in i_rotCubeIndices)
{
Matrix4x4 curM = Cube[idx].GetMatrix();
Matrix4x4 M = R * curM;
Cube[idx].SetMatrix(M);
}
i_rotCounter++;
if (i_rotCounter >= i_rotMaxCount)
{
i_ROTATE = false;
foreach (int idx in i_rotCubeIndices)
{
i_curCubePos[idx] = Cube[idx].GetMatrix() * TH3DMath.ToVector4(c_initCubePos[idx]);
}
}
return;
}
List<int> wL = new List<int>();
if (Input.GetKeyDown(KeyCode.U))
{
for (int i = 0; i < i_curCubePos.Length; i++)
{
if (i_curCubePos[i].y >= 2.0f - 0.01f)
{
wL.Add(i);
}
}
i_rotAxis = Vector3.up;
}
else if (Input.GetKeyDown(KeyCode.R))
{
for (int i = 0; i < i_curCubePos.Length; i++)
{
if (i_curCubePos[i].x >= 2.0f - 0.01f)
{
wL.Add(i);
}
}
i_rotAxis = Vector3.right;
}
else
{
return;
}
i_rotCubeIndices = wL.ToArray();
i_ROTATE = true;
i_rotCounter = 0;
i_addDeg = THUtil.IsShiftDown() ? (-90 / i_rotMaxCount) : (90 / i_rotMaxCount);
指定のキーが1回押されるとCubeの回転が始まるが、その回転角度は $90$°である。4行目の i_rotMaxCount は、その $90$°の回転を何フレームかけて行うかを表す変数であり、ここでは $30$ が設定されているが、これはCubeの $90$°の回転が30フレームかけて行われることを意味する。i_rotCounter は30フレームかけて行われる回転において、今は何フレーム目かを表す変数である。この変数は回転のためのキーが押されるたびに $0$ にセットされる。
i_rotCubeIndices は回転を行うCubeのインデックス配列である。ここでは適当な要素数で初期化されている。
また、本節の上部で述べたように、ルービックキューブを構成する各Cubeは初期状態においてそれぞれの指定の位置に配置されている。したがって、transform.localPosition(あるいは transform.position)などを用いても、3D空間上でのCubeの位置(中心座標)を取得することはできない。そのために各Cubeの位置を常に保持しておくインスタンス変数が必要になるわけであるが、このプログラムでは i_curCubePos というVector3[]型の配列がそれにあたる。ある時点でのCube[i]の位置は i_curCubePos[i] にセットされている。
8行目の for文において i_curCubePos の各要素に初期値を設定するが、その値は各Cubeの初期状態での位置である。c_initCubePos は初期状態における各Cubeの位置がセットされているので、ここではそれらの値を i_curCubePos にコピーしているだけである。
まず、43行目以降から解説する。43行目から68行目は上で解説した その時点での上の段のCube、右の列のCubeのインデックスを取得する部分である。例えば、U が押されると45行目のifブロックに入るが、ここでは その時点で上の段にある9個のCubeのインデックスを List<int>型変数の wL に追加している。
55行目では i_rotAxis という変数に Vector3.up がセットされているが、i_rotAxis はCubeが回転する際の回転軸を表す Vector3型のインスタンス変数である。U が押された場合は上段のCubeが y軸周りに回転することになるので、ここでは i_rotAxis に Vector3.up がセットされているわけである。
R が押された場合は右列のCubeが x軸周りに回転することになるが、67行目では確かに i_rotAxis に x軸プラス方向を表す Vector3.right がセットされている。
U または R が押されると45行目または57行目のifブロックに入るが、何も押されていない場合は69行目の else ブロックに入り そこで return されるので、それ以降に処理が進まない。
しかし、U または R が押された場合には 75行目以降の処理が行われる。ここでは次のフレームからCubeの回転処理が行われるように、回転に必要なインスタンス変数に値をセットしている。
i_rotCubeIndices には、回転するCubeのインデックス配列がセットされる。U または R が押されれば上の部分でList型変数 wL にインデックスがセットされるので、ここではそれを配列の形でコピーしているだけである。i_ROTATE や i_rotCounter については上で述べたとおりである。i_addDeg は1フレームあたりの回転角度であり、i_rotMaxCount の値が$30$なので i_addDeg は $3$ である (Shiftが押されているときは $-3$)。
17行目のifブロックはCubeの回転処理が記述されており、このプログラムの場合は回転対象となるCubeは上の段、あるいは右の列の9個のCubeである。19行目の R は $3$°(あるいは $-3$°)の回転行列であり、回転軸はそのときに押されたキーによって異なるが、ここでは x軸か y軸である。
21行目の foreach文では i_rotCubeIndices にセットされているインデックスのCubeのみを回転させる。このプログラムの場合は i_rotCubeIndices には上段あるいは右列の9個のCubeのインデックスがセットされている。23~25行目のCubeを回転させるコードについては上で述べた方法と同様である。curM は現時点でのCubeの状態を表す変換行列である。curM と R の積 M は、現時点でのCubeをさらに $3$°(あるいは$-3$°)回転させた状態にする行列であり、それをCubeに実行する。毎フレームこのようにCubeを回転させることで各Cubeは30フレームかけて $90$°の回転を行うことになる。そして 上でも述べたように、この方法であればCubeを回転させる際の回転軸はどのような順序にしても構わない。x軸周り、y軸周り、x軸周り であっても y軸周り、x軸周り、x軸周り であっても、そのときにキーで指定した回転軸の周りを回転することになる。
回転処理中は毎フレーム 28行目において i_rotCounter をインクリメントし、その値が $30$ になった時点で回転処理を停止させるために 29行目のifブロックに入る。実際には、ただ i_ROTATE を false にするだけであるが、ここでもう1つ重要な処理がある。それは各Cubeの現在位置の更新である。i_curCubePos には現時点での各Cubeの位置がセットされているが、回転が終わるたびに 回転したCubeの位置を更新しなければならない。33行目の foreach文で行っているのは その更新処理である (位置の更新は回転したCubeのみが対象となるので i_rotCubeIndices が表すCubeだけでよい)。
現時点でのCubeの位置を求める方法は、2-13節において解説した現時点でのオブジェクト上のある位置の求め方と同様である (2-13節における解説は2Dオブジェクトが対象であったが、3Dオブジェクトの場合も同様である。4-12節参照)。
現時点でCubeに実行されている変換行列と 初期状態におけるCubeの位置の同次座標との積を計算すればよい (ただし、位置の場合は同次座標における $w$成分を $1$ にする。ToVector4(..) は引数のVector3型の値をVector4型に変換するカスタムライブラリーのメソッドであるが、その際 $w$成分は $1$ になる。実際には、ここではCubeには回転だけで平行移動が行われることはないので同次座標の $w$成分が $1$ でも $0$ でも算出される値は同じである)。
# Code3
最後は読者用の課題である。ルービックキューブの回転については、一般には以下のように記号が定められている。
-
図10 R : 右の列を回転(x軸周り) -
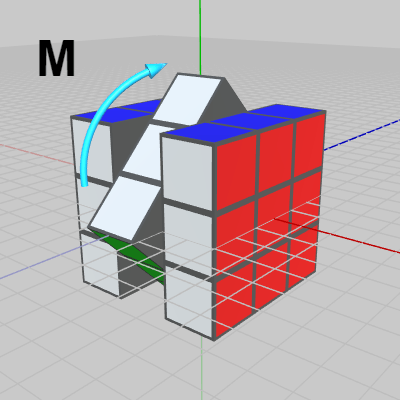図11 M : 中央の列を回転(x軸周り) -
図12 L : 左の列を回転(x軸周り)
-
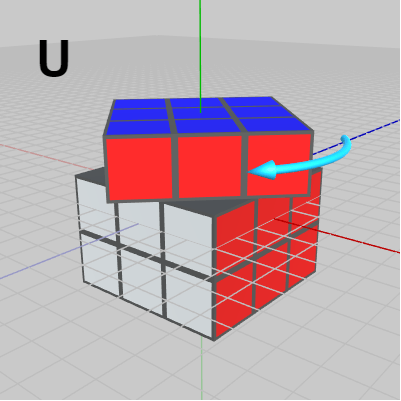図13 U : 上の段を回転(y軸周り) -
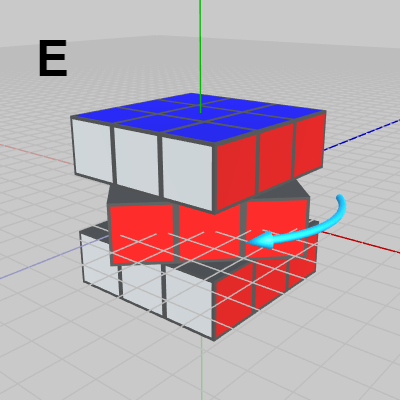図14 E : 中央の段を回転(y軸周り) -
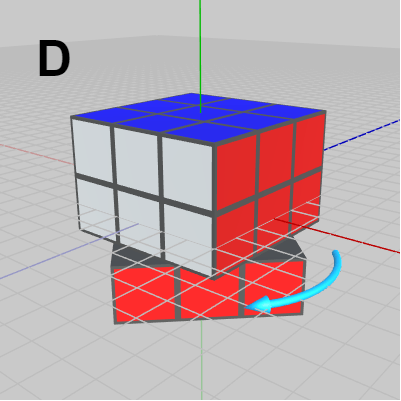図15 D : 下の段を回転(y軸周り)
-
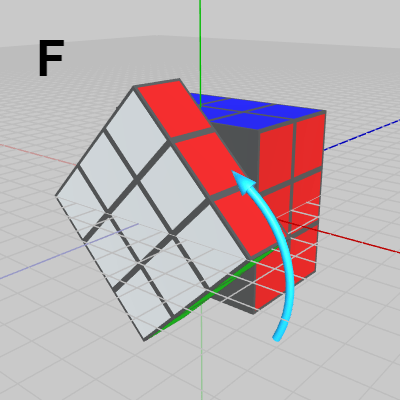図16 F : 手前の列を回転(z軸周り) -
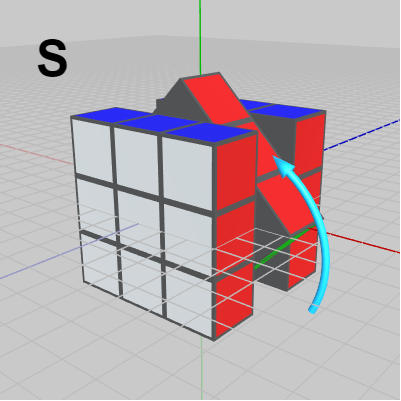図17 S : 中央の列を回転(z軸周り) -
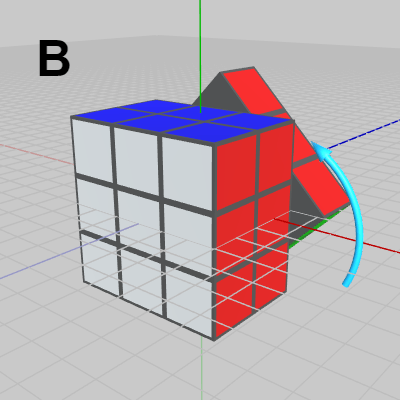図18 B : 奥の列を回転(z軸周り)
-
図19 X : 全体をx軸周りに回転 -
図20 Y : 全体をy軸周りに回転 -
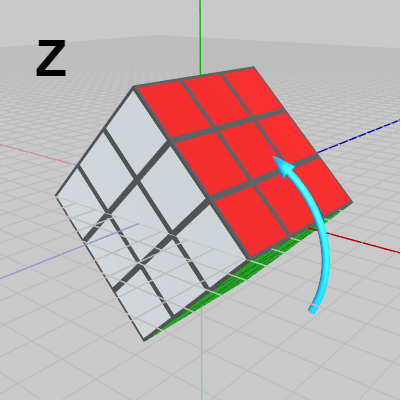図21 Z : 全体をz軸周りに回転
Code2で実装したのはこのうちで U (上の段の回転)、R (右の列の回転) の2つである。
ここでの課題は上図に示される回転を実装し、ルービックキューブの回転プログラムを完成させることである。ただし、上の12種類の回転をすべて実装する必要はない。作成したプログラムが実際のルービックキューブと同じパズルゲームとして成り立つように必要な回転だけを選べばよい。
プログラムはCode3に作成するものとする (Code3は空の初期化ブロックだけ用意されている)。
このプログラムの作成に使用するインスタンス変数を以下に示す (いずれも Code2で使われたものであり、新しいものはない)。
i_ROTATE
: Cubeの回転が行われているかどうかを示すフラグ (Cubeが回転していればtrue)。回転のためのキーが押されるたびに true になる。i_rotMaxCount
: Cubeの回転を何フレームかけて行うかを表す (int型 ; 本節では $30$ という設定であり、Cubeは$30$フレームかけて$90$°回転する)。i_rotCounter
: Cubeの回転が始まって何フレーム目かを表す(int型)。i_addDeg
: 1フレームあたりのCubeの回転角度 (キーを押すたびに$90$°回転するので i_addDeg = 90/i_rotMaxCount である)。i_rotAxis
: Cubeの回転における回転軸。i_rotCubeIndices
: 回転しているCubeのインデックス配列。i_curCubePos
: 現在の各Cubeの位置を保持する配列(Vector3[]型)。Cube配列と同じく要素数は26。c_initCubePos
: 初期状態の各Cubeの位置を保持する配列(Vector3[]型)。解答例は Sec317_Ans.txt 内を参照 (ただし、この課題は容易である。Code2のキー操作の部分を適当に変えてコピーすれば解決する。Sec317_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
© 2020-2024 Redpoll's 60 (All rights reserved)